Lensless Hyperspectral Phase Retrieval via Alternating Direction Method of Multipliers and Spectral Proximity Operators †
Abstract
:1. Introduction
2. Hyperspectral Phase Imaging
2.1. HS Phase Retrieval Solution (HSPhR)
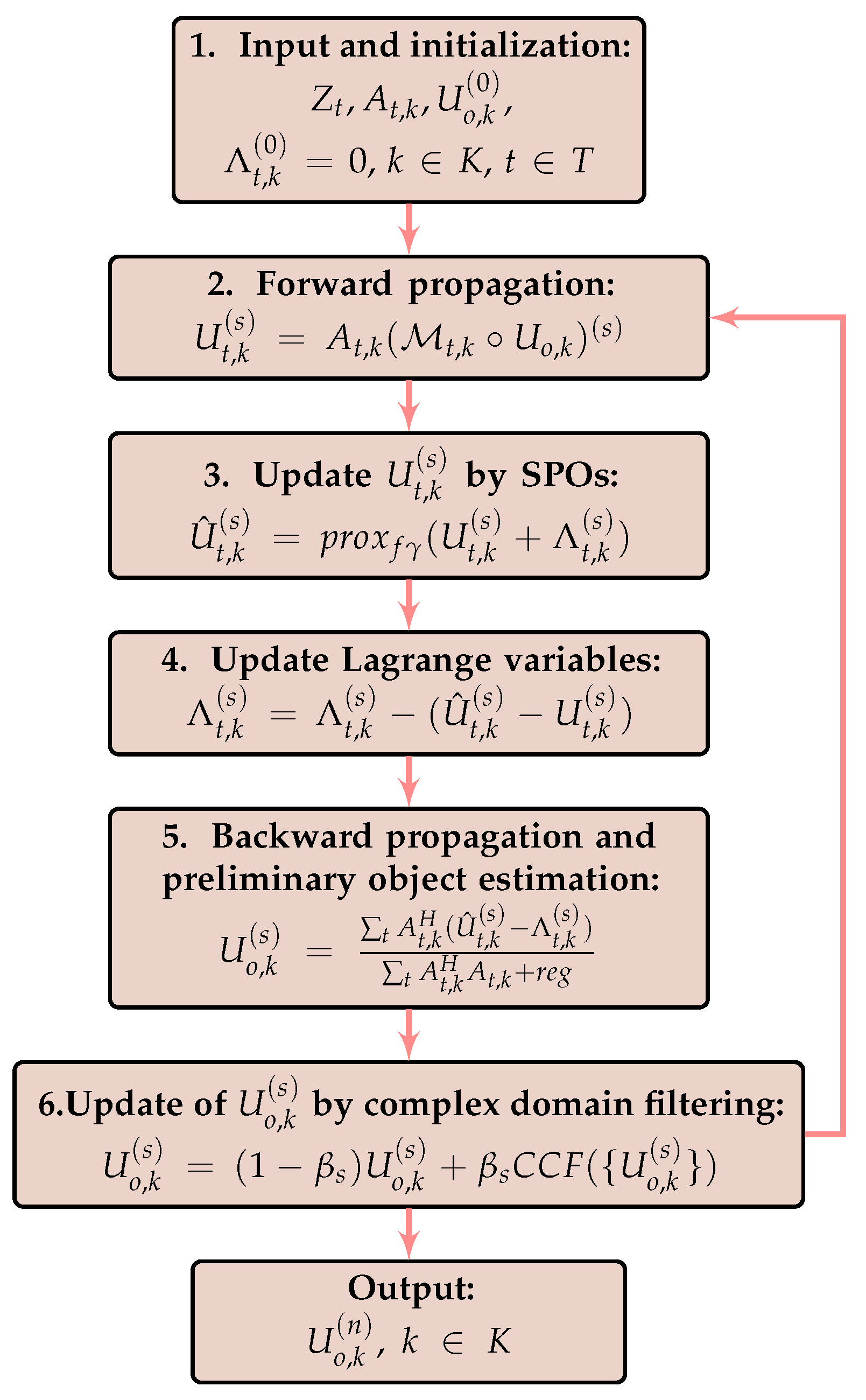
2.2. Developed Algorithm
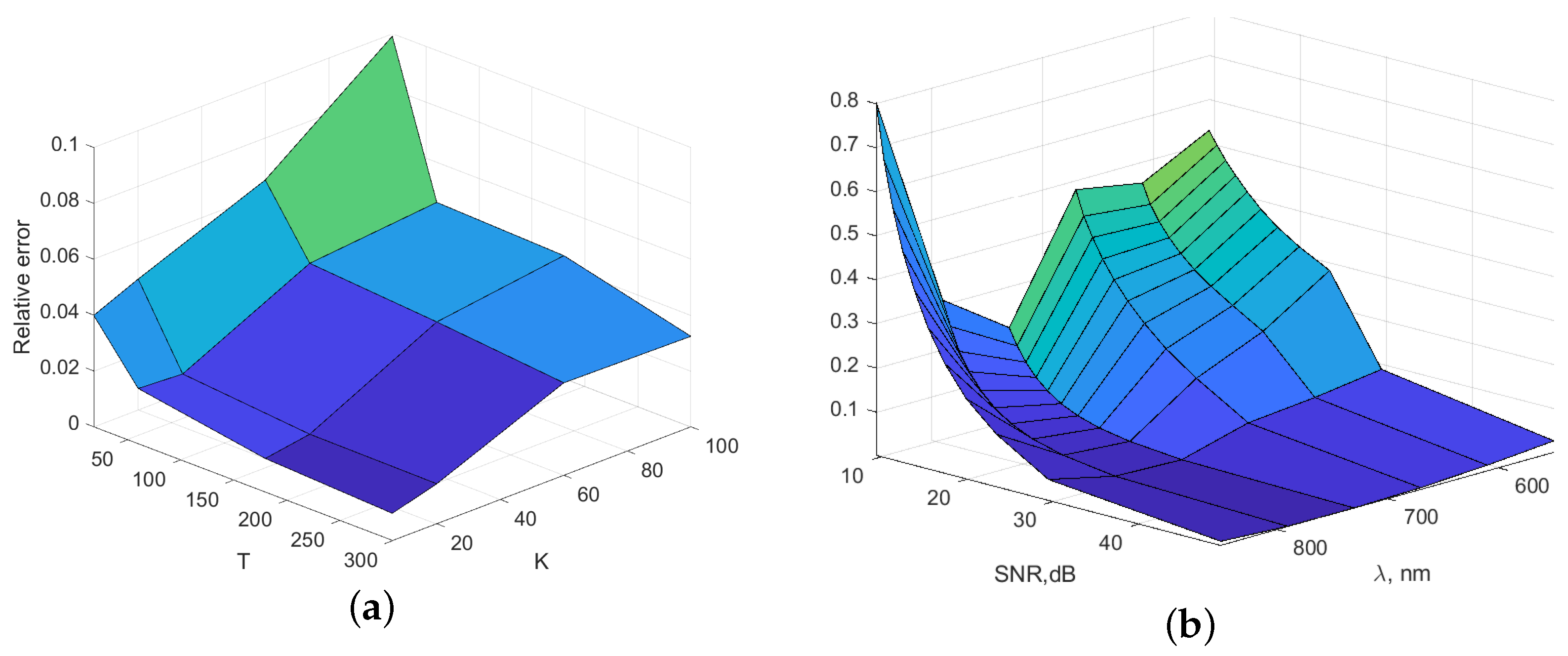
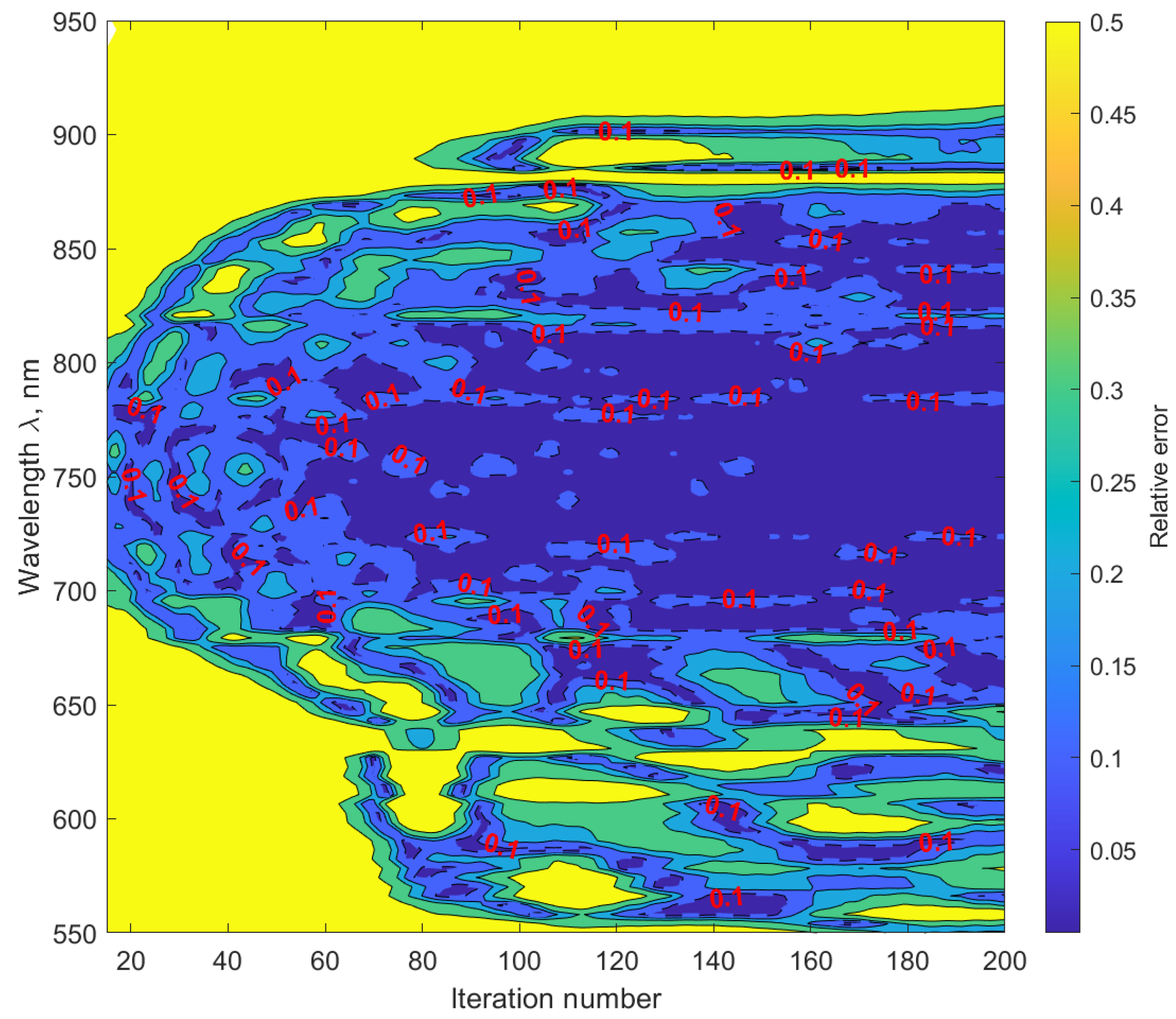
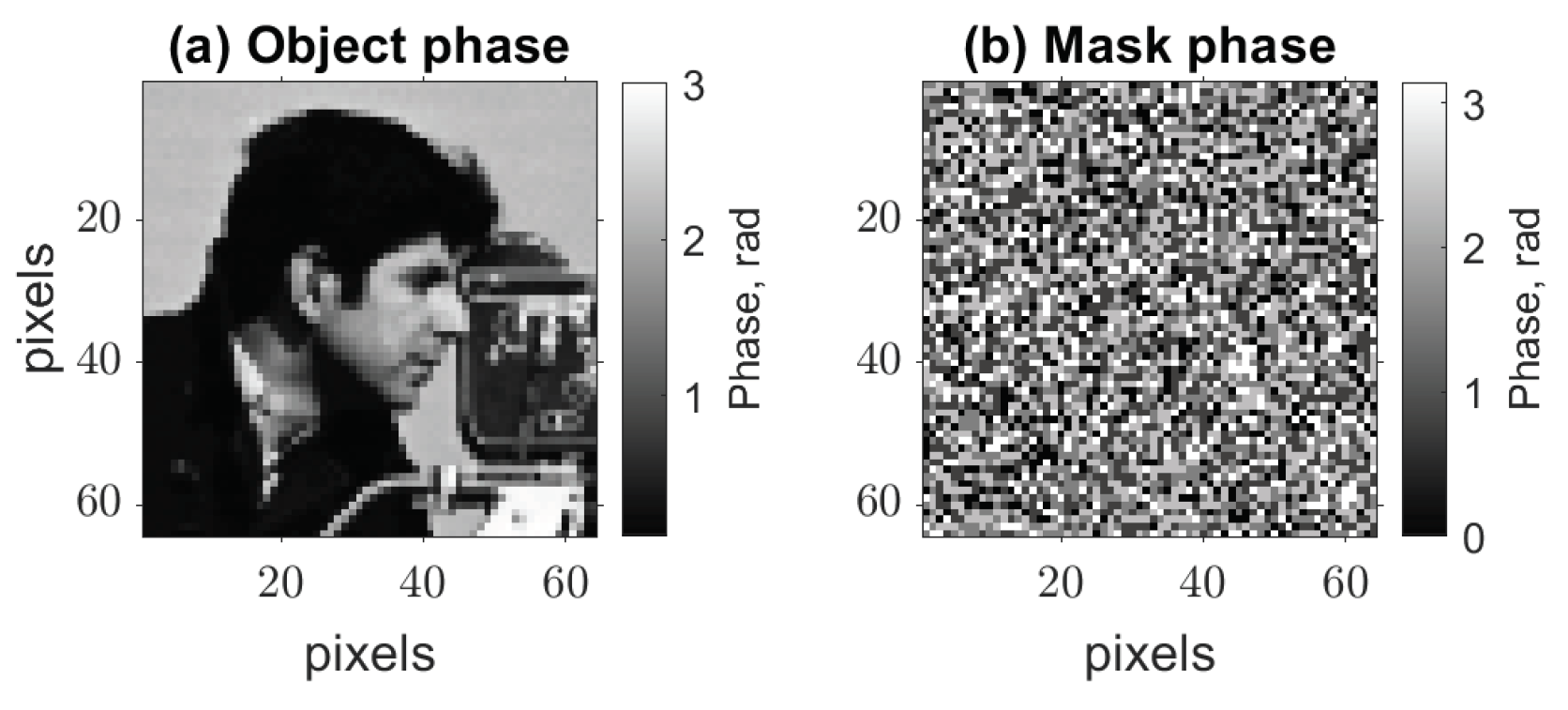
3. Numerical Experiments
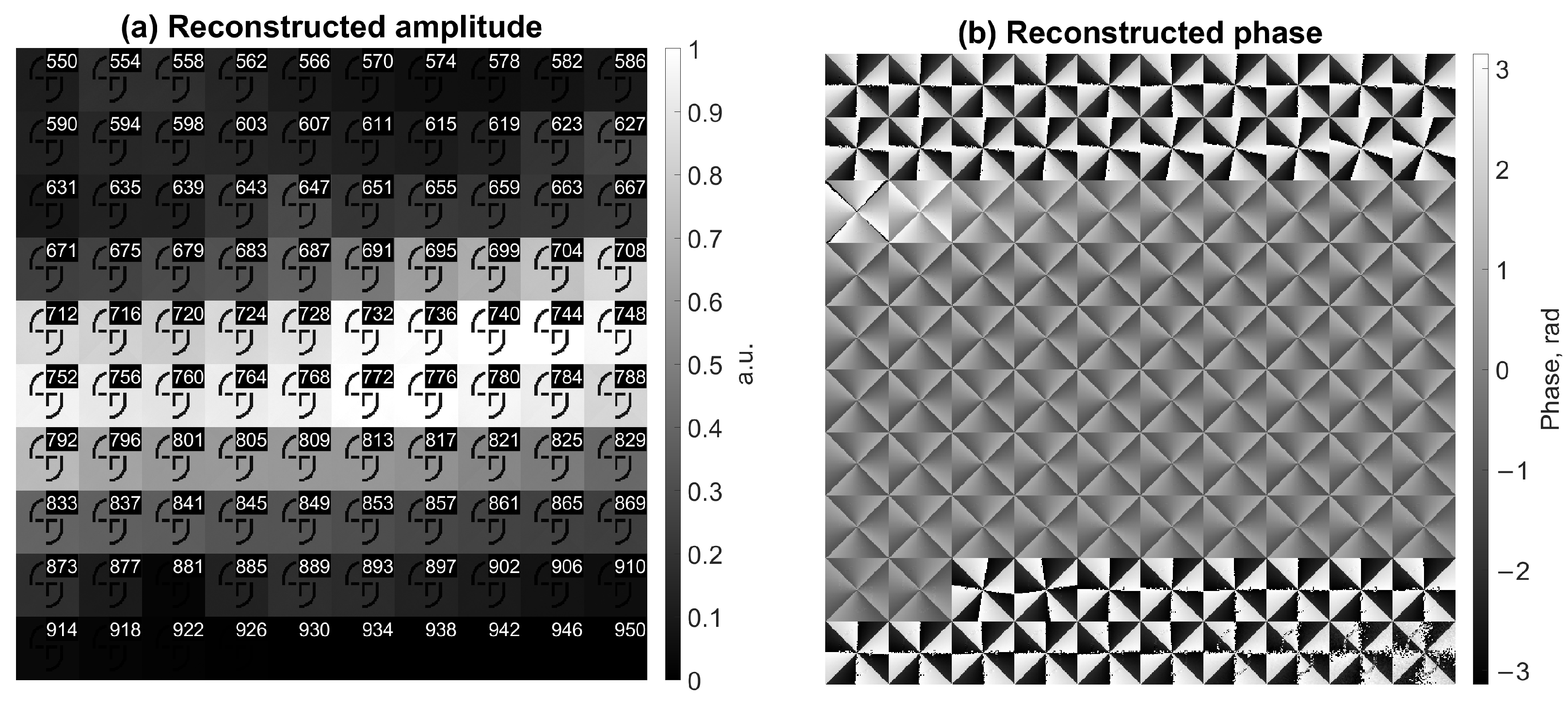
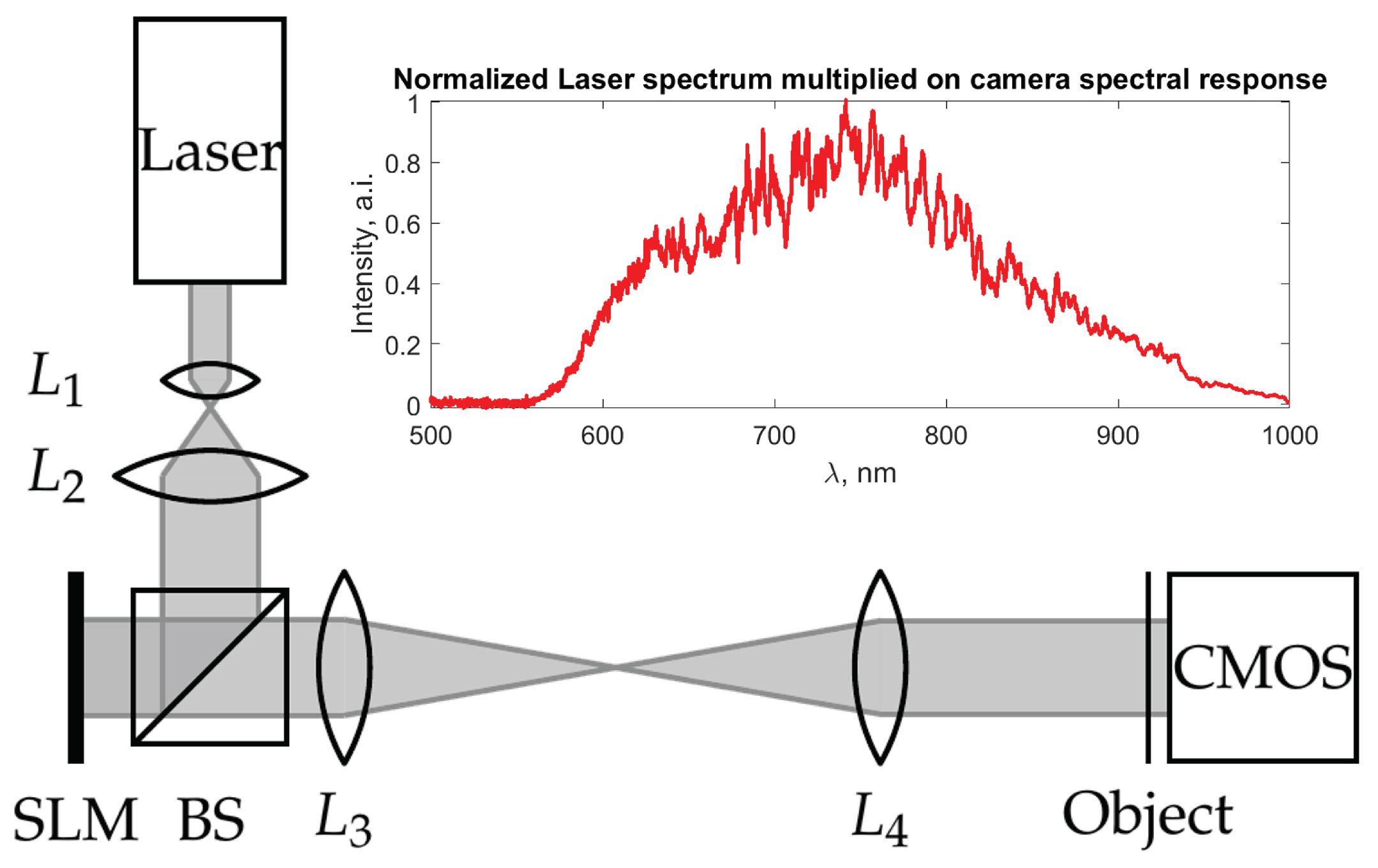
4. Experimental Validation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| BS | Beam Splitter |
| CMOS | Complementary Metal–Oxide–Semiconductor |
| CCF | Complex Cube Filter |
| HSI | HyperSpectral Imaging |
| HSPhR | HyperSpectral Phase Retrieval |
| HSDH | HyperSpectral Digital Holography |
| SPO | Spectral Proximity Operator |
| SNR | Signal-to-Noise Ratio |
References
- Gao, B.C.; Davis, C.; Goetz, A. A review of atmospheric correction techniques for hyperspectral remote sensing of land surfaces and ocean color. In Proceedings of the 2006 IEEE International Symposium on Geoscience and Remote Sensing, Denver, CO, USA, 31 July–4 August 2006; IEEE: New York, NY, USA, 2006; pp. 1979–1981. [Google Scholar]
- Calin, M.A.; Parasca, S.V.; Savastru, D.; Manea, D. Hyperspectral imaging in the medical field: Present and future. Appl. Spectrosc. Rev. 2014, 49, 435–447. [Google Scholar] [CrossRef]
- Ghenim, L.; Allier, C.; Obeid, P.; Hervé, L.; Fortin, J.Y.; Balakirev, M.; Gidrol, X. A new ultradian rhythm in mammalian cell dry mass observed by holography. Sci. Rep. 2021, 11, 1290. [Google Scholar] [CrossRef] [PubMed]
- Belashov, A.V.; Zhikhoreva, A.A.; Bespalov, V.G.; Novik, V.I.; Zhilinskaya, N.T.; Semenova, I.V.; Vasyutinskii, O.S. Refractive index distributions in dehydrated cells of human oral cavity epithelium. J. Opt. Soc. Am. B 2017, 34, 2538–2543. [Google Scholar] [CrossRef]
- Cazac, V.; Meshalkin, A.; Achimova, E.; Abashkin, V.; Katkovnik, V.; Shevkunov, I.; Claus, D.; Pedrini, G. Surface relief and refractive index gratings patterned in chalcogenide glasses and studied by off-axis digital holography. Appl. Opt. 2018, 57, 507. [Google Scholar] [CrossRef] [PubMed]
- Kalenkov, S.G.; Kalenkov, G.S.; Shtanko, A.E. Hyperspectral holography: An alternative application of the Fourier transform spectrometer. J. Opt. Soc. Am. B 2017, 34, B49. [Google Scholar] [CrossRef]
- Claus, D.; Pedrini, G.; Buchta, D.; Osten, W. Accuracy enhanced and synthetic wavelength adjustable optical metrology via spectrally resolved digital holography. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2018, 35, 546–552. [Google Scholar] [CrossRef] [PubMed]
- Katkovnik, V.; Egiazarian, K. Multi-Frequency Phase Retrieval from Noisy Data. In Proceedings of the 2018 26th European Signal Processing Conference (EUSIPCO), Rome, Italy, 3–7 September 2018; IEEE: New York, NY, USA, 2018; pp. 2200–2204. [Google Scholar] [CrossRef]
- Katkovnik, V.; Shevkunov, I.; Petrov, N.V.; Eguiazarian, K. Multiwavelength absolute phase retrieval from noisy diffractive patterns: Wavelength multiplexing algorithm. Appl. Sci. 2018, 8, 719. [Google Scholar] [CrossRef]
- Katkovnik, V.; Shevkunov, I.; Petrov, N.V.; Egiazarian, K. Multiwavelength surface contouring from phase-coded noisy diffraction patterns: Wavelength-division optical setup. Opt. Eng. 2018, 57, 1. [Google Scholar] [CrossRef]
- Shevkunov, I.; Katkovnik, V.; Egiazarian, K. Lensless hyperspectral phase imaging in a self-reference setup based on Fourier transform spectroscopy and noise suppression. Opt. Express 2020, 28, 17944. [Google Scholar] [CrossRef] [PubMed]
- Katkovnik, V.; Shevkunov, I.; Egiazarian, K. Broadband Hyperspectral Phase Retrieval From Noisy Data. In Proceedings of the 2020 IEEE International Conference on Image Processing (ICIP), Abu Dhabi, United Arab Emirates, 25–28 October 2020; IEEE: New York, NY, USA, 2020; pp. 3154–3158. [Google Scholar] [CrossRef]
- Katkovnik, V.; Shevkunov, I.; Egiazarian, K. ADMM and spectral proximity operators in hyperspectral broadband phase retrieval for quantitative phase imaging. Signal Process. 2023, 210, 109095. [Google Scholar] [CrossRef]
- Katkovnik, V.; Shevkunov, I.; Petrov, N.N.V.; Egiazarian, K. Computational wavelength resolution for in-line lensless holography: Phase-coded diffraction patterns and wavefront group-sparsity. Proc. SPIE 2017, 10335, 1033509. [Google Scholar] [CrossRef]
- Hestenes, M.R. Multiplier and gradient methods. J. Optim. Theory Appl. 1969, 4, 303–320. [Google Scholar] [CrossRef]
- Eckstein, J.; Bertsekas, D.P. On the Douglas—Rachford splitting method and the proximal point algorithm for maximal monotone operators. Math. Program. 1992, 55, 293–318. [Google Scholar] [CrossRef]
- Afonso, M.V.; Bioucas-Dias, J.M.; Figueiredo, M.A.T. Fast Image Recovery Using Variable Splitting and Constrained Optimization. IEEE Trans. Image Process. 2010, 19, 2345–2356. [Google Scholar] [CrossRef] [PubMed]
- Afonso, M.V.; Bioucas-Dias, J.M.; Figueiredo, M.A.T. An Augmented Lagrangian Approach to the Constrained Optimization Formulation of Imaging Inverse Problems. IEEE Trans. Image Process. 2011, 20, 681–695. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Wang, X.; Wang, G. Alternating Direction Method of Multipliers for Separable Convex Optimization of Real Functions in Complex Variables. Math. Probl. Eng. 2015, 2015, 104531. [Google Scholar] [CrossRef]
- Shevkunov, I.; Katkovnik, V.; Claus, D.; Pedrini, G.; Petrov, N.V.; Egiazarian, K. Hyperspectral phase imaging based on denoising in complex-valued eigensubspace. Opt. Lasers Eng. 2020, 127, 1–9. [Google Scholar] [CrossRef]
- Candes, E.; Wakin, M. An Introduction To Compressive Sampling. IEEE Signal Process. Mag. 2008, 25, 21–30. [Google Scholar] [CrossRef]
- Fellgett, P.B. On the Ultimate Sensitivity and Practical Performance of Radiation Detectors. J. Opt. Soc. Am. 1949, 39, 970–976. [Google Scholar] [CrossRef] [PubMed]
- Mäkitalo, M.; Foi, A. Noise Parameter Mismatch in Variance Stabilization, With an Application to Poisson–Gaussian Noise Estimation. IEEE Trans. Image Process. 2014, 23, 5348–5359. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shevkunov, I.; Katkovnik, V.; Egiazarian, K. Lensless Hyperspectral Phase Retrieval via Alternating Direction Method of Multipliers and Spectral Proximity Operators. Eng. Proc. 2023, 34, 19. https://doi.org/10.3390/HMAM2-14146
Shevkunov I, Katkovnik V, Egiazarian K. Lensless Hyperspectral Phase Retrieval via Alternating Direction Method of Multipliers and Spectral Proximity Operators. Engineering Proceedings. 2023; 34(1):19. https://doi.org/10.3390/HMAM2-14146
Chicago/Turabian StyleShevkunov, Igor, Vladimir Katkovnik, and Karen Egiazarian. 2023. "Lensless Hyperspectral Phase Retrieval via Alternating Direction Method of Multipliers and Spectral Proximity Operators" Engineering Proceedings 34, no. 1: 19. https://doi.org/10.3390/HMAM2-14146
APA StyleShevkunov, I., Katkovnik, V., & Egiazarian, K. (2023). Lensless Hyperspectral Phase Retrieval via Alternating Direction Method of Multipliers and Spectral Proximity Operators. Engineering Proceedings, 34(1), 19. https://doi.org/10.3390/HMAM2-14146






.png)
