Usage of Geometric Altitude for Radar Plot Position Improvements †
Abstract
:1. Introduction
1.1. Barometric Altitude
1.2. Geometric Altitude in ADS-B
1.3. Three-Dimensional Height in Radars
1.4. Radar Plot Positioning
1.5. Geometric Altitude for Non-ADSB Aircraft
1.6. Scope
- Analysis of geometric/barometric altitude offsets to estimate possible Radar plot position offsets.
- Evaluation of reconstruction of geometric altitudes for all aircraft (also without ADS-B capabilities).
- Comparison of a pressure/temperature-based reconstruction model to real-life meteorological data.
- Assessment of potential benefits by calculating the change in radar position accuracy comparing usage of barometric, reconstructed geometric, and 3D height information (as measured by the used Radar).
2. Results
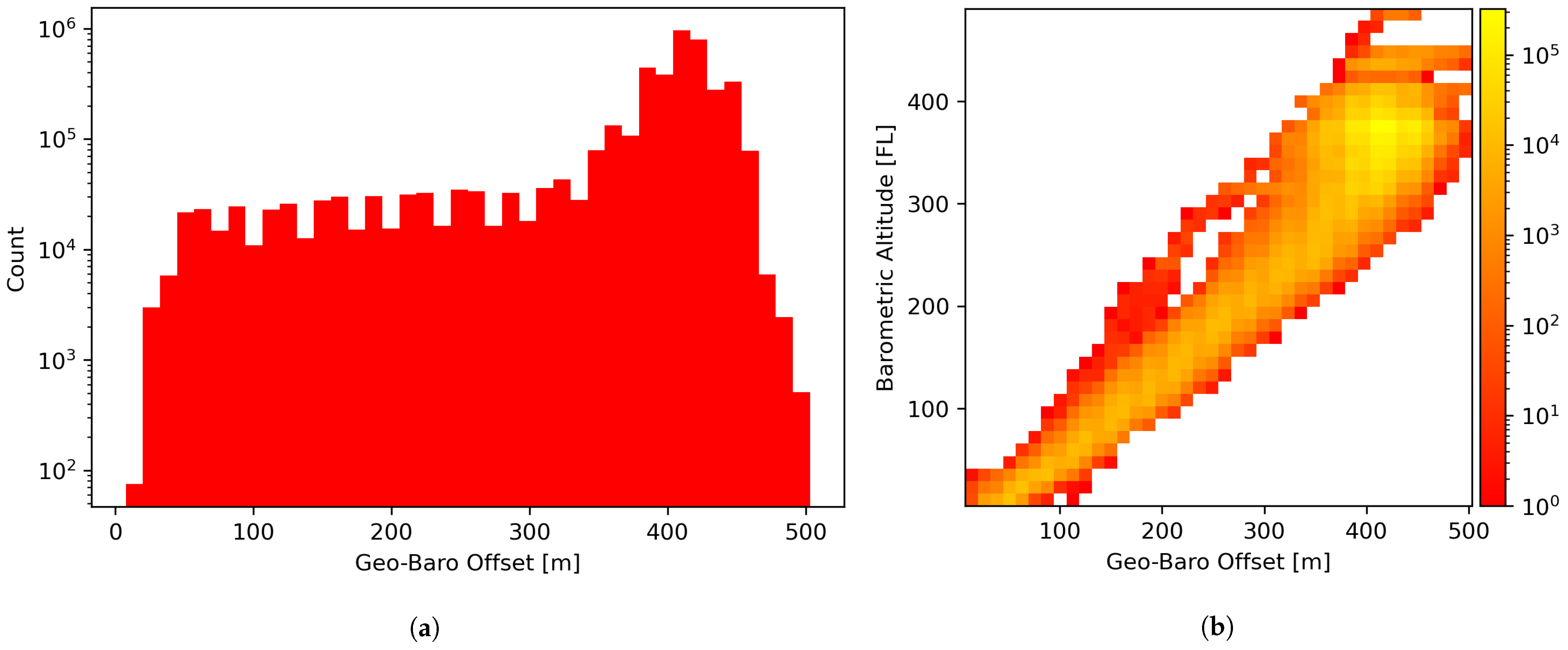
2.1. Geometric/Barometric Altitude Offsets
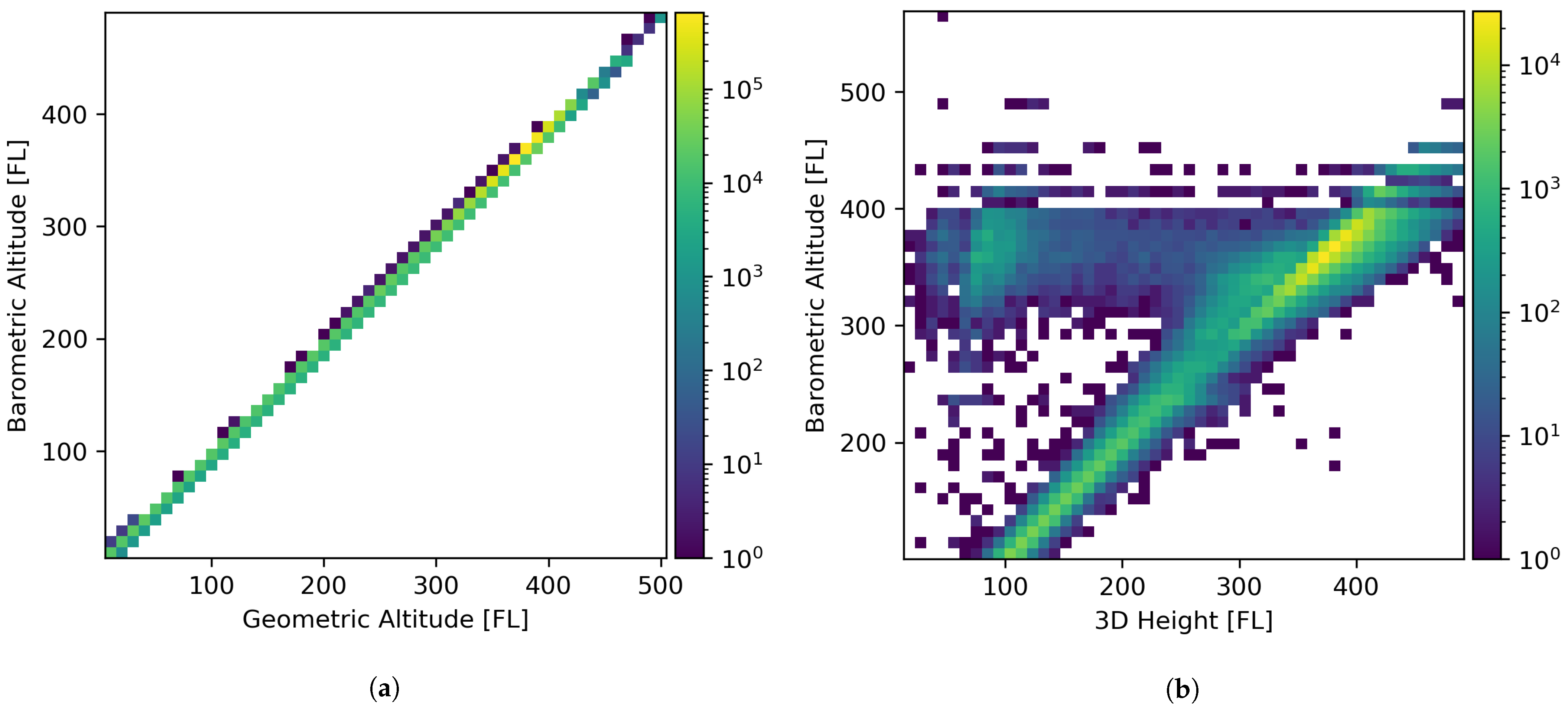
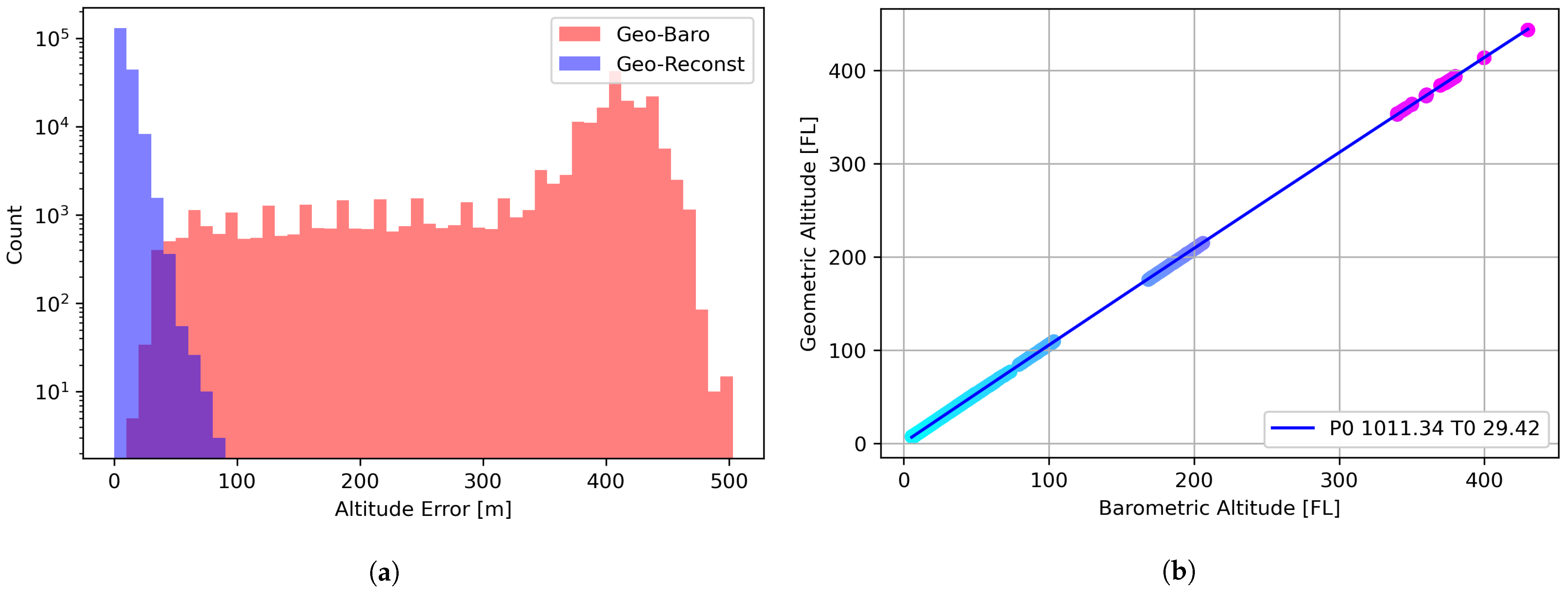
2.2. Geometric Altitude Reconstruction
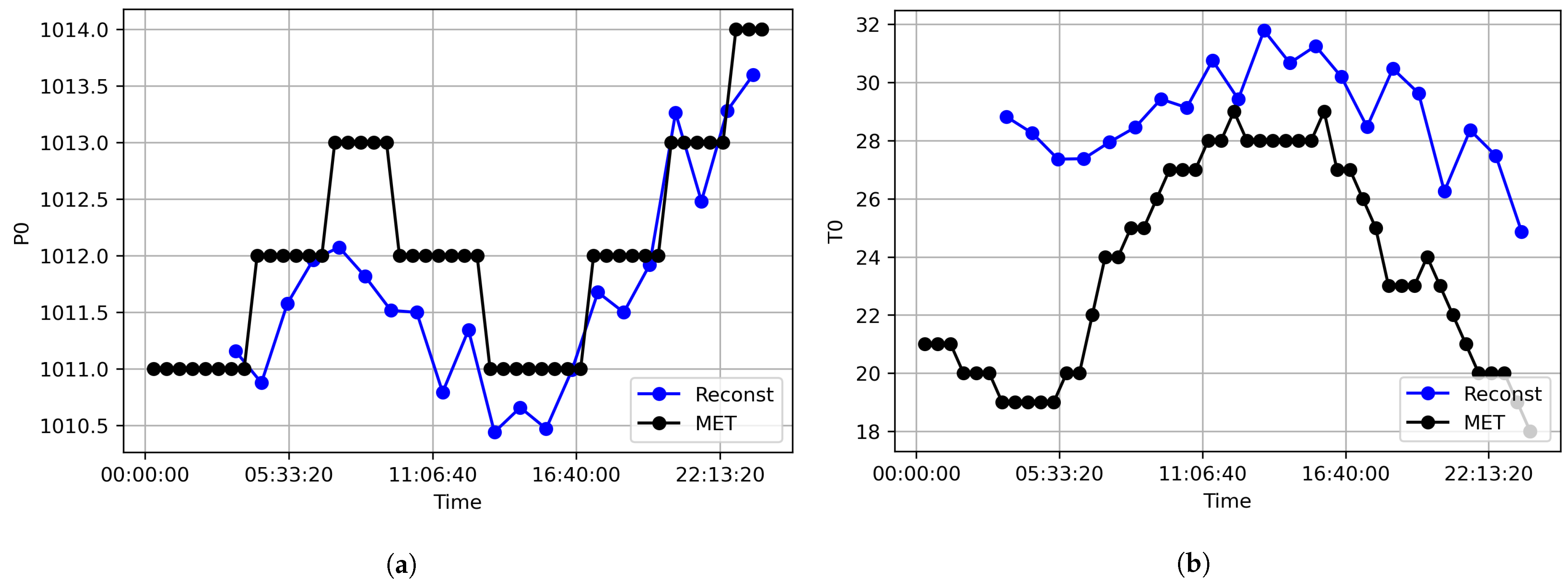
2.3. Pressure/Temperature Reconstruction Assessment
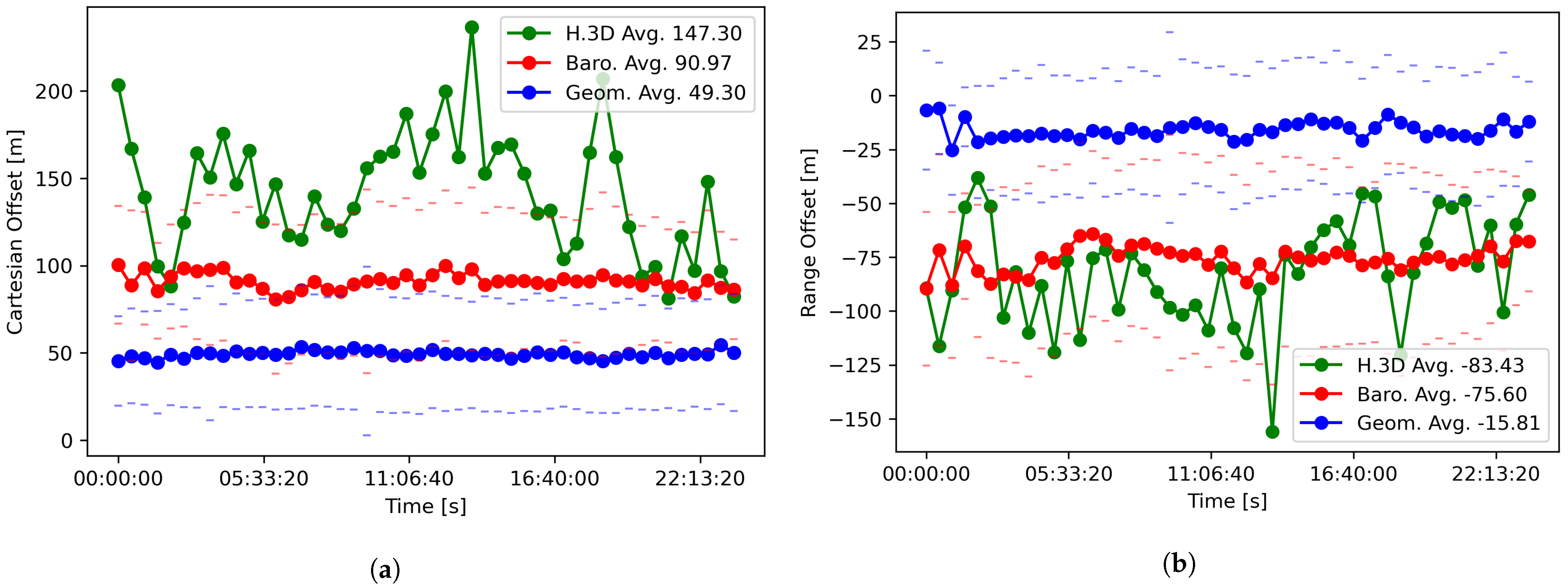
2.4. Comparison of Radar Plot Position Accuracy
3. Discussion
3.1. Reconstruction Model
3.2. Comparison of Radar Plot Position Accuracy
3.3. Radar 3D Height
3.4. Future Work
4. Methods
4.1. Dataset
4.2. Data Filtering
4.2.1. ADS-B Filtering
- MOPS version of 2, NACp ≥ 4,
- Mode C code present, geometric altitude present and valid value (not 204793.75),
- Emitter category 3 or 5 (medium or heavy aircraft).
4.2.2. Radar Filtering
- Data source is the analyzed Radar,
- Mode C code present, Mode C code not garbled, Mode C code valid,
- Three-dimensional height present,
- Mode C code > 100 (FL), range < 62.5 (nm).
4.2.3. Loaded Data Counts
4.3. ADS-B Binning
4.4. Reconstruction Model
4.5. Reconstruction Model Consistency
4.6. Reference Data
4.7. Position Accuracy Measurement
4.8. Source Code
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- GPS Product Team. Global Positioning System (GPS) Standard Positioning Service (SPS) Performance Analysis Report; GPS Product Team: Washington, DC, USA, 2014. [Google Scholar]
- Barton, D.K.; Leonov, S.A. Radar Technology Encyclopedia; Artech House: Norwood, MA, USA, 1998. [Google Scholar]
- International Civil Aviation Organization. Manual on Automatic Meteorological Observing Systems at Aerodromes, 2nd ed.; International Civil Aviation Organization: Montreal, QC, Canada, 2011; Volume 9837. [Google Scholar]
- International Civil Aviation Organization. Manual of the ICAO Standard Atmosphere: Extended to 80 kilometres (262,500 feet); International Civil Aviation Organization: Montreal, QC, Canada, 1993; Volume 7488. [Google Scholar]
- Cavcar, M. The international standard atmosphere (ISA). Anadolu Univ. Turk. 2000, 30, 1–6. [Google Scholar]
- Moré, J.J. The Levenberg-Marquardt algorithm: Implementation and theory. In Numerical Analysis; Springer: Berlin/Heidelberg, Germany, 1978; pp. 105–116. [Google Scholar]
- Specification for Surveillance Data Exchange ASTERIX, Part 12 Category 021, ADS-B Target Reports, 2.6 ed.; EUROCONTROL: Brussels, Belgium, 2021.
| Term | Description | Comment |
|---|---|---|
| p | Pressure at altitude | hPa |
| Standard pressure at MSL | 1013.25 hPa | |
| Temperature gradient over altitude | 0.0065 K/m | |
| Standard temperature at MSL | 273.15 + 15 °K | |
| h | Altitude | m |
| Acceleration of gravity | 9.81 m/s2 | |
| R | Gas constant | 287 J/(kg K) |
| Parameter | Mean (m) | Std.Dev. (m) |
|---|---|---|
| Geo-Baro | 379.24 | 85.20 |
| Geo-Reconst | 7.95 | 6.82 |
| Offset Type | Altitude Source | Mean | Std.Dev. |
|---|---|---|---|
| Cartesian (m) | Barometric | 90.97 | 40.75 |
| Geometric | 49.30 | 32.77 | |
| 3D Height | 147.30 | 440.20 | |
| Azimuth (deg) | (same for all) | 0.0122 | 0.0382 |
| Ground Range (m) | Barometric | −75.60 | 42.96 |
| Geometric | −15.81 | 29.68 | |
| 3D Height | −83.43 | 454.02 |
| Data Source | ASTERIX | Usage |
|---|---|---|
| ADS-B | CAT021 | Generate reconstruction model |
| Analyzed Radar | CAT048 | Accuracy improvement assessment test data |
| Tracker | CAT062 | Accuracy improvement assessment reference |
| Data Source | ASTERIX | Count |
|---|---|---|
| Analyzed Radar | CAT048 | 392,040 |
| ADS-B | CAT021 | 4,217,366 |
| Tracker | CAT062 | 3,057,776 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Puhr, H. Usage of Geometric Altitude for Radar Plot Position Improvements. Eng. Proc. 2022, 28, 8. https://doi.org/10.3390/engproc2022028008
Puhr H. Usage of Geometric Altitude for Radar Plot Position Improvements. Engineering Proceedings. 2022; 28(1):8. https://doi.org/10.3390/engproc2022028008
Chicago/Turabian StylePuhr, Helmut. 2022. "Usage of Geometric Altitude for Radar Plot Position Improvements" Engineering Proceedings 28, no. 1: 8. https://doi.org/10.3390/engproc2022028008
APA StylePuhr, H. (2022). Usage of Geometric Altitude for Radar Plot Position Improvements. Engineering Proceedings, 28(1), 8. https://doi.org/10.3390/engproc2022028008






