Control System Design for a Semi-Finished Product Considering Over- and Underbending †
Abstract
:1. Introduction
1.1. Freeform Bending State of the Art
1.2. Goals and Assumptions
2. Materials and Methods
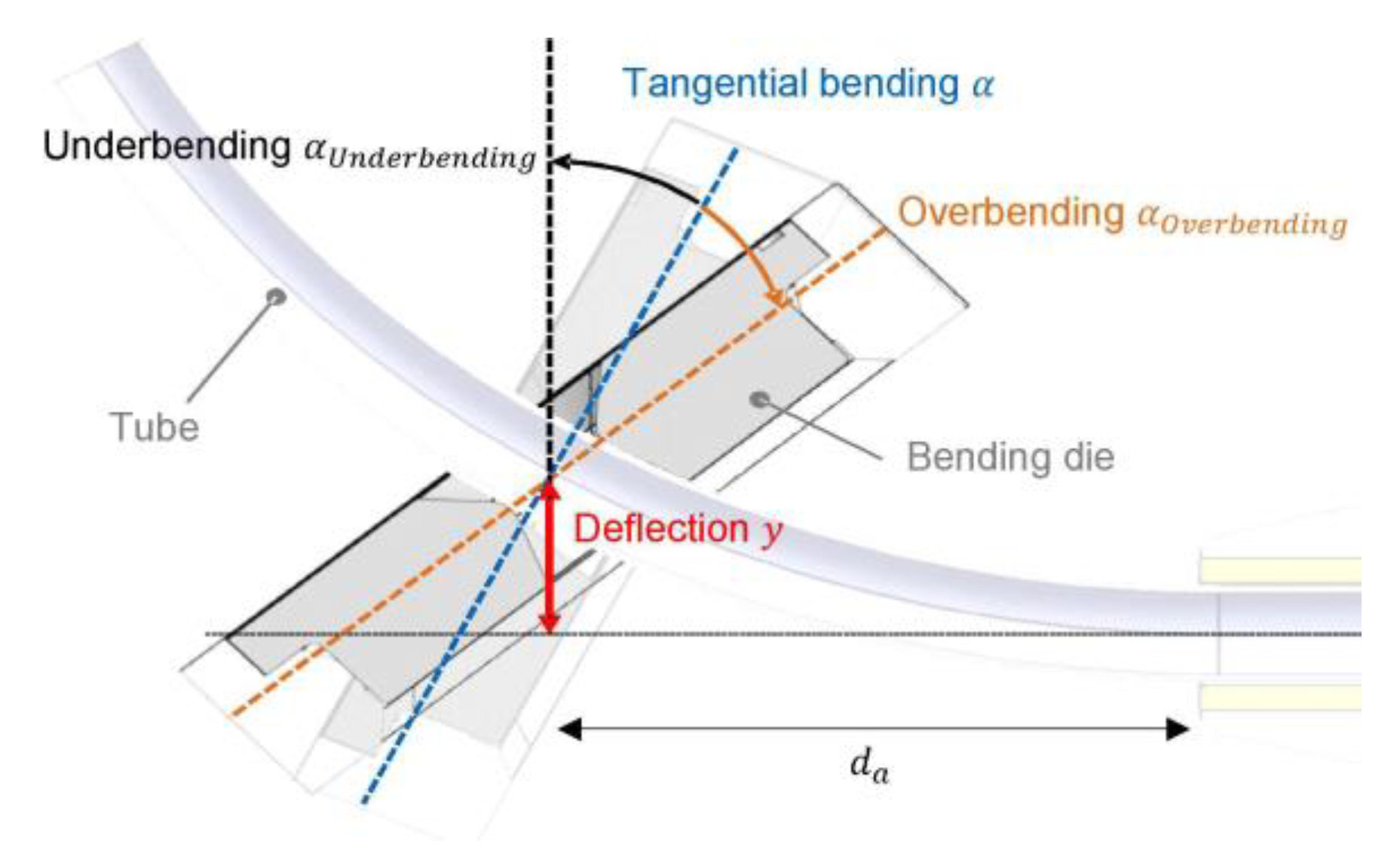
2.1. Mathematical Model for Curvature in Non-Tangential Bending
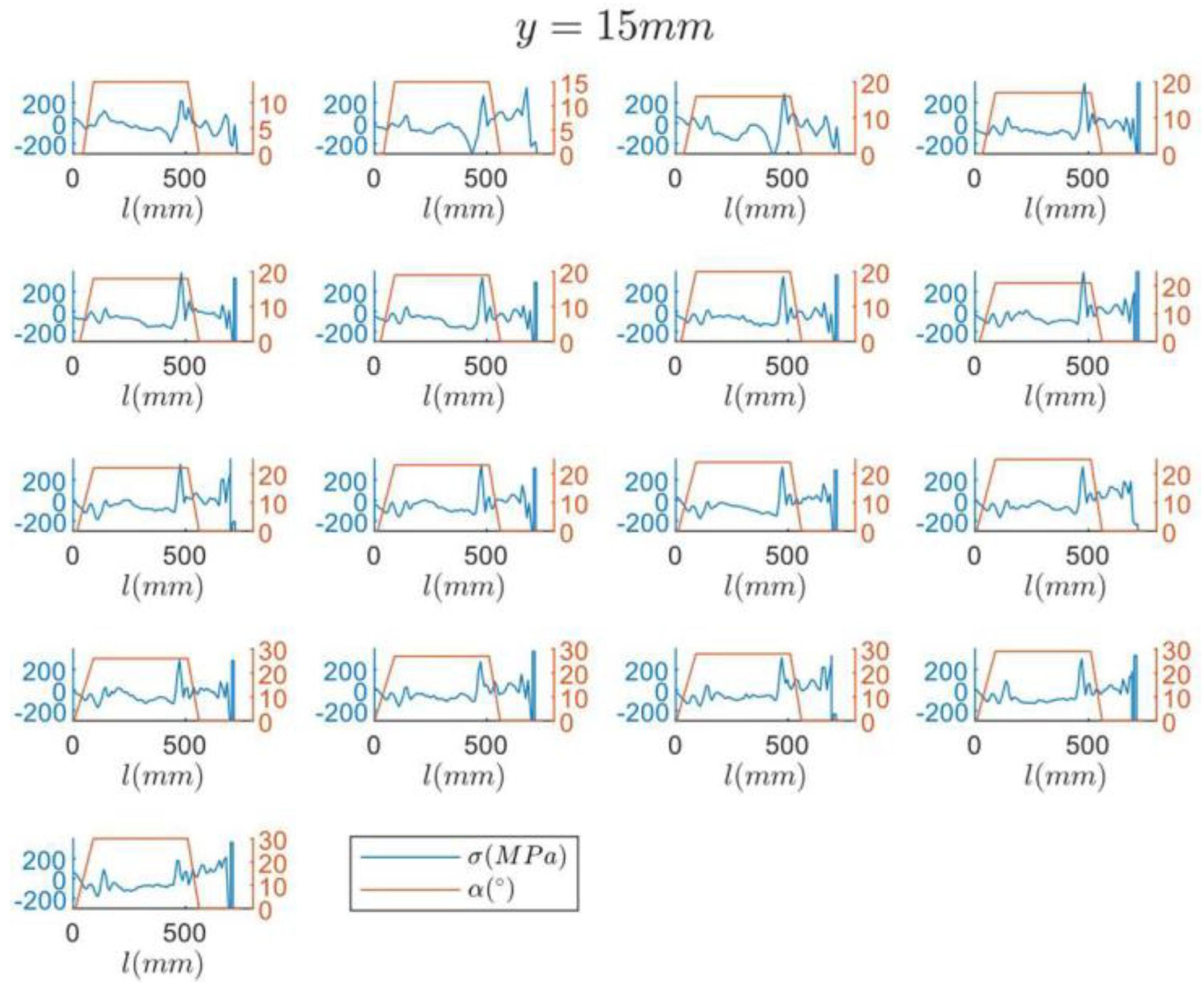
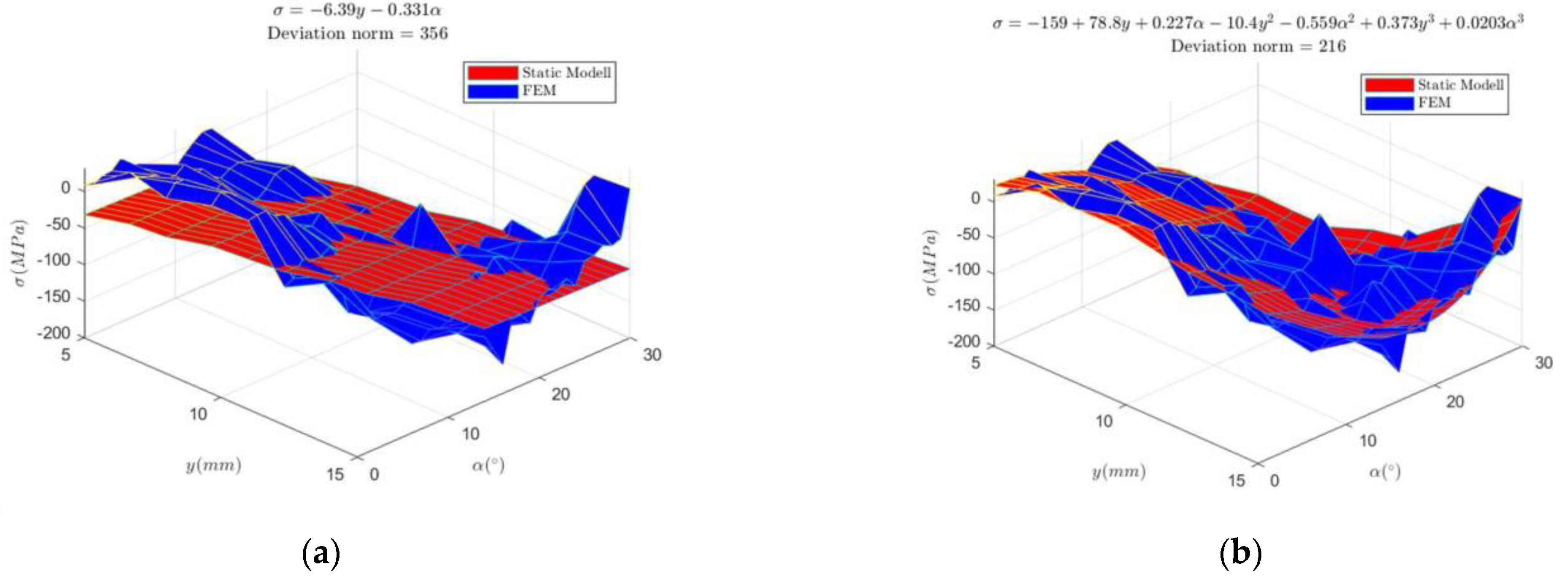
2.2. Mathematical Model for Residual Stresses in Non-Tangential Bending
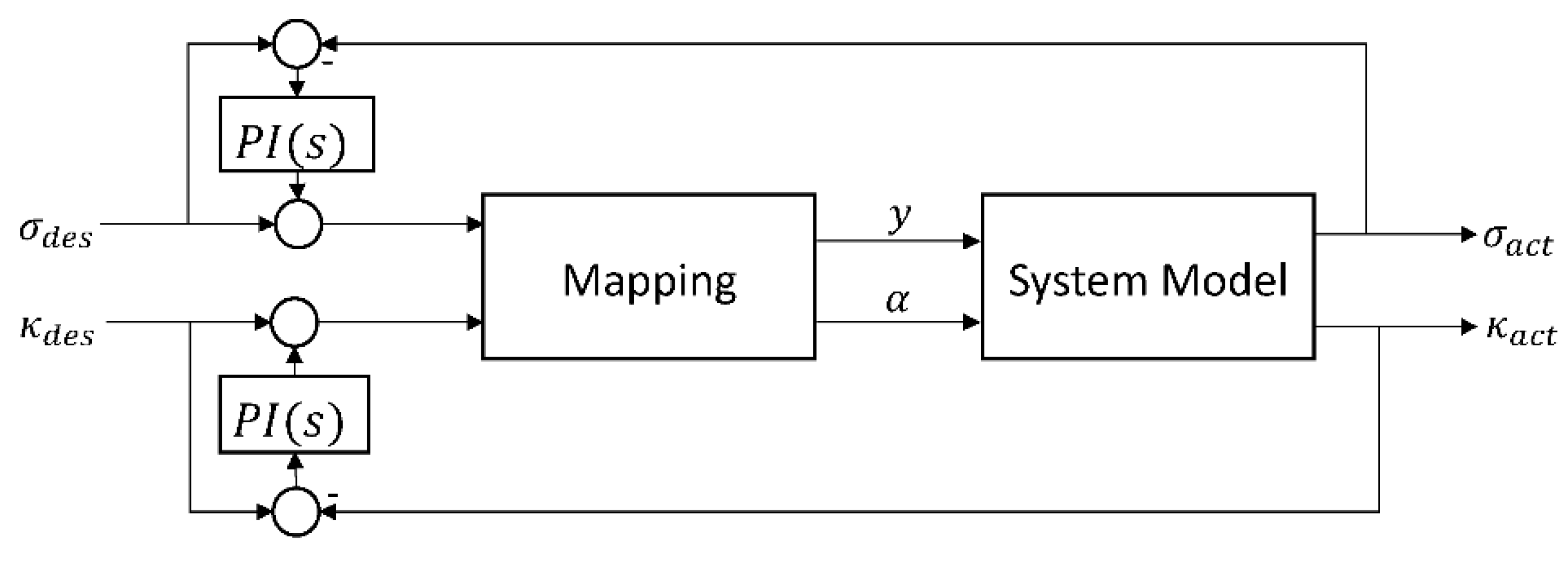
3. Developing a Closed-Loop Control System
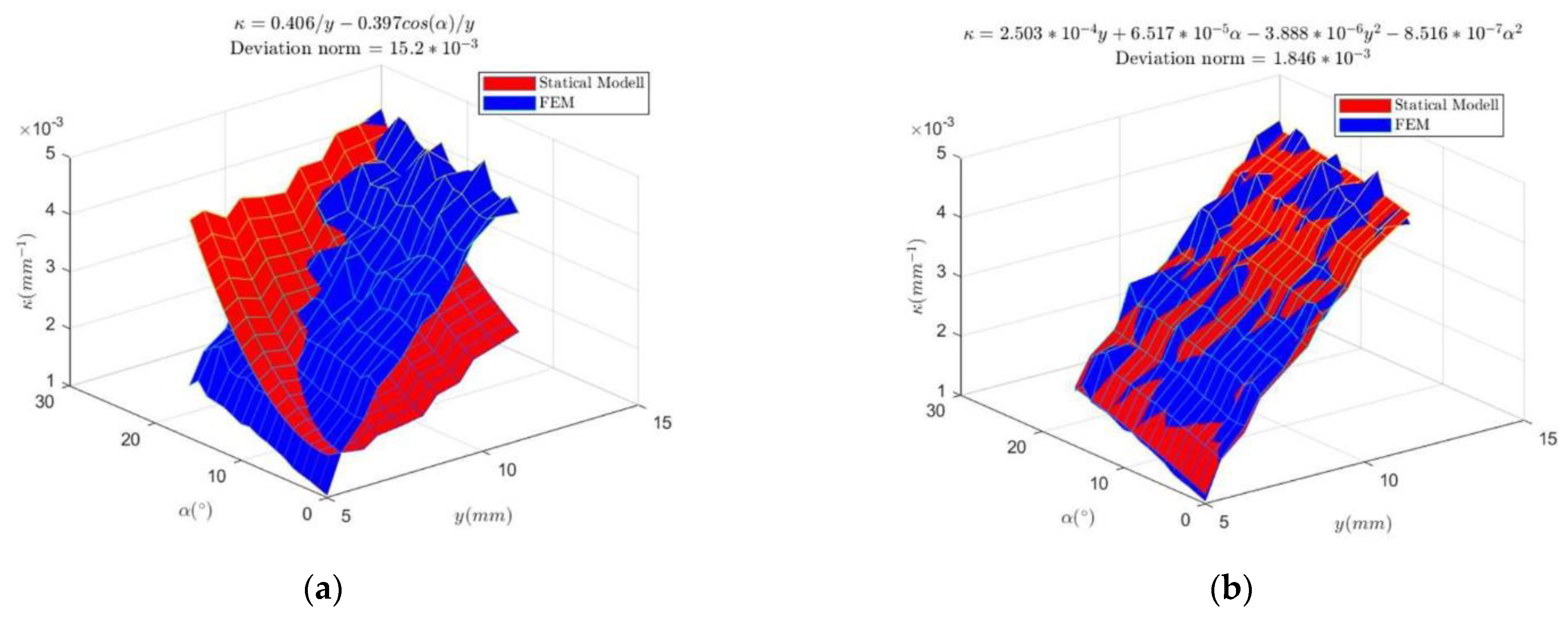
3.1. Deriving the Mathematical Equations for the Mapping Block
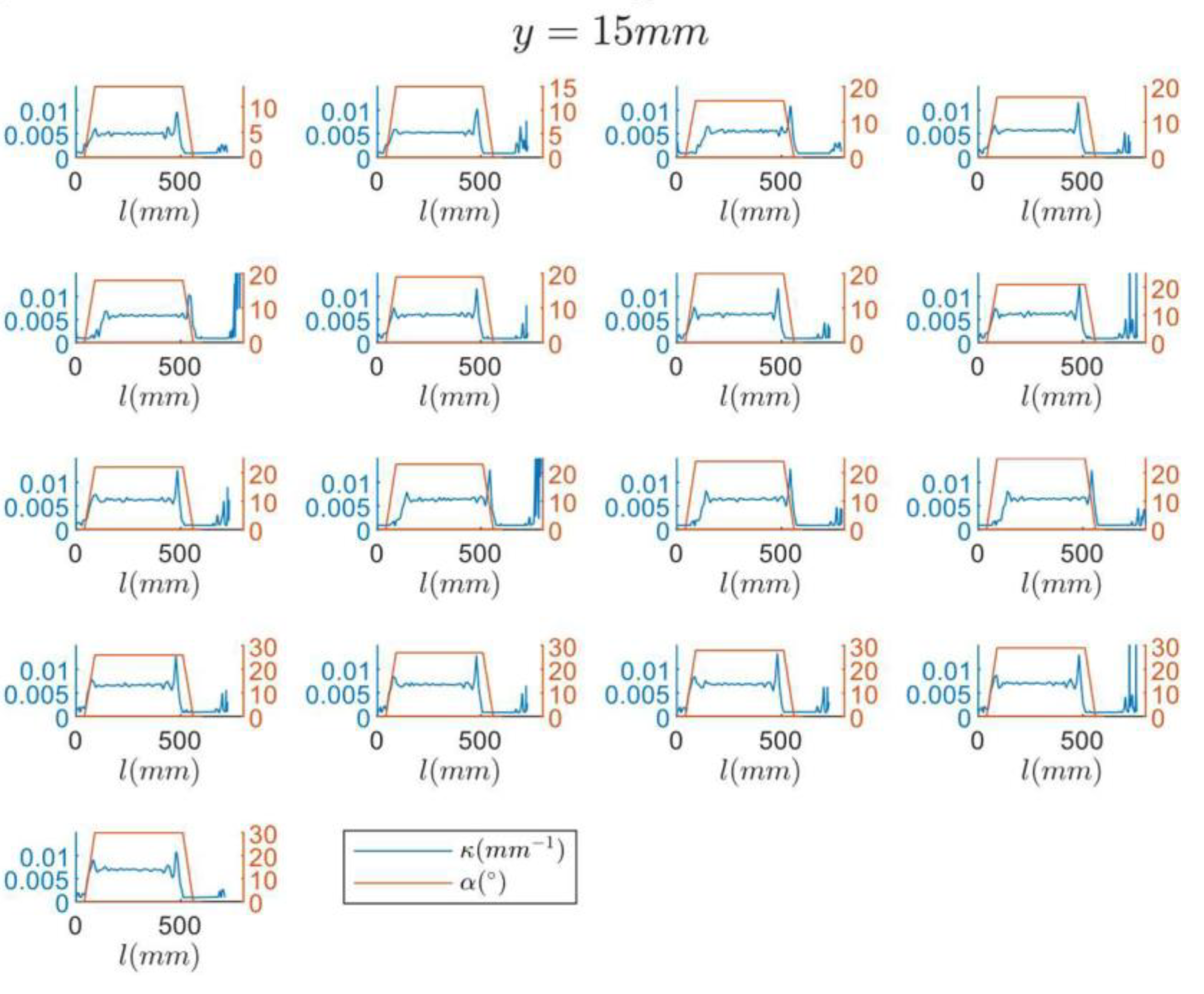
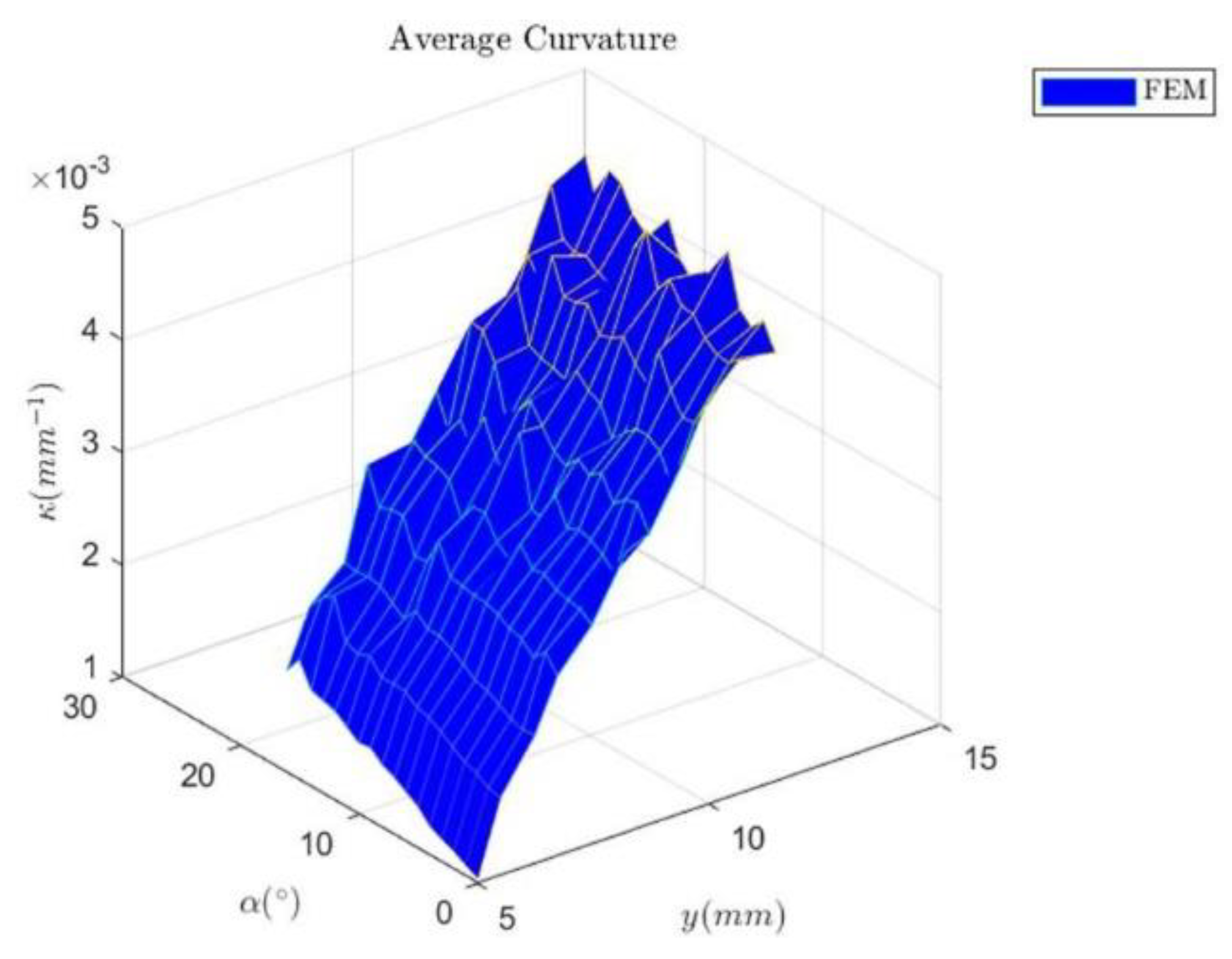
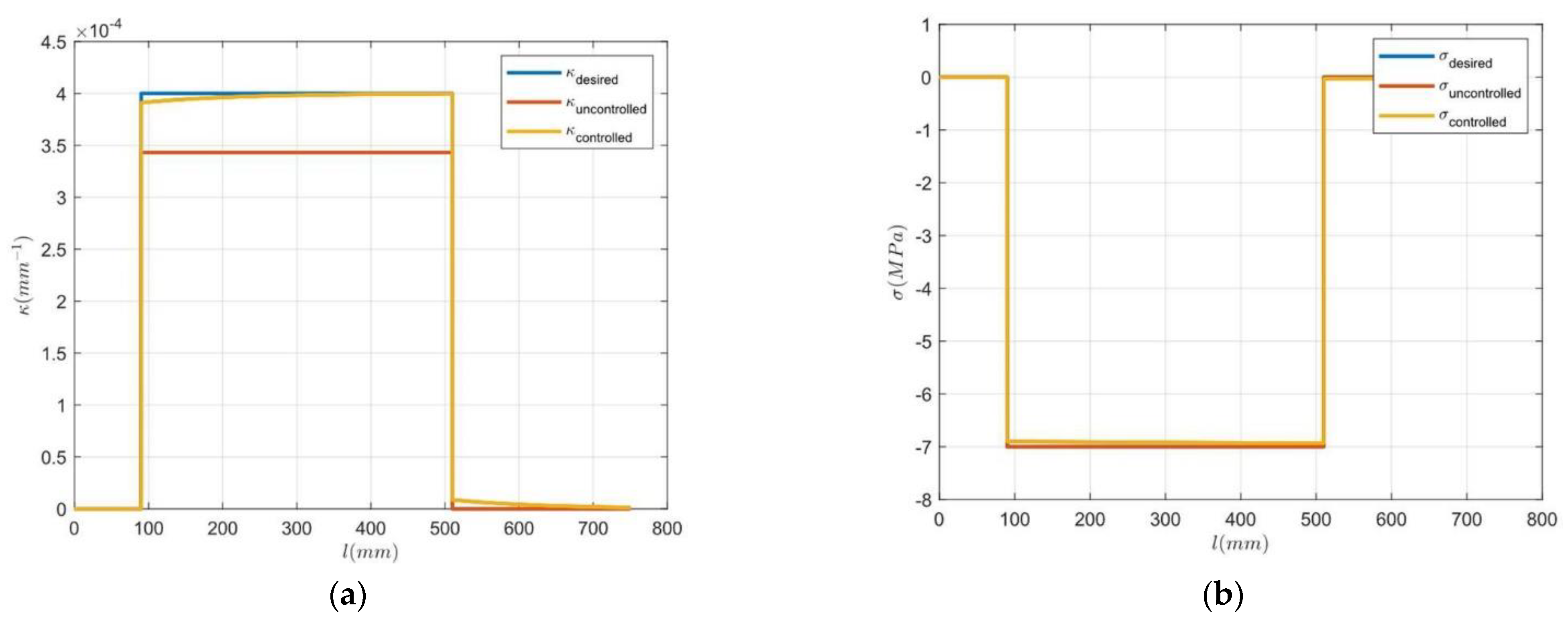
3.2. Simulation Results
4. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ismail, A.; Maier, D.; Stebner, S.; Volk, W.; Münstermann, S.; Lohmann, B. A Structure for the Control of Geometry and Properties of a Freeform Bending Process. IFAC-PapersOnLine 2021, 54, 115–120. [Google Scholar] [CrossRef]
- Maier, D.; Stebner, S.; Ismail, A.; Dölz, M.; Lohmann, B.; Münstermann, S.; Volk, W. The influence of freeform bending process parameters on residual stresses for steel tubes. Adv. Ind. Manuf. Eng. 2021, 2, 100047. [Google Scholar] [CrossRef]
- Stebner, S.C.; Maier, D.; Ismail, A.; Balyan, S.; Dölz, M.; Lohmann, B.; Volk, W.; Münstermann, S. A System Identification and Implementation of a Soft Sensor for Freeform Bending. Materials 2021, 14, 4549. [Google Scholar] [CrossRef] [PubMed]
- Stebner, S.C.; Maier, D.; Ismail, A.; Dölz, M.; Lohman, B.; Volk, W.; Münstermann, S. Extension of a Simulation Model of the Freeform Bending Process as Part of a Soft Sensor for a Property Control. In Key Engineering Materials; Trans Tech Publications Ltd.: Bäch, Switzerland, 2022; Volume 926, pp. 2137–2145. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning, 3rd ed.; Adaptive Computation and Machine Learning series; MIT Press: Cambridge, MA, USA, 2008. [Google Scholar]
- Wu, J.; Liang, B.; Yang, J. Trajectory prediction of three-dimensional forming tube based on Kalman filter. Int. J. Adv. Manuf. Technol. 2022, 121, 5235–5254. [Google Scholar] [CrossRef]
- Maier, D.; Kerpen, C.; Werner, M.K.; Scandola, L.; Lechner, P.; Stebner, S.C.; Ismail, A.; Lohmann, B.; Münstermann, S.; Volk, W. Development of a partial heating system for freeform bending with movable die. In Hot Sheet Metal Forming of High-Performance Steel, Proceedings of the 8th International Conference, Barcelona, Spain, 20–22 April 2022; Oldenburg, M., Hardell, J., Casellas, D., Eds.; Wissenschaftliche Scripten: Auerbach/Vogtland, Germany, 2022; pp. 767–774. [Google Scholar]
| y (mm) | α (°) | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 6 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 7 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 8 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 9 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 10 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 11 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 12 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 13 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 14 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 15 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ismail, A.; Maier, D.; Stebner, S.; Volk, W.; Münstermann, S.; Lohmann, B. Control System Design for a Semi-Finished Product Considering Over- and Underbending. Eng. Proc. 2022, 26, 16. https://doi.org/10.3390/engproc2022026016
Ismail A, Maier D, Stebner S, Volk W, Münstermann S, Lohmann B. Control System Design for a Semi-Finished Product Considering Over- and Underbending. Engineering Proceedings. 2022; 26(1):16. https://doi.org/10.3390/engproc2022026016
Chicago/Turabian StyleIsmail, Ahmed, Daniel Maier, Sophie Stebner, Wolfram Volk, Sebastian Münstermann, and Boris Lohmann. 2022. "Control System Design for a Semi-Finished Product Considering Over- and Underbending" Engineering Proceedings 26, no. 1: 16. https://doi.org/10.3390/engproc2022026016
APA StyleIsmail, A., Maier, D., Stebner, S., Volk, W., Münstermann, S., & Lohmann, B. (2022). Control System Design for a Semi-Finished Product Considering Over- and Underbending. Engineering Proceedings, 26(1), 16. https://doi.org/10.3390/engproc2022026016






