Virtual Model-Based Trajectory Optimization Algorithm for Aliquoting Robotic System ^†

Abstract

This work was devoted to the optimization of the trajectory of a robotic system for aliquoting biosamples, consisting of serial and parallel manipulators. The optimization consisted of two stages. At the first stage, we considered the optimization constraints associated with the workspace, taking into account the ranges of permissible values of the angles of the drive rotational joints, the link interference, and the singularities. The workspace in the space of input and output coordinates was represented as a partially ordered set of integers. At the second stage, constraints were formed related to the objects in the workspace during the aliquoting process, such as the body of the robotic system, test tubes, and racks. The condition for excluding collisions of the manipulator with other objects was provided by the geometric decomposition of objects and the exclusion of areas corresponding to external objects from the set describing the workspace of the manipulator. Optimization was performed in the space of input coordinates. The objective function was proportional to the duration of movement along the trajectory. The possibility of applying evolutionary algorithms to solve this problem is analyzed. An assessment of the performance is given. The optimization and export of the resulting trajectory were implemented in software, which enabled verification of the optimization results on a virtual model. The simulation results are presented.

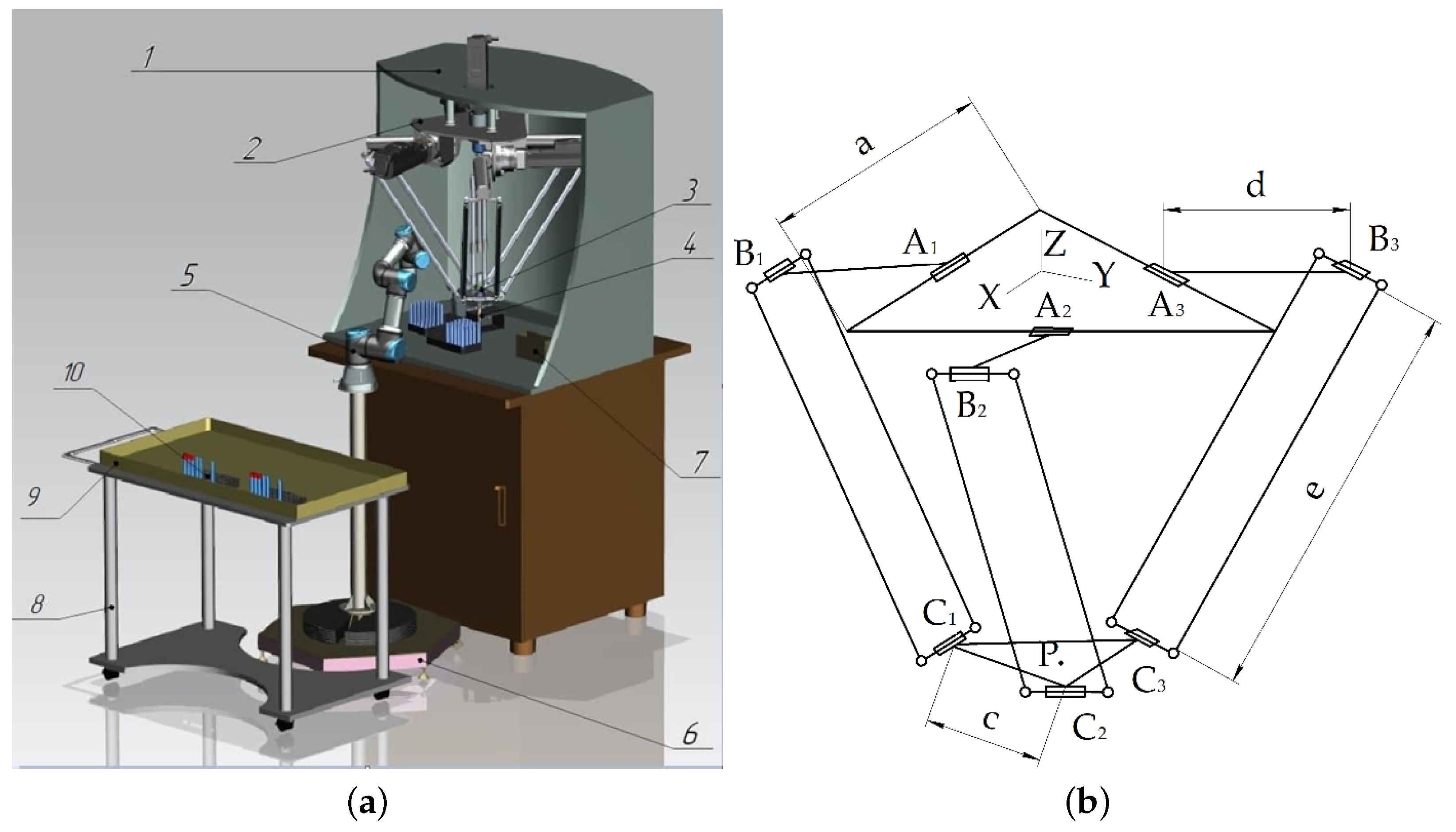
1. Introduction

When automating technological processes in a wide range of industries, trajectory planning tasks are very important. The boundaries of the workspace, singularities, and intersections of robot links can be considered as obstacles. Currently, there are various methods for trajectory planning. Some methods are based on the spatial decomposition into geometric shapes of various shapes [1,2]. Discrete search methods allow using heuristic estimates of the perspective of the trajectories, speeding up the solution of trajectory planning problems [3]. An important family of motion planning methods consists of potential field methods, originally developed for mobile robot navigation and real-time obstacle avoidance [4]. Sampling methods allow us to solve problems of planning the trajectory of movement with a high level of complexity, for spaces with a large number of obstacles and mechanisms with a significant number of degrees of freedom [5]. The Probabilistic Roadmap Method [6] is widely applied to solve path finding problems in both local and global settings. One of the ways to reduce the number of vertices in a graph is the method of constructing randomized route networks based on scopes [7]. There are also currently a number of efficient stochastic methods that can be applied to the trajectory planning of manipulators [8,9].

The application of evolutionary algorithms makes it possible to solve optimization problems, including planning a trajectory with high-performance indicators. In this regard, within the framework of this paper, an original approach is proposed based on the application of evolutionary algorithms to find the optimal trajectory inside the workspace of robots, taking into account the singularities, intersections of links, and the constraints on the drive coordinates. The optimization problem is solved using the example of a delta robot, which can be applied for a wide range of tasks, including biometric aliquoting [10]. During this task, it becomes necessary to avoid obstacles such as test tubes and racks.

2. Setting an Optimization Problem

The delta robot (Figure 1b) included in the robotic system for biomaterial aliquoting (Figure 1a) has three degrees of freedom and includes three kinematic chains RUU. In each of the chains, the drive rotary joint $A_i$ is used to connect to the base. Universal joints $C_i$ are used to connect to the moving platform. Universal joints $B_i$ are used to connect two links to each other. The end-effector is the center P of the mobile platform.

The delta robot can move relatively freely along a certain arbitrary trajectory, taking into account the limitations determined by the workspace and the singularities and intersections of the robot links. The duration of the robot movement should be minimized as much as possible. Since the duration of the movement in time is determined by the duration of the operation of the robot drives required for the corresponding movement, it is advisable to optimize the trajectory in the space of input coordinates. So, for a delta robot, the input coordinates are the angles ${\theta }_i$ of rotation of the drive rotary joints $A_i$. An arbitrary trajectory can be represented as a set of movements (steps) in the space of $m=3$ input coordinates. As a criterion function, we used a function based on the Chebyshev metric, as well as the Euclidean metric, taken with some small weight coefficient $ϵ$ [11]:

$$F=\sum _{i=1}^n\left(\underset{j\in \{1,2,\dots ,m\}}{max}\left|{\theta }_{i,j}-{\theta }_{i-1,j}\right|+\epsilon \sqrt{\sum _{j=1}^m{\left({\theta }_{i,j}-{\theta }_{i-1,j}\right)}^2}\right)\to min.$$

(1)

Optimization should be carried out within the constraints on the size of the workspace. In the framework of previous works, the authors proposed to use the representation of the workspace in the form of a partially ordered set of integers A [12]. Therefore, checking the opt-in constraint consisted of two steps.

2.1. The First Stage: Definition of the Set B of the Trajectory Coordinates in the Space of Integers

For this purpose, an algorithm was modified from Bresenham’s algorithm [13], which assumes that the trajectory is represented as a polyline consisting of many segments. In this case, the coordinates must correspond to the covering set of the workspace, represented as a partially ordered set of integers; they must be obtained taking into account the accuracy of the approximation ${\Delta }_j$ and the displacement $k_j$ along the j coordinate axes by the formula

$$x_i=\frac{{\theta }_{i,1}+k_1}{{\Delta }_1},y_i=\frac{{\theta }_{i,2}+k_2}{{\Delta }_2},z_i=\frac{{\theta }_{i,3}+k_2}{{\Delta }_2}.$$

(2)

2.2. The Second Stage: Determination of Whether the Resulting Set B A Belongs to the Workspace Set A

Thus, the optimization constraint condition has the form

$$B_i\subset A,i\in 1,\dots ,n$$

(3)

where n is the number of segments that make up the trajectory.

Thus, the optimization problem looked like this.

-

Parameters: the coordinates of the intermediate points of the trajectory $x_i,y_i,z_i,i\in 1,\dots ,(n-1)$. For a delta robot, the coordinates are the rotation angles of the drive rotary joints, i.e., ${\left[\left(x_i{y}_i{z}_i\right)\right]}^T={\left[\left({\theta }_{i,1}{\theta }_{i,2}{\theta }_{i,3}\right)\right]}^T$.

-

Parameter change range: the overall dimensions of the workspace in the space of input coordinates ${\theta }_{(i,j)}\in [{\theta }_{jmin};{\theta }_{jmax}]$.

-

Criterion: the function F calculated by formula (1).

-

Constraint: condition (3).

To increase the efficiency of the optimization in the presence of obstacles, we transferred the optimization constraint to the criterion function

$$F^{\prime }=F+\sum _{i=1}^n\left({\vartheta }_i\left(p_1\sqrt{\sum _{j=1}^m{\left({\theta }_{i,j}-{\theta }_{i-1,j}\right)}^2}+p_2\right)\right)\to min,$$

(4)

where $p_1$,$p_2$ are the penalty coefficient, and ${\vartheta }_i$ is the Heaviside function:

$${\vartheta }_i=\left\{\begin{array}{c}0,\mathrm{if}{B}_i\subset A\\ 1-\mathrm{otherwise}.\end{array}\right.$$

(5)

We used the Genetic algorithm (GA), Particle Swarm Optimization (PSO), and Grey Wolf Optimization (GWO) to solve the optimization problem.

3. Numerical Results

The workspace of the delta robot is limited by the range of permissible rotation angles in the hinges, the area of sign constancy, the Jacobian, and the condition that there are no intersections of links. The problem of determining the workspace $B_P$ for a delta robot in the space of output coordinates was considered by the authors in [10]. Figure 2 shows the results for the following delta robot parameters: a = 600 mm, c = 100 mm, d = 350 mm, e = 800 mm, and ${\Delta }_j=4^{\circ }$.

An object was added as an obstacle with a parallelepiped shape (Figure 3a). The updated workspace virtual models are shown in Figure 3b,c.

We performed trajectory optimization inside the workspace of a delta robot. A C++ software package was developed for this purpose. Parallel computing was implemented using the OpenMP library. Visualization was performed by exporting an ordered set of integers describing the workspace in STL format and arrays of co-ordinates of trajectory points in JSON format, and then importing thedata in the Blender software package using developed Python scripts. We set the following starting and ending points of the trajectory in the output coordinate space: $x_{p1}=250$ mm, $y_{p1}=250$ mm, $z_{p1}=-500$ mm, $x_{p2}=-270$ mm, $y_{p2}=-270$ mm, and $z_{p2}=-450$ mm, and the number of vertices of the trajectory $n=3$. Accordingly, the number of optimization parameters $p=3n=9$. The weight coefficient $ϵ=0,1$, the penalty coefficients $p_1=5$, $p_2=500$.

The parameters of the GA algorithm were the number of individuals in the initial population $H=250$, the number of generations $W=200$, the number of crosses at each iteration $S_{GA}=125$, the number of possible values of each of the parameters $g=2^{25}$, and the probability of mutation $p_m=70\%$.

The parameters of the GWO algorithm were $H=250$, $W=200$, and the number of new individuals at each iteration $S_{GWO}$ = 1000.

The parameters of the PSO algorithm were $H=250$, $W=200$, the number of groups G = 2, and the values of free parameters $\alpha$ = 0.7, $\beta$ = 1.4, and $\gamma$ = 1.4.

The optimization for each of the tests was performed in four stages. At the first stage, the range of parameters was changed to the ranges corresponding to the overall dimensions of the workspace for each of the coordinates. The parameter ranges at each subsequent stage were reduced by a factor of ${10}^2$. At the same time, the center of the ranges corresponded to the best result obtained at the previous stage. The optimization results are shown in

Table 1. Results table, mm.

Trials	GA	GWO	PSO	Trials	GA	GWO	PSO
1	152,499	149,852	149,737	6	131,130	149,863	149,891
2	151,070	150,136	130,477	7	130,719	130,433	130,459
3	131,368	130,477	149,778	8	150,506	131,111	149,915
4	137,201	150,394	130,385	9	152,649	149,941	149,914
5	149,876	150,427	149,674	10	149,772	150,083	149,769
				Average value	143,679	144,272	144,000

. The GA algorithm showed the best average value of the criterion function.

To justify the feasibility of using the criterial modified Chebyshev metric as a criterion function, we analyzed the values of the trajectory length for various metrics and the criterion function for one of the tests.

Table 2. Trajectory optimization results for Test 3, mm.

Trajectory According to Test 3	GA	GWO	PSO
Path length	168,101	163,734	167,705
Chebyshev length (estimation of positioning duration)	114,558	114,104	133,008
Criterion function ($\alpha$ = 0,1)	131,368	130,477	149,778

shows the results of the trajectory optimization for Test 3. The table shows that despite the fact that the trajectory obtained as a result of the PSO optimization by the algorithm was 0.2% shorter in length than the trajectory obtained by the GA algorithm, the length in accordance with the Chebyshev metric and, accordingly, the positioning duration for the PSO trajectory was 14% longer. We can conclude that it is advisable to apply the Chebyshev metric when planning a trajectory.

Figure 4 shows the trajectories for Test 3 inside the workspace virtual model. As can be seen from the figure, the PSO algorithm found only a local minimum of the criterion function for avoiding the obstacle.

4. Conclusions

The application of heuristic algorithms made it possible to solve the problem of planning a trajectory for a 3D workspace, represented as a partially ordered set of integers. The planning of the trajectory in the space of input coordinates and the use of the Chebyshev metric as part of the criterion function made it possible to reduce the duration of the positioning from the initial to the final point of the trajectory. As part of our future work, the choice of the parameters of the optimization algorithms will be examined to achieve the best convergence rates. Various modifications of heuristic algorithms, including hybrid ones, will be applied. A comparative analysis of the effectiveness of the developed methodology with existing methods of trajectory planning will be carried out.