Deep Learning Assisted Composite Clock: Robust Timescale for GNSS Through Neural Network ^†

Abstract

This study introduces the Deep Learning Assisted Composite Clock (DLACC), aiming to improve the robustness of the GNSS timescale. If traditional Kalman filter-based composite clocks are today used in systems like GPS and EGNOS, the non-linear, non-Gaussian, and non-stationary behavior of atomic clocks can impact the performance of such model-based filtering. DLACC, built from the KalmanNet approach, proposes to enhance Kalman filters by computing its gain through a neural network to better model clock dynamics and manage ensemble clock reconfigurations. In particular, this study evaluates this method’s performance against conventional filters, demonstrating its potential for more resilient and adaptive GNSS timescales.

1. Introduction

Clock synchronization is vital for navigation systems that require a stable, available, and resilient common time reference to ensure positioning and timing performance for all users. The composite clock approach, adopted by systems such as GPS and EGNOS, addresses these needs by assembling multiple physical clocks through Kalman filters [1,2]. Such algorithms benefit from the availability of a large clock ensemble and can efficiently detect anomalies in individual clocks, allowing them to adapt their contribution to the overall system time. Yet, tuning such algorithms is a very complex task as the clock’s behaviour can be seen as non-linear, non-Gaussian, and non-stationary, while conventional filtering methods often assume the opposite [3,4]. Significant challenges related to the initialization of such filters and handling the clock’s ensemble reconfiguration can also be faced [5].

In such contexts, this study proposes to introduce the concept of a Deep Learning Assisted Composite Clock (DLACC) for GNSS, leveraging supervised learning methods to dynamically estimate filter parameters in real time and in non-linear environments while also considering partial information. Based on recent research [6], the proposed approach embeds a dedicated neural network within the existing Kalman filter, enhancing their ability to capture complex clock behaviors and ensemble reconfigurations.

Firstly, this paper introduces the general paradigm regarding GNSS composite clocks based on the conventional Kalman filters, highlighting the challenges associated with atomic clock behavior prediction. Then, an evolution of the Kalman filter is presented, based on work detailed in [6]. This KalmanNet system, computing the Kalman gain from a recurrent neural network fed by observed and predicted clocks states, is then evaluated with respect to classic filtering methods.

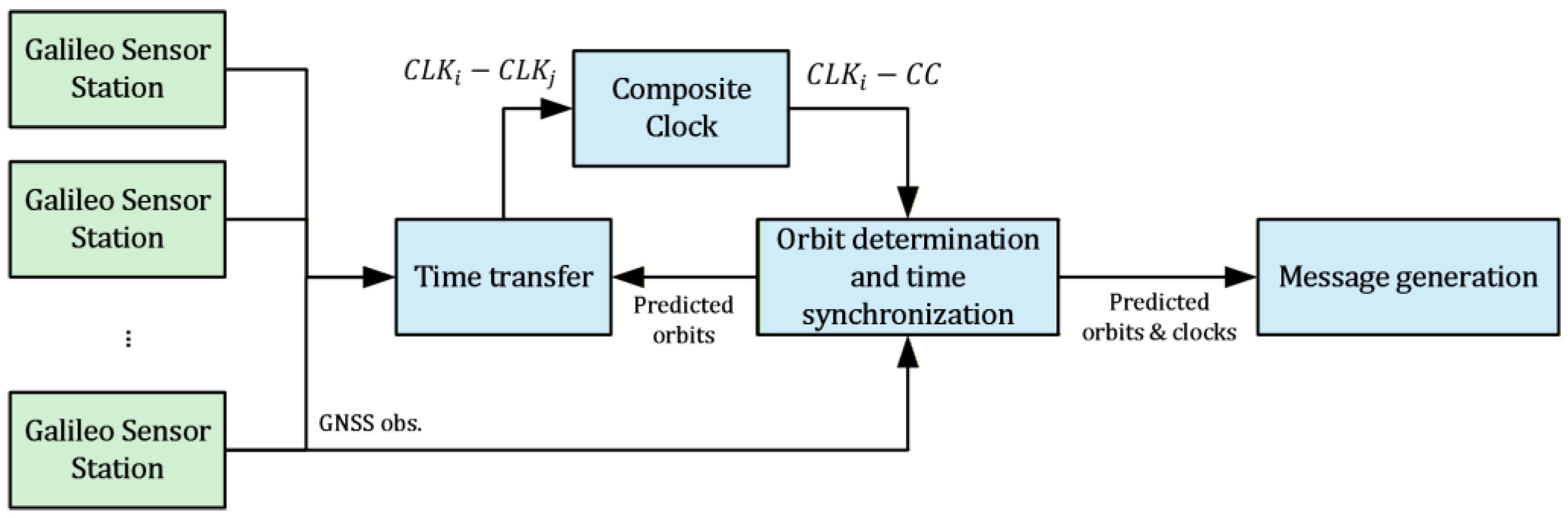
2. Basics of the Composite Clock for GNSS

Precise timing is at the core of the satellite navigation, as associated service relies on the precise knowledge of the satellite clock’s state. In order to synchronize these clocks and other system assets and to compute precise satellite clock predictions for broadcasting in the navigation message, Global Navigation Satellite Systems (GNSS) typically establish an internal timescale: the system time. The work of K. Brown [1] presented the solution to compute the GNSS reference time (as used for satellite clock prediction) from a combination of clocks using a Kalman filter. This ensemble timescale, commonly called a composite clock, has obvious benefits for overall timescale availability and robustness as well as for the monitoring of the contributing clocks for detection and isolation of anomalies.

In [1], the ensemble timescale itself is defined as the implicit Kalman mean that is not directly observable, but the states of the individual clock states (phase, frequency, and frequency drift) are de facto estimated versus it. The blocks of the process covariance matrix $Q$ corresponding to the clock $i$ are defined as follows:

$$Q_i=\left(\begin{array}{ccc}{q}_{i,1}\tau +{\displaystyle \frac{q_{i,2}{\tau }^3}{3}}+{\displaystyle \frac{q_{i,3}{\tau }^5}{20}}& {\displaystyle \frac{q_{i,2}{\tau }^2}{2}}+{\displaystyle \frac{q_{i,3}{\tau }^4}{8}}& {\displaystyle \frac{q_{i,3}{\tau }^3}{6}}\\ *& q_{i,2}\tau +{\displaystyle \frac{q_{i,3}{\tau }^3}{3}}& {\displaystyle \frac{q_{i,3}{\tau }^2}{2}}\\ *& *& q_{i,3}\tau \end{array}\right)$$

(1)

The coefficients $q$ are related to the Allan variance of the corresponding clock, as shown in [7], where ${\mathrm{q}}_0{,\mathrm{q}}_1,{\mathrm{q}}_2,{\mathrm{q}}_3$ correspond to the white phase modulation, white frequency modulation, frequency random walk, and frequency random run, respectively:

$${\sigma }_y^2\left(\tau \right)={\displaystyle \frac{3q_0}{{\tau }^2}}+{\displaystyle \frac{q_1}{\tau }}+{\displaystyle \frac{q_2\tau }{3}}+{\displaystyle \frac{q_3{\tau }^3}{20}}$$

(2)

Important practical considerations regarding the computation and tuning of the clock covariances are presented in [7,8].

Brown’s composite clock implementation suffered from the common problem of the early Kalman filter timescales: the uncontrolled growth of the covariance of the estimated states. This happens because the input measurements are de facto clock differences, while the model assumes estimation of the absolute clock states, which are not observable. In other words, the number of independent observations is always less than the number of clocks that the Kalman filter estimates. This leads to uncontrolled covariance growth, as shown in [9] (although the Kalman gain remains steady), and can result in numerical problems. In [1], the covariance growth is addressed through regular covariance reductions.

A solution to improve the system’s observability by adding constraints on the continuity of the estimated clock states was proposed by S. Stein in [10]. This approach was adopted in the timescale algorithm proposed for the International GPS Service (IGS, now International GNSS Service) [2,11].

Under an ESA contract for the Galileo Ground Mission Segment, Thales Alenia Space France (TAS-F) has investigated options to adapt the IGS timescale algorithm for Galileo [12]. The timescale computation is proposed to be implemented separately from the legacy orbit determination and time synchronization algorithm ODTS (see Figure 1).

While re-using the basic structure of the covariance matrix from (1), [12] proposed scaling factors $Avail$ and $Anom$ to manage i-th clock exclusion/re-introduction because of data availability or clock weight reductions due to an anomaly, similarly to the approach in [11]:

$$w_{i,phase}={\displaystyle \frac{{Avail}_i·{Anom}_i}{q_{1,i}\tau +\frac{q_{2,i}{\tau }^3}{3}+\frac{q_{3,i}{\tau }^5}{20}}}$$

(3a)

$$w_{i,frequency}={\displaystyle \frac{{Avail}_i·{Anom}_i}{\frac{q_{2,i}{\tau }^2}{2}+\frac{q_{3,i}{\tau }^4}{8}}}$$

(3b)

$$w_{i,drift}={\displaystyle \frac{{Avail}_i·{Anom}_i}{\frac{q_{3,i}{\tau }^2}{2}}}$$

(3c)

In the context of future operational implementation of such an algorithm in GNSS, one of the main challenges is refining and automating the dynamic estimation of the process covariance matrix. This is particularly important considering relatively frequent reconfigurations of the system clock ensemble and the general non-stationarity of process noises. This issue becomes even more critical in cases where additional weighting factors to manage clock introduction/exclusion are introduced, as proposed in [12]. Such tuning requires a long-term operational experience and expert knowledge. To increase the level of automation of the GNSS operations and consequently reduce the dependence on expert knowledge and mitigate human error factors, we will consider application of the neural network and machine learning.

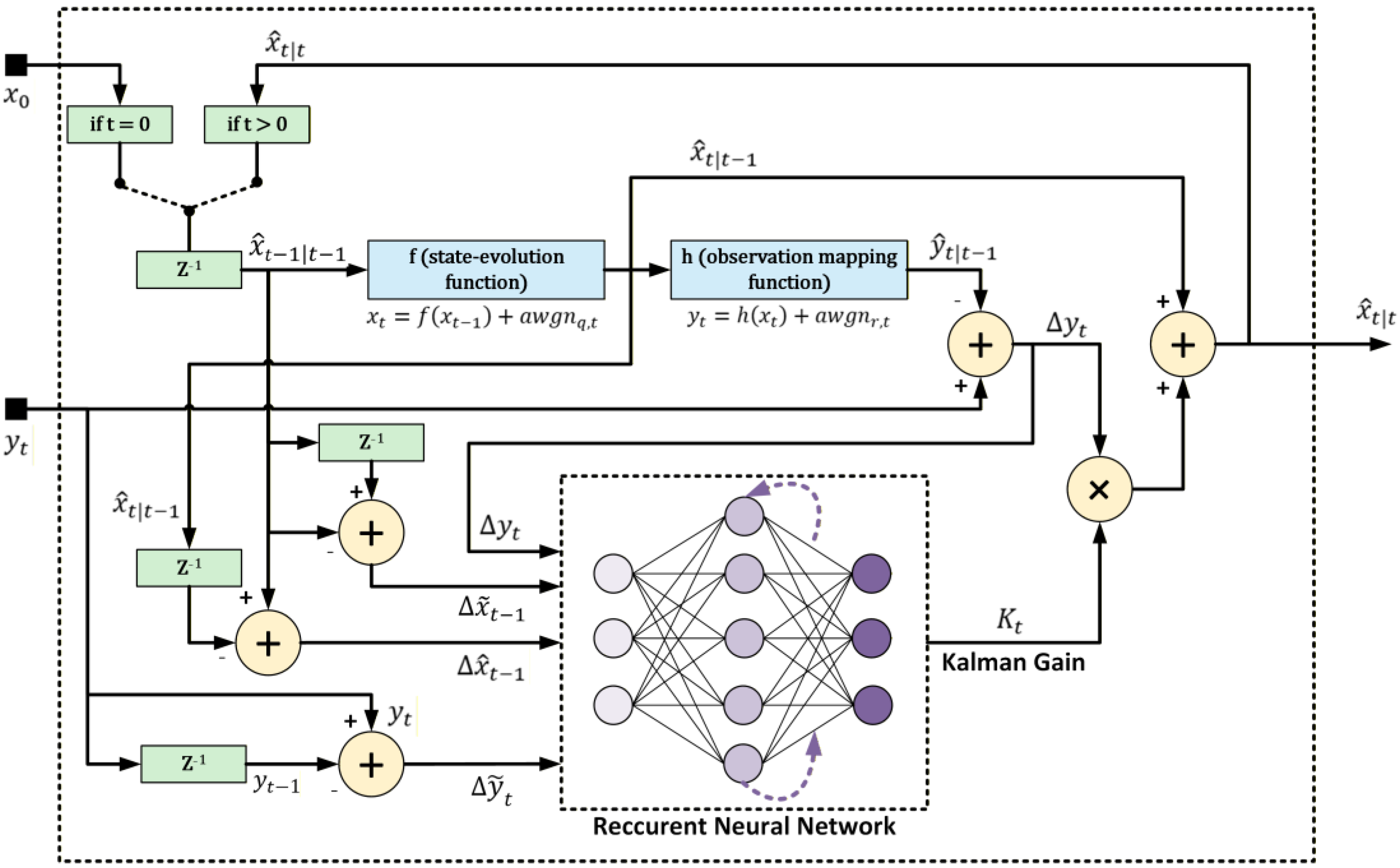
3. Machine Learning Assisted Kalman Filter

As introduced above and detailed in [12], the Kalman gain $K_t$ is for now based on the predicted covariance ${\widehat{P}}_t$ and the observation noise $R$ and thus requires full knowledge of the underlying model, which also admits an efficient linear and recursive structure. In such a context, it appears clear that any mismatch with respect to the model can degrade the overall performance of the Kalman filter, as it can lead to a wrong Kalman gain computation. Yet, in experimental and operational conditions, such mismatches are easily encountered:

• Any anomalies in given clock behavior (frequency and/or phase drift, data gaps) can affect the next state prediction and thus $K_t$ computation.
• Atomic clocks embedded in GNSS (ground segment and space vehicles clocks) can be seen as non-linear, non-Gaussian, and non-stationary system, with which model-based methods cannot fully comply ([3,4,5]).

If any clock with anomalies can be easily taken out of the system by pre-processing the block in charge of detecting and isolating such anomalies, the clock’s behavior can affect the Kalman filter process and therefore the composite clock’s performance.

Based on the work described in [6], the limitations of the model-based approach can be bypassed through usage of a deep learning aided Kalman filter, KalmanNet, where the Kalman gain $K_t$ is computed through a recurrent neural network (RNN) fed by a set of inputs laying on knowledge of the underlying statistics, directly coming from the data stream. In the context of a composite clock, this KalmanNet solution has been adapted to use as inputs the residual observation difference $∆\widetilde{y_t}$, the residual difference $∆y_t$, the forward evolution difference $∆{\tilde{x}}_{t-1}$, and the forward update difference $∆{\widehat{x}}_{t-1}$:

$$∆{\tilde{y}}_t=y_t-y_{t-1}$$

(4a)

$$∆y_t=y_t-{\widehat{y}}_{t|t-1}$$

(4b)

$$∆{\tilde{x}}_{t-1}={\widehat{x}}_{t-1|t-1}-{\widehat{x}}_{t-2|t-2}$$

(4c)

$$∆{\widehat{x}}_{t-1}={\widehat{x}}_{t-1|t-1}-{\widehat{x}}_{t-1|t-2}$$

(4d)

Figure 2 presents the block diagram of this Deep Learning Assisted Composite Clock (DLACC) Kalman filter, introduced in [6] in a more general context. In this new approach, the prediction step is the same as in the model-based Kalman filter, except that only the first-order statistical moments are predicted (upper block, ${\widehat{x}}_{t|t-1}$). After that, a prior estimate for the current observation ${\widehat{y}}_{t|t-1}$ is computed from ${\widehat{x}}_{t|t-1}$. Regarding the update step, the new observation $y_t$ is used to compute the current state posterior ${\widehat{x}}_t$ from the previously computed prior state ${\widehat{x}}_{t|t-1}$, and using the innovation difference $∆y_t$ and the Kalman gain $K_t$. Yet, here, the computation of $K_t$ is not given explicitly and instead learned from data using an RNN, as per [6]. This RNN, thanks to its inherent memory, allows for implicitly tracking the second-order statistical moments (${\widehat{P}}_t$ ahead) without requiring knowledge of the underlying noise statistics.

The advantage of such implementation is that it does not imply huge impact in terms of general implementation of composite clock algorithms, such as the one proposed in [12]. Here, ${\left({\widehat{x}}_t\right)}_i$ represents the predicted state estimate vector of phase, frequency, and frequency drift of a given clock ${CLK}_i$ with respect to the composite clock $CC$:

$${\left({\widehat{x}}_t\right)}_i= \left[\begin{array}{c}{\left({CLK}_i-CC\right)}_{phase}\\ {\left({CLK}_i-CC\right)}_{frequency}\\ {\left({CLK}_i-CC\right)}_{drift}\end{array}\right]$$

(5)

Yet, even if the general paradigm remains unchanged, the main challenge is now to feed the recurrent neural network and find the perfect balance between the number of neurons (linear input and output layers), Gated Recurrent Unit (GRU) interfaces, the number of epochs, and the minimum stream duration to reach a stable Root Mean Square Error (RMSE) between the training dataset and the test one. To perform this, a dataset first needs to be created.

4. Dataset Construction, Recurrent Neural Network Settings and Performance Evaluation

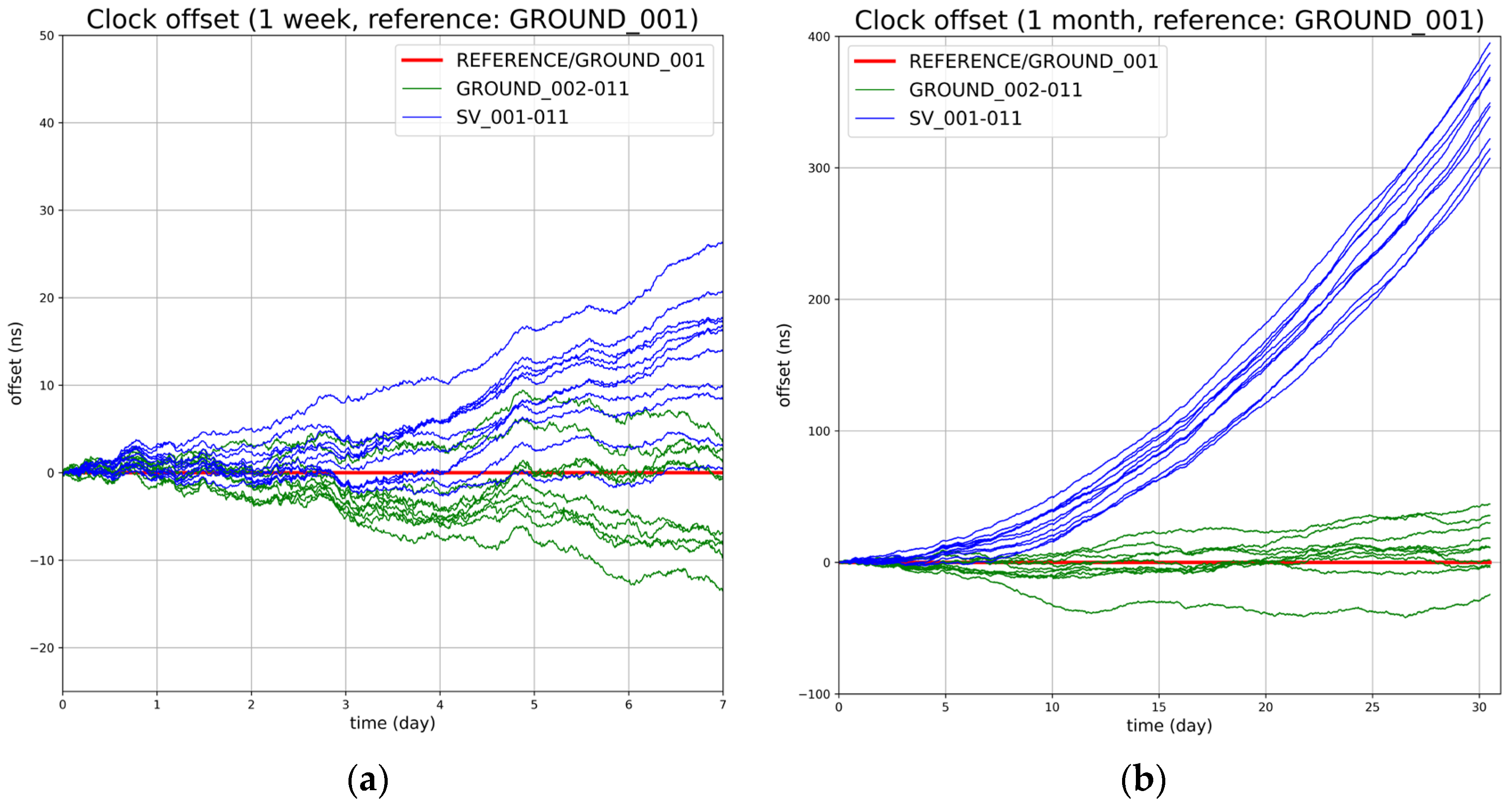
4.1. Dataset Construction

As with any machine learning process, the neural network proposed in the previous section needs to be trained to be correctly parameterized. In the context of DLACC, the main challenge is to retrieve a representative dataset of clock phases. This dataset should emulate the behavior of both ground and space clocks, and, for a very large period, also evaluate nominally the convergence time of the neural network with respect to the time series length, as well as its stability. While the use of real data extracted from actual GNSS systems or laboratories was initially discussed, it was preferred to generate emulated time series using STABLE32 software (version 1.62) [13], as our goal at this stage was to evaluate KalmanNet’s ability to model the process noise for different types of clocks. Besides the possibility of generating long-term time series, these time series cannot suffer from data gaps commonly found in real datasets.

Table 1. Ground and space clocks’ parameters.

Clock Type	Time Series Configuration
Ground	$\tau =600 \mathrm{s}$$, ∆t=100 \mathrm{y}\mathrm{e}\mathrm{a}\mathrm{r}\mathrm{s} (\mathrm{5,259,600} \mathrm{p}\mathrm{o}\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{s})$
	$RWFM=0$ (Random-Walk Frequency Modulation)
	$FFM=8.0\times {10}^{-15}$ (Flicker Frequency Modulation)
	$WFM=4.5\times {10}^{-12}$(White Frequency Modulation)
	$f_{drift}=0 \mathrm{H}\mathrm{z}/\mathrm{s}$ (frequency drift)
Space	$\tau =600 \mathrm{s}$$, ∆t=100 \mathrm{y}\mathrm{e}\mathrm{a}\mathrm{r}\mathrm{s} (\mathrm{5,259,600} \mathrm{p}\mathrm{o}\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{s})$
	$RWFM=0$ (Random-Walk Frequency Modulation)
	$FFM=1.0\times {10}^{-14}$ (Flicker Frequency Modulation)
	$WFM=1.0\times {10}^{-12}$ (White Frequency Modulation)
	$f_{drift}=1.0\times {10}^{-19} \mathrm{H}\mathrm{z}/\mathrm{s}$ (frequency drift)

introduces the parameters that have been used to generate the 11 ground and the 11 space clocks time series, and Figure 3 represents the different clock offset with respect to first ground (a) or space (b) clock time series generated (reference clock in red).

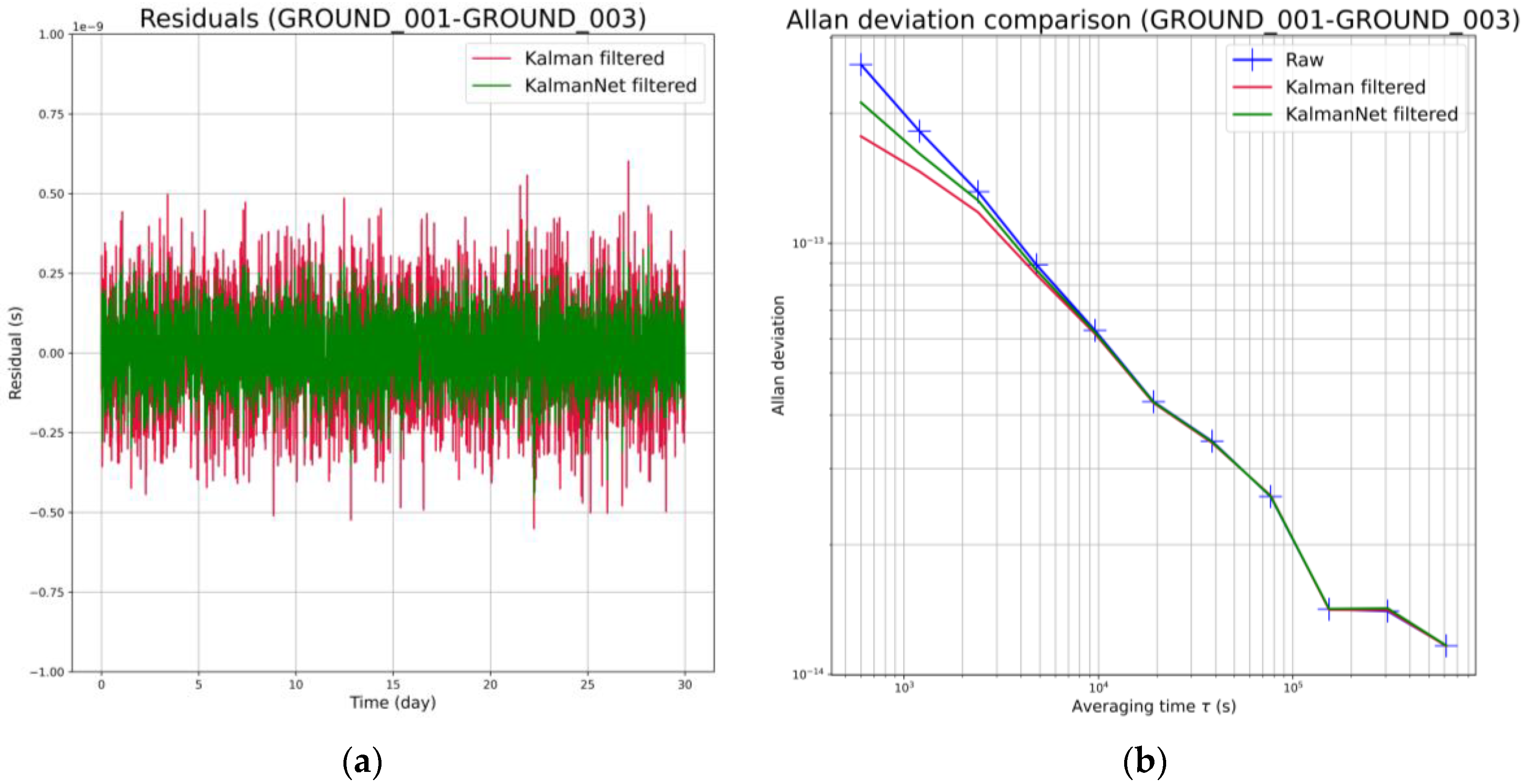
4.2. Recurrent Neural Network Settings and Performance Evaluation

The heart of the KalmanNet filter introduced in [12] and Figure 2 is the recurrent neural network (RNN). This neural network, as with any other one, needs to be parameterized. This setting phase concerns the following:

• $n_{neuron}$: The number of neurons embedded into the RNN. In the context of KalmanNet usage and for convenience, $n_{neuron}$ will represent the number of neurons embedded in each different layer of the RNN (all layers share the same number of neurons).
• $n_{epoch}$: The number of times the entire dataset is passed through the RNN.
• $n_{sample}$: The number of samples injected to train the neural network.
• $l_{batch}$: Batch size, representing the number of samples that will be propagated through the network at the same time.

In addition, the overall architecture of the RNN has been considered as a parameter, too, to test both architectures that are introduced in [12]:

• 1-GRU: Architecture that considers one Gated Recurrent Unit (GRU) between the linear input and linear output layers. This architecture can be considered fully connected, giving more independence to the RNN to formulate the Kalman gain $K_t$.
• 3-GRU: Architecture that considers 3 GRU, with each one dedicated to the prediction of the process covariance $Q$, the state estimate covariance $P$, and the residuals covariance $S$. This architecture more significantly constrains the RNN, reducing the overall abstraction and number of trainable parameters, leading generally to better performance in terms of computation time. At $t=0$, it has been chosen to initialize this parameter as in a traditional Kalman filter, which are then adjusted at each RNN round of computation.

To evaluate the overall performance of the KalmanNet with respect to the traditional Kalman filter, 6600 rounds of simulations have been performed, considering different values for parameters described above and different clock ensembles.

Table 2. Performance evaluation of KalmanNet filter to reproduce clock offset in GNSS context (worst value for 100 runs).

Clock Ensemble	Config.	Arch.	${\mathit{n}}_{\mathit{n}\mathit{e}\mathit{u}\mathit{r}\mathit{o}\mathit{n}}$	${\mathit{n}}_{\mathit{e}\mathit{p}\mathit{o}\mathit{c}\mathit{h}}$	${\mathit{n}}_{\mathit{s}\mathit{a}\mathit{m}\mathit{p}\mathit{l}\mathit{e}}$	${\mathit{l}}_{\mathit{b}\mathit{a}\mathit{t}\mathit{c}\mathit{h}}$	${\mathit{t}\mathit{i}\mathit{m}\mathit{e}}_{\mathit{c}}$ (s)	${\mathit{R}\mathit{M}\mathit{S}}_{\mathit{r}\mathit{e}\mathit{s},\mathit{K}\mathit{N}\mathit{e}\mathit{t}}$	${\mathit{R}\mathit{M}\mathit{S}}_{\mathit{r}\mathit{e}\mathit{s},\mathit{E}\mathit{K}\mathit{F}}$
GROUND_001 - GROUND_003	1	1-GRU	40	25	1000	100	323	1.72489 × 10−10	1.60188 × 10−10
	2	1-GRU	40	25	4000	1000	931	1.56059 × 10−10	1.60188 × 10−10
	3	1-GRU	40	50	1000	100	524	1.39614 × 10−10	1.60188 × 10−10
	4	1-GRU	40	50	4000	1000	1738	1.24873 × 10−10	1.60188 × 10−10
	5	3-GRU	40	25	1000	100	253	1.39167 × 10−10	1.60188 × 10−10
	6	3-GRU	40	25	4000	1000	853	1.31466 × 10−10	1.60188 × 10−10
	7	3-GRU	40	50	1000	100	413	1.01084 × 10−10	1.60188 × 10−10
	8	3-GRU	40	50	4000	1000	1473	1.00498 × 10−10	1.60188 × 10−10
GROUND_001 - SV_007	1	1-GRU	40	25	1000	100	316	1.70944 × 10−10	1.20055 × 10−10
	2	1-GRU	40	25	4000	1000	953	1.44622 × 10−10	1.20055 × 10−10
	3	1-GRU	40	50	1000	100	523	1.33926 × 10−10	1.20055 × 10−10
	4	1-GRU	40	50	4000	1000	1697	1.18975 × 10−10	1.20055 × 10−10
	5	3-GRU	40	25	1000	100	259	1.38892 × 10−10	1.20055 × 10−10
	6	3-GRU	40	25	4000	1000	838	1.31793 × 10−10	1.20055 × 10−10
	7	3-GRU	40	50	1000	100	427	1.02095 × 10−10	1.20055 × 10−10
	8	3-GRU	40	50	4000	1000	1438	1.01168 × 10−10	1.20055 × 10−10

introduces the summary of these results for two clock ensembles and different configurations. In green is represented the configuration that seems to bring the best residuals of RMS value (${RMS}_{res,KNet}$) with respect to computation time (${time}_c$, equal to the time needed to retrieve the Kalman gain value $K_t$, that is to say, when $n_{epoch}$ is reached). The simulations have been performed using Python 3.10.11 on a Windows 11 24H2 desktop computer equipped with an i9-12900K 3.20 GHz CPU and an Nvidia GeForce RTX 4090 GPU. Regarding $n_{sample}$ and $l_{batch}$, their duration is expressed in number of points, where the time between two points represent 600 s. Please also note that if 4 different $n_{neuron}$ values have been used for the simulations, Table 2 only shows results considering 40 neurons, as it represents the perfect trade-off between computation time and performance.

As per Table 2, the configuration that seems to bring to best performance is configuration #7. Figure 4 presents results obtained with this configuration with clock ensemble GROUND_001 and GROUND_003. In comparison with the traditional Kalman filter, it seems that performances are better when using KalmanNet.

5. Outlook and Conclusions

It appears that the usage of a neural network enhanced Kalman filter provides very promising results to estimate a clock’s state. KalmanNet can provide real-time state estimation using continuous learning that seems to overcome model mismatches and non-linearities that can be encountered using a Kalman filter. Following these encouraging results, the application of a KalmanNet filter for a composite clock is quite direct; as described in Section 3, it consists of changing the Kalman filter generally deployed today with this new approach. In the GNSS context, this approach can consist of embedding this KalmanNet filter into the composite clock, as in [1] or [12]. Based on this, the Deep Learning Assisted Composite Clock (DLACC) can finally emerge and will be the heart of the next studies that will be performed with this new approach.

In this study, the measurement noise and KalmanNet integration into a composite clock have not been considered. In such a context, additional work is planned to evaluate performance in a more realistic context with respect to measurements, which bring more uncertainties into state estimation. In addition, the clock datasets used here represent ideal behaviors without considering any clock anomalies (such as data gaps or unusual and sudden drifts) and need to be injected into KalmanNet to test their robustness in this context. In parallel, the computation performance of such a filter needs to be better optimized. Indeed, if computation performance introduced in Table 2 using configuration #7 is satisfactory considering that new measurements are performed every 10 min ($\tau =600 \mathrm{s}$), clear optimization can be made at this moment with the current KalmanNet implementation by better parallelizing computation performed inside of the RNN. Finally, the insertion of KalmanNet inside of a real composite clock algorithm (including anomaly detection) will become the priority in the coming months, including tests with experimental clock data.