Mine Water Inrush Propagation Modeling and Evacuation Route Optimization ^†

Abstract

We modeled water inrush propagation in mines and the optimization of evacuation routes. By constructing a water flow model, the propagation process of water flow through the tunnel network is simulated to explore branching, superposition, and water level changes. The model was constructed based on breadth-first search (BFS) and a time-stepping algorithm. Furthermore, by integrating Dijkstra’s algorithm with a spatio-temporal expanded graph, miners’ evacuation routes were planned, optimizing travel time and water level risk. In scenarios with multiple water inrush points, we developed a multi-source asynchronous model that enhances route safety and real-time performance, enabling efficient emergency response during mine water disasters. For Problem 1 defined in this study, a graph structure and BFS algorithm were used to calculate the filling time of tunnels at a single water inrush point. For Problem 2, we combined the water propagation model with dynamic evacuation route planning, realizing dynamic escape via a spatio-temporal state network and Dijkstra’s algorithm. For Problem 3, we constructed a multi-source asynchronous water inrush dynamic network model to determine the superposition and propagation of water flows from multiple inrush points. For Problem 4, we established a multi-objective evacuation route optimization model, utilizing a time-expanded graph and a dynamic Dijkstra’s algorithm to integrate travel time and water level risk for personalized evacuation decision-making.

1. Introduction

Due to the complex hydrogeological conditions in mines, water disaster accidents cannot be completely avoided. In water disasters, the propagation process of the water inrush flow can be simulated to formulate scientific rescue plans and escape routes, reducing the danger to personnel at risk and minimize economic losses. Mine tunnel systems comprise complex three-dimensional network structures with intersections, which makes the water propagation process and escape route planning complex and difficult. Therefore, establishing an accurate water inrush propagation model and accordingly designing optimal escape routes for miners is significant for ensuring miners’ lives and safety and reducing losses from mine water disasters. To establish the model, the following problems must be identified and solved.

The first problem (Problem 1) is water inrush propagation. A mathematical model needs to be established to capture the flow and propagation of water inrush within the tunnel network. This model must account for tunnel geometry (e.g., rectangular cross-sections), initial water conditions (e.g., water level and inrush volume), and flow division at branch nodes. The model is used to predict the spatial path and temporal dynamics of water movement, including the arrival time of water at each node and the time required for complete flooding of individual tunnels.

The second problem (Problem 2) is dynamic escape route planning. Based on the water propagation model, Problem 2 involves designing optimal escape routes for miners. Travel speed must be adjusted according to water depth as follows: 4 m/s in dry tunnels, 1 m/s against the current and 2 m/s with the current when water depth is less than 0.3 m, with passage prohibited when depth exceeds 0.3 m. Assuming an evacuation alert is issued one minute after the onset of water inrush, the model should compute individualized escape paths and times from each miner’s initial position to the designated exit.

The third problem (Problem 3) is multiple water inrush point modeling. When two water inrush points occur simultaneously, the propagation process becomes substantially complex. In such scenarios, it is necessary to re-examine the hydrodynamic interactions and construct an extended mathematical model that considers the independent and combined effects of multiple inrush sources.

The fourth problem (Problem 4) is the escape route adjustment under multiple inrush conditions. Following the occurrence of a second water inrush point, the safety management department must rapidly revise evacuation plans in response to the altered flow dynamics. Based upon the model for Problem 3, and assuming that an updated evacuation directive is issued one minute after the second inrush begins, the system recalculates optimal escape routes for all miners within the tunnel network.

In this study, we constructed models to solve Problems 1–4 and discussed the results in this study.

2. Problem Analysis

2.1. Problem 1

Problem 1 concerns simulating the dynamic process of water flow originating from the inrush point and propagating through the tunnel network over time. To achieve this, a graph-structured model [1] and a three-dimensional coordinate representation of the tunnels must be constructed. Once the tunnel network is represented as a graph, the mathematical relationships among water propagation velocity, inrush volume, and tunnel cross-sectional area are elucidated based on the principles of mass conservation and the fluid continuity equation. The propagation pattern of water flow within the tunnels must then be analyzed. At tunnel branch points, the flow is assumed to split equally into horizontal and descending tunnels, while maintaining the initial water level. Considering the topological complexity of the tunnel system, particularly the treatment of branch nodes, the model tracks the water flow path and updates the water level and flow rate at each node according to the splitting rule. Finally, breadth-first search is employed to simulate the propagation process, calculate the arrival time of water at each endpoint, and estimate tunnel filling time (defined as the water level rising to 3 m) based on flow rate and tunnel volume.

2.2. Problem 2

Based on the water inrush propagation model established in Problem 1 [2], the second problem involves determining the time at which water arrives at and fills each tunnel, and designing escape routes accordingly. Given the miner’s initial location, travel speed under varying water conditions, and the delay in issuing an escape notification, the escape path must be determined by (1) prioritizing tunnels without water inrush or those where water arrives later, avoiding tunnels already filled or imminently filled, (2) accounting for the miner’s travel speed relative to water arrival time, ensuring safe exit before inundation; and (3) selecting the shortest possible escape route under these constraints. The tunnel network is represented as a directed graph, and escape paths are planned using graph-theoretic methods. Dynamic programming and greedy algorithms are applied to iteratively select the nearest safe access point from the miner’s current position.

2.3. Problem 3

Problem 3 addresses complex dynamics that arise when multiple water inrush points occur simultaneously. In this case, water arrival times, filling times, and escape route planning require re-modeling and analysis. A multi-source asynchronous dynamic network model is established by abstracting the tunnel system into a directed graph, where nodes represent water inrush points, branch nodes, and access points, and edges represent tunnel segments. Each edge is assigned attributes such as length, cross-sectional area, and flow rate. A time-stepping method is adopted, incorporating data initialization and dynamic updates of water flow. At each time step, the state of the tunnels is updated, and tunnel segments are checked to determine whether water volume has reached the capacity calculated as follows.

Capacity = Length × Cross-sectional area

(1)

Segments that reach capacity are marked as “filled,” and the corresponding time is recorded. For multiple inrush points, water propagation is processed separately at each time step, with real-time detection of convergence events. Boundary conditions must also be considered, such as treating water as discharged when it reaches an access point, and marking filled tunnel segments blocked to prevent redundant processing.

2.4. Problem 4

Problem 4 involves dynamically adjusting miners’ escape routes in scenarios where two water inrush points occur sequentially. The delayed initiation of the second inrush point alters the original propagation pattern, potentially obstructing or delaying previously safe passages. Based on the dual-source water flow model developed in Problem 3, water levels in each tunnel must be updated in real time, and route passability re-evaluated. By integrating miner locations and access point information, a dynamic graph model with time as the weight is constructed [3]. Optimal escape routes are determined using shortest-path algorithms. Particular attention is given to high-water-level no-go zones and the influence of water flow velocity on travel speed, ensuring that escape routes remain viable within the required evacuation timeframe. This approach enables safe and efficient evacuation under complex multi-inrush conditions.

3. Model Construction

3.1. Assumption

It is assumed that the initial water level at the water inrush point is 0.1 m and remains constant during the splitting process (no energy loss). When water flow reaches a branch node, it splits equally into horizontal tunnels and descending tunnels. Slope, resistance, or flow rate differences are not considered in the model. It is also assumed that the escape command is issued 1 min after the initial water inrush (Problem 2) or 1 min after the second water inrush point (Problem 4). All workers receive the command simultaneously and act immediately. Workers always choose the path with the shortest escape time. Congestion or individual differences are not considered.

If two water flows reach the same tunnel, the water level change is calculated based on their independent progression. The highest water level is taken as the state of that tunnel without considering dynamic interactions.

Symbols used in the model are described in

Table 1. Symbol Description.

Number	Symbol	Description
1	t1	Endpoint arrival time
2	h0	Initial water level
3	Q	Flow rate entering the tunnel
4	t2	Time when the tunnel is completely filled
5	$t_{arrive}$	Time when water reaches the endpoint
6	$t_{full}$	Time when the tunnel is filled
7	S0	Initial cross-sectional area of the branch
8	$Q_{\mathit{initial} \mathit{inflow}}$	Initial inflow rate into the tunnel
9	$Q_{in}$	Inflow rate
10	$Q_{out}$	Flow rate in each branch
11	$Q_{total}$	Flow rate at the water inrush point
12	$Q_i$	If a node has k feasible flow tunnels, the flow rate allocated to each tunnel
13	$v_{water}$	Water volume
14	$v_{tunnel}$	Tunnel capacity

.

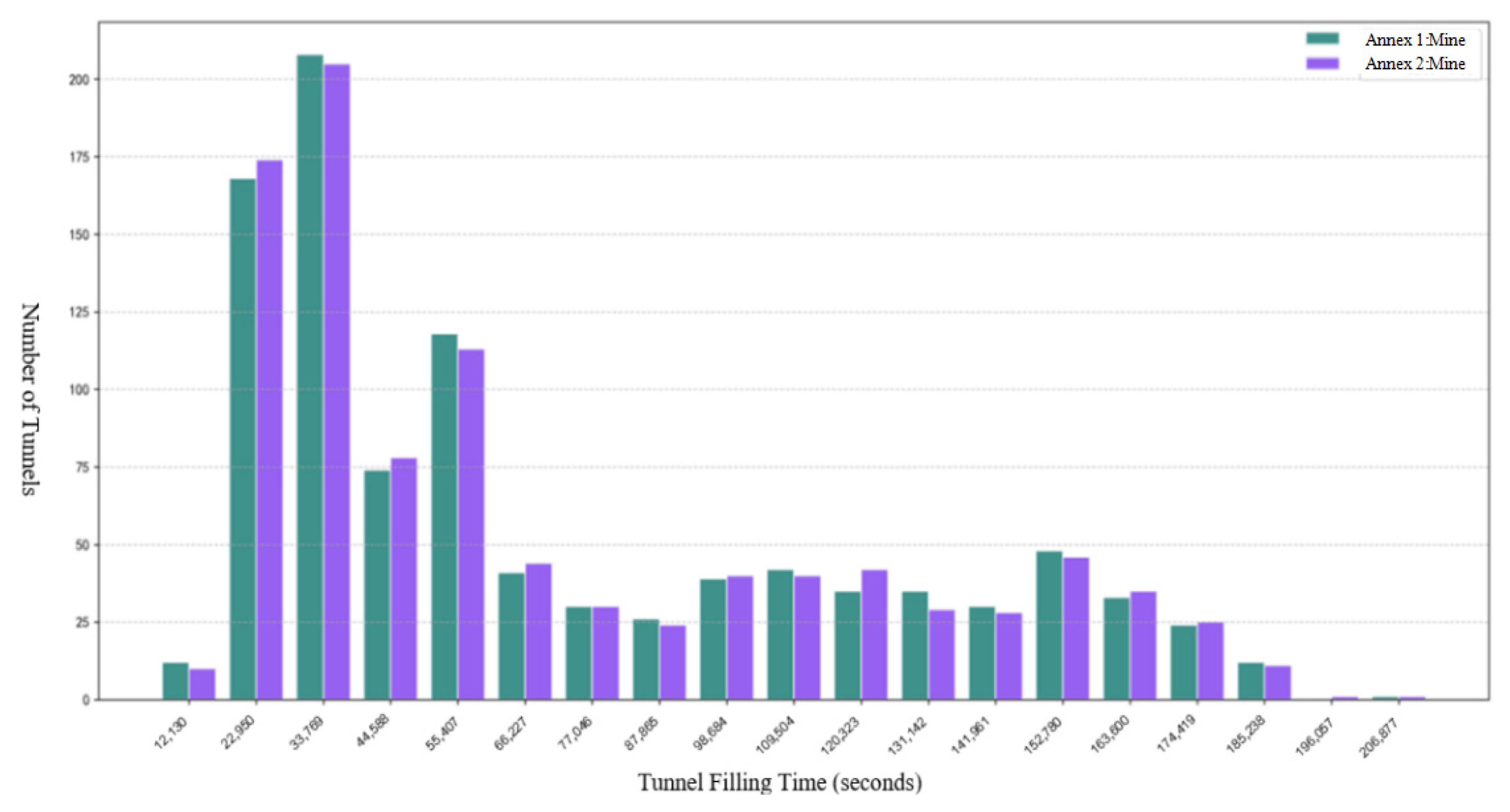
3.2. Water Inrush Flow Propagation Model in Tunnel

Based on endpoint coordinates and tunnel connection relationships, a graph structure model is constructed, treating tunnels as edges and endpoints as nodes and calculating the length of each tunnel. To accurately describe the spatial layout of the tunnels, each node is assigned three-dimensional coordinate information on the x, y, and z axes to determine its specific position in space (Figure 1).

A tunnel is represented by the line connecting its two endpoints P1($x_1, y_1{, z}_1$) and P2($x_2,y_2{, z}_2$), and its length L is the Euclidean distance between the two points in Equation (2).

$$L=\sqrt{(x_2-x_1{)}^2+(y_2-y_1{)}^2+(z_2-z_1{)}^2}$$

(2)

The propagation process within a single tunnel consists of the initial water level advancement stage (where water advances from the water inrush end towards the far end) and the complete filling stage (if the water height reaches the tunnel top during advancement, it enters the filling stage). The time is calculated in the following two scenarios.

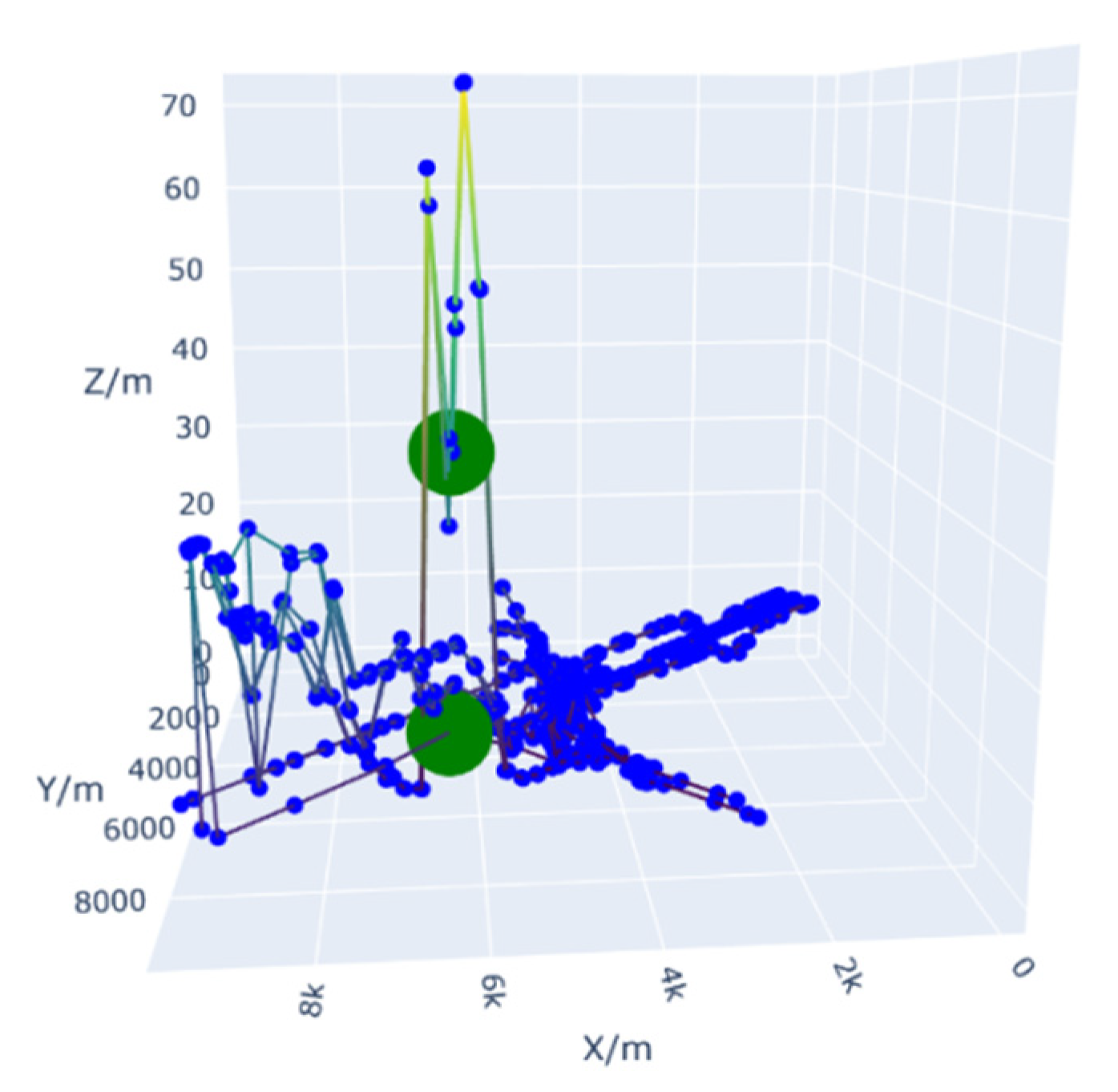
• Scenario 1

The water flow reaches the endpoint before the tunnel is full ($t_{arrive}<t_{full}$). At endpoint arrival time t₁, the water advances with the initial water level h₀. The volume to be filled is calculated as initial cross-sectional area × tunnel length. When the flow rate is Q (the flow rate entering this tunnel), the following equation is applied.

$$t_{arrive}={\displaystyle \frac{S_0\times L}{Q_{in}}}={\displaystyle \frac{0.4L}{Q_{in}}}$$

(3)

At tunnel filling time t₂, the water needs to fill the entire tunnel volume. Therefore, the following must be satisfied.

$$t_{full}={\displaystyle \frac{S_{full}\times L}{Q_{in}}}={\displaystyle \frac{12L}{Q_{in}}}$$

(4)

When $t_{arrive}<t_{full}$, the water flow reaches the endpoint first and then continues to fill the tunnel to the top.

• Scenario 2

The water flow does not reach the endpoint when the tunnel is filled ($t_{full}\le t_{arrive}$). When the tunnel is extremely short (e.g., L < 30/Q), it is filled before the water flow advances to the endpoint. In this case, $t_{full}={\displaystyle \frac{12L}{Q_{in}}}$, ${ t}_{arrive}$ becomes meaningless since the tun1hence $t_{full}=t_{arrive}$.

In both scenarios, the final timing for a single tunnel is defined as follows.

$$t_{arrive}=\mathit{min}({\displaystyle \frac{0.4L}{Q_{in}}},{\displaystyle \frac{12L}{Q_{in}}})={\displaystyle \frac{0.4L}{Q_{in}}}, t_{full1}=12L_1/Q_{in}$$

(5)

The inflow rate $Q_{in}=30 {\mathrm{m}}^3/\min$. This leads to the following calculations.

Endpoint arrival time $t_{arrive1}=0.4L_1/30$, while tunnel filling time $t_{full1}=12L_1/30$.

For Tunnel 1, the arrival time at the starting point (A1) = 0, the arrival time at the endpoint (P3) = $t_{arrive}$, and the filling time = $t_{full}$.

When the water flow reaches a branch node, it splits equally into the horizontal tunnel and the descending tunnel, with the initial water level remaining unchanged. The following three aspects must be considered.

• Water flow distribution: Let the inflow rate at the node be Q. If the node is connected to n branches (horizontal + descending), then the outflow rate for each branch Q_out = Q_in/n
• Constant initial water level: After splitting, the initial water level in each branch remains 0.1 m. Therefore, the initial cross-sectional area of the branch (S₀ = 0.4 m²) remains unchanged, and the propagation time calculation still follows the single tunnel model.
• Time connection: The propagation time for the branch is counted from the time the water flow reaches the node. That is, the branch’s endpoint arrival time = node arrival time + the branch’s own $t_{arrive}$, and the branch’s tunnel filling time = node arrival time + the branch’s own $t_{full}$. The flow diffusion process in different time units is simulated by using A1, as shown in Figure 2.

The entire mine tunnel network is treated as a graph structure composed of nodes and edges. Nodes are tunnel endpoints/branch points, and edges are single tunnels. Breadth-first search (BFS) is used to traverse the network to achieve global propagation time calculation. Based on the water inrush point locations (A1 and A2), the initial tunnels where the inrush occurs are identified. The inflow rate for the initial tunnel $Q_{initial \mathit{inf}low}=30 {\mathrm{m}}^3/\mathrm{m}\mathrm{i}\mathrm{n}$, and the water inrush starting time t = 0. Then, $t_{arrive}$ and $t_{full}$ are calculated for the initial tunnel.

The far-end node of the initial tunnel is added to the node queue pending processing, and the arrival time at this node ($t_{arrive}$ of the initial tunnel) is recorded. A node is taken from the queue, and it is determined whether this node is a branch point (connected to ≥2 unprocessed tunnels). If it is a branch point, the flow is distributed to each branch according to the principle of equal splitting ($Q_{out}=Q_{in}/n$, n is the number of branches). For each branch, $t_{arrive}$ (node arrival time + the branch’s own $t_{arrive}$) and $t_{full}$ (node arrival time + the branch’s own $t_{full}$) are calculated, and the far-end node of the branch is added to the queue. When all nodes in the queue are processed, the calculation is terminated, indicating that the propagation time calculation for all tunnels is complete. A node from the queue is selected in first-in, first-out order (e.g., process P3 first). When a node type is determined as a non-branching node (connected to only 1 tunnel), the propagation time for this tunnel is calculated, and its far-end node is added to the queue.

When the branch node is connected to more than two unprocessed tunnels, e.g., horizontal + descending tunnels, flow distribution is determined as follows. According to the principle of equal splitting, the flow rate for each branch $Q_{out}=Q_{in}/n$ (where n is the number of branches, e.g., when n = 2, $Q_{out}$= 15 m³/min).

In branch propagation, the following is calculated for each branch tunnel: the branch length L₂ (e.g., the Euclidean distance for P3 and P4), the branch’s $t_{arrive2}$= node arrival time (e.g., $t_{arrive1}$) + (0.4 × L₂) /$Q_{out}$, and the branch’s $t_{full2}$= node arrival time + (12 × L₂)/$Q_{out}$. Enqueue child nodes are identified by adding the far-end node of the branch to the queue and recording its arrival time. When the BFS queue is empty, the propagation time calculation for all tunnel segments is complete.

4. Escape Route Planning

4.1. Mine Water Inrush Propagation Model

Problem 2 involves designing the optimal escape route for miners based on the water propagation model from Problem 1 for safety. The model is constructed based on mass conservation and flow splitting rules, employing a time-stepping algorithm for dynamic simulation. The tunnel system is abstracted as a graph structure G = (N,E), where N is the set of nodes (tunnel intersections) and E is the set of edges (tunnel segments). Each tunnel $e\in E$ has a length L, a rectangular cross-sectional area A = 4 × 3 = 12 m², and its elevation difference is calculated from the endpoint coordinates.

The physical quantities for water propagation are flow distribution and water level rise. The flow rate at the water inrush point is set to $Q_{total}$ = 30 m³/min = 0.5 m³/s. When the water front reaches a node, all its downstream tunnels (i.e., tunnels with elevation not higher than that node) are identified. If a node has k feasible flow tunnels, the flow rate allocated to each tunnel $Q_i$= $Q_{in}$/k, where $Q_{in}$ is the total flow rate entering the node.

For a tunnel segment e that is being filled, its water level height h(e,t) increases linearly over time. Starting from the time $t_0$ when the water arrives, its water level change is calculated using the following equations.

$$h(e,t)=\mathit{min}(3,h_0+{\displaystyle \frac{Q_i}{A}}(t-t_0))$$

(6)

where h₀ = 0.1 m is the initial water level. The time t filled for the tunnel to be completely filled with water is obtained by solving h(e,t) = 3 as follows.

$$t_{full}=t_0+{\displaystyle \frac{(3-0.1)\times A}{Q_i}}$$

(7)

The propagation velocity $v_{flow}$ of the water flow within this tunnel is determined by using the flow rate and the cross-sectional area.

$$v_{flow}={\displaystyle \frac{Q_i}{A}}={\displaystyle \frac{Q_i}{12}}$$

(8)

Therefore, the time required for the water flow to fill a tunnel segment of length L_e is defined as follows: $\Delta {\mathrm{t}}_{full}=L_e/v_{flow}$. The propagation velocity refers to the movement speed of the water front, not the rate of water level rise.

4.2. Dynamic Escape Route Planning Model

This model is designed to address the challenge of determining optimal escape routes for miners operating within hazardous environments. By incorporating the temporal dimension, a spatio-temporal state network is established, thereby transforming the dynamic route-planning problem into an extended static shortest-path problem within a network framework [4]. In this equation, each state is defined by spatial location and time, represented as a spatio-temporal state node ($n$,$t$), which denotes that a worker is positioned at node n at time t.

Transitions between states are modeled using spatio-temporal edges to capture the possible movements of workers in spatial and temporal dimensions. Spatio-temporal edges are divided into two types: movement edges and waiting edges. A movement edge connects state ($n_i$, t) to ($n_j$,t+Δt), indicating that the worker enters tunnel e = ($n_i$,$n_j$) at time t through the node $n_i$ and arrives at $n_j$ after a duration Δt. Its weight is the traversal time Δt, $n_j$ is not fixed but depends on the water flow condition in the tunnel at the departure time [5].

$$\mathit{\Delta }t={\displaystyle \frac{L_e}{v\left(t\right)}}$$

(9)

Here, v(t) is the speed determined jointly by the real-time water level data h(e,t) provided by the first model and the relative direction between the worker’s movement and the water flow. When h(e,t)= 0, v(t) = 4; When 0 < h(e,t) ≤ 0.3 and moving with the current, v(t) = 2; When 0 < h(e,t) ≤ 0.3 and moving against the current, v(t) = 1; When h(e,t) > 0.3, v(t) = $\infty$ (indicating impassable).

A waiting edge connects state (n,t) to (n,t+$\mathit{\Delta }{t}_{\mathit{wait}}$), allowing the worker to remain at the node. However, in this problem, since the water level rises monotonically, waiting usually worsens the subsequent passage conditions. Therefore, the weight $\Delta {\mathrm{t}}_{\mathrm{wait}}$ of waiting edges is typically set to a large value [6].

The water flow condition is one of the key factors affecting the escape route. In the model, the real-time water level data h(e,t) is used to reflect the water flow condition within the tunnel. The worker’s movement speed v(t) is a piecewise function that depends on the tunnel’s water flow condition and the relative direction between the worker’s movement and the water flow [7].

It is required to consider the flow distribution and water level rise in the water flow to accurately simulate its propagation process within the tunnels [8]. When the water flow reaches a node, it is distributed to the downstream tunnels according to the splitting rules. The water level in each tunnel rises over time, and its rate of increase depends on the flow rate entering that tunnel and the tunnel’s cross-sectional area. The time for a tunnel to be completely filled with water can be obtained by solving an equation, while the propagation speed of the water flow within the tunnel is jointly determined by the flow rate and the cross-sectional area. When solving for the shortest path, we adopt the Dijkstra’s algorithm. During the solution process, we consider the weights of both movement edges and waiting edges to ensure that the found path is not only the shortest but also safe, as shown in Figure 3.

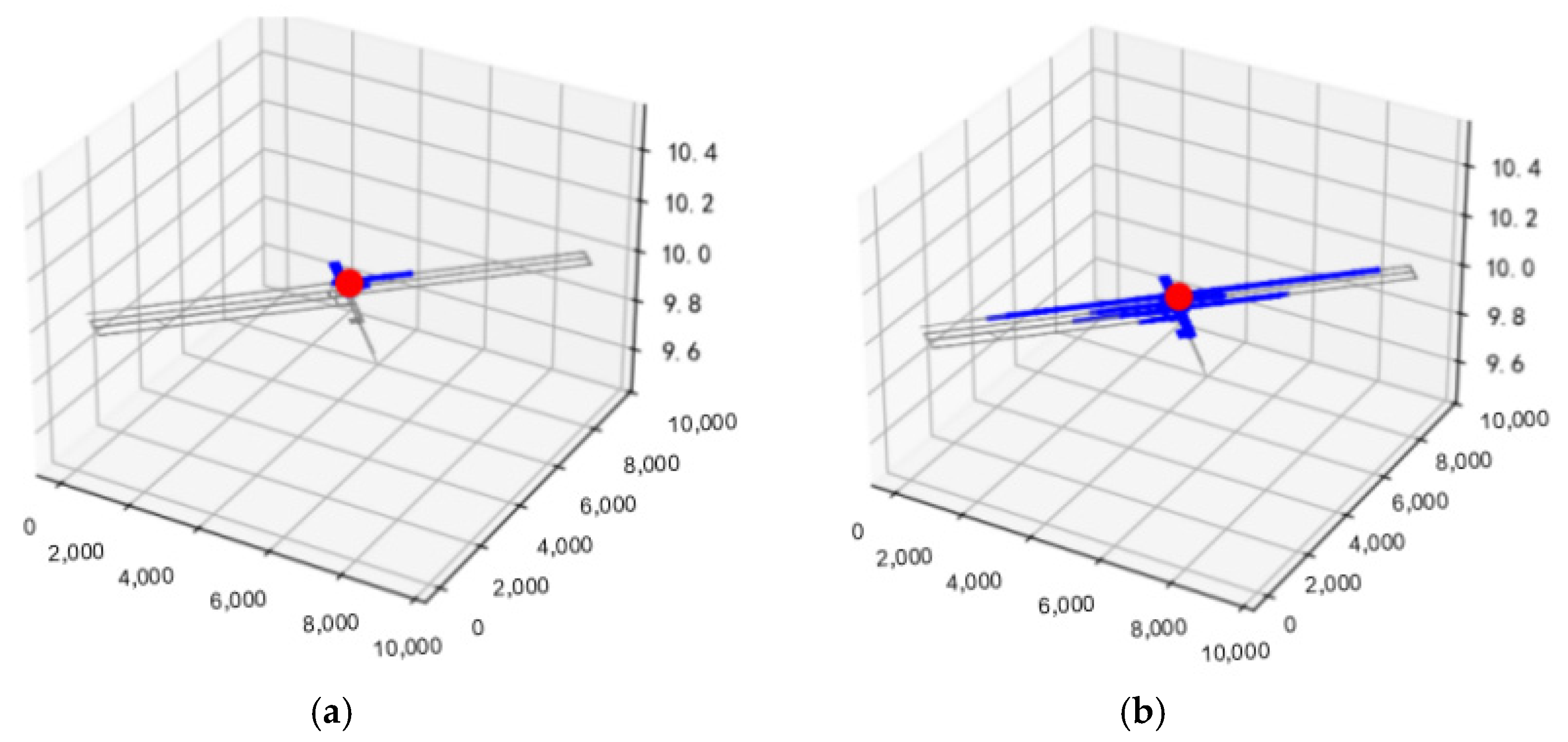
4.3. Water Propagation Model for Multiple Water Inrush Points

For the scenario where two water inrush points occur in the mine, it is necessary to establish a water propagation model capable of handling dynamic superposition from multiple water sources. The second water inrush point starts some time after the first one, requiring consideration of the timing of the water flow processes and their superposition.

4.3.1. Coupling of Three-Dimensional Network Flow and Fluid Dynamics

In a single water inrush point scenario, it is assumed that one inrush point discharges water at a flow rate of 0.5 m³/s. The flow velocity depends on the tunnel’s shape (e.g., for a rectangular cross-section of 12 m², the velocity is the flow rate divided by the area). In a multiple water inrush point scenario, if the water flows from two inrush points meet within a tunnel, their flow rates are summed up. The flow velocity is then recalculated based on this combined total flow rate and the tunnel’s geometry.

The water level h in the tunnel changes over time, with the initial water level $h_0$ = 0.1 m. When the water volume $v_{water}=Q\times t$ reaches the tunnel capacity $v_{\mathrm{tunnel}}=L\times A$, the water level rises to the tunnel height H = 3 m. At this point, the tunnel is completely filled, and water propagation stops. Then, the filling time $t_{full}$ satisfies the following equation.

$$t_{fill,new}={\displaystyle \frac{L\times A}{Q_1+Q_2}}$$

(10)

4.3.2. Dynamic Network Flow Model for Multi-Source Asynchronous Water Inrush

The mine tunnel network is represented as a directed graph G = (V, E), where V is the set of nodes. Each edge e ∈ E is associated with attributes (L, A, Δz, Q, h, $t_{\mathit{arrival}}$, $t_{\mathit{fill}}$), representing length, cross-sectional area, elevation difference, flow rate, water level, endpoint arrival time, and filling time, respectively.

In the initial condition, the first water inrush point activates at time t = 0 with a flow rate of 0.5 m³/s. The second water inrush point activates after a delay (e.g., 4 or 5 min), also with a flow rate of 0.5 m³/s. The initial water level in all tunnel segments is 0, indicating they are not yet covered by water flow. In the boundary conditions, access/egress nodes are considered sink nodes. Once water flow reaches them, it is discharged from the system and does not affect the internal flow distribution within the network. For any tunnel segment e = (u,v) (directed from node u to v), the position of the water front x(t) changes over time as follows.

$$x(t)=\mathit{min}(L,\int {\displaystyle \frac{t}{t_{arrival,u}}}v(t\prime )dt\prime )$$

(11)

Here, $t_{\mathrm{arrival},\mathrm{u}}$ is the time the water flow reaches node u, and the flow velocity v(t) = Q(t)/A. When x(t) = L, the water flow reaches node v and subsequently splits according to the distribution rules.

When two flows, $Q_1$ and $Q_2$, meet either within a tunnel segment e or at a node v, the flow rates merge, and $Q_{total}=Q_1+Q_2$, while the flow velocity $v_{new}=A{Q}_{total}$, and the water level $h_{new}=A{v}_{water}{Q}_{total}$ ($v_{water}$ is the merged water flow velocity). When the flows are merged, and then the combined flow is distributed to adjacent tunnels according to the splitting rules. The initial water level in each adjacent tunnel is $h_0$ = 0.1 m.

The state of each tunnel segment is continuously updated as the time-stepping procedure advances. At the conclusion of each time step, the water volume within each segment is evaluated to determine whether it has reached its maximum capacity. Segments that reach capacity are designated as filled, and the corresponding filling time is recorded. Concurrently, variations in water flow across all segments are stored in a results file, which includes critical information such as endpoint water arrival times and tunnel segment filling times, as illustrated in Figure 4.

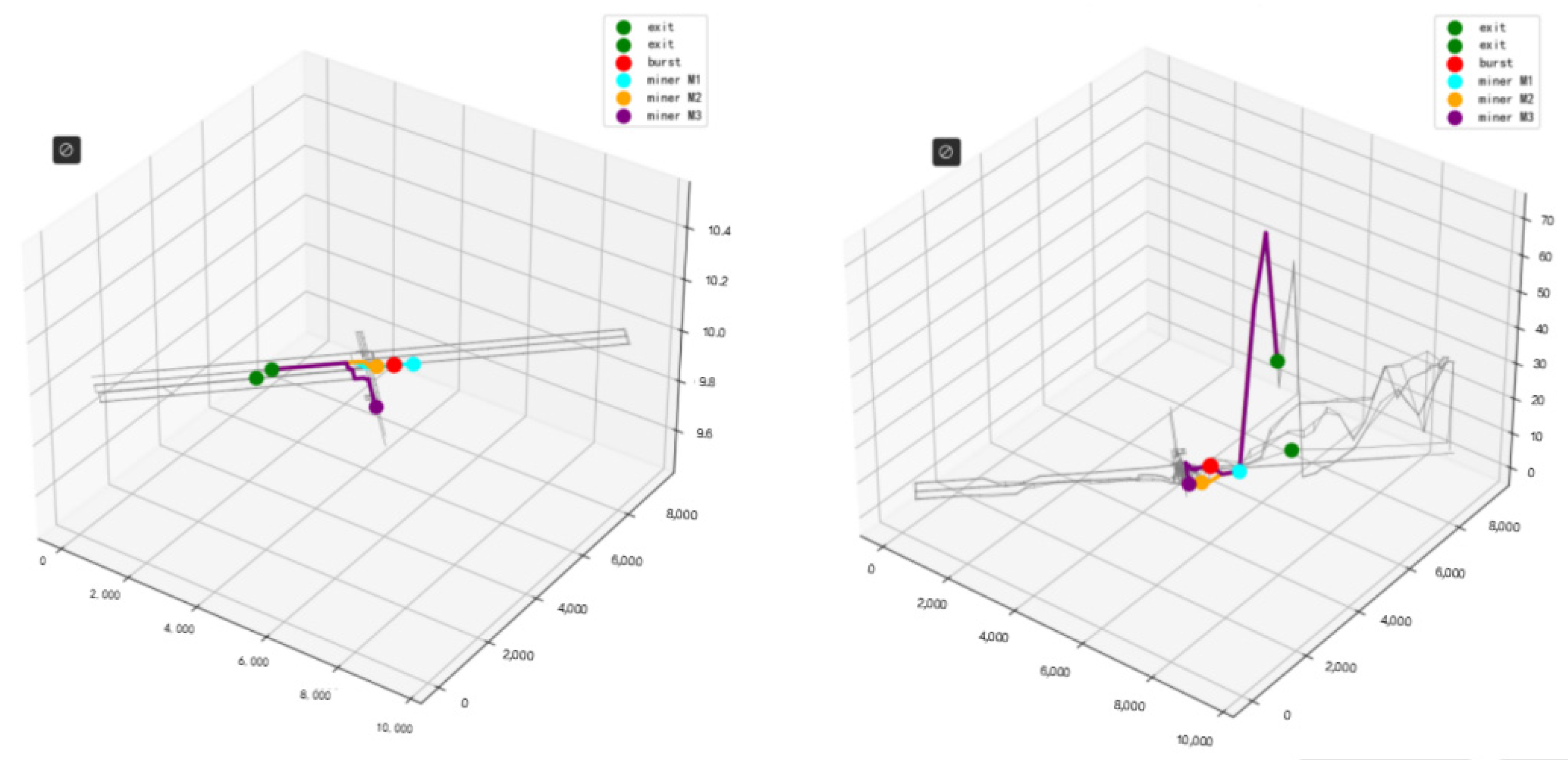
4.4. Adjustment of Escape Routes with Multiple Water Inrush Points

4.4.1. Multi-Objective Evacuation Route Optimization

In the initial stages of a mine water disaster, the safety management strategy is developed for planning escape routes using a static representation of the tunnel network by applying algorithms such as Dijkstra or A* to compute the shortest paths. However, once a second water inrush point is activated, water rapidly propagates through the tunnel system, leading to flooding or rising water levels in certain segments and rendering previously identified shortest paths impassable. To ensure effective evacuation under dual inrush conditions, it is essential to design a dynamic route-planning model capable of responding in real time to evolving water propagation, continuously assessing path safety, and promptly generating optimal escape strategies.

One minute after the activation of the second water inrush point, escape routes must be recalculated for each miner from their current location to a designated safe exit. These routes must satisfy three critical criteria: temporal optimality, minimal risk, and practical passability. Using the water propagation model established in Problem 3, the initial water arrival times and the functions describing water level variation over time for each tunnel segment are obtained. Based on this propagation data, the connectivity of the tunnel network is updated dynamically, with flooded or high-risk segments marked accordingly. Miners’ positions are assumed to be available in real time through a positioning system (e.g., radio frequency identification tags) or inferred from workface distribution. The safety of each exit is then evaluated dynamically, considering its spatial location, distance from water sources, and current water level conditions, with priority assigned to exits associated with lower risk.

4.4.2. Dynamic Dijkstra’s Algorithm Based on Time-Expanded Graph (TEG)

The traditional Dijkstra’s algorithm is appropriate for calculating the shortest path in static networks but cannot handle edge weight changes caused by dynamic water propagation. To address this, the TEG method is employed. This method transforms the dynamic network into a series of static snapshots, where each snapshot represents the state of the network at a specific time. These snapshots are connected by temporal edges, thereby converting the dynamic path planning problem into a shortest path problem on a static graph.

If the initial water arrival time for a tunnel segment is $t_{arrive}$, then its availability at time $t_{current}$ (1 min after the second water inrush point activates) is determined as follows.

• If $t_{current}\ge t_{arrive}$, the tunnel segment is flooded and impassable.
• If $t_{current}<t_{arrive}$, the tunnel segment is passable, but the water level risk when the miner reaches any point in this segment needs to be calculated.

For passable tunnel segments, the weight considers not only the travel time but also incorporates a risk cost due to the rising water level. The risk weight is then calculated using the following equations.

$$w(t)={\displaystyle \frac{L}{v}}+\alpha \cdot {\int }_{t_{start}}^{t_{end}}h(t^{\prime })d{t}^{\prime }$$

(12)

Here, L represents the tunnel length, v is the travel speed, h(t) is the function describing water level change over time, and α is the risk coefficient.

To optimize for both time and risk simultaneously, the weighted sum is used to transform the dual objectives into a single objective.

$$\mathrm{Total} Cost=w_{time}\cdot T+w_{risk}\cdot R$$

(13)

Here, T represents the total travel time, R represents the total risk cost, $w_{time}$ and $w_{risk}$ are weighting coefficients (adjustable based on actual requirements, e.g., being $w_{time}=1$, $w_{risk}=0.1$ when prioritizing time optimality).

5. Conclusions

The water propagation and the escape route optimization models developed in this study demonstrate strong applicability for emergency response in mine water disaster scenarios. The water propagation model effectively simulates the dynamic behavior of water flow under both single-point and multi-point inrush conditions through a time-stepping algorithm, accurately capturing flow-splitting phenomena at branch nodes and superposition effects within tunnel segments. The escape route optimization model introduces an innovative application of the TEG method, which transforms the dynamic path-planning problem into a shortest-path search on a static graph. This approach enables the joint optimization of time efficiency and risk minimization through a weighted sum strategy.

In the following studies, the numerical stability of the calculations needs to be refined, and the weighting coefficients need to be determined for an element of subjectivity. These influence the accuracy and robustness of the model when applied to complex real-world mining environments. It is also necessary to enhance computational stability and develop objective methods for parameter selection to improve the reliability of the proposed framework in practical applications.