Next Article in Journal
Sensitive Electrochemical Detection of the Nitrite Ion Using an ISEM-3 Graphite Electrode and Comparison with Other Carbon-Containing Materials
Previous Article in Journal
Wireless Soil Health Beacons: An Intelligent Sensor-Based System for Real-Time Monitoring in Precision Agriculture
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Engineering Proceedings
Volume 118
Issue 1
10.3390/ECSA-12-26551
engproc-logo
Submit to this Journal
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Proceeding Paper

Impact of Electrical Noise on the Accuracy of Resistive Sensor Measurements Using Sensor-to-Microcontroller Direct Interface †

by
Marco Grossi
* and
Martin Omaña
Department of Electrical Energy and Information Engineering “Guglielmo Marconi” (DEI), University of Bologna, 40136 Bologna, Italy
*
Author to whom correspondence should be addressed.
†
Presented at the 12th International Electronic Conference on Sensors and Applications, 12–14 November 2025; Available online: https://sciforum.net/event/ECSA-12.
Eng. Proc. 2025, 118(1), 14; https://doi.org/10.3390/ECSA-12-26551
Published: 7 November 2025
(This article belongs to the Proceedings of The 12th International Electronic Conference on Sensors and Applications)
Browse Figures
Versions Notes

Abstract

Wireless sensor networks (WSNs) implemented in the paradigm of the Internet of Things (IoT) are characterized by a large number of distributed sensor nodes that make measurements in-the-field and communicate with other sensor nodes and servers in the cloud by means of wireless technology. Sensor-to-microcontroller direct interface (SMDI) is a technique used for the measurement of resistive sensors without the use of an ADC. In SMDI-based measurements, the sensor is directly interfaced with the digital input–output pins of the general-purpose input–output (GPIO) interface of microcontrollers and FPGAs. Compared with the measurements performed with an ADC, SMDI is characterized by lower cost and lower power consumption. In this paper, the impact of noise on the accuracy of resistive sensor measurements using SMDI is investigated. This study was carried out by LTSpice electrical-level simulations and validated by preliminary experimental measurements, where a set of resistances in the range from 100 Ω to 10 kΩ were measured by SMDI under different levels of noise. For each operative condition, the simulations were also carried out in the case of measurements performed with a 12-bit ADC, and the achieved accuracy for the measured resistances was compared with the results achieved by SMDI. The results have shown that noise can seriously impact the measured accuracy of resistive sensors by SMDI and, unlike the ADC measurements, the accuracy cannot be improved by averaging on multiple measurements. A mitigation strategy to estimate the noise level and to improve the measurement accuracy of resistive sensors by SMDI was also proposed.

1. Introduction

Sensors are devices capable of accurately measuring different types of quantities and are normally used in different types of applications, such as environmental monitoring [1,2,3,4], food quality and safety analysis [5,6,7,8,9,10], structural health monitoring of civil infrastructures [11,12,13,14], microbial contamination detection [15,16,17,18,19], and Industry 4.0 applications [20,21,22,23]. In particular, the integration of low-power computing devices, sensors, and wireless communication technologies has led to the development of wireless sensor networks (WSNs), where large amounts of data are acquired and shared with other sensor nodes and servers in the cloud [24,25,26,27]. Sensor data are normally acquired by microcontrollers or Field-Programmable Gate Arrays (FPGAs) using analog-to-digital converters (ADCs), either integrated in the computing device or externally [28,29,30,31].
WSNs are usually powered by batteries and/or energy harvesting devices; thus, the sensor node power consumption is of paramount importance [32,33,34]. From this point of view, sensor-to-microcontroller direct interface (SMDI) is a technique that can be used to acquire sensor data without the use of an ADC, thus providing significant advantages in terms of low power consumption [35,36]. SMDI exploits the Schmitt triggers integrated in the general-purpose input–output (GPIO) interface of microcontrollers and FPGAs to directly interface the sensors’ analog output signal with the digital input pins of the computing device. SMDI has been exploited for the measurement of different types of sensors, such as resistive sensors [37,38,39,40], capacitive sensors [41,42,43,44], inductive sensors [45,46,47], and sensors featuring an output voltage signal [48].
As known, noise affects the reliability of electronic systems and can produce a severe limitation of the system reliability [49,50]. In particular, in the case of sensors, noise contributes to the decrease in the signal-to-noise ratio and the measurement accuracy. Thus, we have investigated the impact of noise on the measurement accuracy of resistive sensors using the SMDI technique. Different types of electrical noise can impact the reliability of electronic circuits, and they are typically classified in two different groups: intrinsic (or internal) noise and external noise [51]. Intrinsic noise refers to all the noise types that are generated inside an electronic device, such as thermal noise (produced by the random thermal agitation of electrons and holes in a conductor), shot noise (produced by the random arrival of electrons and holes at a discontinuous interface inside a device), flicker noise (that is usually found in transistors operating at low frequency), and transit time noise (produced by the energy transfer between electrons and ions). External noise, instead, refers to all types of noise that are generated outside of electronic devices, such as crosstalk noise and electromagnetic noise. Another classification for noise types is related to the shape of their power spectral density (PSD), as a function of frequency (f). White noise presents a flat PSD, while pink noise features a PSD proportional to f−1, red noise features a PSD proportional to f−2, blue noise features a PSD proportional to f, and violet noise features a PSD proportional to f2. Our study considers only white noise as electrical noise source. The study was carried out by electrical-level simulations with LTSpice [51] (with validation on preliminary experimental measurements), using a set of standard resistors with values between 100 Ω and 10 kΩ to represent a realistic working range for the values of a resistive sensor, and comparing the results with the case of measurements carried out using a 12-bit ADC for reference. The results have shown that measurements carried out using SMDI are strongly affected by noise, and different noise types (gaussian white noise or uniform white noise) can have a different impact on the measurement accuracy. Moreover, the presence of noise can seriously degrade the measurement accuracy also in the case the measured sensor value is averaged on a large number of samples. In order to address these issues, we have proposed a mitigation strategy that can compensate for the impact of noise on the measurement accuracy. It is based on the idea of using a programmable potentiometer in order to compensate the impact of noise by performing periodic calibrations on its value.
This paper is structured as follows. In Section 2, the simulation setups for the resistive sensor measurements using the SMDI technique and the 12-bit ADC are presented. In Section 3, the simulation results are presented and the accuracy achieved with the SMDI-based measurements and the ADC-based measurements are compared. In Section 4, the simulation results are discussed and a mitigation strategy to improve the measurement accuracy for the SMDI technique is presented. In Section 5, the simulations results are validated by experimental measurements on a microcontroller. Finally, conclusions are presented in Section 6.

2. Simulation Setup

This study was carried out by electrical-level simulations with LTSpice [52], considering a 180 nm CMOS technology. In Section 2.1, the simulation setup for the case of SMDI-based measurements is presented, while in Section 2.2, the simulation setup for the case of ADC-based measurements is presented.

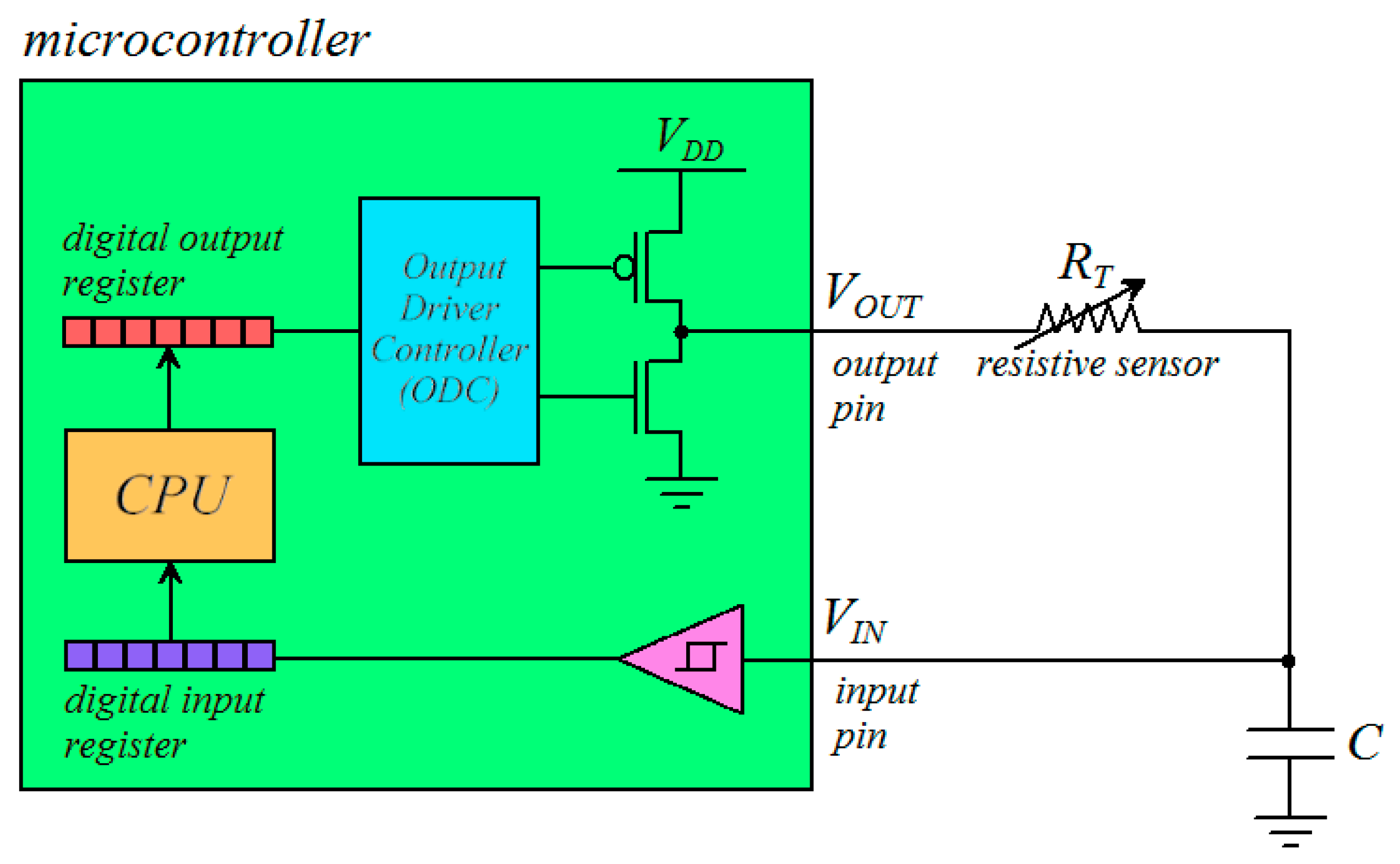
2.1. SMDI-Based Measurements

Sensor-to-microcontroller direct interface (SMDI) is a technique that can be used to acquire sensor data without the use of an ADC, by interfacing the sensor directly to digital input–output pins of a microcontroller. The simulation setup for a resistive sensor RT, measured with a microcontroller using the SMDI technique, is shown in Figure 1, where C is a discrete external capacitance.
SMDI exploits the Schmitt triggers integrated in the GPIO interface of microcontrollers to create an astable oscillator (with time constant RTC) whose period is measured, using the digital timers integrated in the microcontroller, to estimate the resistive sensor value RT. The analog voltage VIN on an input pin of the microcontroller is fed to the non-inverting Schmitt trigger integrated in the GPIO interface of the microcontroller. The Schmitt trigger features two threshold voltages (VH and VL) so that, if VIN > VH, then the Schmitt trigger output is VDD, while if VIN < VL, then the Schmitt trigger output is 0 V.
The microcontroller CPU acquires the digital value at the Schmitt trigger output and controls the Output Driver Controller (ODC) module so that the voltage at the output pin (VOUT) is the complement of the Schmitt trigger output value.
The working principle of the measurement of RT using SMDI can be defined as follows. Initially, it is VIN = VL, VOUT = VDD, and the capacitance C is charged with time constant RTC (i.e., VIN increases). When it is VIN = VH, the Schmitt trigger output switches from 0 V to VDD and VOUT switches from VDD to 0 V. Then, the charging step of the capacitance (whose duration is indicated with tH) terminates and the discharging of the capacitance C starts. When it is VIN = VL, the Schmitt trigger output switches from VDD to 0 V and VOUT switches from 0 V to VDD. Then, the discharging step of the capacitance (whose duration is indicated with tL) terminates and the charging of the capacitance C starts again. The values of tH and tL can be expressed as [40]
t H = R T C ∫ V L V H 1 V D D − V I N d V I N = R T C · l o g V D D − V L V D D − V H
t L = − R T C ∫ V H V L 1 V I N d V I N = R T C · l o g V H V L
The oscillation period TP of the signals VIN and VOUT can be measured using the digital timers integrated in the microcontroller and can be expressed as
T P = t H + t L = R T C · l o g V H V D D − V L V L V D D − V H
and the value of the resistive sensor can be calculated as
R T = T P C · l o g V H V D D − V L V L V D D − V H
The simulation setup of Figure 1 was implemented in LTSpice by using an ideal non-inverting Schmitt trigger with threshold voltages of VH = 1.9 V and VL = 1.4 V, a power supply of VDD = 3.3 V, a value for the capacitance C of 100 nF, and seven different values for the resistive sensor RT (100 Ω, 250 Ω, 500 Ω, 1000 Ω, 2500 Ω, 5000 Ω, 10,000 Ω). The choice of fixed Schmitt trigger thresholds (VH = 1.9 V and VL = 1.4 V) has been considered as a case study. As discussed in [48], these thresholds can present significantly different values for different devices. Moreover, slight differences in the Schmitt trigger thresholds for a single device also occur due to parameter dispersion introduced during manufacturing. Thus, to make accurate estimations of the sensor value, the exact values of the Schmitt trigger thresholds must be determined before the measurements. The operations performed by the microcontroller CPU were emulated by connecting a NOT digital gate between the output of the Schmitt trigger and the microcontroller output pin. The impact of the noise on the sensor measurement accuracy was evaluated by placing a white noise voltage generator (uniformly distributed) in series with the input pin of Figure 1. Nine different values of the white noise peak-to-peak voltage were evaluated (1.25 mV, 2.5 mV, 5 mV, 10 mV, 20 mV, 33.3 mV, 40 mV, 50 mV, 100 mV).

2.2. ADC-Based Measurements

The standard technique for sensor measurement by a microcontroller is based on the use of an ADC (integrated in the microcontroller or external) to acquire the analog information from the sensor and translate it to a digital format for data processing. In the case of a resistive sensor, a typical measurement setup is presented in Figure 2.
The measurement setup shown in Figure 2 exploits a Wheatstone bridge to generate a differential voltage (VIN+ − VIN−) that is used to estimate the resistive sensor value RT. If we consider a reference resistor of known value (RREF), the voltage VIN+ can be expressed as:
V I N + = R T R T + R R E F V D D
Since it is VIN− = VDD/2, then it is
V I N + − V I N − = V D D 2 R T − R R E F R T + R R E F
The differential voltage VIN+ − VIN− is sampled and quantized by the ADC and a digital word D11D10 … D1D0 is generated and fed to the microcontroller for data processing.
The simulation setup shown in Figure 2 was implemented in LTSpice considering a 12-bit differential input ADC (LTC2311-12) [53], a power supply of VDD = 3.3 V, a value for the reference resistor RREF of 1 kΩ, and seven different values for the resistive sensor RT (100 Ω, 250 Ω, 500 Ω, 1000 Ω, 2500 Ω, 5000 Ω, 10,000 Ω). The impact of the electrical noise on the sensor measurement accuracy was evaluated by placing a white noise voltage generator (uniformly distributed) between the node VIN+ and the non-inverting input of the ADC in Figure 2. Nine different values of the white noise peak-to-peak voltage were evaluated (1.25 mV, 2.5 mV, 5 mV, 10 mV, 20 mV, 33.3 mV, 40 mV, 50 mV, 100 mV). The characteristic of the 12-bit ADC output as a function of the resistive sensor value RT in the case of noise-free operating conditions is presented in Figure 3, where VOUT,ADC represents the analog equivalent of the ADC digital output D11D10 … D1D0. As can be seen, the characteristic is quasi-linear, with deviations from the linear behavior when the sensor resistance RT deviates from the reference resistance RREF of about one order of magnitude.

3. Simulation Results

The accuracy achieved in the case of a resistive sensor RT was evaluated for both the SMDI-based measurements and the ADC-based measurements according to the operative conditions described in Section 2.1 and Section 2.2, respectively. The measured RT was evaluated in terms of the average value and standard deviation, by carrying out 100 simulations for each operative condition. The simulation results for the case of the SMDI-based measurements are reported in Section 3.1, while the simulations results for the case of the ADC-based measurements are reported in Section 3.2.

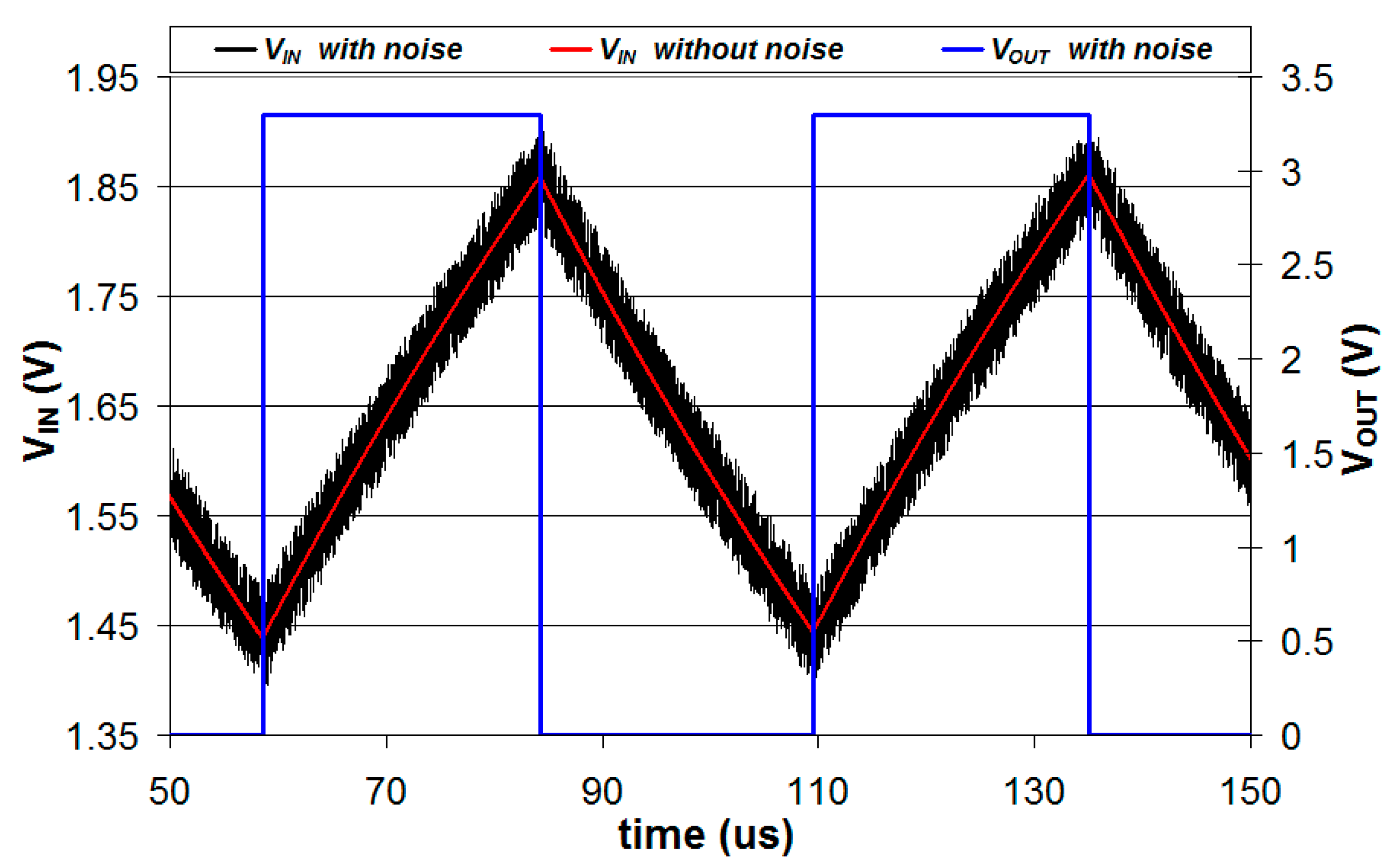
3.1. SMDI-Based Measurements

The average value of the measured resistive sensor RT is plotted in Figure 4 as a function of the peak-to-peak voltage noise (Vnoise,PP), for the case of a sensor resistance of nominal value 5 kΩ. As can be seen, the average value of measured RT decreases linearly with the increase in Vnoise,PP and deviates from its nominal value as Vnoise,PP increases.
The measured values of RT are presented in Table 1, in terms of average value (μ) and standard deviation (σ), as a function of the nominal value of the sensor resistance and the peak-to-peak voltage noise.
As can be seen, as Vnoise,PP increases, the average value of the measured RT decreases and deviates from its nominal value, while the standard deviation increases. Thus, in the case of high levels of noise, even if the measured value of RT is averaged on a large number of measurements, a good level of accuracy cannot be achieved.
The relative error (in percent) of the measured resistance RT is evaluated using the parameter ΔERROR, which is defined by
∆ E R R O R = 100 · R T , m e a s − R T R T
where RT,meas is the measured value of the sensor while RT is its nominal value.
The obtained values of ΔERROR are presented as a function of the nominal value of RT in Figure 5 for the case of the minimum level of electrical noise (Vnoise,PP = 1.25 mV), and in Figure 6 for the case of the maximum level of noise (Vnoise,PP = 100 mV).
Data presented in Figure 5 and Figure 6 confirms the results of Table 1. In the case of low levels of noise (Vnoise,PP = 1.25 mV), the SMDI technique achieves a very good accuracy with a relative error always lower than 1%, and even lower than 0.2% for values of RT of 500 Ω or higher. In the case of high levels of noise (Vnoise,PP = 100 mV), instead, the achieved relative error is always very high (>10%).

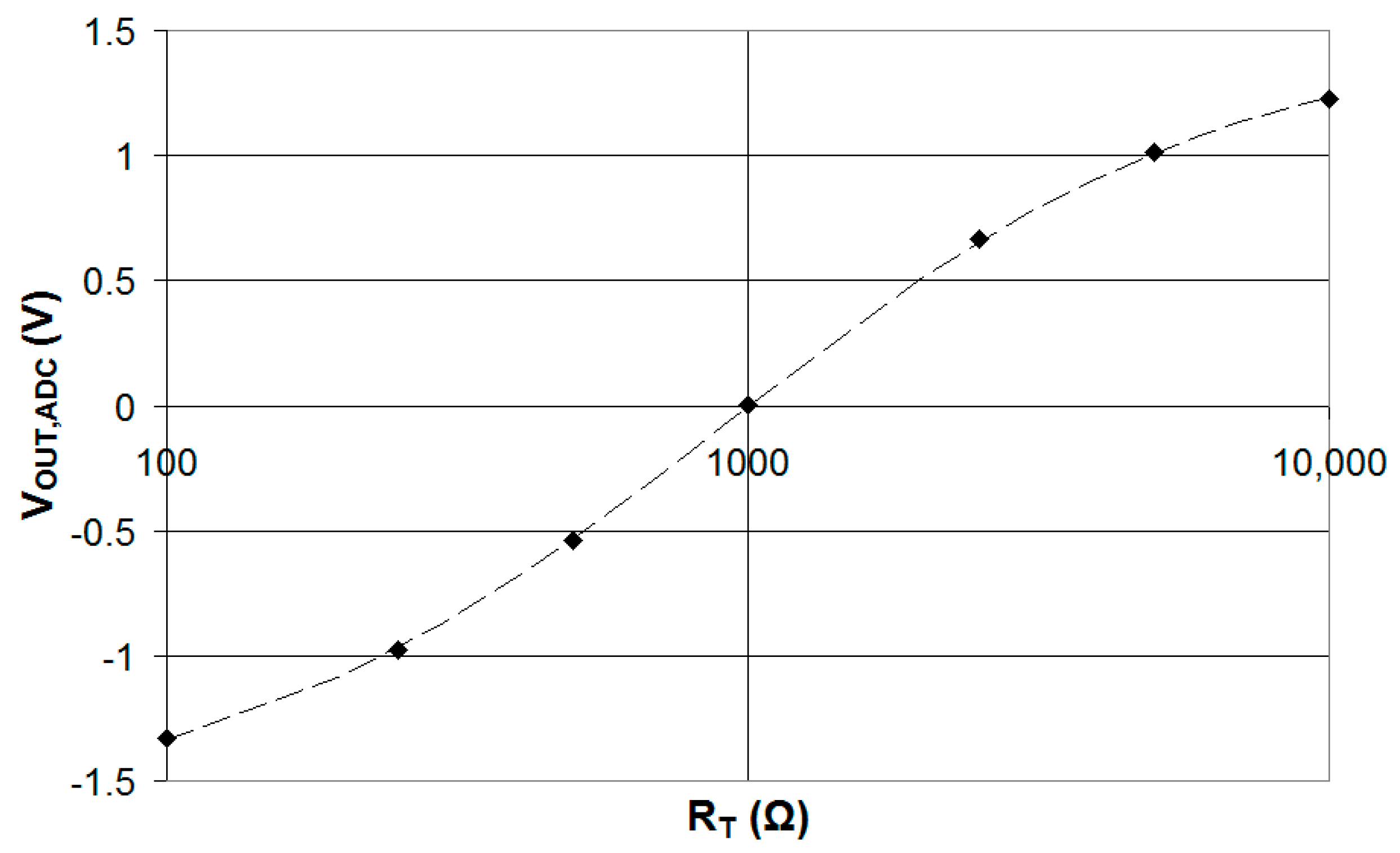
3.2. ADC-Based Measurements

The measured values of RT are presented in Table 2, in terms of the average value (μ) and standard deviation (σ), as a function of the nominal value of the sensor resistance and the peak-to-peak voltage noise. As can be seen, similarly to the case of SMDI-based measurements, the measured RT standard deviation increases with the level of noise. However, unlike SMDI-based measurements, the average value of the measured RT is almost independent of the noise level. Thus, in the case of ADC-based measurements, accurate values of the resistive sensor value can be achieved also in a noisy environment, if RT is calculated by averaging on a large number of measurements.
The values of the relative error (ΔERROR), as defined in Equation (7), are presented as a function of the nominal value of RT in Figure 7 for the case of the minimum level of noise (Vnoise,PP = 1.25 mV) and in Figure 8 for the case of the maximum level of noise (Vnoise,PP = 100 mV).
As can be seen, in the case of low levels of noise (Vnoise,PP = 1.25 mV), measurements carried out by the SMDI technique are more accurate (average ΔERROR of 0.28%) than the ADC-based measurements (average ΔERROR of 1.29%). On the contrary, in the case of high levels of noise (Vnoise,PP = 100 mV), measurements carried out by the SMDI technique are less accurate (average ΔERROR of 15.88%) than the ADC-based measurements (average ΔERROR of 3.27%).

4. Discussion

The results presented in Section 3 have shown that, as expected, higher levels of noise degrade the accuracy of sensor measurements, both in the case of ADC-based measurements and SMDI-based measurements. In the case of ADC-based measurements, however, the average value of sensor data is almost unaffected by the level of noise; thus, a higher measurement accuracy can be achieved by averaging on a large number of samples. This is not the case for SMDI-based measurements, where the average value of the sensor resistance deviates from its nominal value as the noise level increases, thus preventing the possibility to improve the measurement accuracy by averaging on multiple samples. In this section, the reasons for the strong impact of noise on the accuracy of SMDI-based measurements are investigated, and a possible mitigation strategy to improve the accuracy of SMDI-based measurements in a noisy environment is presented.
The waveforms of the voltage signals acquired during a simulation of the resistive sensor measurement with SMDI are presented in Figure 9. With reference to Figure 1, the voltage VIN (input of the Schmitt trigger integrated in the microcontroller GPIO interface) is presented in the case of a signal with high electrical noise level (100 mV peak-to-peak amplitude) as well as in the case of the noise-free signal.
As can be seen, the presence of the noise results in the triggering of the Schmitt trigger thresholds (VH and VL) before the noise-free voltage signal reaches these thresholds. This results in an increase in the detected VL and a decrease in the detected VH, and thus in a decrease in the measured period TP as defined by Equation (3). Then, in accordance with Equation (4), this results in a decrease in the measured sensor resistance RT, as also shown in the results of Section 3.1 (Figure 4 and Table 1). Moreover, the impact of the noise on the measurement accuracy is higher in the case of slower variations in the signal VIN and thus in the case of higher nominal values of RT, as also shown in Figure 6.
To investigate how different types of noise impact on the accuracy of SMDI-based measurements, we evaluated the detected average values of the Schmitt trigger thresholds (VL and VH) during an SMDI measurement under different levels of electrical noise, for RT = 10 kΩ, and two different types of noise: uniformly distributed white noise signal and Gaussian-distributed white noise signal. The results are shown as a function of the noise standard deviation (σnoise) in Figure 10 for the voltage threshold VL and in Figure 11 for the voltage threshold VH, with the average values of VL and VH calculated by averaging 1000 measurements. As expected, the threshold voltage VL increases with noise level, while the threshold voltage VH decreases with noise level. Moreover, the amount of deviation of the detected Schmitt trigger threshold voltages from their nominal value changes for different types of noise: the deviation is stronger for Gaussian-distributed white noise than for uniformly distributed white noise.
Based on the obtained results, in order to achieve an acceptable measurement accuracy, it is of paramount importance to design a strategy to mitigate the impact of the noise for resistive sensor measurements carried out by the SMDI technique. A possible solution is to replace the standard SMDI measurement setup presented in Figure 1 with the proposed measurement setup shown in Figure 12.
The resistor RT in Figure 12 represents the resistive sensor under test, while Rref is a digital potentiometer, and SW is an analog switch controlled by the microcontroller digital output pins (CSSW and CSPOT). In normal operating conditions, the switch SW connects the resistive sensor RT between the microcontroller input and output pins, and the sensor value is measured using the procedure described in Section 2.1. The sensor value (RT) is calculated by comparing the measured period (TP) with a set of reference values determined during a calibration procedure and stored in a look-up table.
The calibration procedure is carried out at regular time intervals to guarantee that all the measurements carried out after the calibration experience the same noise level as during the calibration.
During the calibration procedure, the switch SW is set to disconnect the sensor RT and connect the digital potentiometer Rref between the microcontroller input and output pins. At this point, the period TP defined in Equation (2) is measured (by averaging on an adequate number of measurements) for each value of the digital potentiometer Rref (between 0 Ω and the digital potentiometer full-scale resistance with step ΔRref). The look-up table presenting the measured resistance value for the different values of the measured period is stored in the microcontroller memory. During normal operating conditions, this look-up table is used to estimate the sensor resistance from the measured period TP. More accurate estimation of the sensor resistance RT is possible by using a digital potentiometer with higher resolution (i.e., lower ΔRref) but at the cost of higher memory occupation to store the calibration look-up table.
Simulations were carried out to evaluate the maximum error in RT estimation as a function of the digital potentiometer resolution. The simulations were performed for the case of uniform white noise with a 40 mV peak-to-peak voltage. Both the sensor RT (during the normal operating conditions) and the potentiometer Rref (during the calibration procedure) are determined by averaging 50 measurements. A dataset of 50 different RT values was generated with a uniform probability distribution between 100 Ω and 10 kΩ. The simulation results have shown that the sensor relative error (ΔERROR as defined in Equation (7)) decreases, as expected, by increasing the digital potentiometer resolution (i.e., decreasing ΔRref): we obtained a value of ΔERROR of 2.49% for ΔRref = 25 Ω, a value of ΔERROR of 2.02% for ΔRref = 20 Ω, a value of ΔERROR of 1.25% for ΔRref = 12.5 Ω, a value of ΔERROR of 0.85% for ΔRref = 10 Ω, and a value of ΔERROR of 0.46% for ΔRref = 3.33 Ω. Decreasing ΔRref below 3.33 Ω does not produce any improvement in the measurement accuracy.

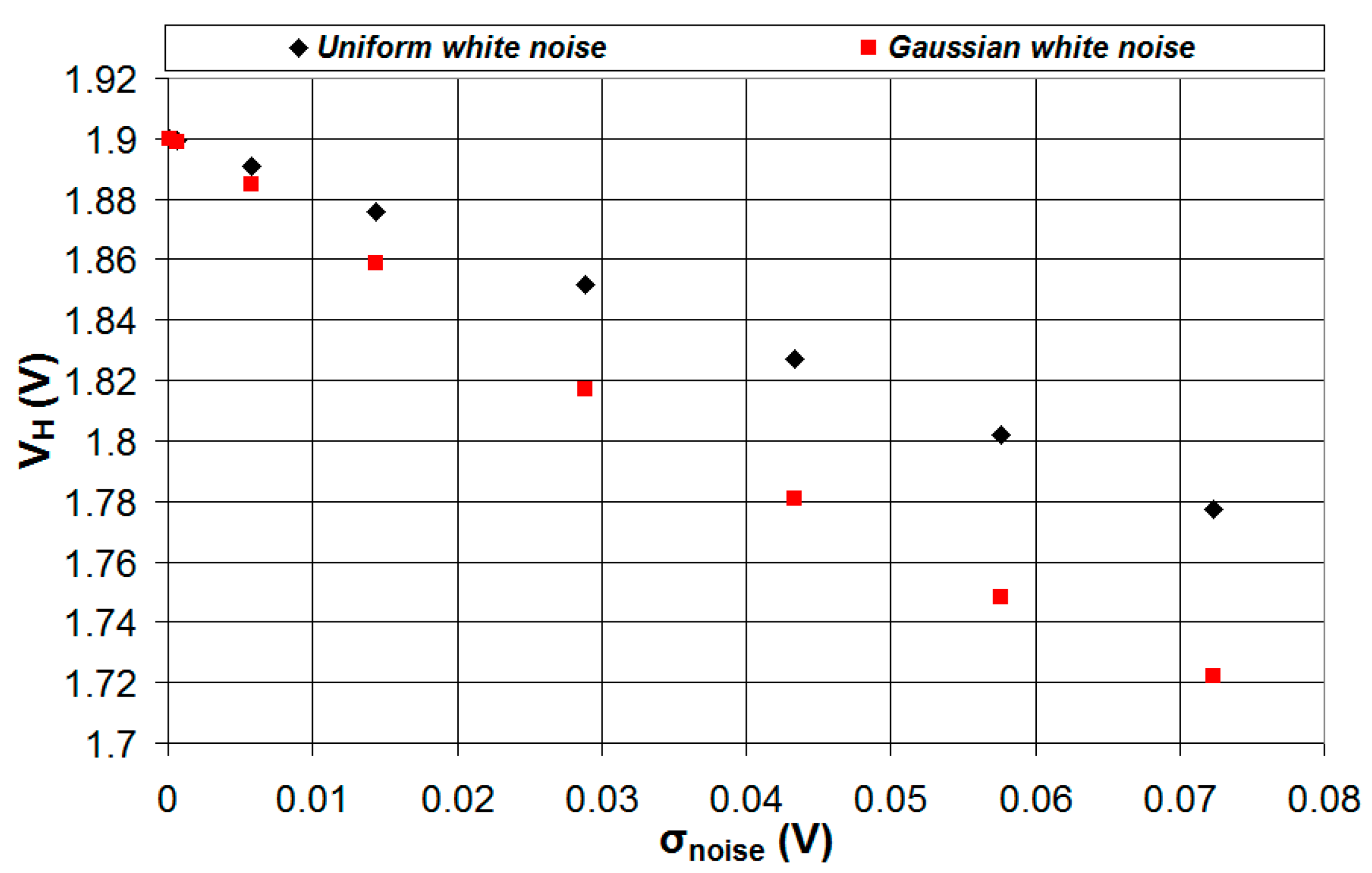
5. Experimental Measurements on a Microcontroller

In this section, the simulation results presented in the previous sections are validated by experimental measurements carried out on a low-cost microcontroller.
The measurement setup is shown in Figure 13. It consists of a Nucleo-L152RE development board that integrates an STM32L152RET6 microcontroller (ST Microelectronics, Geneva, Switzerland) and a laptop PC that is used to communicate with the microcontroller board using the USB-UART interface.
The threshold voltages (VH and VL) of the Schmitt trigger integrated in an input pin of the microcontroller were measured (using the integrated 12-bit DAC) under different noise levels, with the following procedure.
  • The output of the microcontroller DAC is shorted with the input pin to be tested using a cable. Cables of three different lengths (11.5 cm, 26.5 cm, and 102.5 cm) were tested, since the longer the cable, the higher the probability that electromagnetic interference degrades the signal-to-noise ratio.
  • Meanwhile, the microcontroller generates an analog voltage at the DAC output that increases from 0 V to 3.3 V, with steps of 12.89 mV. After the DAC output voltage is increased to a new value, the microcontroller waits 2 ms to allow the voltage stabilization, and then reads the value of the digital input pin. The Schmitt trigger threshold VH is estimated as the DAC output voltage for which the input pin logic value switches from 0 to 1.
  • Then, the microcontroller generates an analog voltage at the DAC output that decreases from 3.3 V to 0 V, with steps of 12.89 mV. Again, after the DAC output voltage is decreased to a new value, the microcontroller waits 2 ms to allow the voltage stabilization, and then reads the value of the digital input pin. The Schmitt trigger threshold VL is estimated as the DAC output voltage for which the input pin logic value switches from 1 to 0.
The values of VH and VL were measured 100 times and the measured values (average value and standard deviation) are reported in Figure 14 (for VH) and in Figure 15 (for VL) as function of the cable length.
As can be seen, the measured Schmitt trigger threshold voltage VH (VL) decreases (increases) linearly (high determination coefficient, R2 > 0.998) with the cable length, and thus with the electrical noise level. These experimental measurements confirm the simulation results, where the estimated Schmitt trigger threshold voltages change linearly with the standard deviation of the white noise signal (Figure 10 and Figure 11).

6. Conclusions

In this paper, we evaluated the impact of noise on the accuracy of resistive sensor measurements carried out by the sensor-to-microcontroller direct interface (SMDI) technique. This study was carried out by electrical-level simulations with the software LTSpice (version XVII) and preliminary experimental measurements. The measurement accuracy of a resistive sensor was evaluated under different levels of white noise both in the case of SMDI-based measurements and ADC-based measurements. The simulation results have shown that, while in the case of ADC-based measurements, the impact of the noise can be mitigated by averaging on a large number of measurements, in the case of SMDI-based measurements, this solution is ineffective. Thus, a mitigation strategy was proposed to allow accurate measurements of resistive sensors using the SMDI technique in a noisy environment.

Author Contributions

Conceptualization, M.G.; methodology, M.G.; software, M.G.; validation, M.G.; formal analysis, M.G.; investigation, M.G.; resources, M.G.; data curation, M.G.; writing—original draft preparation, M.G.; writing—review and editing, M.G. and M.O.; visualization, M.G. and M.O.; supervision, M.G. and M.O.; project administration, M.G. and M.O. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data sharing is not applicable to this article.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Dhall, S.; Mehta, B.R.; Tyagi, A.K.; Sood, K. A review on environmental gas sensors: Materials and technologies. Sens. Int. 2021, 2, 100116. [Google Scholar] [CrossRef]
  2. Han, P.; Mei, H.; Liu, D.; Zeng, N.; Tang, X.; Wang, Y.; Pan, Y. Calibrations of low-cost air pollution monitoring sensors for CO, NO2, O3, and SO2. Sensors 2021, 21, 256. [Google Scholar] [CrossRef]
  3. Gavrilaș, S.; Ursachi, C.Ș.; Perța-Crișan, S.; Munteanu, F.D. Recent trends in biosensors for environmental quality monitoring. Sensors 2022, 22, 1513. [Google Scholar] [CrossRef]
  4. Liang, L. Calibrating low-cost sensors for ambient air monitoring: Techniques, trends, and challenges. Environ. Res. 2021, 197, 111163. [Google Scholar] [CrossRef]
  5. Grossi, M.; Valli, E.; Bendini, A.; Gallina Toschi, T.; Riccò, B. A Portable Battery-Operated Sensor System for Simple and Rapid Assessment of Virgin Olive Oil Quality Grade. Chemosensors 2022, 10, 102. [Google Scholar] [CrossRef]
  6. Grossi, M.; Bendini, A.; Valli, E.; Gallina Toschi, T. Field-deployable determinations of peroxide index and total phenolic content in olive oil using a promising portable sensor system. Sensors 2023, 23, 5002. [Google Scholar] [CrossRef] [PubMed]
  7. Sohrabi, H.; Sani, P.S.; Orooji, Y.; Majidi, M.R.; Yoon, Y.; Khataee, A. MOF-based sensor platforms for rapid detection of pesticides to maintain food quality and safety. Food Chem. Toxicol. 2022, 165, 113176. [Google Scholar] [CrossRef]
  8. Lu, L.; Hu, Z.; Hu, X.; Li, D.; Tian, S. Electronic tongue and electronic nose for food quality and safety. Food Res. Int. 2022, 162, 112214. [Google Scholar] [CrossRef] [PubMed]
  9. Dodero, A.; Escher, A.; Bertucci, S.; Castellano, M.; Lova, P. Intelligent packaging for real-time monitoring of food-quality: Current and future developments. Appl. Sci. 2021, 11, 3532. [Google Scholar] [CrossRef]
  10. Grossi, M.; Valli, E.; Glicerina, V.T.; Rocculi, P.; Gallina Toschi, T.; Riccò, B. Optical determination of solid fat content in fats and oils: Effects of wavelength on estimated accuracy. Eur. J. Lipid Sci. Technol. 2022, 124, 2100071. [Google Scholar] [CrossRef]
  11. Kaartinen, E.; Dunphy, K.; Sadhu, A. LiDAR-based structural health monitoring: Applications in civil infrastructure systems. Sensors 2022, 22, 4610. [Google Scholar] [CrossRef] [PubMed]
  12. Mishra, M.; Lourenço, P.B.; Ramana, G.V. Structural health monitoring of civil engineering structures by using the internet of things: A review. J. Build. Eng. 2022, 48, 103954. [Google Scholar] [CrossRef]
  13. Jayawickrema, U.M.N.; Herath, H.M.C.M.; Hettiarachchi, N.K.; Sooriyaarachchi, H.P.; Epaarachchi, J.A. Fibre-optic sensor and deep learning-based structural health monitoring systems for civil structures: A review. Measurement 2022, 199, 111543. [Google Scholar] [CrossRef]
  14. Rossi, M.; Bournas, D. Structural health monitoring and management of cultural heritage structures: A state-of-the-art review. Appl. Sci. 2023, 13, 6450. [Google Scholar] [CrossRef]
  15. Grossi, M.; Parolin, C.; Vitali, B.; Riccò, B. Computer vision approach for the determination of microbial concentration and growth kinetics using a low cost sensor system. Sensors 2019, 19, 5367. [Google Scholar] [CrossRef]
  16. Grossi, M.; Parolin, C.; Vitali, B.; Riccò, B. A portable sensor system for bacterial concentration monitoring in metalworking fluids. J. Sens. Sens. Syst. 2018, 7, 349–357. [Google Scholar] [CrossRef]
  17. Canciu, A.; Tertis, M.; Hosu, O.; Cernat, A.; Cristea, C.; Graur, F. Modern analytical techniques for detection of bacteria in surface and wastewaters. Sustainability 2021, 13, 7229. [Google Scholar] [CrossRef]
  18. Spagnolo, S.; De La Franier, B.; Davoudian, K.; Hianik, T.; Thompson, M. Detection of E. coli bacteria in milk by an acoustic wave aptasensor with an anti-fouling coating. Sensors 2022, 22, 1853. [Google Scholar] [CrossRef]
  19. Nnachi, R.C.; Sui, N.; Ke, B.; Luo, Z.; Bhalla, N.; He, D.; Yang, Z. Biosensors for rapid detection of bacterial pathogens in water, food and environment. Environ. Int. 2022, 166, 107357. [Google Scholar] [CrossRef]
  20. Kanoun, O.; Khriji, S.; Naifar, S.; Bradai, S.; Bouattour, G.; Bouhamed, A.; El Houssaini, D.; Viehweger, C. Prospects of wireless energy-aware sensors for smart factories in the industry 4.0 era. Electronics 2021, 10, 2929. [Google Scholar] [CrossRef]
  21. Varshney, A.; Garg, N.; Nagla, K.S.; Nair, T.S.; Jaiswal, S.K.; Yadav, S.; Aswal, D.K. Challenges in sensors technology for industry 4.0 for futuristic metrological applications. Mapan 2021, 36, 215–226. [Google Scholar] [CrossRef]
  22. Majid, M.; Habib, S.; Javed, A.R.; Rizwan, M.; Srivastava, G.; Gadekallu, T.R.; Lin, J.C.W. Applications of wireless sensor networks and internet of things frameworks in the industry revolution 4.0: A systematic literature review. Sensors 2022, 22, 2087. [Google Scholar] [CrossRef] [PubMed]
  23. Soori, M.; Arezoo, B.; Dastres, R. Internet of things for smart factories in industry 4.0, a review. Internet Things Cyber-Phys. Syst. 2023, 3, 192–204. [Google Scholar] [CrossRef]
  24. Gulati, K.; Boddu, R.S.K.; Kapila, D.; Bangare, S.L.; Chandnani, N.; Saravanan, G. A review paper on wireless sensor network techniques in Internet of Things (IoT). Mater. Today Proc. 2022, 51, 161–165. [Google Scholar] [CrossRef]
  25. Stankovic, J.A. Wireless sensor networks. Computer 2008, 41, 92–95. [Google Scholar] [CrossRef]
  26. Khalil, N.; Abid, M.R.; Benhaddou, D.; Gerndt, M. Wireless sensors networks for Internet of Things. In Proceedings of the 2014 IEEE Ninth International Conference on Intelligent Sensors, Sensor Networks and Information Processing (ISSNIP), Singapore, 21–24 April 2014; pp. 1–6. [Google Scholar]
  27. Kandris, D.; Nakas, C.; Vomvas, D.; Koulouras, G. Applications of wireless sensor networks: An up-to-date survey. Appl. Syst. Innov. 2020, 3, 14. [Google Scholar] [CrossRef]
  28. Chen, C.H.; He, T.; Zhang, Y.; Temes, G.C. Incremental analog-to-digital converters for high-resolution energy-efficient sensor interfaces. IEEE J. Emerg. Sel. Top. Circuits Syst. 2015, 5, 612–623. [Google Scholar] [CrossRef]
  29. Krasilenko, V.G.; Nikolskyy, A.I.; Lazarev, A.A. Multichannel serial-parallel analog-to-digital converters based on current mirrors for multi-sensor systems. Opt. Syst. Des. 2012, 8550, 598–609. [Google Scholar]
  30. Schroeder, D. Adaptive low-power analog/digital converters for wireless sensor networks. In Proceedings of the Third International Workshop on Intelligent Solutions in Embedded Systems, Hamburg, Germany, 20 May 2005; pp. 70–78. [Google Scholar]
  31. Huang, J.S.; Kuo, S.C.; Chen, C.H. A multistep multistage fifth-order incremental delta sigma analog-to-digital converter for sensor interfaces. IEEE J. Solid-State Circuits 2023, 58, 2733–2744. [Google Scholar] [CrossRef]
  32. Singh, J.; Kaur, R.; Singh, D. Energy harvesting in wireless sensor networks: A taxonomic survey. Int. J. Energy Res. 2021, 45, 118–140. [Google Scholar] [CrossRef]
  33. Hu, H.; Han, Y.; Yao, M.; Song, X. Trust based secure and energy efficient routing protocol for wireless sensor networks. IEEE Access 2021, 10, 10585–10596. [Google Scholar] [CrossRef]
  34. Bhushan, S.; Kumar, M.; Kumar, P.; Stephan, T.; Shankar, A.; Liu, P. FAJIT: A fuzzy-based data aggregation technique for energy efficiency in wireless sensor network. Complex Intell. Syst. 2021, 7, 997–1007. [Google Scholar] [CrossRef]
  35. Reverter, F. The art of directly interfacing sensors to microcontrollers. J. Low Power Electron. Appl. 2012, 2, 265–281. [Google Scholar] [CrossRef]
  36. Reverter, F. Power consumption in direct interface circuits. IEEE Trans. Instrum. Meas. 2012, 62, 503–509. [Google Scholar] [CrossRef]
  37. Reverter, F. A microcontroller-based interface circuit for three-wire connected resistive sensors. IEEE Trans. Instrum. Meas. 2022, 71, 2006704. [Google Scholar] [CrossRef]
  38. Reverter, F. A direct approach for interfacing four-wire resistive sensors to microcontrollers. Meas. Sci. Technol. 2022, 34, 037001. [Google Scholar] [CrossRef]
  39. Grossi, M.; Omaña, M. Accuracy of NTC Thermistor Measurements Using the Sensor to Microcontroller Direct Interface. Eng. Proc. 2024, 82, 12. [Google Scholar]
  40. Grossi, M.; Omaña, M.; Metra, C. Impact of aging on temperature measurements performed using a resistive temperature sensor with sensor-to-microcontroller direct interface. Microelectron. Reliab. 2025, 169, 115729. [Google Scholar] [CrossRef]
  41. Czaja, Z. A measurement method for lossy capacitive relative humidity sensors based on a direct sensor-to-microcontroller interface circuit. Measurement 2021, 170, 108702. [Google Scholar] [CrossRef]
  42. Czaja, Z. A measurement method for capacitive sensors based on a versatile direct sensor-to-microcontroller interface circuit. Measurement 2020, 155, 107547. [Google Scholar] [CrossRef]
  43. Reverter, F.; Casas, Ò. Interfacing differential capacitive sensors to microcontrollers: A direct approach. IEEE Trans. Instrum. Meas. 2009, 59, 2763–2769. [Google Scholar] [CrossRef]
  44. Gaitán-Pitre, J.E.; Gasulla, M.; Pallas-Areny, R. Analysis of a direct interface circuit for capacitive sensors. IEEE Trans. Instrum. Meas. 2009, 58, 2931–2937. [Google Scholar] [CrossRef]
  45. Kokolanski, Z.; Jordana, J.; Gasulla, M.; Dimcev, V.; Reverter, F. Direct inductive sensor-to-microcontroller interface circuit. Sens. Actuators A Phys. 2015, 224, 185–191. [Google Scholar] [CrossRef]
  46. Kokolanski, Z.; Jordana, J.; Gasulla, M.; Dimcev, V.; Reverter, F. Microcontroller-based interface circuit for inductive sensors. Procedia Eng. 2014, 87, 1251–1254. [Google Scholar] [CrossRef][Green Version]
  47. Asif, A.; Ali, A.; Abdin, M.Z.U. Resolution enhancement in directly interfaced system for inductive sensors. IEEE Trans. Instrum. Meas. 2018, 68, 4104–4111. [Google Scholar] [CrossRef]
  48. Grossi, M. Efficient and Accurate Analog Voltage Measurement Using a Direct Sensor-to-Digital Port Interface for Microcontrollers and Field-Programmable Gate Arrays. Sensors 2024, 24, 873. [Google Scholar] [CrossRef]
  49. Jones, B.K. Electrical noise as a reliability indicator in electronic devices and components. IEE Proc.-Circuits Devices Syst. 2002, 149, 13–22. [Google Scholar] [CrossRef]
  50. Demir, A.; Sangiovanni-Vincentelli, A. Analysis and Simulation of Noise in Nonlinear Electronic Circuits and Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 425. [Google Scholar]
  51. Vasilescu, G. Electronic Noise and Interfering Signals: Principles and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
  52. LTSpice Circuit Simulator. Available online: https://www.analog.com/en/resources/design-tools-and-calculators/ltspice-simulator.html (accessed on 15 May 2025).
  53. LTC2311-12 ADC. Available online: https://www.analog.com/en/products/ltc2311-12.html (accessed on 15 May 2025).
Engproc 118 00014 g001
Figure 1. Simulation setup for a resistive sensor RT measured using the SMDI technique.
Figure 1. Simulation setup for a resistive sensor RT measured using the SMDI technique.
Engproc 118 00014 g001
Engproc 118 00014 g002
Figure 2. Simulation setup for a resistive sensor RT measured using a 12-bit ADC.
Figure 2. Simulation setup for a resistive sensor RT measured using a 12-bit ADC.
Engproc 118 00014 g002
Engproc 118 00014 g003
Figure 3. Characteristic of the 12-bit ADC output as a function of RT.
Figure 3. Characteristic of the 12-bit ADC output as a function of RT.
Engproc 118 00014 g003
Engproc 118 00014 g004
Figure 4. Average value of the measured RT as a function of the peak-to-peak voltage noise in the case of a sensor of nominal value 5 kΩ.
Figure 4. Average value of the measured RT as a function of the peak-to-peak voltage noise in the case of a sensor of nominal value 5 kΩ.
Engproc 118 00014 g004
Engproc 118 00014 g005
Figure 5. Measured ΔERROR as a function of the nominal value of RT for SMDI-based measurements in the case of the minimum level of noise (Vnoise,PP = 1.25 mV).
Figure 5. Measured ΔERROR as a function of the nominal value of RT for SMDI-based measurements in the case of the minimum level of noise (Vnoise,PP = 1.25 mV).
Engproc 118 00014 g005
Engproc 118 00014 g006
Figure 6. Measured ΔERROR as a function of the nominal value of RT for SMDI-based measurements in the case of the maximum level of noise (Vnoise,PP = 100 mV).
Figure 6. Measured ΔERROR as a function of the nominal value of RT for SMDI-based measurements in the case of the maximum level of noise (Vnoise,PP = 100 mV).
Engproc 118 00014 g006
Engproc 118 00014 g007
Figure 7. Measured ΔERROR as a function of the nominal value of RT for ADC-based measurements in the case of the minimum level of noise (Vnoise,PP = 1.25 mV).
Figure 7. Measured ΔERROR as a function of the nominal value of RT for ADC-based measurements in the case of the minimum level of noise (Vnoise,PP = 1.25 mV).
Engproc 118 00014 g007
Engproc 118 00014 g008
Figure 8. Measured ΔERROR as a function of the nominal value of RT for ADC-based measurements in the case of the maximum level of noise (Vnoise,PP = 100 mV).
Figure 8. Measured ΔERROR as a function of the nominal value of RT for ADC-based measurements in the case of the maximum level of noise (Vnoise,PP = 100 mV).
Engproc 118 00014 g008
Engproc 118 00014 g009
Figure 9. Waveforms of the voltage signals acquired during a simulation of the resistive sensor measurement using SMDI, in presence and absence of noise.
Figure 9. Waveforms of the voltage signals acquired during a simulation of the resistive sensor measurement using SMDI, in presence and absence of noise.
Engproc 118 00014 g009
Engproc 118 00014 g010
Figure 10. Average value of the detected Schmitt trigger threshold VL as a function of the noise level.
Figure 10. Average value of the detected Schmitt trigger threshold VL as a function of the noise level.
Engproc 118 00014 g010
Engproc 118 00014 g011
Figure 11. Average value of the detected Schmitt trigger threshold VH as a function of the noise level.
Figure 11. Average value of the detected Schmitt trigger threshold VH as a function of the noise level.
Engproc 118 00014 g011
Engproc 118 00014 g012
Figure 12. Proposed measurement setup to mitigate the impact of noise in SMDI-based measurements of resistive sensors.
Figure 12. Proposed measurement setup to mitigate the impact of noise in SMDI-based measurements of resistive sensors.
Engproc 118 00014 g012
Engproc 118 00014 g013
Figure 13. Experimental measurement setup to estimate the Schmitt trigger threshold voltages under different noise levels.
Figure 13. Experimental measurement setup to estimate the Schmitt trigger threshold voltages under different noise levels.
Engproc 118 00014 g013
Engproc 118 00014 g014
Figure 14. Measured values of the Schmitt trigger threshold voltage VH as a function of the cable length.
Figure 14. Measured values of the Schmitt trigger threshold voltage VH as a function of the cable length.
Engproc 118 00014 g014
Engproc 118 00014 g015
Figure 15. Measured values of the Schmitt trigger threshold voltage VL as a function of the cable length.
Figure 15. Measured values of the Schmitt trigger threshold voltage VL as a function of the cable length.
Engproc 118 00014 g015
Table 1. Measured values of RT (average value and standard deviation) using the sensor-to-microcontroller direct interface technique in the case of different nominal values for the sensor resistance and for different values of the noise level.
Table 1. Measured values of RT (average value and standard deviation) using the sensor-to-microcontroller direct interface technique in the case of different nominal values for the sensor resistance and for different values of the noise level.
RT (Ω)
10025050010002500500010,000
Vnoise,PP (mV)μσμσμσμσμσμσμσ
1.25101.000.08251.040.21500.890.351000.50.642498.41.044993.61.669984.53.65
2.5100.990.16250.880.38500.490.56999.011.032494.21.784985.63.399965.65.31
5100.910.27250.680.61498.840.87996.331.702484.43.104963.84.479925.47.05
10100.680.49249.120.93496.431.48989.592.722465.94.394919.67.799835.812.9
2099.410.73246.091.54488.472.01971.343.282417.07.084840.710.89644.919.6
33.397.950.89242.022.33476.362.38950.236.572366.311.94723.020.09416.532.7
4097.181.18237.502.14472.033.92941.655.422331.813.34661.118.49302.224.9
5095.991.70234.423.09464.784.35925.237.402286.816.44546.818.59100.234.1
10088.492.67214.404.68424.736.46841.968.532064.629.04062.719.58154.946.5
Table 2. Measured values of RT (average value and standard deviation) using the 12-bit ADC LTC2311-12 in the case of different values for the sensor resistance and for different values of the noise level.
Table 2. Measured values of RT (average value and standard deviation) using the 12-bit ADC LTC2311-12 in the case of different values for the sensor resistance and for different values of the noise level.
RT (Ω)
10025050010002500500010,000
Vnoise,PP (mV)μσμσμσμσμσμσμσ
1.25102.480.16247.910.10495.260.191003.00.642534.91.825025.34.419739.920.2
2.5102.450.22247.860.28495.320.351003.00.642535.31.965027.25.949742.227.8
5102.430.41247.840.47495.310.611003.01.022535.53.075027.29.169741.334.3
10102.400.83247.790.91495.231.191002.91.912535.35.555026.716.09740.252.5
20102.311.62247.701.82495.182.311002.83.832534.810.95026.230.89737.098.6
33.3102.162.76247.553.06495.053.841002.76.322534.517.95025.750.89737.0159
40102.103.31247.523.70495.014.621002.57.592534.321.45025.560.49734.5190
50102.014.14247.444.63494.895.791002.59.422534.126.45024.874.99732.8236
100101.618.28247.039.23494.5511.61002.118.92533.353.55022.51529740.8470
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Grossi, M.; Omaña, M. Impact of Electrical Noise on the Accuracy of Resistive Sensor Measurements Using Sensor-to-Microcontroller Direct Interface. Eng. Proc. 2025, 118, 14. https://doi.org/10.3390/ECSA-12-26551

AMA Style

Grossi M, Omaña M. Impact of Electrical Noise on the Accuracy of Resistive Sensor Measurements Using Sensor-to-Microcontroller Direct Interface. Engineering Proceedings. 2025; 118(1):14. https://doi.org/10.3390/ECSA-12-26551

Chicago/Turabian Style

Grossi, Marco, and Martin Omaña. 2025. "Impact of Electrical Noise on the Accuracy of Resistive Sensor Measurements Using Sensor-to-Microcontroller Direct Interface" Engineering Proceedings 118, no. 1: 14. https://doi.org/10.3390/ECSA-12-26551

APA Style

Grossi, M., & Omaña, M. (2025). Impact of Electrical Noise on the Accuracy of Resistive Sensor Measurements Using Sensor-to-Microcontroller Direct Interface. Engineering Proceedings, 118(1), 14. https://doi.org/10.3390/ECSA-12-26551

Article Metrics

Back to TopTop