Visual Mapping and Autonomous Navigation Using AprilTags in Omnidirectional Mobile Robots: A Realistic ROS-Gazebo Simulation Framework ^†

Abstract

This paper presents a modular, high-fidelity simulation framework for the autonomous navigation of omnidirectional mobile robots using visual localization with AprilTags. The proposed system integrates realistic robot dynamics, a dual-layer path planning architecture, and interchangeable trajectory tracking controllers, all within the ROS Noetic and Gazebo simulation environment. AprilTags are employed as low-cost fiducial markers for map construction, eliminating the need for LiDAR or GPS. The architecture supports global path planning via the A* algorithm and local reactive replanning to avoid unexpected obstacles while preserving trajectory continuity. Three control strategies—Lyapunov-based, null-space Lyapunov, and proportional–integral (PI) control—are implemented and evaluated in multiple maze-like environments. Experimental results in the simulation demonstrate accurate trajectory tracking, successful visual mapping, and effective obstacle avoidance under realistic conditions.

1. Introduction

Omnidirectional mobile robots can move in any direction without needing to rotate their chassis, offering superior maneuverability in constrained environments. One common approach to achieve omnidirectional motion is the use of Mecanum wheels—wheels fitted with angled rollers that translate wheel rotation into lateral movement components [1,2,3]. Robots equipped with four Mecanum wheels can control motion in the plane X–Y and rotation about the yaw axis, enabling holonomic motion capabilities.

Simulation of omnidirectional mobile robots with Mecanum wheels has become a fundamental tool in the design and validation of navigation and control algorithms before real-world deployment. Several simulation frameworks exist within the ROS ecosystem, with Gazebo standing out for its flexibility and integration with ROS middleware. However, simulating realistic omnidirectional robot behavior—especially for platforms with Mecanum wheels—poses significant challenges due to the complex interaction between wheels and the ground, as well as high sensitivity to model parameters. Existing plugins such as the gazebo_planar_move_plugin plugin or more specialized omnidirectional drive plugins [4,5,6] provide basic functionality, but often lack precise interfaces to control individual wheel speeds.

Visual-based navigation using fiducial markers such as AprilTags has been widely studied for indoor autonomous mobile robots [7,8,9]. These tags serve as robust landmarks for localization, mapping, and path correction. Mapping strategies based on AprilTag detection have been employed for SLAM and global localization [10,11], often enhanced through optimization techniques or probabilistic filtering. Furthermore, local path planning methods leveraging A* algorithms continue to be a preferred choice due to their deterministic nature and computational efficiency [12]. Integration of global and local planning with dynamic obstacle avoidance has also been explored in modular ROS architectures. However, despite the robustness of these components individually, few simulation environments accurately integrate realistic robot dynamics, AprilTag-based navigation, and modular planning and control pipelines under noisy and uncertain conditions.

It is worth mentioning that this work does not take into consideration the robot’s relocalization or simultaneous localization and mapping tools, which will be addressed in future efforts. Despite the robustness of traditional methods such as A* and cubic B-spline smoothing, few works integrate them with realistic Mecanum dynamics, AprilTag-based navigation, and multiple trajectory controllers under noisy conditions, which constitutes the main novelty of this framework.

The main contributions of this paper are as follows: (i) the development of a realistic simulation framework in Gazebo/ROS for omnidirectional robots with Mecanum wheels, including detailed wheel–ground interaction modeling; (ii) the integration of AprilTag-based visual navigation to construct occupancy grids as a cost-effective alternative to LiDAR, supporting robust mapping and path correction; (iii) a modular planning and control architecture that allows interchangeable use of trajectory planners (such as A*) and trajectory-following controllers (Lyapunov, null-space Lyapunov, and PI); and (iv) extensive validation through simulation experiments in maze-like environments under noise and uncertainty, demonstrating robustness of the integrated pipeline. The remainder of this paper presents the methodology, experimental results, discussion, and conclusions.

2. Methodology

The proposed navigation architecture is designed to enable smooth, responsive, and visually guided motion in omnidirectional mobile robots. It consists of two complementary path planning modules: a global and a local planner, that allow reactive autonomous navigation with time-parameterized trajectories. We rely on a B-spline smoothing scheme for the computed trajectories to ensure soft maneuvers. The following sections bring details about the mentioned components.

2.1. Offline Visual Mapping

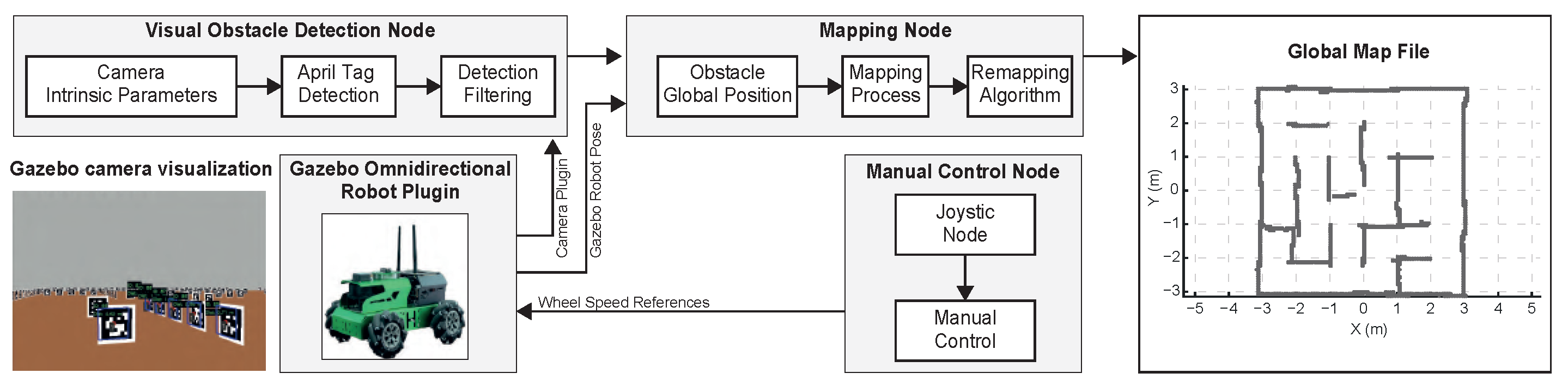
The offline visual mapping stage comprises a sequence of interconnected nodes designed to detect visual obstacles, update a global occupancy grid, and provide manual teleoperation capabilities for data acquisition. Figure 1 describes the overall workflow, from raw image acquisition to the generation of the static global map used by the global planner. Each block in this diagram corresponds to a specific processing node, which is described in detail in the following paragraphs.

2.2. Visual Obstacle Detection Node

The first stage of the mapping system is carried out in a simulated environment using the Gazebo simulator. An omnidirectional robot equipped with a monocular camera plugin navigates through a maze populated with fiducial tags (AprilTags), which act as visual obstacles. The camera captures real-time images of the environment, which are fed to a detection node responsible for identifying and localizing these markers, as illustrated in the lower left corner of Figure 1.

The visual detection pipeline begins with intrinsic calibration to ensure geometric consistency in the projection of image points. AprilTag detection is then performed using OpenCV, which returns the 3D pose of each tag relative to the camera frame noted as ${\mathbf{T}}_{\mathrm{tag}}^{\mathcal{C}}=\left[\mathbf{R}\right|\mathbf{t}]\in SE\left(3\right)$. The resulting transform has rotational $\mathbf{R}$ and translational $\mathbf{t}$ components in 3D. Note that the Z-axis component will not be used.

To ensure reliable mapping, a filtering stage is applied to discard noisy or spurious detections. A tag observation is only accepted if the following conditions are simultaneously satisfied: (i) the robot is stationary or almost stopped, determined by monitoring the velocities of the wheels and comparing them to a small threshold ≤0.5 rad/s; (ii) the distance between the robot and the tag is ≤1.5 m; and (iii) the same tag has been observed multiple consecutive times, indicating temporal stability.

Once validated, the tag pose is transformed from the camera frame $\mathcal{C}$ to the global map frame $\mathcal{W}$ using the following SE(3) transformation chain:

$${\mathbf{T}}_{\mathrm{tag}}^{\mathcal{W}}={\mathbf{T}}_{\mathcal{R}}^{\mathcal{W}}·{\mathbf{T}}_{\mathcal{C}}^{\mathcal{R}}·{\mathbf{T}}_{\mathrm{tag}}^{\mathcal{C}}\mathrm{with}:{\mathbf{T}}_{\mathcal{C}}^{\mathcal{R}}=\left[\begin{array}{cccc}0& 0& 1& 0.096\\ -1& 0& 0& 0.0\\ 0& -1& 0& 0.14\\ 0& 0& 0& 1\end{array}\right]$$

(1)

where the transform from the robot to the global frame ${\mathbf{T}}_{\mathcal{R}}^{\mathcal{W}}$ is computed using odometry. Note that ${\mathbf{T}}_{\mathcal{C}}^{\mathcal{R}}$ is a fixed transform from the camera frame to the robot frame based on the sensor disposition. It is worth mentioning that we assume a constant Z value for all tags, and we used only the $X,Y$ components to build the occupancy grid.

2.3. Mapping Node

The mapping node is responsible for updating a two-dimensional occupancy grid with the estimated positions of obstacles. Each fiducial marker is projected as a rectangular region centered at its global location. The dimensions of this region are fixed at 0.15 m in length and 0.05 m in width, corresponding to the approximate tag of the visual obstacle. The environment is discretized into a 2D grid, where each cell represents the occupancy state of a specific area of the map. Initially, all cells are marked as free. As new detections are received, the corresponding grid regions are updated and set to an occupied value. The mapping is performed incrementally and accumulates information over time, enabling the construction of the environment based solely on visual input.

To ensure the consistency and accuracy of the 2D occupancy map, a remapping algorithm is implemented to update previously mapped AprilTags when new detections suggest a significantly different spatial configuration. Remapping occurs if the robot’s orientation changes by more than ${15}^{°}$, or if the Euclidean distance to the tag differs by $0.3$ m or more compared to the prior mapping instance. Additionally, the global position of the tag is recomputed and compared against its stored location. If the discrepancy exceeds a defined threshold, the occupancy map is updated by repositioning the associated rectangle in the new estimated location. The resulting occupancy grid is exported as a static global map file, which serves as the input for the global planner.

Manual Control Node

During the mapping stage, the robot is operated remotely using a wireless Bluetooth joystick whose inputs are interpreted as desired linear forward/backward velocities $V_x$ and lateral velocities $V_y$, as well as angular rotations around the Z axis. The robot’s direct and inverse kinematics that allow handling the system’s velocities are expressed as:

$$\left[\begin{array}{c}{v}_x\\ v_y\\ {\theta }_z\end{array}\right]={\displaystyle \frac{r}{4}}\left[\begin{array}{cccc}1& 1& 1& 1\\ -1& 1& 1& -1\\ -{\displaystyle \frac{1}{l_x+l_y}}& {\displaystyle \frac{1}{l_x+l_y}}& -{\displaystyle \frac{1}{l_x+l_y}}& {\displaystyle \frac{1}{l_x+l_y}}\end{array}\right]\left[\begin{array}{c}{\omega }_1\\ {\omega }_2\\ {\omega }_3\\ {\omega }_4\end{array}\right]={\displaystyle \frac{1}{r}}\left[\begin{array}{ccc}1& -1& -(l_x+l_y)\\ 1& 1& (l_x+l_y)\\ 1& 1& -(l_x+l_y)\\ 1& -1& (l_x+l_y)\end{array}\right]\left[\begin{array}{c}{v}_x\\ v_y\\ {\theta }_z\end{array}\right]$$

(2)

where r is the wheel radius, $l_x=0.0975\mathrm{m}$ is the longitudinal distance from the robot’s center to each wheel, $l_y=0.103\mathrm{m}$ is the lateral distance, and ${\omega }_i$ are the angular velocities of the wheels. This ensures that the omnidirectional motion commanded by the operator is accurately translated into coordinated wheel movements.

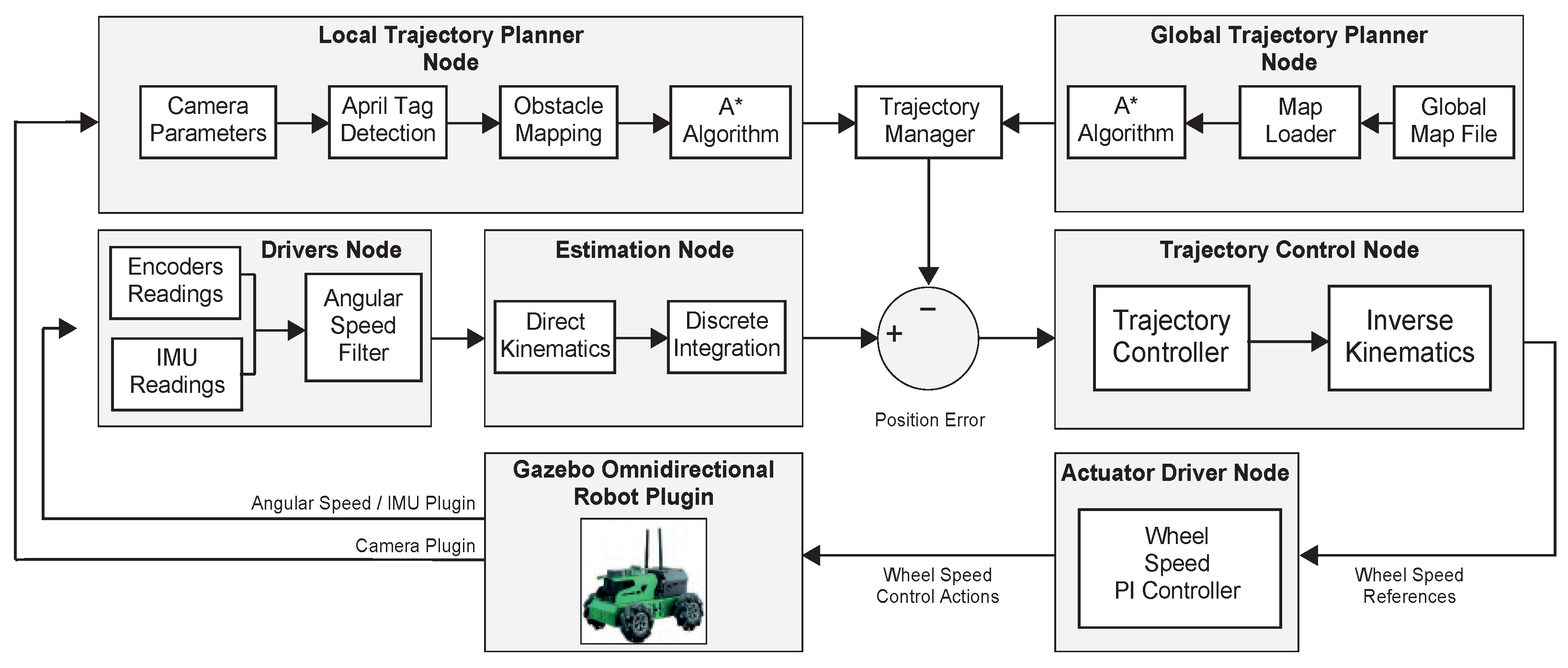
2.4. Global Trajectory Planning

The global planning subsystem shown in Figure 2 requires a map loading and binarizationprocess to plan a suitable trajectory for the robot. The module reads an input image in .png format that represents the layout of the environment. The image is first converted to grayscale, resulting in an intensity matrix $M(x,y)\in$ [0–255], where each pixel encodes a position in the environment (255 free space, 0 occupied space). The map file is converted into a binary matrix $B\in {\{0,255\}}^{H\times W}$ named a occupancy grid, where each cell represents a discrete navigable or blocked location. The regions around obstacles contain a safety margin of $5\times 5$ blocks per cell This prevents trajectories from being planned too close to narrow corridors or wall edges.

The resulting binary map is used to plan the robot’s global trajectory, the process of which requires the start and goal point in grid coordinates, yielding:

$$i_s=⌊{\displaystyle \frac{X_s-X_{min}}{\mathsf{\Delta }}}⌋,j_s=⌊{\displaystyle \frac{Y_s-Y_{min}}{\mathsf{\Delta }}}⌋\mathrm{and},i_g=⌊{\displaystyle \frac{X_g-X_{min}}{\mathsf{\Delta }}}⌋,j_g=⌊{\displaystyle \frac{Y_g-Y_{min}}{\mathsf{\Delta }}}⌋,$$

(3)

where $(X_s,Y_s)$ denotes the starting point and $(X_g,Y_g)$ the final point of the trajectory in the global frame. $(X_{\min },Y_{\min })$ are the minimum coordinate bounds of the map; $\mathsf{\Delta }$ is the map resolution (meters per cell), and $(i,j)$ is a point in the grid frame. Note that the Euclidean distance from the start to the goal must be larger than a threshold to avoid trivial short trajectories.

2.4.1. Trajectory Planning Algorithm

In this work we rely on the A* algorithm for finding the least-cost path on a weighted graph by combining the exact path cost from the start with a heuristic estimate of the cost to the goal [13]. Here, the environment is represented as the binary occupancy grid provided by the global mapping node. Formally, given a directed graph $G=(V,E)$ induced by the free cells of the grid and non-negative edge costs $c:E\to {\mathbb{R}}_{\ge 0}$, a start node $s\in V$, and a goal node $t\in V$, the algorithm assigns each vertex $v\in V$ a cost-to-come $g\left(v\right)$, representing the best-known cost from s to v, and a heuristic cost-to-go $h\left(v\right)$, representing an estimate of the optimal cost from v to t.

The evaluation function is defined as $f\left(v\right)=g\left(v\right)+h\left(v\right)$, which orders nodes in a priority queue (OPEN list) from which the next node to expand is selected. The algorithm initializes $g\left(s\right)=0$, $g\left(v\right)=+\infty$ for $v\ne s$, and inserts s into the queue with key $f\left(s\right)=h\left(s\right)$. At each step, it extracts $u=\arg {\min }_{v\in \mathcal{O}}f\left(v\right)$ from OPEN; if $u=t$, the optimal path is reconstructed by backtracking predecessors $\pi \left(v\right)$. Otherwise, for each neighbor v of u, the tentative cost is computed as $\tilde{g}\left(v\right)=g\left(u\right)+c(u,v),$ and if $\tilde{g}\left(v\right)<g\left(v\right)$, the values $g\left(v\right)\leftarrow \tilde{g}\left(v\right)$, $\pi \left(v\right)\leftarrow u$, and $f\left(v\right)\leftarrow g\left(v\right)+h\left(v\right)$ are updated, inserting v into OPEN if not already present. The choice of $h\left(v\right)$ typically reflects the Euclidean or Manhattan distance between v and t in the grid. A heuristic h is admissible if $h\left(v\right)\le h^{*}\left(v\right)$ for all v, where $h^{*}\left(v\right)$ is the true minimal cost from v to t; it is consistent if $h\left(u\right)\le c(u,v)+h\left(v\right)$ for all $(u,v)\in E$. When h is admissible, A* guarantees an optimal solution; with consistency, the algorithm never needs to reopen nodes. The resulting path is post-processed using a B-spline smoothing technique to produce a continuous and dynamically feasible trajectory.

2.4.2. Trajectory Smoothing Algorithm

In the post-processing stage of both the global and local planners, a trajectory smoothing algorithm is applied to reduce abrupt directional changes and ensure continuity in both position and curvature, thereby facilitating more accurate controller tracking. The cubic spline method is a widely used technique for generating smooth trajectories through a set of n given points [14], $P=[P_1,P_2,\dots ,P_n]$. The goal is to determine the second derivatives $M=[M_1,M_2,\dots ,M_n]$ at each point such that the spline is twice continuously differentiable. For natural splines, $M_1=0$ and $M_n=0$. For $i=2,\dots ,n-1$, the system to solve is

$${\displaystyle \frac{h_{i-1}}{6}}{M}_{i-1}+{\displaystyle \frac{h_{i-1}+h_i}{3}}{M}_i+{\displaystyle \frac{h_i}{6}}{M}_{i+1}={\displaystyle \frac{P_{i+1}-P_i}{h_i}}-{\displaystyle \frac{P_i-P_{i-1}}{h_{i-1}}},$$

where $h_i=x_{i+1}-x_i$ is the spacing between consecutive points along the independent variable. This leads to the tridiagonal system $D·M=Y$ with:

$$D=\left(\begin{array}{ccccc}1& 0& 0& \dots & 0\\ {\displaystyle \frac{h_1}{6}}& {\displaystyle \frac{h_1+h_2}{3}}& {\displaystyle \frac{h_2}{6}}& \dots & 0\\ 0& {\displaystyle \frac{h_2}{6}}& {\displaystyle \frac{h_2+h_3}{3}}& {\displaystyle \frac{h_3}{6}}& ⋮\\ ⋮& \ddots & \ddots & \ddots & {\displaystyle \frac{h_{n-2}}{6}}\\ 0& \dots & 0& 0& 1\end{array}\right),Y=\left(\begin{array}{c}0\\ y_2\\ y_3\\ ⋮\\ 0\end{array}\right),$$

(4)

where $y_i={\displaystyle \frac{P_{i+1}-P_i}{h_i}}-{\displaystyle \frac{P_i-P_{i-1}}{h_{i-1}}}$. The solution is obtained as $M=D^{-1}Y$. Here, $P_i$ are the known positions, $h_i$ the segment lengths, and $M_i$ the spline’s second derivatives at each knot. Recall that the global trajectory planner node and the local trajectory planner node apply this smoothing process. The smoothed trajectory is now passed as a trajectory message for either of the planner nodes.

2.5. Local Trajectory Planning

The local planner operates as a reactive navigation layer that complements the global trajectory. As illustrated in Figure 2, the system continuously receives updated obstacle information from the visual detection module and triggers a short replanning whenever an AprilTag is detected at less than $0.6\mathrm{m}$ from the robot. Let the robot pose be ${\mathbf{p}}_R=(x_R,y_R,{\theta }_R)$ and the pre-computed global path be ${\mathcal{P}}_{\mathrm{global}}=\{{\mathbf{g}}_0,\dots ,{\mathbf{g}}_N\}$. A temporary goal ${\mathbf{p}}_{\ell }\in {\mathcal{P}}_{\mathrm{global}}$ is chosen ahead of the robot, at least $1.0\mathrm{m}$ away, within a forward viewing angle of $\pi /2$, and located in a free cell of the occupancy grid.

The local path ${\mathcal{P}}_{\mathrm{loc}}=\{{\mathbf{q}}_0,\dots ,{\mathbf{q}}_M\}$ is computed from ${\mathbf{p}}_R$ to ${\mathbf{p}}_{\mathcal{\ell }}$ using the A* algorithm with the same formulation as in the global planner, but including an obstacle-proximity penalty to favor safer clearance. The resulting waypoints are refined by cubic B-spline smoothing with reduced tension, allowing tighter curvature radii for effective obstacle evasion.

To merge back into the global path, the last $\rho M$ points of the smoothed local path when $\rho =0.1$–$0.2$ are replaced by the corresponding waypoints of ${\mathcal{P}}_{\mathrm{global}}$ starting from index $k^{*}$, defined as the closest forward waypoint to ${\mathbf{q}}_M$. When no new obstacles are detected within the safety radius, tracking resumes along ${\mathcal{P}}_{\mathrm{global}}$ from $k^{*}$, restoring the replanning path with minimal deviation.

2.6. Trajectory Following Control

The trajectory following stage ensures that the robot accurately tracks the planned reference ${\mathbf{x}}_{\mathrm{ref}}=[x_{\mathrm{ref}},y_{\mathrm{ref}},{\theta }_{\mathrm{ref}}]$ by converting tracking errors into coordinated wheel commands according to the kinematic model in (2). Three controllers were implemented for comparison: kinematic proportional, null-space, and PI. Note that the control actions for all controllers denoted with $\mathbf{u}$, $\mathbf{w}$, and $\mathbf{a}$ in the following subsections represent a $4\times 1$ vector with the angular speed for each wheel required to position the robot according to a trajectory.

2.6.1. Kinematic Proportional Controller

The kinematic proportional controller minimizes the error between the robot’s estimated state $\mathbf{x}=[x,y,\theta ]$ and the current reference ${\mathbf{x}}_{\mathbf{d}}=[x_d,y_d,{\theta }_d]$. The control action $\mathbf{u}$ is computed as a virtual acceleration proportional to the error $\mathbf{e}=\mathbf{x}-{\mathbf{x}}_{\mathbf{d}}$ as $\mathbf{a}={\mathbf{K}}_p\mathbf{e}\mathrm{with}:\mathbf{a}={[a_x,a_y,a_{\omega }]}^{\top }.$ These accelerations are mapped into wheel angular velocities via the inverse Jacobian, yielding $\mathbf{u}={\displaystyle \frac{1}{r}}{J}^{-1}\left(\theta \right)\mathbf{a}$, where $J^{-1}\left(\theta \right)$ is the analytically derived inverse kinematic matrix of the Mecanum configuration stated in Equation (2).

2.6.2. Null-Space Controller

The null-space controller extends the standard proportional law by introducing a secondary task for orientation control that is projected onto the null space of the main x–y tracking task. The reduced Jacobian for the x–y task is denoted ${\mathbf{J}}_{1k}$; let ${\theta }_1=\theta +{\displaystyle \frac{\pi }{4}}$. The $2\times 4$ reduced Jacobian that maps wheel speeds to planar linear velocities is the first two rows of the full Jacobian in (2) is (5).

$${\mathbf{J}}_{1k}={\displaystyle \frac{r}{4}}\left[\begin{array}{cccc}\sqrt{2}cos{\theta }_1& \sqrt{2}sin{\theta }_1& \sqrt{2}cos{\theta }_1& \sqrt{2}sin{\theta }_1\\ \sqrt{2}sin{\theta }_1& -\sqrt{2}cos{\theta }_1& \sqrt{2}sin{\theta }_1& -\sqrt{2}cos{\theta }_1\end{array}\right]$$

(5)

And the corresponding null-space projection matrix is ${\mathbf{N}}_1={\mathbf{I}}_4-{\mathbf{J}}_{1k}^{†}{\mathbf{J}}_{1k}$, yielding the control law:

$$\mathbf{w}={\mathbf{J}}_{1k}^{-1}\left(\dot{{\mathbf{x}}_{\mathbf{d}}(x,y)}+k_{\mathrm{NS}}{\mathbf{e}}_{(x,y)}\right)+{\mathbf{N}}_1{\mathbf{J}}_{1k}^{-1}\left({\dot{{\mathbf{x}}_{\mathbf{d}}}}_{\left(\theta \right)}+k_{\mathrm{NS}}{\mathbf{e}}_{\left(\theta \right)}\right)$$

(6)

where $k_{\mathrm{NS}}$ is a proportional gain. The first term drives position tracking, while the second adjusts orientation without disturbing the primary task.

2.6.3. PI Controller

The PI controller also uses the inverse mapping from (2) but augments the proportional term with an integral component to eliminate steady-state error as $mathbfa={\mathbf{K}}_p\mathbf{e}+{\mathbf{K}}_i\int \mathbf{e}dt$ where ${\mathbf{K}}_i$ is the integral gain matrix.

3. Results

To evaluate the proposed trajectory controllers, two 6 × 6 m maze-like environments were created in Gazebo using the same Python-based generation algorithm to ensure comparable complexity and obstacle density. AprilTags were placed on maze walls as visual landmarks for obstacle detection. The three controllers tested were (i) a Lyapunov-based proportional controller with gain $K_p=3.1$, (ii) a null-space Lyapunov controller with orientation gain $k_{NS}=1.5$, and (iii) a PI controller with gains $K_p=1.9$ and $K_i=0.015$.

The evaluation comprised two stages. In the offline mapping phase, the robot detected AprilTags and built an occupancy grid of the static environment, from which a global path was planned with A*. In the second phase, additional AprilTags simulated dynamic obstacles. When the front-facing monocular camera detected a new tag within 0.6 m, local replanning was triggered using A* on the updated map. The robot followed the local path until the obstacle cleared, then progressively rejoined the global path. Three controllers were tested in both mazes under identical trajectories and replanning strategies, recording position tracking errors and control effort for performance metrics.

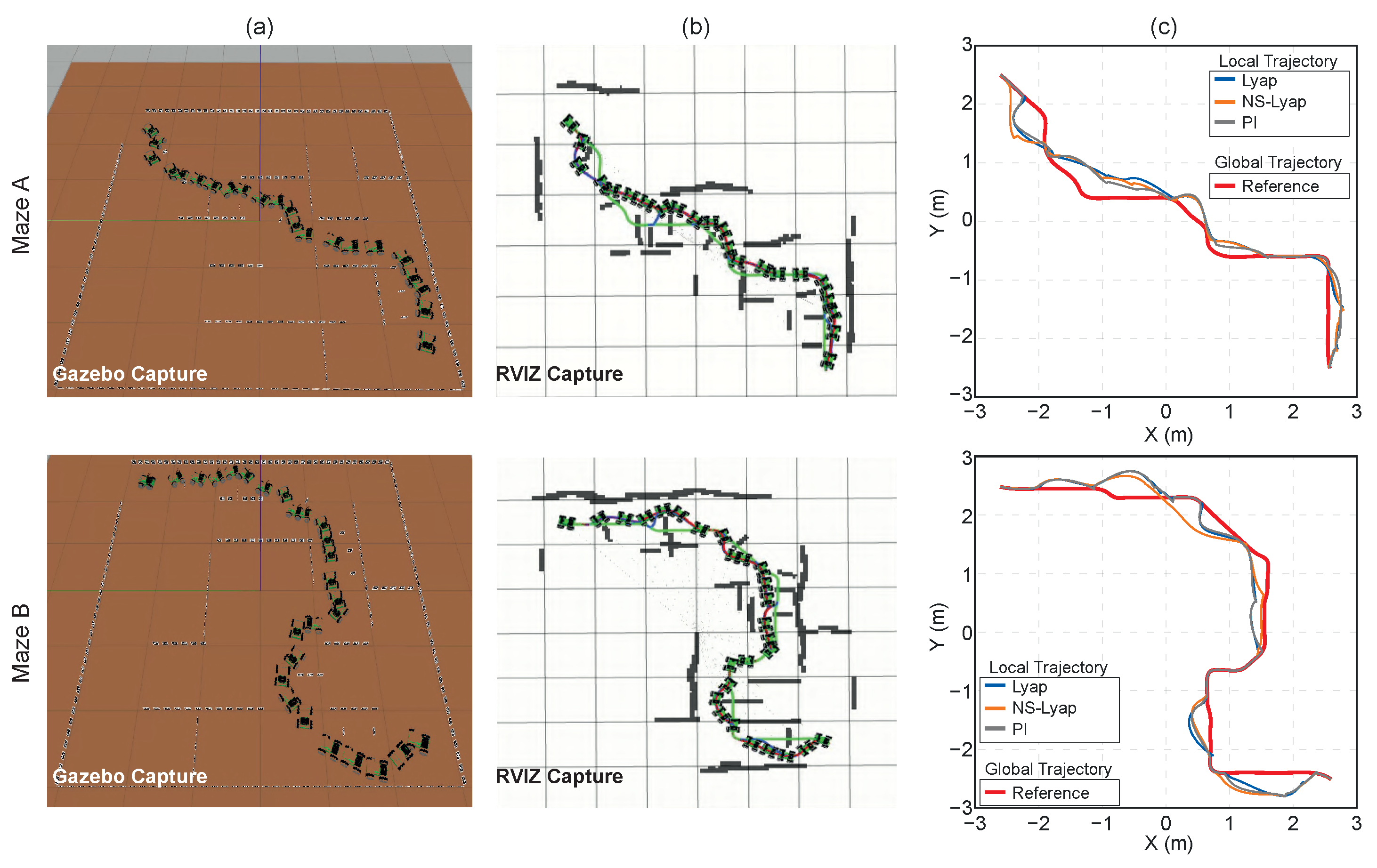
Figure 3 shows the navigation results in two test environments: (a) Maze A and (b) Maze B. The red curve is the initial global path, the green curve is the locally replanned path triggered by AprilTag-based detection of unmapped obstacles, and the black curve is the robot’s actual trajectory. Blue rectangles mark dynamically detected AprilTags absent from the initial occupancy map. The results demonstrate the robot’s ability to avoid unforeseen obstacles and rejoin the original path, validating the integration of local planning with visual perception.

Figure 4 summarizes the experiments in both mazes with three trajectory-tracking controllers: (a) Gazebo setup for Maze A/B with JetAuto following the reference; (b) RViz overlays the robot’s estimated pose and trajectory on the AprilTag-based occupancy grid; (c) comparison of the reference trajectories and the actual robot trajectories. The apparent deviations from the global path occurred when the robot performed local replanning upon detecting new obstacles. In these cases, the controllers correctly followed the local reference, allowing the robot to bypass obstacles safely before rejoining the global path.

Table 1. Performance metrics for trajectory tracking in Maze A and Maze B. Position metrics include ISE, RMSE, and maximum deviation, while MTE corresponds to control effort.

Controller	Maze A				Maze B
	ISE [m2·s]	RMSE [m]	Max. Dev. [m]	MTE [rad/s]	ISE [m2·s]	RMSE [m]	Max. Dev. [m]	MTE [rad/s]
Lyap	13.2599	0.5155	0.8284	1.4003	15.5878	0.4943	0.9554	2.4671
NS-Lyap	5.9513	0.3450	0.7045	1.6868	5.0709	0.2824	0.5632	2.0070
PI	33.7037	0.8235	1.3612	1.8244	38.1450	0.7690	1.4428	1.8193

shows that NS-Lyap consistently achieved the best tracking in both mazes, yielding the lowest ISE, RMSE, and maximum deviation, and remaining accurate even during local replanning triggered by obstacle detections. By contrast, the PI controller produced the largest positional errors and the highest peak deviations, although it required the least control effort with lowest MTE. The standard Lyapunov controller was intermediate, balancing accuracy and command smoothness.

4. Conclusions

This work presented a complete simulation framework for autonomous navigation of an omnidirectional mobile robot using AprilTags as visual landmarks, integrating high-fidelity modeling, global and local planning, trajectory smoothing, and trajectory tracking controllers within the ROS and Gazebo environment. The proposed system addresses the challenges of navigation in dynamic environments by combining an offline mapping stage with global planning based on the A* algorithm, and an online local replanning strategy triggered by real-time detection of previously unmapped obstacles. The incorporation of morphological dilation in the occupancy grid generation proved essential for increasing path safety margins, while the trajectory smoothing stage—implemented via collinearity reduction and cubic B-splines—ensured continuous, dynamically feasible paths for the controller. Simulation results in two maze-like environments validated the ability of the system to detect and avoid dynamic obstacles, rejoin the global path, and maintain high tracking precision despite trajectory deviations. This confirms the robustness of the integrated planning–perception–control pipeline under uncertainty and noise conditions.

Future work will focus on extending the validation to real-world platforms, incorporating additional perception modalities such as LiDAR or depth cameras, and exploring adaptive control strategies to further enhance robustness in highly dynamic and unstructured environments.