Local and Global Optimization Methods for Power System Models: A Case Study on the Optimal Charging and Discharging Scheduling of Vehicle-to-Grid (V2G) Systems †
Abstract
1. Introduction
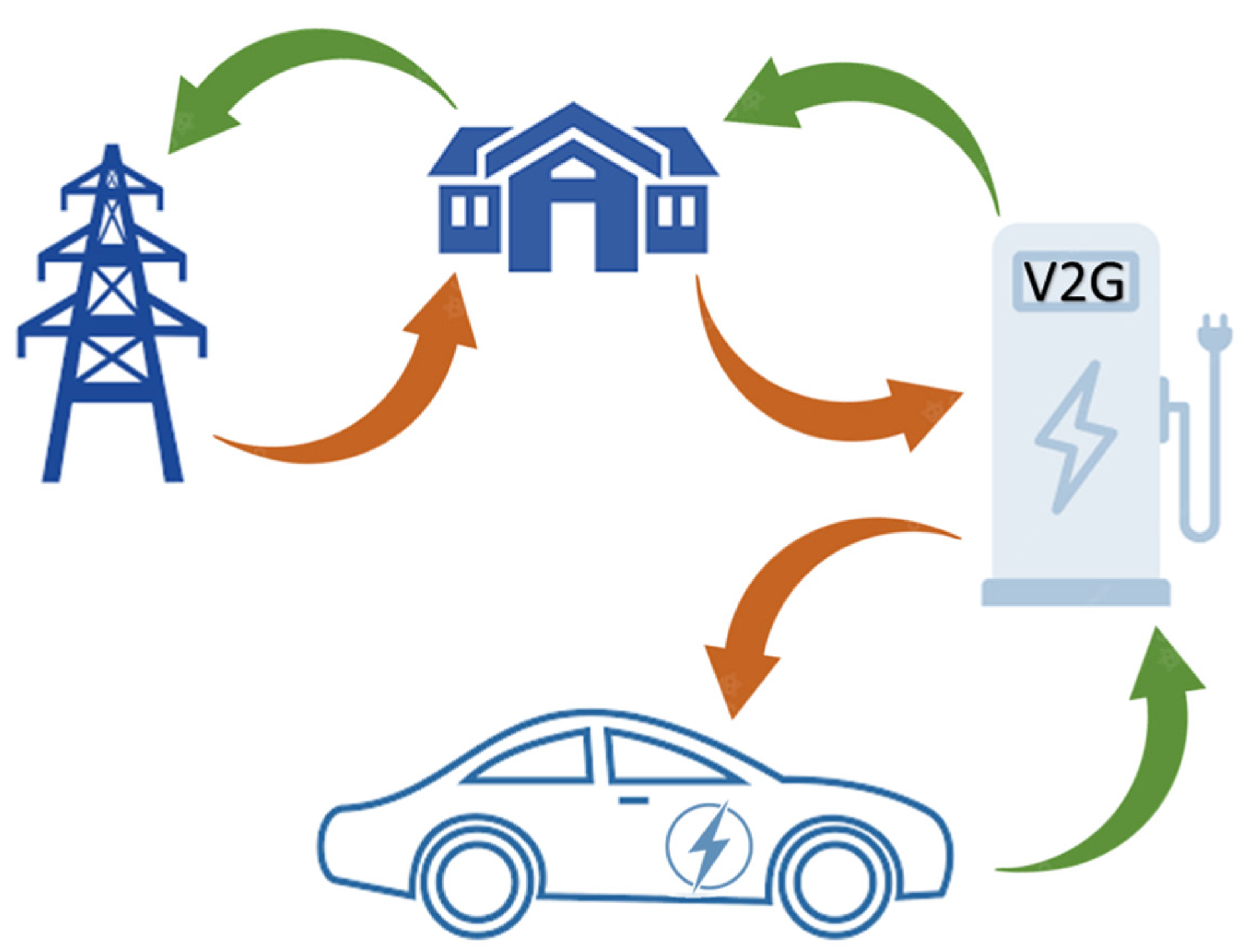
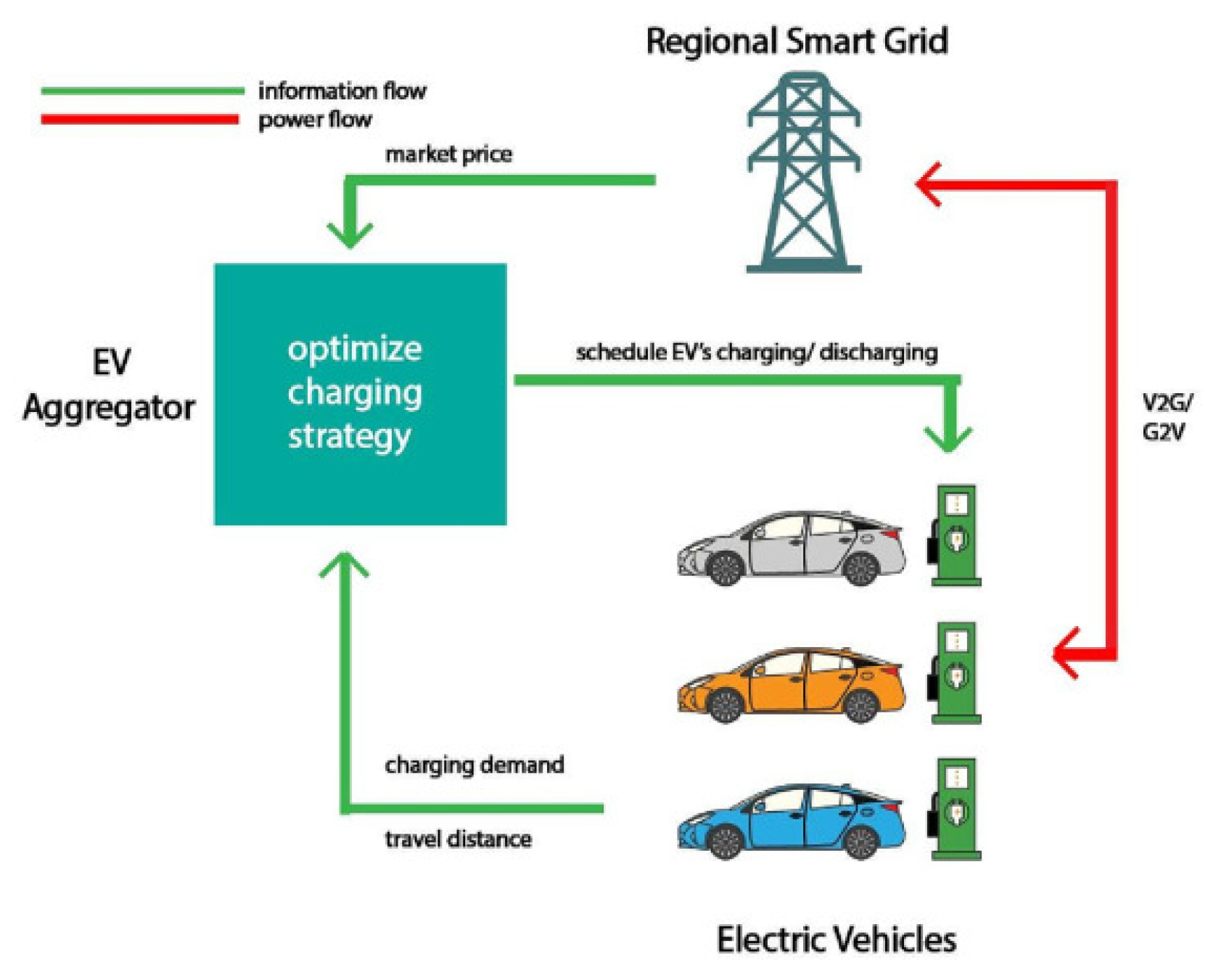
2. Vehicle-to-Grid (V2G) Schemes
3. Charging and Discharging Process of Electric Vehicles
- Uncoordinated Strategies: This strategy is very commonly used and involves a scheme that does not take scheduling into account. As it is a process that does not consider coordination, it does not make use of optimization techniques or price tracking mechanisms. It can be related to a purely random process, simply taking into account the connection of the electric vehicle to the grid [17].
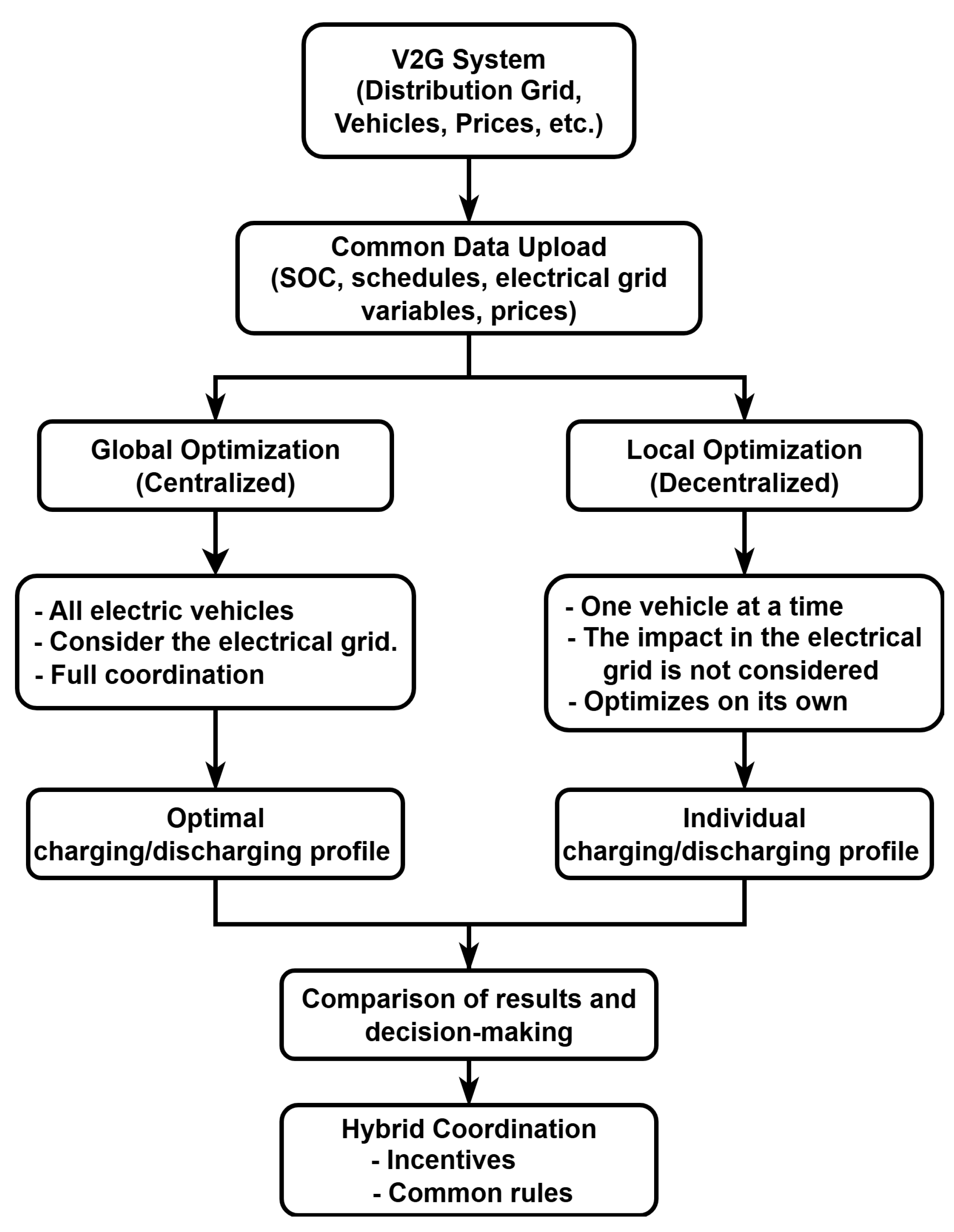
4. Global and Local Optimization Methods
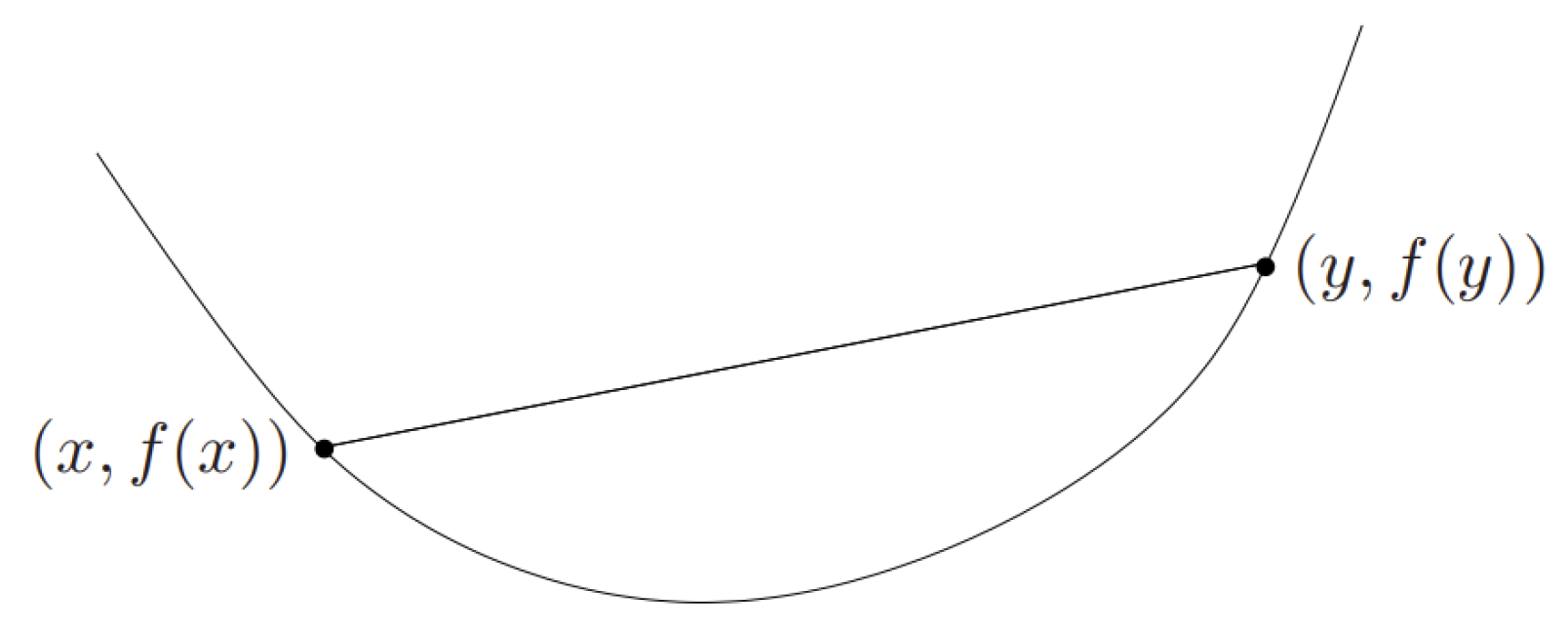
5. Convex Method Algorithm for Solving Global and Local Optimization
6. Materials and Methods
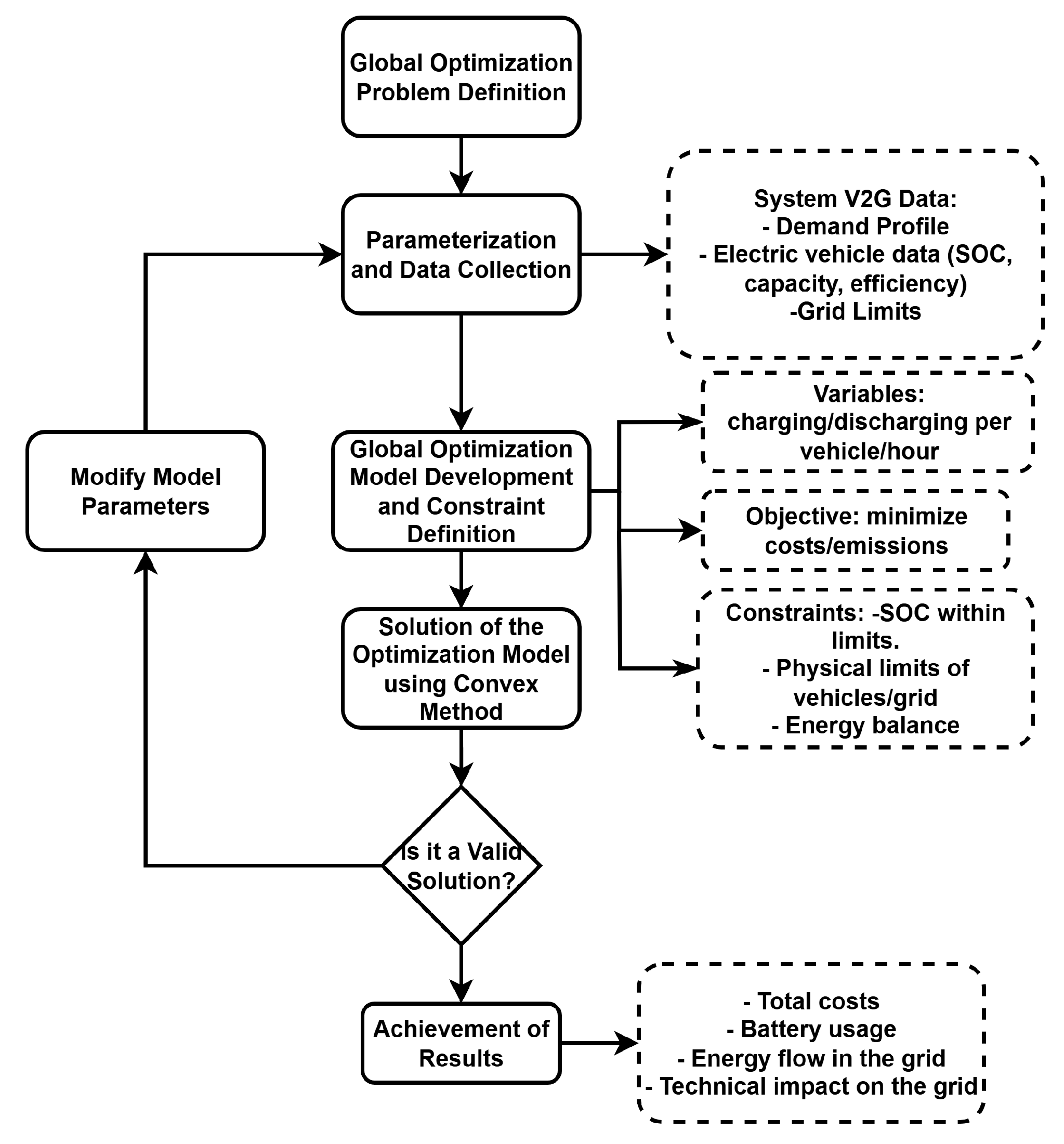
6.1. Global Optimization Process
- Active Power Limits per Electric Vehicle:
- Evolution and Dynamics of SOC:
- SOC Limits:
- Required SOC Final:
- Global Power Balance per Hour:
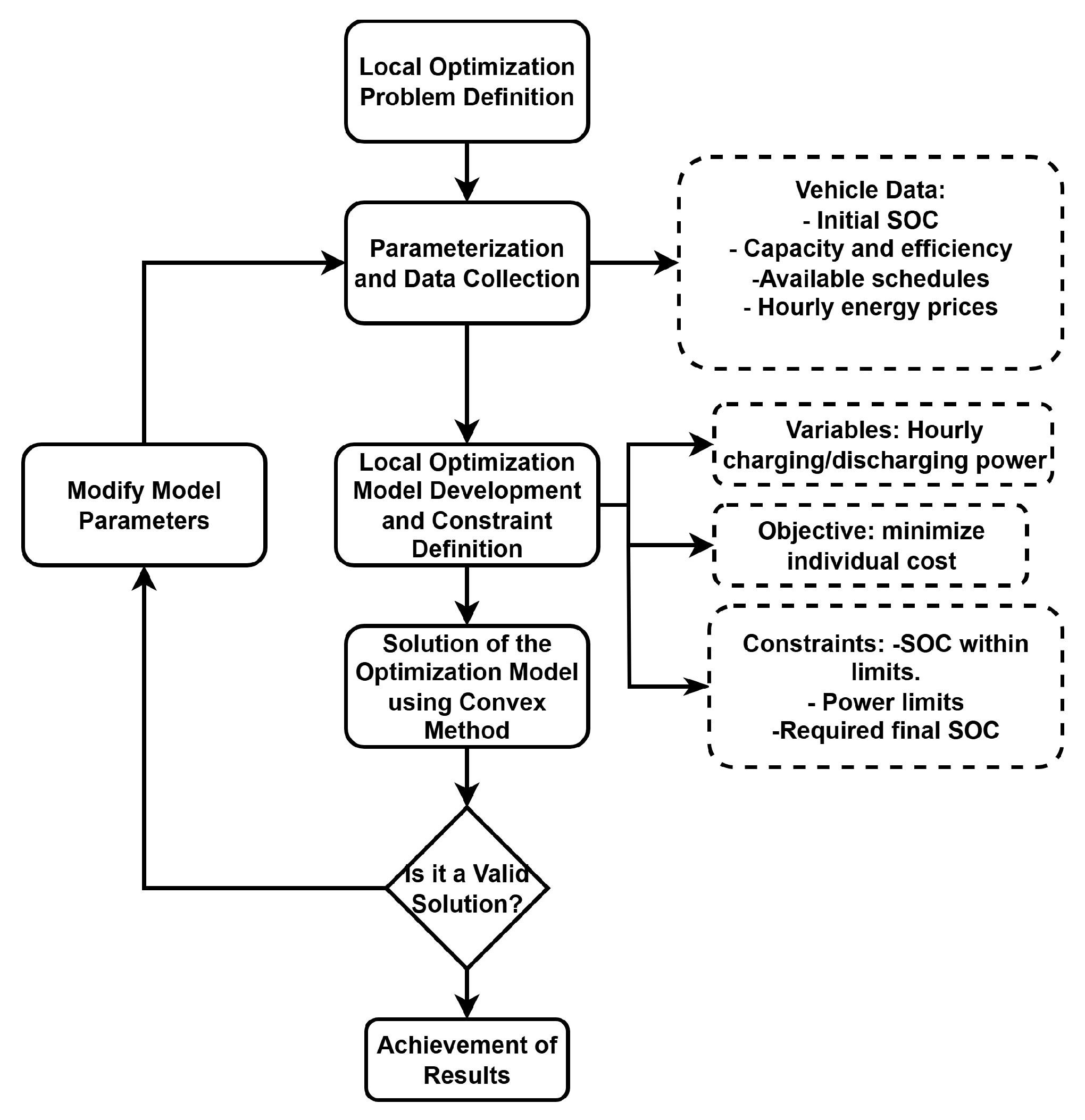
6.2. Local Optimization Process
- Objective Function:
- Limits EV Charging and Discharging Power per Hour:
- Evolution and Dynamics of SOC:
- SOC Limits:
7. Results and Discussion
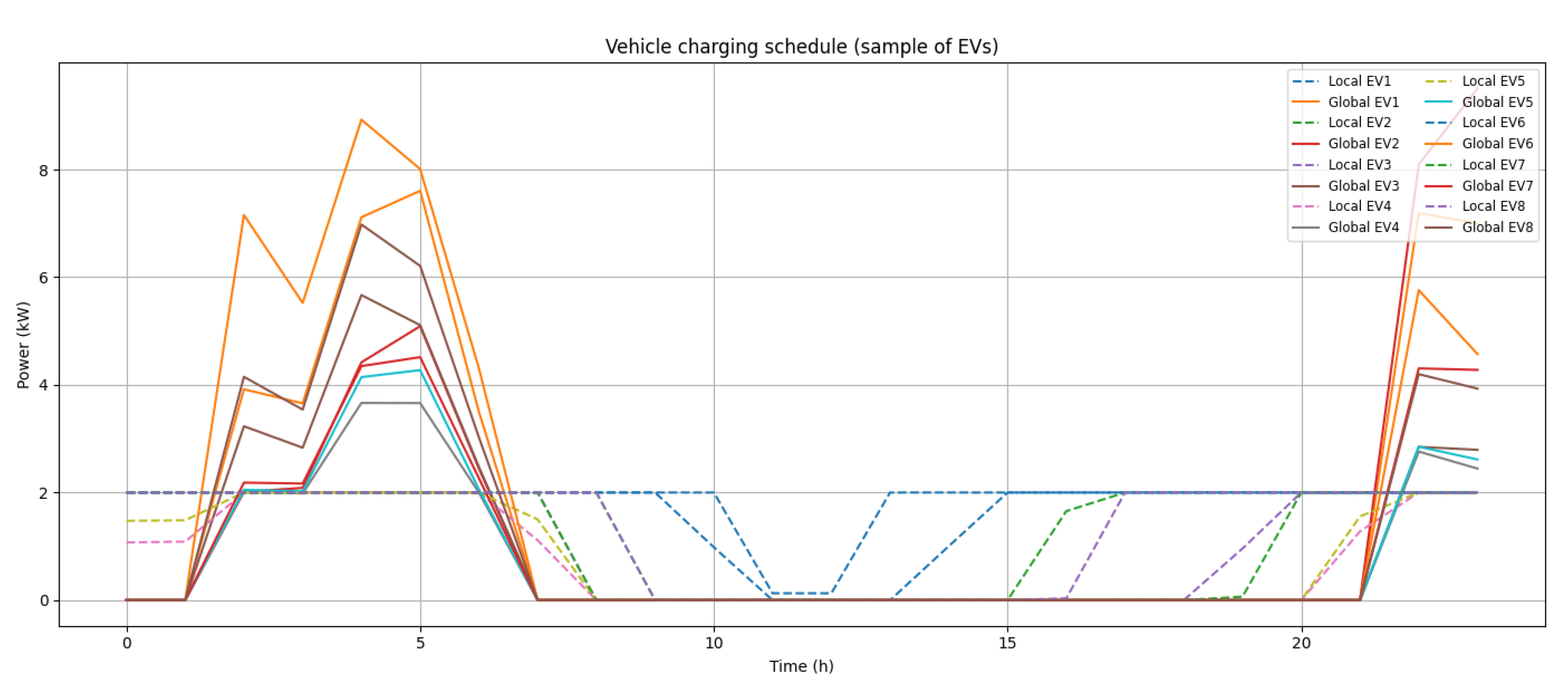
- Local Optimization: A specific power limit per hour is defined for each vehicle. Planning is carried out independently for each EV.
- Global Optimization: A total power limit is defined, which is shared by all EVs every hour. Planning is carried out jointly for all EVs, and the minimum total cost of the system is sought.
- Local: The maximum power allocated per vehicle = 2 kW per hour.
- Global: total power available per hour = 6 kW.
- Local Optimization Scenario: each vehicle will be charged independently, and its maximum individual power (2 kW) will be limited, without sharing resources with other vehicles.
- Global Optimization Scenario: all vehicles will share a total power limit of 6 kW. In addition, the optimization process will decide how to distribute this energy to minimize the total cost.
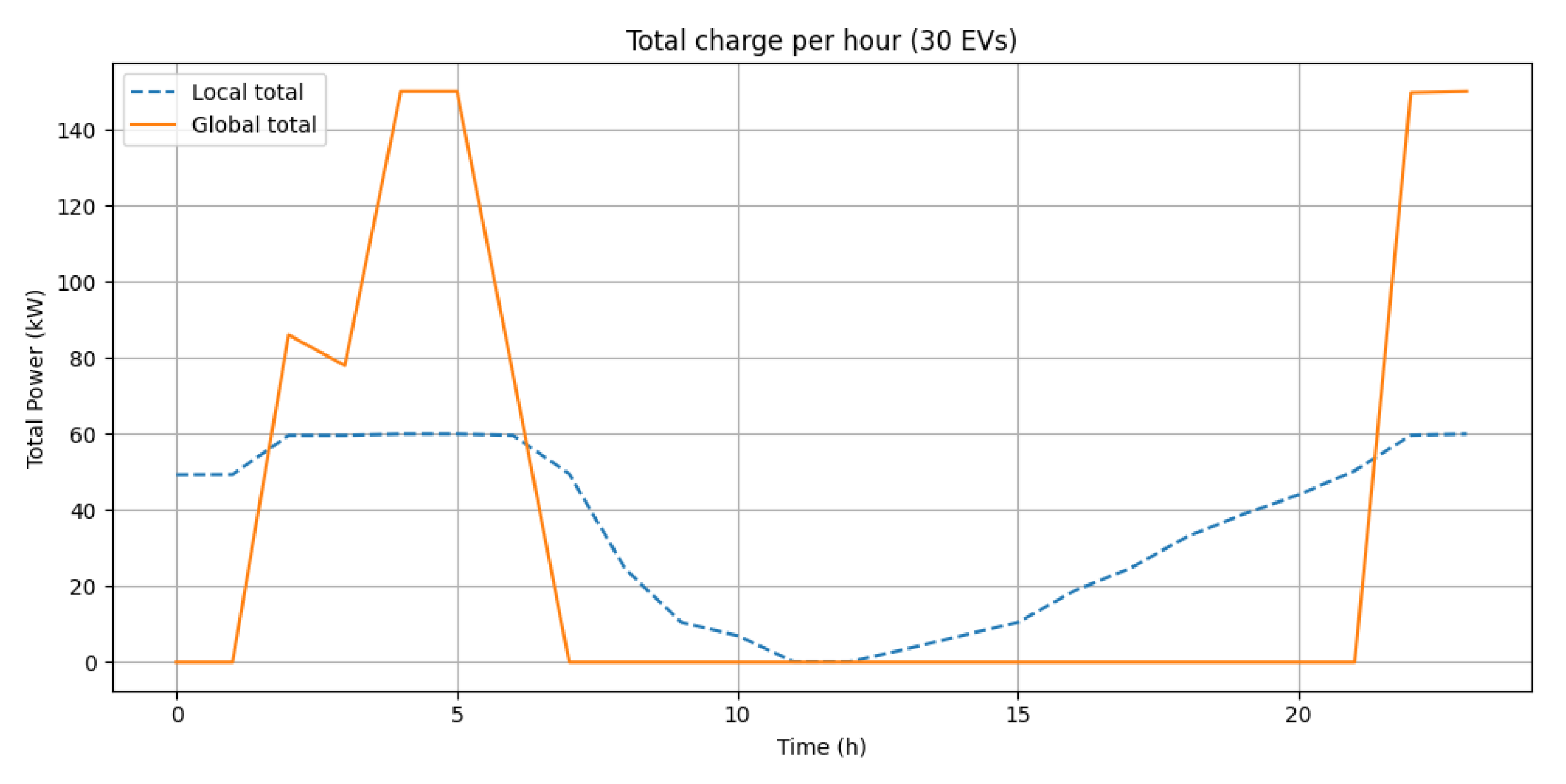
Case of Study
- Total energy charged (Local): 839.35 kWh;
- Total energy charged (global): 839.35 kWh.
- Total cost (Local): $106.23;
- Total cost (Global): $87.83.
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Total number of electric vehicles | |
| T | Number of time intervals (hours) |
| Grid energy price over time t [$/kWh] | |
| Maximum charging/discharging power of the vehicle v [kW] | |
| , | Charging and discharging efficiency |
| , | Charge status limits [kWh] |
| E | Battery capacity [kWh] |
| Vehicle battery capacity v [kWh] | |
| D(t) | Grid demand over time t [kW] |
| G(t) | Renewable generation available over time t [kW] |
| Minimum SOC required at the end of the horizon [kWh] |
References
- Kempton, W.; Tomić, J. Vehicle-to-Grid power implementation: From stabilizing the grid to supporting large-scale renewable energy. J. Power Sources 2005, 144, 280–294. [Google Scholar] [CrossRef]
- Lascano, J.; Chiza, L.; Saraguro, R.; Quinatoa, C.; Tapia, J. Demand Estimation for an Electric Vehicles Charging Station Through the Application of Probabilistic Methods. Rev. Técnica Energía 2023, 20, 52–64. [Google Scholar] [CrossRef]
- Bortotti, M.F.; Rigolin, P.; Udaeta, M.E.M.; Grimoni, J.A.B. Comprehensive Energy Analysis of Vehicle-to-Grid (V2G) Integration with the Power Grid: A Systemic Approach Incorporating Integrated Resource Planning Methodology. Appl. Sci. 2023, 13, 11119. [Google Scholar] [CrossRef]
- Shaheen, H.I.; Rashed, G.I.; Yang, B.; Yang, J. Optimal electric vehicle charging and discharging scheduling using metaheuristic algorithms: V2G approach for cost reduction and grid support. J. Energy Storage 2024, 90, 111816. [Google Scholar] [CrossRef]
- Yang, J.; He, L.; Fu, S. An improved PSO-based charging strategy of electric vehicles in electrical distribution grid. Appl. Energy 2024, 128, 82–92. [Google Scholar] [CrossRef]
- Amir, M.; Zaheeruddin; Haque, A. Optimal scheduling of charging/discharging power and EVs pattern using stochastic techniques in V2G system. In Proceedings of the 2021 IEEE Transportation Electrification Conference (ITEC-India), New Delhi, India, 16–19 December 2021; IEEE: New York, NY, USA, 2021. [Google Scholar]
- Zheng, Z.; Yang, S. Particle swarm optimisation for scheduling electric vehicles with microgrids. In Proceedings of the 2020 IEEE Congress on Evolutionary Computation (CEC), Glasgow, UK, 19–24 July 2020; IEEE: New York, NY, USA, 2020. [Google Scholar]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Mosammam, Z.M.; Ahmadi, P.; Houshfar, E. Multi-objective optimization-driven machine learning for charging and V2G pattern for plug-in hybrid vehicles: Balancing battery aging and power management. J. Power Sources 2024, 608, 234639. [Google Scholar] [CrossRef]
- Jones, D. A Taxonomy of Global Optimization Methods Based on Response Surfaces. J. Glob. Optim. 2001, 21, 345–383. [Google Scholar] [CrossRef]
- Bertsimas, D.; Margaritis, G. Global optimization: A machine learning approach. J. Glob. Optim. 2025, 91, 1–37. [Google Scholar] [CrossRef]
- Floudas, C.A.; Visweswaran, V. A global optimization algorithm (GOP) for certain classes of nonconvex NLPs—I. Theory. Comput. Chem. Eng. 1990, 14, 1397–1417. [Google Scholar] [CrossRef]
- Bagirov, A.M.; Rubinov, A.; Zhang, J. Local Optimization Method with Global Multidimensional Search. J. Glob. Optim. 2005, 32, 161–179. [Google Scholar] [CrossRef]
- Mantica, S.; Cominelli, A.; Mantica, G. Combining Global and Local Optimization Techniques for Automatic History Matching Production and Seismic Data. SPE J. 2001, 7. [Google Scholar] [CrossRef]
- He, C.; Peng, J.; Jiang, W.; Wang, J.; Du, L.; Zhang, J. Vehicle-To-Grid (V2G) Charging and Discharging Strategies of an Integrated Supply–Demand Mechanism and User Behavior: A Recurrent Proximal Policy Optimization Approach. World Electr. Veh. J. 2024, 15, 514. [Google Scholar] [CrossRef]
- Qiu, Z. Research and Analysis on V2G Technology and Its Application. Highlights Sci. Eng. Technol. 2023, 68, 141–149. [Google Scholar] [CrossRef]
- El-Bayeh, C.Z.; Alzaareer, K.; Aldaoudeyeh, A.-M.I.; Brahmi, B.; Zellagui, M. Charging and Discharging Strategies of Electric Vehicles: A Survey. World Electr. Veh. J. 2021, 12, 11. [Google Scholar] [CrossRef]
- Khodayar, M.E.; Wu, L.; Shahidehpour, M. Hourly coordination of electric vehicle operation and volatile wind power generation in SCUC. IEEE Trans. Smart Grid 2012, 3, 1271–1279. [Google Scholar] [CrossRef]
- Mahmud, I.; Medha, M.B.; Hasanuzzaman, M. Global challenges of electric vehicle charging systems and its future prospects: A review. Res. Transp. Bus. Manag. 2023, 49, 101011. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]



| Parameter | Value |
|---|---|
| Number of EV | 30 |
| Time Horizon | 24 h |
| Battery Capacity | (40, 45, 50) [kWh] Average |
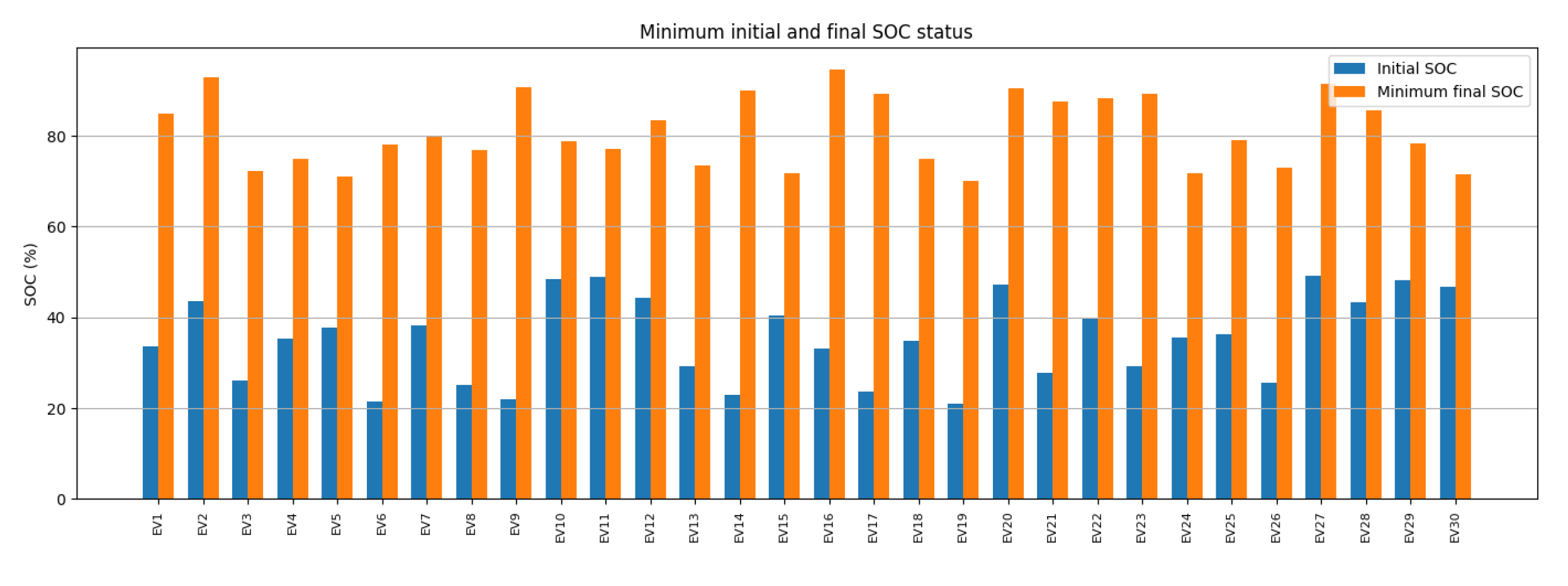
| Initial SOC | (0.2, 0.3, 0.4) Average |
| Final Min SOC | (0.9, 0.85, 0.8) Average |
| Electricity Prices | changing per hour [$/kWh] |
| Energy | Total |
|---|---|
| Local Energy [kWh] | 839.35 |
| Global Energy [kWh] | 839.35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chiza, L.; Aguayo, A.; Chiza, M. Local and Global Optimization Methods for Power System Models: A Case Study on the Optimal Charging and Discharging Scheduling of Vehicle-to-Grid (V2G) Systems. Eng. Proc. 2025, 115, 25. https://doi.org/10.3390/engproc2025115025
Chiza L, Aguayo A, Chiza M. Local and Global Optimization Methods for Power System Models: A Case Study on the Optimal Charging and Discharging Scheduling of Vehicle-to-Grid (V2G) Systems. Engineering Proceedings. 2025; 115(1):25. https://doi.org/10.3390/engproc2025115025
Chicago/Turabian StyleChiza, Luis, Adrián Aguayo, and Marck Chiza. 2025. "Local and Global Optimization Methods for Power System Models: A Case Study on the Optimal Charging and Discharging Scheduling of Vehicle-to-Grid (V2G) Systems" Engineering Proceedings 115, no. 1: 25. https://doi.org/10.3390/engproc2025115025
APA StyleChiza, L., Aguayo, A., & Chiza, M. (2025). Local and Global Optimization Methods for Power System Models: A Case Study on the Optimal Charging and Discharging Scheduling of Vehicle-to-Grid (V2G) Systems. Engineering Proceedings, 115(1), 25. https://doi.org/10.3390/engproc2025115025






