Developing Longitudinal Vehicle Dynamics Model of Electric Bicycles for Virtual Validation of Active Safety Systems ^†

Abstract

The increasing adoption of electric bicycles (e-bikes) has led to a growing need for advanced active safety systems, such as anti-lock braking systems (ABSs), to enhance rider safety. In recent years, both hydraulic and electromechanical ABSs were researched. To support the development and validation of these systems, this paper presents a longitudinal vehicle dynamics model of an electric bicycle. The model captures key physical interactions, including drivetrain, transmission, braking, and tire–road contact, to accurately simulate longitudinal motion. By leveraging this model, future studies can perform virtual validation of active safety components in a controlled and repeatable environment, reducing the dependency on costly and time-intensive physical testing. The proposed model lays the foundation for a model-based design approach, enabling early-stage performance assessment and optimization of safety-critical functions in electric bicycles.

1. Introduction

In the past ten years, the shift towards electrification has revolutionized personal transportation by introducing electric scooters and electric bicycles. This trend of electrification provides an efficient and environmentally friendly option for urban travel. However, with the increasing popularity of electric bicycles (e-bikes) comes challenges, particularly in maintaining rider safety due to their increased speeds and weights compared to regular bicycles. A significant aspect of this challenge is to ensure reliable braking performance. Active safety systems, such as antilock brake systems (ABSs), have demonstrated potential in preventing wheel lockup and improving stability during emergency stops [1].

Recent studies indicate a growing interest in ABS solutions and active safety systems being implemented for e-bikes. The development and validation of these systems remain resource-intensive and require repeated field tests and costly hardware iterations. Simulations and virtual validation methods address the challenges associated with prototype-driven physical development by using simulation models and model-based development instead of prototype-driven development [2].

This work focuses on the development of a high-fidelity longitudinal vehicle dynamics model of an electric bicycle. The model presented in this paper captures the main components of an electronic bike, including the vehicle body, drivetrain, transmission, brakes, and tire–road contact.

The model is used to evaluate the braking performance of a specific e-bike under different road conditions. Road conditions represent dry, wet, snowy, and icy road conditions, and the effects of the tire–road interaction under different conditions are evaluated. With this work, a baseline is created for evaluating different control algorithms for e-bike ABSs; thus the significance of this model for virtual verification of ABS solutions is crucial.

2. Materials and Methods

The scope of this section is to highlight the methods and modeling techniques for creating a longitudinal vehicle model of an e-bike that can evaluate the braking performance of a bicycle. The method for creating the longitudinal model is model-based design (MBD). Using MBD we can model both a control loop and the physical model that serves as a plant model for control verification and validation. When it comes to control system modeling, casual modeling techniques are used, where signal-driven systems are developed. However, for plant models, acausal modeling techniques are used, where instead of a signal-driven modeling philosophy, component-driven modeling is used [3,4].

The modeling process is carried out in Simulink and Simscape, which support acausal, equation-based representation. Using Simulink for the modeling method, we achieve a modeling environment for virtual experimentation under a wide range of operating conditions without the need for physical prototypes.

2.1. Longitudinal Model of the Electric Bicycle

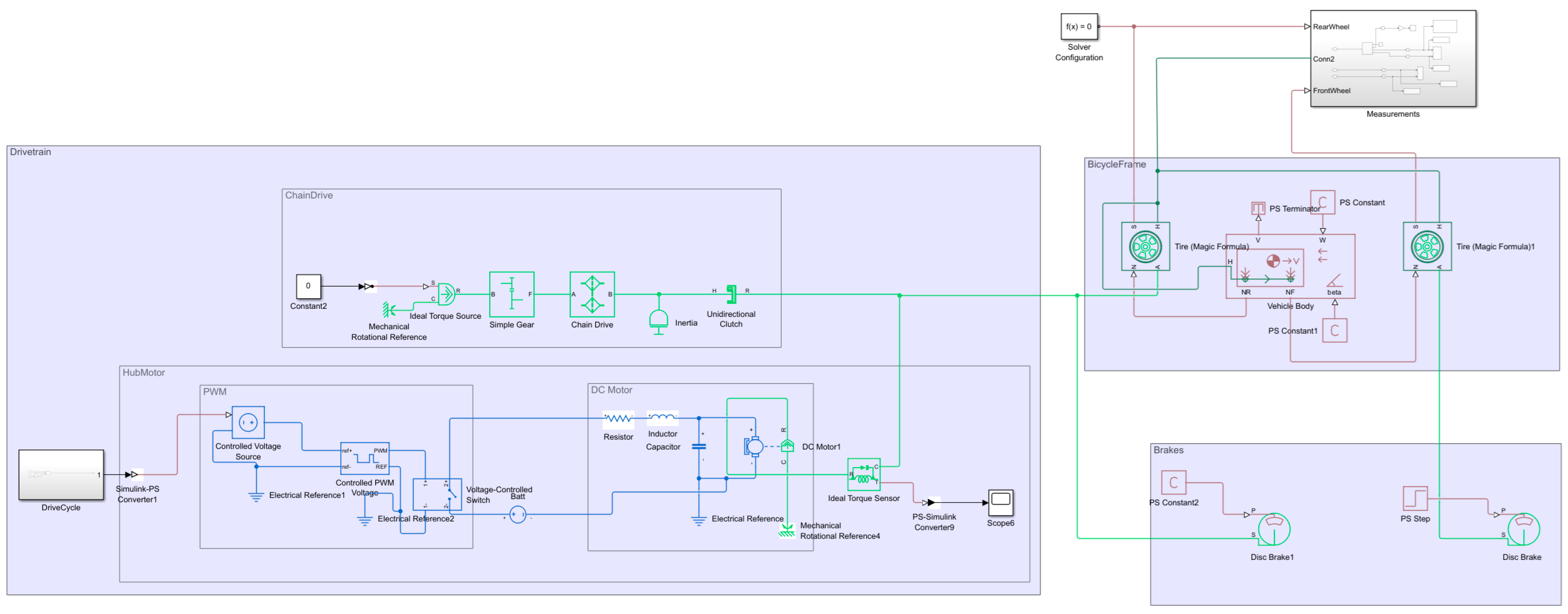
For developing the model of the e-bike, it was crucial to choose the right level of model fidelity that is appropriate for validating active safety functions. In order to capture the wheel slip for later ABS development, it is necessary to have realistic tire–road interaction. On the other hand, the lateral motion of the bicycle was neglected, and only longitudinal motion was modeled. We created a simulation model with the previously described requirements, which consists of the following main components:

• Bicycle frame;
• Wheels and brakes;
• Drivetrain.

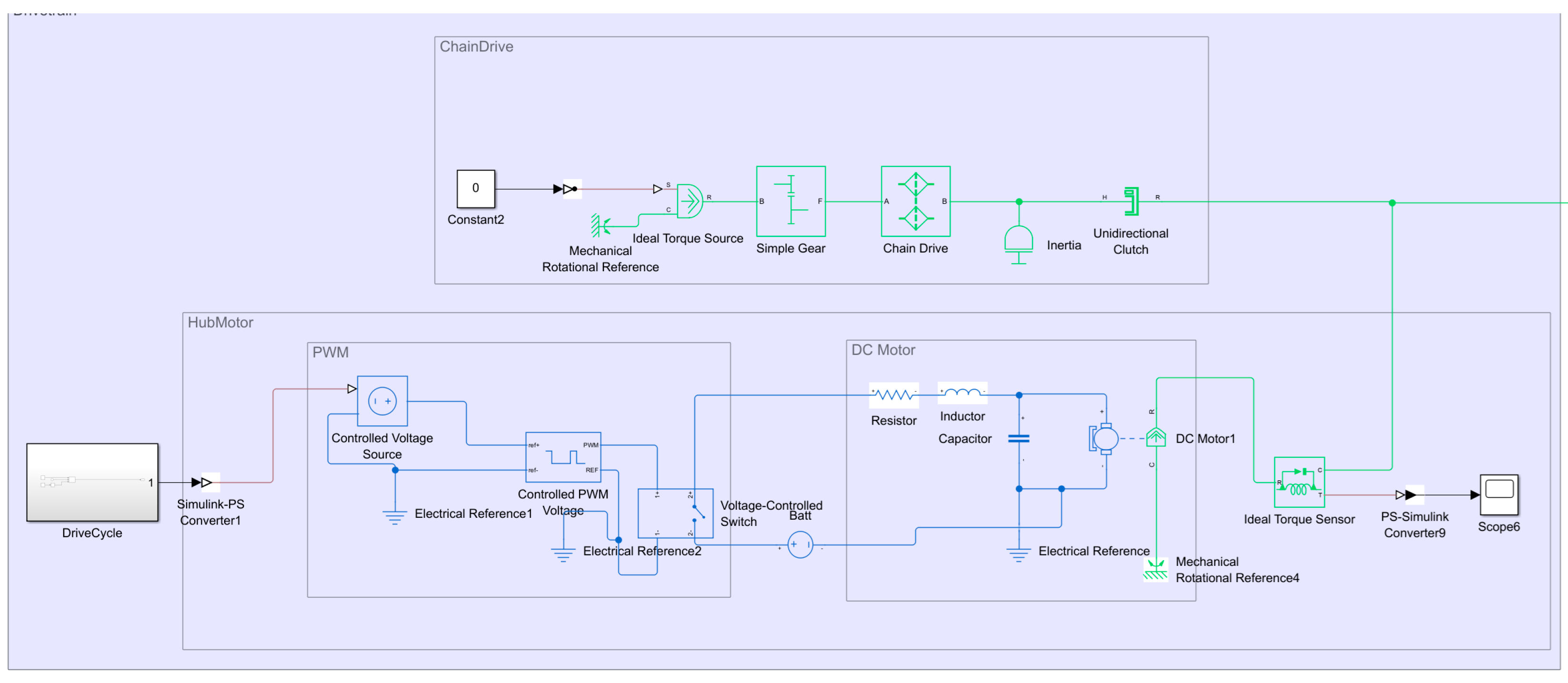
The components and their interfaces are represented in Figure 1.

2.1.1. Bicycle Frame

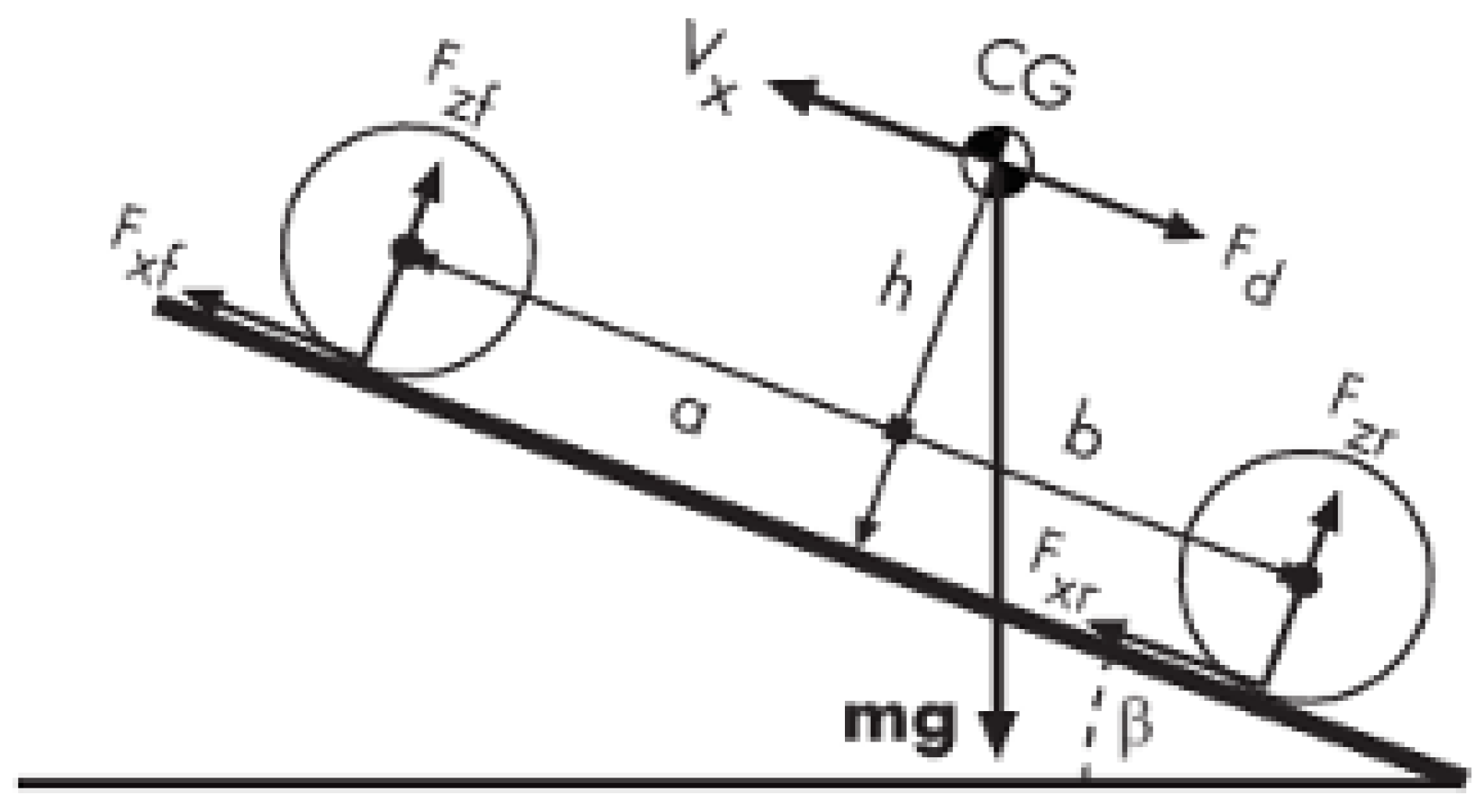
The bicycle frame is at the center of development and is modeled as a rigid body, characterized by its geometry and mass distribution. The bicycle frame also determines the number of wheels per axle and the distribution of the axles throughout the geometry of the bicycle. The bicycle frame also defines the center of gravity (COG).

Figure 2 shows the mechanical model of the bicycle frame used for the model. The frame represents a two-axle vehicle, where the axles are parallel to each other and form a plane.

The equations for the vehicle body are as follows:

$$m\dot{V_x}= F_x-F_d-mg sin\beta$$

(1)

where $F_x$ and $F_d$ are

$$F_x= n\left(F_{x}f+F_{x}r \right)$$

(2)

$$F_d= {\displaystyle \frac{1}{2}}{C}_d\rho A\left(V_x+V_w\right)\cdot sgn\left(V_x+V_w\right)$$

(3)

The variables and parameters used in Equations (1)–(3) are described in

Table 1. Variables of the vehicle model equations.

Symbol	Note
$m$	Mass of the vehicle, including rider
$h$	Height of bicycle’s center of gravity (CoG)
$g$	Gravitational acceleration
$\beta$	Road inclination angle
$a,b$	Distance of front and rear axles from the CoG
$V_x$	Velocity of the vehicle—positive value means forward movement
$V_w$	Velocity of the wind—positive value means headwind
$n$	Number of wheels per axle
$F_{x_f},F_{x_r}$	Longitudinal forces on each wheel
$F_{z_f},F_{z_r}$	Normal load forces on each wheel
$A$	Vehicle frontal area
$C_d$	Aerodynamic drag coefficient
$\rho$	Density of air
$F_d$	Aerodynamic drag force

.

2.1.2. Wheels and Brakes

The wheels and brake models are important for this study, as we are developing models to evaluate the braking distance and time for the bicycle and will use the developed model to evaluate ABS algorithms in later studies. In the following, we describe both the wheels and brake models.

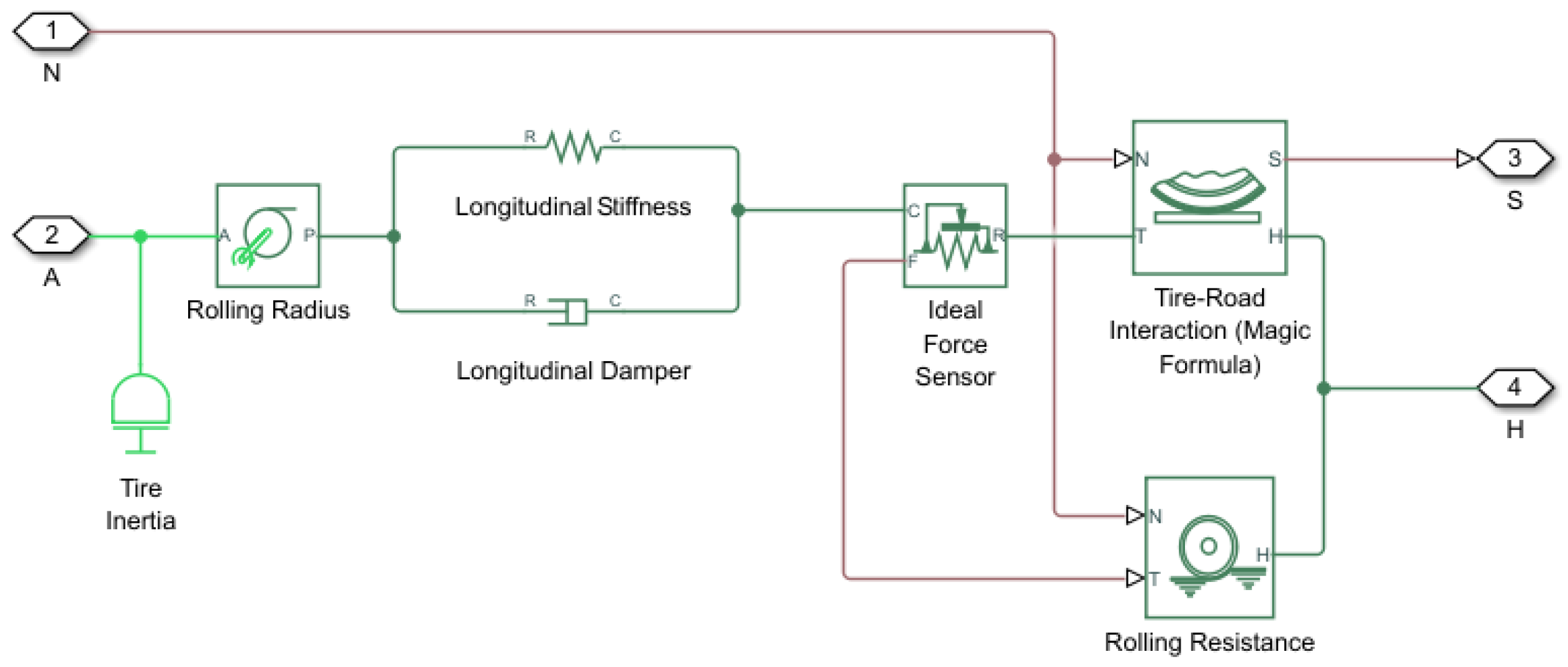
2.1.3. Wheels and Tires

The wheels represent a longitudinal wheel model, with tire dynamics being defined by the Magic Formula. The longitudinal motion axis of the wheels is the same as the longitudinal motion axis of the vehicle frame. The model considers that the wheel is in contact with the road and is subject to wheel slip. When torque is applied to the axle of the wheel, it causes the wheel to rotate. This rotation is transmitted through the tire to generate a longitudinal force, $F_x$, at the contact patch with the road surface. In response, the road applies an equal and opposite reaction force to the tire, which propels the wheel, and thus the bicycle, forward, resulting in longitudinal motion [6,7].

The general form of the Magic Formula is as follows:

$$y=D sin sin \left\{C arctan arctan \left[Bx-E\left(Bx-arctan arctan \left(Bx\right) \right)\right] \right\}$$

(4)

The coefficients $B,C,D,E$ are empirical coefficients called fitting coefficients [6]. A representation of the tire and wheel model is shown in Figure 3.

The tire–road interaction can be influenced by modifying the parameters B, C, D, and E. Within simulations, 3 road conditions are modeled, and the effects of different road surfaces are investigated. The parameters and the road surfaces are shown in

Table 2. Magic Formula parameters for different road surfaces [9].

Surface	B	C	D	E
Dry Tarmac	10	1.9	1	0.97
Wet Tarmac	12	2.3	0.82	1
Snow	5	2	0.3	1
Ice	4	2	0.1	1

[7].

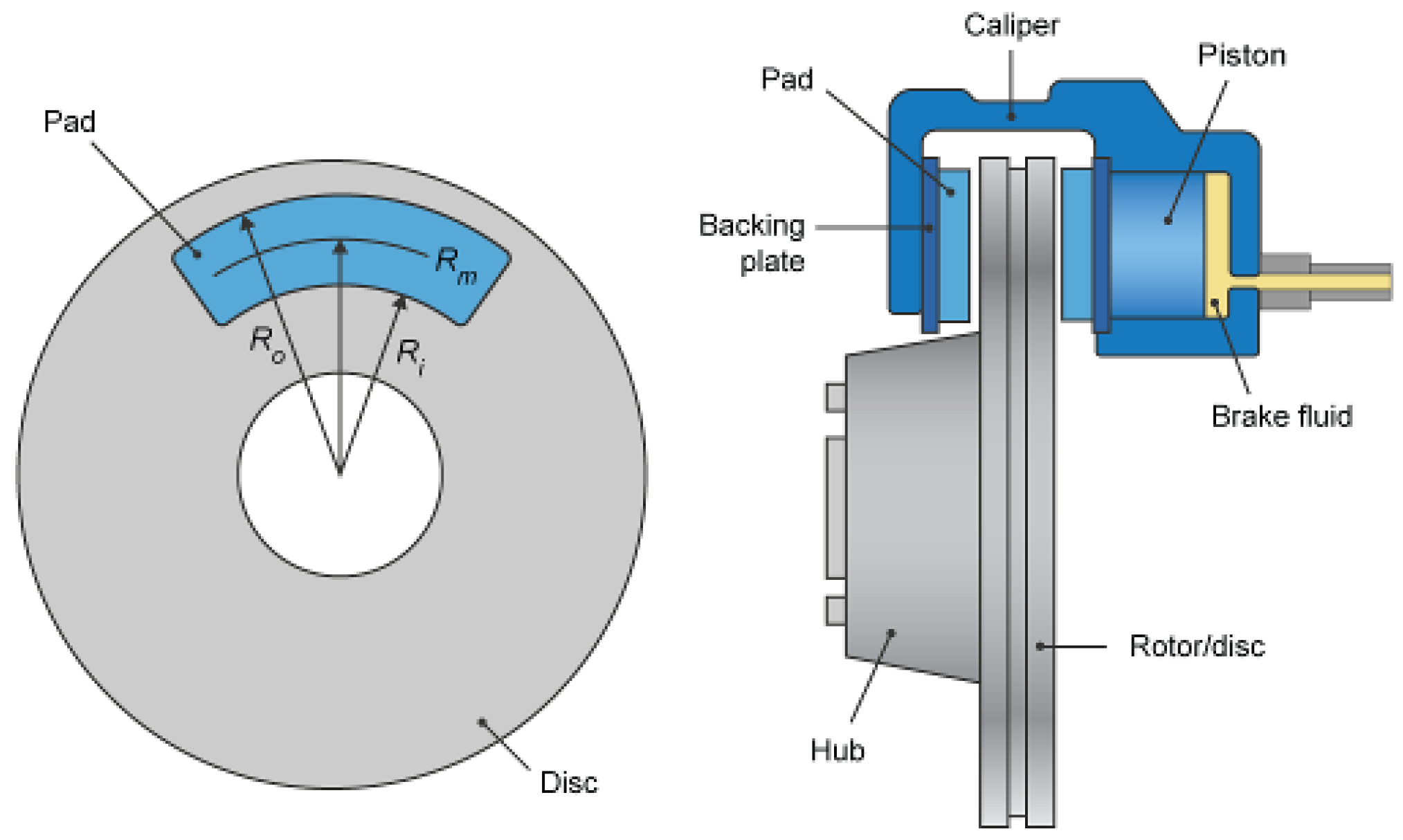
2.1.4. Brakes

Disk brakes are modeled, where the braking force is exerted through the brake cylinders and transformed to the braking force through the brake pads. The braking force is applied at the mean radius of the brake pad. Figure 4 shows the characteristics of the disk brakes.

2.1.5. Drivetrain

The drivetrain consists of a chain drive that transfers the human pedal force through the system and an electric hub motor that represents the electrical system. A representation of the models is shown in Figure 5.

The chain drive is modeled as a simple torque input, and throughout the simulation, no human input is added, so the torque on the chaindrive is $T_h=0 \mathrm{N}\mathrm{m}$. The hub motor is modeled as a DC motor mounted on the rear axle of the bicycle and is powered via a 48 V battery that is modeled as an ideal voltage source. The motor is controlled through pulse width modulation (PWM), where the duty cycle of the PWM is $d = 85\%$ while the bicycle is accelerating [11].

2.1.6. Driving Scenario

For simulating the braking distance and braking time of the bicycle, we set up a driving scenario. The details of the test setup were as follows:

• Acceleration for 80s with $d = 85\%$ duty cycle;
• Bicycle reaches speed of $36 \mathrm{k}\mathrm{m}/\mathrm{h}$
• At time $80.2 \mathrm{s}$ full braking is applied to stop the bicycle.

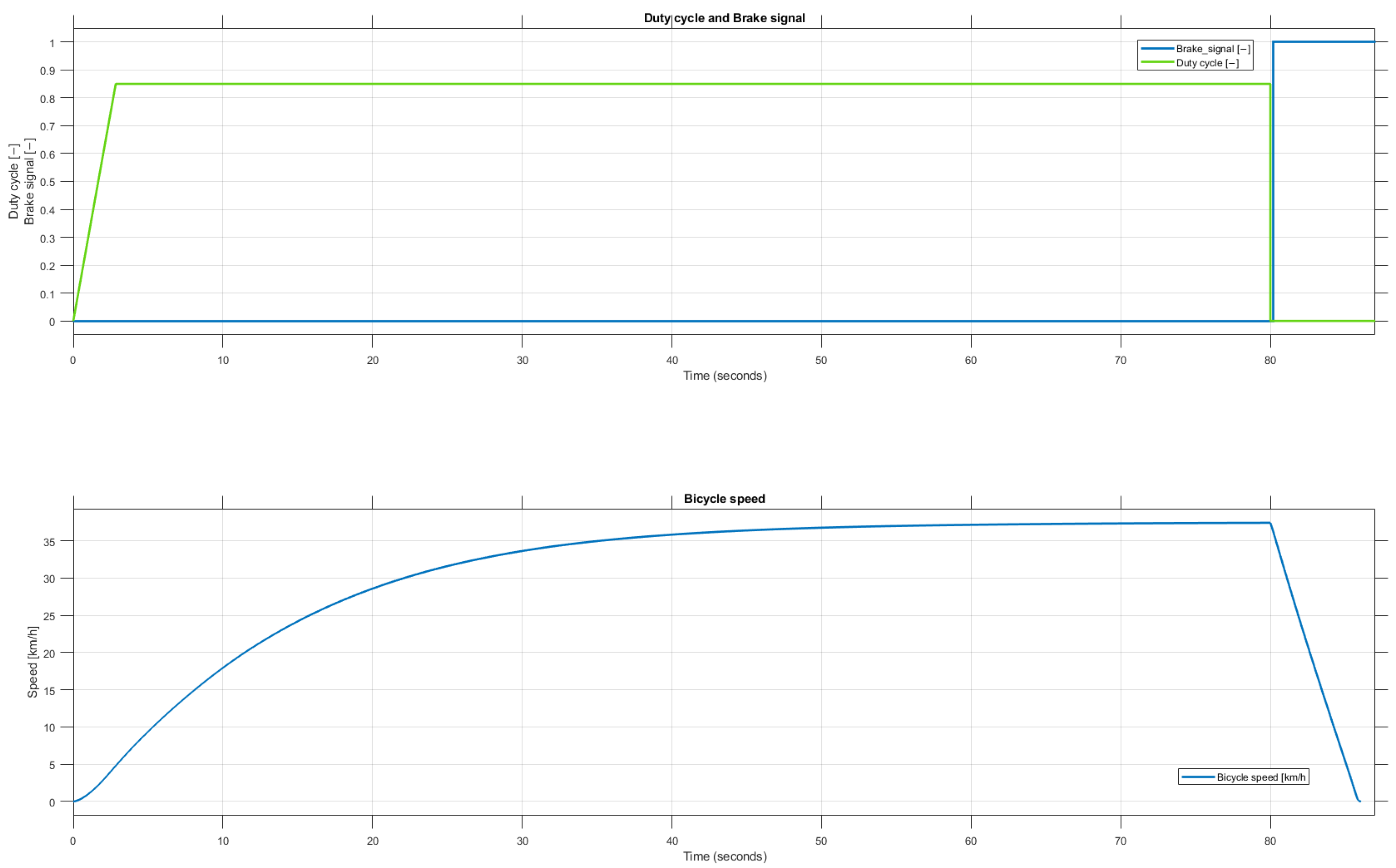
Figure 6 shows the driving scenario and the model response on a dry tarmac surface. The figure shows how the PWM and brake signals are changing at the top of the figure and how the bicycle speed is changing accordingly [12].

3. Results

Simulations were performed for four different road conditions. We will repeat the same drive cycle for the road conditions listed in Table 2:

• Dry tarmac;
• Wet tarmac;
• Snow;
• Ice.

For simulations, the main parameters of the e-bike are listed in

Table 3. E-bike’s main parameter values for simulation.

Value	Parameter/Variable
$m=102 \mathrm{k}\mathrm{g}$	Mass of the vehicle, including rider
$h=1150 \mathrm{m}\mathrm{m}$	Height of bicycle’s center of gravity (CoG)
$a+b=1143 \mathrm{m}\mathrm{m}$	Wheelbase of the bicycle
$r_b=150 \mathrm{m}\mathrm{m}$	Disk brake mean radius
$T_m=65 \mathrm{N}\mathrm{m}$	Hub motor, stall torque
${\omega }_m=540 \mathrm{r}\mathrm{p}\mathrm{m}$	Hub motor, no load speed

.

After postprocessing the simulations, the results indicate the following performance metrics of the bicycle for the braking scenario:

• Braking time [s]—time for decceleration from $36\mathrm{k}\mathrm{m}/\mathrm{h}$ to $0\mathrm{k}\mathrm{m}/\mathrm{h}$;
• Braking distance [m]—distance traveled while braking;
• Wheel slip [−]—wheel slip parameter calculated via the Pacejka tire model.

The driving profiles of dry tarmac and snow are also demonstrated to compare differences in vehicle speed and wheel slip coefficient in the simulation time domain.

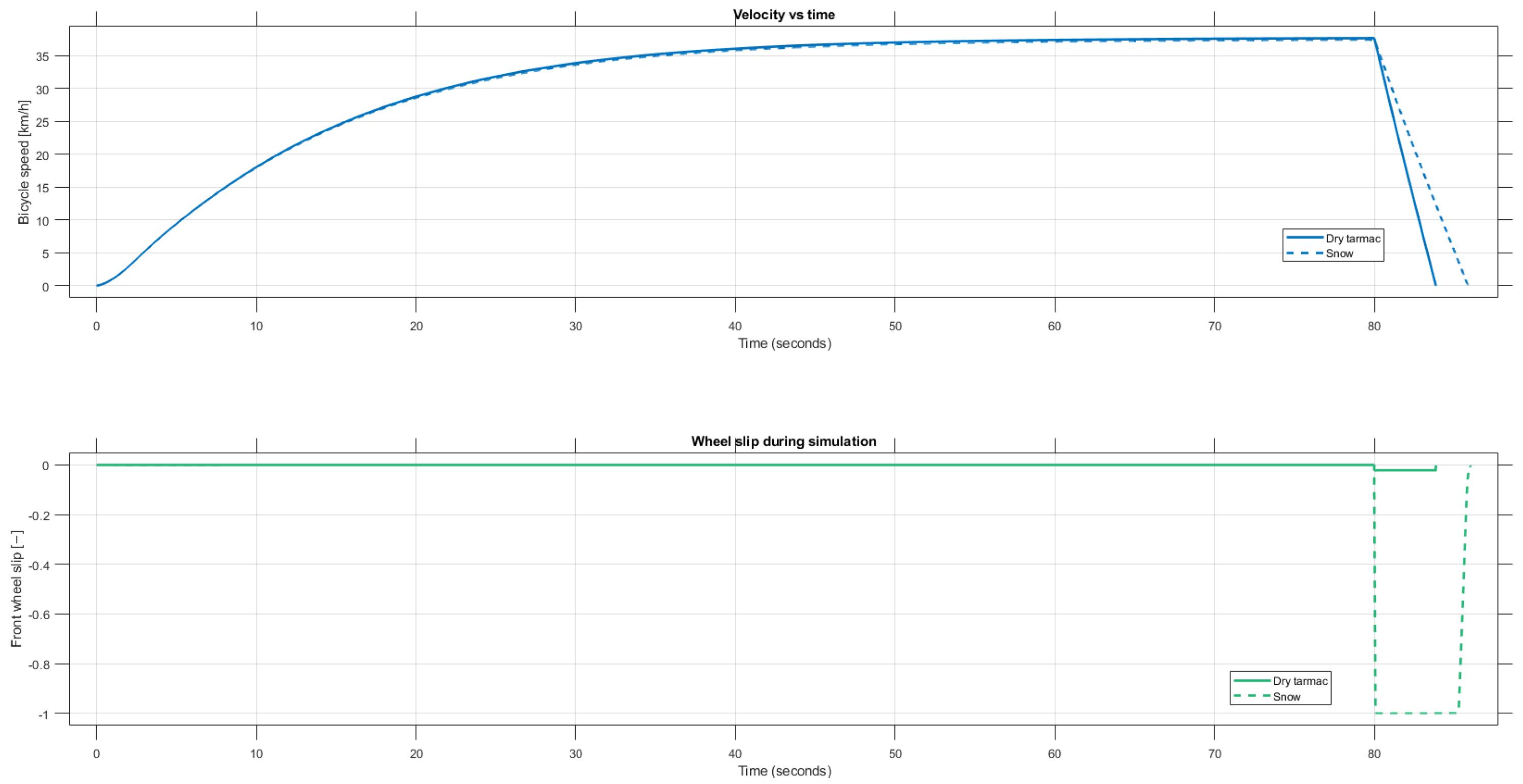
3.1. Driving Scenario Results—Dry Tarmac vs. Snow

Figure 7 shows that in the acceleration phase, for both road conditions the e-bike is capable of accelerating with a comparable gradient; however, when the braking maneuver starts at 80 s, the simulations show a significant difference. For dry tarmac, the bicycle can stop with small wheel slip values, without locking the wheels. However, for the snowy road, the wheel slip is −1, meaning that the front wheel is locked, and it is not rolling, but slipping over the road surface. From the vehicle speed we also see major differences, the speed decrease is less significant for the snowy road conditions [13].

3.2. Comparison of Evaluated Braking Characteristics

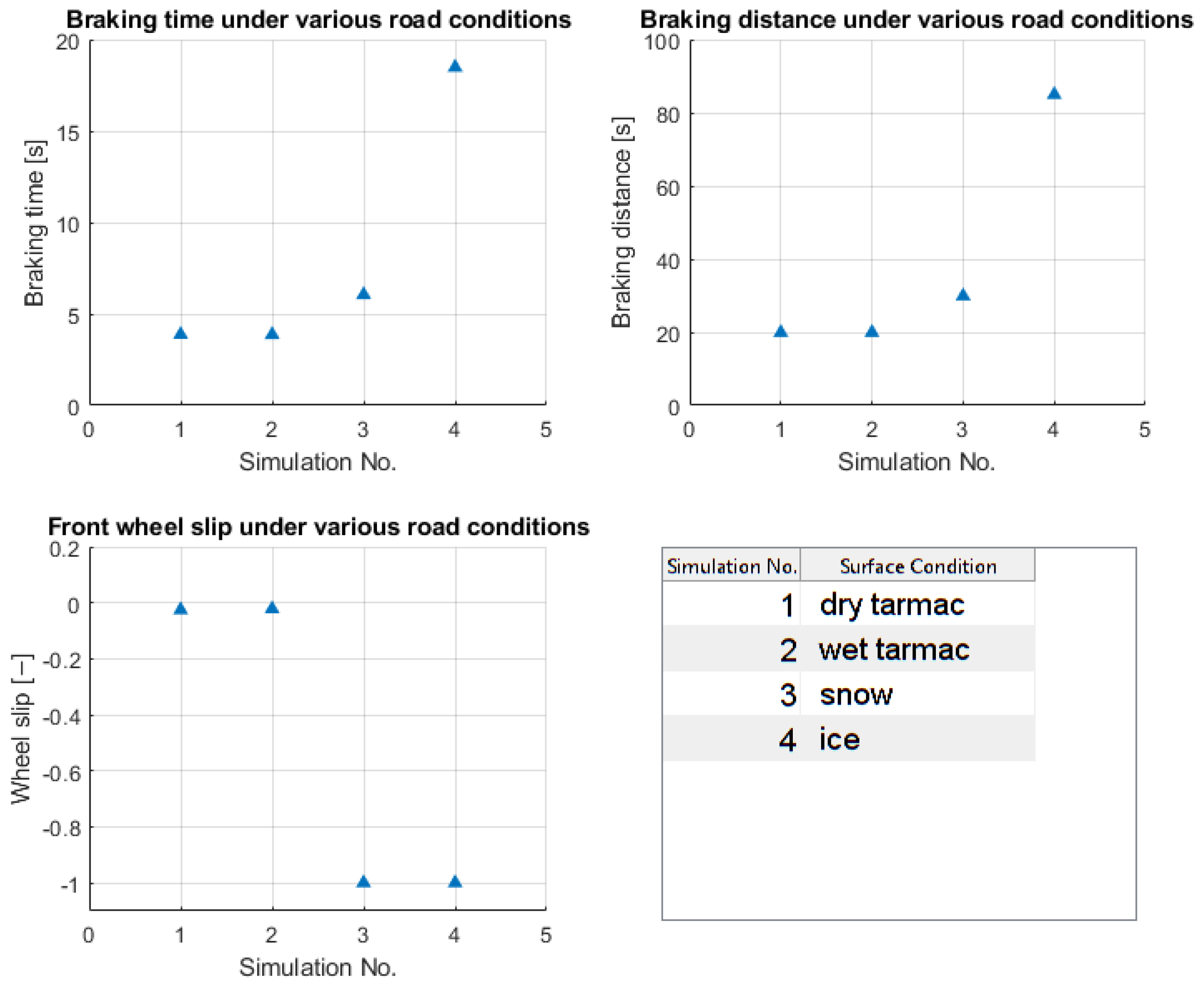
The simulation results for all road conditions are compared in Figure 8.

The three plots of Figure 8 show the relevant parameters, and we can see that for dry and wet tarmac, the wheel slip is 0 throughout the simulation, and also there are no differences in the braking time and braking distances. However, for snowy and icy road conditions, in both cases it comes to a wheel lockup, and the braking time and braking distance increase. For the snowy road condition, the braking distance increases by 50%, and for the icy road condition, the increase is over 400%, which is significant [14].

The simulation results presented in Figure 8 demonstrate that the developed longitudinal vehicle dynamics model produces realistic and physically consistent behaviors across different road conditions.

3.3. Validation of the Simulation Model

To assess the accuracy of the developed longitudinal dynamics simulation model, its outputs were compared with experimental stopping distance data reported by Lyubenov et al. in Experimental Determination of Bicycles and Electric Bicycle Stopping Distance [15].

The comparison was conducted for initial velocities ranging from 5 km/h to 35 km/h. In each case, the simulated stopping distance was calculated using identical input conditions to those described in the reference study.

Table 4. Validation of the simulation results based on the measurements of Lyubenov et al. [15].

	Velocity, km/h
	5	10	15	20	25	30	35
	Distance, m
$Measurement$ [15]	1.88	4.18	6.91	10.07	13.64	17.65	22.08
$Simulation$	2.07	4.35	7.36	10.58	14.64	18.96	25.26
	Error %
	9.18	3.91	6.11	4.82	6.83	6.91	12.59

presents the measured and simulated stopping distances, along with the percentage errors between them.

The results show that the simulation model predicts stopping distances with a maximum error of 13%. At lower speeds, the slightly higher relative error (9.18% at 5 km/h) is likely due to the increased influence of the rider reaction time and brake application variability in the experimental data, which are difficult to model precisely.

The validation indicates that the developed simulation model reproduces the experimental stopping distance trends with satisfactory accuracy for virtual testing and design evaluation purposes, particularly in the operational speed range of typical e-bike usage.

Overall, the outcomes confirm that the proposed e-bike model is sensitive to changes in tire–road friction and dynamic braking behavior, which are essential requirements for simulating safety-critical scenarios. As such, this model provides a credible foundation for the virtual development and testing of ABS algorithms. It enables the controlled study of wheel slip and braking response, supporting future research aimed at improving braking stability and safety in electric bicycles [14].