Experimental Study of the Interaction of UHF Electromagnetic Waves with Fuel-Contaminated Water †
Abstract
1. Introduction
2. Interaction of Electromagnetic Waves with Fluids
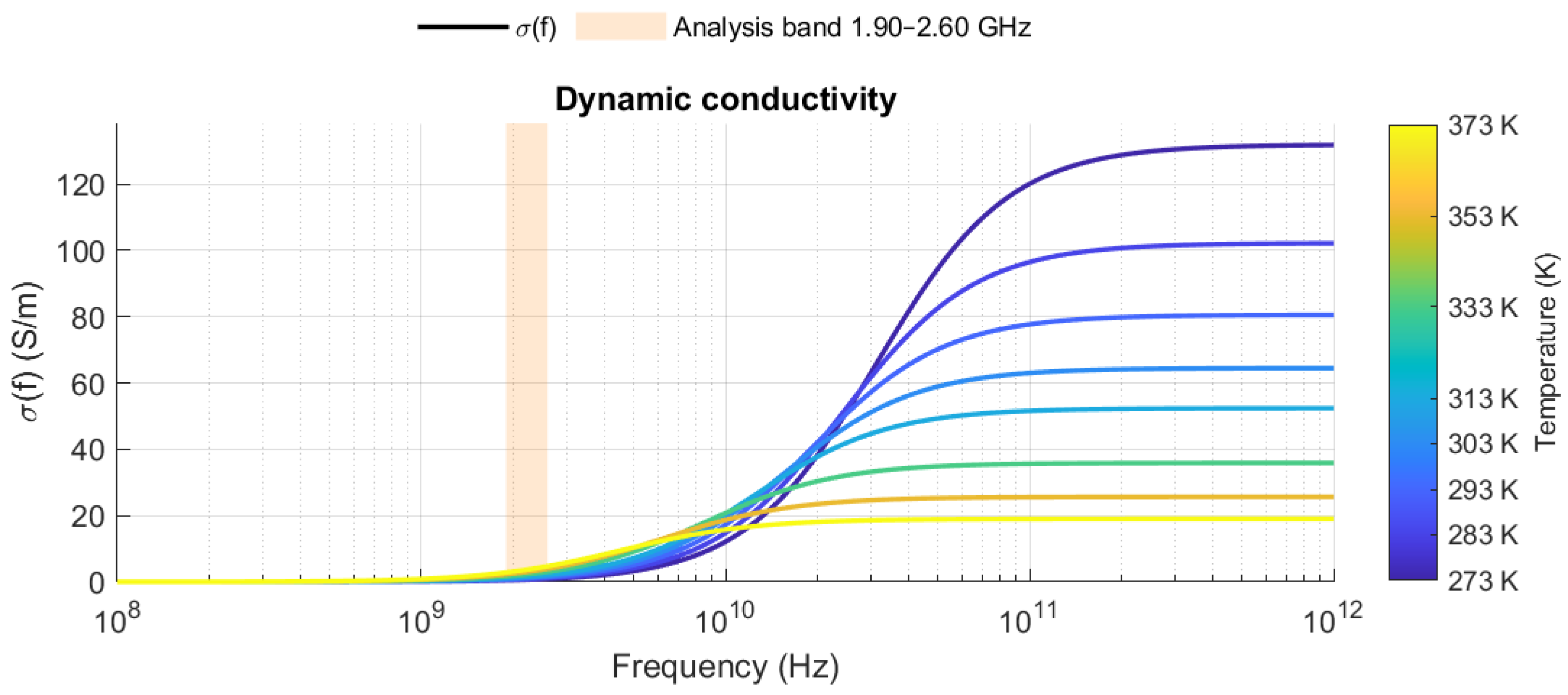
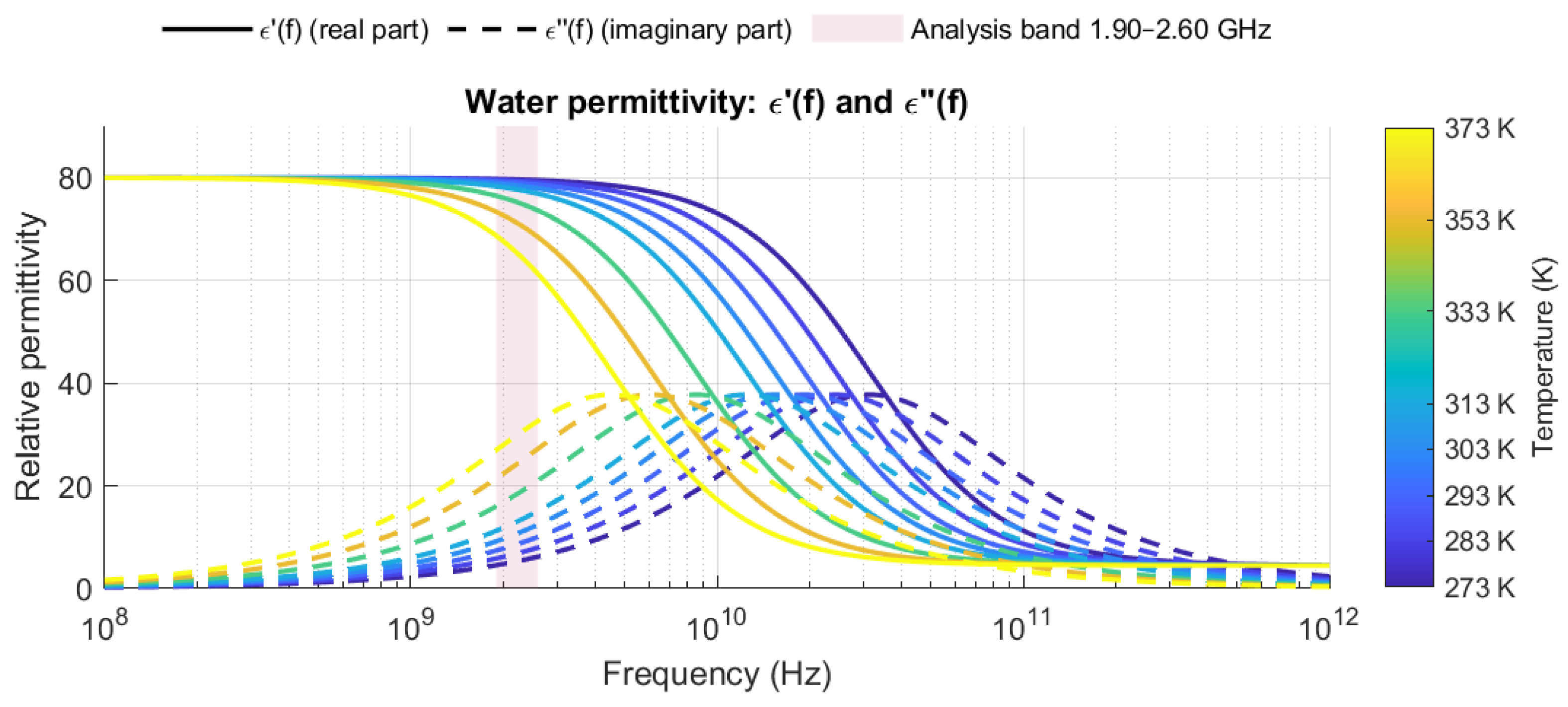
2.1. Water as a Dielectric and Its Behavior at High Frequencies
2.2. Reflection Coefficient in Electromagnetic Waves
2.3. Relative Permittivity in Aqueous Mixtures
2.4. Propagation of Electromagnetic Waves
2.5. Electromagnetic Reflection Coefficient in the Interaction Between Water and Different Aqueous Media
2.6. Estimation of the Reflection Coefficient
2.7. Theoretical Reference Model: Free-Space Propagation
3. Equipment and Methodology
3.1. Experimental Methodology
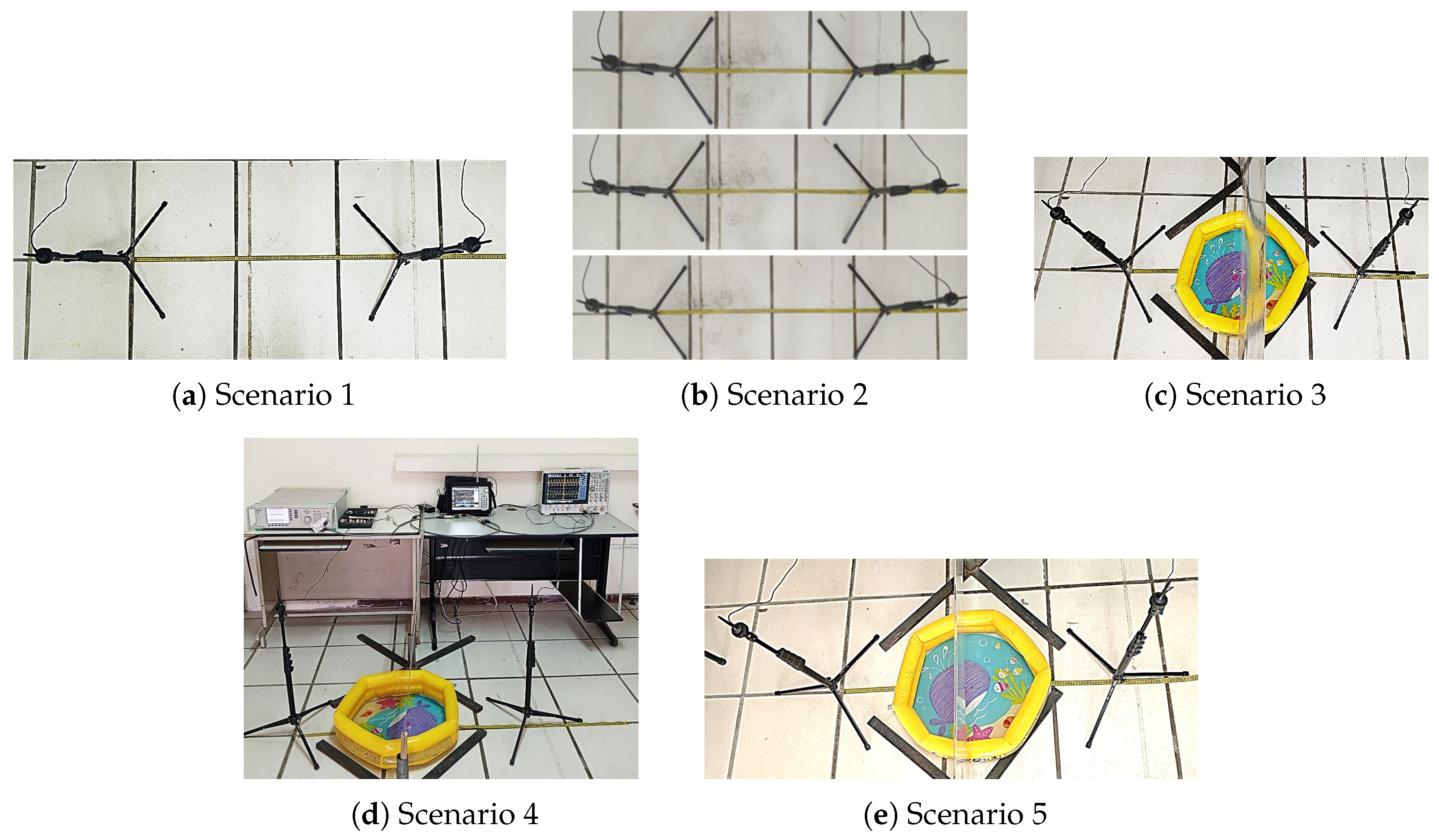
3.1.1. Description of the Experimental System
3.1.2. Physical Details of the Measurement Scenario and System Limitations
4. Experimental Scenarios
4.1. Scenario 1: Direct Transmission at Fixed Distance with Frequency Sweep
4.2. Scenario 2: Direct Transmission at Multiple Distances and Frequencies
4.3. Scenario 3: Transmission with Obstruction and Pool with Pure Water
4.4. Scenario 4: Transmission with Obstruction and Pool with Pure Gasoline
4.5. Scenario 5: Transmission with Obstruction and Pool with Water–Gasoline Mixture
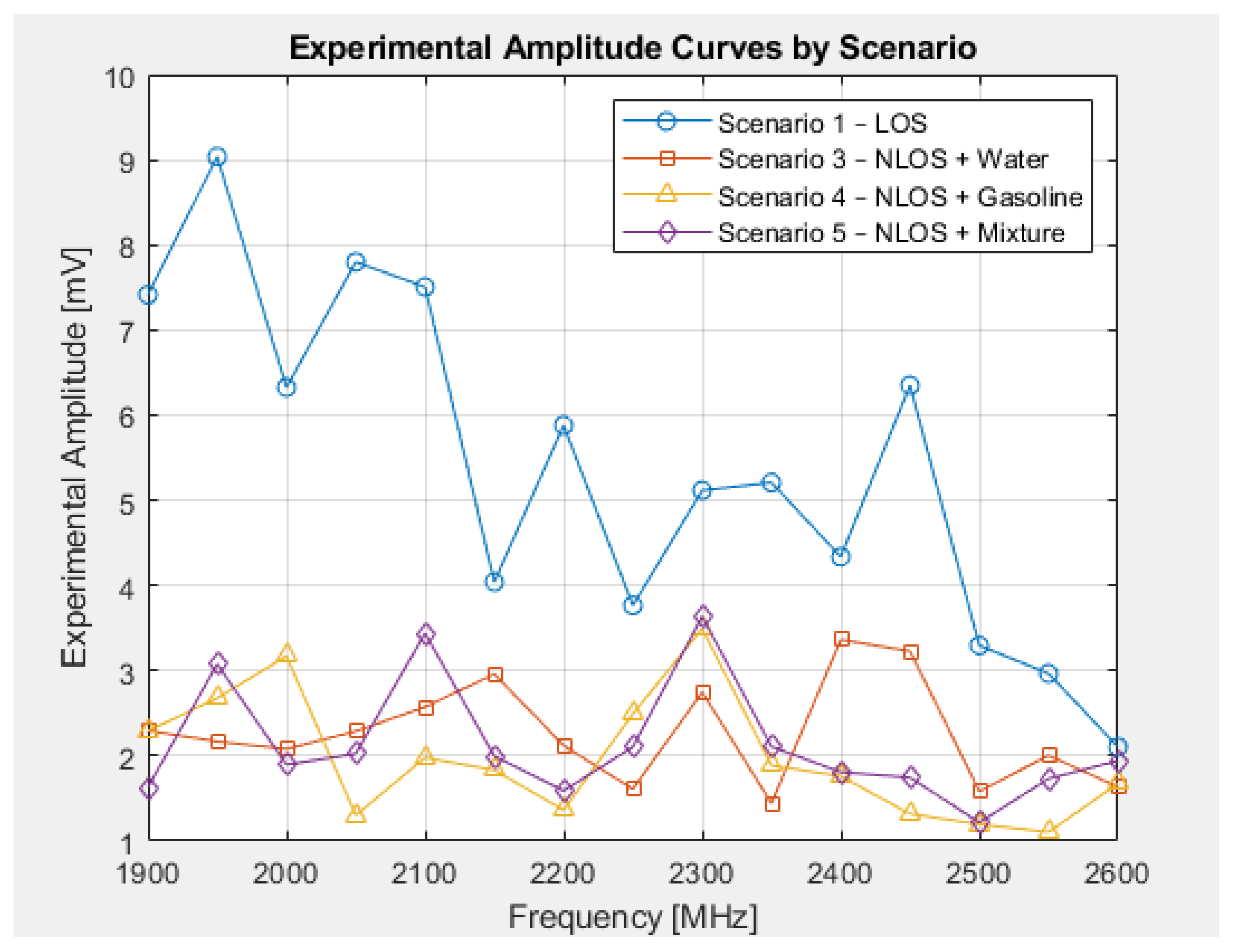
5. Results
Analysis of the Scenarios and Experimental Estimation of the Reflection Coefficient
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Westerhoff, P.; Alvarez, P.J.; Kim, J.; Li, Q.; Alabastri, A.; Halas, N.J.; Villagran, D.; Zimmerman, J.; Wong, M.S. Utilizing the Broad Electromagnetic Spectrum and Unique Nanoscale Properties for Chemical-Free Water Treatment. Curr. Opin. Chem. Eng. 2021, 33, 100709. [Google Scholar] [CrossRef] [PubMed]
- Artemov, V. The Electrodynamics of Water and Ice; Springer Series in Chemical Physics; Springer: Cham, Switzerland, 2021; Volume 124. [Google Scholar] [CrossRef]
- Kremer, F.; Schönhals, A. (Eds.) Broadband Dielectric Spectroscopy; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar] [CrossRef]
- Pozar, D.M. Microwave Engineering, 4th ed.; Wiley: Hoboken, NJ, USA, 2025; Available online: https://www.wiley.com/en-us/Microwave+Engineering%2C+4th+Edition-p-9781118213636 (accessed on 11 July 2025).
- Balanis, C.A. Advanced Engineering Electromagnetics, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2012; Available online: http://ndl.ethernet.edu.et/bitstream/123456789/88007/4/Balanis-AdvancedEngineeringElectromagnetics-2012.pdf (accessed on 12 July 2025).
- Hernandez-Gomez, E.-S.; Olvera-Cervantes, J.L.; Corona-Chavez, A.; Corona-Vasquez, B.; Kataria, T.K.; Sosa-Morales, M.E. Detection of an emerging contaminant in water by dielectric properties in microwave range. J. Microw. Power Electromagn. Energy 2020, 54, 273–290. [Google Scholar] [CrossRef]
- Kong, J.A.; Ali, S.M.; Einziger, P.; Habashy, T.M.; Poh, S.Y.; Shin, R.T. Electromagnetic Wave Theory and Applications; Research Laboratory of Electronics, MIT: Cambridge, MA, USA, 1988; Available online: https://dspace.mit.edu/bitstream/handle/1721.1/57071/RLE_PR_131_02_03s_01.pdf?sequence=1 (accessed on 10 July 2025).
- Ishimaru, A. Electromagnetic Wave Propagation, Radiation, and Scattering: From Fundamentals to Applications; Wiley: Hoboken, NJ, USA, 2017. [Google Scholar]
- Shi, Q.; Xuan, X.-W.; Nie, H.-K.; Wang, Z.-Y.; Wang, W. Antenna Sensor Based on AMC Array for Contactless Detection of Water and Ethanol in Oil. IEEE Sens. J. 2021, 21, 21503–21510. [Google Scholar] [CrossRef]
- Balanis, C.A. Antenna Theory: Analysis and Design, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Kraus, J.D.; Marhefka, R.J. Antennas for All Applications; McGraw-Hill: Columbus, OH, USA, 2002. [Google Scholar]
- Balsbaugh, J.C.; Assaf, A.G.; Oncley, J.L. Dielectric Properties of Hydrocarbons and Hydrocarbon Oils. Ind. Eng. Chem. 1942, 34, 92–100. [Google Scholar] [CrossRef]
- Reina, F.; García, A.; Ibáñez, L. Determinación de las propiedades dieléctricas de los combustibles, sus mezclas y del suelo, así como su impacto en un uso eficiente de los recursos energéticos y en la determinación de la contaminación ambiental. Int. J. Manag. Sci. Oper. Res. 2019, 4, 1. [Google Scholar] [CrossRef]
- Abdolrazzaghi, M.; Daneshmand, M.; Iyer, A.K. Strongly Enhanced Sensitivity in Planar Microwave Sensors Based on Metamaterial Coupling. IEEE Trans. Microw. Theory Tech. 2018, 66, 1843–1855. [Google Scholar] [CrossRef]
- Bo, Ø.; Nyfors, E. Application of Microwave Spectroscopy for the Detection of Water Fraction and Water Salinity in Water/Oil/Gas. J.-Non-Cryst. Solids 2002, 305, 345–353. [Google Scholar] [CrossRef]
- Montagnier, L.; Del Giudice, E.; Aïssa, J.; Lavallee, C.; Motschwiller, S.; Capolupo, A.; Polcari, A.; Romano, P.; Tedeschi, A.; Vitiello, G. Transduction of DNA information through water and electromagnetic waves. Electromagn. Biol. Med. 2015, 34, 106–112. [Google Scholar] [CrossRef] [PubMed]
- SMARTEQ. 1140.26-SMA Antenna; SMARTEQ Wireless AB: Kista, Sweden, 2025; Available online: https://www.radwell.com/es-ES/Buy/SMARTEQ/SMARTEQ/1140.26-SMA (accessed on 30 July 2025).
- Anritsu. RF/Microwave Signal Generator MG3691C; Anritsu Corporation: Atsugi, Japan, 2025; Available online: https://www.anritsu.com/en-us/test-measurement/products/mg3690c (accessed on 30 July 2025).
- Keysight. MSOX6004A Mixed Signal Oscilloscope: 1 GHz – 6 GHz, 4 Analog Plus 16 Digital Channels; Keysight Technologies: Santa Rosa, CA, USA, 2025; Available online: https://www.keysight.com/us/en/product/MSOX6004A/mixed-signal-oscilloscope-1ghz-6ghz-4-analog-16-digital-channels.html (accessed on 30 July 2025).
- Anritsu. Spectrum Master Handheld Spectrum Analyzer MS2711E; Anritsu Corporation: Atsugi, Japan, 2025; Available online: https://www.anritsu.com/en-us/test-measurement/products/ms2711e (accessed on 30 July 2025).
- Fujikura Ltd. 5D-2W Coaxial Cable Specification Sheet; Fujikura Ltd.: Tokyo, Japan, 2021; Available online: https://www.fujikura-dia.co.jp/pdf/catalog/catalog-pihfc-cable.pdf (accessed on 30 July 2025).
- Belden Inc. RG-174 Coaxial Cable Technical Data Sheet; Belden Inc.: Richmond, IN, USA, 2019; Available online: https://catalog.belden.com/techdata/EN/8216_techdata.pdf (accessed on 30 July 2025).




| Interface | Reflected Power [%] | Phase Shift | |||
|---|---|---|---|---|---|
| Air–Water | 80.0 | 42.15 | 63.8 | ||
| Air–Gasoline | 2.2 | 254.17 | 3.8 | ||
| Air–Mixture | 16.01 | 94.22 | 36.0 |
| Scenario | Distance (m) | Sweep (GHz) | Obstruction | Medium |
|---|---|---|---|---|
| 1. Direct transmission (reference) | 1.05 | 1.90–2.60 | None | None |
| 2. Transmission at multiple distances | 0.40–1.20 | 1.90–2.60 | None | None |
| 3. Transmission with obstruction and water pool | 1.05 | 1.90–2.60 | Metallic plate | 3.0 L water |
| 4. Transmission with obstruction and gasoline pool | 1.05 | 1.90–2.60 | Metallic plate | 2.6 L gasoline |
| 5. Transmission with obstruction and water–gasoline mixture | 1.05 | 1.90–2.60 | Metallic plate | 1.5 L water + 1.4 L gasoline |
| Scenario | Medium | Average || | Reflected Power [%] |
|---|---|---|---|
| 3 | Pure Water | 0.5289 | 27.97 |
| 4 | Pure Gasoline | 0.5950 | 35.40 |
| 5 | Water–Gasoline Mixture | 0.5611 | 31.48 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arteaga, K.I.; Batallas, G.P.; Morillo, P.L.; Osorio, D.F. Experimental Study of the Interaction of UHF Electromagnetic Waves with Fuel-Contaminated Water. Eng. Proc. 2025, 115, 11. https://doi.org/10.3390/engproc2025115011
Arteaga KI, Batallas GP, Morillo PL, Osorio DF. Experimental Study of the Interaction of UHF Electromagnetic Waves with Fuel-Contaminated Water. Engineering Proceedings. 2025; 115(1):11. https://doi.org/10.3390/engproc2025115011
Chicago/Turabian StyleArteaga, Kevin Iza, Gabriel Palma Batallas, Pablo Lupera Morillo, and Darwin Flores Osorio. 2025. "Experimental Study of the Interaction of UHF Electromagnetic Waves with Fuel-Contaminated Water" Engineering Proceedings 115, no. 1: 11. https://doi.org/10.3390/engproc2025115011
APA StyleArteaga, K. I., Batallas, G. P., Morillo, P. L., & Osorio, D. F. (2025). Experimental Study of the Interaction of UHF Electromagnetic Waves with Fuel-Contaminated Water. Engineering Proceedings, 115(1), 11. https://doi.org/10.3390/engproc2025115011








