Finite Element Assessment of Temperature Effects on the Performance of Bituminous Pavement Materials ^†

Abstract

This study investigates the effectiveness of the finite element method for predicting the performance of flexible pavements subjected to varying traffic-loading and environmental conditions. A two-dimensional axisymmetric finite element model of a flexible pavement structure was developed using ABAQUS software v2022. In order to estimate the necessary pavement stiffness for reducing the likelihood of rutting and fatigue failure, the impacts of loading and operational characteristics of modern trucks were taken into consideration. Detailed parametric analyses were conducted to comprehensively assess the effect of substrate temperature profile variations on pavement performance. The findings demonstrate that utilization of a stiffer binder results in substantial reductions in critical tensile and compressive strains.

1. Introduction

Road structure is an essential part of a well-outlined transportation system. The structure of a road impacts the efficiency of the road for transportation usage, the efficiency of vehicles traversing the road, and the safety with which drivers are able to use the road. From environmental conditions to material availability, the factors affecting road structures have different impacts on them. The climatic conditions of an area can affect the type of road structure; these conditions mainly include environmental temperature, humidity, groundwater levels, and wind speed. The thicknesses of pavement layers and their material properties are well-known parameters which can govern the cost-effectiveness of a flexible pavement and can thus define its reliability as well [1,2,3,4,5].

The rise in the number of commercial vehicles and the excessive overloading of trucks, in addition to fluctuating environmental conditions, have a significant impact on flexible pavements. This is because these factors contribute to a decrease in the durability and performance of flexible pavements. In India, rates of pavement distresses and, thus, of premature failures can potentially increase exponentially due to the extreme temperature changes that occur there. When exposed to high temperatures, flexible pavements begin to soften and become more readily deformed. Conversely, when exposed to low temperatures, they become more rigid and brittle, which shortens their lifespan. In order to address these problems, it is vital to take advantage of modern analytical techniques that are capable of accurately simulating the reaction of pavements to a variety of loads and climatic conditions, in order to enhance design and improve performance forecasts [6,7,8,9].

A flexible pavement is comprised either of a single layer or a combination of layers (surface, base, and subgrade) where each plays an important role in distributing inherent traffic-induced stresses. Primarily asphalt, the top layer directly interacts with vehicle loads and is subjected to the highest stresses. These stresses are transmitted through the base layer to the subgrade, and overall pavement thickness is primarily a function of the modulus of the subgrade soil [10,11,12,13,14].

Although they are advantageous, flexible pavements are still vulnerable to distress due to heavy traffic loadings, environmental conditions, and material deterioration over time. There are different types of distress mechanisms, but one of the most severe is rutting (longitudinal depression on the wheel path), which is common in hot climates. If not dealt with, rutting deteriorates pavement performance due to increases in skidding and hydroplaning. Because the severity of rutting varies, depending on repeated traffic loads, climate, and the properties of materials, its mitigation is a critical aspect in pavement design [15,16,17,18,19].

This study aims to evaluate the effectiveness of 2D axisymmetric finite element analysis in predicting flexible pavement performance under varying temperature conditions. Following the standards established by IRC:37-2016 as well as major performance metrics, the analysis focuses on the influence of the thickness of the bituminous layer and the qualities of the material while keeping the thickness of the base layer constant. In order to build a framework for pavement design that is optimal, it is necessary to evaluate the horizontal tensile strain at the bottom of the bituminous layer as well as the vertical compressive strain at the tip of the subgrade.

2. Methodology

2.1. Flexible Pavement Modelling

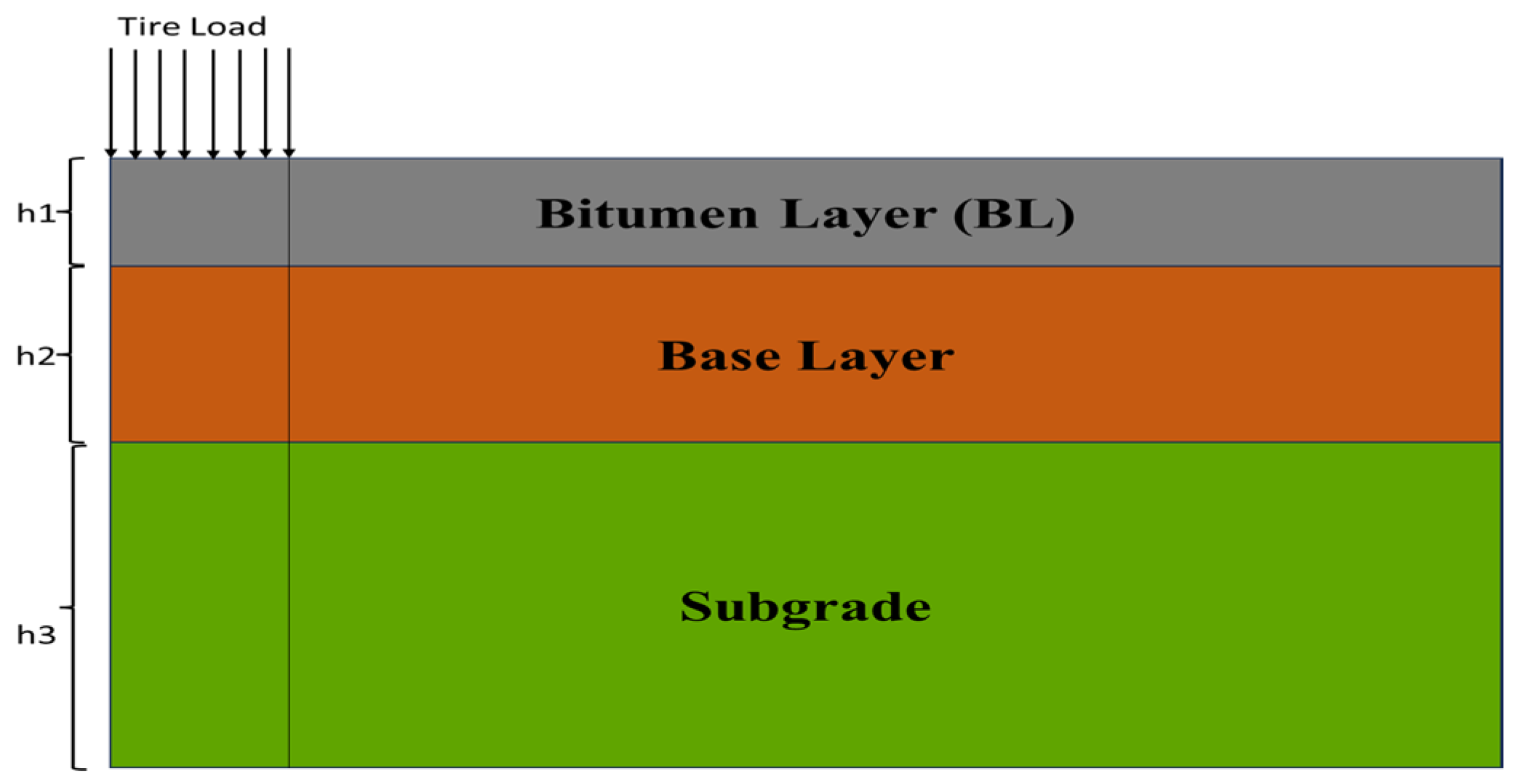
The current study considers a three-layer flexible pavement model, as presented in Figure 1. The top layer is made up of bitumen concrete (BC) and dense bituminous macadam (DBM). The thickness of the bitumen concrete is considered as 50 mm and the thickness of the DBM layer varies in 50 mm increments from 50 mm up to 200 mm. This means that thicknesses of the top bituminous layer (h1) ranging from 100 to 250 mm are considered for the analysis of the pavement structure. The resilient modulus of the BC layer is taken as EBC = 1700 MPa, and the Poisson ratio (ν) is taken as 0.35. The resilient modulus of the DBM layer varies according to the material properties of bitumen at various temperatures. The layer below the bitumen layer is the granular base, which is 450 mm thick and comprised of compacted soil and crushed rock with consistent material properties. The resilient modulus of the granular base layer is E_Base = 450 MPa, and the Poisson ratio (ν) is taken as 0.35.

The bottommost layer represents finite extensions of subgrade, and its depth is chosen in such a way that it could represent the finite zone where the influence of tire load and deformation of the subgrade is significant. The resilient modulus of subgrade layer is E_subgrade = 80 MPa, and the Poisson ratio (ν) is taken as 0.35. Tire load is applied as a uniformly distributed load over a circular area which is equal to tire load divided by tire pressure. The effect of temperature is incorporated into the model by changing the material properties of the DBM layer at temperatures ranging from 20 °C to 40 °C. The material properties of the bitumen layer, the base layer, and the subgrade are considered constant for these temperature changes.

2.2. Bitumen Material Characteristics

In the current analysis, we considered roads in India, where the average temperature of flexible pavement is around 35 °C. The resilient modulus of the bitumen indicates the load distribution characteristics of the flexible pavements. A higher resilient modulus means a stiffer pavement layer which can distribute traffic loads over a wider area, reducing stress on the underlying layers. Based on IRC: 37-2018 guidelines, the temperature sensitivity of specific types of bitumen expressed as resilient modulus (in MPa) is presented in

Table 1. Resilient modulus of bitumen (in MPa) for different types of bitumen under various temperatures.

Type of Bitumen	Resilient Modulus (in MPa) for Various Temperatures of Flexible Pavement
	20 °C	25 °C	30 °C	35 °C	40 °C
VG 10 bitumen	2300	2000	1450	1000	800
VG 30 bitumen	3500	3000	2500	1700	1250
VG 40 bitumen	6000	5000	4000	3000	2000
Modified bitumen	5700	3800	2400	1650	1300

.

Bitumen is graded in terms of its VG; this stands for “Viscosity Grade” and measures resistance to flow at 60 °C. Higher values of VG indicate stiffer bitumen. As pavement temperature increases from 20 °C to 40 °C, the resilient modulus roughly halves, or even drops by more than half in some cases. As a result, it can be deduced that changes in pavement temperature, both on a daily and seasonal basis, have a significant impact on the resilient modulus of the pavement. It has been shown that modified bitumen has increased stiffness at lower temperatures, but may be more prone to softening at higher temperatures, in comparison to other grades with higher variable viscosity (VG).

2.3. Finite Element Modelling

A semi-infinite soil structure contains one axis of symmetry; in analysis of such structures, only axial and radial behavior is considered, and circumferential displacements are ignored. Three-dimensional analyses of these structures can be reduced to a two-dimensional axisymmetric analysis in ABAQUS software. A 2D sketch of the model is created, and material properties are applied for each layer. Meshing is carried out as per the requirements of accuracy. Very fine meshing is assigned for the region which comes directly under the load, and coarser meshing is assigned for the subgrade region. Uniform loading is applied as tire load over a radius of 150 mm. The nodes at the bottom of the subgrade are restrained in both the radial (r) and axial (z) directions, as shown in Figure 2. The nodes over the axis of the symmetry are restrained in the radial direction. It is assumed that due to the indefinite lateral extent of the pavement section, the nodes over the extreme vertical face of the pavement, i.e., at a horizontal distance of 1050 mm from the centerline of the wheel loading, do not suffer radial displacements. Hence, these nodes are treated as restrained in the radial (r) direction.

3. Results and Discussion

The objective of mesh refinement is to achieve a solution that is invariant to the mesh size. The outcomes derived from mesh refining are physically relevant and independent of the degree of discretization. The results are dependent upon the mesh size. As the mesh is modified, the computed values fluctuate, indicating that the initial coarse meshes were insufficiently detailed to accurately represent the solution. Precision and the cost of computing are two aspects that are distinct from one another. The coarser the mesh size, the more accurate the results will be; the finer the mesh size, the more precise the results will be. However, computation times will be considerably longer for finer meshes. For the purpose of improvement, it is necessary to determine the ideal equilibrium between the appropriate level of precision and the available computational resources. A three-layer axisymmetric finite element model is developed for the analysis. The top layer has modulus of elasticity E = 689 MPa, the middle layer has E = 400 MPa and the bottom layer has E = 68.9 MPa. The Poisson ratio for all layers is taken as 0.3.

The finite element formulation uses Boussinesq theory to calculate stresses and displacements in homogeneous, elastic, isotropic, and semi-infinite soil mass, validating results against analytical solutions. Figure 3 presents variations in vertical stress with increases in soil depth for various mesh sizes.

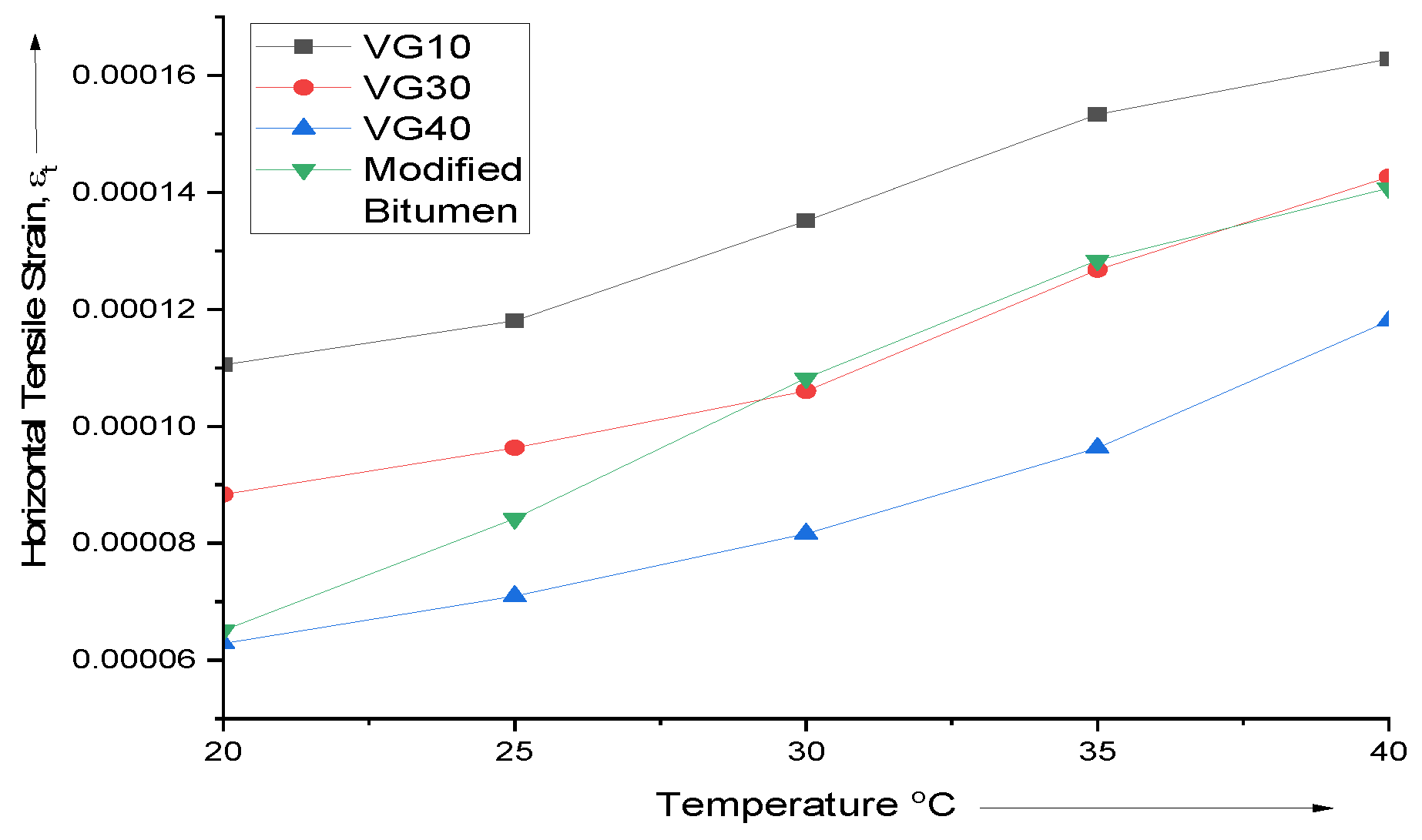
Figure 4 shows that increasing temperature decreases tensile strain across all tested bitumen grades (VG10, VG30, VG40, and Modified Bitumen). Warmer temperatures enhance bitumen flexibility, reducing strain. VG10 has the highest strain values, while Modified Bitumen has the lowest strain values. These findings highlight the importance of selecting bitumen grades that can manage tensile strains to prevent cracking and ensure long-term pavement performance.

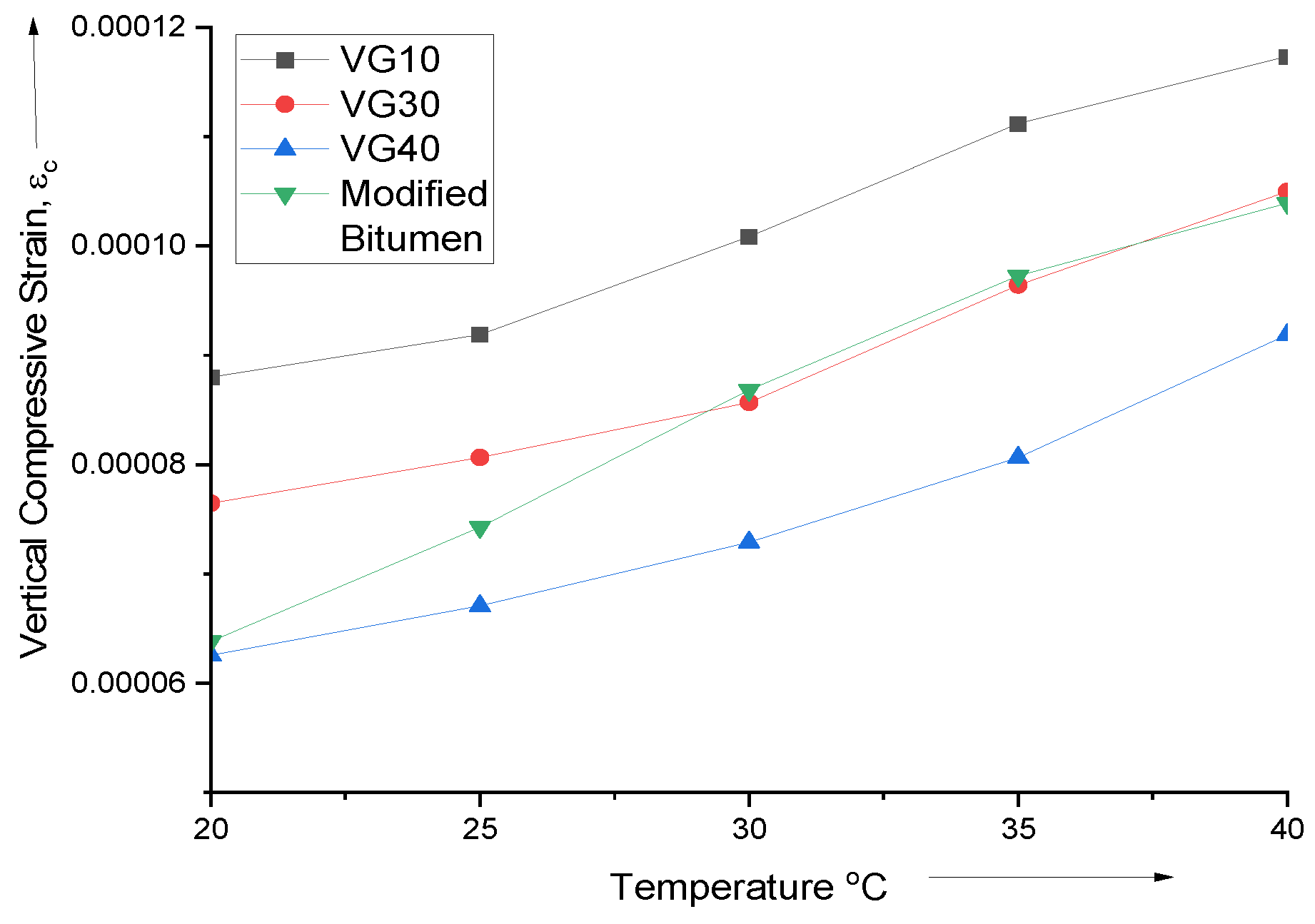
Figure 5 shows that increasing temperature increases vertical compressive strain across all tested bitumen types (VG10, VG30, VG40, and Modified Bitumen). This is due to the softening of upper pavement layers, transferring more vertical load to the base layer. In particular, when temperatures are lower, VG10 has the highest strain whereas VG40 has the lowest strain. The significance of selecting the appropriate bitumen grade to effectively handle vertical compressive stresses is brought into focus by this.

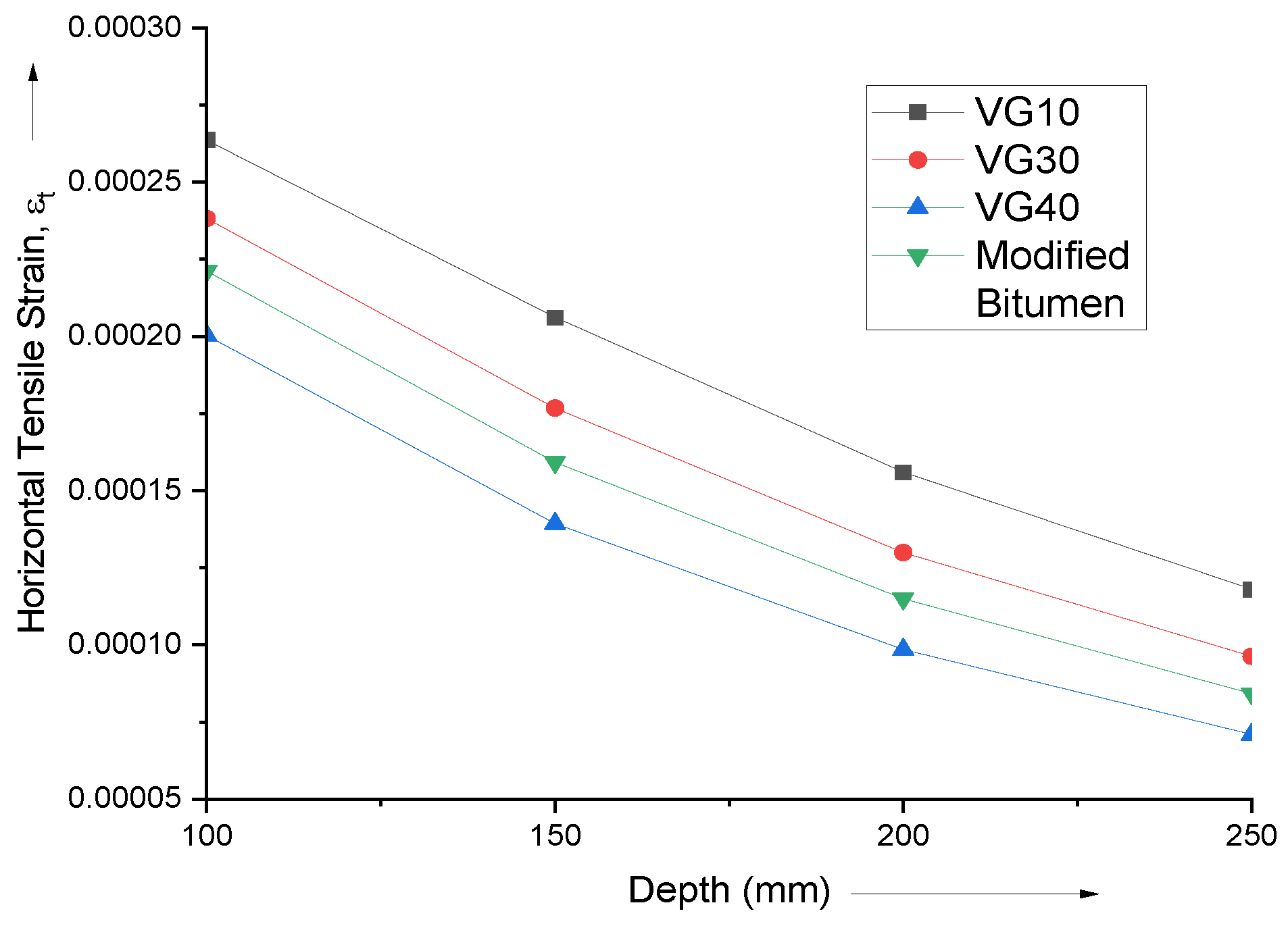
Figure 6 shows that as the depth of the bitumen layer increases, the horizontal tensile strain decreases for all bitumen grades (VG10, VG30, VG40, and Modified Bitumen). A thicker layer experiences less strain at its bottom, with VG10 being the most susceptible. Modified Bitumen offers the greatest resistance to horizontal tensile forces, followed by VG40 and VG30. This highlights the importance of bitumen layer thickness in pavement design.

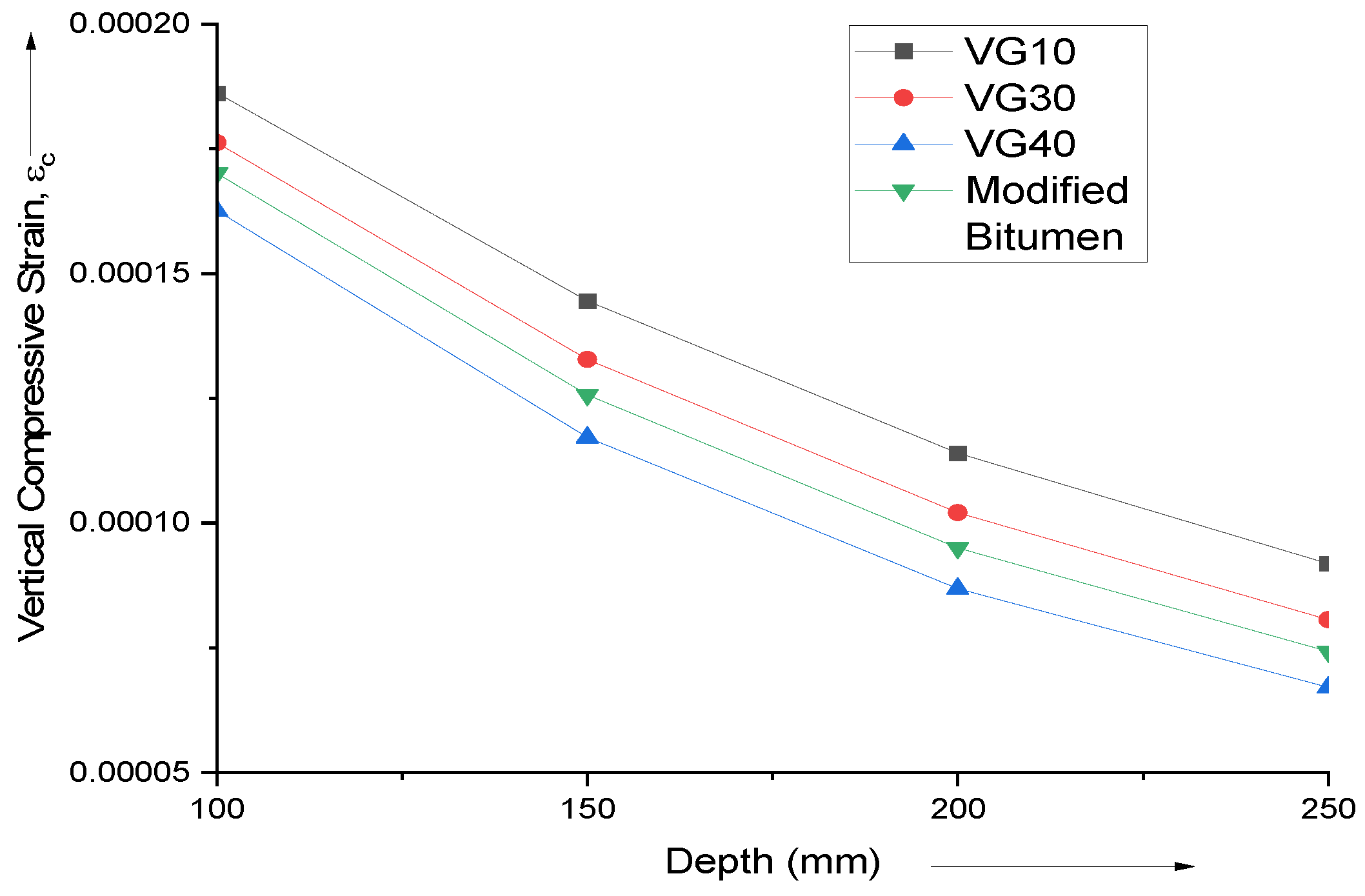
Figure 7 shows that as the depth of the bitumen layer increases, the vertical compressive strain decreases for all tested bitumen types (VG10, VG30, VG40, and Modified Bitumen). A thicker bitumen layer distributes vertical loads more effectively, resulting in lower compressive strain in the base layer. VG10 experiences the most compression, while VG40 minimizes vertical strain, suggesting its potential for more durable pavements resistant to vertical deformation.

4. Conclusions

The following are the major considerations which can be drawn from the present research work:

• There is a trade-off between precision and computing expense, and the importance of mesh refinement in obtaining solution invariance is discussed. Additionally, the correlation coefficients offer a quantifiable measurement of the improvement that occurs with finer meshes. It is noted that coarser meshes result in greater variability, particularly at lower soil depths.
• The finite element model is validated against the analytical Boussinesq theory for vertical stress; results converge at deeper soil depths across different mesh sizes.
• The superior performance of Modified Bitumen in resisting tensile strain is remarkable, as is the performance of VG40 in minimizing compressive strain.
• The effect of increasing bitumen layer thickness reduces both horizontal tensile strain at the bottom of the bitumen layer and vertical compressive strain at the bottom of the base layer.
• At higher temperatures, the effect of a thicker bitumen layer becomes more crucial in terms of limiting strain on the base layer. This is a significant practical interpretation of the phenomenon.