Torque Profile Optimization for Shell Eco-Marathon Urban Category Race ^†

Abstract

In this paper, we analyze the possibilities of optimizing the driving strategy for energy-efficient electric vehicles competing in the Shell Eco-marathon race. The base method we already developed and successfully applied for several years—winning the Urban Concept Battery Electric competition of the 2022, 2023, and 2024 Shell Eco-marathon races—was further tested, with small modifications to our optimization method. We only used an optimizer tool based on a genetic algorithm. We were interested in determining how a modification to the minimalization problem could help our optimizer find the best driving cycle to reach the minimum energy consumption. We successfully applied the modification to our method at the 2025 competition, where we beat our own record and proved its practical applicability.

1. Introduction

We sought to improve the applied driving cycle optimization procedure in anticipation of the 2025 race season, allowing for faster optimization and improved results. We have already published papers showing that our method [1,2] places a heavy burden on the nature of the racetrack—most importantly, the differences in altitude [3,4,5]—since the track is often the largest force component in such a race, as opposed to the running resistance of the vehicle or even the powertrain system. The method involves dividing the track into 10 m sections where the optimizer determines the positions at which the drive should and should not be run—i.e., it calculates the acceleration and deceleration sections. The results confirm that on a racetrack that is nearly flat, the acceleration and coasting sections are limited to a narrow speed range, while on a racetrack with larger climbs and descents, the acceleration and coasting sections are longer [4,6,7,8]. Along with searching for acceleration positions on the track, the optimizer also searches for a shift speed at which the torque reference of the vehicle drive is lowered to an equally optimized torque. The initial full acceleration phase—maximum traction provided by the drive system—is important to limit the amount of desired vehicle acceleration in the rest of the trajectory, reducing and minimizing the time the drive of the vehicle is in operation. The use of an optimized torque value above the shifting speed is important to ensure the drivetrain is applying a highly efficient workload on the track, which is crucial for the efficiency of the drive [9]. The competition rules do not emphasize battery preservation. Our objective is to complete the race distance with a lightweight battery that meets performance and range expectations. Therefore, high charge and discharge currents are tolerated if they yield improved consumption results, even at the expense of battery longevity.

2. Optimization Methods

We aimed to improve the method, i.e., make things easier on the optimizer, by restricting the search space to a reasonable boundary or modifying the torque reference calculation method. For this purpose, we aimed to test 3 additional new methods. Along with basic optimization, we further bounded the lower and upper bounds for optimized torque. In the other two cases, we changed the optimization problem by searching for the third-degree coefficients and a linear polynomial to determine the torque rather than searching for change speeds and a reduced torque value in the optimization. The basic method using acceleration sections on 10 m sections of the track area was still included in the vector.

The optimization problem and objective function are unchanged from the presented method [1,10] only the optimization vector and the torque mapping are changed to compare the methods.

The basic optimization vector searches for a 1280 m long racetrack—in 2025, the racetrack is 1283 m long (Equation (1)):

$${opt}_{base}=[d_0\dots d_{128}, v_{limit}, M_{opt}]$$

(1)

where d is the applied drive based on position on the racetrack—powertrain switched on —and v_limit is the speed where the drive changes to M_opt torque.

$$d=[d_0,d_1\dots d_{128}] \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} d_i \in \{0,1\} \mathrm{for} \mathrm{all} \mathrm{i}=0, \dots , 128$$

(2)

$$v_{limit} \in \mathrm{R} \mathrm{such} \mathrm{that} 0 \le v_{limit} \le 40$$

(3)

$$M_{opt} \in \mathrm{R} \mathrm{such} \mathrm{that} 1 \le v_{limit} \le 40$$

(4)

The drive torque applied by the drive chain in the simulations is determined by the equation below (Equation (5)):

$$\begin{array}{lll}M\left(s\right)& =& \\ M_{max},& & if d_s=1 and {v \le v}_{limit}\\ M_{opt},& & {if d}_s=1 and {v> v}_{limit}\\ 0,& & if d_s=0\end{array}$$

(5)

where s is the actual position on the track.

In the modified method, we changed only the bounds in M_opt possible values (Equation (6)). We named this method the narrower torque range optimization method:

$$M_{opt} \in \mathrm{R} \mathrm{such} \mathrm{that} 15 \le v_{limit} \le 21$$

(6)

We can easily agree with this limitation if we examine the efficiency curves of the drivetrain (Figure 1), which clearly shows that the optimum efficiency—red thin lines on the figure—is within the torque-limited range between 200 and 320 rpm. The thick red line delimits the working area that the powertrain can provide.

In the following two developed methods, the drive is not operated with discrete torque values (which were M_max and M_opt in the base method), but a third-degree and a linear polynomial give the actual drive torque that is dependent on speed.

The torque calculation equation for the third-degree polynomial method is (Equation (7))

$$\begin{array}{lll}M\left(s\right)=& & \\ M=a{v}^3+b{v}^2+cv+d,& & if d_s=1\\ 0,& & if d_s=0\end{array}$$

(7)

where v is the actual speed of the vehicle.

The optimization vector modified to this formula is

$${opt}_{3rd polinom}=[d_0\dots d_{128}, a, b,c,d]$$

(8)

$$a,b,c,d \in \mathrm{R}$$

(9)

The torque calculation equation for the linear method is (Equation (10))

$$\begin{array}{lll}M\left(s\right)=& & \\ M=av+b,& & if d_s=1\\ 0,& & if d_s=0\end{array}$$

(10)

The optimization vector modified to this formula is

$${opt}_{3rd polinom}=[d_0\dots d_{128}, a, b]$$

(11)

$$a,b \in \mathrm{R}$$

(12)

We compared these four different optimization methods in our simulations, where our main goal was to achieve the best result. We did not investigate the sensitivity of the other parameters of the optimization method. Our investigations were only focused on the torque signal training methods.

3. Simulations and Results

The optimization process was tested based on the 2025 Shell Eco-marathon Europe competition, which has a total length of 1283 m. The optimizer minimizes the electrical energy absorbed by the drivetrain. The model for the vehicle and track was based on measured data and implemented with selected LUTs [1] The Simulink model had a simulation time step interval of 0.1 s, which gave a run time of less than a second for a specific race lap. The optimizing genetic algorithm was sub-applied.

The objective function tracks the distance traveled by the vehicle and the time spent to travel the specified distance and penalizes the optimization individuals if the time and distance objectives are not satisfied. The distance traveled must be 1283 m in less than 190 s. If the vehicle speed is negative during the simulation, the simulation of the course is terminated and the individual is penalized by the objective function as well.

In the optimization process, 130 generations were run for each method and the population consisted of 1300 individuals. The first 129 elements of the optimization vector were searched as integer values, while the remaining values were searched as floatingpoint values corresponding to the optimization method.

The results of the optimization methods can be seen in

Table 1. Results of optimization methods.

Optimization Method	Energy Consumption [J]
Base	18.295
Narrower torque range	17.649
Third-degree polynomial	20.462
Linear polynomial	17.985

.

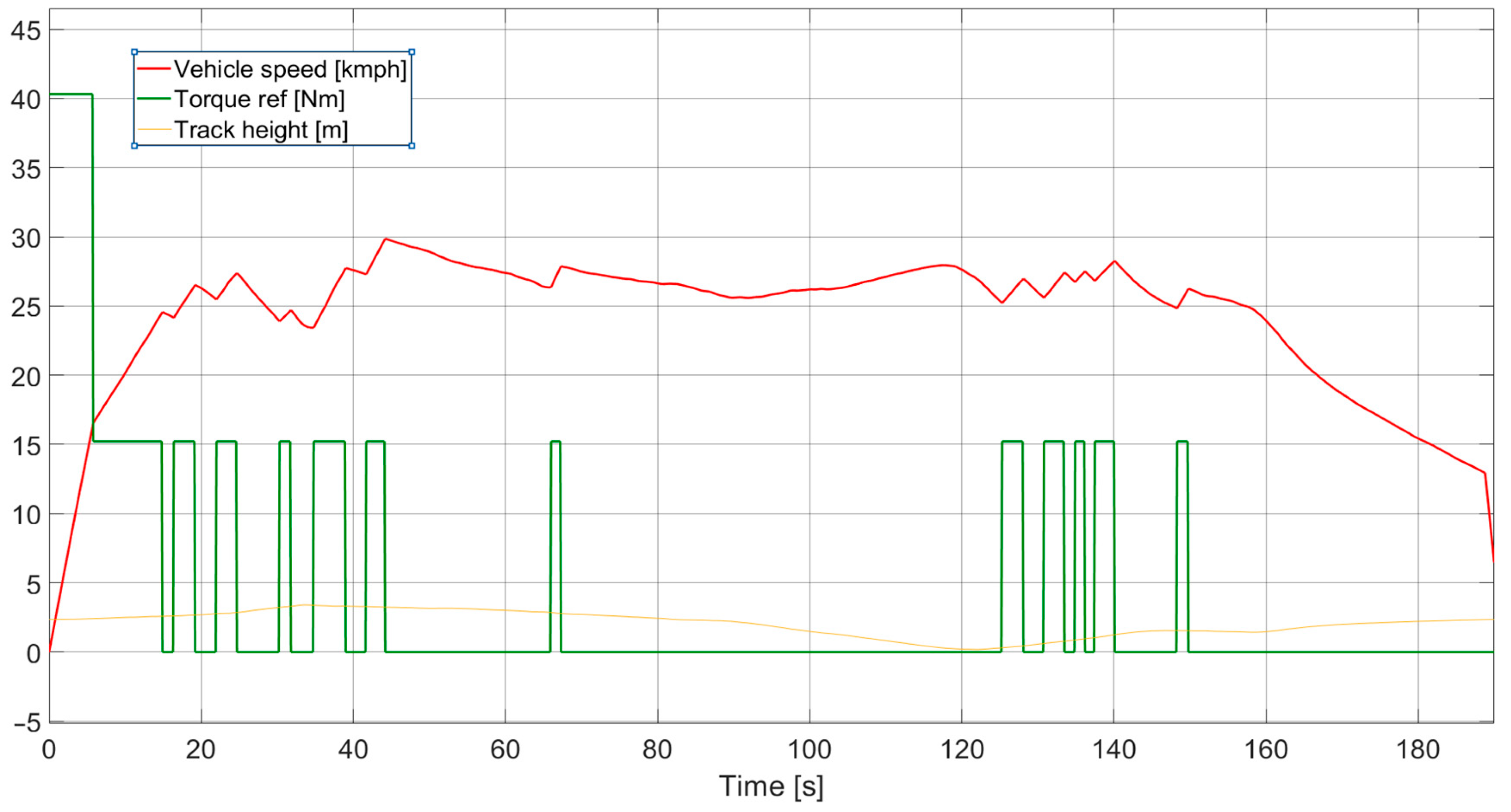
The basic method achieved the third best result (the result can be seen in Figure 2), but in repeated runs, it showed quite a large variance in the best result. This is probably because a large torque range has a large impact on the vehicle dynamics and the method cannot fully minimize the running time of the drivetrain.

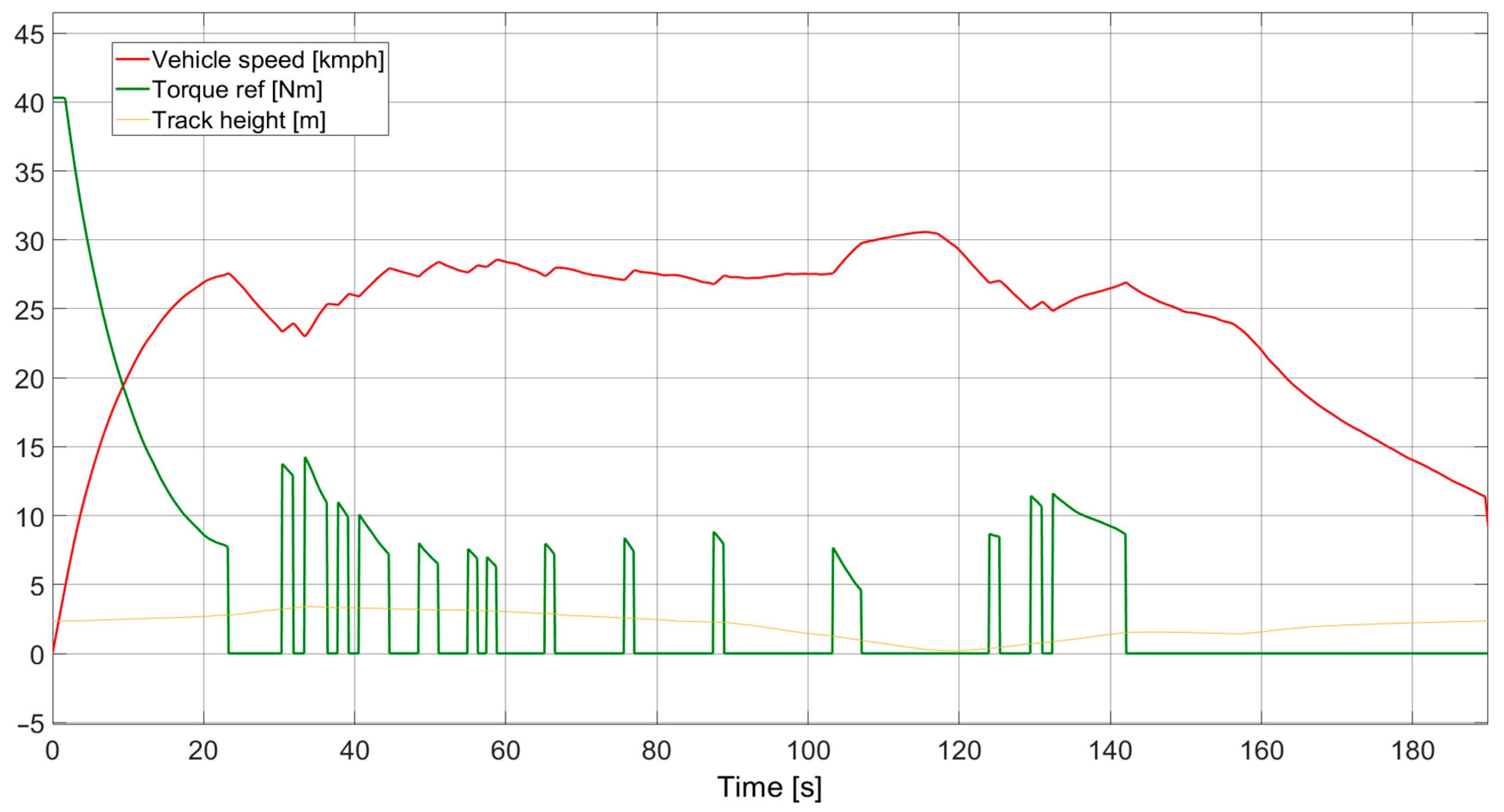
The narrower torque range procedure (the result can be seen in Figure 3) yielded the best results as the optimizer searched over a small torque range in the speed-maintaining sections. The smaller torque range helped the optimizer minimize the drivetrain operating time. It can also be clearly seen that the method takes advantage of the downhill section of the track and does not operate the drive system when the vehicle is only losing a small amount of speed or is accelerating on the downhill. We used this method in the 2025 Shell Eco-marathon, which we won and set a record for the most races with the same set of rules. The new record is 327 km/kWh in this category.

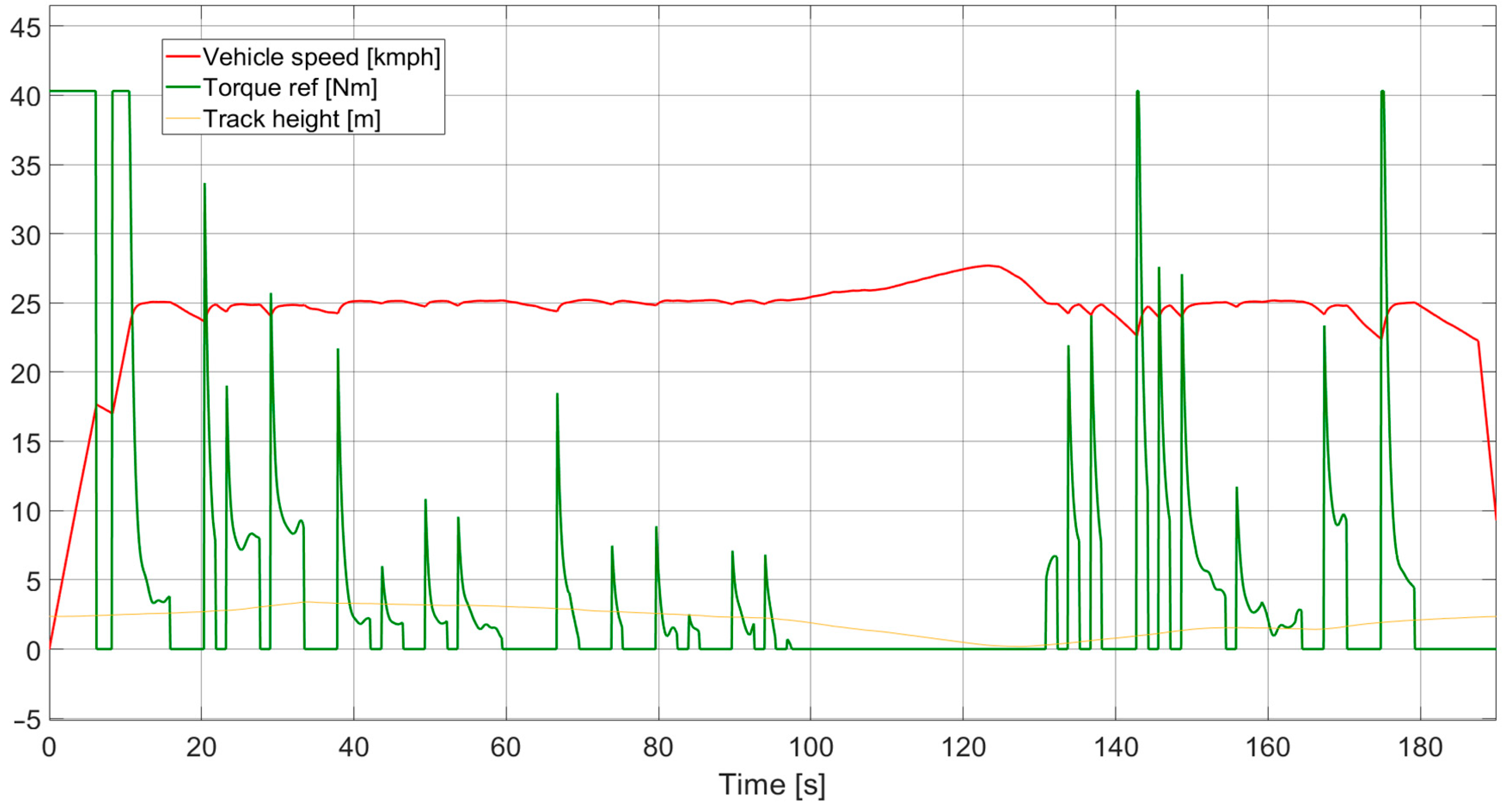
The disadvantage of the third-degree polynomial method (the result can be seen in Figure 4) is that a small change in the parameters produces a torque reference signal with a completely different value, so the optimizer cannot find the right parameters, due to identical optimization settings. It can also be seen from the torque curve that the third-degree polynomial does not give the right value of torque at speeds around 25 km/h and is not able to accelerate the vehicle meaningfully above 25 km/h.

The advantage of the linear polynomial method (the result can be seen in Figure 5) is that the torque generation gives the driver a natural driving experience. Torque reference without large steps results in reduced vehicle acceleration, so the method merits further investigation. This method also nearly minimized the drivetrain operating time, which is why it achieved the second-best result. However, it has the disadvantage that the drive is only able to remain partially in the maximum efficiency range in the speed holding range, because the speed-dependent linear relationship allows this only if the starting torque is high.

4. Conclusions

It can be concluded that the three new methods perform very close to the original optimization method. The optimization using the discrete torque shift method with a reduced torque range yields the best results, since we reduce the search space in it. The linear velocity-dependent torque training method achieves a more uniform torque application and is easier to implement in the vehicle control software.

The results of the presented methods show that GA is able to find the best result when the torque signal calculation is simple [11]. The optimizer cannot perform well if small changes in the parameters that result in the torque signal have a large effect on the vehicle dynamics—hence, the third-degree polynomial method did not perform well. The results also show that the best performing optimizations minimize the drive-operating time durations.

The optimization results are presented to the driver in practice during the race via a GUI (Graphical User Interface) that displays the optimal energy-saving strategy (reference speed and actual speed as well as drive engagement phases). The driver can visually follow the indicated strategy, which is especially important in a learning or racing environment where full automation has not been implemented. Real-time torque control based on vehicle speed (reference torque signal generation) is handled by the vehicle control unit (VCU), so the driver does not have to interpret the detailed output of the optimizer.