Strain Rate Dependence of PLC Effect in AlMg4.5 Alloys †
Abstract
1. Introduction
2. Materials and Methods
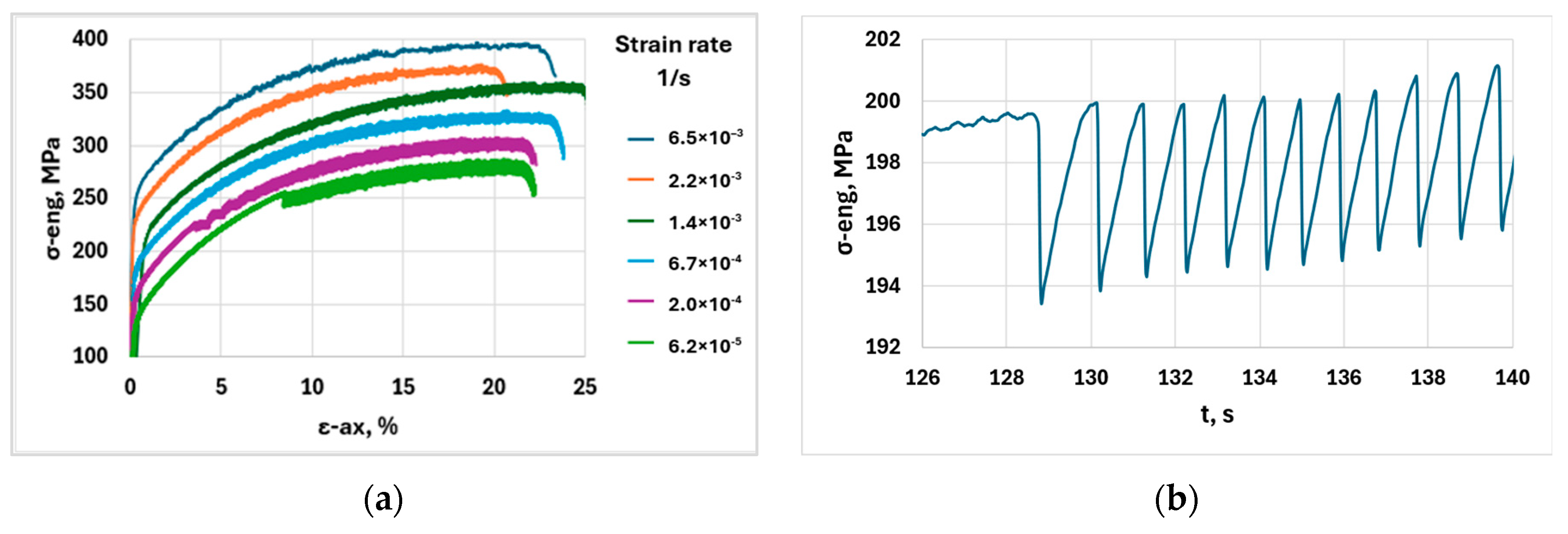
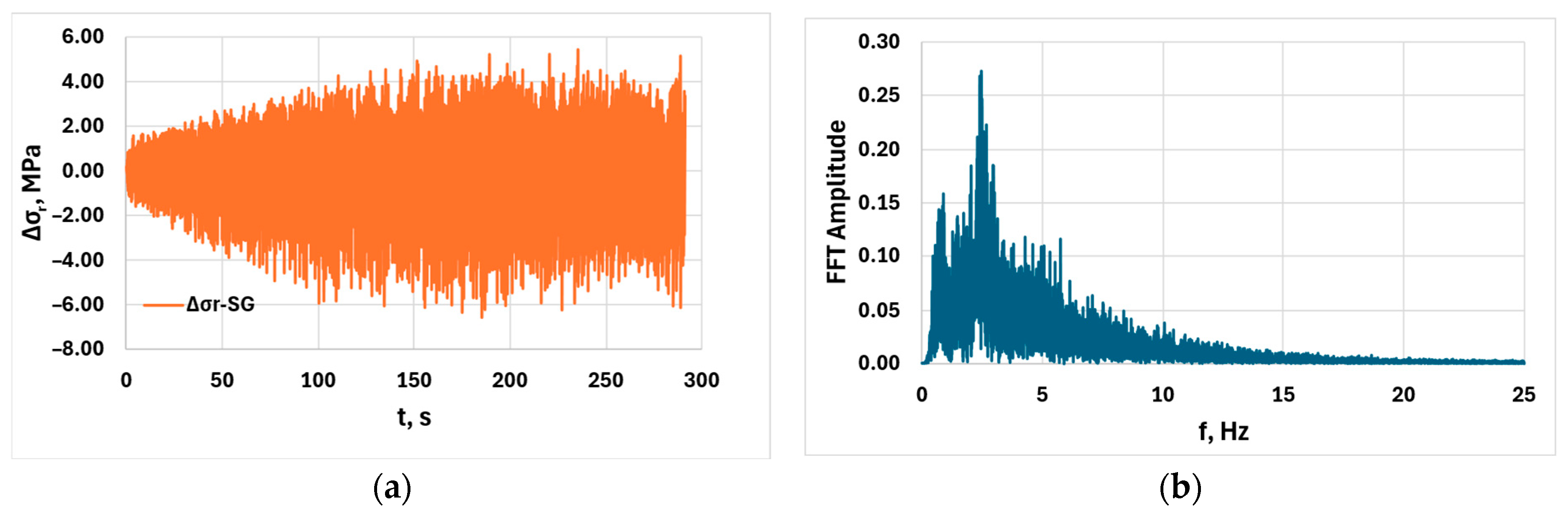
3. Results
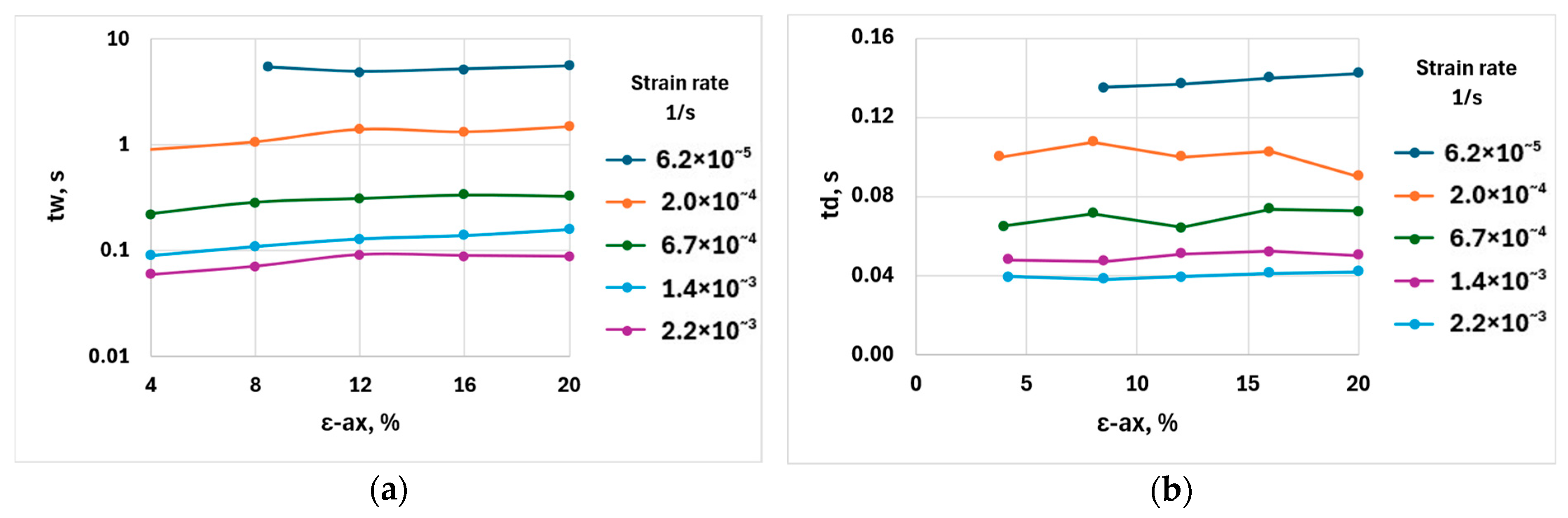
4. Discussion
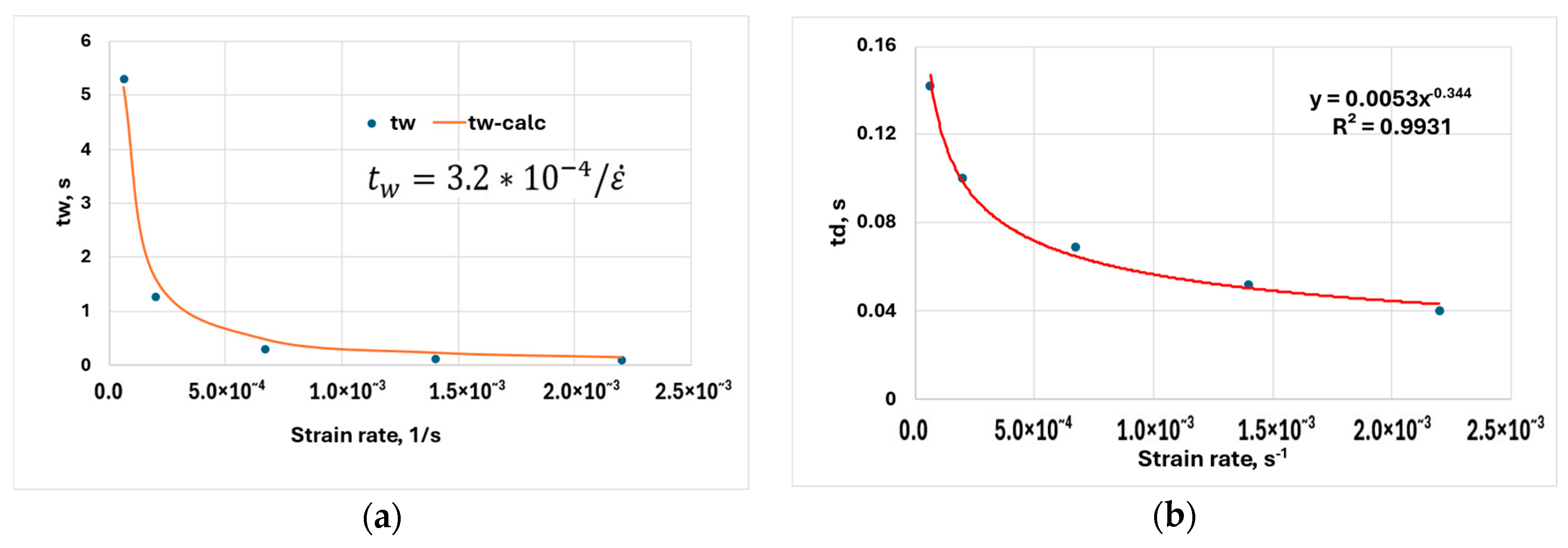
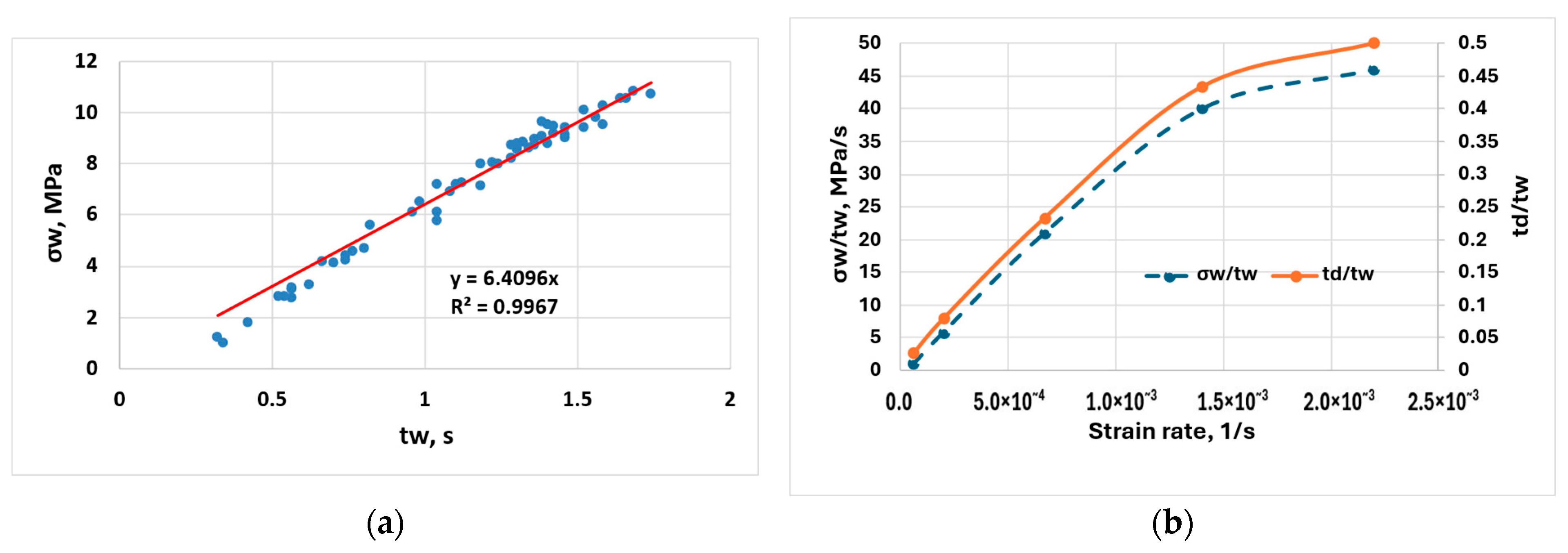
4.1. Analysis of the Parameters of the Reference Function
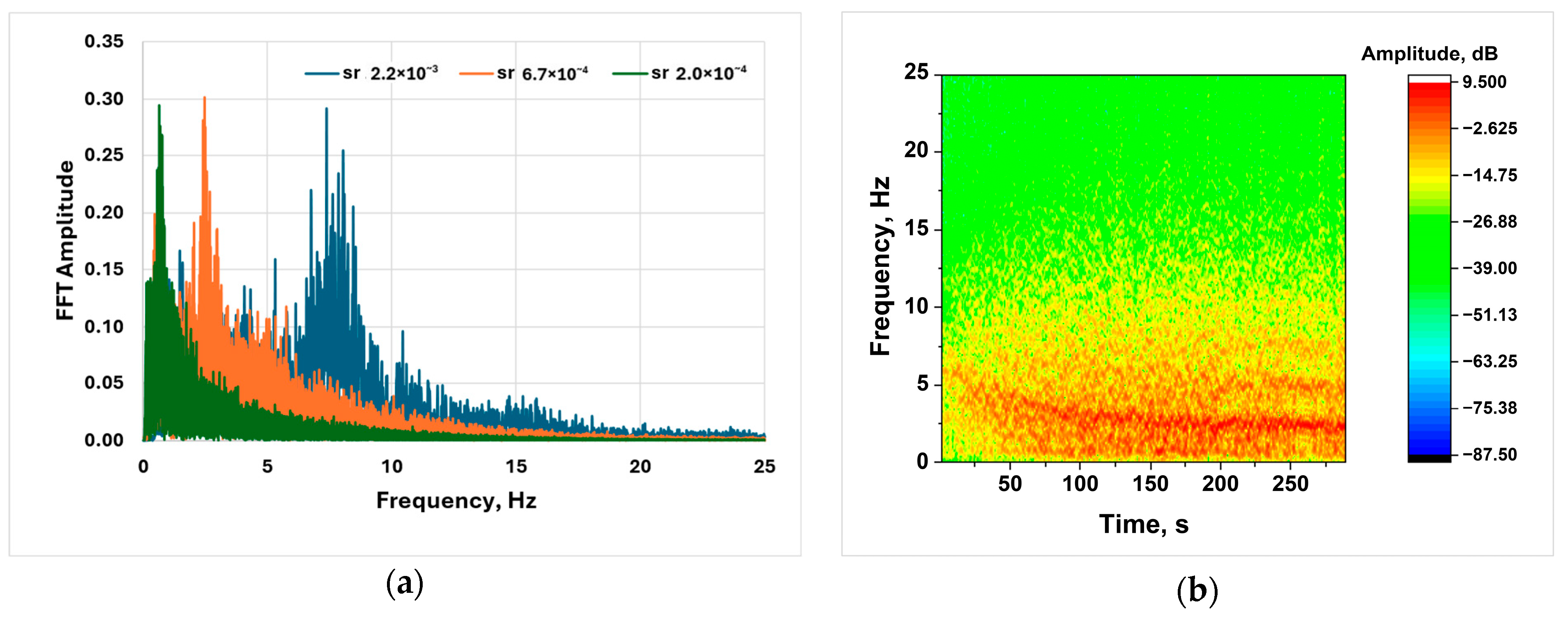
4.2. Effect of Strain Rate on PLC Characteristics
5. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Portevin, A.; Le Chatelier, F. On a phenomenon observed during the tensile testing of alloys undergoing transformation. C. R. Acad. Sci. Paris 1923, 176, 507–510. (In French) [Google Scholar]
- Saad, G.; Fayek, S.A.; Fawzy, A.; Soliman, H.N.; Nassr, E. Serrated flow and work hardening characteristics of Al-5356 alloy. J. Alloys Compd. 2010, 502, 139–146. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, J.P.; Chen, S.Y.; Xie, X.; Liaw, P.K.; Dahmen, K.A.; Qiao, J.W.; Wang, Y.L. Serration and noise behaviors in materials. Prog. Mater. Sci. 2017, 90, 358–460. [Google Scholar] [CrossRef]
- Tian, N.; Wang, G.; Zhou, Y.; Liu, K.; Zhao, G.; Zuo, L. Study of the Portevin-Le Chatelier (PLC) characteristics of a 5083 aluminum alloy sheet in two heat treatment states. Materials 2018, 11, 1533. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Z.; Li, F.; He, M. Fast Fourier transform on analysis of Portevin-Le Chatelier effect in Al 5052. Mater. Sci. Eng. A 2011, 530, 389–395. [Google Scholar] [CrossRef]
- Ait-Amokhtar, H.; Fressengeas, H.; Bouabdallah, K. On the effects of the Mg content on the critical strain for the jerky flow of Al-Mg alloys. Mater. Sci. Eng. A 2015, 636, 180–186. [Google Scholar] [CrossRef]
- McCormick, P.G. Effect of grain size on serrated yielding in an Al-Mg-Si alloy. Philos. Mag. A 1971, 23, 949–956. [Google Scholar] [CrossRef]
- Kovács, Z.; Lendvai, J.; Vörös, G. Localized deformation bands in Portevin–Le Chatelier plastic instabilities at a constant stress rate. Mater. Sci. Eng. A 2000, 279, 179–184. [Google Scholar] [CrossRef]
- Reed, J.M.; Walter, M.E. Observations of serration characteristics and acoustic emission during serrated flow of an Al–Mg alloy. Mater. Sci. Eng. A 2003, 359, 1–10. [Google Scholar] [CrossRef]
- Wen, W.; Morris, J.G. The effect of cold rolling and annealing on the serrated yielding phenomenon of AA5182 aluminum alloy. Mater. Sci. Eng. A 2004, 373, 204–216. [Google Scholar] [CrossRef]
- Gopinath, K.; Gogia, A.K.; Kamat, S.V.; Ramamurty, U. Dynamic strain ageing in Ni-base superalloy 720Li. Acta Mater. 2009, 57, 1243–1253. [Google Scholar] [CrossRef]
- Saadat, Z.; Moghanaki, S.K.; Kazeminezhad, M.; Goodarzi, M.; Afjeh, S.M.B.G. Effect of two steps annealing on the microstructure and dynamic strain aging behavior of Al-6Mg alloy. Mater. Sci. Eng. A 2020, 798, 140097. [Google Scholar] [CrossRef]
- Kubin, L.P.; Estrin, Y. Evolution of dislocation densities and the critical conditions for the Portevin-Le Chatelier effect. Acta Metall. Mater. 1990, 38, 697–708. [Google Scholar] [CrossRef]
- Lee, S.Y.; Chettri, S.; Sarmah, R.; Takushima, C.; Hamada, J.; Nakada, N. Serrated flow accompanied with dynamic type transition of the Portevin–Le Chatelier effect in austenitic stainless steel. J. Mater. Sci. Technol. 2023, 133, 154–164. [Google Scholar] [CrossRef]
- Ait-Amokhtar, H.; Boudrahem, S.; Fressengeas, C. Spatiotemporal aspects of jerky flow in Al–Mg alloys, in relation with the Mg content. Scr. Mater. 2006, 54, 2113–2118. [Google Scholar] [CrossRef]

| s−1 | Rp0.2; MPa | Rm; MPa | Ag; % | At; % | n | r |
|---|---|---|---|---|---|---|
| 6.5 × 10−3 | 132 | 269 | 20.1 | 23.0 | 0.31 | 0.81 |
| 2.2 × 10−3 | 131 | 269 | 18.2 | 21.2 | 0.31 | 0.83 |
| 1.4 × 10−3 | 141 | 281 | 21.8 | 25.2 | 0.31 | 0.78 |
| 6.7 × 10−4 | 140 | 283 | 21.3 | 24.1 | 0.31 | 0.84 |
| 2.0 × 10−4 | 135 | 282 | 22.1 | 22.2 | 0.32 | 0.85 |
| 6.2 × 10−5 | 136 | 267 | 22.1 | 22.3 | 0.33 | 0.81 |
| s−1 | tw, s | td, s | t = tw + td, s | fave, Hz | p | fmin, Hz |
|---|---|---|---|---|---|---|
| 2.2 × 10−3 | 0.080 | 0.040 | 0.120 | 8.333 | 49 | 50 |
| 1.4 × 10−3 | 0.120 | 0.052 | 0.172 | 5.814 | 69 | 38 |
| 6.7 × 10−4 | 0.297 | 0.069 | 0.366 | 2.732 | 147 | 29 |
| 2.0 × 10−4 | 1.258 | 0.100 | 1.403 | 0.713 | 561 | 20 |
| 6.2 × 10−5 | 5.294 | 0.142 | 5.436 | 0.184 | 2173 | 14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Czinege, I.; Harangozó, D. Strain Rate Dependence of PLC Effect in AlMg4.5 Alloys. Eng. Proc. 2025, 113, 25. https://doi.org/10.3390/engproc2025113025
Czinege I, Harangozó D. Strain Rate Dependence of PLC Effect in AlMg4.5 Alloys. Engineering Proceedings. 2025; 113(1):25. https://doi.org/10.3390/engproc2025113025
Chicago/Turabian StyleCzinege, Imre, and Dóra Harangozó. 2025. "Strain Rate Dependence of PLC Effect in AlMg4.5 Alloys" Engineering Proceedings 113, no. 1: 25. https://doi.org/10.3390/engproc2025113025
APA StyleCzinege, I., & Harangozó, D. (2025). Strain Rate Dependence of PLC Effect in AlMg4.5 Alloys. Engineering Proceedings, 113(1), 25. https://doi.org/10.3390/engproc2025113025






