Urban Mobility Modeling: Application to Seoul Bike-Sharing Data †
Abstract
1. Introduction
2. The Normal Variance–Mean Mixture Model
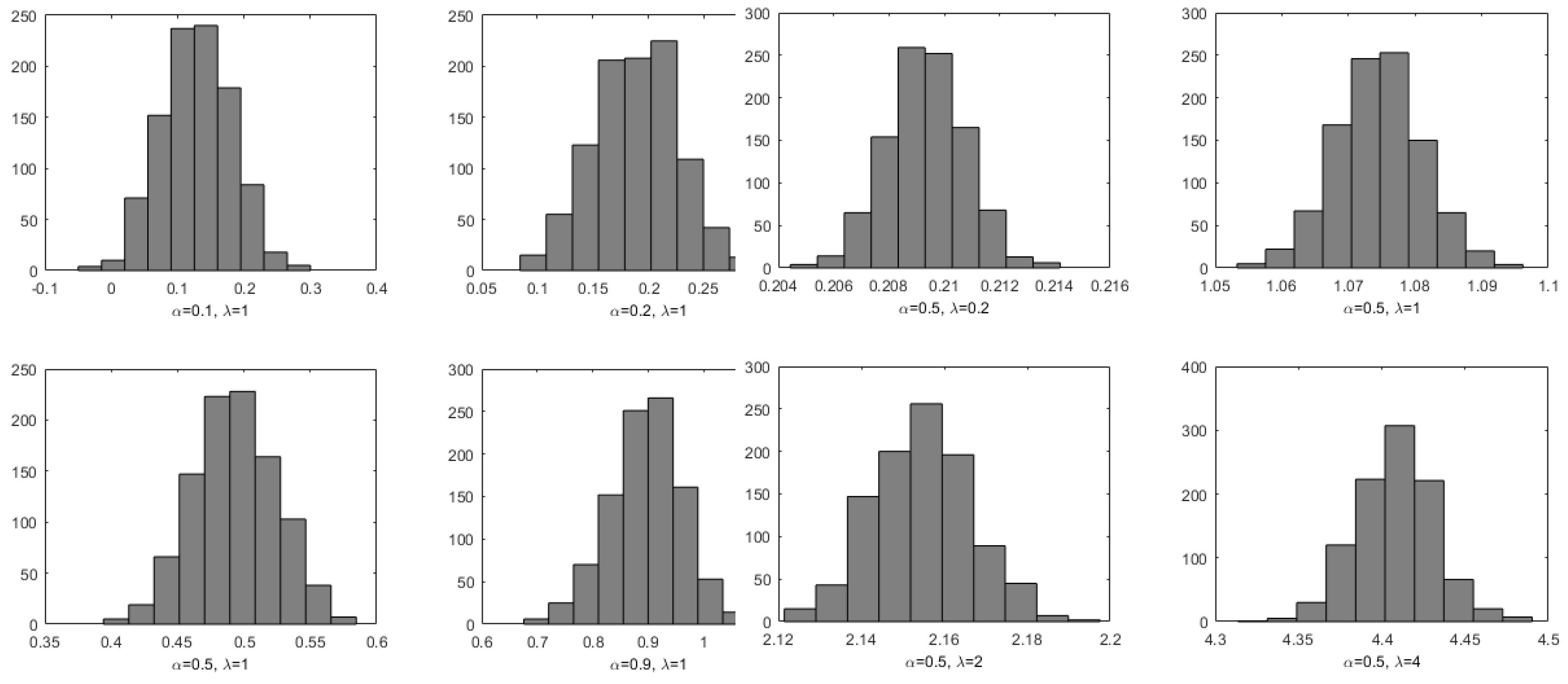
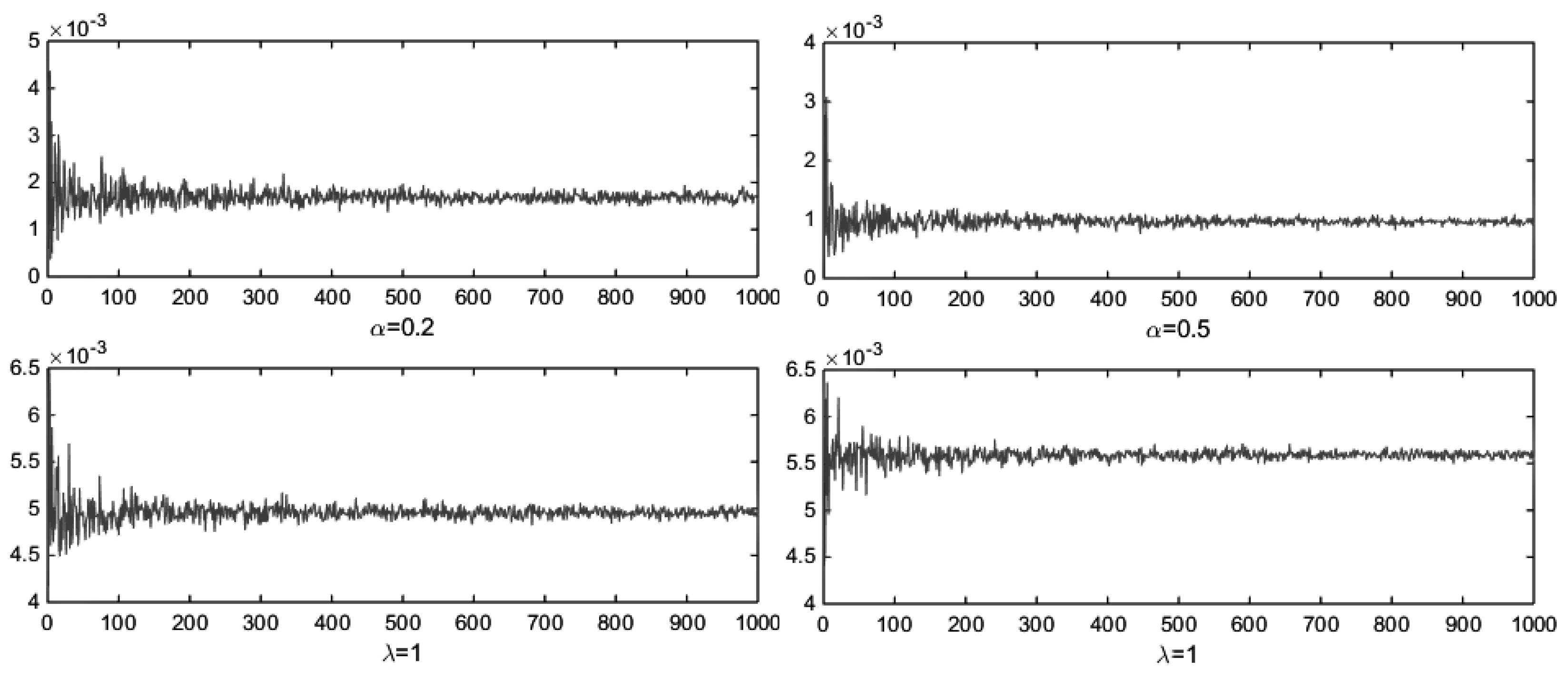
2.1. Estimation
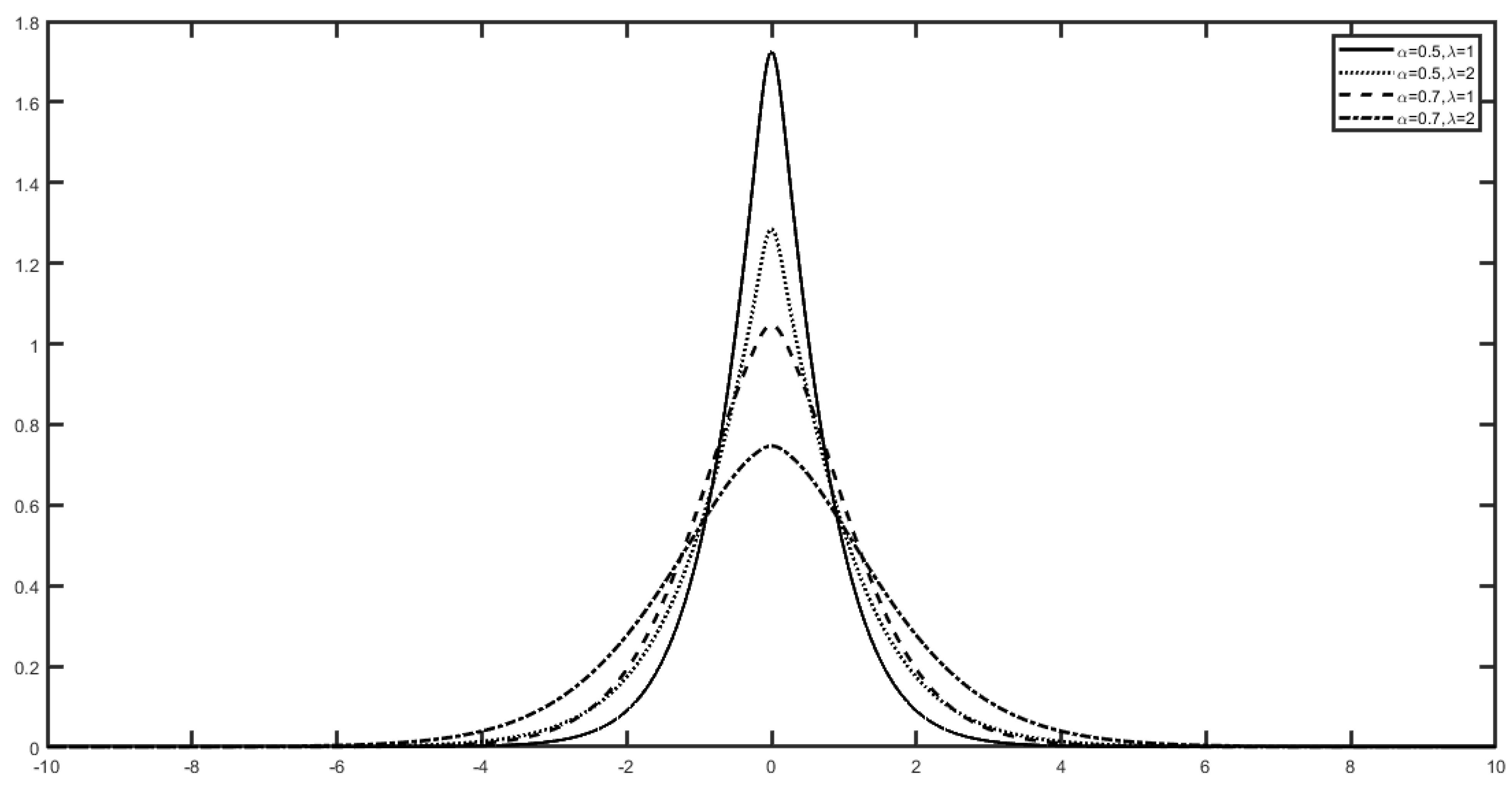
2.2. Numerical Illustration
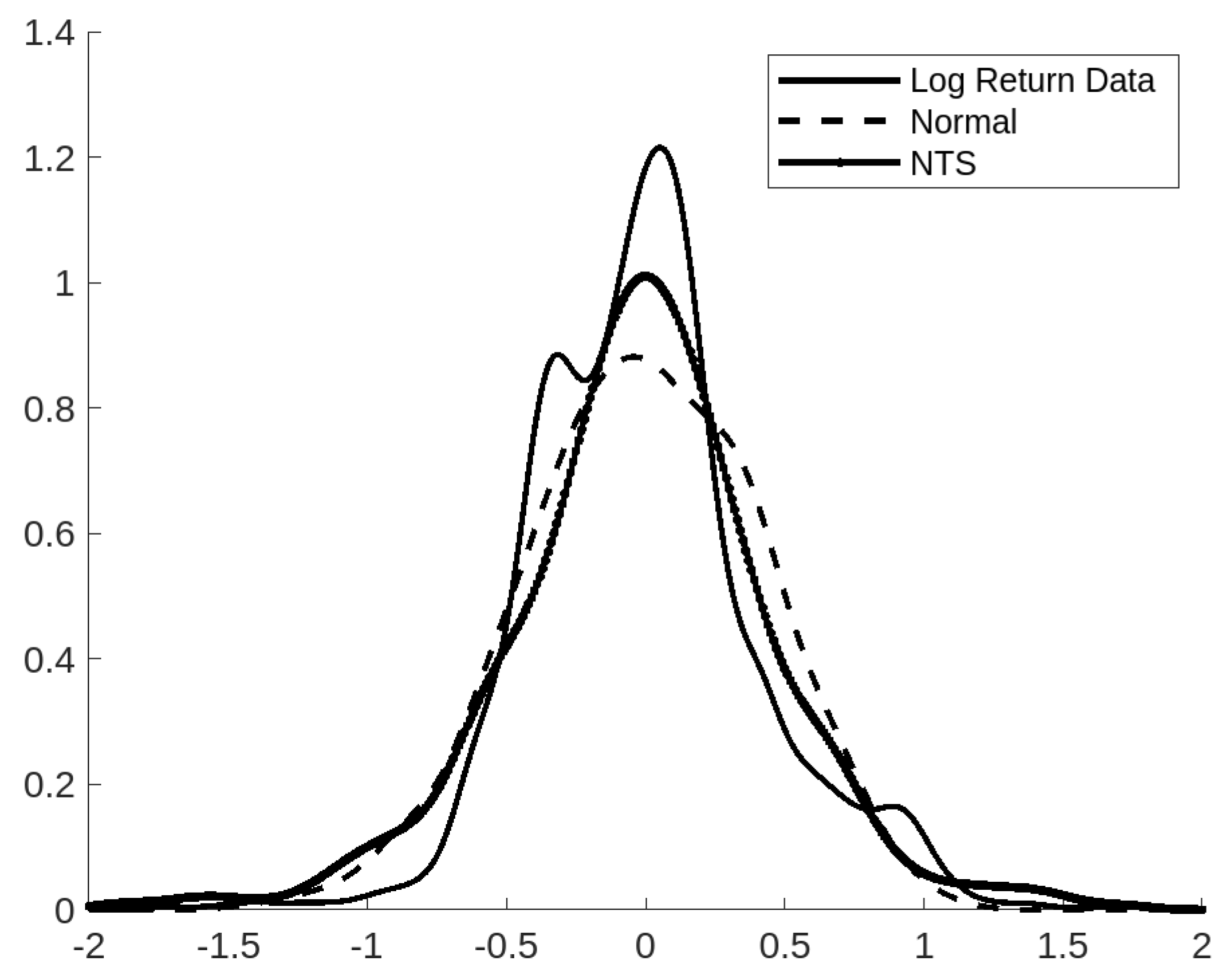
3. Modeling Bike-Sharing Data
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- El Amrani, A.M.; Fri, M.; Benmoussa, O.; Rouky, N. The integration of urban freight in public transportation: A systematic literature review. Sustainability 2024, 16, 5286. [Google Scholar] [CrossRef]
- Benjdiya, O.; Rouky, N.; Benmoussa, O.; Fri, M. On the use of machine learning techniques and discrete choice models in mode choice analysis. LogForum 2023, 19, 321–336. [Google Scholar] [CrossRef]
- Charfi, S.; Mselmi, F. Modeling exchange rate volatility: Application of GARCH models with a Normal Tempered Stable distribution. Quant. Financ. Econ. 2022, 6, 206–222. [Google Scholar] [CrossRef]
- Fri, M. Lead time prediction using advanced deep learning approaches: A case study in the textile industry. LogForum 2024, 20, 145–155. [Google Scholar] [CrossRef]
- Oucheikh, R.; Fri, M.; Fedouaki, F.; Hain, M. Deep anomaly detector based on spatio-temporal clustering for connected autonomous vehicles. In Proceedings of the International Conference on Ad Hoc Networks, Paris, France, 17 November 2020; pp. 201–212. [Google Scholar]
- Barndorff-Nielsen, O.E.; Shephard, N. Normal modified stable processes. Theor. Probab. Math. Stat. 2001, 65, 1–19. [Google Scholar]
- Bianchi, M.L.; Tassinari, G.L. Estimation for multivariate normal rapidly decreasing tempered stable distributions. J. Stat. Comput. Simul. 2024, 94, 103–125. [Google Scholar] [CrossRef]
- Xia, Y.; Grabchak, M. Estimation and simulation for multivariate tempered stable distributions. J. Stat. Comput. Simul. 2022, 92, 451–475. [Google Scholar] [CrossRef]
- Baeumer, B.; Kovács, M. Approximating multivariate tempered stable processes. J. Appl. Probab. 2012, 49, 167–183. [Google Scholar] [CrossRef][Green Version]
- Mselmi, F. Lévy processes time-changed by the first-exit time of the inverse Gaussian subordinator. Filomat 2018, 32, 2545–2552. [Google Scholar] [CrossRef]
- Mselmi, F. Characterization of the inverse stable subordinator. Stat. Probab. Lett. 2018, 140, 37–43. [Google Scholar] [CrossRef]
- Rencher, A.C.; Christensen, W.F. Methods of Multivariate Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Bianchi, M.L.; Tassinari, G.L.; Fabozzi, F.J. Riding with the four horsemen and the multivariate normal tempered stable model. Int. J. Theor. Appl. Financ. 2016, 19, 1650027. [Google Scholar] [CrossRef]
- Sabino, P. Normal tempered stable processes and the pricing of energy derivatives. SIAM J. Financ. Math. 2023, 14, 99–126. [Google Scholar] [CrossRef]
- Sabino, P. Exact simulation of normal tempered stable processes of OU type with applications. Stat. Comput. 2022, 32, 81. [Google Scholar] [CrossRef]
- Nolan, J.P. Stable Distributions: Models for Heavy Tailed Data; Birkhäuser: Boston, MA, USA, 2008. [Google Scholar]
- Geweke, J. Monte Carlo simulation and numerical integration. Handb. Comput. Econ. 1996, 1, 731–800. [Google Scholar]
- UCI Machine Learning Repository. Bike Sharing. Available online: https://archive.ics.uci.edu/dataset/275/bike+sharing+dataset (accessed on 25 June 2025).

| 1 | |||||||
| 2 | |||||||
| 1 | |||||||
| 2 | |||||||
| 1 | |||||||
| 2 |
| − | − | |||
| − | − |
| Normal Model | Normal Tempered Stable Model | |
|---|---|---|
| MSE | 0.013002 | 0.0076658 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mselmi, F.; Fri, M.; Rouky, N. Urban Mobility Modeling: Application to Seoul Bike-Sharing Data. Eng. Proc. 2025, 112, 51. https://doi.org/10.3390/engproc2025112051
Mselmi F, Fri M, Rouky N. Urban Mobility Modeling: Application to Seoul Bike-Sharing Data. Engineering Proceedings. 2025; 112(1):51. https://doi.org/10.3390/engproc2025112051
Chicago/Turabian StyleMselmi, Farouk, Mouhsene Fri, and Naoufal Rouky. 2025. "Urban Mobility Modeling: Application to Seoul Bike-Sharing Data" Engineering Proceedings 112, no. 1: 51. https://doi.org/10.3390/engproc2025112051
APA StyleMselmi, F., Fri, M., & Rouky, N. (2025). Urban Mobility Modeling: Application to Seoul Bike-Sharing Data. Engineering Proceedings, 112(1), 51. https://doi.org/10.3390/engproc2025112051






