Phase-Field Simulation of Bubble Evolution and Heat Transfer in Microchannels Under Subcooled and Saturated Flow Boiling †
Abstract
1. Introduction
2. Numerical Model
- Inlet (x = 0):
- Bottom Wall:
- Outlet (x = 1000 μm):
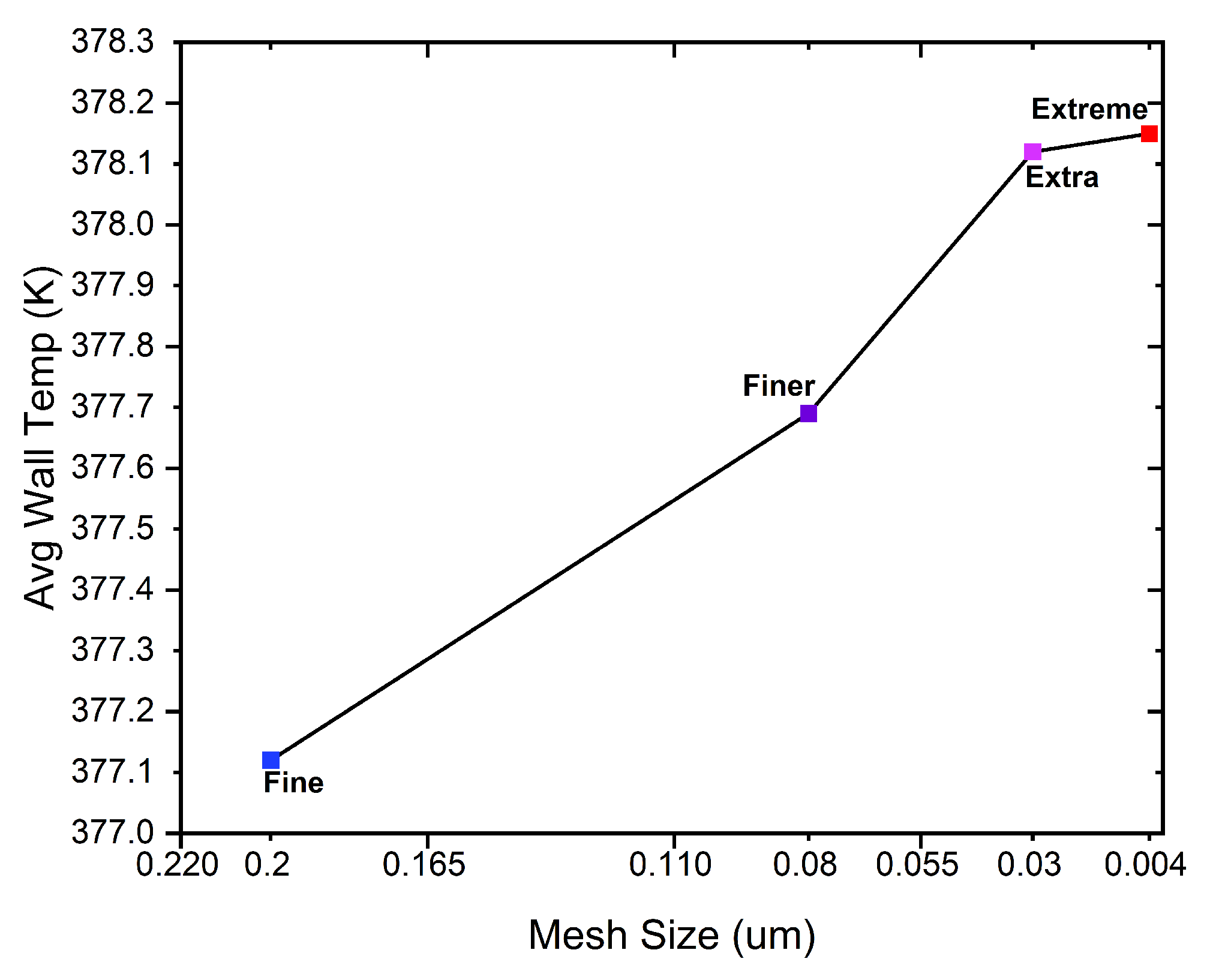
Mesh Independence Study
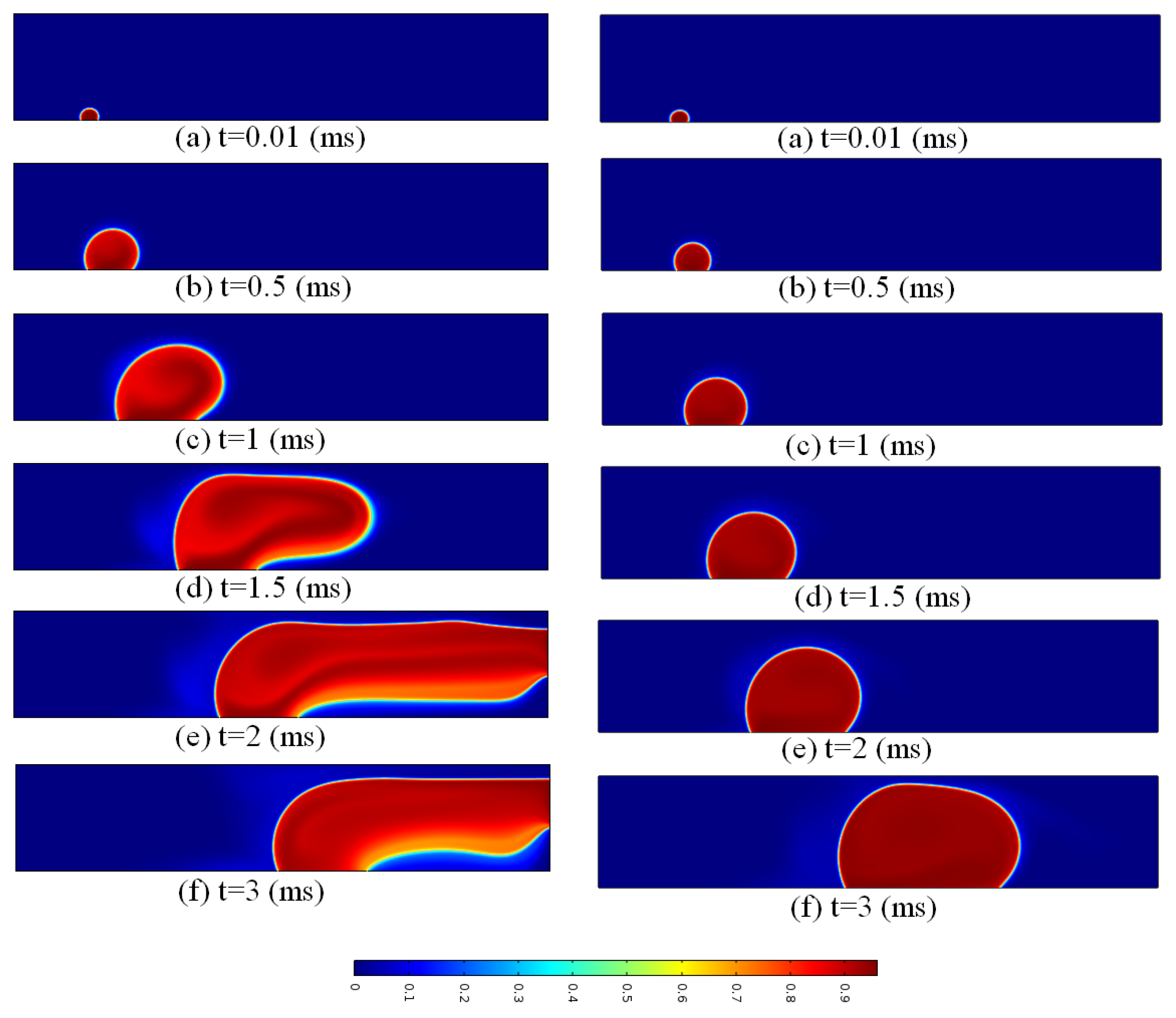
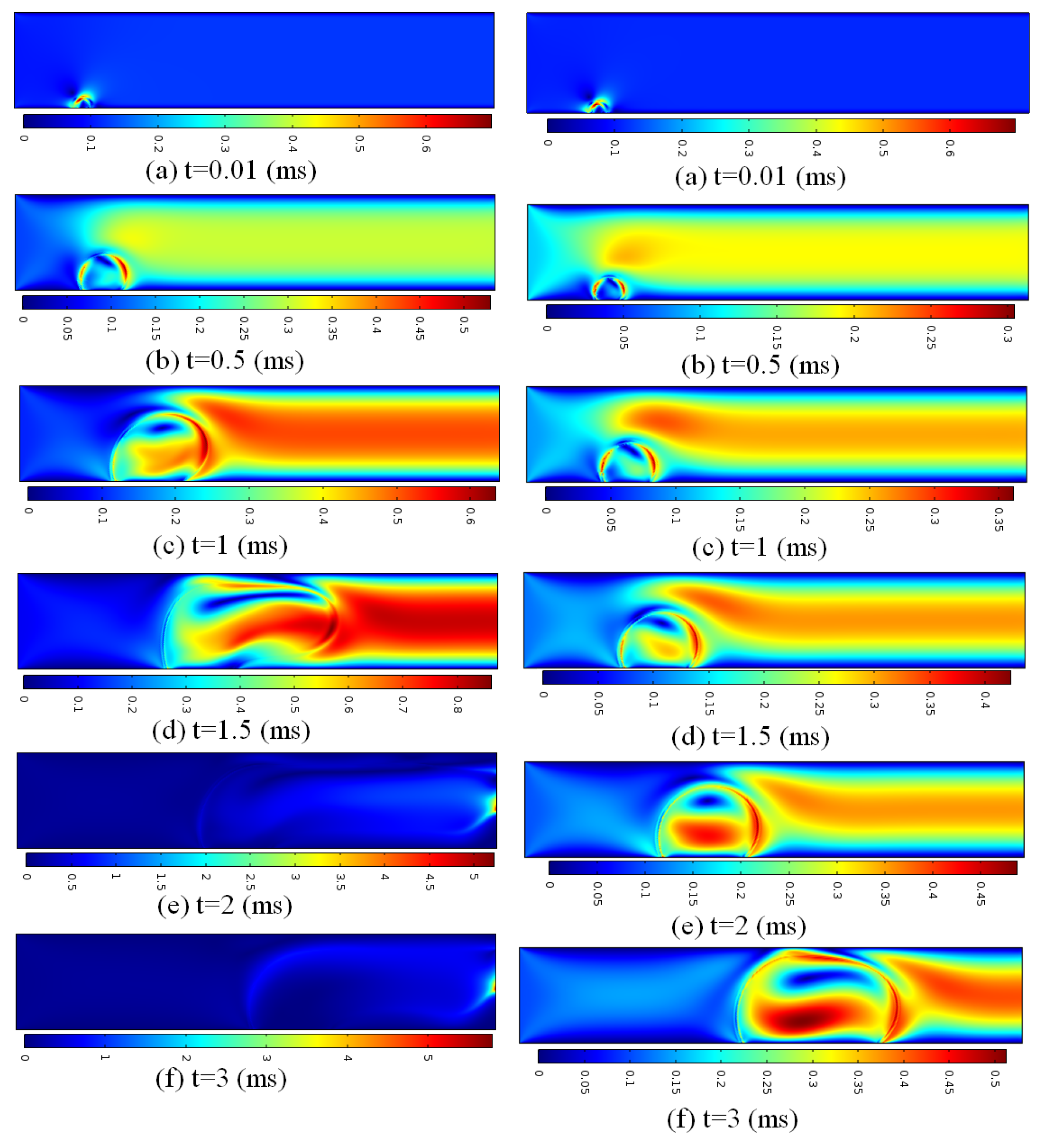
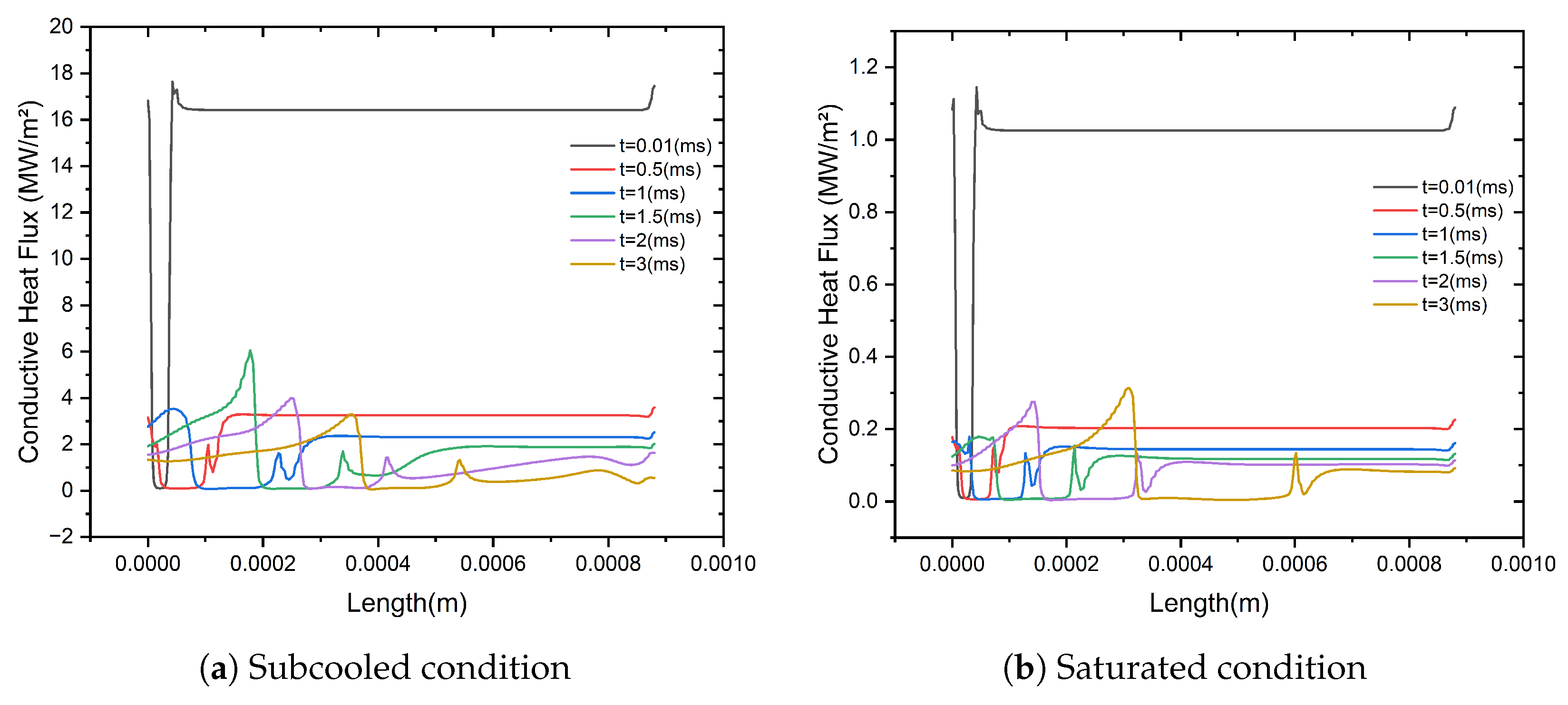
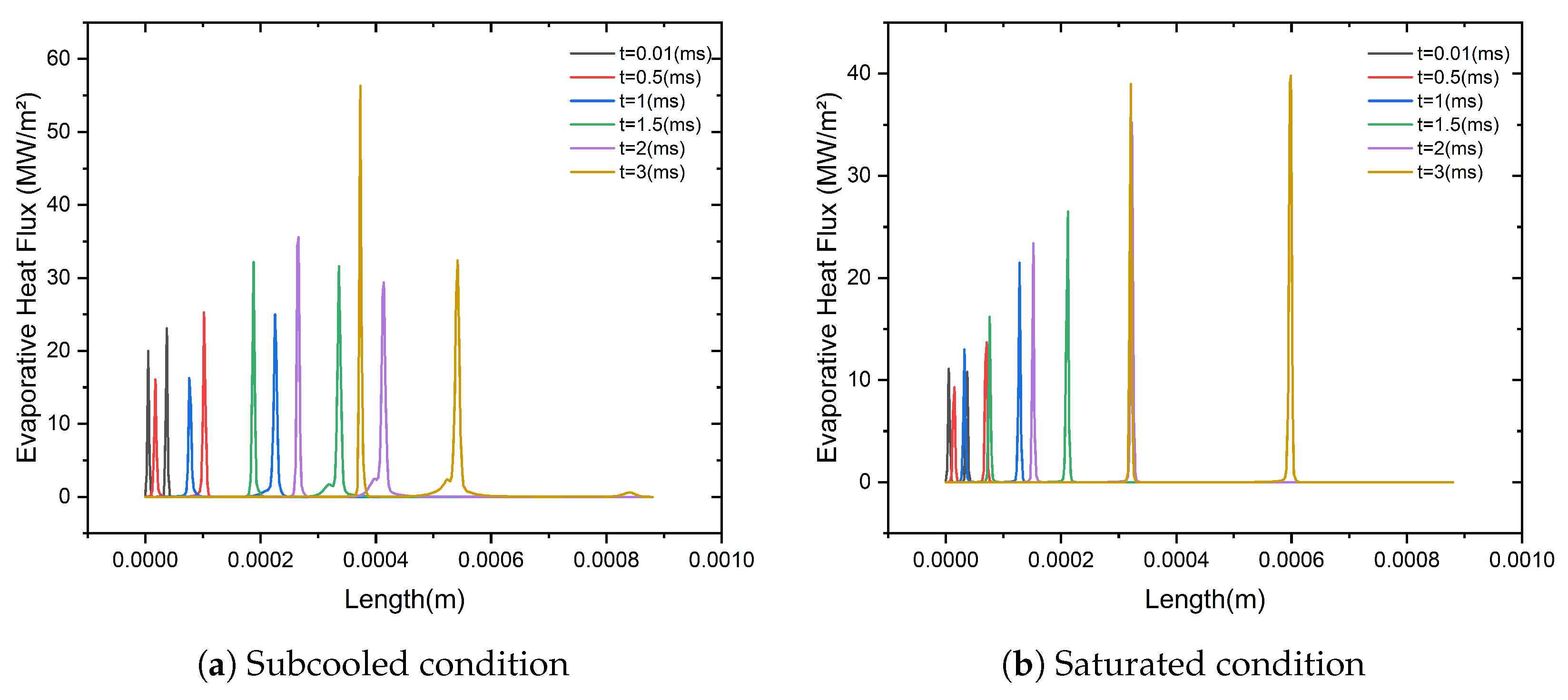
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wu, X.; Wang, X.; Liu, Y.; Li, L. Numerical Investigation of Subcooled Boiling Flow and Patterns’ Transitions in a High-Heat-Flux Rectangular Small Channel. Water 2025, 17, 1580. [Google Scholar] [CrossRef]
- Luo, Y.; Zhang, J.; Li, W. Simulation of subcooled flow boiling in manifold microchannel heat sink. In Proceedings of the International Conference on Nanochannels, Microchannels, and Minichannels, Virtual, 13–15 July 2020; American Society of Mechanical Engineers: New York, NY, USA, 2020; Volume 83693, p. V001T16A003. [Google Scholar] [CrossRef]
- Okajima, J.; Stephan, P. Numerical simulation of liquid film formation and its heat transfer through vapor bubble expansion in a microchannel. Int. J. Heat Mass Transf. 2019, 136, 1241–1249. [Google Scholar] [CrossRef]
- Municchi, F.; El Mellas, I.; Matar, O.K.; Magnini, M. Conjugate heat transfer effects on flow boiling in microchannels. Int. J. Heat Mass Transf. 2022, 195, 123166. [Google Scholar] [CrossRef]
- Rajkotwala, A.H.; Boer, L.L.; Peters, E.A.J.F.; van der Geld, C.W.M.; Kuerten, J.G.M.; Kuipers, J.A.M.; Baltussen, M.W. A numerical study of flow boiling in a microchannel using the local front reconstruction method. AIChE J. 2022, 68, e17598. [Google Scholar] [CrossRef]
- Soleimani, A.; Hanafizadeh, P.; Sattari, A. Subcooled two-phase flow boiling in a microchannel heat sink: Comparison of conventional numerical models. J. Comput. Appl. Mech. 2020, 51, 37–45. [Google Scholar]
- Jain, S.; Jayaramu, P.; Gedupudi, S. Modeling of pressure drop and heat transfer for flow boiling in a mini/micro-channel of rectangular cross-section. Int. J. Heat Mass Transf. 2019, 140, 1029–1054. [Google Scholar] [CrossRef]
- Roccon, A. Boiling heat transfer by phase-field method. Acta Mech. 2024, 235, 1–16. [Google Scholar] [CrossRef]
- Mukherjee, A.; Kandlikar, S.G. Numerical simulation of growth of a vapor bubble during flow boiling of water in a microchannel. Microfluid. Nanofluid. 2005, 1, 137–145. [Google Scholar] [CrossRef]
- Kandlikar, S.G. Handbook of Thermal Science and Engineering, 1st ed.; Springer International Publishing AG: Cham, Switzerland, 2018; Chapter 48. [Google Scholar]
- Karayiannis, T.G.; Mahmoud, M.M. Flow boiling in microchannels: Fundamentals and applications. Appl. Therm. Eng. 2017, 115, 1372–1397. [Google Scholar] [CrossRef]
- Odumosu, O.A.; Li, H.; Wang, T.; Che, Z. Conjugate heat transfer effects on bubble growth during flow boiling heat transfer in microchannels. Phys. Fluids 2024, 36, 12. [Google Scholar] [CrossRef]
- Mukherjee, A.; Kandlikar, S.G.; Edel, Z.J. Numerical study of bubble growth and wall heat transfer during flow boiling in a microchannel. Int. J. Heat Mass Transf. 2011, 54, 3702–3718. [Google Scholar] [CrossRef]
- Darshan, M.B.; Magnini, M.; Matar, O.K. Numerical modelling of flow boiling inside microchannels: A critical review of methods and applications. Appl. Therm. Eng. 2024, 257, 124464. [Google Scholar] [CrossRef]
- Okajima, J.; Komiya, A.; Maruyama, S. Analysis of evaporative heat transfer by expansion bubble in a microchannel for high heat flux cooling. J. Therm. Sci. Technol. 2012, 7, 740–752. [Google Scholar] [CrossRef]
- Suzuki, K.; Torikai, K.; Satoh, H.; Ishimaru, J.; Tanaka, Y. Boiling heat transfer of subcooled water in a horizontal rectangular channel: Observation of MEB and MEB generation. Heat Transf.—Asian Res. 2001, 30, 426–438. [Google Scholar] [CrossRef]
- Anderson, D.M.; McFadden, G.B.; Wheeler, A.A. Diffuse-interface methods in fluid mechanics. Annu. Rev. Fluid Mech. 1998, 30, 139–165. [Google Scholar] [CrossRef]
- Jacqmin, D. Calculation of two-phase Navier–Stokes flows using phase-field modeling. J. Comput. Phys. 1999, 155, 96–127. [Google Scholar] [CrossRef]
- Kim, J. Phase-field models for multi-component fluid flows. Commun. Comput. Phys. 2012, 12, 613–661. [Google Scholar] [CrossRef]
- Dong, S.; Shen, J. A time-stepping scheme involving constant-coefficient matrices for phase-field simulations of two-phase incompressible flows with large density ratios. J. Comput. Phys. 2012, 231, 5788–5804. [Google Scholar] [CrossRef]
- Lee, W.H. A pressure iteration scheme for two-phase flow modeling. In Multiphase Transport Fundamentals, Reactor Safety, Applications; ANS Winter Meeting: New Orleans, LA, USA, 1980. [Google Scholar]
- Hardt, S.; Wondra, F. Evaporation model for interfacial flows based on a continuum-field representation of the source terms. J. Comput. Phys. 2008, 227, 5871–5895. [Google Scholar] [CrossRef]
- Lee, J.; Lowengrub, J.S.; Goodman, J.; Smereka, P. Modeling pinchoff and reconnection in a Hele–Shaw cell. Phys. Fluids 2002, 14, 492–513. [Google Scholar] [CrossRef]
- Cahn, J.W.; Hilliard, J.E. Free energy of a nonuniform system. I. Interfacial free energy. J. Chem. Phys. 1958, 28, 258–267. [Google Scholar] [CrossRef]
- Teshigawara, R.; Onuki, A. Droplet evaporation in one-component fluids: Dynamic van der Waals theory. Europhys. Lett. 2008, 84, 36003. [Google Scholar] [CrossRef]
- Welch, S.W.J.; Wilson, J. A volume of fluid based method for fluid flows with phase change. J. Comput. Phys. 2000, 160, 662–682. [Google Scholar] [CrossRef]
- Sun, Y.; Beckermann, C. Sharp interface tracking using the phase-field equation. J. Comput. Phys. 2007, 225, 138–166. [Google Scholar] [CrossRef]
- Jacqmin, D. Contact-line dynamics of a diffuse fluid interface. J. Fluid Mech. 2000, 402, 57–88. [Google Scholar] [CrossRef]
- Yue, P.; Zhou, C.; Feng, J.J. Sharp-interface limit of the Cahn–Hilliard model for moving contact lines. J. Fluid Mech. 2010, 645, 279–294. [Google Scholar] [CrossRef]
- Lee, W.; Son, G. Bubble dynamics and heat transfer during nucleate boiling in a microchannel. Numer. Heat Transf. A 2008, 53, 1074–1090. [Google Scholar] [CrossRef]
- Odumosu, O.A.; Xu, H.; Wang, T.; Che, Z. Growth of Elongated Vapor Bubbles During Flow Boiling Heat Transfer in Wavy Microchannels. Appl. Therm. Eng. 2023, 223, 119987. [Google Scholar] [CrossRef]




| Case | Inlet Temp (K) | Wall Temp (K) | Velocity (m/s) | Pressure (atm) |
|---|---|---|---|---|
| Saturated | 373.15 | 378.15 | 0.1 | 1 |
| Subcooled | 370.15 | 378.15 | 0.1 | 1 |
| State | Temp (K) | Density (kg/m3) | Viscosity (Pa·s) | Thermal Conductivity (W/m·K) | Surface Tension (N/m) |
|---|---|---|---|---|---|
| Liquid (Subcooled) | 370.15 | 979.8 | 0.639 | 0.0589 | |
| Liquid (Saturated) | 373.15 | 958.4 | 0.679 | 0.0589 | |
| Vapor (Saturated) | 373.15 | 0.597 | 0.025 | – |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jamali, J.A.; He, Y. Phase-Field Simulation of Bubble Evolution and Heat Transfer in Microchannels Under Subcooled and Saturated Flow Boiling. Eng. Proc. 2025, 111, 27. https://doi.org/10.3390/engproc2025111027
Jamali JA, He Y. Phase-Field Simulation of Bubble Evolution and Heat Transfer in Microchannels Under Subcooled and Saturated Flow Boiling. Engineering Proceedings. 2025; 111(1):27. https://doi.org/10.3390/engproc2025111027
Chicago/Turabian StyleJamali, Jawed Ahmed, and Ying He. 2025. "Phase-Field Simulation of Bubble Evolution and Heat Transfer in Microchannels Under Subcooled and Saturated Flow Boiling" Engineering Proceedings 111, no. 1: 27. https://doi.org/10.3390/engproc2025111027
APA StyleJamali, J. A., & He, Y. (2025). Phase-Field Simulation of Bubble Evolution and Heat Transfer in Microchannels Under Subcooled and Saturated Flow Boiling. Engineering Proceedings, 111(1), 27. https://doi.org/10.3390/engproc2025111027






