Experimental and Numerical Analysis of Hybrid Silica Sand–Basalt Rock Thermal Energy Storage for Enhanced Heat Retention and Discharge Control †
Abstract
1. Introduction
2. Problem Formulation
3. Methodology
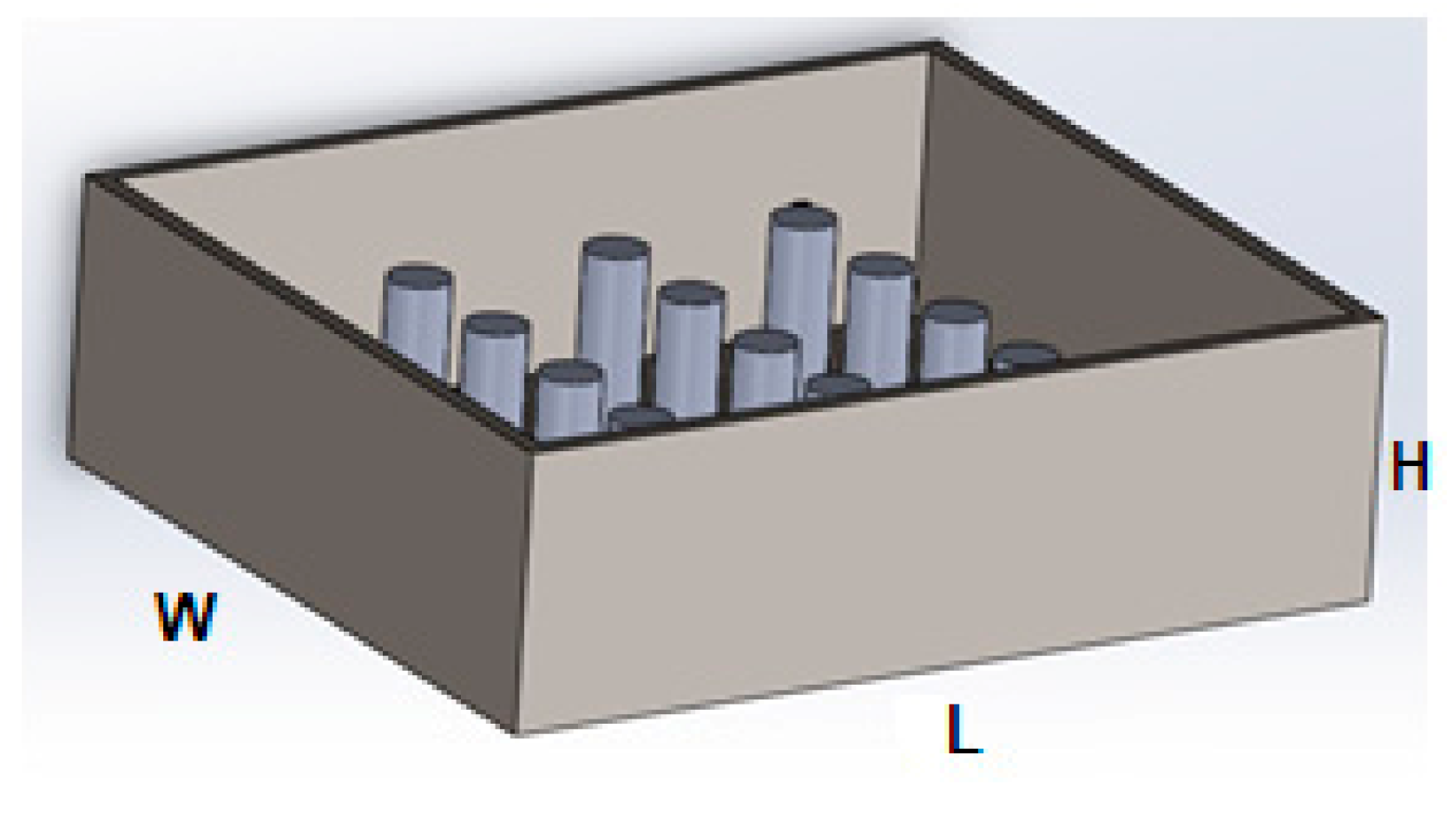
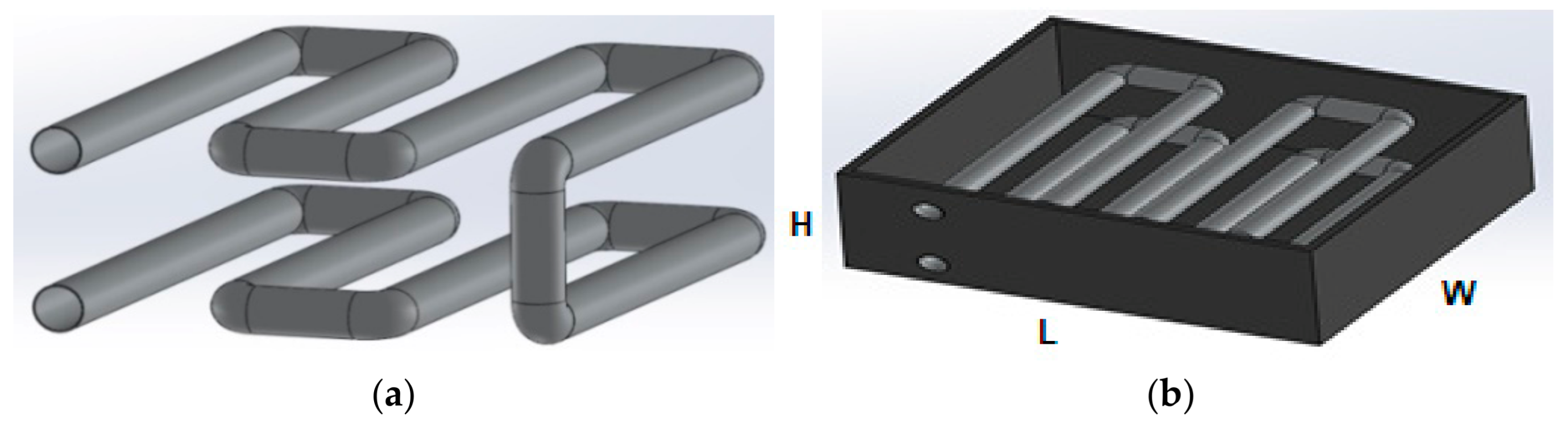
3.1. CAD Modeling
3.1.1. Conduction
3.1.2. Convection
3.2. Mathematical Modeling
Thermal Energy Storage Calculation
- mT = Total mass of mixture (kg)
- cps, cpr = Specific heat capacity of sand and rocks (J/kg·K)
- T = Rise in temperature (°C)
- ms, mr = Mass of silica sand and basalt rocks, respectively.
4. Numerical Study
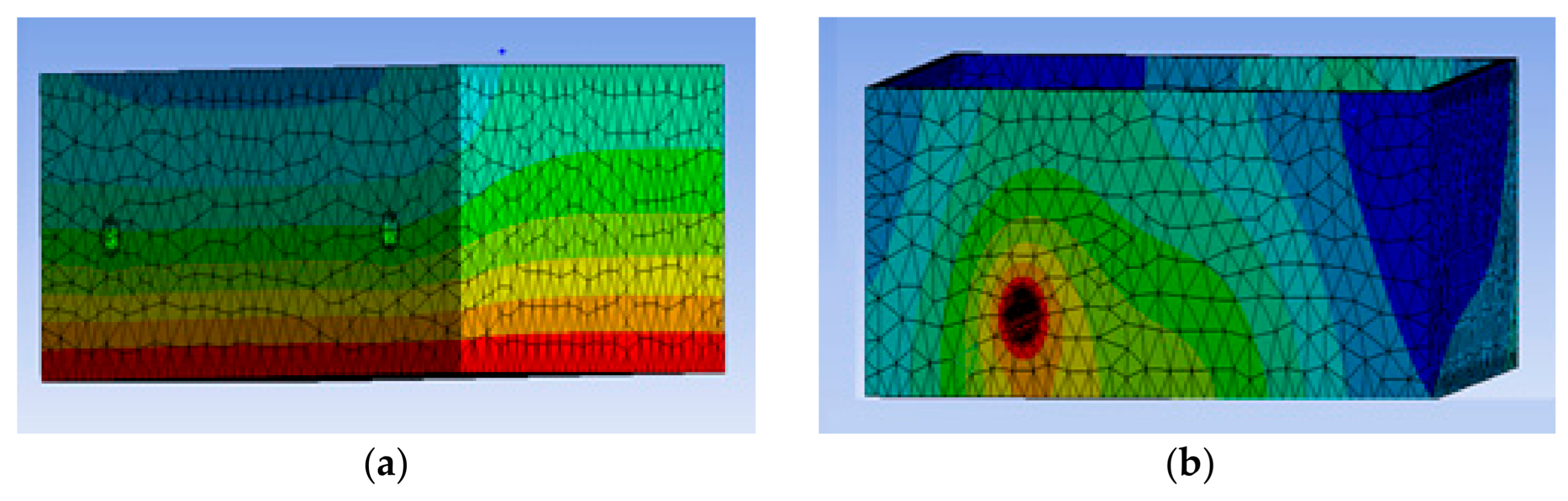
4.1. Mesh Independence
4.2. Mesh Sizing, Solver Settings, and Boundary Conditions
4.3. Simulations
5. Experimental Setup
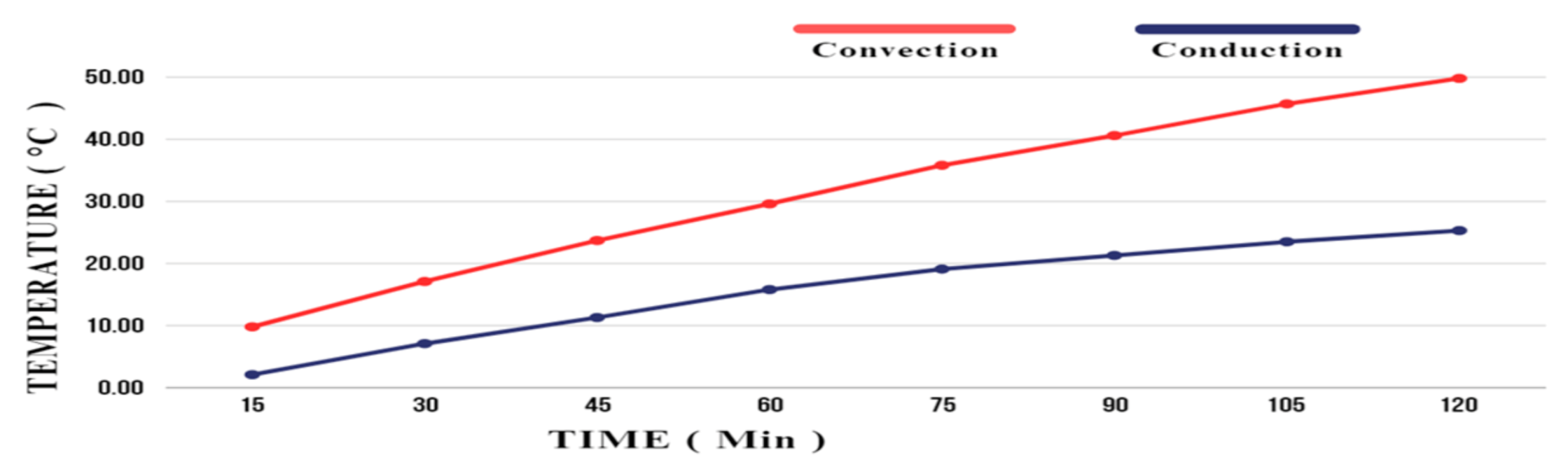
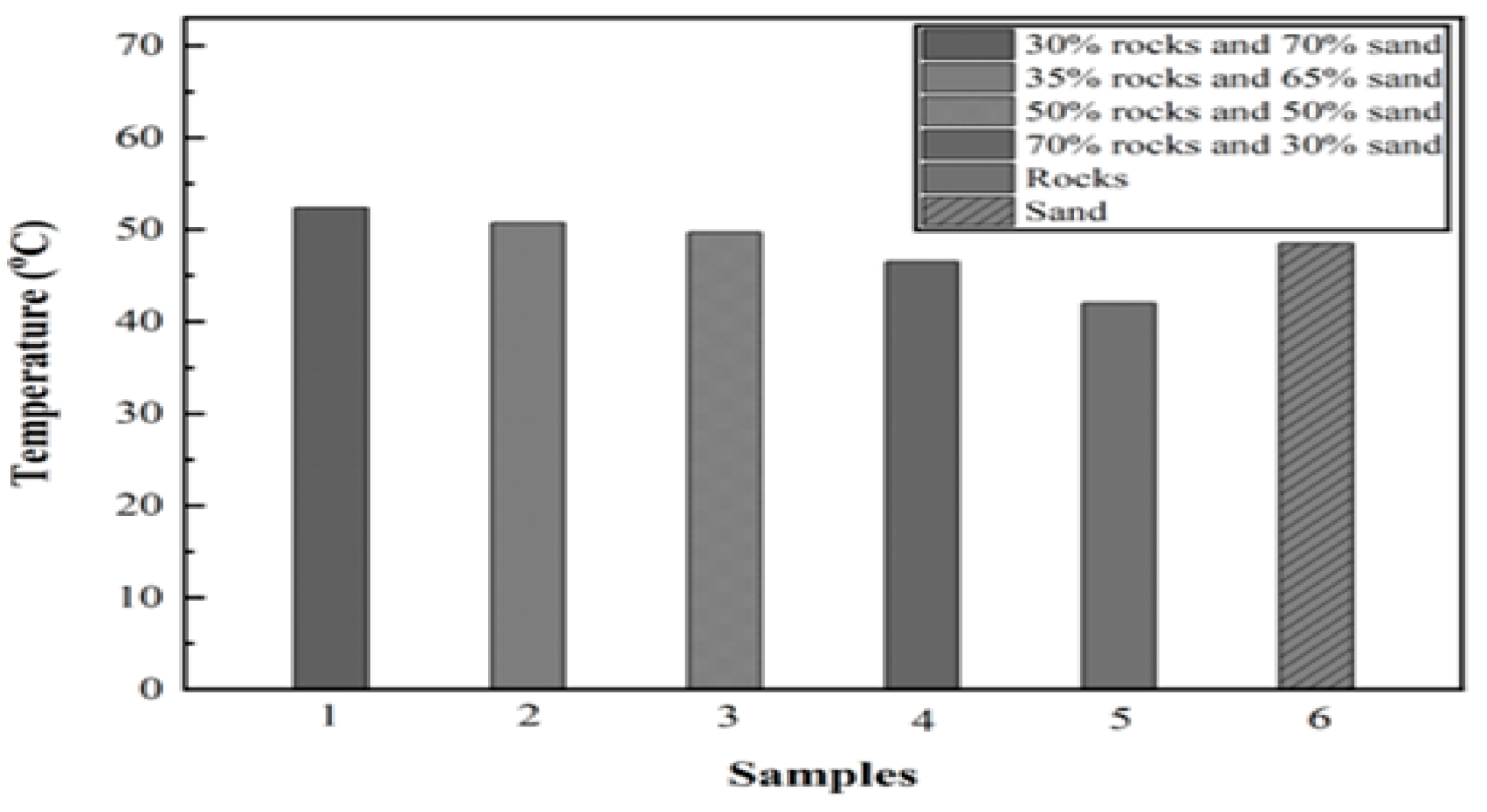
6. Results and Discussion
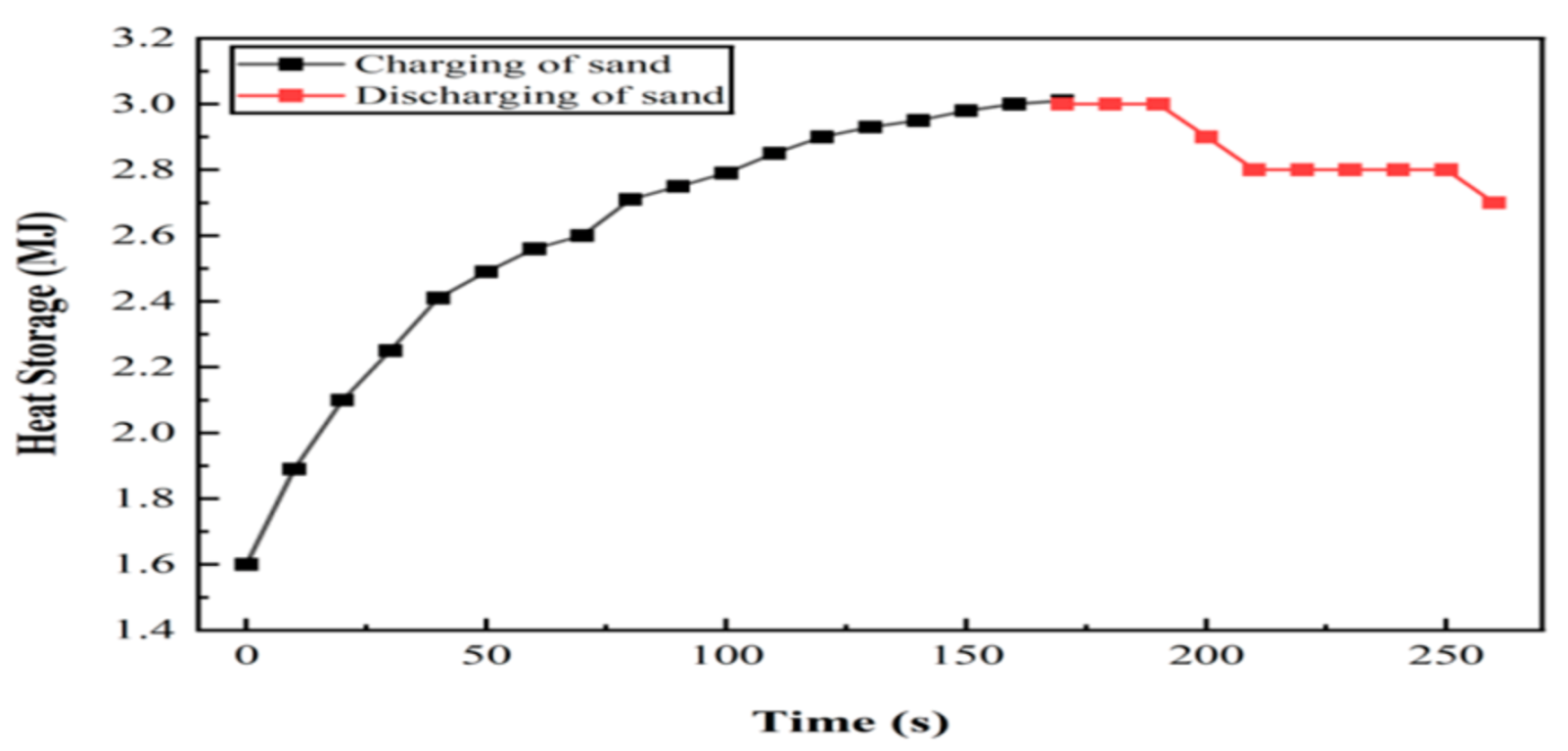
6.1. Experiment 01: 100% Silica Sand
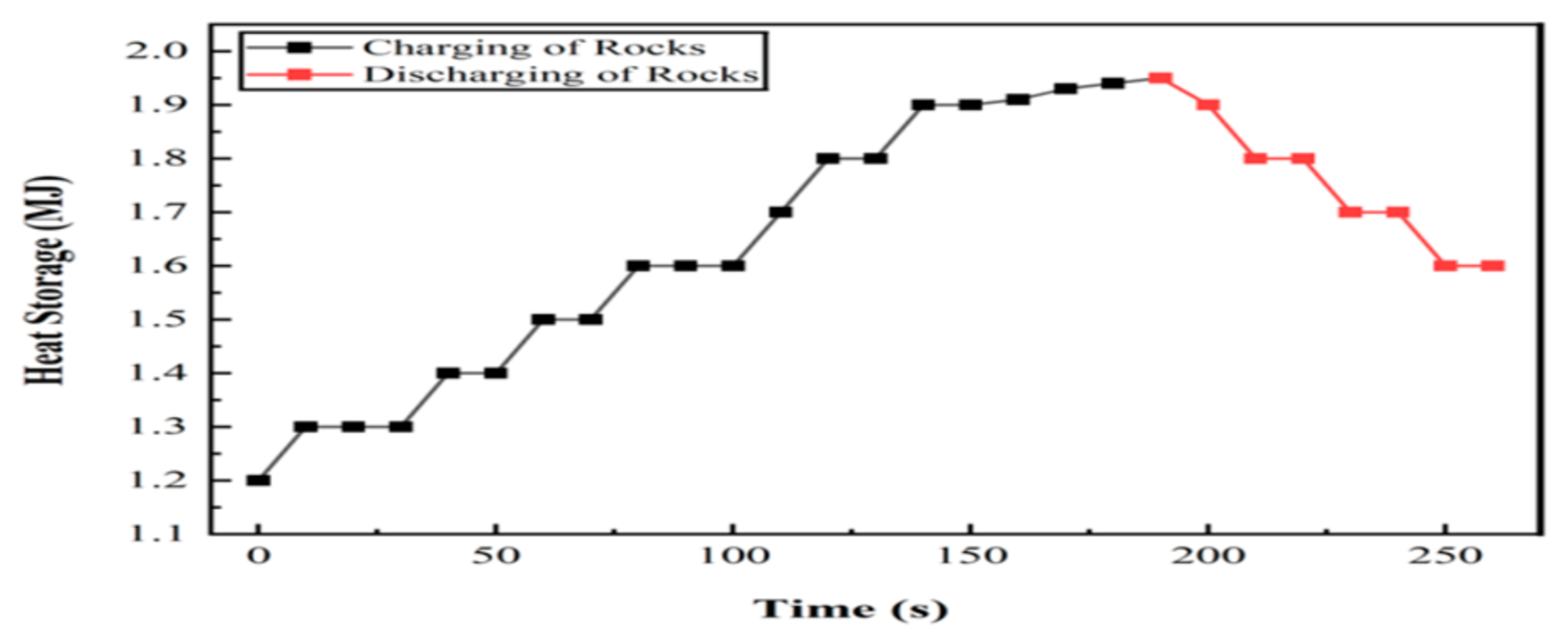
6.2. Experiment 02: 100% Basalt Rocks
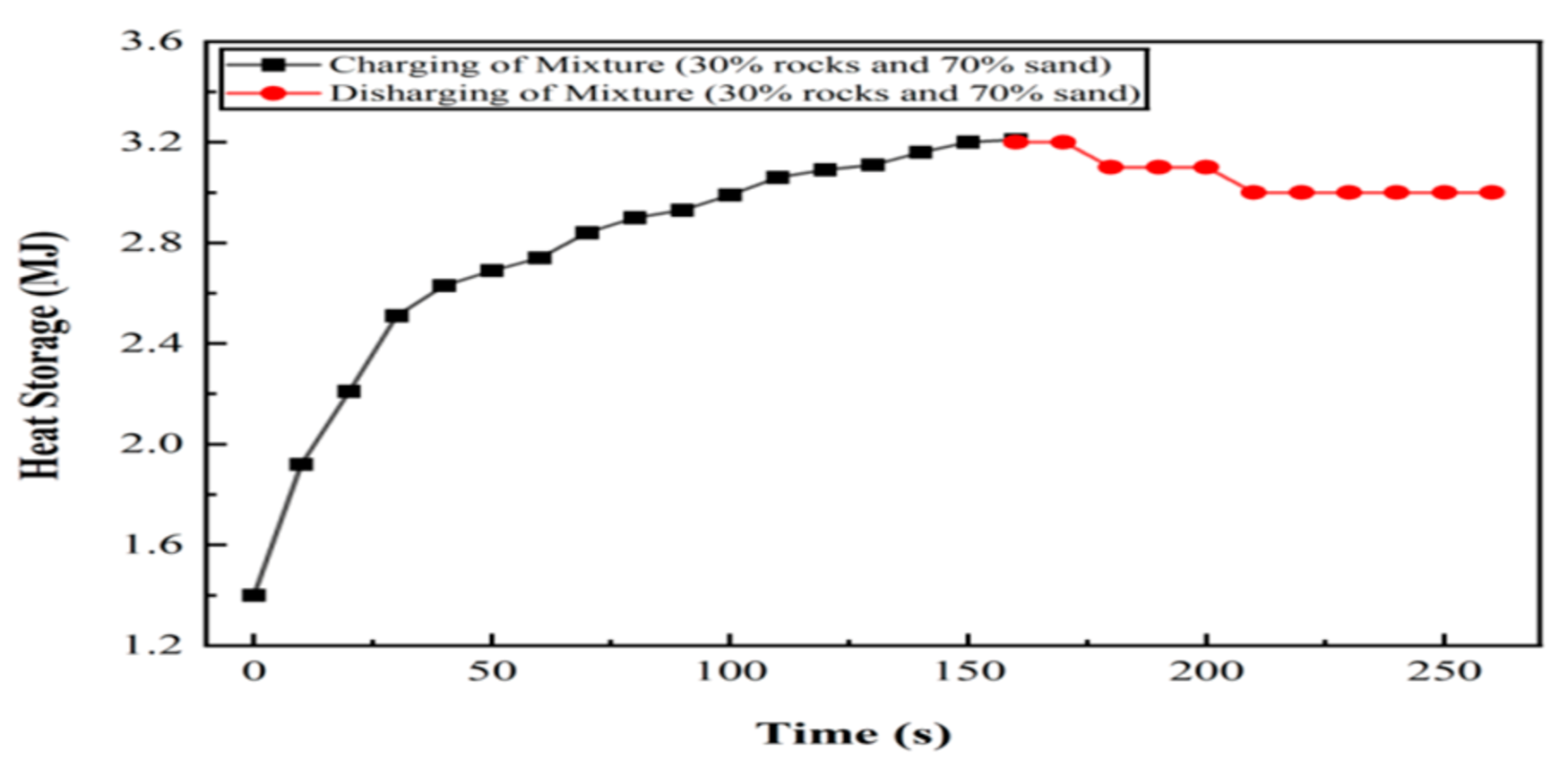
6.3. Experiment 03: 30% Silica Sand and 70% Basalt Rocks
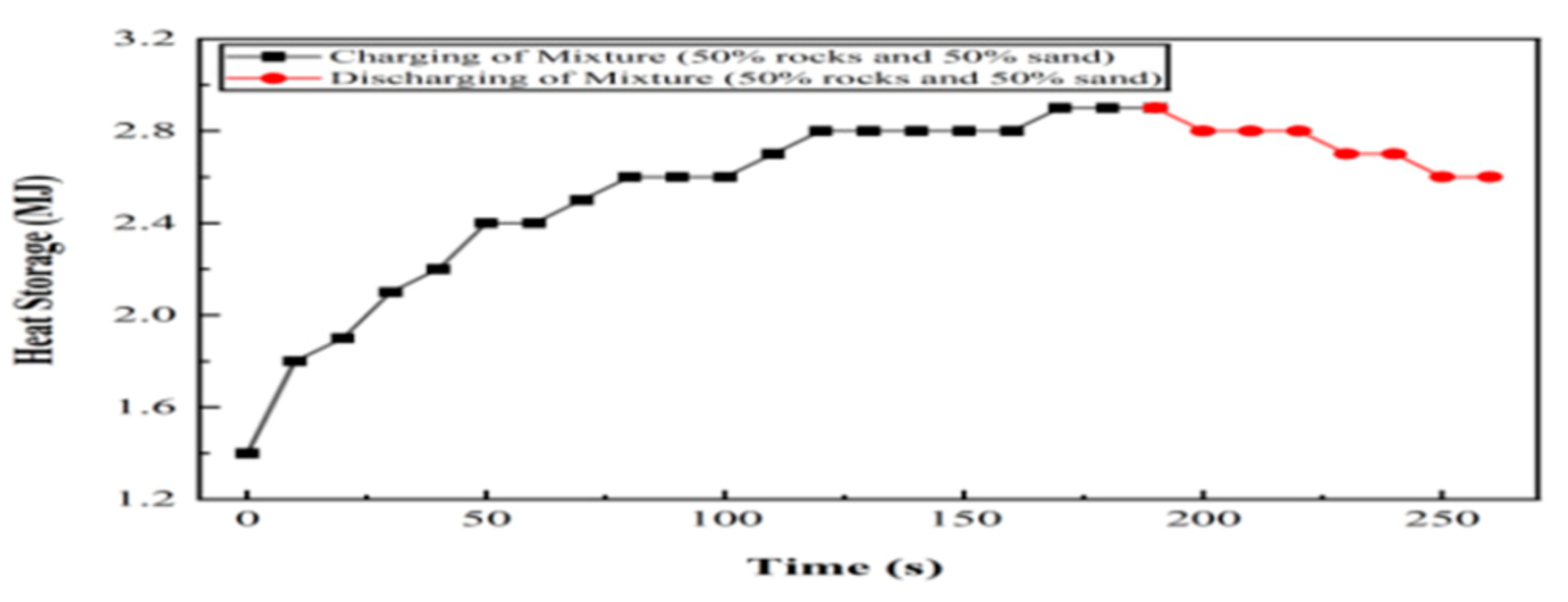
6.4. Experiment 04: 50% Silica Sand and 50% Basalt Rocks
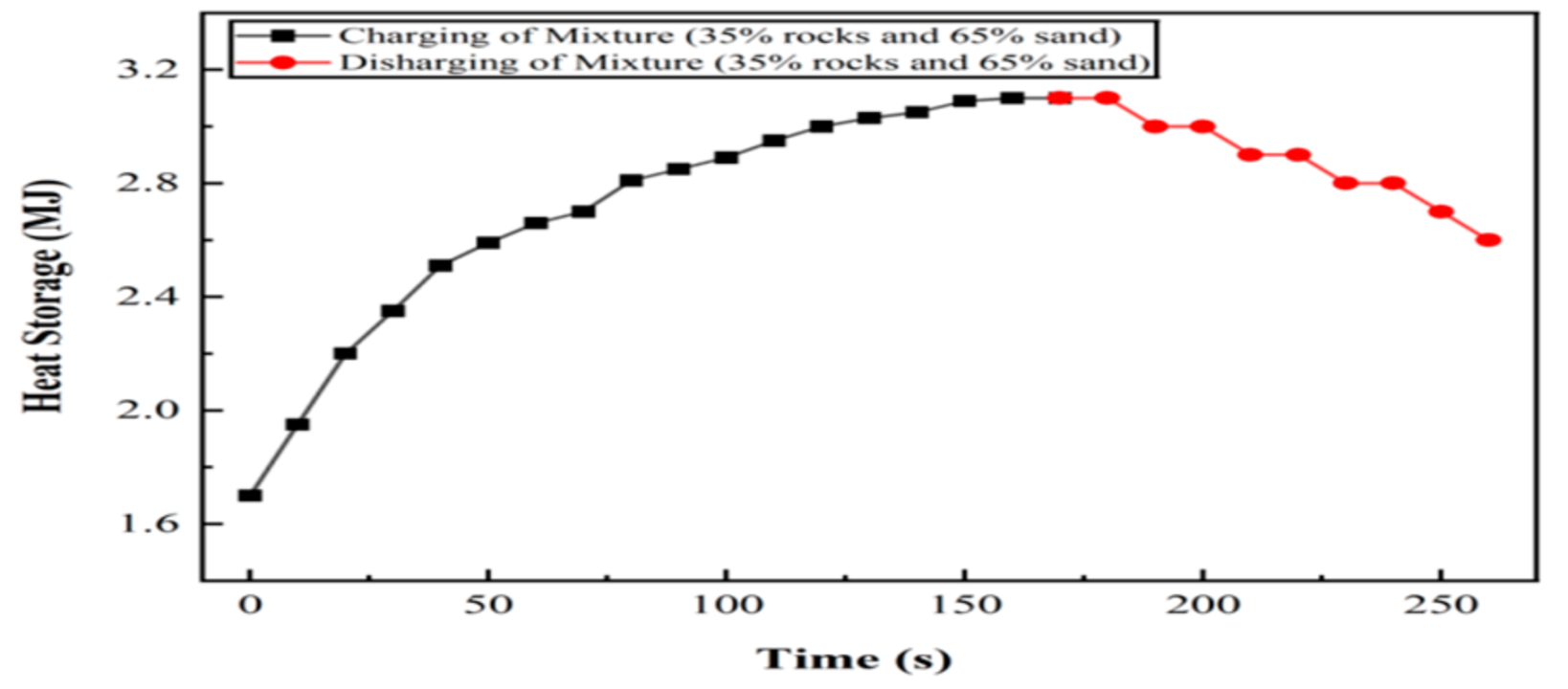
6.5. Experiment 05: 65% Silica Sand and 35% Basalt Rocks
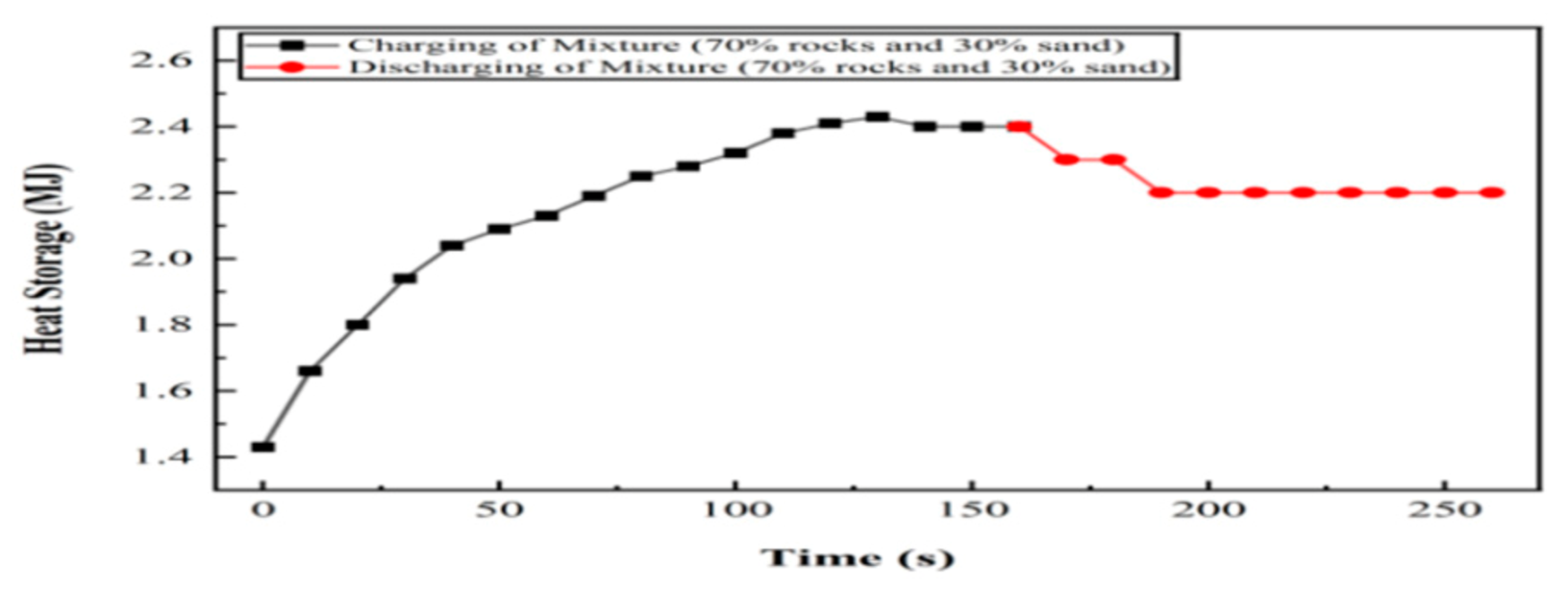
6.6. Experiment 06: 70% Silica Sand and 30% Basalt Rocks
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| TES | Thermal Energy Storage |
| CAD | Computer-Aided Design |
| COP | Coefficient of Performance |
| 3D | Three-Dimensional |
| CO2 | Carbon Dioxide |
References
- Radwan, O.A.; Humphrey, J.D.; Hakeem, A.S.; Zeama, M. Evaluating Properties of Arabian Desert Sands for Use in Solar Thermal Technologies. Sol. Energy Mater. Sol. Cells 2021, 231, 111335. [Google Scholar] [CrossRef]
- Chung, K.M.; Chen, R. Black Coating of Quartz Sand towards Low-Cost Solar-Absorbing and Thermal Energy Storage Material for Concentrating Solar Power. Sol. Energy 2023, 249, 98–106. [Google Scholar] [CrossRef]
- Agrawal, K.K.; Misra, R.; Das Agrawal, G. Improving the Thermal Performance of Ground Air Heat Exchanger System Using Sand-Bentonite (in Dry and Wet Condition) as Backfilling Material. Renew. Energy 2020, 146, 2008–2023. [Google Scholar] [CrossRef]
- Jemmal, Y.; Zari, N.; Asbik, M.; Maaroufi, M. Experimental Characterization and Thermal Performance Comparison of Six Moroccan Rocks Used as Filler Materials in a Packed Bed Storage System. J. Energy Storage 2020, 30, 101513. [Google Scholar] [CrossRef]
- Tetteh, S.; Juul, G.; Järvinen, M.; Santasalo-Aarnio, A. Improved Effective Thermal Conductivity of Sand Bed in Thermal Energy Storage Systems. J. Energy Storage 2024, 86, 111350. [Google Scholar] [CrossRef]
- El Alami, K.; Asbik, M.; Agalit, H. Identification of Natural Rocks as Storage Materials in Thermal Energy Storage (TES) System of Concentrated Solar Power (CSP) Plants—A Review. Sol. Energy Mater. Sol. Cells 2020, 217, 110599. [Google Scholar] [CrossRef]
- Al Edhari, A.J.; Ngo, C.C. Experimental Study of Thermal Energy Storage Using Natural Porous Media. In ASME International Mechanical Engineering Congress and Exposition; American Society of Mechanical Engineers: New York, NY, USA, 2017. [Google Scholar]
- Schlipf, D.; Schicktanz, P.; Maier, H.; Schneider, G. Using Sand and Other Small Grained Materials as Heat Storage Medium in a Packed Bed HTTESS. Energy Procedia 2015, 69, 1029–1038. [Google Scholar] [CrossRef]
- Bandyopadhyay, D.; Forsberg, C. Selecting Rock Types for Very-Low-Cost Crushed Rock Heat Storage Systems with Nitrate Salt Heat Transfer. J. Energy Storage 2023, 61, 106664. [Google Scholar] [CrossRef]
- Hrifech, S.; Agalit, H.; Jarni, A.; Mouguina, E.M.; Grosu, Y.; Faik, A.; Bennouna, E.G.; Mimet, A. Characterization of Natural Rocks as Filler Materials for Medium-Temperature Packed Bed Thermal Energy Storage System. J. Energy Storage 2020, 32, 101822. [Google Scholar] [CrossRef]
- Barbhuiya, S.; Das, B.B.; Idrees, M. Thermal Energy Storage in Concrete: A Comprehensive Review on Fundamentals, Technology and Sustainability. J. Build. Eng. 2023, 82, 108302. [Google Scholar] [CrossRef]
- Yapicioglu, A.; Dincer, I. A Newly Developed Renewable Energy Driven Multigeneration System with Hot Silica Sand Storage for Power, Hydrogen, Freshwater and Cooling Production. Energy Technol. Assess. 2023, 55, 102938. [Google Scholar] [CrossRef]
- Kothari, R.; La Seta, A.; Hemmingsen, C.S.; Desai, N.B.; Haglind, F. Numerical analysis of measures to minimize the thermal instability in high temperature packed-beds for thermal energy storage systems. J. Energy Storage 2024, 94, 112431. [Google Scholar] [CrossRef]
- Serrano, M.I.R.; Knobloch, K.; Giuliano, S.; Engelbrecht, K.; Hirsch, T. Retrofit of a Coal-Fired Power Plant with a Rock Bed Thermal Energy Storage. J. Energy Storage 2024, 75, 109238. [Google Scholar] [CrossRef]
- Knobloch, K.; Ulrich, T.; Bahl, C.; Engelbrecht, K. Degradation of a Rock Bed Thermal Energy Storage System. Appl. Therm. Eng. 2022, 214, 118823. [Google Scholar] [CrossRef]
- Jaber, H.; Maalouf, E.; Yehya, A.; Salah, M.K.; Bou-Hamdan, K.; Harb, M. The Effect of Temperature on the Mechanical and Hydraulic Properties of Sedimentary Rocks. Geoenergy Sci. Eng. 2024, 235, 212702. [Google Scholar] [CrossRef]
- Sarbu, I.; Sebarchievici, C. A Comprehensive Review of Thermal Energy Storage. Sustainability 2018, 10, 191. [Google Scholar] [CrossRef]
- Maldonado, J.M.; Verez, D.; de Gracia, A.; Cabeza, L.F. Comparative Study between Heat Pipe and Shell-And-Tube Thermal Energy Storage. Appl. Therm. Eng. 2021, 192, 116974. [Google Scholar] [CrossRef]
- Hosseini, H.; Ashrafi, M.M.A.; Asadi, Z.; Ganji, D.D. Development in Household Water Heaters by Replacing the Shell and Tube Heat Exchangers by Inclined Flat Ones Having Rectangular Fins. Case Stud. Therm. Eng. 2021, 28, 101490. [Google Scholar] [CrossRef]
- Cahya, A.H.; Permatasari, R. Design of Shell ands Tube Heat Exchanger for Waste Water Using Heat Transfer Using Heat Transfer Research Inc. Adv. Sci. Technol. 2020, 29, 611–622. [Google Scholar]
- Nikiforova, T.; Savytskyi, M.; Limam, K.; Bosschaerts, W. Methods and Results of Experimental Researches of Thermal Conductivity of Soils. Energy Procedia 2013, 42, 775–783. [Google Scholar] [CrossRef]




| Parameters | Features |
|---|---|
| Length of heat exchanger | 45 cm |
| Width of heat exchanger | 40 cm |
| Height of heat exchanger | 15 cm |
| Diameter of fin | 3 cm |
| Length of fin | 10 cm |
| Volume of heat exchanger | 27,000 cm3 |
| Volume of fins | 85 cm3 |
| Volume of mixture | 26,915 cm3 |
| Parameters | Features |
|---|---|
| Length of heat exchanger | 45 cm |
| Width of heat exchanger | 40 cm |
| Height of heat exchanger | 16.2 cm |
| Diameter of pipe | 3 cm |
| Length of pipe | 320 cm |
| Volume of heat exchanger | 29,160 cm3 |
| Volume of pipe | 2197.78 cm3 |
| Volume of mixture | 26,915 cm3 |
| Number of Elements (103) | Average Temperature (°C) |
|---|---|
| 15.7 | 10 |
| 23.9 | 27 |
| 35.4 | 39 |
| 56.7 | 48 |
| 76.5 | 49 |
| 98.6 | 49 |
| Material Properties | Values |
|---|---|
| Sand Thermal Conductivity (W·m−1·k−1) | 2.56 |
| Sand Heat Capacity (J·kg−1·k−1) | 703 |
| Rocks Thermal Conductivity (W·m−1·k−1) | 2.08 |
| Rocks Heat Capacity (J·kg−1·k−1) | 1028 |
| Proportion of Silica Sand | Proportion of Basalt Rocks |
|---|---|
| 85 kg (100%) | 0 |
| 0 | 65 kg (100%) |
| 25.5 kg (30%) | 45.5 kg (70%) |
| 42.5 kg (50%) | 32.5 kg (50%) |
| 55.2 kg (65%) | 22.7 kg (35%) |
| 59.5 kg (70%) | 19.5 kg (30%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Imran, M.; Waseem, Z.; Tayyab, R.; Aziz, H.; Anwar, M.; Khan, T.I. Experimental and Numerical Analysis of Hybrid Silica Sand–Basalt Rock Thermal Energy Storage for Enhanced Heat Retention and Discharge Control. Eng. Proc. 2025, 111, 6. https://doi.org/10.3390/engproc2025111006
Imran M, Waseem Z, Tayyab R, Aziz H, Anwar M, Khan TI. Experimental and Numerical Analysis of Hybrid Silica Sand–Basalt Rock Thermal Energy Storage for Enhanced Heat Retention and Discharge Control. Engineering Proceedings. 2025; 111(1):6. https://doi.org/10.3390/engproc2025111006
Chicago/Turabian StyleImran, Muhammad, Zainab Waseem, Rahaya Tayyab, Hassaan Aziz, Muhammad Anwar, and Talha Irfan Khan. 2025. "Experimental and Numerical Analysis of Hybrid Silica Sand–Basalt Rock Thermal Energy Storage for Enhanced Heat Retention and Discharge Control" Engineering Proceedings 111, no. 1: 6. https://doi.org/10.3390/engproc2025111006
APA StyleImran, M., Waseem, Z., Tayyab, R., Aziz, H., Anwar, M., & Khan, T. I. (2025). Experimental and Numerical Analysis of Hybrid Silica Sand–Basalt Rock Thermal Energy Storage for Enhanced Heat Retention and Discharge Control. Engineering Proceedings, 111(1), 6. https://doi.org/10.3390/engproc2025111006






