Abstract
Quadcopter drones have been extensively researched due to their flexibility and suitability for diverse tasks. In this study, a control strategy tailored for scenarios with restricted network bandwidth is developed. An event-triggered control approach was used to minimize network bandwidth load. Also, a robust fuzzy controller was integrated to enhance the system’s resilience and efficiency. The simulation results confirmed that the developed control strategy fosters stable performance, even under constrained network conditions.
1. Introduction
Drones have been widely employed across various applications, including military operations, geospatial surveying, and environmental monitoring [1,2,3,4,5,6,7,8]. Drones mitigate risks to human operators, enhance the accuracy and efficiency of data acquisition, and enable access to otherwise difficult or hazardous environments. The quadcopter has garnered particular attention among various drones due to its superior maneuverability, vertical takeoff and landing (VTOL) capabilities, cost efficiency, and relatively straightforward mechanical architecture. These attributes increase interest in quadcopter platforms in drone system design and control research.
As quadcopters [4] are used in diverse domains, their reliance on wireless communication networks for data transmission becomes increasingly significant. With the growing number of aerial units operating concurrently, the demand for communication bandwidth increases accordingly. However, wireless bandwidth is a finite resource. When multiple quadcopters share the same network, they compete for limited bandwidth, potentially causing congestion, reduced communication quality, and degraded overall system performance.
To mitigate the impact of constrained communication bandwidth, an event-triggered control (ETC, [9,10,11,12,13,14]) is used for adaptive sampling and transmissions based on state-dependent triggering conditions, which are based on low system error thresholds [12,14,15,16,17,18,19,20,21,22]. This event-driven mechanism effectively lowers the control signal update frequency, resulting in reduced network traffic and enhanced bandwidth utilization. A robust fuzzy control is adopted to compensate for parametric uncertainties and exogenous disturbances affecting the quadcopter’s nonlinear dynamics [16,18,19,22]. The system is represented by a Takagi–Sugeno (T-S) fuzzy model, and controller synthesis is performed through parallel distributed compensation (PDC) to guarantee closed-loop stability. Stability and robustness proofs are conducted using Lyapunov function-based analysis [15], ensuring the system’s convergence properties under bounded disturbances.
In this study, the event-triggered robust fuzzy controller maintained satisfactory tracking performance and system stability despite stringent network bandwidth constraints, validating its practical applicability for quadcopter control in resource-limited communication environments.
The remainder of this manuscript is structured as follows. Section 2 introduces the problem formulation and underlying assumptions. Section 3 details the design methodology of the proposed event-triggered robust fuzzy control scheme. In Section 4, simulation studies are conducted to evaluate and verify the effectiveness of the control approach. Finally, Section 5 summarizes the key findings and concludes the study.
2. Problem Formulation
The kinematic and dynamic models of the quadcopter were established in this study. The quadcopter consists of four rotors mounted symmetrically on a cross-shaped frame, as illustrated in Figure 1 [6]. This configuration is a basis for deriving the system’s motion equations and control dynamics. In the figure, the quadcopter’s attitude , which consists of the roll (ϕ), pitch (θ), and yaw (ψ) angles in the earth-fixed coordinate system (E), the angular velocity of the vehicle in the body-fixed coordinate system (B) is set as , and the inertia in B is .
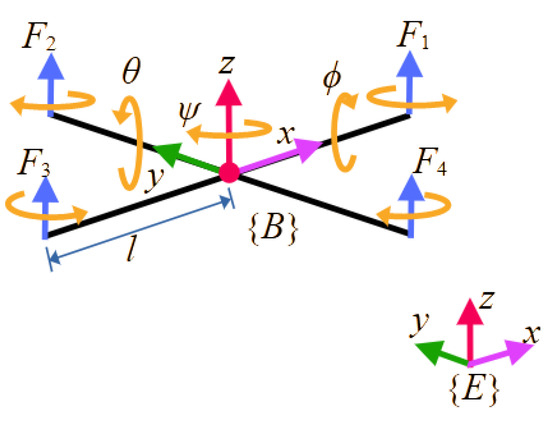
Figure 1.
Quadcopter configuration [6].
The quadcopter’s rotational dynamics are expressed as follows.
where is the notation of the control torque is the notation of the lumped disturbance, including parameterized uncertainties and external disturbances, acting on the quadcopter. The matrix is defined to represent the rotation from B to E as follows.
The control torque vector is generated by the thrust forces of the four propellers, each driven by an individual motor. The relationship between the motor inputs and the resulting torques is described by the following equations.
where is the force generated by the ith propeller (), denotes the thrust coefficient, denotes the propeller rotary speed, is the length of the quadcopter arm, and is the force-to-torque coefficient.
An altitude control module generates a virtual thrust signal, which is then integrated with the computed virtual torque input to construct the complete control vector. This vector is subsequently translated into the corresponding motor control signals for system actuation. By performing the time derivative of Equation (1), the following expression is obtained.
By substituting Equation (1) into (5), the quadcopter dynamic equation is obtained as follows.
where and .
In this study, a controller was designed to stabilize the quadcopter’s state trajectory around a predefined equilibrium point, ensuring asymptotic convergence and overall system stability.
3. Event-Triggered Robust Fuzzy Controller
To fulfill the control objective of stabilizing the quadcopter at a designated equilibrium point, a T-S fuzzy model [15] was constructed to approximate the complex nonlinear input–output characteristics of the system. The ith fuzzy rule of the T-S fuzzy model is designed as
where ; are the premise variables, is the system parameter matrix, is the control input, are the system parameters, and is the fuzzy set of the premise variables.
By using the singleton fuzzifier, the product inference engine, the center-average defuzzifier [15], the output of the T-S fuzzy model (Equation (7)) is expressed as
where
Using Equation (8), the quadcopter’s dynamic behavior is presented as a weighted combination of local linear models to design a controller while preserving essential nonlinearities inherent in the system dynamics.
Based on Equation (8), a robust fuzzy controller was designed corresponding to each local linear model. Therefore, the fuzzy rules of the robust fuzzy controller were designed as
where , and is the control gain matrix. By using the singleton fuzzifier, the product inference engine and the center-average defuzzifier [15], the output of the robust fuzzy controller (Equation (9)) is expressed as
Substituting Equation (10) into Equation (8) yields the following equation.
To reduce network bandwidth requirements, the event-triggered control was adoped. And the triggering instant was set as .
where denotes the known proportional threshold and denotes the symmetric positive definite weighting matrix. Then, the control law (Equation (11)) was rewritten as
Using Equation (13), the control strategy was discontinued when the feedback input was not updated and the output signal varied within a preset range. Therefore, it was unnecessary to transmit system states and control signals at every time instant. Under the network bandwidth constraints, the developed control strategy in this study showed excellent control performance.
4. Simulation Results
To evaluate the effectiveness of the proposed controller, computer simulations were conducted under the following quadcopter parameter settings: an arm length of 0.295 m, a concentrated mass of 0.08 kg representing the engine and propeller assembly, a spherical body mass of 0.75 kg, and a sampling interval of 0.005 s. The target attitude states were specified as . The resulting state trajectories of the quadcopter under control are illustrated in Figure 2, Figure 3 and Figure 4.
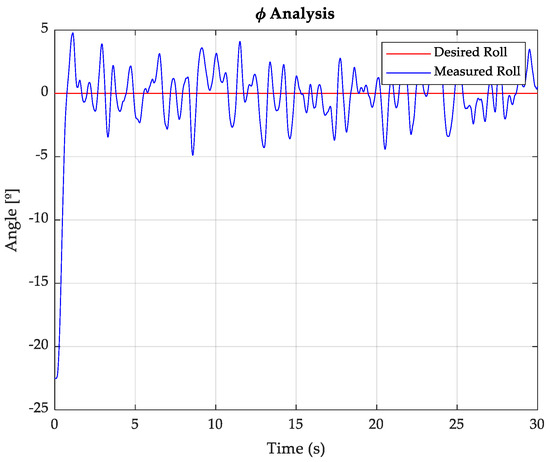
Figure 2.
Trajectory of the roll ().
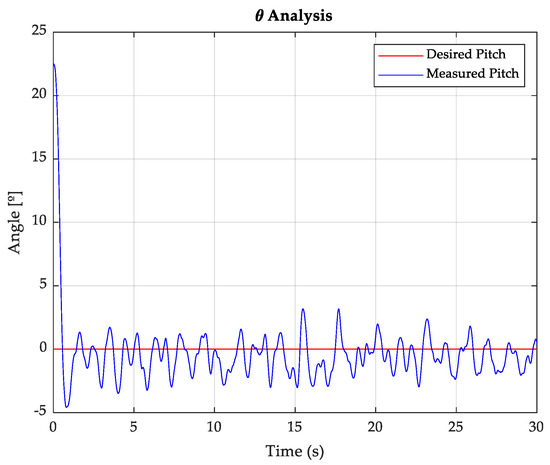
Figure 3.
Trajectory of the pitch (θ).
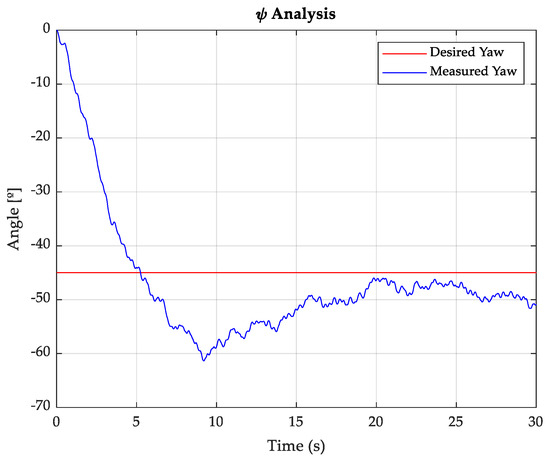
Figure 4.
Trajectory of the yaw (ψ).
The simulation results showed that the developed event-triggered robust fuzzy control strategy stabilized the quadcopter system despite the presence of limited communication resources due to constrained network bandwidth. The controller maintained accurate attitude tracking performance, wherein all state variables converged smoothly to their corresponding reference trajectories without exhibiting noticeable oscillations or delays. The triggering mechanism significantly reduced the frequency of control updates and data transmissions, thereby showing stable control to manage communication constraints efficiently. The consistent tracking behavior under reduced communication highlights both the robustness and the viability of the proposed approach. These results collectively validated the effectiveness of the controller in achieving reliable and stable flight performance in networked control environments with bandwidth limitations.
5. Conclusions
An event-triggered robust fuzzy controller was developed for quadcopter systems subject to network bandwidth limitations. The quadcopter’s nonlinear dynamics were determined using a Takagi–Sugeno fuzzy model to effectively capture the input–output relationship of the system across different operating regions. Building on this model, a fuzzy control strategy based on PDC was developed to stabilize each local linear subsystem to ensure overall system stability. Simulations were performed under constrained network bandwidth scenarios to evaluate the practical performance of the developed controller. The results confirmed that the control scheme reduced communication load through event-triggered mechanisms and guaranteed the robust and stable flight of the quadcopter, validating the effectiveness and applicability of the proposed method in realistic operating environments.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the author on request.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Tayebi, A.; McGilvray, S. Attitude stabilization of a VTOL quadrotor aircraft. IEEE Trans. Contr. Syst. Technol. 2006, 14, 562–571. [Google Scholar] [CrossRef]
- Lee, C.; Lee, S.; Chu, B. Extension of quadcopter flight range based on quadcopter transport system and autonomous ramp flight algorithm. IEEE Access 2020, 8, 156422–156432. [Google Scholar] [CrossRef]
- Labib, N.S.; Brust, M.R.; Danoy, G.; Bouvry, P. The rise of drones in internet of things: A survey on the evolution, prospects and challenges of unmanned aerial vehicles. IEEE Access 2021, 9, 115466–115487. [Google Scholar] [CrossRef]
- Eltayeb, A.; Rahmat, M.F.; Basri, M.A.M.; Eltoum, M.A.M.; Mahmoud, M.S. Integral adaptive sliding mode control for quadcopter UAV under variable payload and disturbance. IEEE Access 2022, 10, 94754–94764. [Google Scholar] [CrossRef]
- Nguyen, M.Q.; Tran, V.H.; Vo, M.T.; Le, M.H. Pose estimation and its impact on quadcopter control: An experimental study. In Proceedings of the 9th International Conference on Applying New Technology in Green Buildings (ATiGB), Danang, Vietnam, 30–31 August 2024; pp. 264–268. [Google Scholar] [CrossRef]
- Nguyen, X.; Won, S.M.; Do, T.D.; Hong, S.K. Improved fixed-time attitude tracking control for quadcopter unmanned aerial vehicles. IEEE Access 2024, 12, 191612–191622. [Google Scholar] [CrossRef]
- Manohar, S.; Kiran, M. Priority based efficient user scheduling in quadcopter assisted 5G network. In Proceedings of the 2024 Control Instrumentation System Conference (CISCON), Manipal, India, 2–3 August 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Mohamed, A.; Mohamed, M. Unmanned Aerial Vehicles in Last-Mile Parcel Delivery: A State-of-the-Art Review. Drones 2025, 9, 413. [Google Scholar] [CrossRef]
- Heemels, W.P.M.H.; Johansson, K.H.; Tabuada, P. An introduction to event-triggered and self-triggered control. In Proceedings of the 2012 IEEE 51st IEEE Conference on Decision and Control (CDC), Maui, HI, USA, 10–13 December 2012. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, J. Periodic event-triggered sliding mode control for switched uncertain T-S fuzzy systems with a logistic adaptive event-triggering scheme. IEEE Trans. Fuzzy Syst. 2022, 30, 4115–4126. [Google Scholar] [CrossRef]
- Chen, G.; Dong, J. Data-driven control for discrete-time nonlinear systems with dual-channel dynamic event-triggered mechanism. IEEE Trans. Circuits Syst. II 2023, 70, 4439–4443. [Google Scholar] [CrossRef]
- Li, Z.M.; Chang, X.H.; Xiong, J. Event-based fuzzy tracking control for nonlinear networked systems subject to dynamic quantization. IEEE Trans. Fuzzy Syst. 2023, 31, 941–954. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, F. Distributed Dynamic event-triggered control for multi-agent systems with quantization communication. IEEE Trans. Circuits Syst. II 2024, 71, 2054–2058. [Google Scholar] [CrossRef]
- Lien, C.H.; Chang, H.C.; Yu, K.W.; Li, H.C.; Yu, C.R.; Vaidyanathan, S. Event-triggered parallel distributed compensator design for nonlinear system with mixed delays and sampling input by T-S fuzzy approach. IEEE Access 2025, 13, 46941–46955. [Google Scholar] [CrossRef]
- Wang, L.X. A Course in Fuzzy Systems and Control; Prentice Hall: Upper Saddle River, NJ, USA, 1997. [Google Scholar]
- Kung, C.C.; Chen, T.H. H∞ tracking based-adaptive fuzzy sliding mode controller design for nonlinear systems. IET Control Theory Appl. 2007, 1, 82–89. [Google Scholar] [CrossRef]
- Bian, B.; Wang, L. A robust fuzzy PD inverse dynamics decoupling control of spherical motion mechanism with fuzzy linear extended state observer. IEEE Access 2021, 9, 40140–40154. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhao, H.; Zhen, S.; He, C.S. Designing robust control for permanent magnet synchronous motor: Fuzzy based and multivariable optimization approach. IEEE Access 2021, 9, 39138–39153. [Google Scholar] [CrossRef]
- Guo, X.; Wang, Z.; Zhang, C.; Zhang, H.; Huang, C. Dual-mode robust fuzzy model predictive control of time-varying delayed uncertain nonlinear systems with perturbations. IEEE Trans. Fuzzy Syst. 2023, 31, 2182–2196. [Google Scholar] [CrossRef]
- Xu, S.; He, B. Robust adaptive fuzzy fault tolerant control of robot manipulators with unknown parameters. IEEE Trans. Fuzzy Syst. 2023, 31, 3081–3092. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Z.; Zou, L.; Dong, H. Observer-based fuzzy PID tracking control under try-once-discard communication protocol: An affine fuzzy model approach. IEEE Trans. Fuzzy Syst. 2024, 32, 2352–2365. [Google Scholar] [CrossRef]
- Yan, W.; Zhao, T.; Niu, B.; Wang, X. Adaptive T-S fuzzy control for an unknown structure system with a self-adjusting control accuracy. IEEE Trans. Automat. Sci. Eng. 2025, 22, 944–957. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).