Finite-Element and Experimental Analysis of a Slot Line Antenna for NV Quantum Sensing †
Abstract
1. Introduction
2. The NV Center
3. Slot Lines for NV Centers
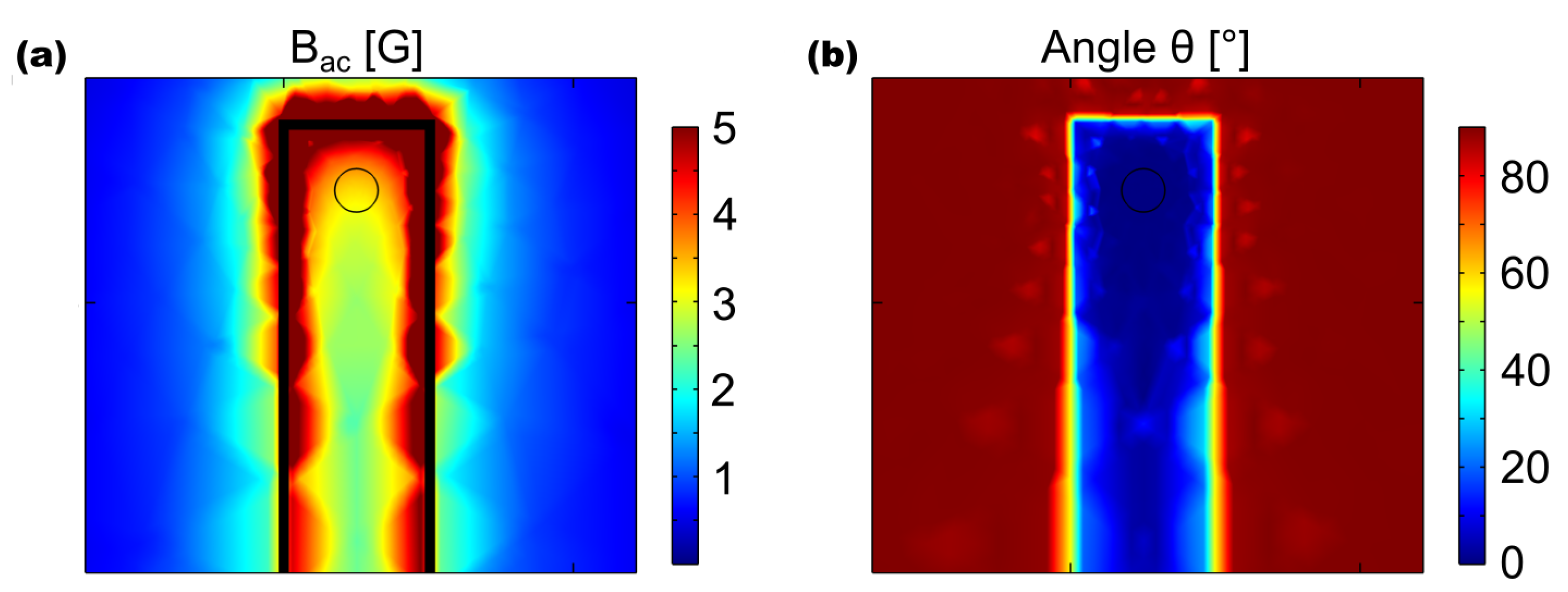
4. Simulations
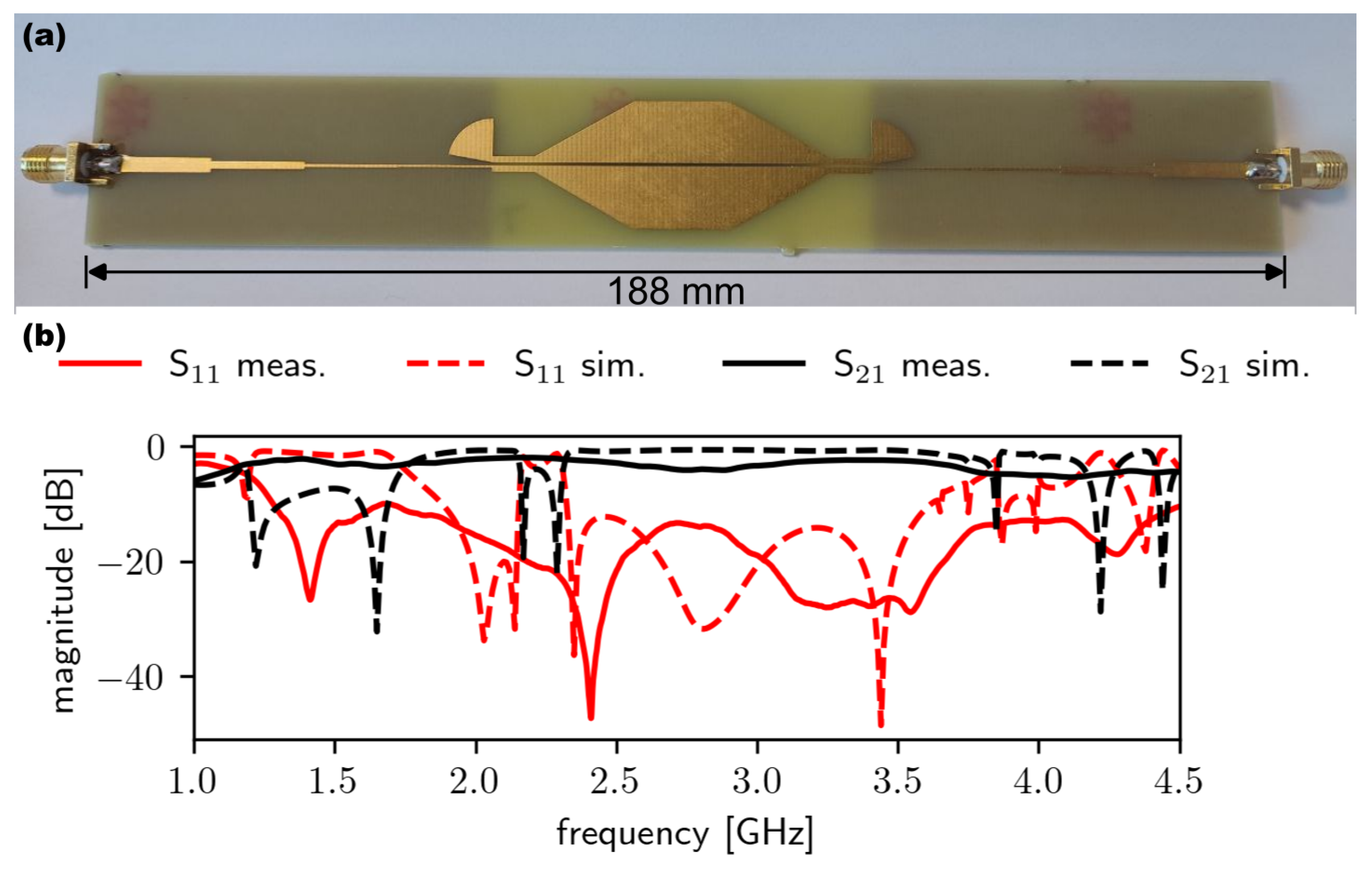
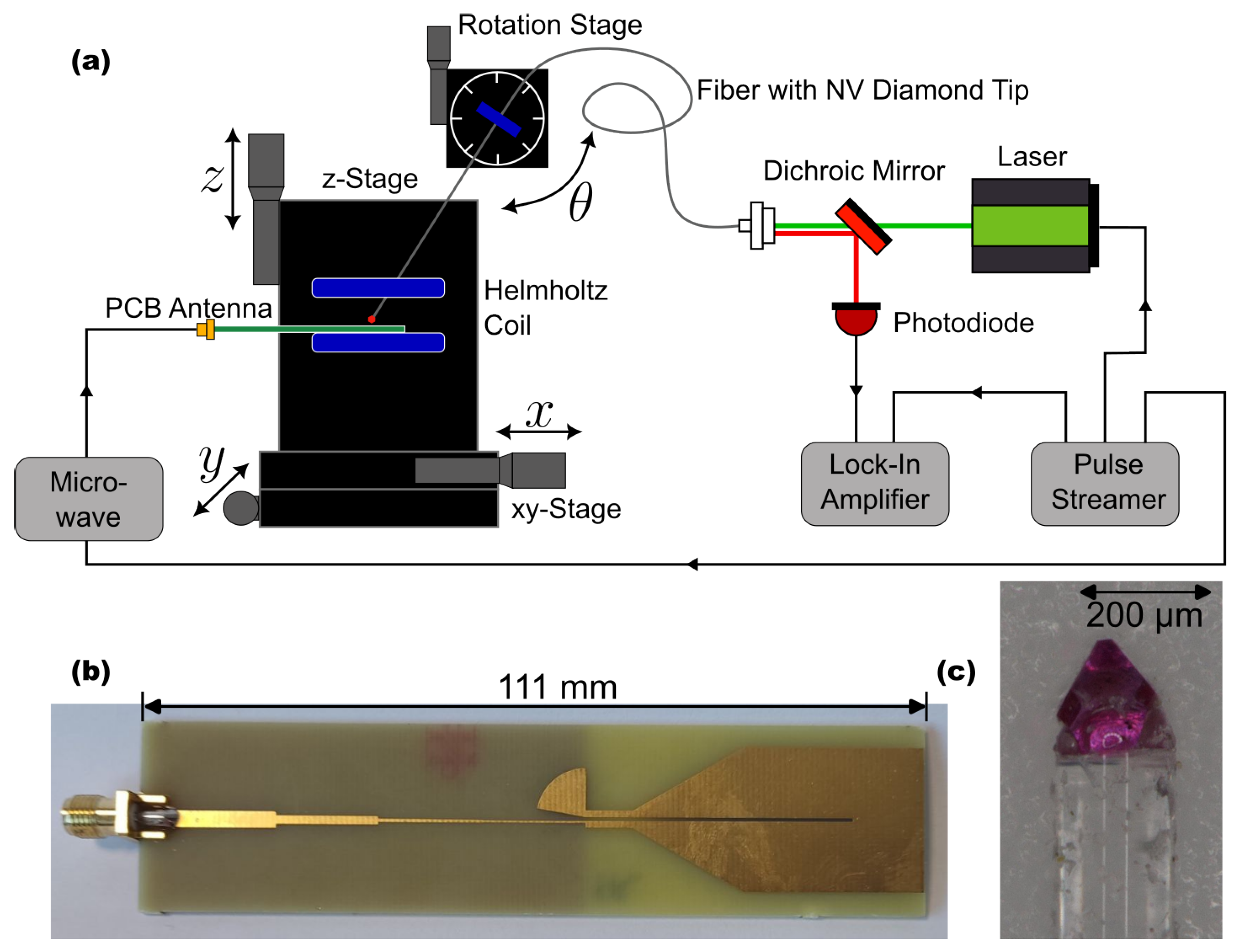
5. Setup and Measurement
6. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| NV | Nitrogen vacancy |
| FEM | Finite element method |
| PCB | Printable circuit board |
| ZFS | Zero field splitting |
| ODMR | Optically detection of magnetic resonances |
| RF4 | Fire retardant |
| CPS | Coplanar strips |
| TEM | Transverse electromagnetic mode |
| ENIG | Electroless nickel iommersion gold |
| VNA | Vector network analyser |
| TOSM | Through-ppen-short-match |
| HPHT | High temperature high pressure |
| NA | Numerical aperture |
| FFT | Fast fourier transformation |
References
- Sasaki, K.; Monnai, Y.; Saijo, S.; Fujita, R.; Watanabe, H.; Ishi-Hayase, J.; Itoh, K.M.; Abe, E. Broadband, large-area microwave antenna for optically detected magnetic resonance of nitrogen-vacancy centers in diamond. Rev. Sci. Instrum. 2016, 87, 053904. [Google Scholar] [CrossRef] [PubMed]
- Bayat, K.; Choy, J.; Baroughi, M.F.; Meesala, S.; Loncar, M. Efficient, uniform, and large area microwave magnetic coupling to NV centers in diamond using double split-ring resonators. Nano Lett. 2014, 14, 1208–1213. [Google Scholar] [CrossRef]
- Eisenach, E.R.; Barry, J.F.; Pham, L.M.; Rojas, R.G.; Englund, D.R.; Braje, D.A. Broadband loop gap resonator for nitrogen vacancy centers in diamond. Rev. Sci. Instrum. 2018, 89, 094705. [Google Scholar] [CrossRef]
- Kapitanova, P.; Soshenko, V.V.; Vorobyov, V.V.; Dobrykh, D.; Bolshedvorskii, S.V.; Sorokin, V.N.; Akimov, A.V. 3D Uniform Manipulation of NV Centers in Diamond Using a Dielectric Resonator Antenna. JETP Lett. 2018, 108, 588–595. [Google Scholar] [CrossRef]
- Zhang, N.; Yuan, H.; Zhang, C.; Xu, L.; Zhang, J.; Bian, G.; Fan, P.; Yuan, H.; Fang, J. Microwave Field Uniformity Impact on DC Magnetic Sensing With NV Ensembles in Diamond. IEEE Sens. J. 2019, 19, 451–456. [Google Scholar] [CrossRef]
- Opaluch, O.R.; Oshnik, N.; Nelz, R.; Neu, E. Optimized Planar Microwave Antenna for Nitrogen Vacancy Center based Sensing Applications. Nanomaterials 2021, 11, 2108. [Google Scholar] [CrossRef]
- Haverkamp, N.; Pusch, A.; Gregor, M.; Heusler, S. Low-cost ODMR experiments with nitrogen-vacancy centers in diamonds: A didactical approach to theory and experiment. EPJ Quantum Technol. 2025, 12, 27. [Google Scholar] [CrossRef]
- Hu, Q.; Huang, K.; Mao, X.; Ran, G.; He, X.; Lin, Z.; Hu, T.; Ran, S. Design of high sensitivity magnetometer based on Diamond Nitrogen-Vacancy Centers and Weak Signal Output Module. Diam. Relat. Mater. 2025, 151, 111858. [Google Scholar] [CrossRef]
- Sewani, V.K.; Vallabhapurapu, H.H.; Yang, Y.; Firgau, H.R.; Adambukulam, C.; Johnson, B.C.; Pla, J.J.; Laucht, A. Coherent control of NV− centers in diamond in a quantum teaching lab. Am. J. Phys. 2020, 88, 1156–1169. [Google Scholar] [CrossRef]
- Lee, J.S.; Lee, G.H.; Mohyuddin, W.; Choi, H.C.; Kim, K.W. Design of an Ultra-Wideband Microstrip-to-Slotline Transition on Low-Permittivity Substrate. Electronics 2020, 9, 1329. [Google Scholar] [CrossRef]
- Lee, G.H.; Mohyuddin, W.; Choi, H.C.; Kim, K.W. Asymmetric Ultra-Wideband Microstrip-to-Coplanar Stripline Transition. IEEE Microw. Wirel. Compon. Lett. 2018, 28, 386–388. [Google Scholar] [CrossRef]
- Lee, G.H.; Mohyuddin, W.; Kumar, S.; Choi, H.C.; Kim, K.W. Compact Wideband Coplanar Stripline-to-Microstrip Line Transition Using a Bended Structure on a Two-Layered Substrate. Electronics 2021, 10, 1272. [Google Scholar] [CrossRef]
- Guo, X.; Zhu, L.; Wang, J.; Wu, W. Wideband Microstrip-to-Microstrip Vertical Transitions Via Multiresonant Modes in a Slotline Resonator. IEEE Trans. Microw. Theory Tech. 2015, 63, 1902–1909. [Google Scholar] [CrossRef]
- Seman, N.S.; Bialkowski, M.E. Microstrip-Slot Transition and Its Applications in Multilayer Microwave Circuits. In Passive Microwave Components and Antennas; Zhurbenko, V., Ed.; InTech: London, UK, 2010. [Google Scholar] [CrossRef]
- Zinieris, M.M.; Sloan, R.; Davis, L.E. A broadband microstrip-to-slot-line transition. Microw. Opt. Technol. Lett. 1998, 18, 339–342. [Google Scholar] [CrossRef]
- Garg, R.; Bahl, I.J.; Bozzi, M. Microstrip Lines and Slotlines, 3rd ed.; Artech House Microwave Library, Artech House: Boston, MA, USA, 2013. [Google Scholar]
- Tu, W.H.; Chang, K. Wide-band microstrip-to-coplanar stripline/slotline transitions. IEEE Trans. Microw. Theory Tech. 2006, 54, 1084–1089. [Google Scholar] [CrossRef]
- Toulali, I.; Lahsaini, M.; Zenkouar, L. Design of a Low Noise Amplifier Using the Quarter Wave Transformers Matching Technique in the Frequency Band [9–13] GHz. Int. J. Commun. Antenna Propag. (IRECAP) 2015, 5, 248. [Google Scholar] [CrossRef]
- Hammerstad, E.O. Equations for Microstrip Circuit Design. In Proceedings of the 1975 5th European Microwave Conference, Hamburg, Germany, 1–4 September 1975; pp. 268–272. [Google Scholar] [CrossRef]
- Darwis, F.; Wijayanto, Y.N.; Setiawan, A.; Mahmudin, D.; Rahman, A.N.; Daud, P. 10 GHz Standing-Wave Coplanar Stripline on LiNbO 3 Crystal for Radio to Optical-Wave Conversion. J. Physics Conf. Ser. 2018, 1011, 012050. [Google Scholar] [CrossRef]
- Janaswamy, R.; Schaubert, D.H. Characteristic Impedance of a Wide Slotline on Low-Permittivity Substrates (Short Paper). IEEE Trans. Microw. Theory Tech. 1986, 34, 900–902. [Google Scholar] [CrossRef]
- Stiegekötter, D.; Pogorzelski, J.; Horsthemke, L.; Hoffmann, F.; Gregor, M.; Glösekötter, P. Microcontroller-Optimized Measurement Electronics for Coherent Control Applications of NV Centers. Sensors 2024, 24, 3138. [Google Scholar] [CrossRef] [PubMed]
- Homrighausen, J.; Hoffmann, F.; Pogorzelski, J.; Glösekötter, P.; Gregor, M. Microscale fiber-integrated vector magnetometer with on-tip field biasing using N-V ensembles in diamond microcrystals. Phys. Rev. Appl. 2024, 22, 034029. [Google Scholar] [CrossRef]
- Saiko, A.P.; Fedaruk, R.; Markevich, S.A. Suppression of electron spin decoherence in Rabi oscillations induced by an inhomogeneous microwave field. J. Magn. Reson. 2018, 290, 60–67. [Google Scholar] [CrossRef] [PubMed]
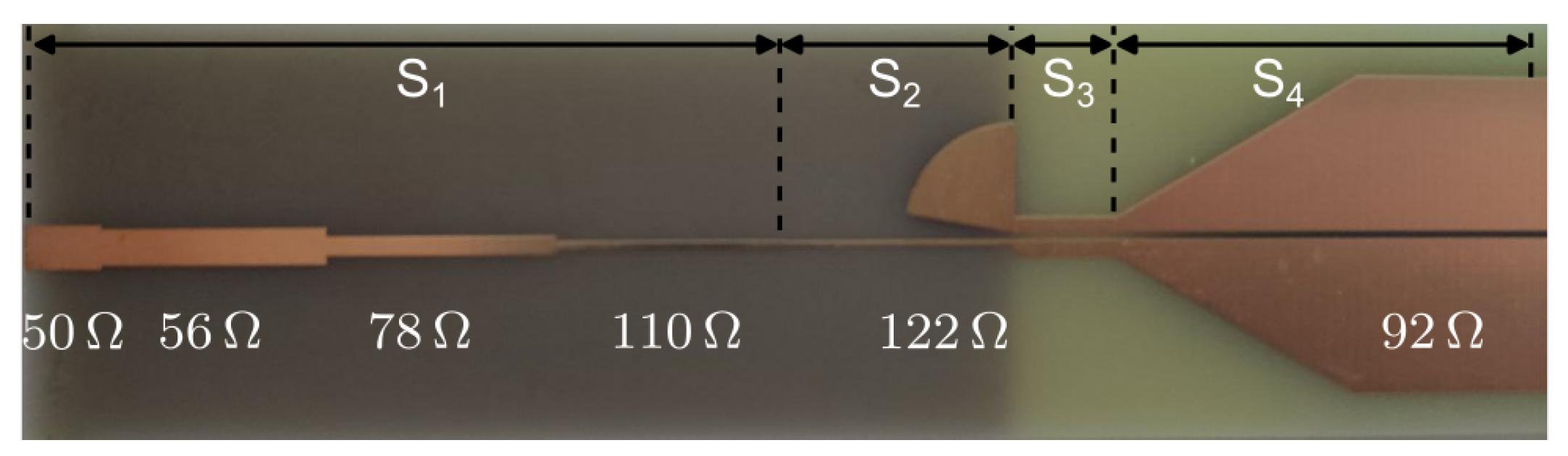


| CPS | SL | Taper | Stub | |||||
|---|---|---|---|---|---|---|---|---|
| W = 2.81 | W = 2.32 | W = 1.19 | W = 0.49 | W = 0.34 | W = 2.5 | W = 10.5 | = 30 | = 80 |
| L = 5 | L = 14.3 | L = 14.6 | L = 14.8 | L = 14.6 | L = 6.73 | L = 15.4 | R = 7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stiegekötter, D.; Homrighausen, J.; Bülter, A.-S.; Horsthemke, L.; Hoffmann, F.; Pogorzelski, J.; Glösekötter, P.; Gregor, M. Finite-Element and Experimental Analysis of a Slot Line Antenna for NV Quantum Sensing. Eng. Proc. 2025, 101, 9. https://doi.org/10.3390/engproc2025101009
Stiegekötter D, Homrighausen J, Bülter A-S, Horsthemke L, Hoffmann F, Pogorzelski J, Glösekötter P, Gregor M. Finite-Element and Experimental Analysis of a Slot Line Antenna for NV Quantum Sensing. Engineering Proceedings. 2025; 101(1):9. https://doi.org/10.3390/engproc2025101009
Chicago/Turabian StyleStiegekötter, Dennis, Jonas Homrighausen, Ann-Sophie Bülter, Ludwig Horsthemke, Frederik Hoffmann, Jens Pogorzelski, Peter Glösekötter, and Markus Gregor. 2025. "Finite-Element and Experimental Analysis of a Slot Line Antenna for NV Quantum Sensing" Engineering Proceedings 101, no. 1: 9. https://doi.org/10.3390/engproc2025101009
APA StyleStiegekötter, D., Homrighausen, J., Bülter, A.-S., Horsthemke, L., Hoffmann, F., Pogorzelski, J., Glösekötter, P., & Gregor, M. (2025). Finite-Element and Experimental Analysis of a Slot Line Antenna for NV Quantum Sensing. Engineering Proceedings, 101(1), 9. https://doi.org/10.3390/engproc2025101009







