On Errors of Signal Estimation Using Complex Singular Spectrum Analysis ^†

Abstract

Singular spectrum analysis (SSA) is a nonparametric method that can be applied to signal estimation. The extension of SSA to the complex-valued case, called CSSA, is considered. The accuracy of signal estimation using CSSA is investigated. An explicit form of the first-order errors is presented for the case of a constant signal and two forms of perturbations: an outlier and white noise. Also, it is shown numerically that (1) the first-order errors describe the full errors well, and (2) the formulas for accurately estimating a constant signal can be applied to a sum of complex exponentials via multiplication by the number of exponentials.

1. Introduction

The analysis of time series with complex values is an important area in signal processing. Although complex-valued time series do not occur directly in real-life data, they are constructed from two related features [1,2] and can also arise as a result of applying the discrete Fourier transform to real data [3,4].

Singular spectrum analysis (SSA) [5,6,7,8] is a powerful method of time series analysis that does not require a parametric model of the time series to be specified in advance. The method has a natural extension to the case of complex time series, called Complex SSA (CSSA) [9,10]. In fact, one could say that SSA is a special case of CSSA. A class of signals governed by linear recurrence relations can be used to obtain theoretical results regarding SSA and CSSA.

Let the observed complex time series be of the form $\mathsf{X}=\mathsf{S}+\mathsf{E}$. To obtain an estimate $S$ of the signal S, we will use the CSSA method.

To analyse the signal estimation error, we use the perturbation theory [11,12], which has been applied to the case of signal extraction by the SSA method in a number of papers: see, for example, [13,14]. Although Kato’s perturbation theory gives a form of the full error, its examination is a difficult task. Therefore, we will only consider the first-order error, which is the part that is linear in the perturbation.

Even for the first-order error, obtaining its explicit form is a rather complicated task. Theoretically, we consider only the case of a constant signal. Two types of perturbation are examined: an outlier and random noise. The theoretical results obtained allow us to study how CSSA deals with signal extraction. The importance of perturbation in the form of noise is quite clear. There are robust variants of the SSA method for analysing time series with possible outliers [15,16,17,18,19], but they are mostly much more time-consuming than the basic version of SSA, so studying the influence of outliers on the basic version of SSA and CSSA is of considerable interest.

Certainly, constant signals are not a common case in time series analysis. Therefore, special attention is given to a possible generalisation of the theoretical results, which are demonstrated numerically.

The rest of the paper is organized as follows. Section 2 contains the CSSA algorithm. Section 3 outlines the theoretical approach to error computation and presents the theoretical results obtained for the constant series. In Section 4, an extension of the theoretical results to the general case of signals is suggested; the assumed results on estimation accuracy are confirmed by numerical experiments. Section 5 concludes this paper.

2. Algorithm CSSA

Let us briefly describe singular spectrum analysis and its features. Algorithm 1 presents the steps of CSSA for estimating the signal.

Algorithm 1: CSSA

1 Input: Complex time series $\mathsf{X}=(x_1,\dots ,x_N)$, window length L, signal rank r. 2 Output: Signal estimate $\tilde{S}$. 3 Algorithm: 1. Embedding. Construct $\mathbf{X}\in {\mathbf{C}}^{L\times K}$, the L-trajectory matrix of the time series X: $$\mathbf{X}={\mathcal{T}}_L\mathsf{X}=[X_1:\dots X_K],$$ where $K=N-L+1$ and $X_i$ are the L-embedding vectors: $X_i={(x_i,\dots ,x_{i+L-1})}^{\mathrm{T}}\in {\mathbf{C}}^L$. 2. Decomposition. Construct the singular value decomposition (SVD) of the matrix X: $\mathbf{X}={\displaystyle \sum _{k=1}^{rank\; X}}\sqrt{{\lambda }_k}{U}_k{V}_k^{\mathrm{H}}={\displaystyle \sum _{k=1}^{rank\; X}}{\widehat{\mathbf{X}}}_k$, where $\mathrm{H}$ means the Hermitian conjugate, $U_k$ and $V_k$ are the left and right singular vectors of the matrix X, $\sqrt{{\lambda }_k}$ are the singular values in decreasing order. 3. Grouping. Group the matrix components ${\widehat{\mathbf{X}}}_k$ associated with the signal: $\widehat{\mathbf{S}}={\sum }_{k=1}^r{\widehat{\mathbf{X}}}_k$. 4. Diagonal averaging. Apply the hankelization (which is the projection into the linear space of Hankel matrices): $\tilde{\mathbf{S}}={\mathrm{\Pi }}_{\mathcal{H}}\widehat{\mathbf{S}}$, and return back to the series form: $\tilde{\mathrm{S}}={\mathcal{T}}_L^{-1}\tilde{\mathbf{S}}$.

Recommendations for the choice of the window length L can be found in [20,21]. The choice of r is a much more sophisticated problem; information criteria for the choice of r are proposed in [22,23].

The SSA/CSSA estimation of the signal can be presented in short form:

$$\tilde{\mathrm{S}}={\mathcal{T}}_L^{-1}\circ {\mathrm{\Pi }}_{\mathcal{H}}\circ {\mathrm{\Pi }}_r\circ {\mathcal{T}}_L\left(\mathsf{X}\right),$$

where ${\mathrm{\Pi }}_{\mathcal{H}}$ is the projector on the space of Hankel matrices (in Frobenius norm), and ${\mathrm{\Pi }}_r$ is the projector on the set of matrices of ranks not larger than r.

The L-rank of a time series is the rank of its trajectory matrix. For further considerations we need to know the ranks of certain series. It is known from [8] that the rank of a complex signal for which its real and imaginary parts are sinusoids with the same frequency $\omega$, $0<\omega <0.5$, is equal to 2 if the absolute phase shift of the sinusoids, given in the interval from $-\pi$ to $\pi$, is not equal to $\pi /2$ and is equal to 1 in the case of a complex exponential. The rank of a real sine wave is 2 under the same frequency constraints. The ranks of complex and real constants are equal to 1 as they can be considered as a special case with $\omega =0$.

The signal is considered to be a sum of r exponentially modulated complex exponentials, with the sum having a rank of r.

3. Application of Perturbation Theory to CSSA

Let us observe $\mathsf{X}=\mathsf{S}\left(\delta \right)$, where $\mathsf{S}\left(\delta \right)=\mathsf{S}+\delta \mathsf{E}$, and let $\tilde{\mathsf{S}}$ be the CSSA estimate of the signal. It is known from [13] that the reconstruction error F has the form $\mathsf{F}=\tilde{\mathsf{S}}-\mathsf{S}={\mathcal{T}}_L^{-1}{\mathrm{\Pi }}_{\mathcal{H}}(\delta {\mathbf{S}}^{\left(1\right)}+{\delta }^2{\mathbf{S}}^{\mathrm{(2)}})$.

For simplicity, let $\delta =1$. We call the first-order reconstruction error the part of the error that is linear in $\delta$: ${\mathsf{F}}^{\mathrm{(1)}}={\mathcal{T}}_L^{-1}{\mathrm{\Pi }}_{\mathcal{H}}\left(\delta {\mathbf{S}}^{\left(1\right)}\right)$. Theorem 2.1 from [13] gives the following formula for ${\mathbf{S}}^{\mathrm{(1)}}\in C^{L\times K}$ in the case of a sufficiently small perturbation:

$${\mathbf{S}}^{\mathrm{(1)}}={\mathbf{P}}_0\mathbf{E}{\mathbf{Q}}_0^{\perp }+{\mathbf{P}}_0^{\perp }\mathbf{E},$$

(1)

where ${\mathbf{P}}_0^{\perp }$ is the projector onto the column space of S; ${\mathbf{Q}}_0^{\perp }$ is the projector onto the row space of S; ${\mathbf{P}}_0=\mathbf{I}-{\mathbf{P}}_0^{\perp }$; $\mathbf{I}$ is the identity matrix.

3.1. Relation Between Complex and Real First-Order Errors for Rank 1

In [13], formulas were derived for ${\mathbf{S}}^{\mathrm{(1)}}$ for real series of ranks 1 and 2. Below, we give the complex form for the case of rank 1. For $rank\mathsf{S}=1$ and the leading left and right singular vectors U and V of the trajectory matrix of the series S,

$${\mathbf{S}}^{\mathrm{(1)}}={\mathbf{S}}^{\mathrm{(1)}}(\mathbf{E},\mathsf{S})=-U^{\mathrm{H}}\mathbf{E}VU{V}^{\mathrm{H}}+U{U}^{\mathrm{H}}\mathbf{E}+\mathbf{E}V{V}^{\mathrm{H}}.$$

(2)

Proposition 1.

Let $rank\mathsf{S}=rankRe(\mathsf{S})=rankIm(\mathsf{S})=1$. Then,

$${\mathsf{F}}^{\mathrm{(1)}}={\mathsf{F}}_{Re}^{\left(1\right)}+\mathrm{i}{\mathsf{F}}_{Im}^{\left(1\right)},$$

where ${\mathsf{F}}^{\mathrm{(1)}}$ is the first-order error of the CSSA estimate of $\mathsf{S},{\mathsf{F}}_{Re}^{\left(1\right)}$ is the first-order error of the SSA estimate of $Re(\mathsf{S})$, and ${\mathsf{F}}_{Im}^{\left(1\right)}$ is the first-order error of the SSA estimate of $Im(\mathsf{S})$.

Proof. 

By the linearity of (2) in,

$${\mathbf{S}}^{\mathrm{(1)}}(\mathbf{E},\mathsf{S})={\mathbf{S}}^{\mathrm{(1)}}(Re\left(\mathbf{E}\right),\mathsf{S})+\mathrm{i}{\mathbf{S}}^{\mathrm{(1)}}(Im\left(\mathbf{E}\right),\mathsf{S}).$$

(3)

Since the rank is equal to 1, the singular vectors of the trajectory matrices of $Re\left(\mathsf{S}\right)$, $Im\left(\mathsf{S}\right)$, and S coincide. We can derive, from (3) using the linearity of the diagonal averaging operation and the equality of the singular vectors, that

$${\mathbf{S}}^{\mathrm{(1)}}(\mathbf{E},\mathsf{S})={\mathbf{S}}^{\mathrm{(1)}}(Re\left(\mathbf{E}\right),Re\left(\mathsf{S}\right))+\mathrm{i}{\mathbf{S}}^{\mathrm{(1)}}(Im\left(\mathbf{E}\right),Im\left(\mathsf{S}\right)).$$

□

Note that although the perturbation E can take any form in the statement of the proposition, the proposition has practical application only if the first-order error adequately describes the full error.

An example where the conditions of Proposition 1 are fulfilled is the constant signal. In Section 3.2, we consider the perturbation in the form of an outlier; in Section 3.3, the perturbation is white noise.

Corollary 1.

Let $Re\left(\mathsf{E}\right)$ and $Im\left(\mathsf{E}\right)$ be independent. Then, in the conditions of Proposition 1,

$$\mathbb{D}{\mathsf{F}}^{\mathrm{(1)}}=\mathbb{D}{\mathsf{F}}_{Re}^{\left(1\right)}+\mathbb{D}{\mathsf{F}}_{Im}^{\left(1\right)}$$

3.2. Case of Constant Signals with Outliers

In this section, we consider the signal $\mathsf{S}=(c_1+\mathrm{i}{c}_2,\dots ,c_1+\mathrm{i}{c}_2)$ perturbed by the outlier $a_1+\mathrm{i}{a}_2$ at position k, i.e., the series E consists of zeros except for the value $a_1+\mathrm{i}{a}_2$ at the k-th position. Based on Proposition 1, it is sufficient to compute the first-order reconstruction error for a real signal $\mathsf{S}=(c,\dots ,c)$ perturbed by an real outlier a at position k.

By substituting $U={\{1/\sqrt{L}\}}_{i=1}^L$, $V={\{1/\sqrt{K}\}}_{i=1}^K$, and $K=N-L+1$ into (2) and then performing the diagonal averaging of the matrix ${\mathbf{S}}^{\mathrm{(1)}}$, an explicit form of the first-order reconstruction error was obtained. It appears that the first-order error does not depend on c, and therefore, the formulas are valid for the complex $c=c_1+\mathrm{i}{c}_2$. Due to linear dependence on a, the obtained formulas are correct for the complex outlier $a=a_1+\mathrm{i}{a}_2$. Below, we present the final results depending on the location of the outlier and the relation between L and K.

Let us consider different locations k of the outlier. For $L\le k\le K$, we have

$$f_l^{\left(1\right)}={\displaystyle \frac{a}{L}}\left\{\begin{array}{cc}{\displaystyle \frac{1}{min(L,l)}}(l-k+L),\hfill & k-L\le l\le k,\hfill \\ {\displaystyle \frac{1}{min(L,N-l+1)}}(L+k-l),\hfill & k<l<L+k,\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(4)

Below we consider the location $k<L$, since case $k>K$ can be reduced to $k<L$ by inverting the time series and taking the outlier at position $N-k+1$.

Define

$$\begin{array}{cc}\hfill A_1& =L+K-k,\hfill \\ \hfill A_2& ={\displaystyle \frac{k(L+K-l)}{l}},\hfill \\ \hfill A_3& ={\displaystyle \frac{K(L+k-l)}{L}},\hfill \\ \hfill A_4& =\left\{\begin{array}{cc}0,\hfill & k<K-L,\hfill \\ {\displaystyle \frac{2KL-l(L+K-k)}{N-l+1}},\hfill & \mathrm{otherwise},\hfill \end{array}\right.\hfill \\ \hfill A_5& =\left\{\begin{array}{cc}{\displaystyle \frac{(L-K)(L-k)}{N-l+1}},\hfill & {\displaystyle \frac{L}{2}}<k<{\displaystyle \frac{K}{2}},\hfill \\ {\displaystyle \frac{(K-l)(L-k)}{N-l+1}},\hfill & \mathrm{otherwise},\hfill \end{array}\right.\hfill \\ \hfill A_6& =-k.\hfill \end{array}$$

Then, the first-order error has the following form:

$$\begin{array}{cc}\hfill f_l^{\left(1\right)}& ={\displaystyle \frac{a}{LK}}\left\{\begin{array}{cc}{A}_1,\hfill & 1\le l\le k,\hfill \\ A_2,\hfill & k<l\le L,\hfill \\ A_3,\hfill & L<l\le min(K,L+k),\hfill \\ A_4,\hfill & min(K,L+k)<l\le max(K,L+k),\hfill \\ A_5,\hfill & max(K,L+k)<l\le K+k,\hfill \\ A_6,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\hfill \end{array}$$

(5)

Comments

It can be seen that the first-order error tends to zero as N tends to infinity only if L and K are proportional to N. Then, the first-order error is proportional to $1/min(L,K)$, i.e., $1/N$. Therefore, the rate of convergence of the first-order error to zero can be estimated as $\mathcal{O}(1/N)$. Since the first-order error does not depend on the signal scale, it is not determined by the signal-to-noise ratio.

Remark 1.

From (4) and (5), one can see that for a fixed L, the first-order error does not tend to 0 as N increases. As will be shown in the next section, the first-order error still describes the full error quite accurately in this case. Therefore, the full error does not tend to 0 as N increases. If L and K are proportional to N, the first-order and full errors tend to zero. The theoretical basis for the real case and the maximum absolute deviation error can be found in [24].

The following proposition can be derived directly from (4) and (5).

Proposition 2.

If $L\le k\le K$, then $f_l^{\left(1\right)}=0$ for $|k-l|>L$, and therefore, the first-order error has a support of length $2L+1$. If $k<L$ and $k+L<K$, then $f_l^{\left(1\right)}=0$ for $k+L\le l<K$, meaning the first-order error has a support of length $2L+k+1$. If $K-L\le k<L$, we have $f_l^{\left(1\right)}=0$ only for $l=2LK/(L+K-k)$ if it is an integer.

It can be seen from Proposition 2 that the number of points where $f_l^{\left(1\right)}\ne 0$ is not continuous with respect to k. For example, for $k=L-1$, it is either N or $N-1$, but for $k=L$, it is $2L+1$.

Proposition 2 shows that increasing the window length causes the errors to spread more widely over the time series. Let us consider $f_k^{\left(1\right)}$ for different values of k. For $L\le k\le K$, $f_k^{\left(1\right)}=a/L$. For $k<L$, $f_k^{\left(1\right)}=a(N-k+1)/\left(LK\right)$. In both cases, a larger value of L gives a smaller absolute value of $f_k^{\left(1\right)}$. Thus, a smaller window length, L, results in more localised errors near the position of an outlier, but with larger values.

3.3. Case of Noisy Constant Signals

Consider the time series S with common terms $s_n=c_1+\mathrm{i}{c}_2$ and the white noise with zero mean and variances of real and imaginary parts ${\sigma }_1^2$ and ${\sigma }_2^2$, respectively. The conditions of Proposition 1 are obviously satisfied, and therefore, by Corollary 1, the variance of the CSSA first-order error is expressed by the variances of the first-order errors of the real and imaginary part of the SSA estimates.

In [25], the analytic formula was obtained for a real constant signal, i.e., for the variances of $F_{Re}^{\left(1\right)}$ and $F_{Im}^{\left(1\right)}$ separately. Let $L=\alpha N$, $\alpha \le {\displaystyle \frac{1}{2}}$, and $\lambda ={lim}_{N\to \infty }2l/N$. Following [25] and correcting an error, we get, for the general complex case,

$$\mathbb{D}{f}_l^{\left(1\right)}=\mathbb{D}{f}_{Re,l}^{\left(1\right)}+\mathbb{D}{f}_{Re,l}^{\left(1\right)}\sim {\displaystyle \frac{{\sigma }_1^2+{\sigma }_2^2}{N}}\left\{\begin{array}{cc}{D}_1(\alpha ,\lambda ),\hfill & 0\le \lambda \le min\left(2\right(1-2\alpha ),2\alpha ),\hfill \\ D_2(\alpha ,\lambda ),\hfill & min\left(2\right(1-2\alpha ),2\alpha )<\lambda \le 2\alpha ,\hfill \\ D_3(\alpha ,\lambda ),\hfill & 2\alpha <\lambda \le 1,\hfill \end{array}\right.$$

(6)

where

$$\begin{array}{cccc}\hfill D_1(\alpha ,\lambda )=& {\displaystyle \frac{1}{3{\alpha }^2{(1-\alpha )}^2}}({\lambda }^2(\alpha +1)-2\lambda {(1+\alpha )}^2+4\alpha (-3\alpha +3+2{\alpha }^2)),\hfill & & \\ \hfill D_2(\alpha ,\lambda )=& {\displaystyle \frac{1}{6{\alpha }^2{\lambda }^2(\alpha -1)}}({\lambda }^4+2{\lambda }^3(3\alpha -2-3{\alpha }^2)+\hfill & & \\ \hfill +& 2{\lambda }^2(3-9\alpha +12{\alpha }^2-4{\alpha }^3)+4\lambda (4{\alpha }^4-4{\alpha }^3-3{\alpha }^2+4\alpha -1)+\hfill & & \\ \hfill +& 8\alpha -56{\alpha }^2+144{\alpha }^3-160{\alpha }^4+64{\alpha }^5,\hfill & & \\ \hfill D_3(\alpha ,\lambda )=& {\displaystyle \frac{2}{3\alpha }}.\hfill \end{array}$$

Formulas are written down for $l\le N/2$. For $l\ge N/2$, the error at l is equal to the error at position $N-l$.

4. Numerical Investigation

4.1. Numerical Comparison of First-Order and Full Signal Estimation Errors

For the case of outlier perturbation, the example with signal $s_l=1+\mathrm{i}1$ and outlier perturbation $a_1+\mathrm{i}{a}_2=10+\mathrm{i}10$ at position $k=L-1$ was considered. The results are shown in

Table 1. Maximum difference between first-order error and full error for the outlier at $k=L-1$.

N	100	1000	10,000	100,000
$k=N/2-1$, $L=N/2$, full	$2.88\times {10}^{-1}$	$2.83\times {10}^{-2}$	$2.83\times {10}^{-3}$	$2.83\times {10}^{-4}$
$k=N/2-1$, $L=N/2$, diff	$4.19\times {10}^{-2}$	$5.47\times {10}^{-4}$	$5.64\times {10}^{-6}$	$5.66\times {10}^{-8}$
$k=20$, $L=20$, full	$7.25\times {10}^{-1}$	$7.09\times {10}^{-1}$	$7.07\times {10}^{-1}$	$7.07\times {10}^{-1}$
$k=20$, $L=20$, diff	$2.80\times {10}^{-2}$	$6.38\times {10}^{-3}$	$6.68\times {10}^{-4}$	$6.71\times {10}^{-5}$
$k=20$, $L=N/2$, full	$5.09\times {10}^{-1}$	$5.70\times {10}^{-2}$	$5.66\times {10}^{-3}$	$5.66\times {10}^{-4}$
$k=20$, $L=N/2$, diff	$5.97\times {10}^{-2}$	$1.60\times {10}^{-3}$	$1.69\times {10}^{-5}$	$1.70\times {10}^{-7}$
$k=N/2-1$, $L=20$, full	$7.07\times {10}^{-1}$	$7.07\times {10}^{-1}$	$7.07\times {10}^{-1}$	$7.07\times {10}^{-1}$
$k=N/2-1$, $L=20$, diff	$5.77\times {10}^{-15}$	$1.82\times {10}^{-14}$	$2.38\times {10}^{-13}$	$9.68\times {10}^{-13}$

. The columns of Table 1 correspond to different time series lengths N. The rows correspond to different outlier locations k and different window lengths L as a function of N. For each pair of k and L, we give the maximum full error (‘full’) and the maximum absolute difference between the full and first-order errors (‘diff’). One can see the convergence of this difference to 0 for all cases, while the full error tends to 0 only for L proportional to N.

The analogous result that the first-order error adequately estimates the full error of signal reconstruction at each point was also verified numerically in the case of noisy constant series (see the example concerning a noisy signal in Section 4.2). For both perturbations, it was verified that this result is valid for signals of larger ranks (not shown).

4.2. Numerical Validation of Generalisation to Larger Ranks

The theoretical results for constant signals seem to be rather limited. In this section, we numerically demonstrate that the shape of the errors for signals of larger ranks is similar to the error for signals of rank 1, and their size differs by a multiplier.

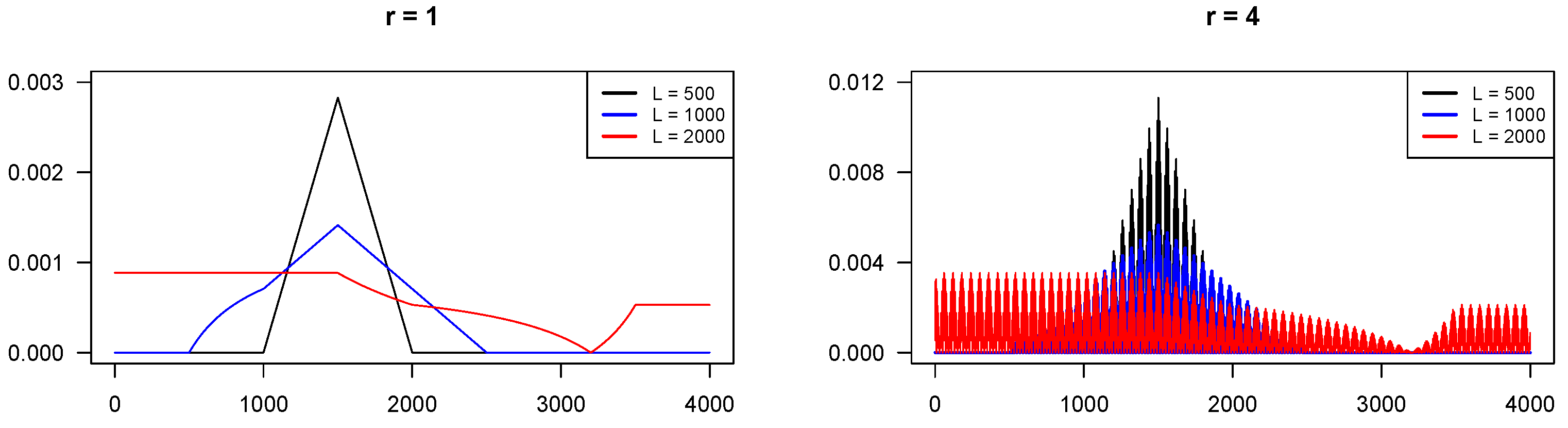
Let us start with a perturbation in the form of an outlier. Set the series length to 3999 and locate the outlier $10+\mathrm{i}10$ at the point $k=1500$. Figure 1 shows the behaviour of the absolute errors as a function of the series point. Figure 1 (left) corresponds to the case $r=1$ (constant signal) and is given by the theoretical formulas presented in Section 3.2. Figure 1 (right) corresponds to the signal $s_n=cos(2\pi n/12)+\mathrm{i}cos(2\pi n/15+\pi /4)$ of rank 4. One can see that the shapes of the errors are similar. The ratio of the summed squared errors is approximately 4 for each of the considered window lengths of 500, 1000, and 2000.

Thus, the theoretical formulas for an elementary case help understand the error behaviour for a general case.

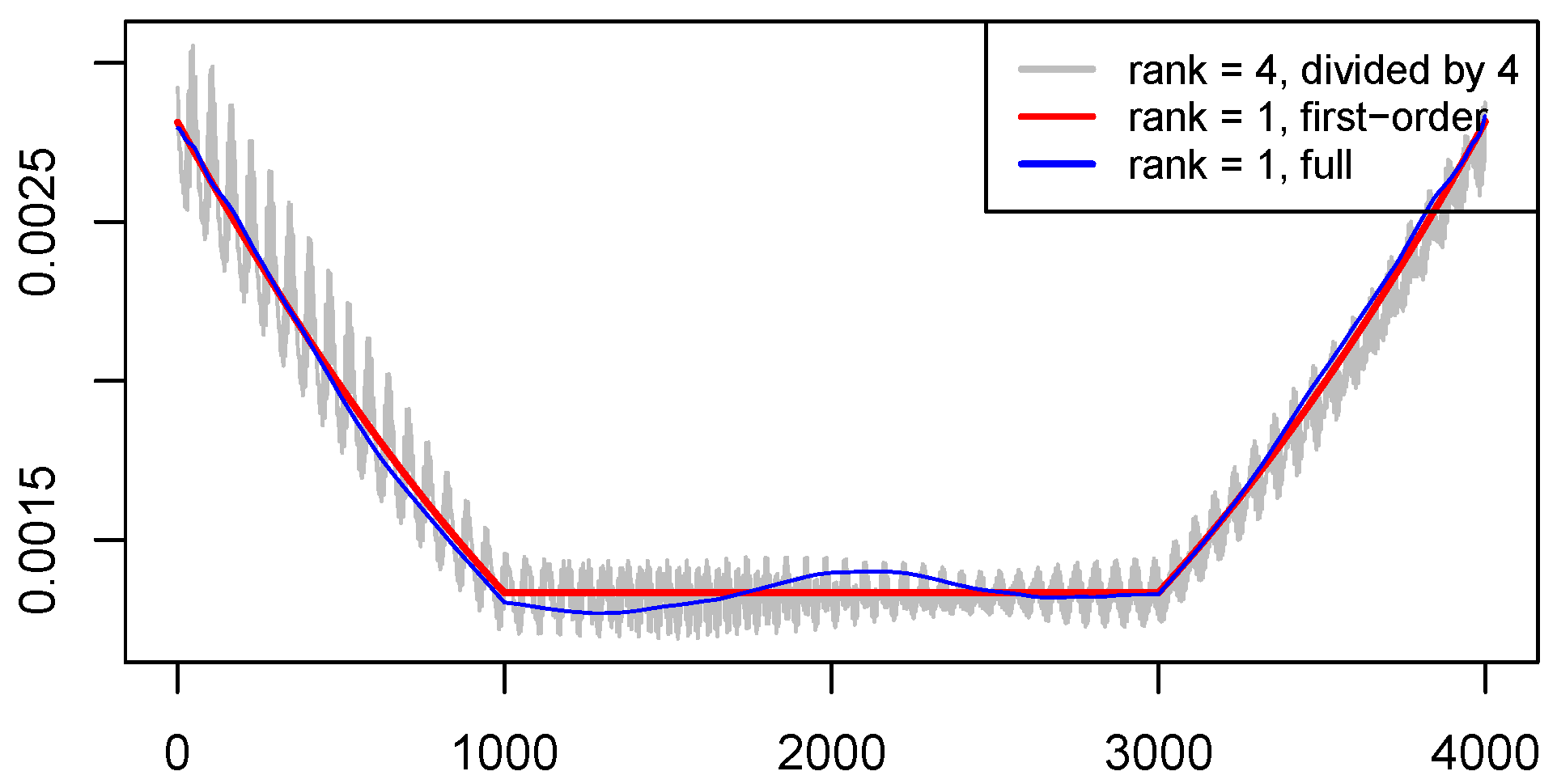
The similar relationship of error variances applies to random noise perturbations. We consider the same signals and the complex independent white Gaussian noise with variance 1 for real and imaginary parts. The MSE for $L=1000$ estimated by 500 realisations of the noise is shown in Figure 2. The ratio of the MSE averaging along the series is about 4; this is confirmed by the proximity of the black and blue lines in Figure 2. We also add the line corresponding to the first-order error calculated by (6). One can see a good agreement between the first-order error and the full error.

All numerical results were obtained using the Rssa package, http://CRAN.R-project.org/package=Rssa, accessed on 3 May 2025 and described in [8]. In the implementation of CSSA, the fast numerical method PRIMME was used to compute the truncated SVDs.

5. Conclusions

An explicit form of the first-order error of signal estimation at each point was obtained for a complex constant signal and for both outliers and random noise perturbations. For the random noise, the error was measured by the variance. It appears that the error does not depend on the signal scale. For both examples, the proximity between the first-order error and the full error was confirmed numerically.

We have demonstrated numerically how the theoretical results on the accuracy of signal estimation in the simple case of a constant signal can help to explain error behaviour in the more general case of a sum of complex exponentials, $s_n={\sum }_{j=1}^r{A}_j{e}^{\mathrm{i}2\pi {\omega }_{j}n}$. These results allow one to use the obtained error formulas in the general case, and they are promising for obtaining theoretical results for ranks larger than one.