Methodology for the Design and Verification of a Securing Structure for Transporting Cylindrical Rollers on Load Bogies ^†

Abstract

The safe transport of cylindrical loads such as metal, paper, or polymer rollers requires specialized securing structures that address the complex dynamic forces encountered during rail movement. This paper presents a structured methodology for the design and verification of such securing systems, combining theoretical analysis, standardized load models, and numerical simulations. The method includes load calculations based on EN 12195-1:2010, EN 15551, and Eurocode 1, and validation through finite element modeling in Ansys Workbench. The proposed structure ensures stability under static and dynamic loads, including acceleration, braking, turning, and wind forces, while optimizing wagon space utilization. Simulation results confirm that the design meets strength and safety criteria without exceeding material stress limits, offering a reliable solution for the secure transport of cylindrical rollers.

1. Introduction

Ensuring the safe and efficient transport of cylindrical loads—such as metal, paper, or polymer rollers—by railway is a critical aspect of modern logistics and industrial practice. The transport of bulky cylindrical objects presents specific challenges due to their geometry, high center of gravity, and propensity to roll or shift if not adequately restrained. Improper securing during rail transport can result in catastrophic incidents, including cargo displacement, wagon derailment, infrastructure damage, and serious safety hazards for operating personnel [1,2].

Although international standards such as EN 12195-1:2010 [3] and ISO 27956:2009 [4] provide general guidance for cargo securing, they are primarily tailored to road transport and are not specifically optimized for the dynamic and complex operational conditions encountered in railway logistics. Similarly, standards like EN 15551:2009 [5] and UIC Code 777-2 [6] outline general securing principles for freight wagons but lack detailed technical solutions for cylindrical or rolling loads under dynamic rail-specific forces. Consequently, the securing of cylindrical objects often relies on traditional methods such as wedges, straps, and friction-enhancing surfaces, which may not provide sufficient resistance under combined static and dynamic loading conditions [7].

Railway transport subjects cargo to a combination of longitudinal (acceleration and braking), transverse (curve negotiation and centrifugal effects), and vertical forces (track irregularities and vibration), all of which act simultaneously and can compromise load stability [8,9]. Experimental studies and operational incident analyses have shown that even relatively small shifts in cylindrical loads during dynamic events can result in progressive movement, increasing the risk of overturning or derailment [10].

Recent advances in numerical modeling, such as multibody dynamics (MBD) and finite element method (FEM) simulations, have improved the ability to predict and mitigate cargo instability under realistic operational scenarios. Multibody simulations, as applied in the dynamic testing of railway vehicles [11], demonstrate that the interaction between wagon dynamics and unsecured or poorly secured loads significantly affects the safety and performance of the transport system [12,13]. Accurate modeling of cargo behavior under dynamic loading is therefore critical for the design and validation of effective securing systems.

Moreover, contemporary engineering research highlights the importance of stress analysis in securing structures. Areas with high stress concentrations, especially around cargo supports and restraint fixtures, are often the initiation points for structural fatigue or failure [14,15]. Methods for reducing stress concentration factors (SCFs)—through improved geometry, material selection, and load distribution—are essential to enhance the long-term reliability of securing structures, particularly under cyclic dynamic loading typical for railway transport [16].

Previous works [17,18] underline that targeted optimization of stress can lead to significant improvements in the fatigue life. Furthermore, studies such as [19,20] emphasize the necessity of integrating dynamic load modeling with structural optimization techniques to ensure both the functional reliability and operational safety of specialized freight securing devices.

In light of these challenges, this paper proposes a systematic methodology for the design and verification of a specialized securing structure intended for the stabilization of cylindrical rollers during railway transport. The methodology integrates the following steps: (i) load analysis considering both static and dynamic railway-specific forces, (ii) verification of structural integrity through finite element simulations under realistic dynamic loading scenarios. The objective is to contribute to the development of standardized and optimized securing solutions for cylindrical cargo, enhancing the safety, efficiency, and reliability of railway freight operations.

2. Methodology for Design of the Structure

The proposed design methodology is based on classical design and verification principles. Figure 1 shows a classical block diagram of the methodology.

Figure 1. Block diagram of the methodology.

In order to formulate a design and verification methodology, a thorough analysis of the input data is necessary. For this case, these are the type of vehicle-freight wagon type Smmps (Figure 1), load dimensions-D = 3 m. L = 1.5 m., mass of the load-30 t.

Figure 2 shows a standard geometric model and the securing scheme of the cylindrical load on the railway wagon.

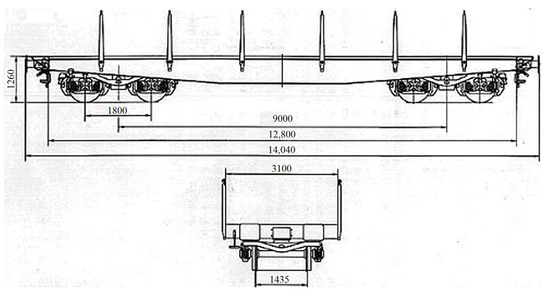
Figure 2. Cargo bogie Smrs.

The first stage of the methodology covers the formation of a design conceptual project. Taking into account the geometry of the load and the vehicle, constraints are imposed on the design of the structure for maximum filling of the wagon, which allows two positions for loading rollers as each position must be a maximum length of 6 m. For this particular task, a conceptual design for a prismatic structure is formed Figure 3.

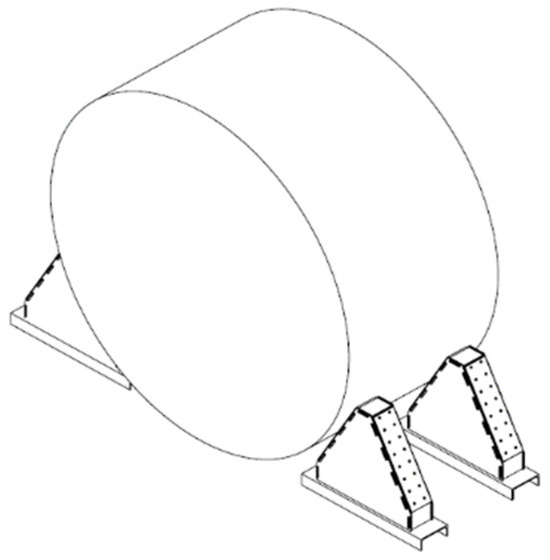
Figure 3. Conceptual design.

The next stage of the methodology is the determination of the loads acting on the securing structure during transportation. This is a fundamental stage in the design process. Dynamic driving conditions, such as acceleration, braking, and cornering, as well as external factors, such as vibrations from the road surface and weathering, generate forces that can compromise the stability of the cylindrical rollers.

Loads are classified into two types: static and dynamic loads [21].

Static loads include the vertical forces due to the self-weight of the rollers and the gravitational acceleration, g = 9.81 m/s²:

$$F_{\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{c}}=m·g$$

(1)

where m is the mass of the pulley and g is the gravitational acceleration.

Dynamic loads arise from changes in vehicle motion and are calculated using dynamic load factors, c_x and c_z, defined in EN 12195-1:2010 according to EN 15551 and UIC 530 [3,5,6].

Longitudinal forces, along the axis of motion, are calculated using Formula (2):

$$F_{\mathrm{x}}=m·c_x·g$$

(2)

where the coefficient c_x ranges from 0.3 to 0.5, the recommended values according to EN 15551 for railway freight wagons. We assume 0.4.

The transverse forces are the sum of the centrifugal forces acting when moving in a turn and the forces generated by natural phenomena, specifically wind. Centrifugal forces are calculated by Formula (3):

$$F_{\mathrm{c}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{f}\mathrm{u}\mathrm{g}\mathrm{a}\mathrm{l}}={\displaystyle \frac{m·v^2}{R}}$$

(3)

where:

• m—mass of the load;
• $v^2$—travel speed depends on the standards of the specific country. For Europe, the maximum speed for freight is 120 km/h, regulated in EN 14363. In particular, the standard in Bulgaria limits the speed to 100 km/h, regulated in the Bulgarian Regulation H-7 for railway infrastructure.
• R—radius of the bend. There is no standard norm, but based on the analysis of UIC 606-1 considering the conditions for the minimum radius of the bend, we assume an average value of 500 m.

Wind force is calculated by Formula (4):

$$F_{wind}=0.5·\rho ·V_{wind}·C_d·A$$

(4)

where:

• ρ—Air density;
• V_wind—Wind speed;
• C_d—Coefficient of aerodynamic drag;
• A—Design area.

A common transverse force appears to be the equilibrium of the two (5):

$$F_y=F_{\mathrm{c}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{f}\mathrm{u}\mathrm{g}\mathrm{a}\mathrm{l}}+F_{wind}$$

(5)

Vertical dynamic forces are the forces associated with the vibrations caused by the roughness of the railway infrastructure. These forces can be calculated by Formula (6):

$$F_z=m·c_z+g$$

(6)

where c_z is the value and reaches up to 0.15 when going over bumps.

On the basis of the described steps for the calculation of the loads, the input data and the assumed coefficients and additional parameters are: travel speed 120 km/h, turning radius 500 m, and wind speed 250 km/h [22], the result of which is shown in Table 1.

Table 1. Results of load calculations.

Load Type	Value (kN)
Static	294.3
Lengthwise (Fx)	117.7
Crosswise (Fy)	76.0
Total dynamic	193.7
Vertical	44.1

The third stage of the methodology involves the verification of the conceptual design based on the resulting loads through computer modeling in the Ansys Workbench engineering product environment. A 3D finite element model using solid elements was constructed for the strength analysis. The finite element size was varied, with a maximum size of 60 mm for the general areas of the structure and a minimum size of 5 mm in the areas of contact between the structure and the coils. Standard finite element quality requirements have been met, and solution convergence has been verified. Appropriate boundary conditions have been applied to ensure adequate performance in the service of the structure. Fixed supports were defined in the connection areas with the main bearing system, limiting the displacements in all directions. The loads to which the structure is subjected are presented in Table 1. The following three verification scenarios have been developed (Table 2):

Table 2. Conditions for the study options.

Designation	I. Vertical Static Loads
VLC1	Mass of the roller–294.3 kN
Designation	II. Combined loads
CHVLC1	Roller mass 294.3 kN + Static force of 76 kN
CHVLC2	Mass of the roller 294.3 kN + Static force of 117.7 kN

For each of the scenarios, boundary conditions are set: related to the material characteristic, number of finite elements and nodes between them, and factor of safety. The specific values are given in Table 3.

Table 3. Boundary conditions.

Characteristic of material	S355J2 according EN 10025 [2]: Remin = 355 N/mm2 and Rm ≥ 470 N/mm2 (for thickness > 3 дo ≤ 16 mm) Remin = 345 N/mm2 and Rm = 470 N/mm2 (for thickness > 16 дo ≤ 40 mm)
Number of end items	239,854
Number of nodes	567,463

The results of the simulations performed under the first option are systematized in Table 4 and visualized in Figure 3 and Figure 4.

Table 4. Option 1 test results.

Mode HLC2
Parameter	Value
Material	S355J2 according EN 10025
Permissible value of stresses	σzul = Re = 355 MPa
Max. value of calculated stresses	σMises = 292.8 MPa

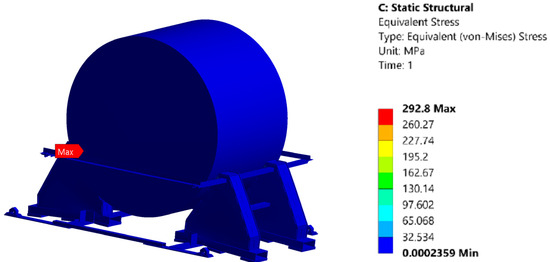
Figure 4. Finite element analysis of securing structure under vertical static load: von Mises stress distribution.

The results of the simulations performed under the first option are systematized in Table 5 and visualized in Figure 5 and Figure 6.

Table 5. Option 2 test results.

Mode CHVLC1
Parameter	Value
Material	S355J2 according EN 10025
Permissible value of stresses	σzul = Re = 355 MPa
Max. value of calculated stresses	σMises = 299.24 MPa

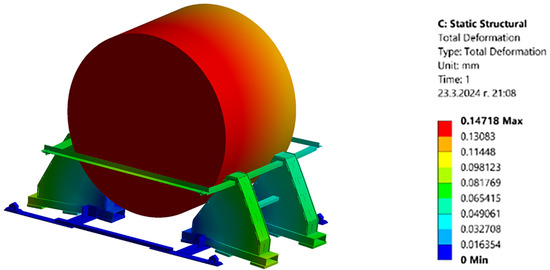
Figure 5. Finite element analysis of securing structure under vertical static load: total deformation distribution.

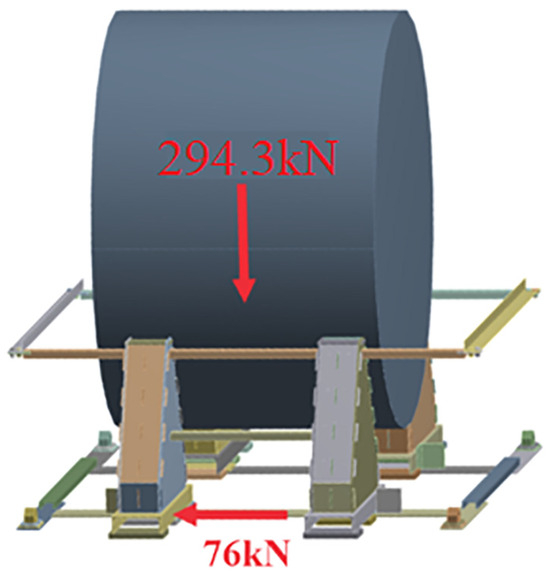
Figure 6. Loading scheme of the securing structure under vertical and transverse forces.

The results of the simulations performed under the first option are systematized in Table 6 and visualized in Figure 7 and Figure 8.

Table 6. Option 3 test results.

Mode CHVLC2
Parameter	Value
Material	S355J2 according EN 10025
Permissible value of stresses	σzul = Re = 355 MPa
Max. value of calculated stresses	σMises = 220.32 MPa

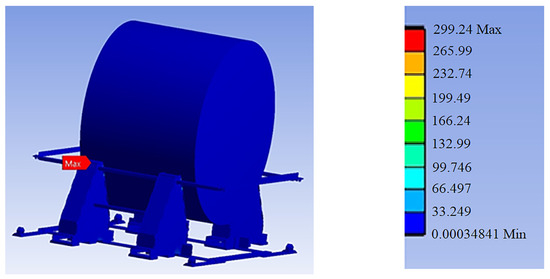
Figure 7. Finite element analysis of securing structure under combined vertical and transverse loads: von Mises stress distribution.

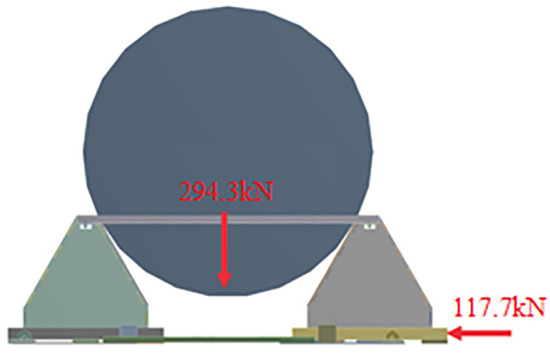
Figure 8. Loading scheme of the securing structure under vertical and axial forces.

Figure 9 shows the result of a finite element analysis (FEM) of the securing structure for the cylindrical load under combined loads.

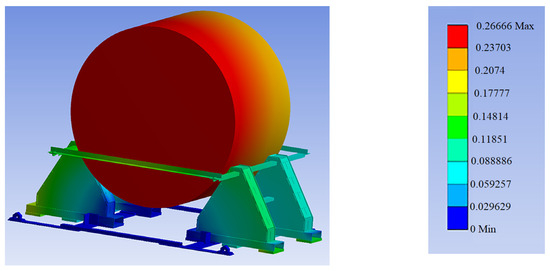
Figure 9. Finite element analysis of securing structure under combined vertical and transverse loads: total deformation distribution.

The studies carried out show that the proposed structure will withstand the expected load. This stage in the methodology is the final one. In the event that the analysis does not confirm that the structure will carry the load, it is necessary to go back to the conceptual design and change the thicknesses of the structural components.

3. Conclusions

The developed methodology presents a structured approach to the design and verification of securing structures for the transport of cylindrical roller loads by rail. It integrates theoretical postulations, standardized norms, and numerical modeling, thus providing a high degree of reliability in the assessment of structural security.

The analysis of acting loads takes into account both static components resulting from the dead weight of the load and dynamic effects, including longitudinal, transverse, and vertical forces due to accelerations, bends, vibrations, and atmospheric conditions. The assumptions used and the parameters assumed (speed, turning radius, wind force) correspond to real operating conditions according to European and national regulations (EN 14363, Eurocode 1, Regulation H-7, etc.).

Numerical simulations implemented in Ansys Workbench allow detailed verification of the stress state of the structure under different loading scenarios. The results obtained show that in all cases considered, the maximum values of the equivalent (von Mises) stresses remain below the allowable limit for the S355J2 material used, including under combined loads. This confirms that the structure meets the strength and safety criteria without any local or global failure risks.

The design solution is in accordance with the geometrical limitations of the transport rolling stock (freight wagons type Smmps), as well as with the requirements for rational load distribution and maximum filling of the loading area.

The possibility of stable positioning of two roller units within 6 m modules is ensured, minimizing the risk of unwanted shifting or overturning during movement.

The flexibility of the proposed methodology allows its easy adaptation to different types of cylindrical loads with varying dimensions, mass, and transport conditions. At the same time, it can be used as a basis for standardizing engineering practices in the field of transport securing systems, as well as a starting point for developing new designs based on numerical simulations and engineering optimization.

In conclusion, this research contributes to improving the safety and efficiency of specialized cargo transportation by applying an interdisciplinary engineering analysis approach combining classical methods with advanced virtual design and verification tools.