Thermal and Structural Analysis of Gasoline Engine Piston at Different Boost Pressures †
Abstract
1. Introduction
2. Materials and Methods
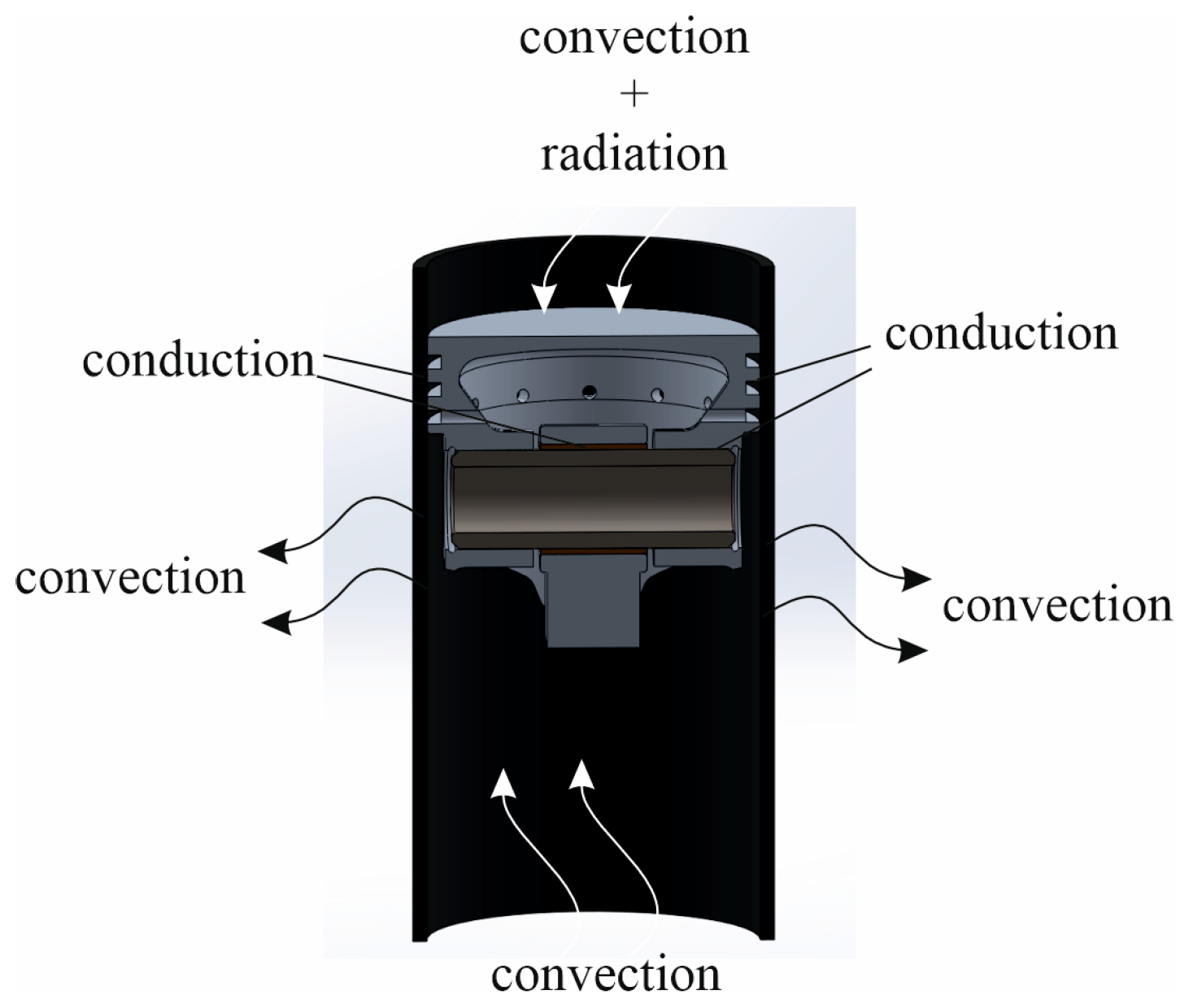
2.1. Thermal Boundary Conditions
2.2. Static Boundary Conditions
2.3. Material Properties
3. Results and Discussion
3.1. Results of Thermal Calculation at ICE
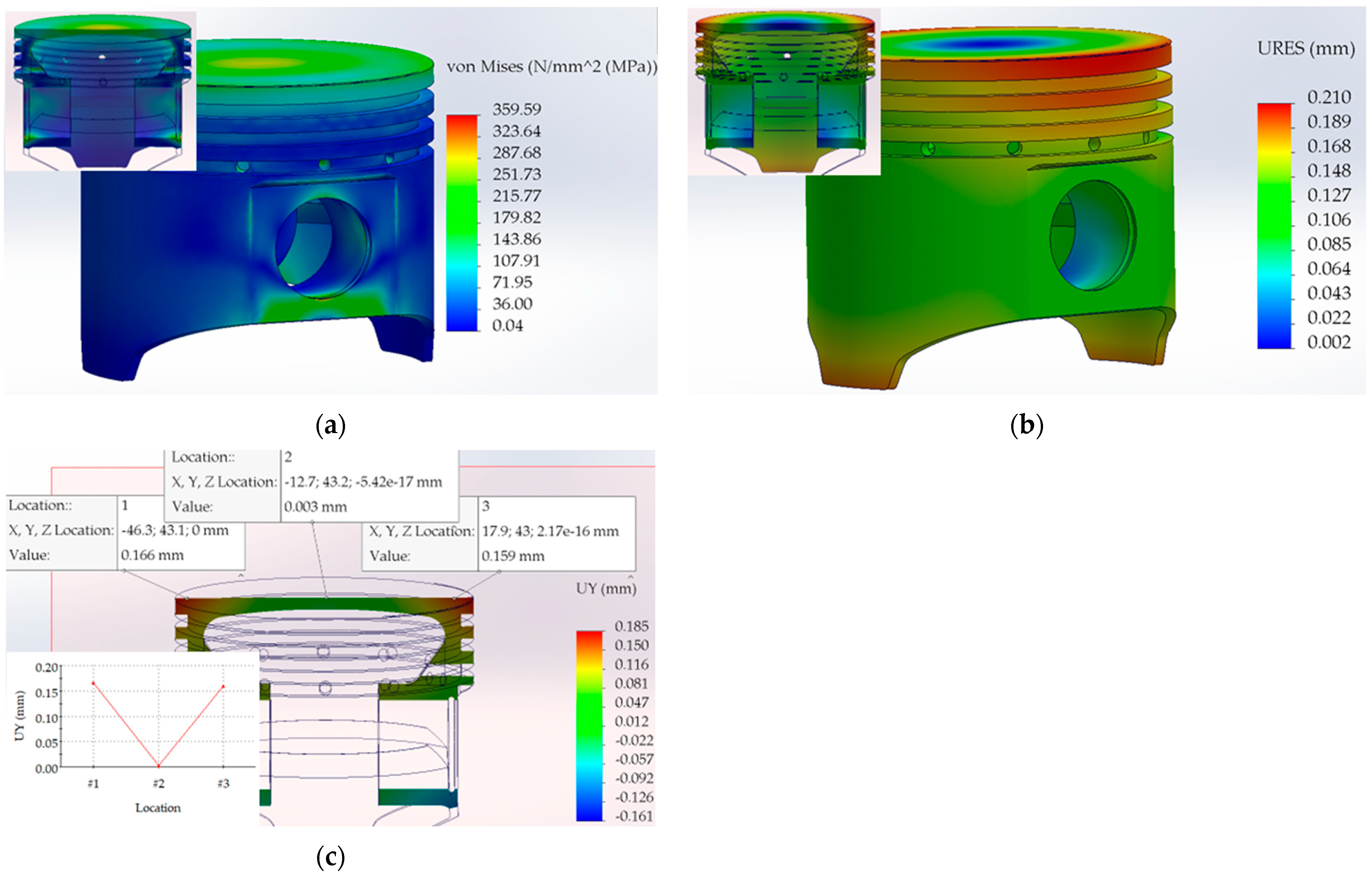
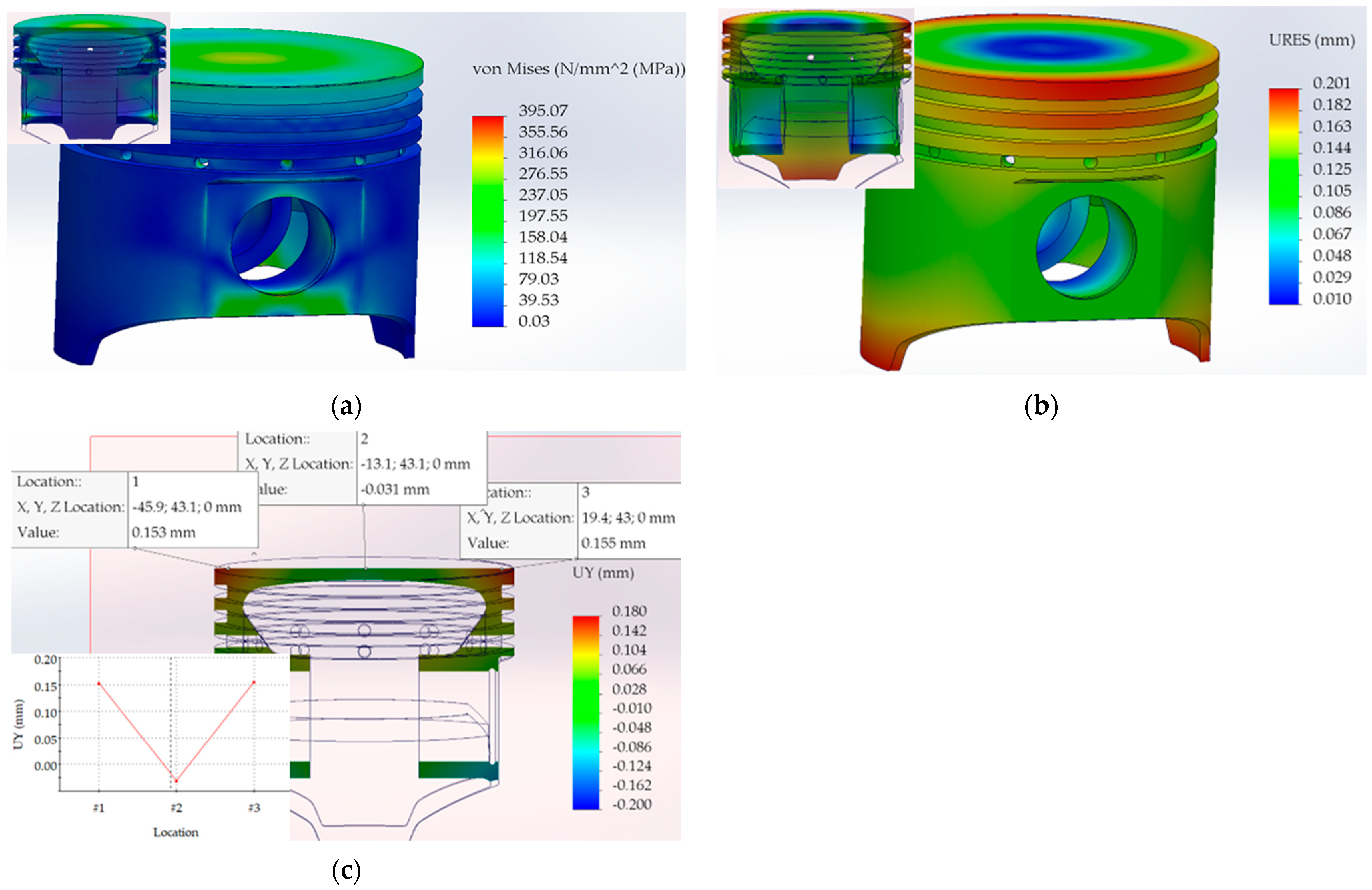
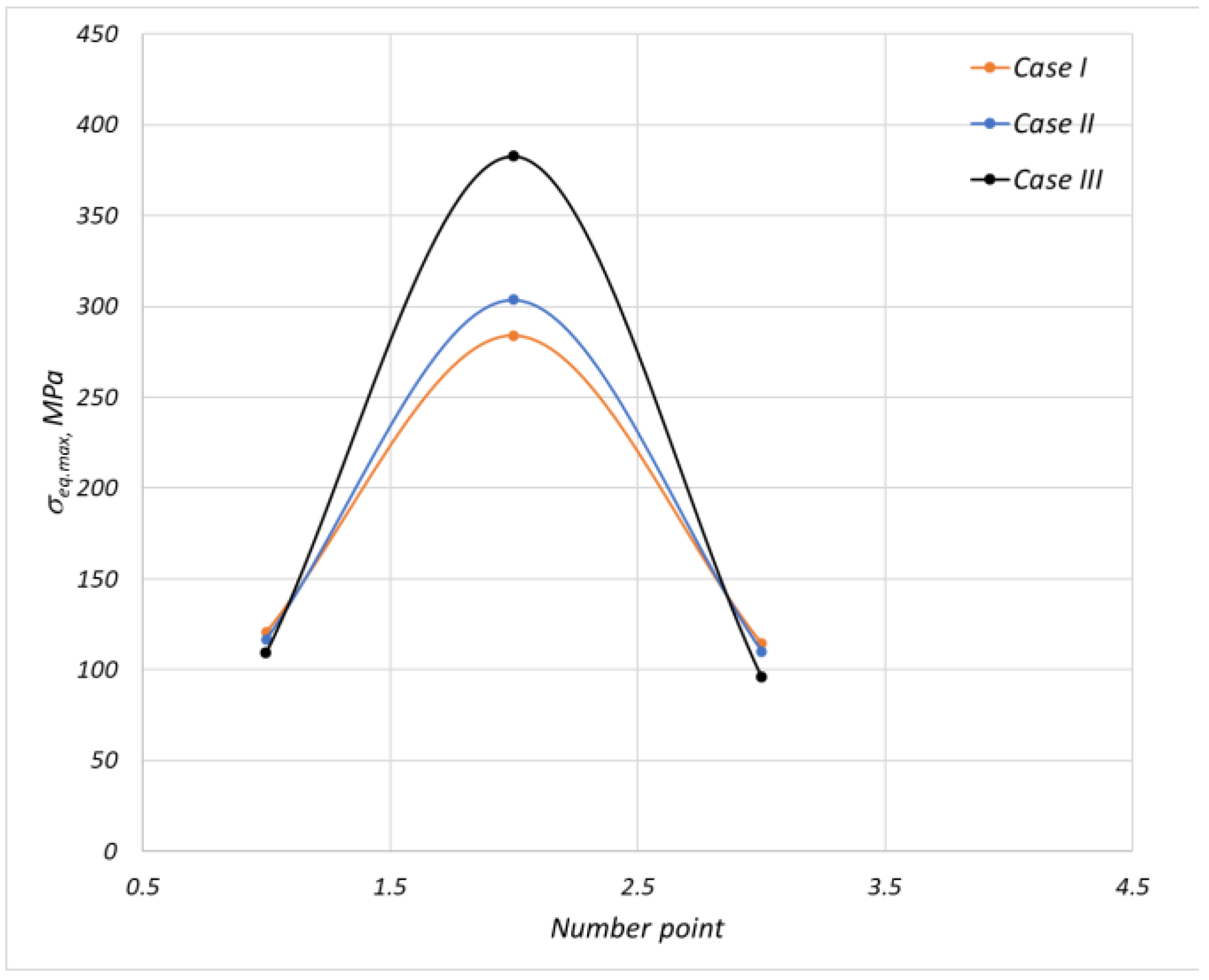
3.2. FEA Results
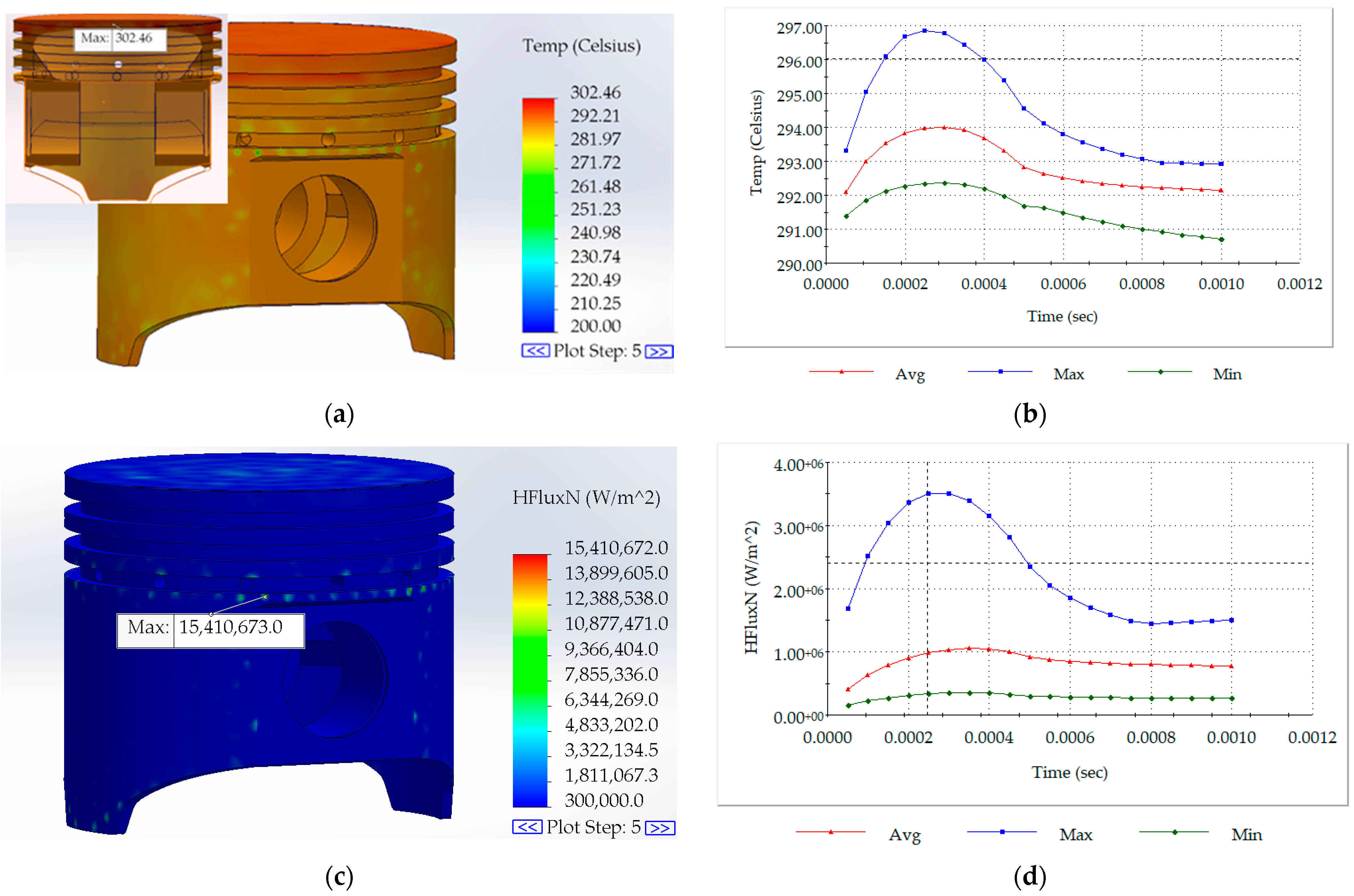
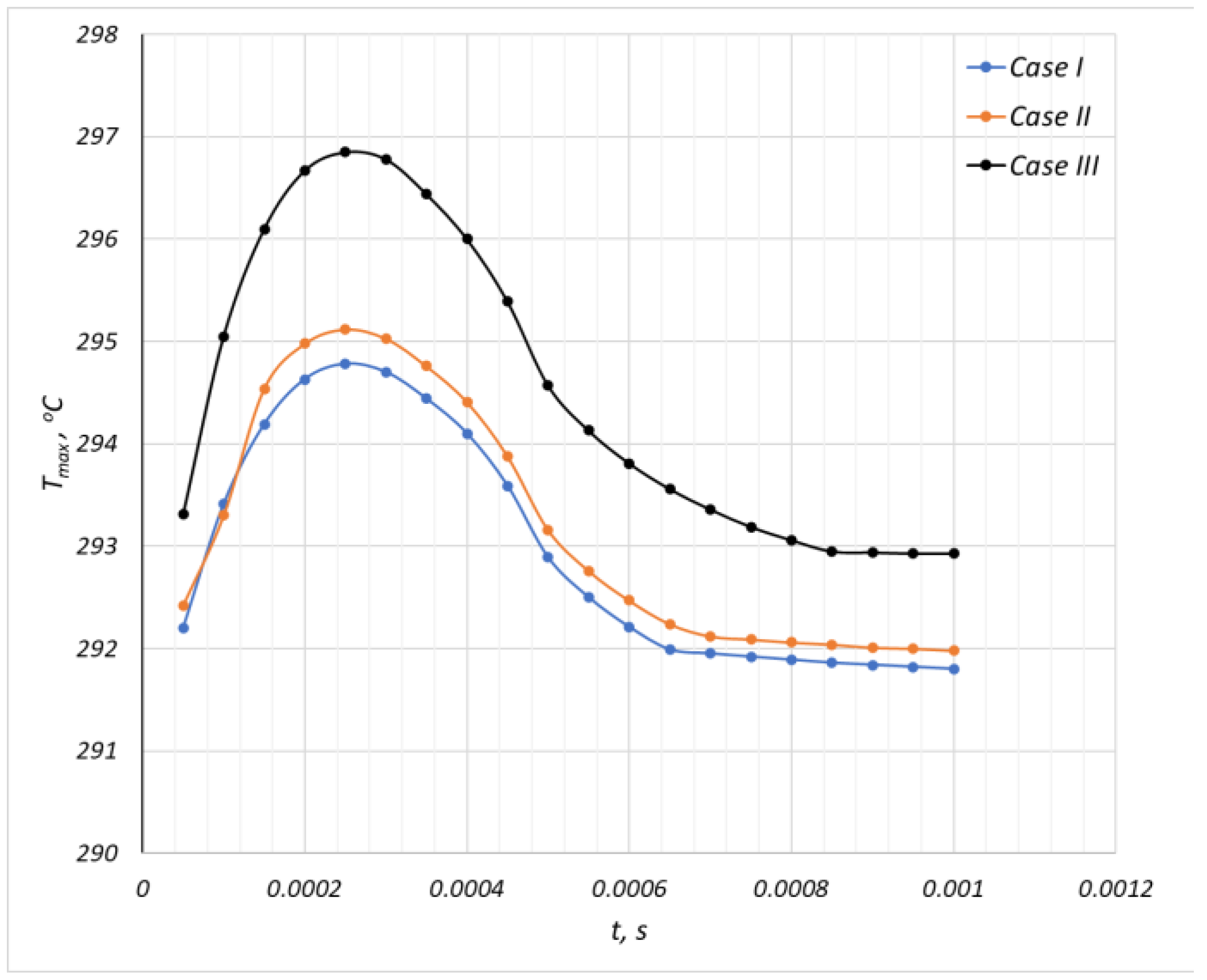
3.2.1. Transient Thermal Analysis Results
3.2.2. Structural Analysis Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Singh, A.R.; Sharma, P.K. Design, Analysis and Optimization of Three Aluminium Piston Alloys Using FEA. Int. J. Eng. Res. Appl. 2014, 4, 94–102. [Google Scholar]
- Kumar, A.; Gangrade, K. Design Thermal and Structural Analysis of Piston with Different Materials Using Finite Element Analysis. Int. J. Res. Publ. Rev. 2022, 3, 3814–3819. [Google Scholar]
- Zhaoju, Q.; Yingsong, L.; Zhenzhong, Y.; Junfa, D.; Lijun, W. Diesel engine piston thermo-mechanical coupling simulation and multidisciplinary design optimization. Case Stud. Therm. Eng. 2019, 15, 100527. [Google Scholar] [CrossRef]
- Dagar, N.; Sharma, R.; Rinawa, M.L.; Gupta, S.; Chaudhary, V.; Gupta, P. Design and analysis of piston using aluminum alloy and composites in SolidWorks and Ansys. Mater. Today Proc. 2022, 67, 784–791. [Google Scholar] [CrossRef]
- Valkov, G.; Nikolov, V. Analysis of stresses and deformations in the chassis of terrain forklifts. IOP Conf. Ser. Mater. Sci. Eng. 2020, 878, 012038. [Google Scholar] [CrossRef]
- Ijagbemi, C.O.; Oladapo, B.I.; Campbell, H.M.; Ijagbemi, C.O. Design and simulation of fatigue analysis for a vehicle suspension system (VSS) and its effect on global warming. Procedia Eng. 2016, 159, 124–132. [Google Scholar] [CrossRef]
- Georgiev, Z.; Kunchev, L. Study of the stresses in the front suspension components of a car passing over speed breakers. IOP Conf. Ser. Mater. Sci. Eng. 2019, 664, 012012. [Google Scholar] [CrossRef]
- Cerit, M.; Coban, M. Temperature and thermal stress analyses of a ceramic-coated aluminum alloy piston used in a diesel engine. Int. J. Therm. Sci. 2014, 77, 11–18. [Google Scholar] [CrossRef]
- Buyukkaya, E. Thermal analysis of functionally graded coating AlSi alloy and steel pistons. Surf. Coat. Technol. J. 2008, 202, 3856–3865. [Google Scholar] [CrossRef]
- Ahmed, A.; Wahab, M.S.; Raus, A.A.; Kamarudin, K.; Bakhsh, Q.; Ali, D. Thermal Effect on the Automobile Piston: A Review. Indian J. Sci. Technol. 2016, 9. [Google Scholar] [CrossRef][Green Version]
- Muhammad, A.; Haruna, S.I. Finite element analysis of the heat transfer in a piston. J. Mod. Manuf. Syst. Technol. 2020, 4, 45–51. Available online: https://www.researchgate.net/publication/340244705 (accessed on 28 April 2025). [CrossRef]
- Esfahanian, V.; Javaheri, A.; Ghaffarpour, M. Thermal analysis of an SI engine piston using different combustion boundary condition treatments. Appl. Ther. Eng. J. 2006, 26, 277–287. [Google Scholar] [CrossRef]
- Borman, G.; Nishiwaki, K. Internal-combustion engine heat transfer. Prog. Energy Combust. Sci. J. 1987, 13, 1–46. [Google Scholar] [CrossRef]
- Yue, Z.; Reitz, R. Numerical investigation of radiative heat transfer in internal combustion engines. Appl. Energy J. 2019, 235, 147–163. [Google Scholar] [CrossRef]
- Subbaraoa, R.; Gupta, S. Thermal and structural analyses of an internal combustion engine piston with suitable different super alloys. Mater. Today Proc. 2020, 22, 2950–2956. [Google Scholar] [CrossRef]
- Kadikyanov, G. Research temperature gradient of aluminum piston with coatings. In Proceedings of the Trans&MOTAUTO’09, Sunny Beach, Bulgaria, 17–19 September 2009; pp. 95–97, ISBN 1313-5031. [Google Scholar]
- Bojadjiev, K.; Traikov, L. Construction, Design and Calculation of ICE.; Technica: Sofia, Bulgaria, 1990. [Google Scholar]
- Heywood, J. Internal Combustion Engine Fundamentals; McGraw-Hill Bock Company: Singapore, 1998. [Google Scholar]
- Available online: https://www.simscale.com/docs/tutorials/heat-transfer-engine-piston/ (accessed on 28 April 2025).
- Available online: https://help.solidworks.com/2023/english/solidworks/cworks/c_Mechanisms_of_Heat_Transfer.htm (accessed on 28 April 2025).
- Soyhan, H.S.; Yasar, H.; Walmsley, H.; Head, B.; Kalghatgi, G.T.; Sorusbay, C. Evaluation of heat transfer correlations for HCCI engine modelling. Appl. Therm. Eng. 2008, 29, 541. Available online: https://hal.science/hal-00498971 (accessed on 28 April 2025). [CrossRef]
- Taneva, S.; Ambarev, K. Thermal analysis of a piston from an internal combustion gasoline engine. J. BulCToMM Mech. Mach. 2025, 133, 85–92. [Google Scholar]





| Properties | Piston | Cylinder | Piston Pin | Piston Pin Bearing | Connecting Rod |
|---|---|---|---|---|---|
| Density (kg/m3) | 2760 | 7100 | 7850 | 7400 | 2810 |
| Thermal conductivity (W/(m.K)) | 146 | 75 | 44,5 | 56 | 130 |
| Expansion coefficient (/K) | 2.2 × 10−5 | 1.1 × 10−5 | 1.23 × 10−5 | 1.7 × 10−5 | 2.36 × 10−5 |
| Elastic modulus (N/mm2) | 74,500 | 120,000 | 205,000 | 110,000 | 72,000 |
| Specific heat (J/(kg.K)) | 875 | 450 | 475 | 380 | 960 |
| Poisson’s ratio | 0.33 | 0.31 | 0.285 | 0.3 | 0.33 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ambarev, K.; Taneva, S. Thermal and Structural Analysis of Gasoline Engine Piston at Different Boost Pressures. Eng. Proc. 2025, 100, 38. https://doi.org/10.3390/engproc2025100038
Ambarev K, Taneva S. Thermal and Structural Analysis of Gasoline Engine Piston at Different Boost Pressures. Engineering Proceedings. 2025; 100(1):38. https://doi.org/10.3390/engproc2025100038
Chicago/Turabian StyleAmbarev, Krasimir, and Stiliyana Taneva. 2025. "Thermal and Structural Analysis of Gasoline Engine Piston at Different Boost Pressures" Engineering Proceedings 100, no. 1: 38. https://doi.org/10.3390/engproc2025100038
APA StyleAmbarev, K., & Taneva, S. (2025). Thermal and Structural Analysis of Gasoline Engine Piston at Different Boost Pressures. Engineering Proceedings, 100(1), 38. https://doi.org/10.3390/engproc2025100038





