A Numerical Parametric Study of the Dynamic Factor in the Rope of a DC-Motor-Driven Hoisting Mechanism ^†

Abstract

This paper presents a numerical parametric study of a dynamic lumped-parameter model of a hoisting mechanism driven by a DC electric motor. The analysis focuses on two operating scenarios: hoisting with an initially tight rope and hoisting with an initially slack rope. The model considers the inertial, elastic, and damping characteristics of the mechanical system, as well as the motor’s dynamic behavior. Systematic simulations are used to evaluate the influence of key design parameters on the rope’s dynamic factor. Sensitivity analysis is carried out by varying each parameter within a ±20% range, and Monte Carlo simulations are employed to compute Pearson correlation coefficients and perform multiple linear regression. The results indicate that the slack rope scenario produces significantly higher peak dynamic loads than those observed in the tight rope scenario, emphasizing its importance for structural sizing and safety. The findings enhance our understanding of parameter influence and support more robust hoisting system design in transient conditions.

1. Introduction

Hoisting mechanisms are parts of lifting and material handling machines. Their elements experience significant dynamic loads during operation, particularly during transient modes. These loads are generated by the operation of the drive motor and the elasticity of components such as shafts, couplings, ropes, and clearances in the kinematic chain. Although the dominant load in hoisting mechanisms is static and is caused by the weight of the load, the uneven movement of heavy masses, combined with elastic elements, turns dynamic impacts into a determining factor for the system’s reliability. Dynamic processes are analyzed by many classic studies using analytical, numerical, and experimental methods [1,2,3,4,5,6].

Modern researchers continue to pay attention to the dynamic modeling of hoisting mechanisms. The monograph [7] focuses on multiparameter studies of crane dynamics, developing and validating precise mathematical models of overhead cranes, and determining their dynamic characteristics. The authors of [8] use models with three degrees of freedom to find an optimal law of motion which reduces dynamic loads through smooth motor speed control. A similar method is also applied in [9], where the motion of a model with three degrees of freedom is studied under a sinusoidal law. A detailed dynamic model of a container crane is created in [10] that considers the gearbox, boom, and rope’s elasticity, and highlights the substantial impact of trapezoidal motion laws on vibrations. A multi-body dynamic model is used in [11] to study the dynamic behavior of a polar crane’s hoisting mechanism under emergency conditions. In emergency stopping by a mechanical brake, in [12], a mathematical model developed using Hamilton’s principle was investigated, and facts useful for design and exploitation practice were established.

The ropes, which are among the most heavily loaded elements of the hoisting mechanisms, require special attention. Acceleration, sudden stops, impacts, vibrations, and load swinging cause them to take on additional loads. Technical and design parameters determine the applied laws of acceleration and speed, which ultimately affect the loads in the ropes. To ensure the safety and reliability of hoisting mechanisms, it is important to study the dynamic factor in the rope. The dynamic factor is the ratio of the rope’s force during the mechanism’s operation to its static force. According to the European standard [13], the dynamic factor should be determined based on the elasticity class of the crane’s metal structure and the speed of hoisting the load. The paper [14] and the extensive monograph [15] compare two models of the steel rope when driving the mechanism by an asynchronous motor with a wound rotor. The findings suggest that the Bouc-Wen hysteresis model offers a precise estimation of the maximum dynamic factor. However, determining the numerical values of the nine constants requires specialized methods [16,17]. An essential aspect of these studies is that a dynamic model of an asynchronous motor was used, allowing for more accurate transient modeling. In paper [18], the dynamics of a bridge crane with a truss metal structure, an asynchronous motor, and a two-stage planetary gear are studied, and a dynamic factor of about 1.93 is obtained. Another interesting study is [19], which considers vibrations caused by dynamic loading during load hoisting with a bridge crane. The finite element method and discrete mass models (2 and 4 degrees of freedom) were compared, and it was determined that the 4-degree-of-freedom model provides more accurate results. The dynamic factor of 107 cranes is analyzed using a phenomenological model with 4 degrees of freedom, and the results are presented in [20]. The authors concluded that the results for the dynamic factor are not more than 20% different from the normative values listed in [13]. A mathematical model of a boom crane has been proposed by the authors of [21], and simulations have revealed severe dynamic overloads when hoisting loads. This study suggests that the use of only design measures to limit dynamic phenomena does not always yield sufficiently effective results. Active motor control through a feedback system implementing smooth motion laws is a practical method for reducing the dynamic factor of the rope. By using this approach, dynamic overloads are reduced from over 25% to about 5% in [22].

Despite the many studies available, these aspects can be noted, which have not been given enough attention: (1) The models do not consider the influence of the characteristics of the drive motor on the dynamic characteristics of the mechanism; (2) The influence of various system parameters on the maximum value of the dynamic factor is not thoroughly investigated. This paper aims to develop a mathematical model of the hoisting mechanism for estimating the maximum dynamic factor in the rope, which considers the inertial, damping, and elastic characteristics of the mechanical system, as well as the specific parameters of the driving DC motor. Through an extensive numerical parametric study, the key design and technical factors with the most decisive influence on the dynamic factor in the rope will be identified, which will improve the design and operational characteristics of the hoisting equipment.

2. Materials and Methods

2.1. Dynamic Model of the Hoisting Mechanism

The subject of the research is a hoisting system with a kinematic chain made up of a DC electric motor connected through an elastic coupling to the input shaft of a two-stage gearbox. The gearbox’s output shaft drives a rope drum, onto which the rope of a paired double-sheave pulley block (providing a 2:1 mechanical advantage) is wound. The load is suspended from this pulley block. The dynamic model of the hoisting mechanism consists of discrete masses and is depicted in Figure 1.

The following elements are included: pos. 1—motor rotor and the rotating elements connected to it with equivalent mass moment of inertia J₁; pos. 2, pos. 3, pos. 4, and pos. 5—gears of the two-stage gearbox with mass moments of inertia J₂, J₃, J₄, and J₅; pos. 6—drum with radius R and mass moment of inertia J₆; pos. 7—lever system with a ratio of arms i₃ = 2, conditionally representing the paired double-sheave pulley block with a total stiffness coefficient c₅ and a damping coefficient b₅; pos. 8—the metal structure of the crane with equivalent mass m₁, stiffness coefficient c₄, and damping coefficient b₄; pos. 9—payload with mass m₂. By c₁ and b₁ are denoted, respectively, the stiffness coefficient of the elastic coupling and the damping coefficient, c₂ and b₂ are the stiffness and damping coefficients of the shaft connecting gears 3 and 4, and c₃ and b₃ are the stiffness and damping coefficients of the output shaft of the gearbox. The gear ratios of the first and second stages of the gearbox are i₁ and i₂, respectively. L₀ indicates the initial length of the rope. The damping coefficients b₆ and b₇ model viscous drag torque, representing energy losses in gears.

2.2. Mathematical Model of the Hoisting Mechanism

Six degrees of freedom are present in the lumped-parameter dynamic model developed, and the generalized coordinate vector given describes the linear displacements and angular rotations of its elements.

$$q={\left[\begin{array}{cccccc}{\phi }_1& {\phi }_2& {\phi }_5& {\phi }_6& y_1& y_2\end{array}\right]}^T$$

(1)

By applying the Lagrange equations of the second kind [14,15], a system of ordinary differential equations is generated that describes the motions in generalized coordinates:

$$M\ddot{q}+B\dot{q}+Cq+G=Q$$

(2)

where the following notations are introduced: $\dot{q}$ and $\ddot{q}$ are the vectors of the generalized velocities and accelerations, respectively; C is the stiffness matrix of the mechanical system with the following elements: $C_{11}=c_1$, $C_{12}=C_{21}=-c_1$, $C_{22}=c_1+c_2/i_1^2$, $C_{23}=C_{32}=-c_2{i}_2/i_1$, $C_{33}=c_3+c_2{i}_2^2$, $C_{34}=C_{43}=-c_3$, $C_{44}=c_3+c_5{R}^2/i_3^2$, $C_{45}=C_{54}=c_{5}R/i_3$, $C_{46}=C_{64}=-c_{5}R/i_3$, $C_{56}=C_{65}=-c_5$, $C_{55}=c_4+c_5$, and $C_{66}=c_5$. The rest of the elements of the matrix are 0. B is the damping matrix, and its elements are the same as the corresponding elements of the matrix C after the formal replacement of the symbol “c” with the symbol “b”, except for the elements $B_{22}=b_1+\left(b_2+b_6\right)/i_1^2$ and $B_{33}=b_3+b_7+b_2{i}_2^2$; G is a vector containing the gravity forces:

$$G={\left[\begin{array}{cccccc}0& 0& 0& 0& m_{1}g& m_{2}g\end{array}\right]}^T$$

(3)

M is the inertia matrix of the system:

$$M=diag\left(J_1, J_2+J_3{i}_1^{-2}, J_5+J_4{i}_2^2, J_6, m_1, m_2\right)$$

(4)

Q is the vector of generalized forces:

$$Q={\left[\begin{array}{cccccc}M& 0& 0& 0& 0& 0\end{array}\right]}^T$$

(5)

where M denotes the torque of the motor. In this study, a DC electric motor is used, the dynamic model of which is as follows [23,24]:

$$T_E\dot{M}+M=a-b{\dot{\phi }}_1$$

(6)

where T_E denotes the electromechanical time constant of the electric motor, and a and b are coefficients determining its characteristics.

The minimum potential energy theorem [25] is used to obtain the initial conditions for generalized coordinates in the presence of a suspended payload:

$$\begin{gathered} {\phi }_1\left(0\right)=0, {\phi }_2\left(0\right)=-{\displaystyle \frac{m_{2}gR}{c_1{i}_1{i}_2{i}_3}}, {\phi }_5\left(0\right)=-{\displaystyle \frac{m_{2}gR\left(c_2+c_1{i}_1^2\right)}{c_1{c}_2{i}_1^2{i}_2^2{i}_3}}, \\ {\phi }_6\left(0\right)=-{\displaystyle \frac{m_{2}gR\left(c_1{c}_3{i}_1^2+c_2\left(c_3+c_1{i}_1^2{i}_2^2\right)\right)}{c_1{c}_2{c}_3{i}_1^2{i}_2^2{i}_3}}, y_1\left(0\right)=-{\displaystyle \frac{\left(m_1+m_2\right)g}{c_4}}, \\ {y}_2\left(0\right)=-{\displaystyle \frac{\left(m_1+m_2\right)g}{c_4}}-m_{2}g\left({\displaystyle \frac{1}{c_5}}+{\displaystyle \frac{R^2\left(c_2{c}_3+c_1{c}_3{i}_1^2+c_1{c}_2{i}_1^2{i}_2^2\right)}{c_1{c}_2{c}_3{i}_1^2{i}_2^2{i}_3^2}}\right); \end{gathered}$$

The initial conditions for the generalized velocities are zero values.

3. Results

Several numerical experiments were carried out to analyze the system’s dynamic behavior and identify the highest values of the dynamic factor in the rope. By integrating the following system of differential equations, the numerical characteristics of the system were obtained:

$$\ddot{q}=M^{-1}\left(Q-B\dot{q}-Cq-G\right)$$

(7)

In (6), the DC motor’s rheostatic starting is simulated using coefficients a_i and b_i for the starting stages, as shown in

Table 1. Numerical values of the coefficients for rheostatic starting.

Stage, i	ai, Nm	bi, Nms	Angular Velocity Range of the Motor ${\dot{\mathit{\phi }}}_{\mathbf{1}}$, rad/s
1	150	0.955	[0, 24.58)
2	177.84	1.133	[24.58, 45.31)
3	210.86	1.343	[45.31, 62.8)
4	250	1.592	[62.8, 157]

.

The motor torque increases from 126.5 to 150 Nm during start-up.

Two typical scenarios of hoisting a payload have been studied numerically. The first scenario involves hoisting a hanging payload “from the air” by using a rope that is initially tight. During the entire period of movement, the payload’s mass remains constant at m₂. The second scenario involves lifting the payload with ropes that are initially slack and a payload on the ground. The hoisting of the payload starts when all the slack in the rope has been eliminated, and at this moment, the motor has already reached the steady state. Here, the mass m₂ is modeled by the following function:

$$m_2=IF t\le t* THEN m_2^{start} ELSE m_2^{final}$$

(8)

This function simulates starting the motor with slack ropes (at a small value of $m_2^{start}$) and changing the mass to the nominal value $m_2^{final}$ after a period t*, which is enough to take up the slack.

The rope is a complex element with nonlinear characteristics and complex physical behavior [26], but for small deformations and a linear model, it can be assumed that its stiffness coefficient c₅ and damping coefficient b₅ are determined by the following relationships [14,15,27]:

$$c_5={\displaystyle \frac{n{E}_{r}S}{L_0-y_2}}$$

(9)

$$b_5=2\xi \sqrt{c_5\left(m_2+m_r\right)}$$

(10)

$$m_r=n\rho S\left(L_0-y_2\right)$$

(11)

where n is the number of ropes on which the payload hangs, E_r is the elasticity modulus of the rope, S is the cross-section of the rope, L₀ is the initial length of the rope, $\xi$ is a dimensionless damping coefficient for steel ropes, m_r is the mass of the rope, and $\rho$ is the density of the steel.

The force in the rope F_r is calculated from the following:

$$F_r=c_5\left(R{\displaystyle \frac{{\phi }_6}{i_3}}+y_1-y_2\right)+b_5\left(R{\displaystyle \frac{{\dot{\phi }}_6}{i_3}}+{\dot{y}}_1-{\dot{y}}_2\right)$$

(12)

In the simulation model, through additional mathematical equations, it is considered that the rope works only in tension.

The dynamic factor in the rope K_d is defined as the ratio of the force in the rope (12) and the static force in the rope caused by the weight of the payload:

$$K_d={\displaystyle \frac{F_r}{\left(m_2+m_r\right)g}}$$

(13)

The following nominal parameter values were used in the simulation: m₁ = 5 × 10³ kg, $m_2^{start}=100 \mathrm{kg}$, $m_2^{final}=2.5\times {10}^3 \mathrm{kg}$, t* = 1.2 s, J₁ = 0.205 kgm², J₂ = J₄ = 1.22 × 10⁻³ kgm², J₃ = J₅ = 1.125 × 10⁻¹ kgm², J₆ = 10.2 kgm², c₁ = 12.5 × 10³ Nm/rad, c₂ = 123 × 10³ Nm/rad, c₃ = 508 × 10³ Nm/rad, c₄ = 4.8 × 10⁶ N/m, R = 0.25 m, g = 9.81 m/s², i₁ = 9.1, i₂ = 9.2, i₃ = 2, b₁ = 1.25 × 10³ Nms, b₂ = 2.5 × 10³ Nms, b₃ = 2.5 × 10³ Nms, b₄ = 2.5 × 10³ Ns/m, ξ = 0.07, E_r = 1.1 × 10¹¹ Pa, b₆ = b₇ = 1 Nms, L₀ = 10 m, n = 4, ρ = 7.85 × 10³ kg/m³, T_E = 0.02 s, and S = 1 × 10⁻⁴ m².

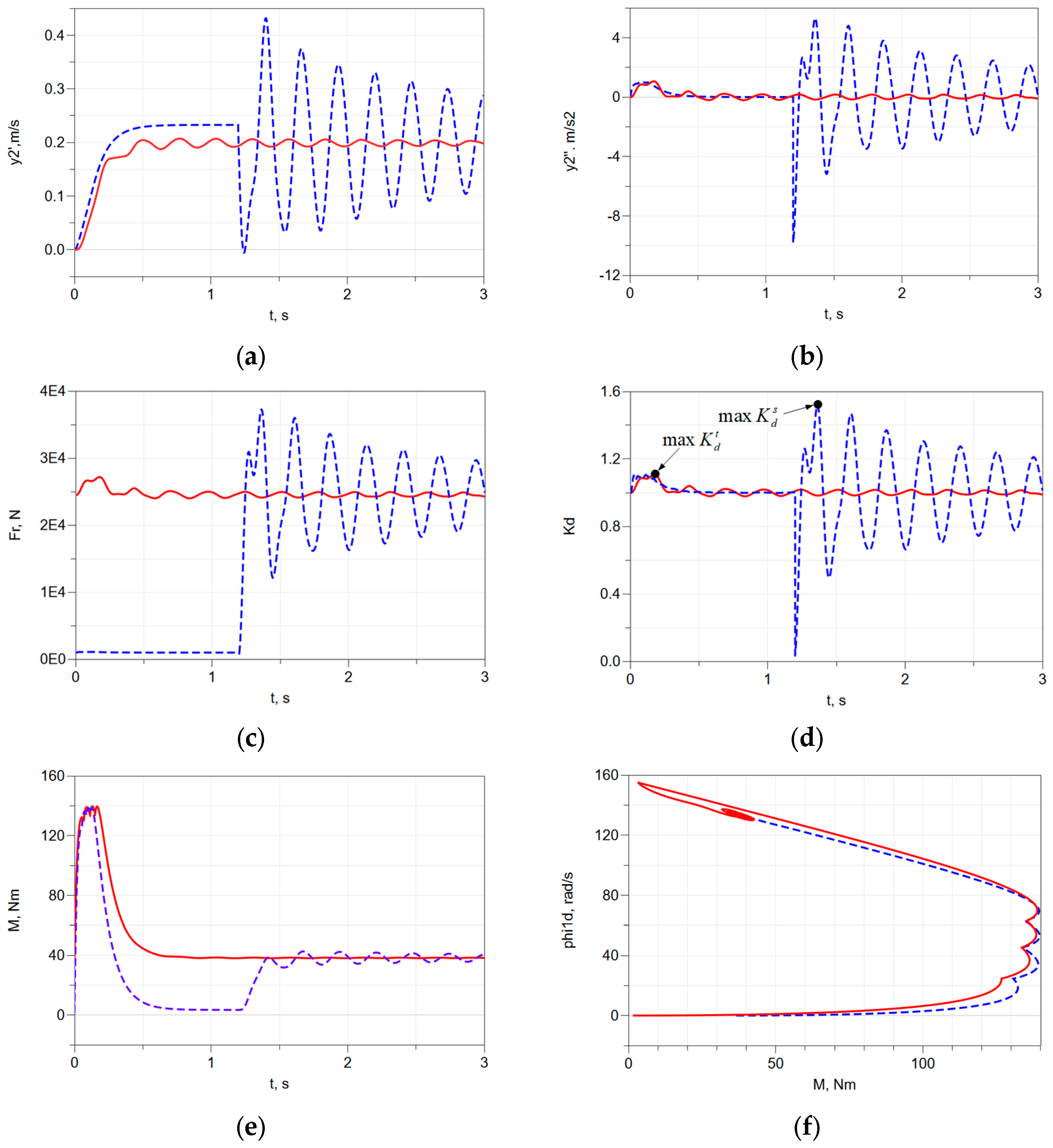
Figure 2 reveals some kinematic and force characteristics of the system through numerical analysis of differential equation (7) using nominal parameters.

A continuous red line is used to represent the characteristics of the tight rope scenario, while a dashed blue line is used to represent the characteristics of the slack rope scenario. The following characteristics are displayed: (1) Figure 2a—the linear velocities of the payload ${\dot{y}}_2$; (2) Figure 2b—the accelerations of the payload ${\ddot{y}}_2$; (3) Figure 2c—the force in the rope F_r; (4) Figure 2d—the dynamic factors for both scenarios, where $max{K}_d^s$ denotes the maximum value of the dynamic factor for the slack rope scenario, and $max{K}_d^t$ is used for the tight rope scenario; (5) Figure 2e—the DC motor torque; (6) Figure 2f—the torque-speed characteristic of the motor ${\dot{\phi }}_1=f\left(M\right)$. The characteristics of the slack rope scenario vary greatly, and the maximum dynamic factor is significantly greater than in the tight rope scenario.

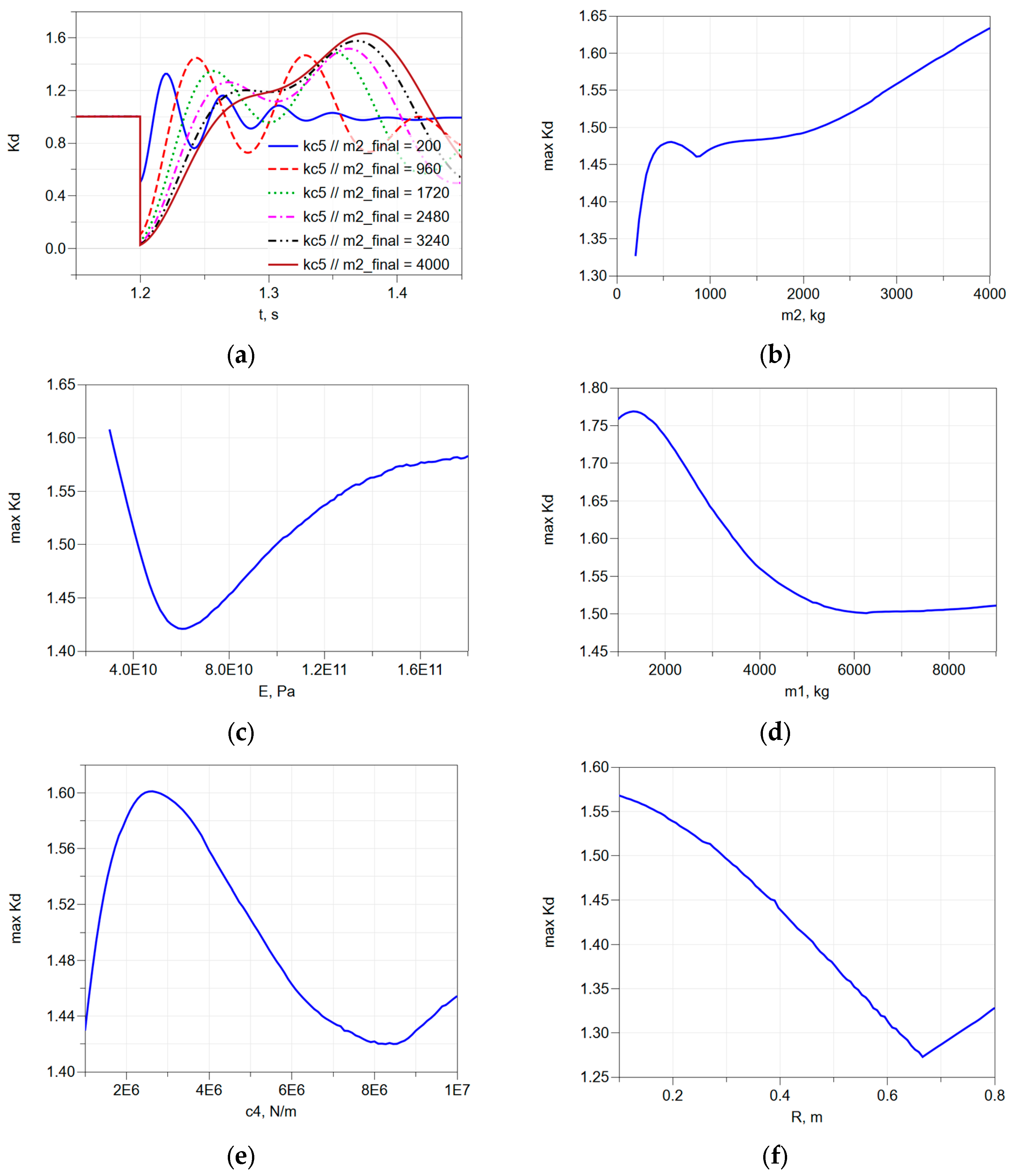
Parametric studies were carried out to determine the relationship between the maximum dynamic factor maxK_d and the system parameters, with parameters changing within specified limits.

Figure 3a displays graphs of the dynamic factor values over time for various payload masses m₂ in the scenario with a slack rope. It can be observed that for a small payload mass (200 kg), the maximum dynamic factor is reached during the first oscillation peak. At approximately 960 kg, the maximum values are nearly identical for the first and second oscillations. As the mass increases further, the second peak becomes dominant. This shift occurs because at lower masses, damping plays a stronger role than inertial forces, causing subsequent oscillations to diminish. Additionally, as the payload mass increases, the oscillation frequency decreases, contributing to this behavior. This leads to the fact that the function maxK_d = f(m₂) is thus highly nonlinear and exhibits a cusp, as shown in Figure 3b. Strong nonlinearity is also noticeable in the graphs of other parameters—maxK_d = f(E_r) is shown in Figure 3c, maxK_d = f(m₁) is shown in Figure 3d, maxK_d = f(c₄) is shown in Figure 3e, and maxK_d = f(R) is shown in Figure 3f. Studying and drawing unambiguous conclusions about maxK_d in a wide range of changes in system parameters is difficult due to these facts. For this reason, a parametric study of maxK_d was conducted using narrower intervals of change in the system parameters, specifically ±20% of the nominal value of the parameter. In these intervals, the dependencies are either linear or can be approximated with high accuracy by a linear function.

The results of the numerical experiments regarding the values of maxK_d ($max{K}_d^t$ for the tight rope scenario and $max{K}_d^s$ for the slack rope scenario) at the lower (P − 20%) and upper (P + 20%) limits of change in the system parameters are systematized in

Table 2. Ranges of the parameter changes in and obtained values of maxK_d for both scenarios.

Parameters	Nominal Value P	P − 20%	P + 20%	$\underset{\mathit{P}-\mathbf{20}\mathbf{\%}}{\mathit{m}\mathit{a}\mathit{x}{\mathit{K}}_{\mathit{d}}^{\mathit{t}}}$	$\underset{\mathit{P}\mathbf{+}\mathbf{20}\mathbf{\%}}{\mathit{m}\mathit{a}\mathit{x}{\mathit{K}}_{\mathit{d}}^{\mathit{t}}}$	$\underset{\mathit{P}\mathbf{-}\mathbf{20}\mathbf{\%}}{\mathit{m}\mathit{a}\mathit{x}{\mathit{K}}_{\mathit{d}}^{\mathit{s}}}$	$\underset{\mathit{P}\mathbf{+}\mathbf{20}\mathbf{\%}}{\mathit{m}\mathit{a}\mathit{x}{\mathit{K}}_{\mathit{d}}^{\mathit{s}}}$
m1	5 × 103	4 × 103	6 × 103	1.112	1.107	1.560	1.502
m2	2.5 × 103	2 × 103	3 × 103	1. 114	1. 103	1.493	1.559
J1	0.205	0.164	0.246	1.131	1.092	1.518	1.522
J6	10.2	8.16	12.24	1. 108	1.108	1.522	1.518
c1	12.5 × 103	10 × 103	15 × 103	1. 108	1.108	1.519	1.519
c4	4.8 × 106	3.84 × 106	5.76 × 106	1.112	1.106	1.569	1.474
R	0.25	0.2	0.3	1.095	1.119	1.539	1.496
b4	5.4 × 103	4.32 × 103	6.48 × 103	1.09	1.080	1.525	1.513
ξ	0.07	0.056	0.084	1.110	1.108	1.537	1.504
Er	1.1 × 1011	8.8 × 1010	1.32 × 1011	1.106	1.110	1.472	1.555
TE	0.02	0.0167	0.024	1.100	1.070	1.521	1.520
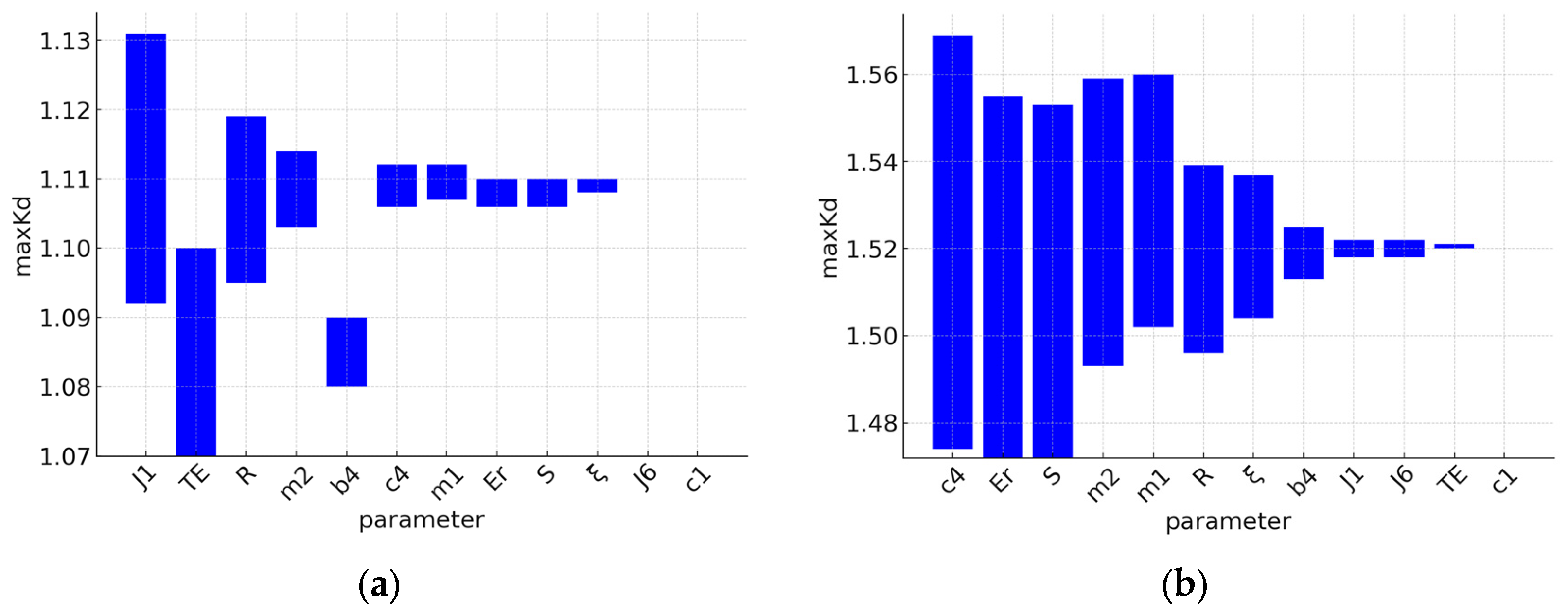
S	1 × 10−4	8 × 10−5	1.2 × 10−4	1.106	1.110	1.472	1.553

. The ranked ranges of changes in the dynamic factor for the two scenarios being considered are shown in Figure 4.

As one can see, the parameters have different influences on the maxK_d values. To determine the influence based on the data from Table 2, a local normalized sensitivity was calculated for both scenarios ($S_E^t$ and $S_E^s$, respectively). The following relationship determines it [28]:

$$S_E={\displaystyle \frac{\Delta max{K}_d}{\Delta P}}{\displaystyle \frac{P}{max{K}_d^{avg}}}$$

(14)

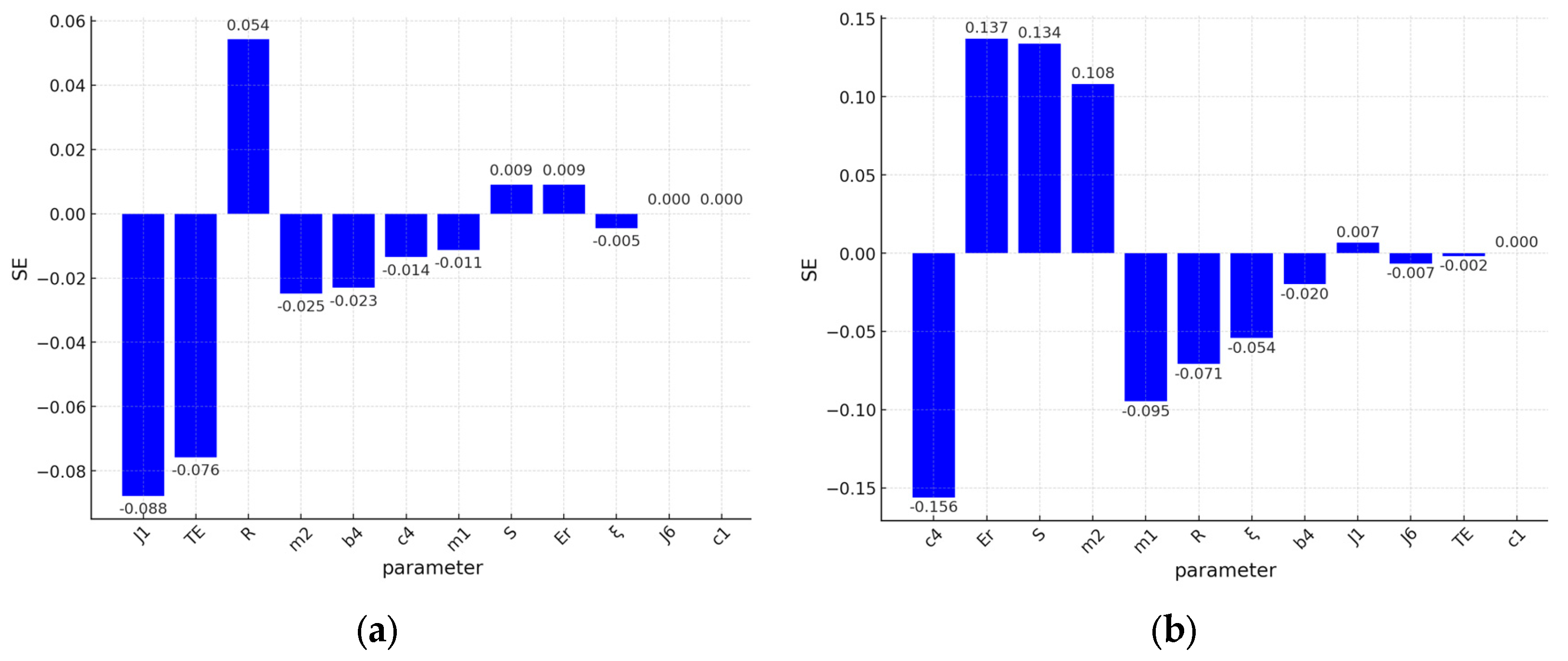
where $\Delta P$ is the interval of change in the parameter, $\Delta max{K}_d$ is the interval of change in $max{K}_d$, $max{K}_d^{avg}$ is the average value of $max{K}_d$ in its interval of change, and P is the nominal value of the parameter. Figure 5a,b show the sensitivities determined by (14) for each parameter, ranked by value. The sensitivities have a positive or negative sign depending on whether $max{K}_d$ increases or decreases with increasing the parameter value. As seen, the sensitivities are different for the two operating scenarios. 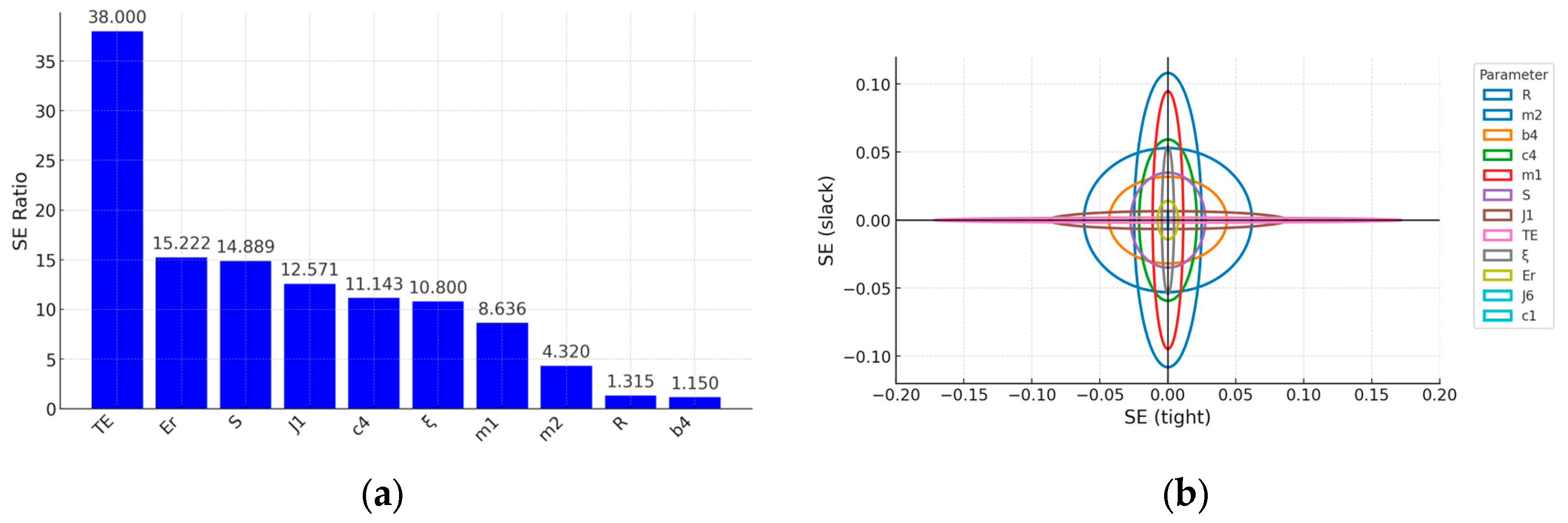In Figure 6a, the sensitivities ratio is shown, calculated by dividing the larger by the smaller value without considering their signs, i.e., $\left|\max \left(S_E^s,S_E^t\right)/\min \left(S_E^s,S_E^t\right)\right|$. Figure 6b shows the sensitivities of all parameters by visualizing them with ellipses, with semi-axes equal to the sensitivities in both scenarios. The ellipses should be circles if both scenarios of operation have the same sensitivity.

4. Discussion

From the analysis of the results in the considered range of parameter changes, it can be seen that the maximum value of the dynamic factor reaches 1.131 for the tight rope scenario (see Figure 4a), while for the slack rope scenario, it increases to 1.569 (see Figure 4b. The significant difference indicates that the slack rope mode results in significantly higher dynamic loads, which should be decisive for the sizing of the mechanism elements, as has been proven in [14,15]. Here, strong transients are caused by shock loading. The dynamic factor is influenced by a different set of parameters in both scenarios considered.

For the scenario of hoisting with a tight rope, the dynamic factor is determined primarily by the moment of inertia of the motor J₁ (see Figure 5a), which, when increased, reduces the dynamic factor (has a negative sensitivity), primarily influencing the decrease in the starting accelerations of the system and giving the system greater stability to applied shock loads. The electromechanical constant of the motor T_E has a negative sensitivity—its increase leads to slower transient processes in the motor and, respectively, less dynamic load on the mechanical system components. Increasing the radius of the drum R increases the dynamic factor (has a positive sensitivity) since its increase leads to an increase in the speed of hoisting the load and an increase in inertial forces. The mass of the payload m₂ has a weaker influence on the dynamic factor, which has a negative sensitivity. Increasing the system’s inertial characteristics by increasing m₂ while maintaining the motor’s power capabilities results in lower starting accelerations, which is the main reason for this. The other parameters examined have a less significant effect. In this mode, the rope parameters E_r and S, which determine its stiffness and deformation, have little effect at positive sensitivity. The primary reason for this is that the stiffness of the rope increases due to the increase in these parameters, which, in turn, increases the dynamic factor. The movement of the payload begins with an already deformed rope that has accumulated potential energy, and transient dynamic processes only result in small additional deformations.

When hoisting with a slack rope, the dynamic factor is significantly higher and has greater sensitivity due to the more significant dynamic processes because of shock loading (see Figure 5b). The analysis shows that in this scenario, the main influence is exerted by the mechanical system elements included in the vertical kinematic chain. The stiffness of the supporting structure c₄ and the mass of the metal structure m₁ have a strong influence and negative sensitivity. The main reason for this is that an increase in both parameters results in smaller crane vibration amplitudes and, in turn, smaller inertial forces that affect the dynamic factor. Increasing the payload mass m₂ increases the dynamic factor, since its value determines the inertial force and the magnitude of the impact load on the system at the moment of rope slack removal. The stiffness characteristics of the rope, defined by the modulus of elasticity E_r and the cross-section S are also highly influential parameters with positive sensitivity. They determine the deformation of the rope, its ability to accumulate and release potential energy, and the magnitude of the impact reaction in it. The relative damping coefficient $\xi$ is responsible for regulating the rate of oscillation damping and decreasing amplitude peaks. Unlike a tight rope scenario, with a slack rope, the drive parameters J₁ and T_E have a weak influence, since the motor only participates in the dynamics of the system after the initial impact. The radius of the drum R, which, according to (12), determines the force in the rope, also has a negative sensitivity.

The analysis of the values of the sensitivity ratio from Figure 6a shows that the sensitivities of T_E, E_r, S, J₁, $\xi$, c₄, m₁, and m₂ change the most, i.e., these parameters influence the value of the maximum dynamic factor the most when the system loading mode changes.

By calculating Pearson’s linear correlation coefficients r, we can determine the strength of the relationship between the input parameters and maxK_d. For this purpose, using the Monte Carlo method with 2 × 10³ numerical experiments, all system parameters in Table 2 were varied simultaneously, and maxK_d was determined for each combination. Figure 7a shows the ranked statistically significant correlation coefficients r for the scenario of hoisting with a tight rope, and Figure 7b shows the same for the slack rope scenario. The values and their signs confirm the results of the sensitivity analysis. For the tight rope scenario, J₁ and R have the strongest influence, and their correlation coefficients are −0.78 and 0.50 respectively. For the slack rope scenario, the strongest influence is seen for the parameters c₄, S, m₂, E_r, m₁, and R, with correlation coefficients of −0.48, 0.40, 0.40, 0.38, −0.36, and −0.24, respectively. The direction of the correlation coincides with that of the sensitivity.

Also, the obtained dataset was used to establish multiple linear regression models that determine the maximum dynamic factor for both scenarios, with only statistically significant coefficients included:

$$\begin{array}{l}max{K}_d^t=1.19-0.471J_1+0.248R-0.285T_E-0.0763\xi -3.24\times {10}^{-6}{m}_1-\\ 4.04\times {10}^{-7}{b}_4-9.20\times {10}^{-6}{m}_2-2.48\times {10}^{-9}{c}_4+9.43\times {10}^{-14}{E}_r+1.63\times {10}^{-4}S\end{array}$$

(15)

$$\begin{array}{l}max{K}_d^s=1.56-3.14\times {10}^{-5}{m}_1+7.25\times {10}^{-5}{m}_2+0.0775J_1-0.440R-1.03\xi -\\ 4.36\times {10}^{-8}{c}_4-4.61\times {10}^{-6}{b}_4+1.57\times {10}^{-12}{E}_r+1.82\times {10}^{-4}S\end{array}$$

(16)

The equations’ adjusted coefficients of determination R² are 0.98 for the tight rope and 0.93 for the slack rope scenarios. To determine how much of the variation in maxK_d is caused by the variation in the corresponding parameter, a calculation of the partial coefficients of determination was also performed, the values of which are presented in

Table 3. Numerical values of partial R² for the two scenarios.

Scenario	J1	R	m2	m1	c4	S	Er	ξ	TE	b4	J6	c1
Part. R2 (TR)	0.636	0.269	0.037	0.018	0.009	0.008	0.007	0.002	0.002	0.000	0.000	0.000
Part. R2 (SR)	0.001	0.058	0.166	0.124	0.225	0.167	0.158	0.032	0.000	0.004	0.000	0.000

. The bolded values indicate the most significant values, and the results validate the results of the sensitivity and correlation coefficients analysis. In the tight-rope case, motor inertia J₁ and drum radius R explain ≈64 % and ≈27 % of the maxK_d variance, respectively. In slack-rope hoisting, support-structure stiffness c₄, rope cross-section S, and payload mass m₂ contribute ≈22%, ≈17% and ≈17%, respectively.

5. Conclusions

In this paper, a mathematical model of a hoisting mechanism is developed, which considers the inertial, elastic, and damping characteristics of the main elements of the system and the dynamic characteristics of the DC motor. With this model, one can accurately simulate transient processes, peak loads, and the system’s real dynamics under different operating conditions. A parametric study of the values of the dynamic factor in the rope has been conducted through numerical experiments. The simulations performed in a specific parameter range (±20% compared to their nominal values) reveal that the dynamic factor in the rope is strongly influenced by the mechanism’s operating mode. The dynamic response of the system in a tight rope hoisting is mostly determined by parameters that relate to the drive and kinematics, and the dynamic factor is relatively low.

But in the slack rope mode, a sharp increase in the dynamic factor and its sensitivity to changes in the system parameters is observed. Here, the parameters of the elements forming the kinematic chain in the vertical direction have a clear dominant influence. Key variables include the modulus of elasticity, rope cross-section, payload mass, and stiffness and mass of the supporting structure. In this mode, the elastic properties significantly impact the absorption and release of kinetic and potential energy, leading to a significant impact on the amplitude of transient processes and the amount of dynamic forces.

The results obtained show that the scenario of hoisting with a slack rope is relevant for the dimensioning of the hoisting system, since in this scenario the highest values of the dynamic factor and the highest peak loads are reached. This has practical significance in engineering practice, as it draws attention to the key design parameters that play a critical role in generating a higher dynamic factor and which must be carefully controlled and optimized to ensure reliability in the operation of the hoisting mechanisms. The developed approach for modeling and analyzing the dynamics of hoisting mechanisms provides a reliable basis for making engineering decisions, allowing for precise identification of critical factors and effective optimization of the system for different operating modes.

Future research will be directed to evaluate the effects of parametric uncertainties and consider different motor rotation laws. Experimental confirmation and model calibration will be carried out to correct model parameters and enhance the quality of dynamic predictions.