Predicting Traffic Load Data: ARIMA and SARIMA Comparison †
Abstract
1. Introduction
1.1. ARIMA and SARIMA Methods
- p: The order of the autoregressive part. It represents the number of lag observations in the model (how many previous time points influence the current point);
- d: The degree of differencing. This is used to make the time series data stationary (i.e., removing trends and seasonality);
- q: The order of the moving average (MA) part. It represents the number of lagged forecast errors in the prediction equation [6].
- p: number of autoregressive (AR) terms;
- d: number of differencing (I) terms;
- q: number of moving average (MA) terms;
- P: seasonal autoregressive terms;
- D: seasonal differencing;
- Q: seasonal moving average terms;
- m: seasonality period (e.g., 12 for monthly data, 7 for weekly data) [6].
1.2. Determining the Parameters of ARIMA and SARIMA
2. Preliminary Analysis
2.1. Purification and Aggregation
- duplicated records (i.e., when a vehicle is detected more than once for less than a few seconds)—these records are erased;
- different lengths are detected for the same plate number—in these cases, the length is substituted by the most frequent value;
- records where speed is negative or greater than 200 km/h—these records are substituted by the N/A value.
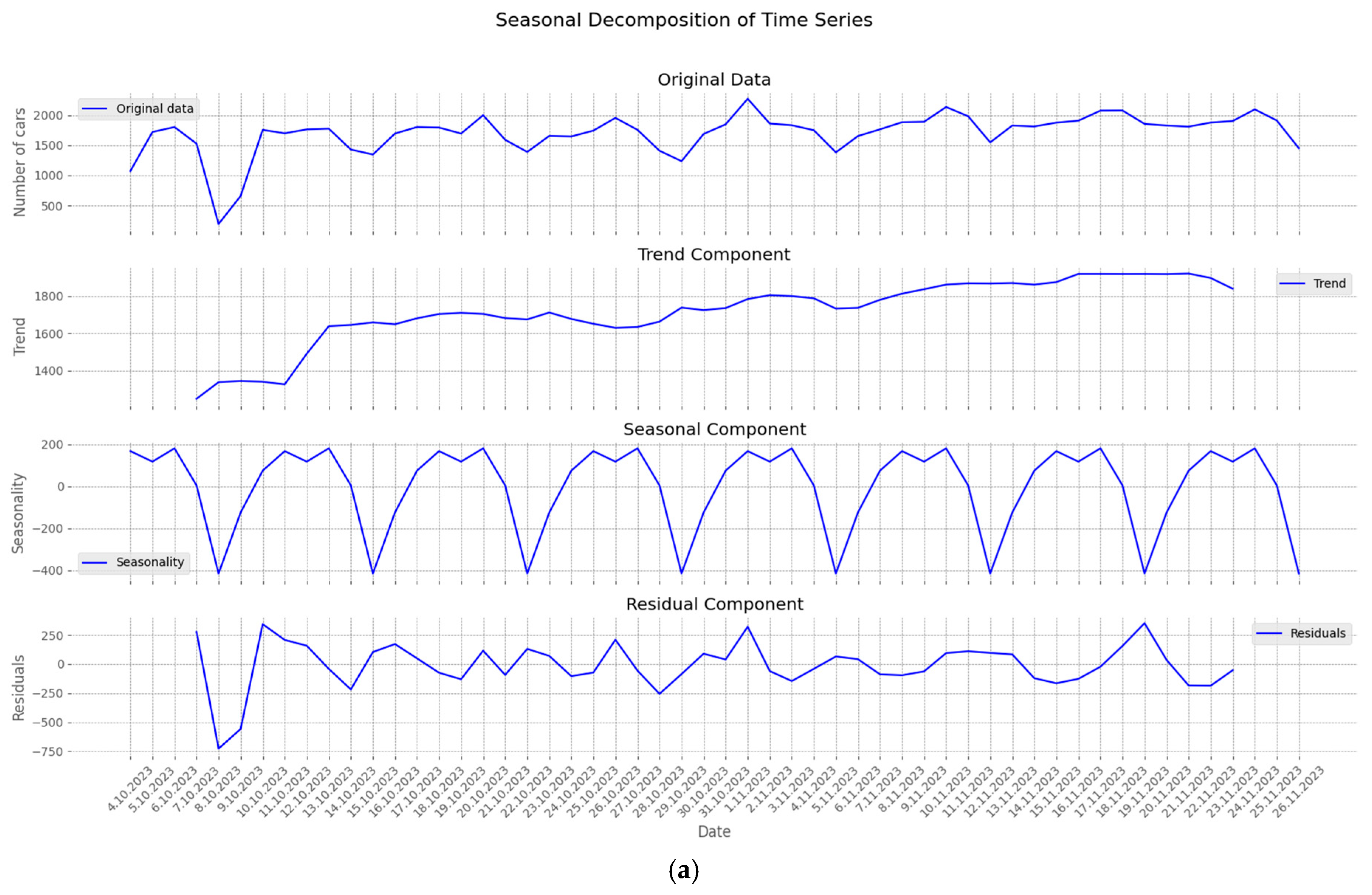
2.2. STL Decomposition
3. ARIMA and SARIMA Configuration and Comparison
3.1. ADF and KPSS Tests
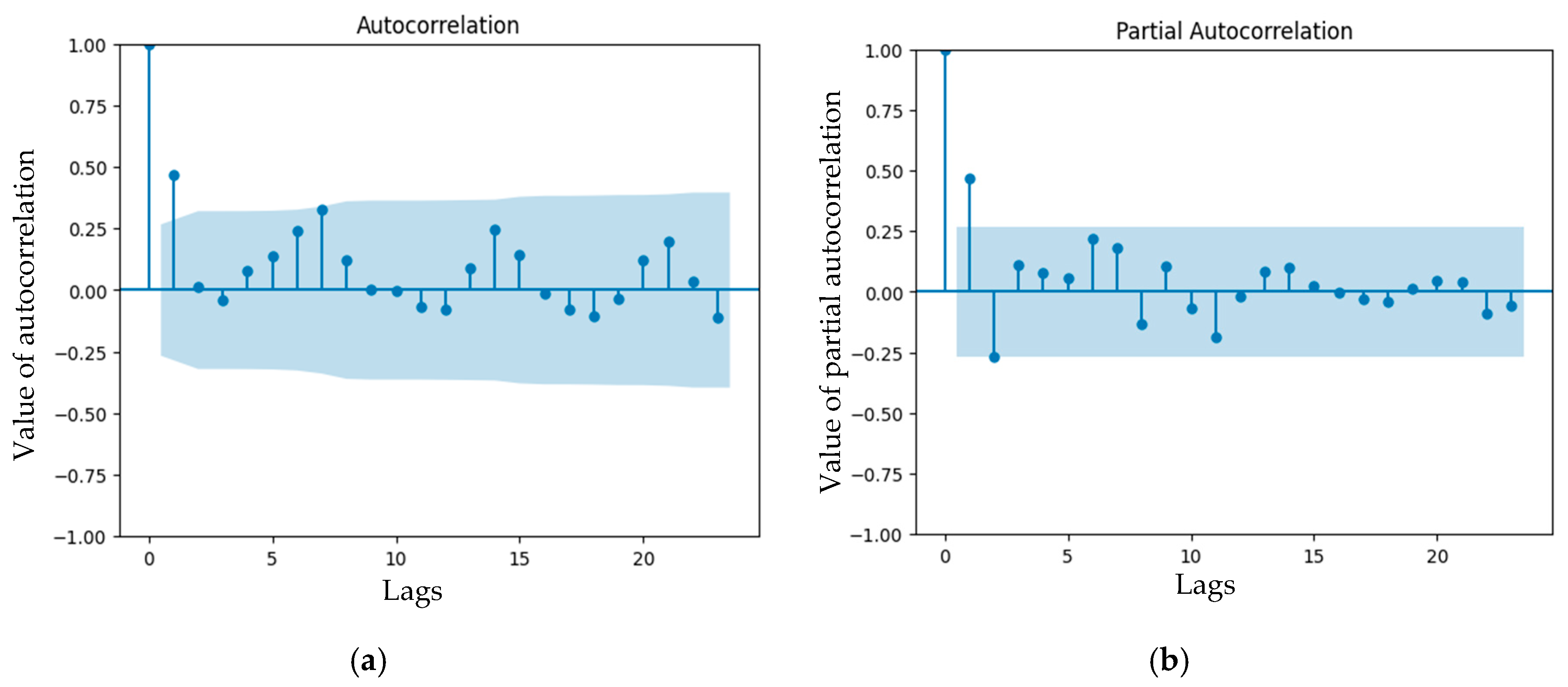
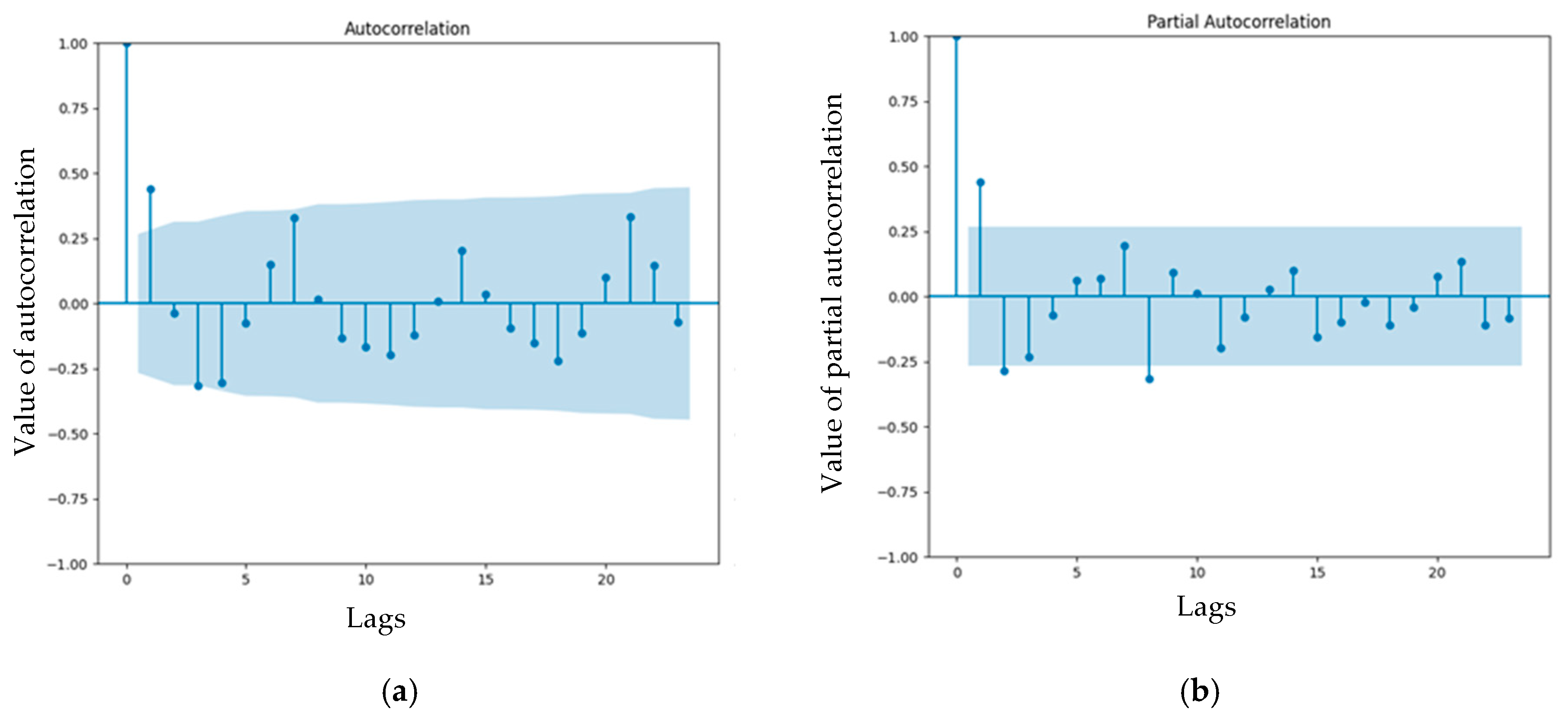
3.2. Analysis of ACF and PACF
3.3. Comparison of MAE, MAPE, and RMSE of Different Configurations of ARIMA
3.4. Comparison of MAE, MAPE, and RMSE of Different Configurations of SARIMA
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ARIMA | Autoregressive Integrated Moving Average |
| SARIMA | Seasonal Autoregressive Integrated Moving Average |
| STL | Seasonal Trend Leftover |
| ACF | Autocorrelation Function |
| PACF | Partial Autocorrelation Function |
| ADF | Augmented Dickey-Fuller |
| KPSS | Kwiatkowski-Phillips-Schmidt-Shin |
| PP | Phillips-Perron |
| ZA | Zivot-Andrews |
| MAE | Mean Absolute Error |
| MAPE | Mean Absolute Percentage Error |
| RMSE | Root Mean Squared Error |
References
- Galkaduwa, C.; Ranasinghe, N. Data Science and Its Importance. Biomed. Sci. Clin. Res. 2024, 3, 1–4. [Google Scholar]
- Lukas, S.; Uhrina, M.; Frnda, J. UHD Database Focus on Smart Cities and Smart Transport. Electronics 2024, 13, 904. [Google Scholar] [CrossRef]
- Chattopadhyay, A.; Lee, C.Y.; Lee, Y.C.; Liu, C.L.; Chen, H.K.; Li, Y.H.; Chuang, E.Y. Twnbiome: A public database of the healthy Taiwanese gut microbiome. BMC Bioinform. 2024, 24, 474. [Google Scholar] [CrossRef] [PubMed]
- Szostek, K.; Mazur, D.; Drałus, G.; Kusznier, J. Analysis of the Effectiveness of ARIMA, SARIMA, and SVR Models in Time Series Forecasting: A Case Study of Wind Farm Energy Production. Energies 2024, 17, 4803. [Google Scholar] [CrossRef]
- Santoso, A.B.; Widodo, T. Predicting the number of forest and land fire hotspot occurrences using the arima and sarima methods. J. Sisfokom. 2024, 13, 119–129. [Google Scholar] [CrossRef]
- Hyndman, R.; Athanasopoulos, G. Forecasting: Principles and Practice; Monash University: Melbourne, VIC, Australia, 2021; Available online: https://otexts.com/fpp3/ (accessed on 7 May 2025).



| 1st Dataset p-Value | 2nd Dataset p-Value | |
|---|---|---|
| ADF test before differentiation | 0.041 | 0.25 |
| ADF test after differentiation | 4.93 × 10−8 | 0.044 |
| KPSS test before differentiation | 0.1 | 0.1 |
| KPSS test after differentiation | 0.1 | 0.1 |
| (1,0,1) | (1,0,2) | (2,0,1) | (2,0,2) | (1,1,1) | (1,1,3) | (3,1,1) | (3,1,3) | (2,1,1) | (1,1,2) | (2,1,2) | (3,1,2) | (2,1,3) | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1st dataset | MAE | 147.85 | 153.17 | 139.07 | 143.68 | 185.48 | 195.08 | 224.87 | 220.16 | 227.58 | 150.17 | 219.69 | 137.06 | 216.25 |
| MPE | 7.82 | 8.11 | 7.27 | 7.56 | 10.56 | 11.5 | 12.88 | 12.60 | 13.08 | 7.86 | 12.59 | 7.06 | 12.30 | |
| RMSE | 244.73 | 250.68 | 242.20 | 242.89 | 244.68 | 264.16 | 280.98 | 283.08 | 282.62 | 247.88 | 281.06 | 241.00 | 280.09 | |
| 2nd dataset | MAE | 129.37 | 115.19 | 244.08 | 262.88 | 153.83 | 127.19 | 147.64 | 415.83 | 99.91 | 132.73 | 136.21 | 98.88 | 123.21 |
| MPE | 7.86 | 7.26 | 14.22 | 15.77 | 9.22 | 7.73 | 8.77 | 24.62 | 6.19 | 8.04 | 8.16 | 6.11 | 7.50 | |
| RMSE | 142.52 | 148.38 | 265.32 | 290.56 | 166.30 | 139.93 | 178.24 | 505.99 | 123.45 | 144.59 | 152.50 | 121.46 | 137.91 |
| (3,1,2), (1,0,1,7) | (1,0,2) (1,0,1,7) | (1,1,2) (1,0,1,7) | (3,1,2), (1,0,2,7) | (1,0,2) (1,0,2,7) | (1,1,2) (1,0,2,7) | (3,1,2) (2,0,1,7) | (1,0,2), (2,0,1,7) | (1,1,2) (2,0,1,7) | (3,1,2) (2,0,2,7) | (1,0,2), (2,0,2,7) | (1,1,2) (2,0,2,7) | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| First dataset | MAE | 221.67 | 186.11 | 153.95 | 257.03 | 217.62 | 155.60 | 246.65 | 230.04 | 142.60 | 260.89 | 168.92 | 134.41 |
| MPE | 13.05 | 10.94 | 8.65 | 15.27 | 12.91 | 8.78 | 14.62 | 13.71 | 7.82 | 15.52 | 9.74 | 7.30 | |
| RMSE | 258.55 | 222.53 | 190.97 | 280.09 | 242.26 | 192.46 | 273.30 | 250.67 | 189.65 | 280.61 | 207.74 | 192.33 | |
| Second dataset | MAE | 116.41 | 186.39 | 102.47 | 136.82 | 263.68 | 132.75 | 124.53 | 237.97 | 119.77 | 164.85 | 273.17 | 145.87 |
| MPE | 7.22 | 11.15 | 6.38 | 8.44 | 15.70 | 8.20 | 7.71 | 14.17 | 7.41 | 10.19 | 16.24 | 8.99 | |
| RMSE | 147.20 | 198.73 | 127.91 | 162.43 | 299.49 | 154.70 | 153.16 | 262.64 | 141.86 | 193.91 | 308.40 | 166.68 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peychinov, T.; Karaivanova, A.; Mecheva, T. Predicting Traffic Load Data: ARIMA and SARIMA Comparison. Eng. Proc. 2025, 100, 29. https://doi.org/10.3390/engproc2025100029
Peychinov T, Karaivanova A, Mecheva T. Predicting Traffic Load Data: ARIMA and SARIMA Comparison. Engineering Proceedings. 2025; 100(1):29. https://doi.org/10.3390/engproc2025100029
Chicago/Turabian StylePeychinov, Todor, Adeliya Karaivanova, and Teodora Mecheva. 2025. "Predicting Traffic Load Data: ARIMA and SARIMA Comparison" Engineering Proceedings 100, no. 1: 29. https://doi.org/10.3390/engproc2025100029
APA StylePeychinov, T., Karaivanova, A., & Mecheva, T. (2025). Predicting Traffic Load Data: ARIMA and SARIMA Comparison. Engineering Proceedings, 100(1), 29. https://doi.org/10.3390/engproc2025100029





