A Wind Tunnel Study of the Aerodynamic Characteristics of Wings with Arc-Shaped Wingtips †
Abstract
1. Introduction
2. Materials and Methods
2.1. Model Details
2.2. Wind Tunnel and Instrumentation
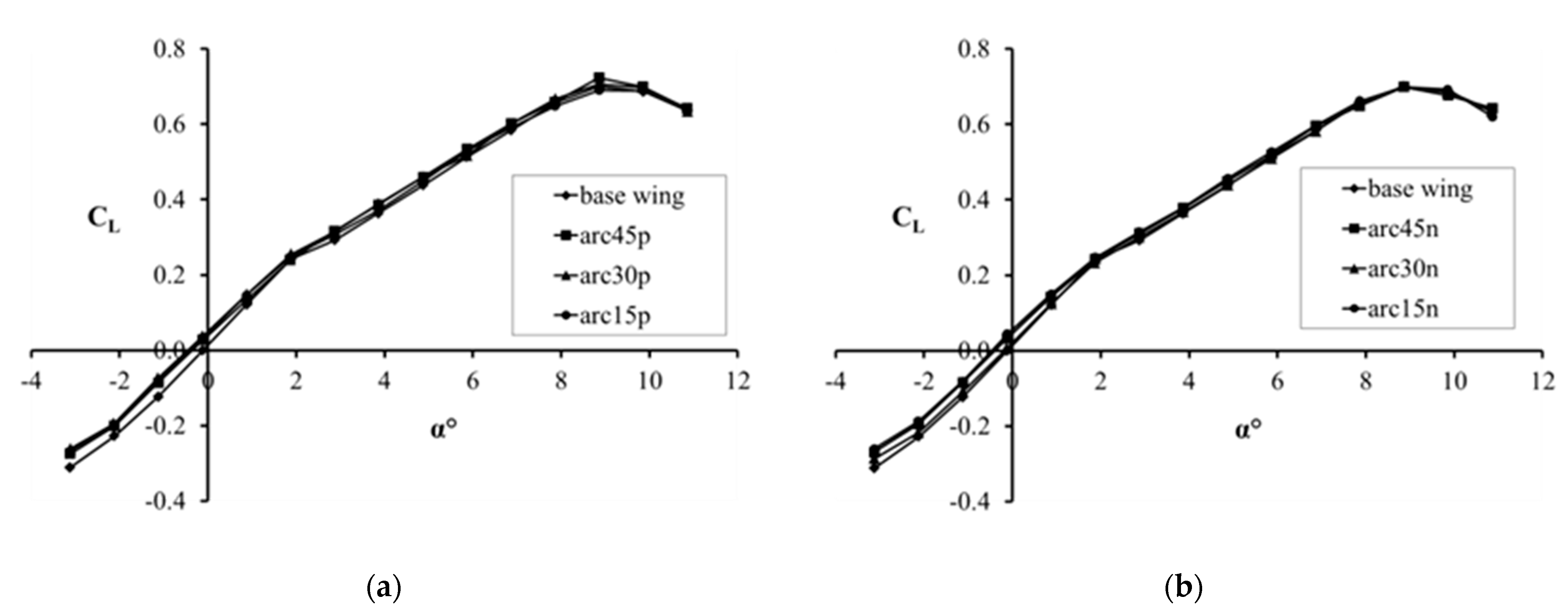
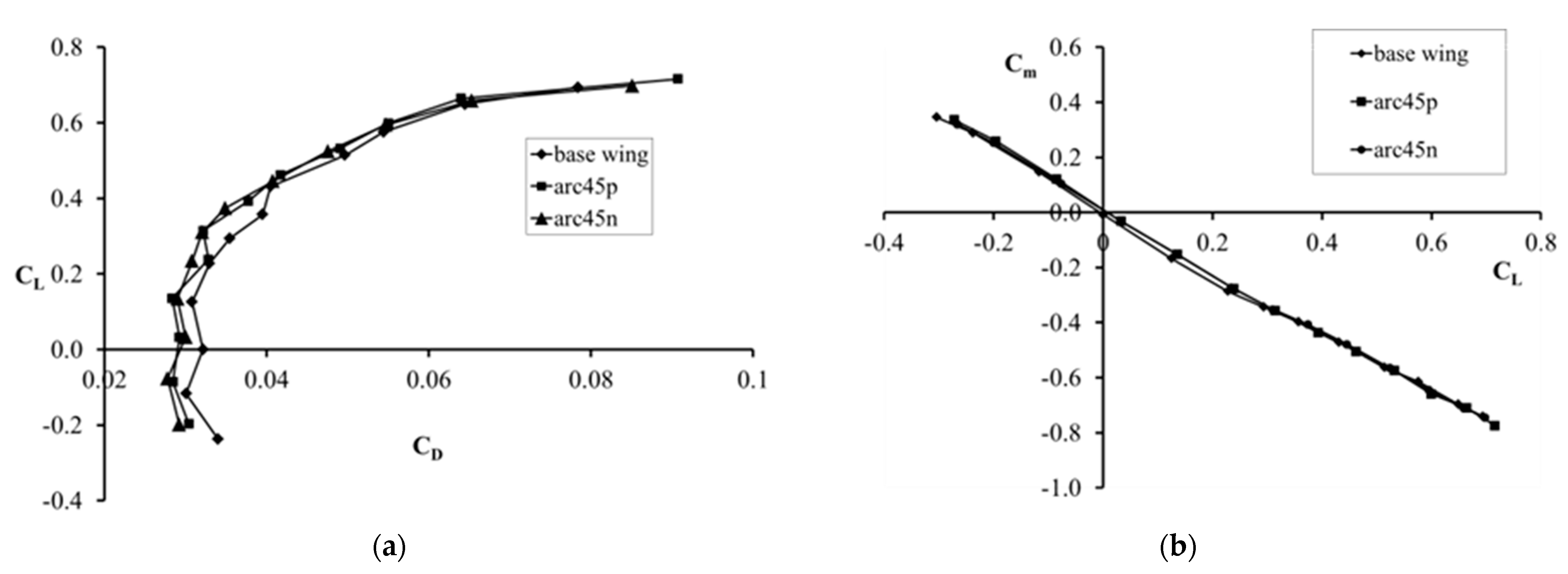
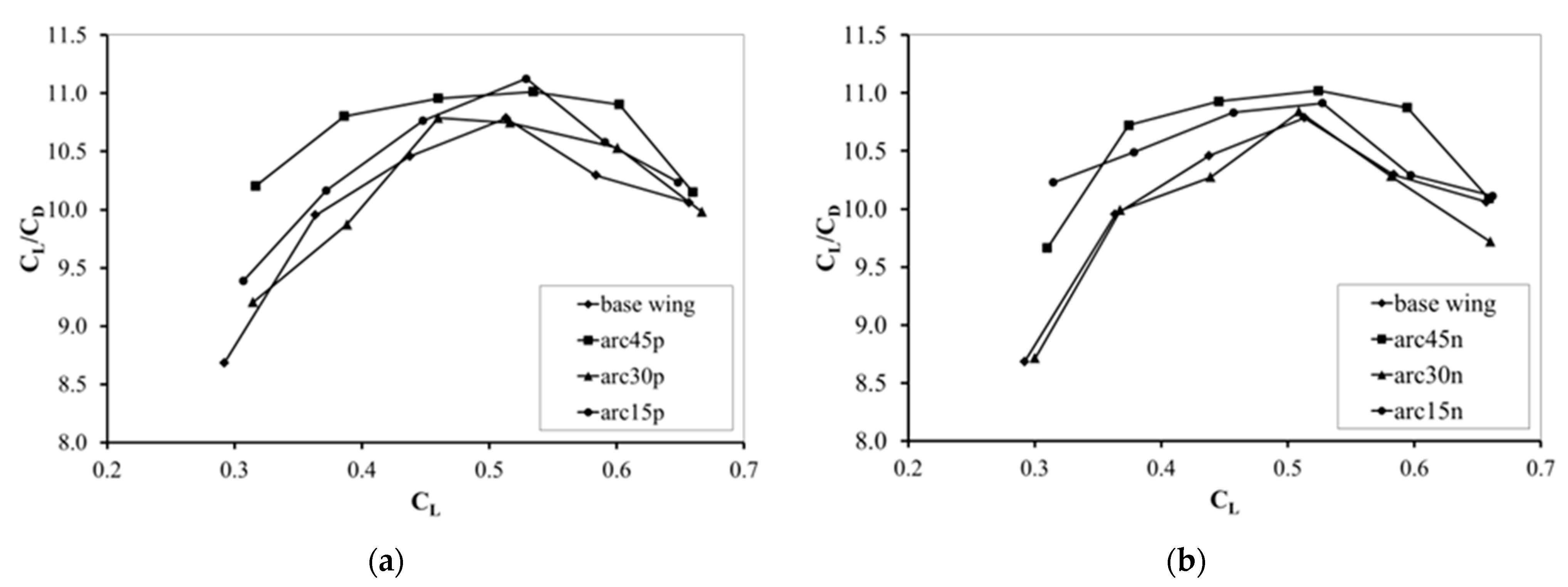
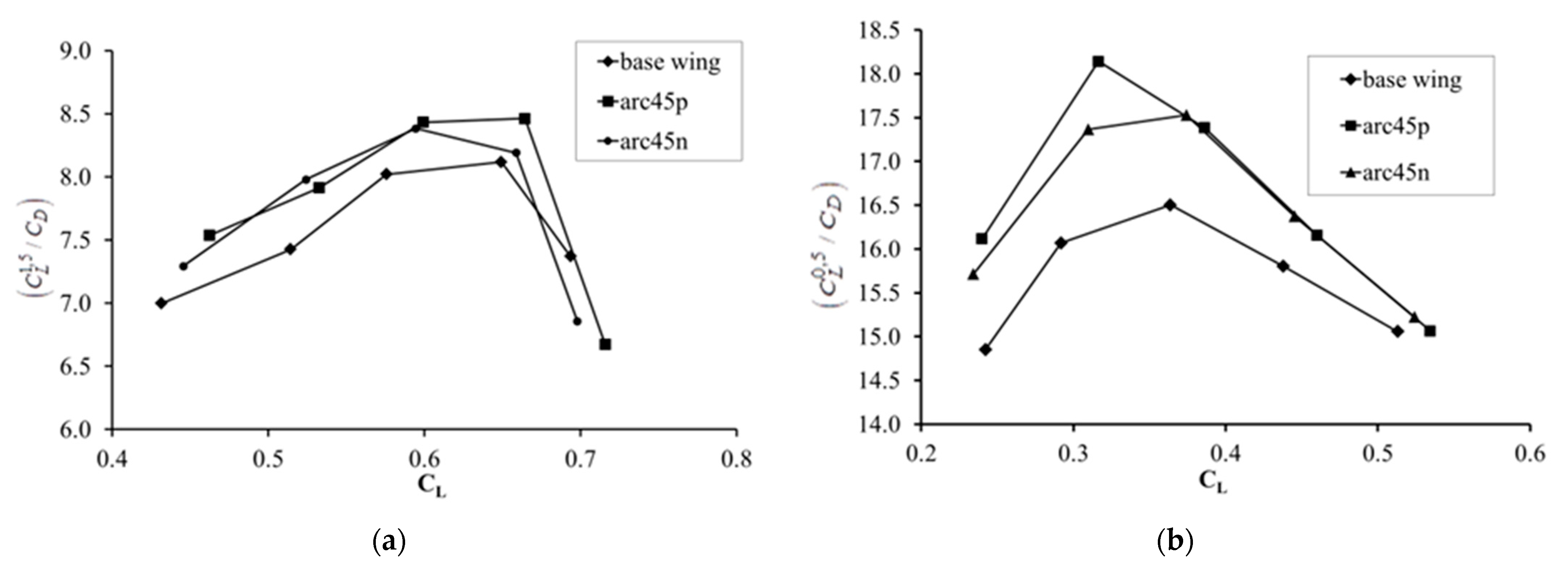
3. Results and Discussion
4. Conclusions
- The winglet models with a ±45° cant angle have increased lift-to-drag ratios, minimum power, and maximum range coefficients.
- It cannot be clearly determined whether configurations with positive or negative dihedral angles have better characteristics.
- The results show that winglet models have a greater increase in aerodynamic efficiency at low angles of attack.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Penchev, S. Study of Aerodynamic Characteristics of Wings with Wingtip Devices. Ph.D. Thesis, Technical University—Sofia, Sofia, Bulgaria, 2018. [Google Scholar]
- Raymer, D.P. Aircraft Design: A Conceptual Approach, 5th ed.; AIAA Education Series; American Institute of Aeronautics and Astronautics Inc.: Washington, DC, USA, 2012. [Google Scholar]
- Inam, M.I.; Mashud, M.; Nahian, A.; Selim, S.M. Induced drag reduction for modern aircraft without increasing the span of the wing by using winglet. Int. J. Mech. Mechatron. 2010, 10, 49–53. [Google Scholar]
- Nikolic, V.R. Planform variations and aerodynamic efficiency of movable tip strakes. J. Aircr. 2007, 44, 340–343. [Google Scholar] [CrossRef]
- Nikolic, V.R. Effect of leading-edge form on performance of wing-movable tip strake configurations. J. Aircr. 2007, 44, 1749–1753. [Google Scholar] [CrossRef]
- Reeder, M.F.; Allen, W.; Phillips, J.M.; Dimmick, R. Wind-tunnel measurements of the E-8C modeled with and without winglets. J. Aircr. 2008, 45, 345–348. [Google Scholar] [CrossRef]
- Arora, P.R.; Hossain, A.; Edi, P.; Jaafar, A.A.; Younis, T.S.; Saleem, M. Drag reduction in aircraft model using elliptical winglet. J.-Inst. Eng. 2005, 66, 1–8. [Google Scholar]
- Berens, M. Potential of Multi-Winglet Systems to Improve Aircraft Performance. Ph.D. Thesis, Technical University Berlin, Berlin, Germany, 2008. [Google Scholar]
- Catalano, F.M.; Ceron-Munoz, H.D. Experimental analysis of aerodynamic characteristics of adaptive multi-winglets. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2006, 220, 209–215. [Google Scholar] [CrossRef]
- Hossain, A.; Rahman, A.; Iqbal, A.; Ariffin, M.; Mazian, M. Drag analysis of an aircraft wing model with and without bird feather like winglet. Int. J. Aerosp. Mech. Eng. 2012, 6, 8–13. [Google Scholar]
- Panayotov, H.; Penchev, S.; Kolibarov, D. Experimental study of canard UAV aerodynamics. MATEC Web Conf. 2017, 133, 01002. [Google Scholar] [CrossRef]
- Britcher, C.; Landman, D. Wind Tunnel Test Techniques, 1st ed.; Academic Press: Cambridge, MA, USA, 2023. [Google Scholar]
- Panayotov, H.; Penchev, S.; Zikyamov, M. Experimental study of turbulence in the test section of wind tunnel. In Proceedings of the 15th International Scientific and Practical Conference “Environment. Technology. Resources”, Rezekne, Latvia, 27–28 June 2024; Volume 3, pp. 217–220. [Google Scholar] [CrossRef]
- Torenbeek, E.; Wittenberg, H. Flight Physics. Essentials of Aeronautical Disciplines and Technology with Historical Notes; Springer: London, UK, 2009. [Google Scholar]
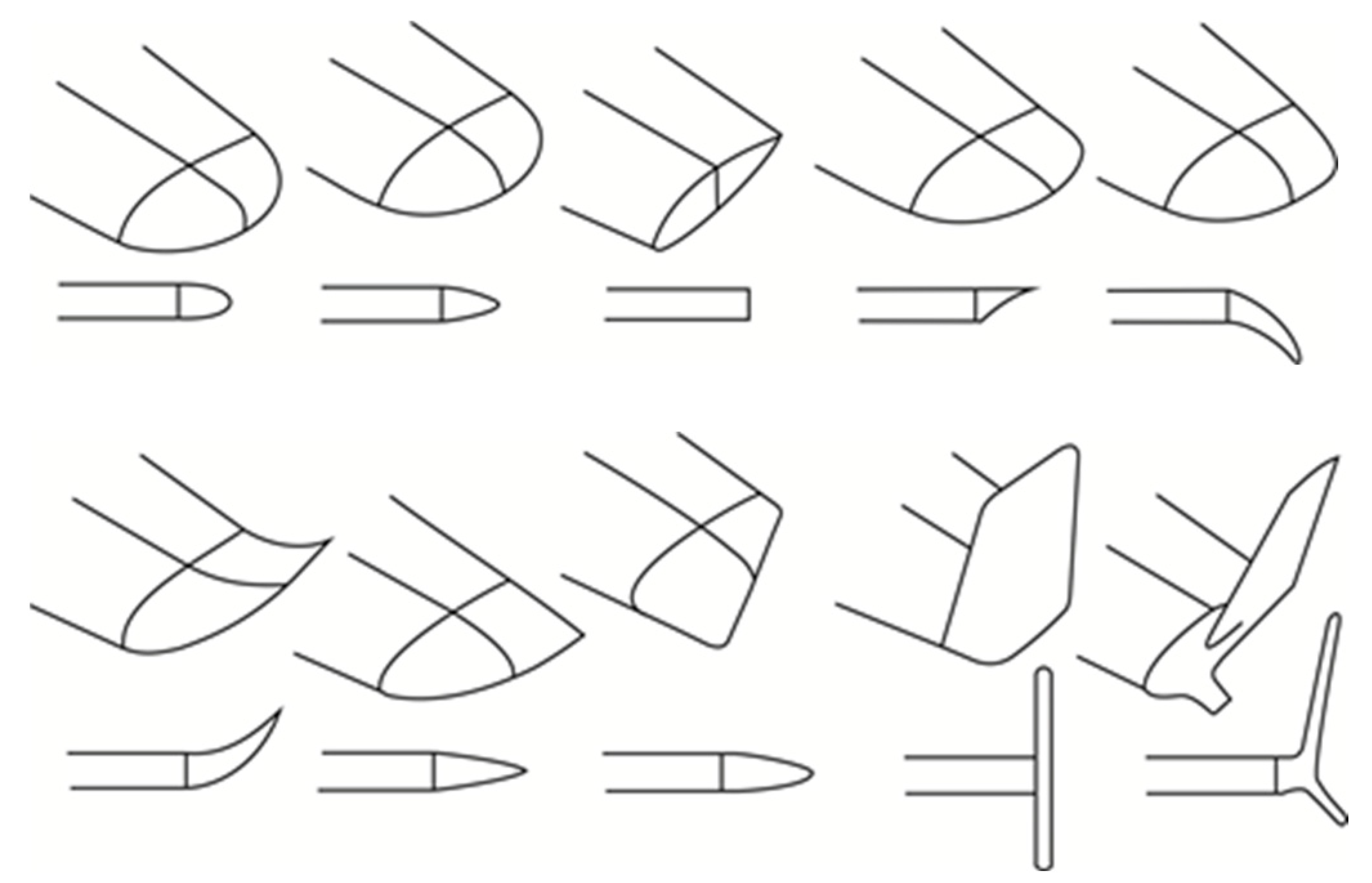
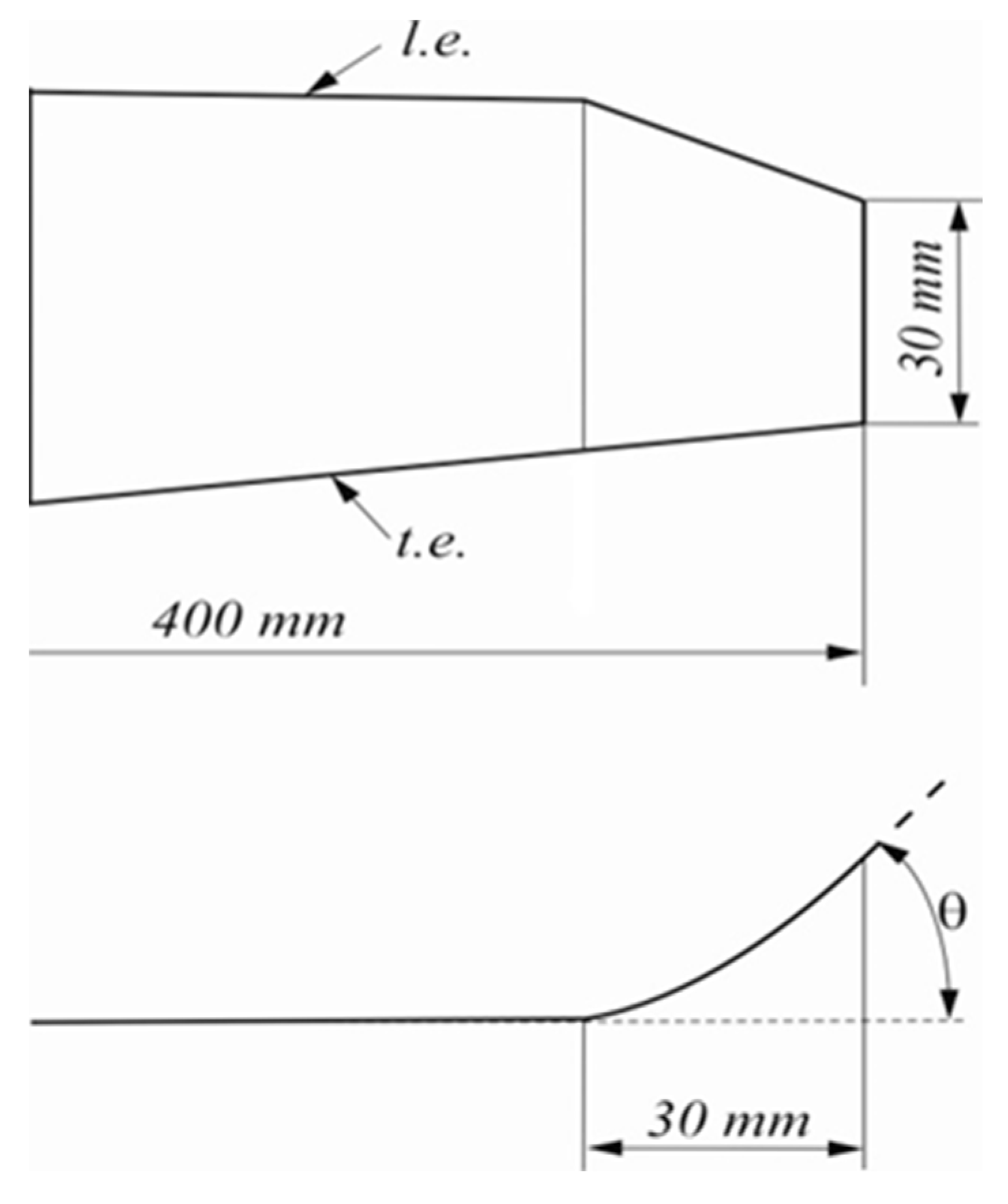


| Test Models | Cant Angle θ | Designation |
|---|---|---|
| Base wing | 0° | base wing |
| Wing with winglets | 15° | arc15p |
| 30° | arc30p | |
| 45° | arc45p | |
| −15° | arc15n | |
| −30° | arc30n | |
| −45° | arc45n |
| Test Models | CLmax | CLα | (CL/CD)max | C1 | C2 |
|---|---|---|---|---|---|
| Base wing | 0.70 | 4.30 | 10.65 | 8.11 | 16.21 |
| arc15p | 0.69 | 4.24 | 11.13 | 8.24 | 16.95 |
| arc30p | 0.71 | 4.16 | 10.78 | 8.19 | 16.41 |
| arc45p | 0.72 | 4.47 | 11.08 | 8.46 | 17.44 |
| arc15n | 0.70 | 4.23 | 10.93 | 7.91 | 16.60 |
| arc30n | 0.70 | 4.28 | 10.84 | 7.95 | 16.47 |
| arc45n | 0.70 | 4.33 | 11.02 | 8.38 | 17.52 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Penchev, S.; Panayotov, H. A Wind Tunnel Study of the Aerodynamic Characteristics of Wings with Arc-Shaped Wingtips. Eng. Proc. 2025, 100, 28. https://doi.org/10.3390/engproc2025100028
Penchev S, Panayotov H. A Wind Tunnel Study of the Aerodynamic Characteristics of Wings with Arc-Shaped Wingtips. Engineering Proceedings. 2025; 100(1):28. https://doi.org/10.3390/engproc2025100028
Chicago/Turabian StylePenchev, Stanimir, and Hristian Panayotov. 2025. "A Wind Tunnel Study of the Aerodynamic Characteristics of Wings with Arc-Shaped Wingtips" Engineering Proceedings 100, no. 1: 28. https://doi.org/10.3390/engproc2025100028
APA StylePenchev, S., & Panayotov, H. (2025). A Wind Tunnel Study of the Aerodynamic Characteristics of Wings with Arc-Shaped Wingtips. Engineering Proceedings, 100(1), 28. https://doi.org/10.3390/engproc2025100028





