Investigation of Technological System Stability During Side Milling ^†

Abstract

This study analyzes technological system stability during side milling by evaluating the influence of two critical parameters: the radial depth of cut (A_e) and feed per tooth (f_z). The experiment was conducted on prismatic samples with stepped geometries to measure deformation at various levels of Ae and f. Regression analysis showed a significant influence of both factors on deformation, with Ae having a stronger effect. The model explains a high level of the variance, confirming the reliability of the experimental data. The results provide guidance for optimizing parameters to improve stability and reduce dimensional deviations.

1. Introduction

The stability of a technological system during milling is crucial for achieving precise dimensions and high surface quality [1,2,3,4]. Uncontrolled deformations [5] may lead to tool wear, workpiece defects, and increased production costs. Side milling, characterized by variable cutting forces, presents specific challenges due to unproper cutter engagement [6]. This study quantitatively evaluates the influence of Ae and f on deformation in machining stepped samples [7,8,9]. The goal is to identify optimal parameter combinations that minimize deformations. Previous studies emphasize the role of cutting parameters, but few analyze their combined effects on stepped geometries.

2. Materials and Methods

Experiments were conducted on a CNC milling machine with the following parameters: maximum spindle power of 22.4 kW, speed up to 12,000 rpm, and feed rate up to 22.9 m/min. A 12 mm diameter solid carbide end mill with 4 teeth, a helix angle of 35°, a length of −26 mm, and am overall length −83 mm was used. Prismatic samples made of steel 10 45 [10] with pre-machined steps were utilized to control the radial engagement (Figure 1 and Figure 2).

A Central Composite Design (CCD) [11,12] with two factors (A_e and f_z) was applied. The radial depth of cut (Ae) varied from 0.18 mm to 5.82 mm, and the feed per tooth (f_z) ranged from 0.011 mm/z to 0.068 mm/z. The cutting speed (V_c) was kept constant at 120 m/min. Thirteen experiments were conducted, including central points and axial points.

Table 1. Experimental plan.

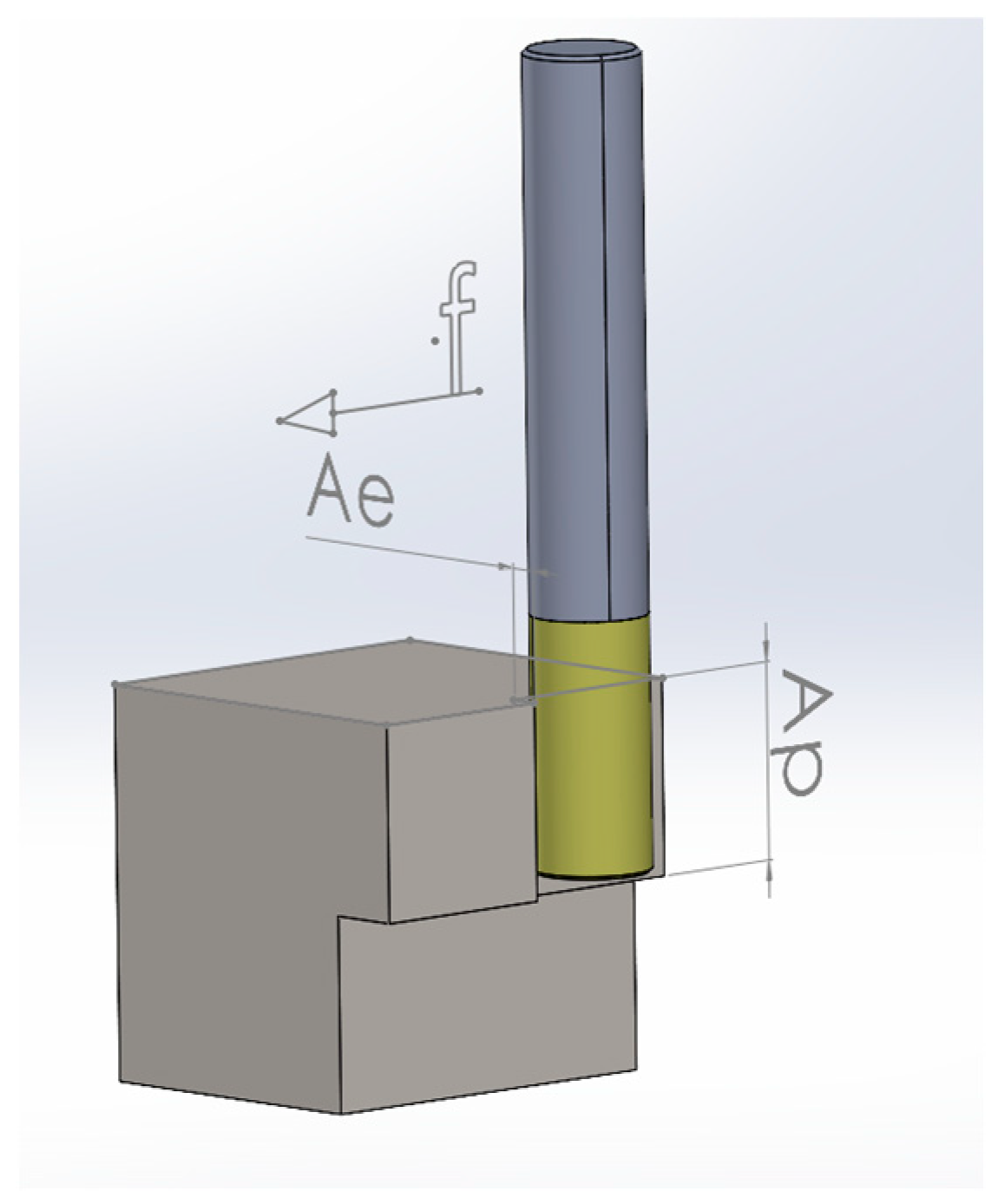
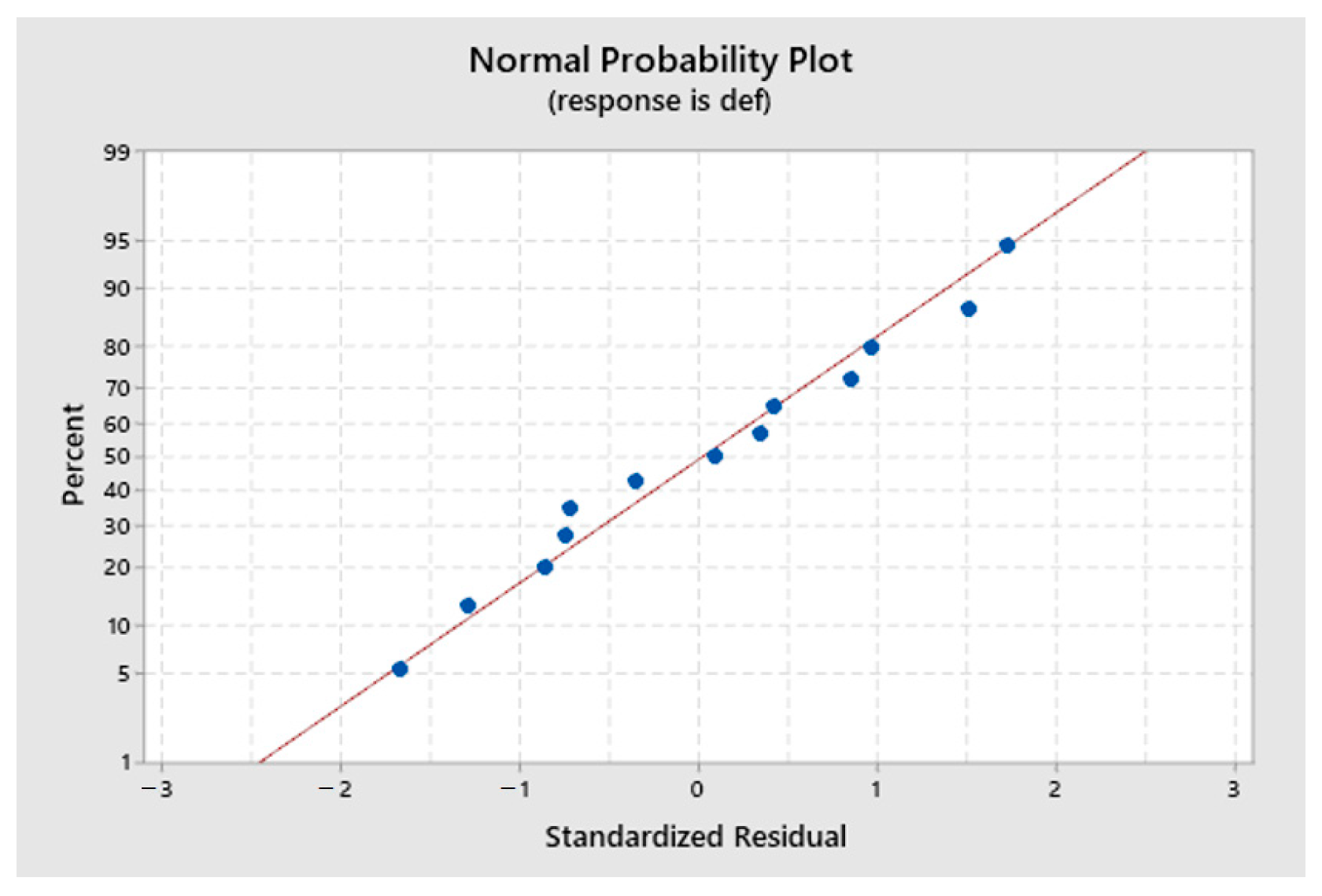
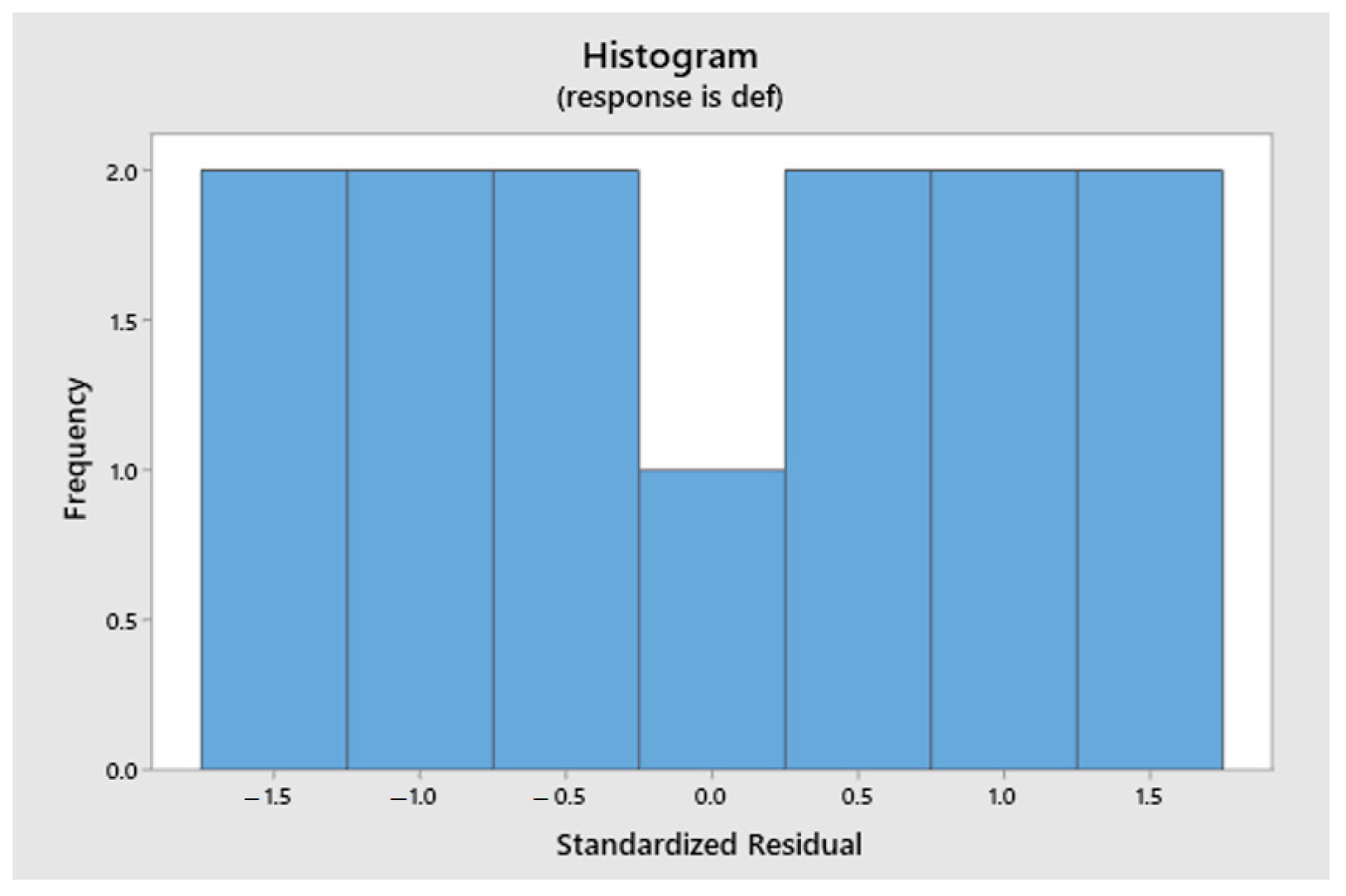
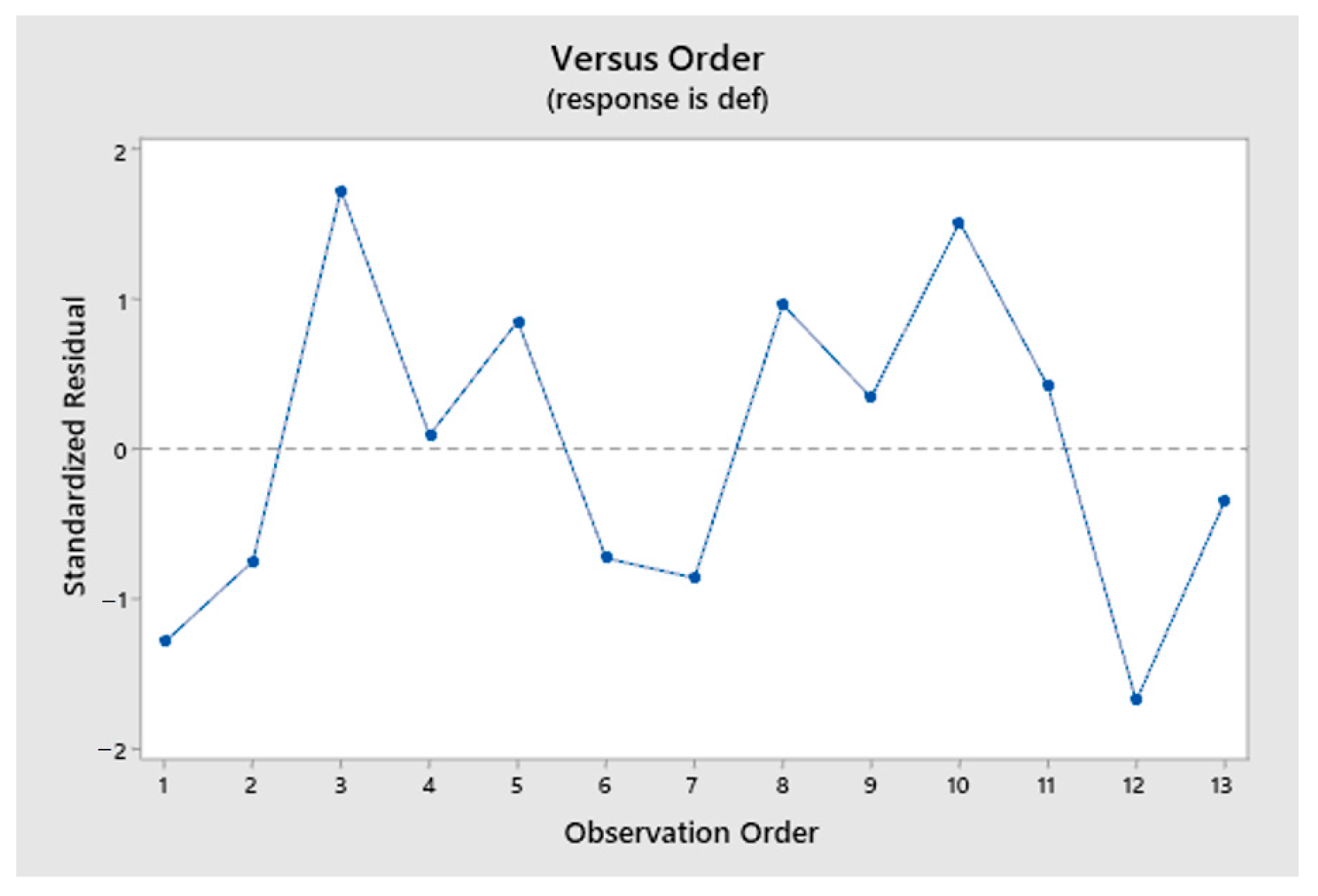
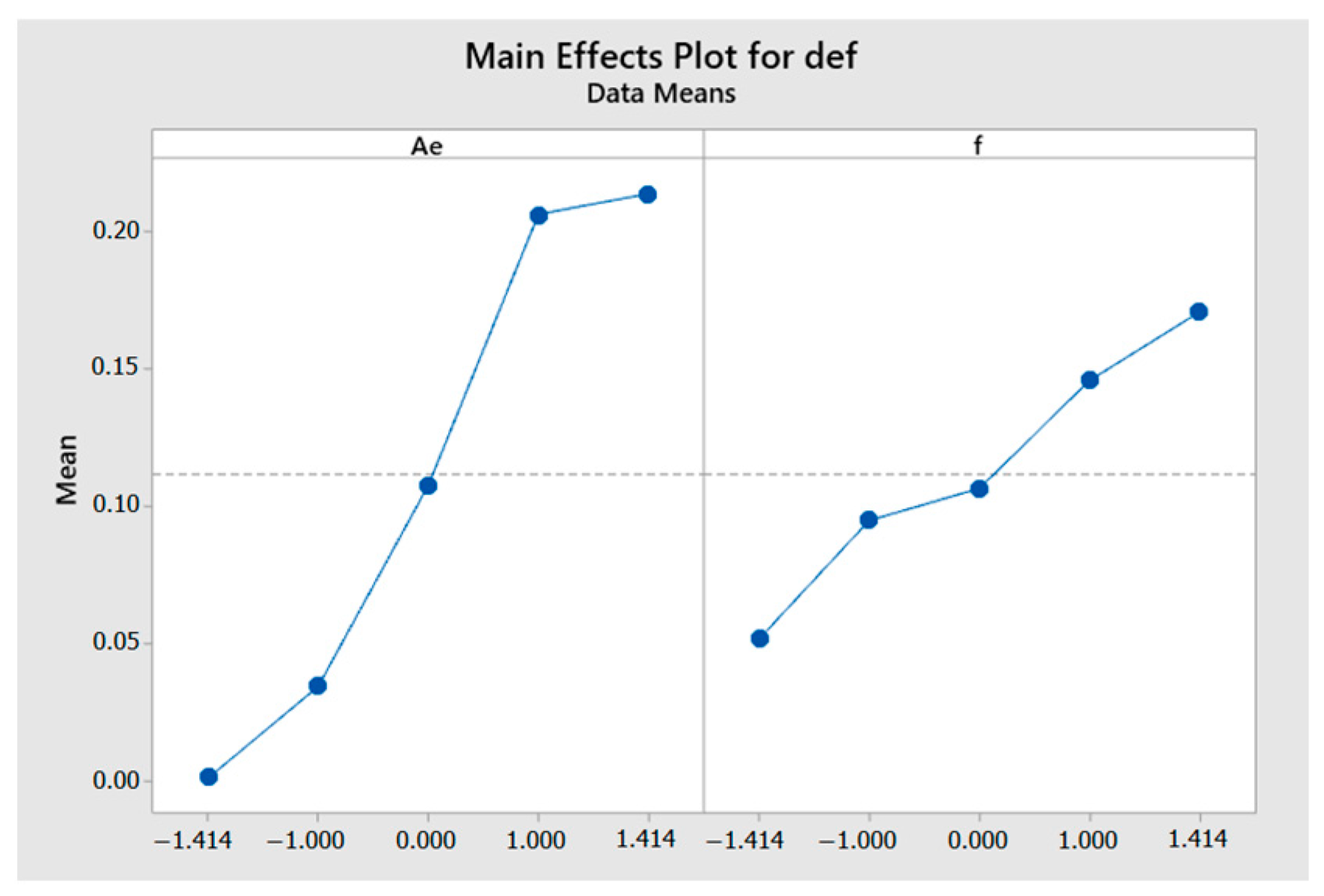
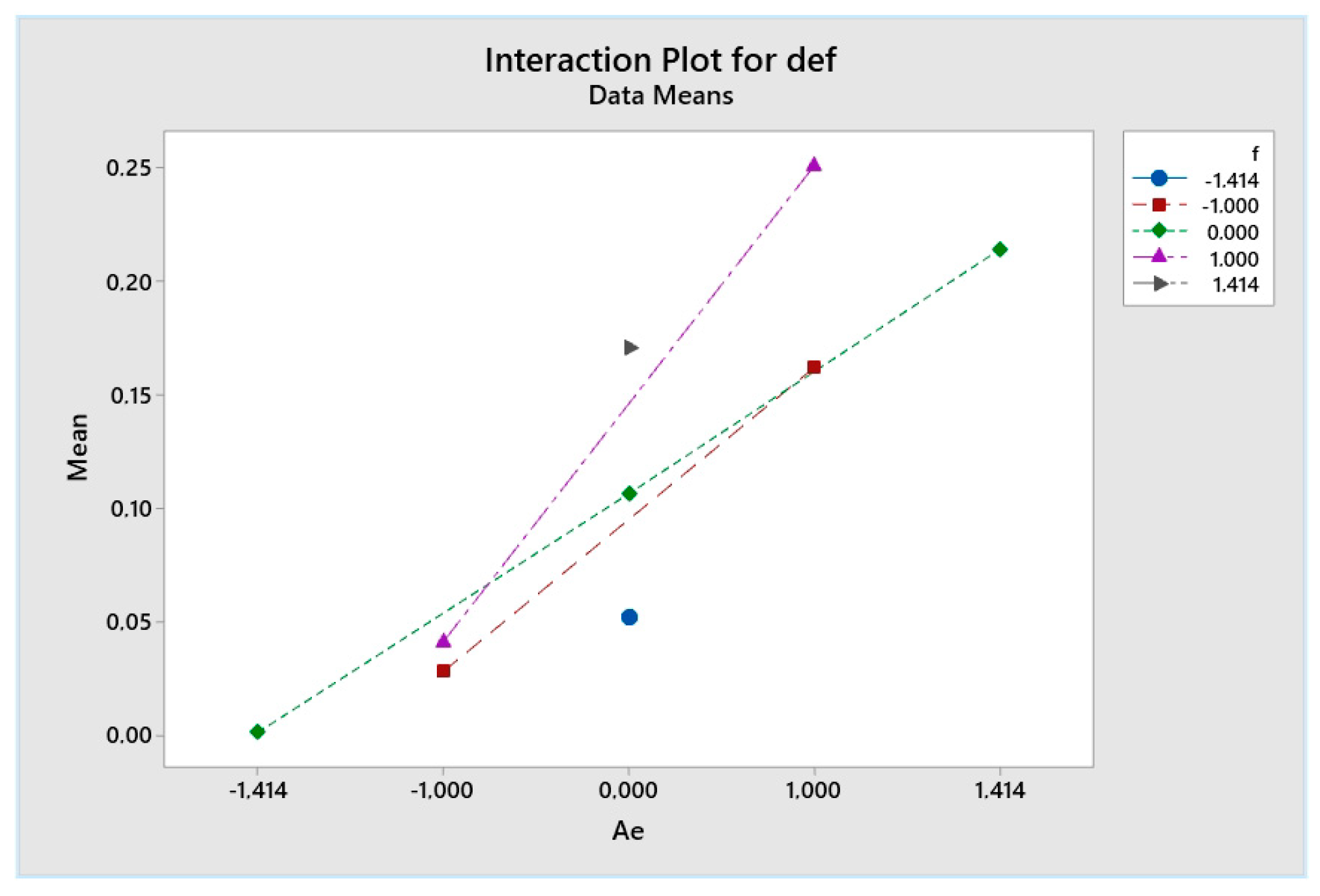
#	Level Ae	Level f	Ae Mm	Fz mm/z	Vc m/min
1	0	0	3	0.04	120
2	0	0	3	0.04	120
3	−1	−1	1	0.06	120
4	0	0	3	0.04	120
5	0	1.414	3	0.068	120
6	0	−1.414	3	0.011	120
7	1.414	0	5.82	0.04	120
8	0	0	3	0.04	120
9	1	−1	5	0.02	120
10	1	1	5	0.06	120
11	−1.414	0	0.18	0.04	120
12	−1	1	1	0.06	120
13	0	0	3	0.04	120

summarises the experimental design data.

Deformations, expressed as dimensional deviations, were measured using the CNC machine’s Renishaw probing system shown in Figure 3 [13,14,15,16].

3. Results

The experimental results are summarized in

Table 2. Experimental results.

#	Level Ae	Level Fz	Response mm
1	0	0	0.090
2	0	0	0.099
3	−1	−1	0.028
4	0	0	0.112
5	0	1.414	0.171
6	0	−1.414	0.052
7	1.414	0	0.214
8	0	0	0.126
9	1	−1	0.162
10	1	1	0.251
11	−1.414	0	0.001
12	−1	1	0.041
13	0	0	0.105

. Dimension deviation ranged from 0.001 mm to 0.251 mm.

Regression analysis gave the equation

def = 0.11058 + 0.08138·Ae + 0.03457·f,

(1)

The results of the statistical processing such as coefficients, model summary, analysis of variance are shown in

Table 3. Coefficients.

Term	Coef	SE Coef	95% CI	T-Value	p-Value	VIF
Constant	0.11058	0.00458	(0.10037, 0.12079)	24.13	0.000
Ae	0.08138	0.00584	(0.06836, 0.09440)	13.93	0.000	1.00
fz	0.03457	0.00584	(0.02155, 0.04759)	5.92	0.000	1.00

,

Table 4. Model summary.

S	R-sq	R-sq (adj)	PRESS	R-sq (pred)	AICc	BIC
0.0165261	95.82%	94.98%	0.0051733	92.07%	−60.19	−62.93

and

Table 5. Analysis of variance.

Source	DF	Seq SS	Contribution	Adj SS	Adj MS	F-Value	p-Value
Regression	2	0.062541	95.82%	0.062541	0.031270	114.50	0.000
Ae	1	0.052979	81.17%	0.052979	0.052979	193.98	0.000
fz	1	0.009562	14.65%	0.009562	0.009562	35.01	0.000
Error	10	0.002731	4.18%	0.002731	0.000273
Lack of Fit	6	0.001995	3.06%	0.001995	0.000332	1.81	0.295
Pure Error	4	0.000737	1.13%	0.000737	0.000184
Total	12	0.065272	100.00%

.

The Pareto chart presented in Figure 4 ranks the standardized effects of the model terms from most to least influential with respect to the response variable. A reference line indicating the threshold for statistical significance is included. It is evident that both factors—the radial depth of cut (A_e) and feed per tooth (f_z)—exceed this threshold, confirming their significant contribution to the response. This graphical validation is consistent with the numerical findings from the regression and reinforces the importance of both parameters in predicting deformation during side milling.

The standardized residuals, defined as the ratio between the raw residuals and their estimated standard deviation, provide a reliable diagnostic tool for assessing model adequacy. Unlike raw residuals, standardized values offer a consistent scale for comparison. As illustrated in Figure 5 and Figure 6, all residuals fall within the range of ±2, indicating the absence of outliers or gross deviations. This observation supports the assumption that the regression model satisfies the fundamental conditions of normality, linearity, and homoscedasticity, and thus can be considered statistically robust. The histogram of the response (Figure 7) and the plot of residuals versus order (Figure 8) further confirm the absence of systematic errors or trends over time.

Both factors had a statistically significant positive effect (p < 0.001), with Ae contributing 81.17% and f contributing 14.65% to the total variance −R² = 95.82%. The high predictive ability—R²(pred) = 92.07%—confirms the reliability of the model.

The results of the ANOVA—F-value = 114.50 and p < 0.001—and residual diagnostics—normal plots and Pareto plots—showed no significant deviations [17].

Figure 9 and Figure 10 present the main effects plots for the two investigated factors—the radial depth of cut (A_e) and feed per tooth (f_z), respectively—based on measured and model-predicted deformation values. It is clearly visible that the lines are not horizontal, indicating the presence of statistically significant main effects for both factors. This confirms that variations in Ae and f lead to notable changes in deformation, with the influence of Ae being more pronounced. The regression results show that Ae accounts for 81.17% of the total deformation variation, while f contributes 14.65%. The alignment between the experimental and predicted average values, supported by the high coefficient of determination (R² = 95.82%), further validates the adequacy of the developed regression model.

Figure 11 illustrates the interaction plot between Ae and f. The non-parallel lines indicate a significant interaction effect, meaning that the impact of one factor on deformation depends on the level of the other. This interaction becomes especially evident at higher values of the radial depth of cut. The presence of this interaction suggests that optimal cutting performance cannot be achieved by tuning only one parameter, and both factors must be considered simultaneously in process optimization for side milling.

4. Discussion

The dominant influence of Ae on deformation aligns with theoretical expectations, as increased radial depth intensifies cutting forces and cutting temperature. The linear relationship suggests that even small changes in Ae can significantly affect stability [18]. The high R² value highlights the model’s efficiency, although this study was limited to a constant cutting speed (V_c). Future research should investigate the interactions between V_c, A_e, and f_z [19].

5. Conclusions

This study successfully quantified the influence of radial depth (A_e) and feed per tooth (f_z) on dimensions’ errors during side milling. Main findings include the following:

• The radial depth of cut (A_e) is the dominant factor, responsible for 81.17% of variance.
• Feed per tooth (f_z) has a secondary, yet statistically significant effect.
• The regression model provides a reliable tool for predicting deformations and optimizing parameters.

These results are beneficial for manufacturers seeking to improve machining accuracy and extend tool life. Future studies should incorporate dynamic cutting conditions and various workpiece geometries.