Solving the Inter-Ring Distances Optimization Problem for Pentapolar and Sextopolar Concentric Ring Electrodes Based on the Negligible Dimensions Model of the Electrode †
Abstract
:1. Introduction
2. Methods
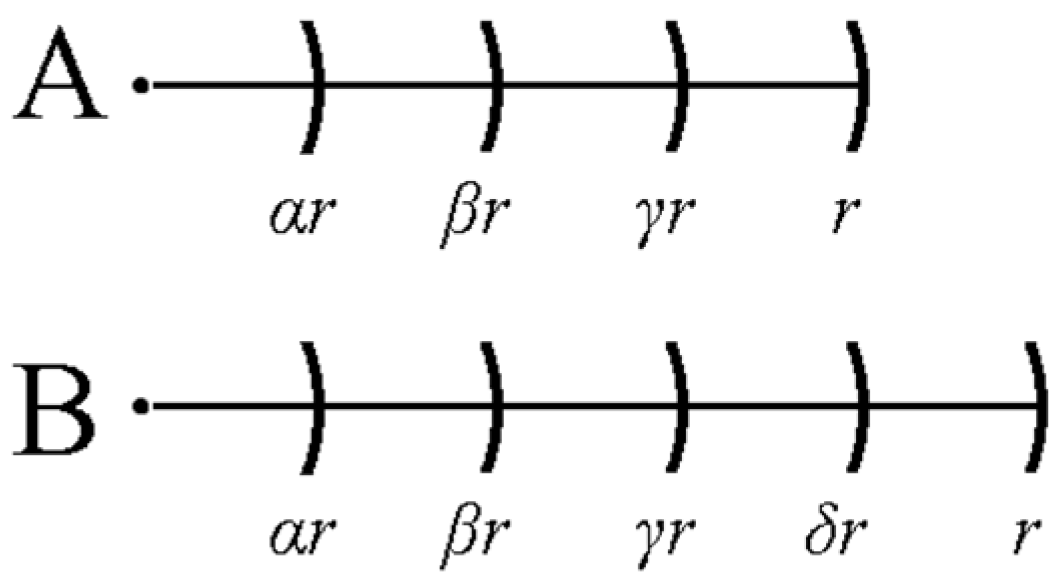
2.1. Defining the Inter-Ring Distances Optimization Problem for PCRE and SCRE Configurations
2.2. Solving the Inter-Ring Distances Optimization Problem for PCRE and SCRE Configurations
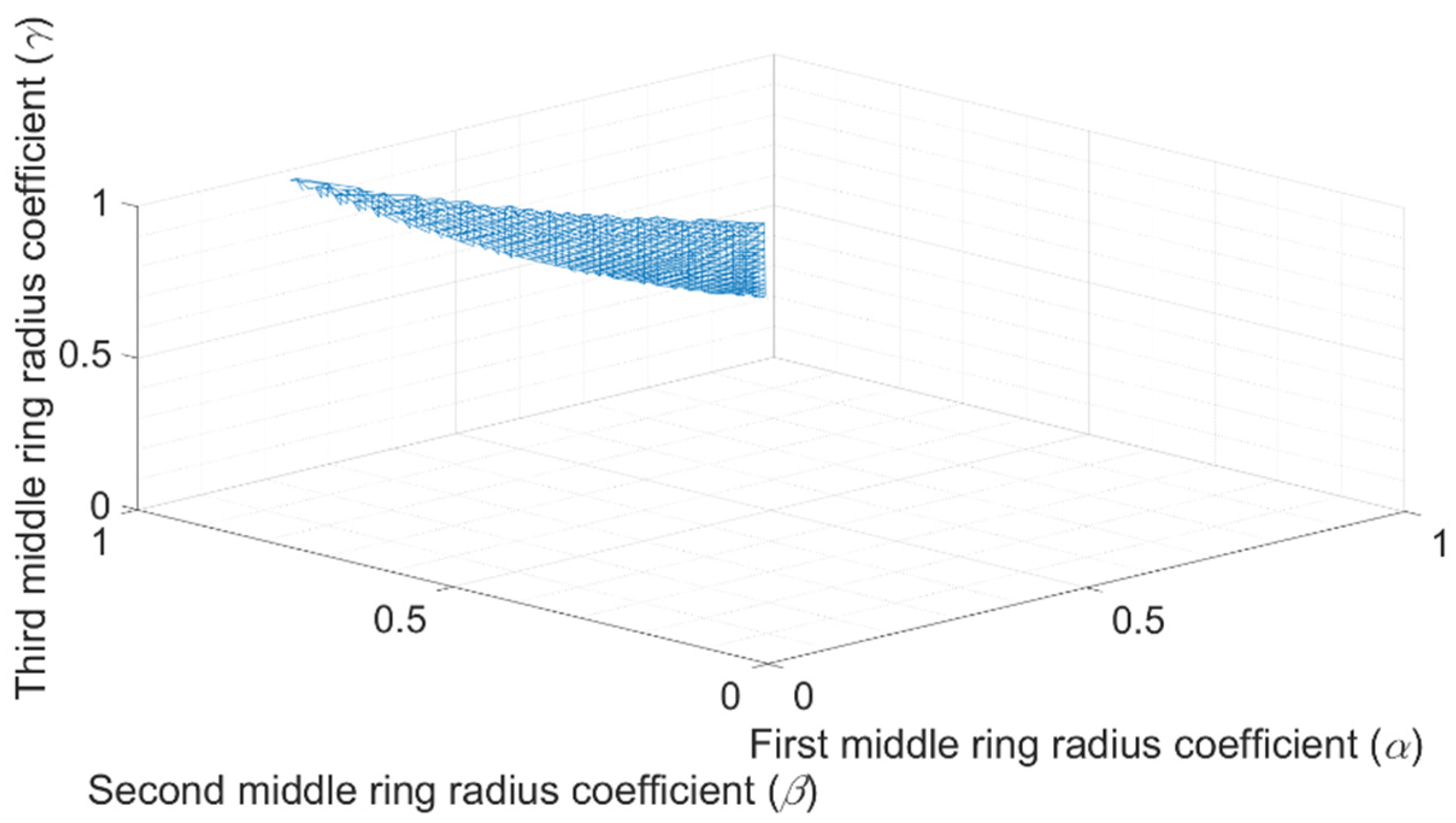
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, K.; Parekh, U.; Pailla, T.; Garudadri, H.; Gilja, V.; Ng, T.N. Stretchable Dry Electrodes with Concentric Ring Geometry for Enhancing Spatial Resolution in Electrophysiology. Adv. Healthc. Mater. 2017, 6, 1700552. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zena-Giménez, V.; Garcia-Casado, J.; Ye-Lin, Y.; Garcia-Breijo, E.; Prats-Boluda, G. A Flexible Multiring Concentric Electrode for Non-Invasive Identification of Intestinal Slow Waves. Sensors 2018, 18, 396. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Prats-Boluda, G.; Ye-Lin, Y.; Pradas-Novella, F.; Garcia-Breijo, E.; Garcia-Casado, J. Textile Concentric Ring Electrodes: Influence of Position and Electrode Size on Cardiac Activity Monitoring. J. Sens. 2018, 2018, e7290867. [Google Scholar] [CrossRef]
- Nasrollaholhosseini, S.H.; Mercier, J.; Fischer, G.; Besio, W. Electrode-Electrolyte Interface Modeling and Impedance Characterizing of Tripolar Concentric Ring Electrode. IEEE Trans. Biomed. Eng. 2019, 66, 2897–2905. [Google Scholar] [CrossRef] [PubMed]
- Toole, C.; Martinez-Juárez, I.E.; Gaitanis, J.N.; Sunderam, S.; Ding, L.; DiCecco, J.; Besio, W.G. Source Localization of High-Frequency Activity in Tripolar Electroencephalography of Patients with Epilepsy. Epilepsy Behav. 2019, 101, 106519. [Google Scholar] [CrossRef] [PubMed]
- Makeyev, O.; Musngi, M.; Moore, L.; Ye-Lin, Y.; Prats-Boluda, G.; Garcia-Casado, J. Validating the Comparison Framework for the Finite Dimensions Model of Concentric Ring Electrodes Using Human Electrocardiogram Data. Appl. Sci. 2019, 9, 4279. [Google Scholar] [CrossRef] [Green Version]
- Garcia-Casado, J.; Ye-Lin, Y.; Prats-Boluda, G.; Makeyev, O. Evaluation of Bipolar, Tripolar, and Quadripolar Laplacian Estimates of Electrocardiogram via Concentric Ring Electrodes. Sensors 2019, 19, 3780. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Aghaei-Lasboo, A.; Inoyama, K.; Fogarty, A.S.; Kuo, J.; Meador, K.J.; Walter, J.J.; Le, S.T.; Graber, K.D.; Razavi, B.; Fisher, R.S. Tripolar Concentric EEG Electrodes Reduce Noise. Clin. Neurophysiol. 2020, 131, 193–198. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Makeyev, O.; Besio, W. Improved Spatial Resolution of Electroencephalogram Using Tripolar Concentric Ring Electrode Sensors. J. Sens. 2020, 2020, 6269394. [Google Scholar] [CrossRef]
- Estrada-Petrocelli, L.; Torres, A.; Sarlabous, L.; Rafols-de-Urquia, M.; Ye-Lin, Y.; Prats-Boluda, G.; Jane, R.; Garcia-Casado, J. Evaluation of Respiratory Muscle Activity by Means of Concentric Ring Electrodes. IEEE Trans. Biomed. Eng. 2021, 68, 1005–1014. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Casado, J.; Prats-Boluda, G.; Ye-Lin, Y.; Restrepo-Agudelo, S.; Perez-Giraldo, E.; Orozco-Duque, A. Evaluation of Swallowing Related Muscle Activity by Means of Concentric Ring Electrodes. Sensors 2020, 20, 5267. [Google Scholar] [CrossRef] [PubMed]
- Makeyev, O. Solving the General Inter-Ring Distances Optimization Problem for Concentric Ring Electrodes to Improve Laplacian Estimation. Biomed. Eng. Online 2018, 17, 117. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Makeyev, O.; Besio, W.G. Improving the Accuracy of Laplacian Estimation with Novel Variable Inter-Ring Distances Concentric Ring Electrodes. Sensors 2016, 16, 858. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Makeyev, O.; Ding, Q.; Besio, W.G. Improving the Accuracy of Laplacian Estimation with Novel Multipolar Concentric Ring Electrodes. Measurement 2016, 80, 44–52. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- King, M.R.; Mody, N.A. Numerical and Statistical Methods for Bioengineering: Applications in MATLAB; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]

| Percentile | Tripolar CRE | Quadripolar CRE | PCRE | SCRE | ||||
|---|---|---|---|---|---|---|---|---|
| m | R2 | m | R2 | m | R2 | m | R2 | |
| 1st | 0.098 | - | 0.094 | 0.997 | 0.096 | 0.989 | 0.092 | 0.986 |
| 3rd | 0.171 | - | 0.166 | 0.998 | 0.165 | 0.994 | 0.158 | 0.991 |
| 5th | 0.221 1 | - | 0.214 1 | 0.998 1 | 0.213 | 0.995 | 0.204 | 0.992 |
| 10th | 0.313 1 | - | 0.303 1 | 0.998 | 0.3 | 0.996 | 0.288 | 0.991 |
| 15th | 0.383 | - | 0.372 | 0.998 | 0.367 | 0.995 | 0.352 | 0.99 |
| 20th | 0.442 | - | 0.43 | 0.998 | 0.424 | 0.995 | 0.407 | 0.989 |
| 25th | 0.494 | - | 0.481 | 0.998 | 0.474 | 0.994 | 0.455 | 0.987 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Makeyev, O.; Lee, A.; Begay, A. Solving the Inter-Ring Distances Optimization Problem for Pentapolar and Sextopolar Concentric Ring Electrodes Based on the Negligible Dimensions Model of the Electrode. Eng. Proc. 2021, 10, 8. https://doi.org/10.3390/ecsa-8-11280
Makeyev O, Lee A, Begay A. Solving the Inter-Ring Distances Optimization Problem for Pentapolar and Sextopolar Concentric Ring Electrodes Based on the Negligible Dimensions Model of the Electrode. Engineering Proceedings. 2021; 10(1):8. https://doi.org/10.3390/ecsa-8-11280
Chicago/Turabian StyleMakeyev, Oleksandr, Alana Lee, and Ashton Begay. 2021. "Solving the Inter-Ring Distances Optimization Problem for Pentapolar and Sextopolar Concentric Ring Electrodes Based on the Negligible Dimensions Model of the Electrode" Engineering Proceedings 10, no. 1: 8. https://doi.org/10.3390/ecsa-8-11280
APA StyleMakeyev, O., Lee, A., & Begay, A. (2021). Solving the Inter-Ring Distances Optimization Problem for Pentapolar and Sextopolar Concentric Ring Electrodes Based on the Negligible Dimensions Model of the Electrode. Engineering Proceedings, 10(1), 8. https://doi.org/10.3390/ecsa-8-11280






