Chalcogen–Nitrogen Bond: Insights into a Key Chemical Motif ^†

Abstract

Chalcogen–nitrogen chemistry deals with systems in which sulfur, selenium or tellurium is linked to a nitrogen nucleus. This chemical motif is a key component of different functional structures, ranging from inorganic materials and polymers to rationally designed catalysts, to bioinspired molecules and enzymes. The formation of a selenium–nitrogen bond, and its disruption, are rather common events in organic Se-catalyzed processes. In nature, along the mechanistic path of glutathione peroxidase, evidence of the formation of a Se–N bond in highly oxidizing conditions has been reported and interpreted as a strategy to protect the selenoenzyme from overoxidation. Selenium is also bonded to nitrogen in the well-known ebselen, a selenenylamide with antioxidant, antimicrobic and cytoprotective activity and its formation/disruption has a crucial role for its pharmacological action. Focusing on examples taken from selenium organic chemistry and biochemistry, the selenium–nitrogen bond is described, and its strength and reactivity are quantified using accurate computational methods applied to model molecular systems. Significant trends show up when comparing to sulfur/tellurium–nitrogen bonds, also reaffirming the peculiar and valuable role of selenium in chemistry and life in this context.

1. Introduction

The chalcogen–nitrogen bond (X–N, X = S, Se, Te) is an important motif in chemistry present in many different structures, ranging from inorganic and organic materials, catalysts, protein mimics, and potential drugs [1,2,3,4]. In the lab, the formation of an X–N bond is typically obtained from benzanilide, using ortholithiation, chalcogen insertion, and oxidative cyclization [5,6,7,8], and by intramolecular cyclocondensation of chalcogenic acids [9,10,11].

The Se–N bond is present in the isoselenazole ring of ebselen (2-phenyl-1,2-benzisoselenazol-3(2H)-one), which is described as the oldest and most popular glutathione peroxidase (GPx) mimic. So far, the mechanistic details of its catalytic activity have not been fully elucidated [12,13,14,15,16], although a computational investigation has provided an exhaustive picture of the possible paths [17], disclosing that the chemistry of the Se–N bond plays a crucial role in triggering the antioxidant effects [3,18].

Importantly, it has been demonstrated that ebselen is a potent inhibitor of the SARS-CoV-2 main protease (Mpro), suggesting its potential therapeutic use for COVID-19 treatment. The reaction between the thiol moiety from the cysteine residue of Mpro active site and the isoselenazole ring can break the Se–N bond, leading to the formation of an Se–S bond and subsequent enzyme inhibition [19,20].

An early overview on the structure and on the electronic as well as steric features of Se–N and Te–N bonds was reported by Bjorgvinsson and Roesky in 1991 [21]. The structures of several X–N bond-containing heterocycles were also reported. Mahmudov and colleagues provided an updated perspective on the relevance of covalent and non-covalent chalcogen bonding in several trending branches of modern solid state and solution chemistry. Organic and inorganic synthesis, catalysis, material sciences and molecular recognition are just some of the fields in which the X–N bond can direct and assist chemical reactivity [22].

In biochemistry and medicinal chemistry, besides ebselen and other GPx mimics, compounds based on heterocyclic scaffolds containing one or multiple Se–N bonds are being studied as antibiotic, antifungal, anticancer, anti-inflammatory, analgesic, and antimicrobial agents [1,3,14]. Particularly, selenazolinium salts appear as promising candidates because of their good reactivity and selectivity towards thiol groups in peptides, proteins, and enzymes [23].

In this work, the X–N bond is described and its strength and reactivity changes upon varying the chalcogen are quantified using accurate computational methods applied to model molecular systems, which enable the drawing of conclusions of general validity for the very different systems above described.

2. Methods

All calculations were performed with the Amsterdam Density Functional (ADF) program [24,25]. Geometry optimizations were performed with the GGA BLYP functional [26,27,28,29] in conjunction with a triple-ζ slater basis set with a double set of polarization functions (TZ2P). Core electrons were kept frozen: up to 1s for C and N, up to 2p for S, up to 3p for Se, and up to 4p for Te, and the zeroth-order regular approximation (ZORA) was used to take relativistic effects into account [30,31,32,33]. Grimme’s empirical dispersion correction with Becke–Johnson damping was added to correct the underestimation of non-bonded forces by this functional [34]. This level of theory will be referred to as ZORA-BLYP-D3(BJ)/TZ2P. For the bonding analysis, based on the activation strain model [35,36], a more accurate level of theory was employed, i.e., using a full electron quadruple-ζ slater basis set (QZ4Pae). Moreover, the bonding analysis was carried out with the meta-hybrid M06-2X functional [37,38] due to its excellent performance with radical systems [39]. Single points calculation performed at this level of theory are denoted as ZORA-M06-2X/QZ4Pze//ZORA-BLYP-D3(BJ)/TZ2P. The X–N bond strength was calculated as the interaction energy between the two molecular fragments obtained after homolytic cleavage.

3. Results

The models chosen for the analysis of the chalcogen–nitrogen bonds have the general formula RX–NR’₂ in which X can be S, Se or Te, and R and R’ vary between H, CH₃ and CF₃. A selection of optimized molecular structures is reported in Figure 1.

Analysis of the optimized geometries showed how the X–N bond length can vary upon changing the chalcogen or the substituents R and R’. Particularly, descending along the group we assist in a lengthening of the bond with all substituents, caused by the increase in the van der Waals radius of the increasingly bigger chalcogen. The variation upon modification of the substituents in series with the same chalcogen is smaller and does not follow the same trend for all the chalcogens. However, the structures showing the longest and shortest bond length are the same for all the chalcogens with the combination having CF₃ on the chalcogen and CH₃ on the nitrogen displaying the shortest bond length, whereas the specular combination, i.e., R,R’=CH₃,CF₃ leads to the longest bond length (e.g., in the case of selenium the values are 1.86 and 1.92 Å).

To obtain a more exhaustive picture on the variation of the X–N bond strength upon changing the chalcogen or substituent, an accurate analysis on the interaction energy between the two molecular fragments obtained after homolytic cleavage of the X–N bond was carried out at two different levels of theory. The reaction investigated was:

RX–NR’₂ → RX^• + ^•NR’₂ (X = S, Se or Te; R,R’=H, CH₃ or CF₃)

(1)

Results, reported in

Table 1. ∆E_int for the model molecules. Structure definitions are reported in Figure 1. Level of theory: ZORA-M06-2X/QZ4Pze//ZORA-BLYP-D3(BJ)/TZ2P.

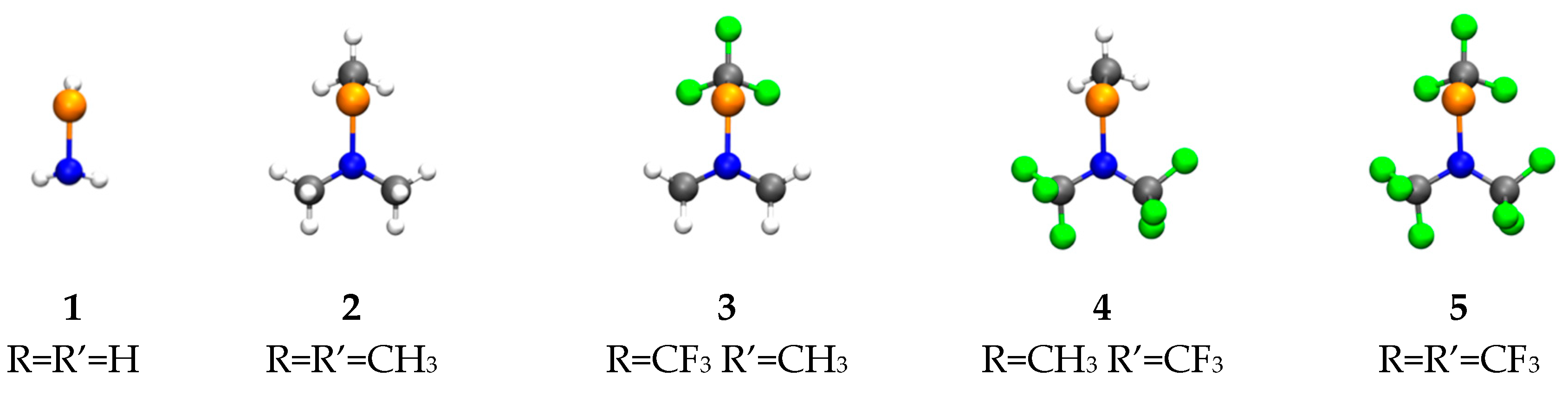
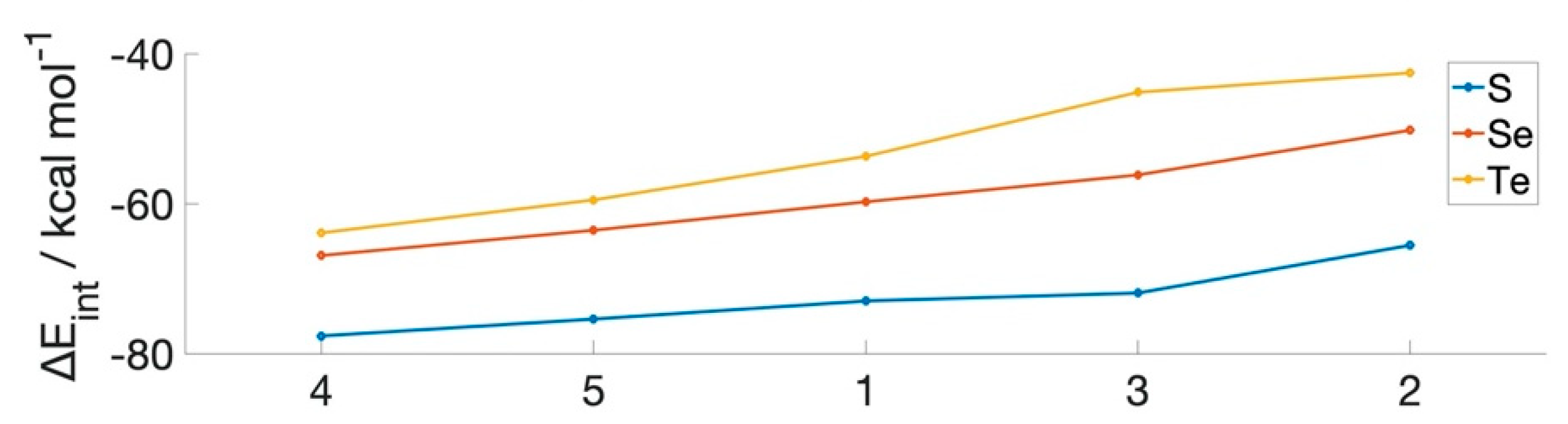
RX–NR’2			∆Eint (kcal mol−1)
Molecule	R	R’	S	Se	Te
1	H	H	−73.0	−59.8	−53.7
2	CH3	CH3	−65.5	−50.2	−42.6
3	CF3	CH3	−71.9	−56.2	−45.1
4	CH3	CF3	−77.6	−66.9	−63.9
5	CF3	CF3	−75.4	−63.5	−59.5

, show how the interaction diminishes as the chalcogen atom increases in size. For example, with R,R’=CH₃, it rises from −65.5 kcal mol⁻¹ in the presence of sulfur to −42.6 in the presence of tellurium. The same trend is found for all the substituents combination, and also when energies are computed with the accurate M06-2X functional combined with the QZ4Pae basis set (Table 1).

If we focus on the effect of the substituent effect, a clear trend is found that is common for all the chalcogens. The interaction energy becomes progressively less negative in the sequence 4 < 5 < 1 < 3 < 2 (Figure 2).

4. Discussion

The orbital analysis of the radical fragments obtained after homolytic cleavage of the X–N bond shows that upon variation of the chalcogen atom along the group, we assist a decrease in the interaction energy, which becomes less negative, due to the fact that the fragment containing the chalcogen has its singly occupied molecular orbital (SOMO) orbital that becomes progressively more diffused. This makes the fragment “softer”. On the other hand, the amino fragment contains a “hard” center, i.e., the N atom, and this worsens the interaction with the heavier chalcogens. The same behavior is found with all the different substituents, upon variation of the chalcogen.

The variation of the substituent on the interaction energy can be rationalized, analyzing the effects that the different moieties have on the orbitals responsible for the X–N bond. This translates to differently stabilized partially filled orbitals in the chalcogen and nitrogen molecular fragments depending on the substituent they contain. Electron donating substituents (e.g., CH₃) give rise to fragments with higher energy frontier orbitals, whereas electron withdrawing ones (e.g., CF₃) form fragments with lower frontier energy orbitals. Moreover, energetic separation of the two SOMOs is related to ∆E_int and the calculations show that if the gap between the two SOMOs increases, the interaction energy becomes more stabilizing, due to the formation of a more stabilized filled orbital.

5. Conclusions

In this work, we have analyzed with modern quantum mechanical techniques the nitrogen–chalcogen bond. The results show that sulfur has a better interaction with nitrogen than selenium or tellurium due to the higher “hardness” of sulfur with respect to the other chalcogens. Besides, a correlation between the electron donating and electron withdrawing character of the substituents and the orbital energy of the molecular fragments can explain the different interaction energy calculated for the different species. These results can open new perspectives on the fine tuning of the chalcogen–nitrogen bond amenable of application in many biological and pharmaceutical studies targeted towards the development of novel bio-active compounds and antioxidant drugs.