An Efficient Finite Element Model to Predict the Mechanical Response of Metallic-Reinforced Pressure Vessels
Abstract
1. Introduction
2. Materials and Methods
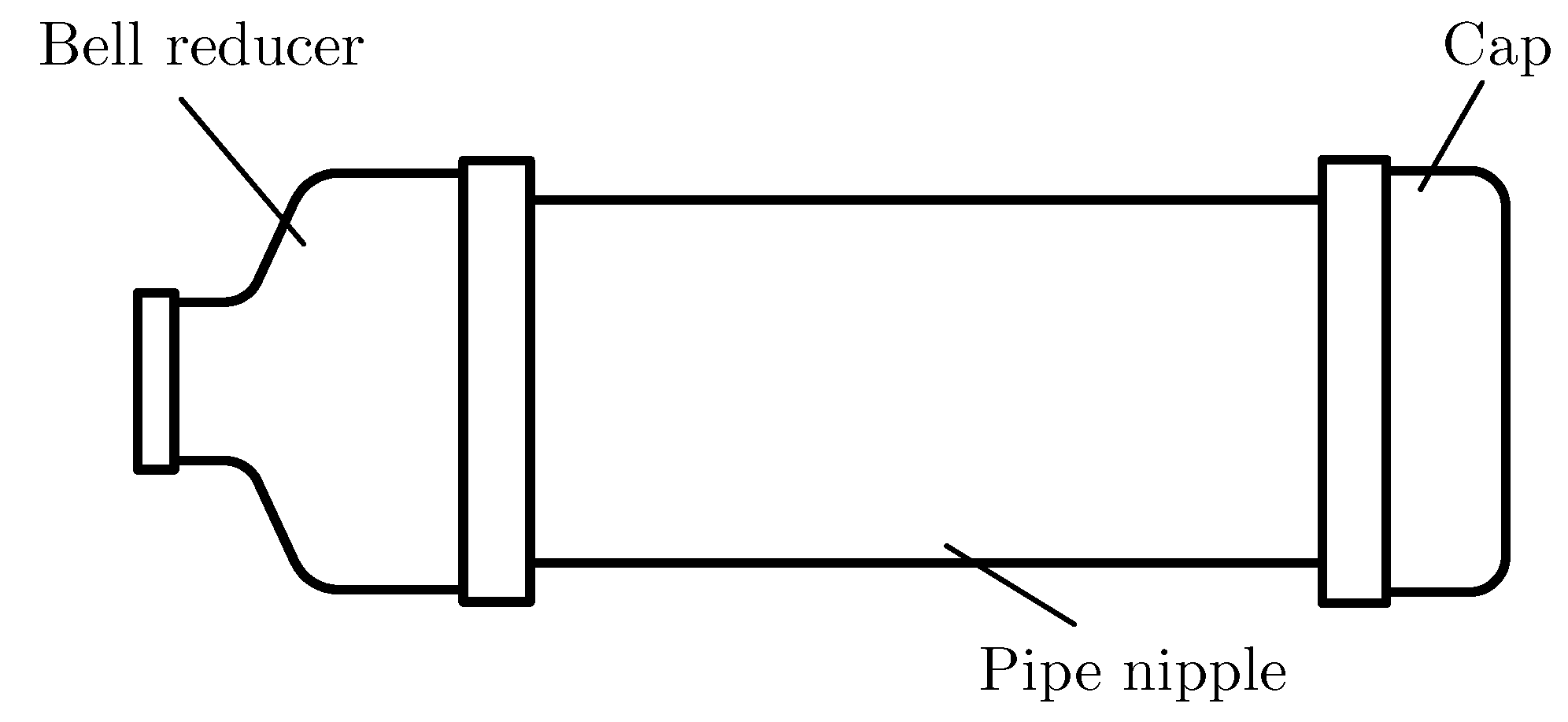
2.1. Pressure Vessel Geometry
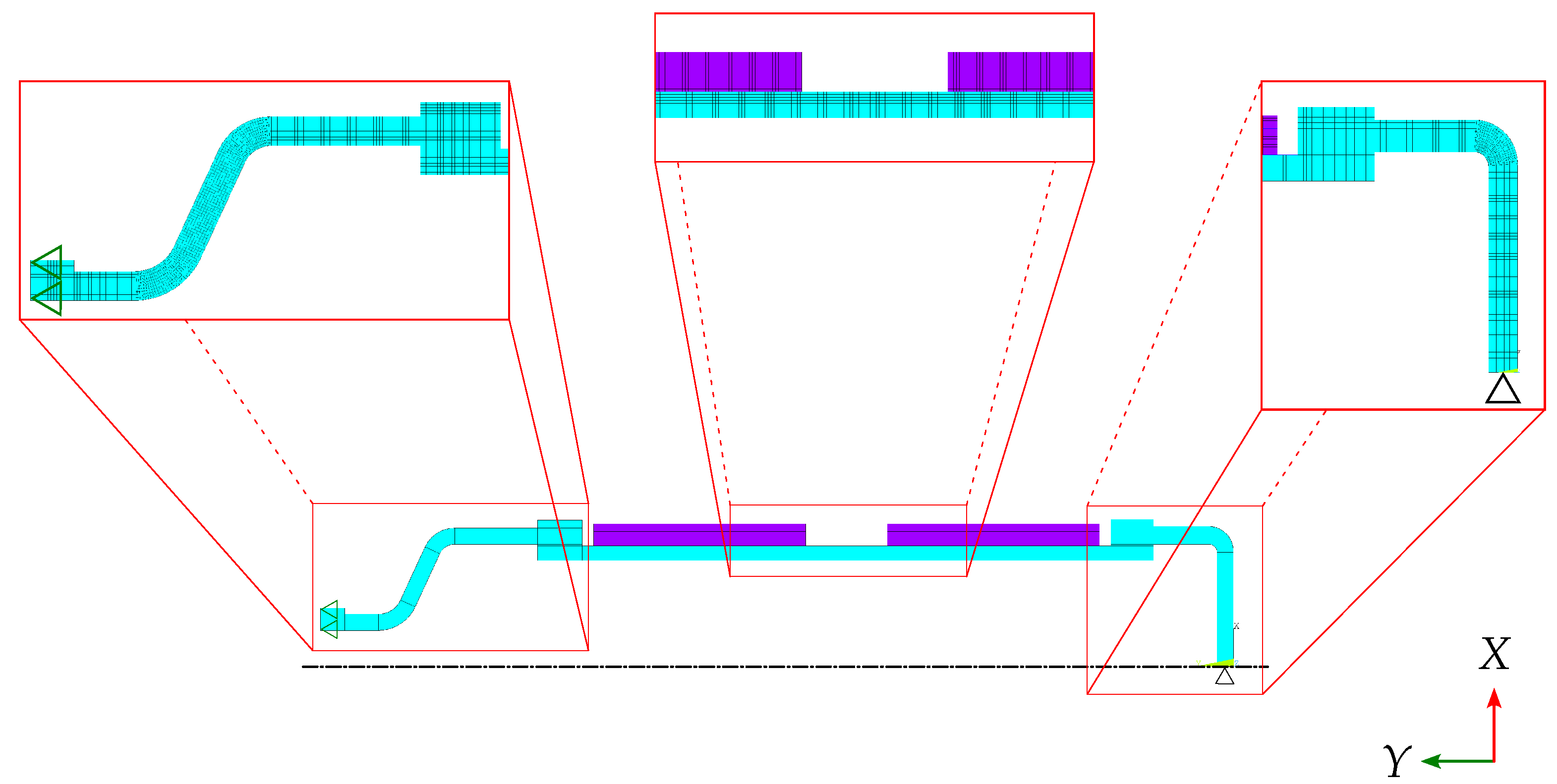
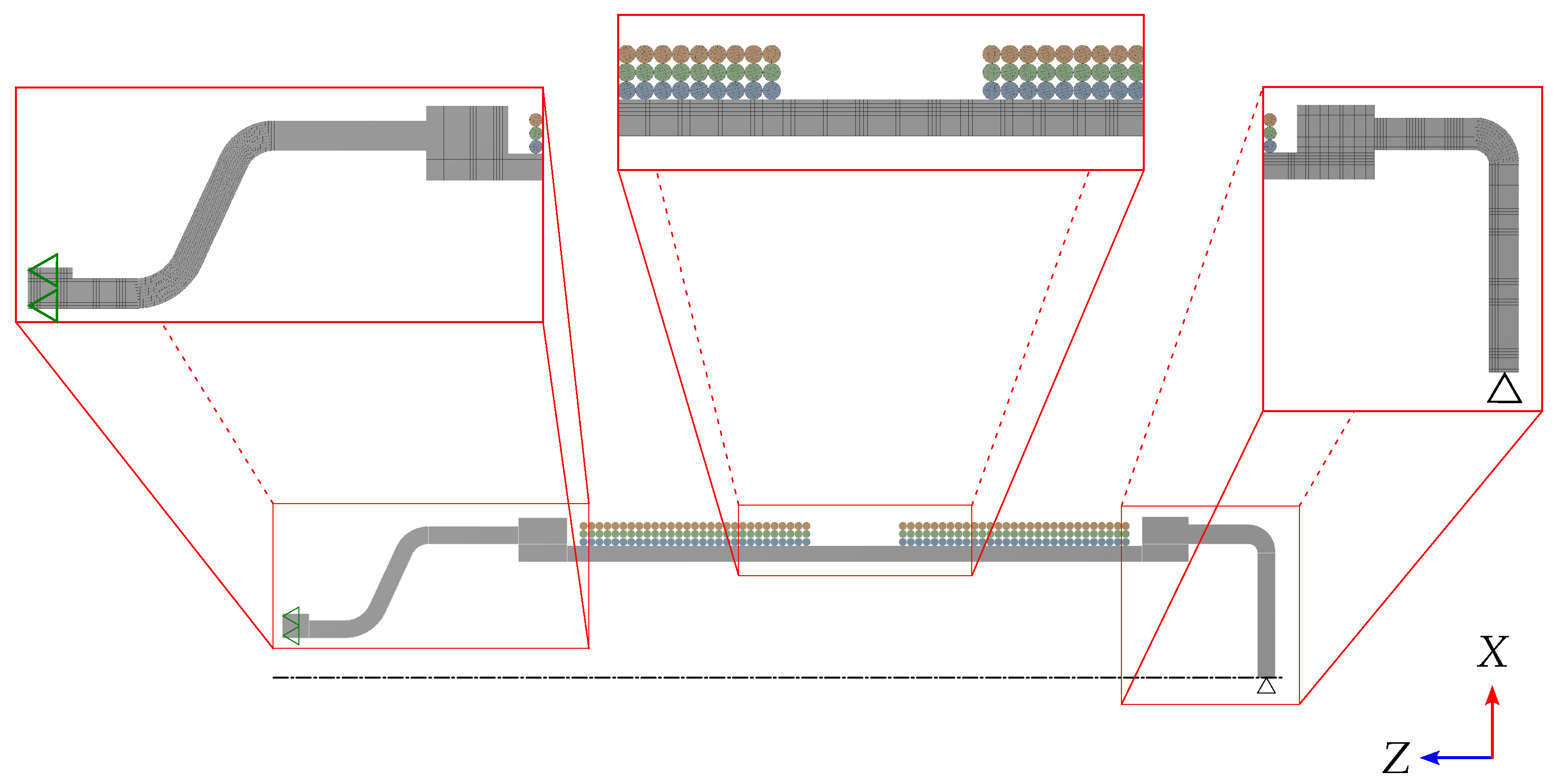
2.2. Finite Element Models
2.3. Prototype Fabrication
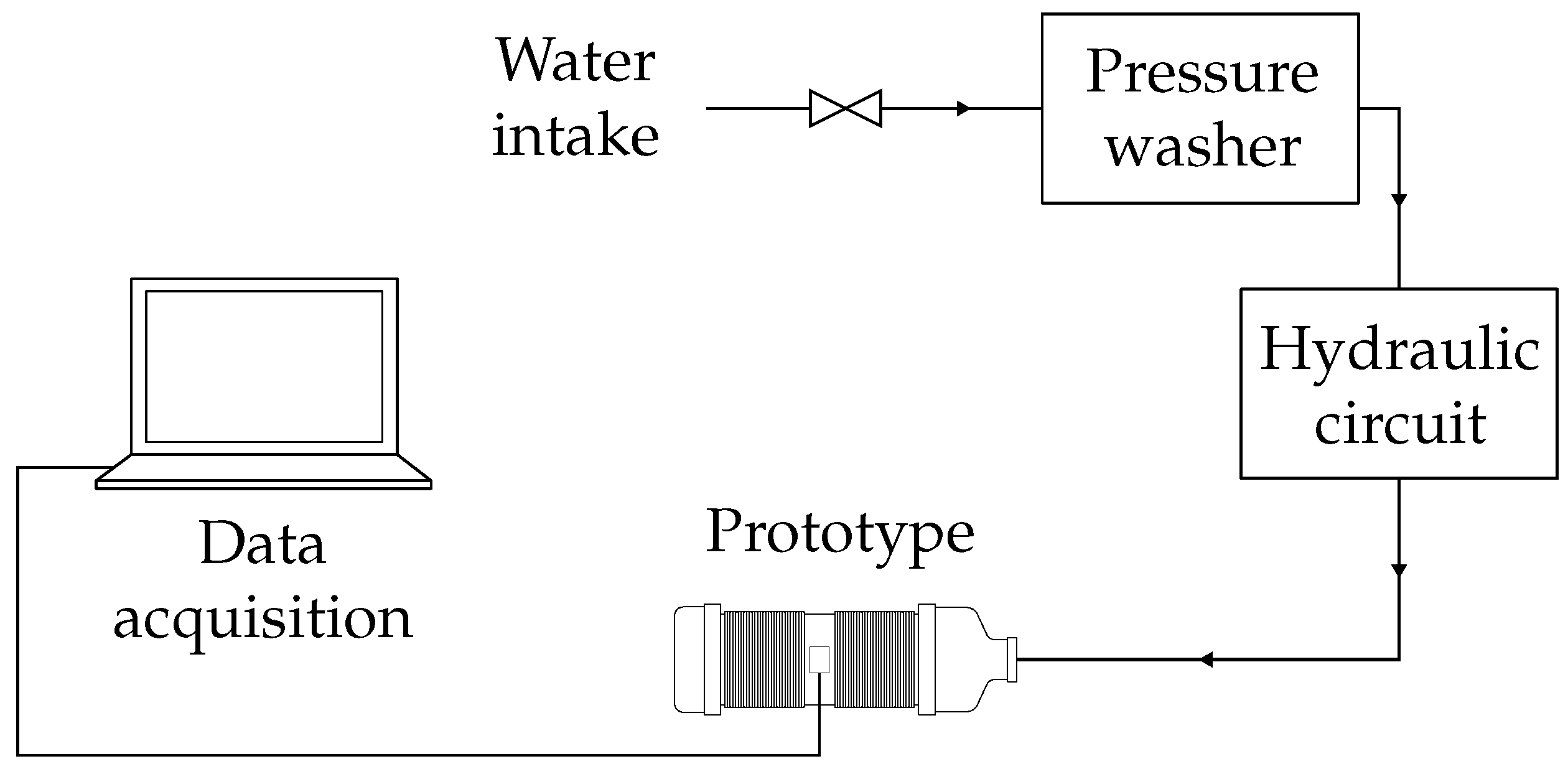
2.4. Experimental Setup
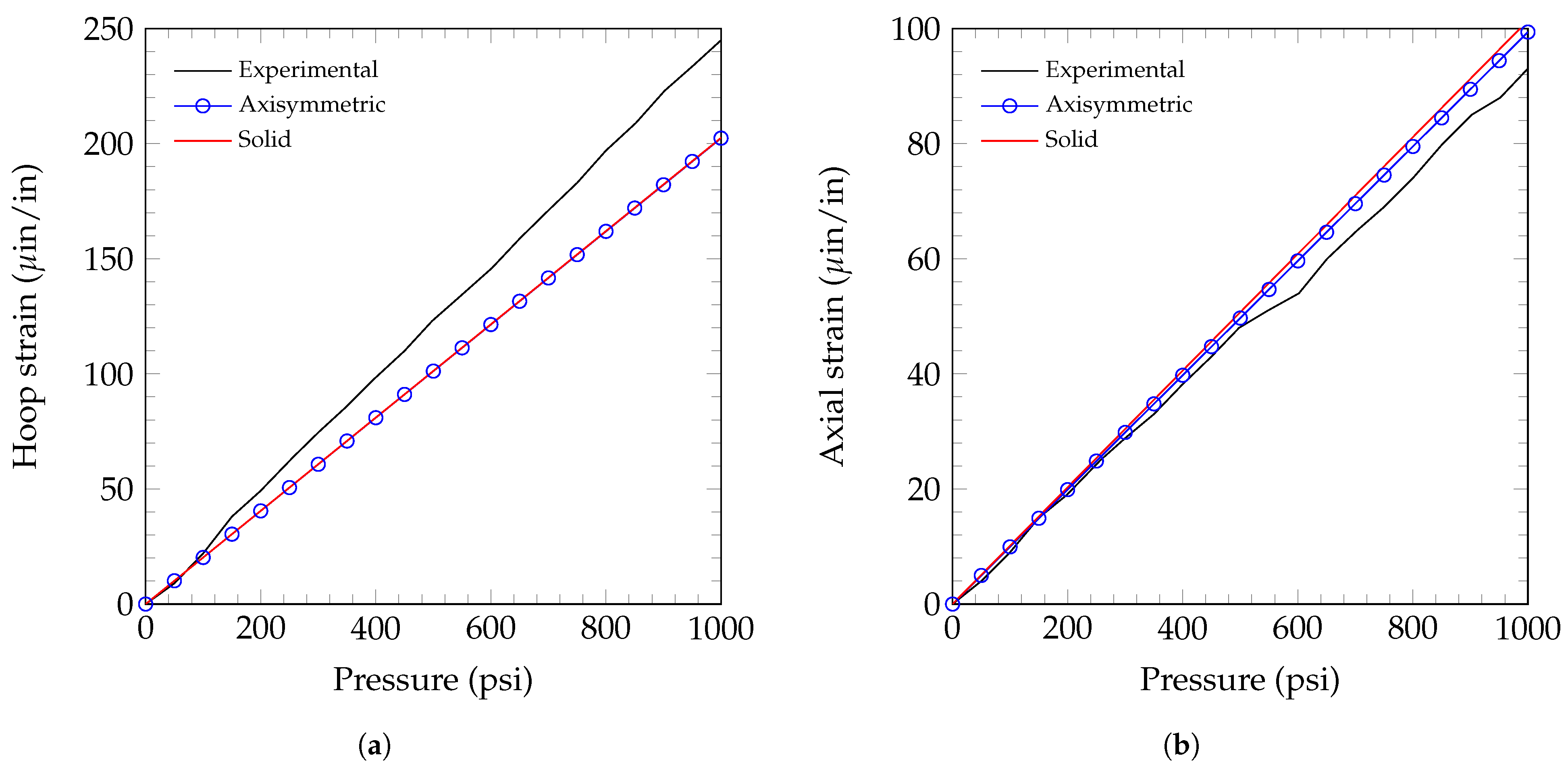
2.5. Validation
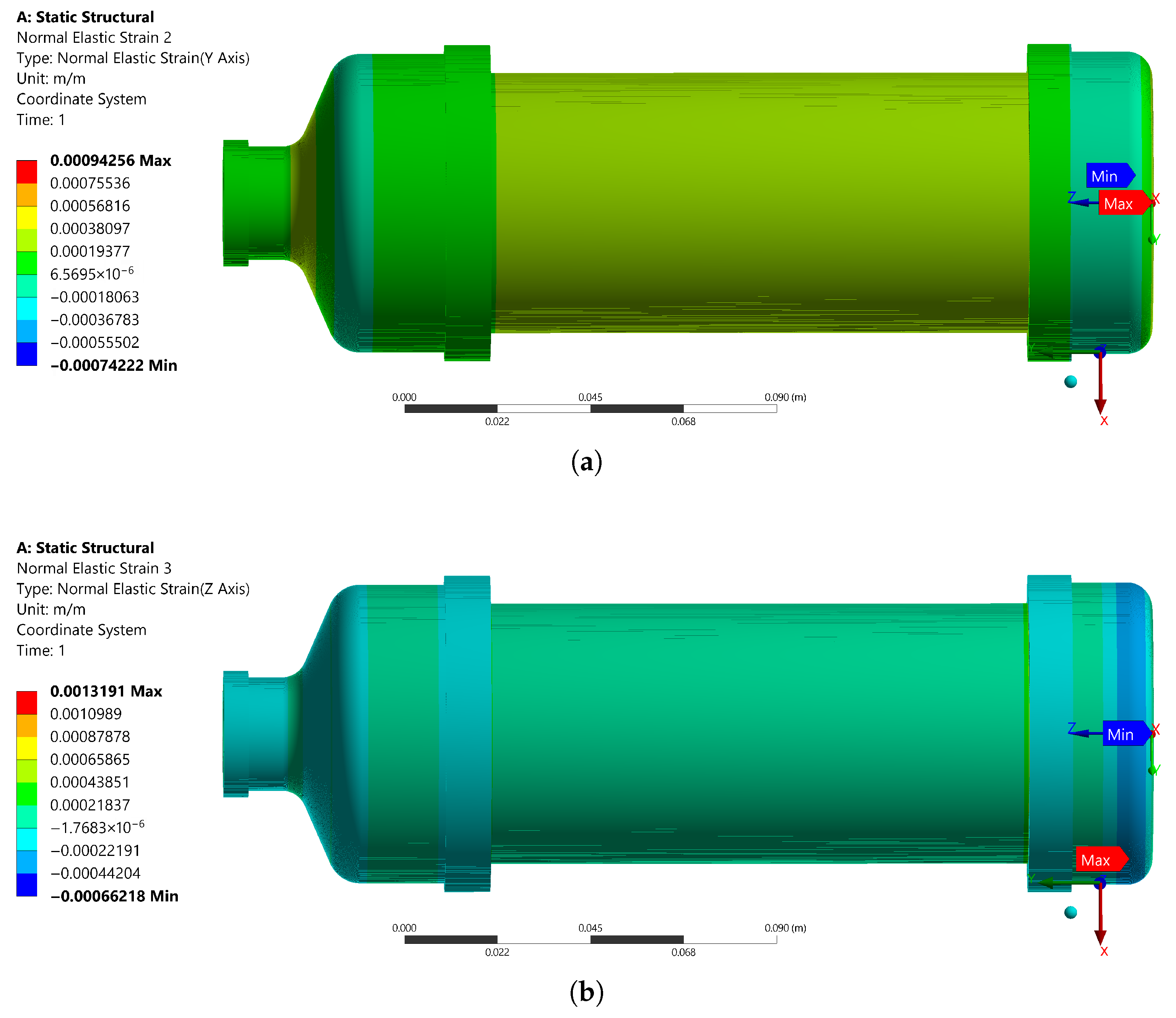
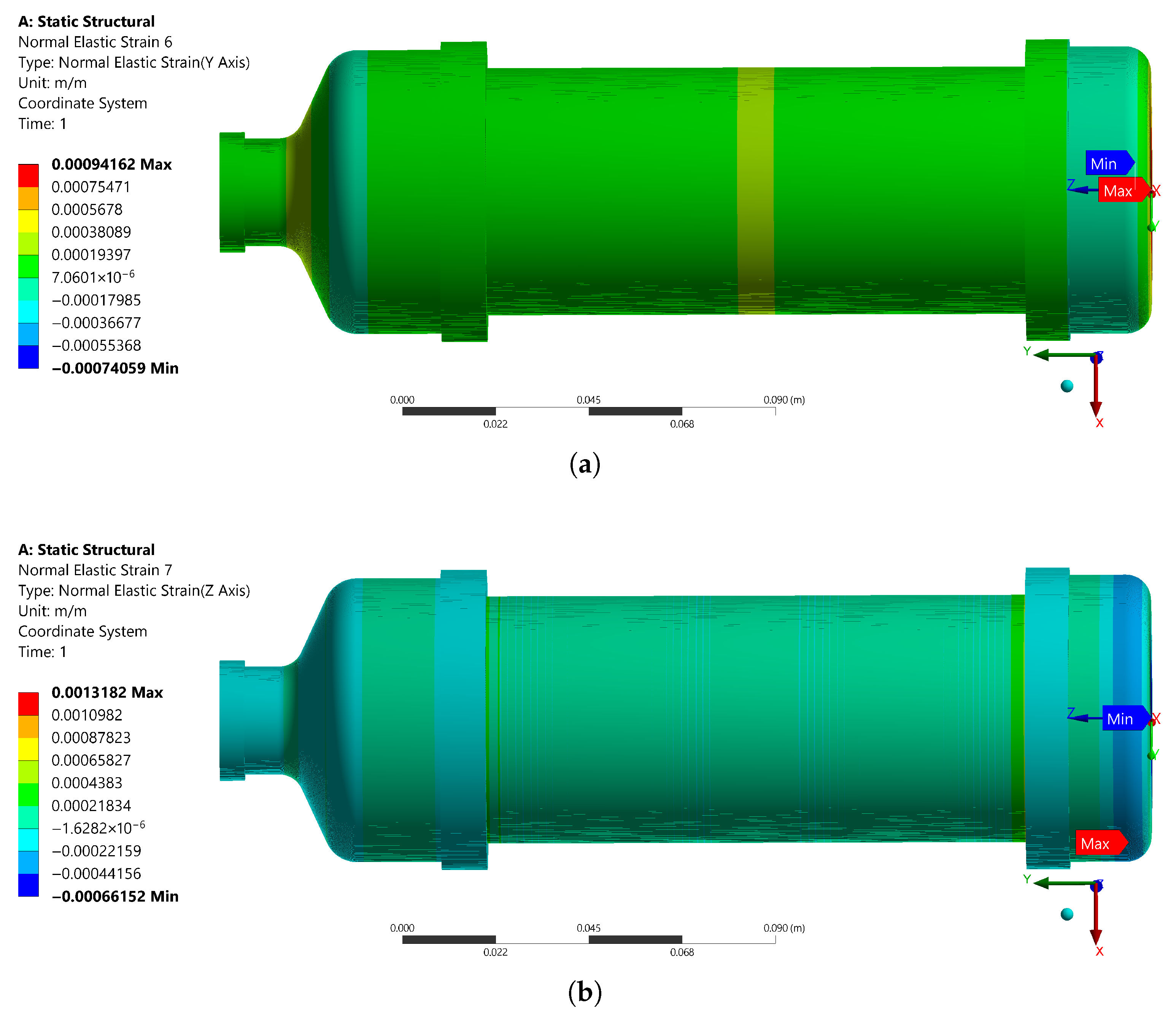
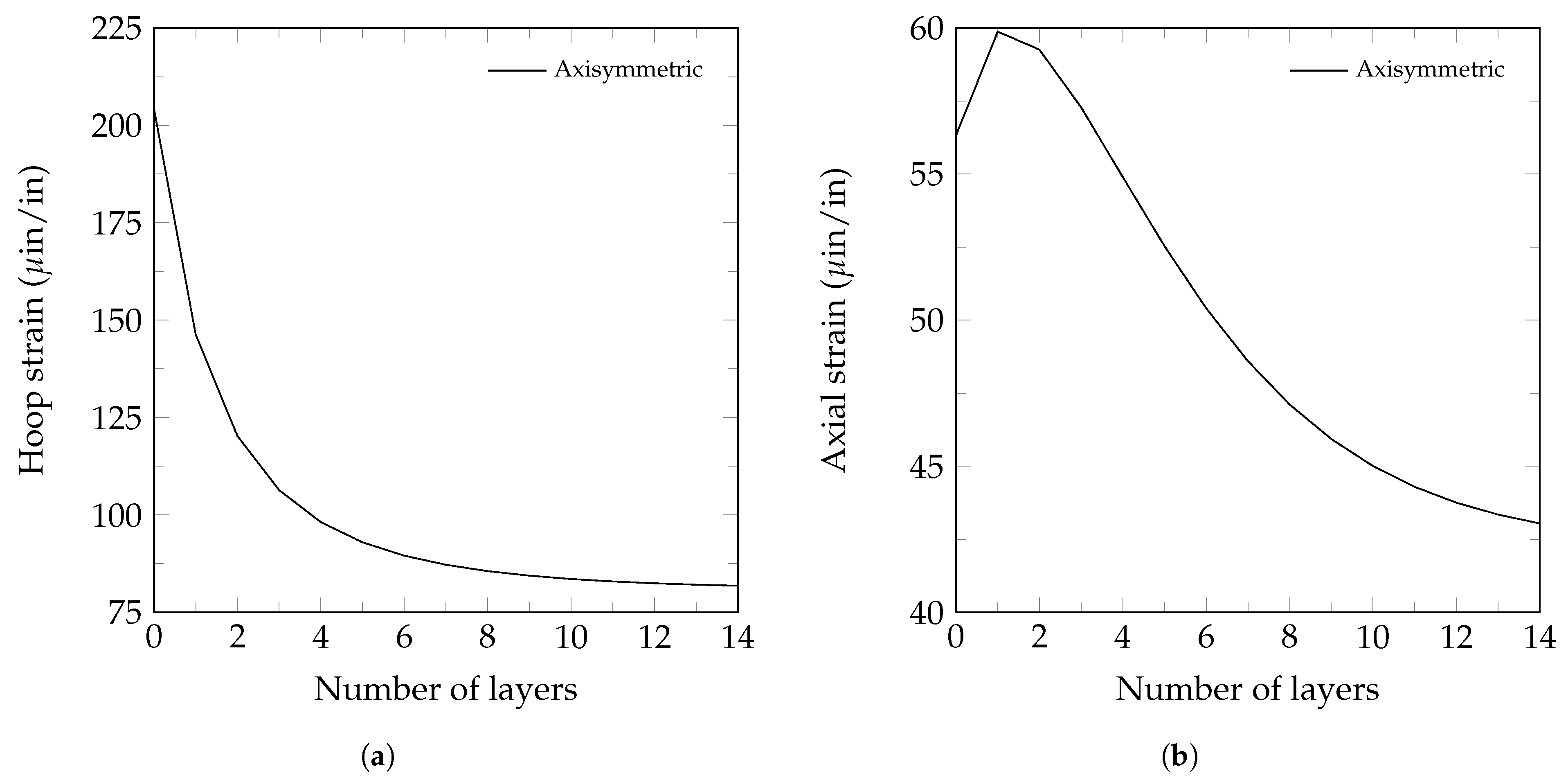
3. Numerical Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cheng, Q.; Zhang, R.; Shi, Z.; Lin, J. Review of common hydrogen storage tanks and current manufacturing methods for aluminium alloy tank liners. Int. J. Lightweight Mater. Manuf. 2024, 7, 269–284. [Google Scholar] [CrossRef]
- Ahad, M.T.; Bhuiyan, M.M.H.; Sakib, A.N.; Becerril Corral, A.; Siddique, Z. An overview of challenges for the future of hydrogen. Materials 2023, 16, 6680. [Google Scholar] [CrossRef]
- Kadirgama, K.; Samylingam, L.; Aslfattahi, N.; Kiai, M.S.; Kok, C.K.; Yusaf, T. Advancements and challenges in numerical analysis of hydrogen energy storage methods: Techniques, applications, and future direction. Int. J. Hydrogen Energy 2025, 125, 67–85. [Google Scholar] [CrossRef]
- Ma, N.; Zhao, W.; Wang, W.; Li, X.; Zhou, H. Large scale of green hydrogen storage: Opportunities and challenges. Int. J. Hydrogen Energy 2024, 50, 379–396. [Google Scholar] [CrossRef]
- Abdalla, A.M.; Hossain, S.; Nisfindy, O.B.; Azad, A.T.; Dawood, M.; Azad, A.K. Hydrogen production, storage, transportation and key challenges with applications: A review. Energy Convers. Manag. 2018, 165, 602–627. [Google Scholar] [CrossRef]
- Nachtane, M.; Tarfaoui, M.; Abichou, M.A.; Vetcher, A.; Rouway, M.; Aâmir, A.; Mouadili, H.; Laaouidi, H.; Naanani, H. An overview of the recent advances in composite materials and artificial intelligence for hydrogen storage vessels design. J. Compos. Sci. 2023, 7, 119. [Google Scholar] [CrossRef]
- Batul, B.; Sohail, A.; Aizaz, A.; Jamil, Z. Application of structural similitude for scaling of a pressure vessel. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Kuala Lumpur, Malaysia, 29–30 August 2019; IOP Publishing: Bristol, UK, 2019; Volume 642, p. 012004. [Google Scholar]
- Zhang, Q.; Xu, H.; Jia, X.; Zu, L.; Cheng, S.; Wang, H. Design of a 70 MPa type IV hydrogen storage vessel using accurate modeling techniques for dome thickness prediction. Compos. Struct. 2020, 236, 111915. [Google Scholar] [CrossRef]
- Kumar, S.S.; Bibin, C.; Ramachandran, M. Design and analysis of hydrogen storage tank with different materials by ansys. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Mumbai, India, 23–24 December 2019; IOP Publishing: Bristol, UK, 2020; Volume 810, p. 012016. [Google Scholar]
- Kwak, H.S.; Park, G.Y.; Kim, C. Design of compressed natural gas pressure vessel (Type II) to improve storage efficiency and structural reliability. J. Press. Vessel Technol. 2020, 142, 011303. [Google Scholar] [CrossRef]
- Park, G.; Jang, H.; Kim, C. Design of composite layer and liner for structure safety of hydrogen pressure vessel (type 4). J. Mech. Sci. Technol. 2021, 35, 3507–3517. [Google Scholar] [CrossRef]
- Nguyen, B.N.; Roh, H.S.; Merkel, D.R.; Simmons, K.L. A predictive modeling tool for damage analysis and design of hydrogen storage composite pressure vessels. Int. J. Hydrogen Energy 2021, 46, 20573–20585. [Google Scholar] [CrossRef]
- Celaya Garcia, L.; Gutierrez Rivera, M.; Ledesma Orozco, E.; Aceves, S.M.; Martinez Ramirez, I. Equivalent properties of pure metallic reinforcement for pressure vessels using the finite element method. J. Braz. Soc. Mech. Sci. Eng. 2021, 43. [Google Scholar] [CrossRef]
- Błachut, A.; Wollmann, T.; Panek, M.; Vater, M.; Kaleta, J.; Detyna, J.; Hoschützky, S.; Gude, M. Influence of fiber tension during filament winding on the mechanical properties of composite pressure vessels. Compos. Struct. 2023, 304, 116337. [Google Scholar] [CrossRef]
- Wu, X.; Yang, B.; Zhou, S. Strength and Failure Analysis of Fiber-Wound Composite Gas Cylinder via Numerical Simulation. Materials 2024, 17, 717. [Google Scholar] [CrossRef]
- Azeem, M.; Hamdan, H.Y.; Alam, M.A.; Kumar, M.; Sajid, Z.; Gohery, S.; Maziz, A.; Gemi, L.; Abdullah, S.S.; Khan, S.H. Influence of winding angles on hoop stress in composite pressure vessels: Finite element analysis. Results Eng. 2024, 21, 101667. [Google Scholar] [CrossRef]
- Katsumata, S.; Ogasawara, T.; Uchino, T.; Hirayama, N.; Sakata, K.; Uzawa, K. Experimental and analytical study of a high-pressure hydrogen storage tank made of CFRP with dome–cylinder split molding structure for fuel cell vehicles. Int. J. Hydrogen Energy 2025, 101, 269–279. [Google Scholar] [CrossRef]
- Reda, R.; Ataya, S.; Ashraf, A. Finite Element Modeling of Different Types of Hydrogen Pressure Vessels Under Extreme Conditions for Space Applications. Processes 2025, 13, 1429. [Google Scholar] [CrossRef]
- Koutsawa, Y.; Bouhala, L. Uncertainty analysis in the design of Type-IV composite pressure vessels for hydrogen storage. Compos. Part C Open Access 2025, 16, 100544. [Google Scholar] [CrossRef]
- Syed, Z.A.H.; Che, J.l.; Chang, S.H. Design of a Type-III hydrogen pressure vessel with an elliptical dome for stress reduction in the composite layer. Int. J. Hydrogen Energy 2025, 103, 937–950. [Google Scholar] [CrossRef]
- Barthélémy, H.; Weber, M.; Barbier, F. Hydrogen storage: Recent improvements and industrial perspectives. Int. J. Hydrogen Energy 2017, 42, 7254–7262. [Google Scholar] [CrossRef]
- Hassan, I.; Ramadan, H.S.; Saleh, M.A.; Hissel, D. Hydrogen storage technologies for stationary and mobile applications: Review, analysis and perspectives. Renew. Sustain. Energy Rev. 2021, 149, 111311. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Y.; Afshan, S.; Hjalmarsson, J. A review of metallic tanks for H2 storage with a view to application in future green shipping. Int. J. Hydrogen Energy 2021, 46, 6151–6179. [Google Scholar] [CrossRef]
- Zhou, W.; Wang, J.; Pan, Z.B.; Liu, J.; Ma, L.H.; Zhou, J.Y.; Su, Y.F. Review on optimization design, failure analysis and non-destructive testing of composite hydrogen storage vessel. Int. J. Hydrogen Energy 2022, 47, 38862–38883. [Google Scholar] [CrossRef]
- Li, J.; Chai, X.; Gu, Y.; Zhang, P.; Yang, X.; Wen, Y.; Xu, Z.; Jiang, B.; Wang, J.; Jin, G.; et al. Small-scale high-pressure hydrogen storage vessels: A review. Materials 2024, 17, 721. [Google Scholar] [CrossRef] [PubMed]
- Bohorquez Rico, H.A. Diseño y Simulación de un Tanque Tipo II Revestido con Alambre de Acero SA-905. Master’s Thesis, Universidad de Guanajuato, Guanajuato, Mexico, 2018. Available online: http://repositorio.ugto.mx/handle/20.500.12059/392 (accessed on 19 June 2025).
- Saxena, A.; Prakash, A.; Sharp, G.; Thomson, W.; David, T.; Harless, F.; Vain, J.; Miller, I.; Nagpal, V.; Peters, D.T.; et al. Low Cost Hydrogen Storage at 875 Bar Using Steel Liners and Steel Wire Wraps; Technical report; WireTough Cylinders, LLC: Bristol, VA, USA, 2019. [Google Scholar]
- MatWeb, LLC. ASTM A36 Steel, Plate. 2025. Available online: https://www.matweb.com/search/DataSheet.aspx?MatGUID=afc003f4fb40465fa3df05129f0e88e6 (accessed on 26 June 2025).
- American Society of Mechanical Engineers. ASME Boiler and Pressure Vessel Code, 2021st ed.; ASME: New York, NY, USA, 2021. [Google Scholar]





| Mechanical Property | Value | Units |
|---|---|---|
| Modulus of elasticity | 200 | GPa |
| Poisson’s ratio | 0.26 | - |
| Mechanical Property | Value | Units |
|---|---|---|
| Elastic modulus | 160.0 | GPa |
| Elastic modulus | 21.0 | GPa |
| Elastic modulus | 21.0 | GPa |
| Shear modulus | 26.2 | GPa |
| Shear modulus | 26.2 | GPa |
| Shear modulus | 25.4 | GPa |
| Poisson’s ratio | 0.16 | - |
| Poisson’s ratio | 0.16 | - |
| Poisson’s ratio | 0.07 | - |
| Iteration | von Mises Stress (MPa) | Change | Nodes | Elements |
|---|---|---|---|---|
| 1 | 41.973 | 725 | 146 | |
| 2 | 42.338 | 0.94% | 2241 | 530 |
| 3 | 42.568 | −0.11% | 7199 | 1978 |
| 4 | 42.566 | 0.16% | 11,394 | 3271 |
| 5 | 42.654 | −0.33% | 25,388 | 7633 |
| 6 | 42.706 | −0.14% | 29,338 | 8861 |
| 7 | 42.709 | 0.04% | 37,592 | 11,497 |
| Iteration | von Mises Stress (MPa) | Change | Nodes | Elements |
|---|---|---|---|---|
| 1 | 42.875 | 43,090 | 6220 | |
| 2 | 42.611 | −0.92% | 48,938 | 7212 |
| 3 | 42.670 | −0.35% | 68,349 | 10,888 |
| 4 | 42.629 | −0.15% | 82,669 | 13,696 |
| 5 | 42.644 | −0.05% | 140,868 | 25,340 |
| Mechanical Property | Value | Units |
|---|---|---|
| Modulus of elasticity | 200 | GPa |
| Poisson’s ratio | 0.3 | - |
| Layers | % of Mass Added | % of Hoop Stress Reduction | % of Axial Stress Reduction |
|---|---|---|---|
| 1 | 18.2 | 27.3 | 13.0 |
| 2 | 37.7 | 39.8 | 20.8 |
| 3 | 58.3 | 46.7 | 26.6 |
| 4 | 80.2 | 50.9 | 31.1 |
| 5 | 103.3 | 53.7 | 34.7 |
| 6 | 127.6 | 55.6 | 37.6 |
| 7 | 153.1 | 56.9 | 40.0 |
| 8 | 179.8 | 57.9 | 41.8 |
| 9 | 207.7 | 58.6 | 43.2 |
| 10 | 236.8 | 59.1 | 44.3 |
| 11 | 267.2 | 59.5 | 45.1 |
| 12 | 298.7 | 59.8 | 45.8 |
| 13 | 331.5 | 60.0 | 46.2 |
| 14 | 365.5 | 60.2 | 46.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
León Razo, A.L.; Gutierrez Rivera, M.E.; Valencia Murillo, C.E.; Ledesma Orozco, E.R.; Martinez Ramirez, I. An Efficient Finite Element Model to Predict the Mechanical Response of Metallic-Reinforced Pressure Vessels. Hydrogen 2025, 6, 55. https://doi.org/10.3390/hydrogen6030055
León Razo AL, Gutierrez Rivera ME, Valencia Murillo CE, Ledesma Orozco ER, Martinez Ramirez I. An Efficient Finite Element Model to Predict the Mechanical Response of Metallic-Reinforced Pressure Vessels. Hydrogen. 2025; 6(3):55. https://doi.org/10.3390/hydrogen6030055
Chicago/Turabian StyleLeón Razo, Ana Lucía, Miguel Ernesto Gutierrez Rivera, Carlos Enrique Valencia Murillo, Elias Rigoberto Ledesma Orozco, and Israel Martinez Ramirez. 2025. "An Efficient Finite Element Model to Predict the Mechanical Response of Metallic-Reinforced Pressure Vessels" Hydrogen 6, no. 3: 55. https://doi.org/10.3390/hydrogen6030055
APA StyleLeón Razo, A. L., Gutierrez Rivera, M. E., Valencia Murillo, C. E., Ledesma Orozco, E. R., & Martinez Ramirez, I. (2025). An Efficient Finite Element Model to Predict the Mechanical Response of Metallic-Reinforced Pressure Vessels. Hydrogen, 6(3), 55. https://doi.org/10.3390/hydrogen6030055







