Natural Gas Pyrolysis in a Liquid Metal Bubble Column Reaction System—Part I: Experimental Setup and Methods
Abstract
1. Introduction
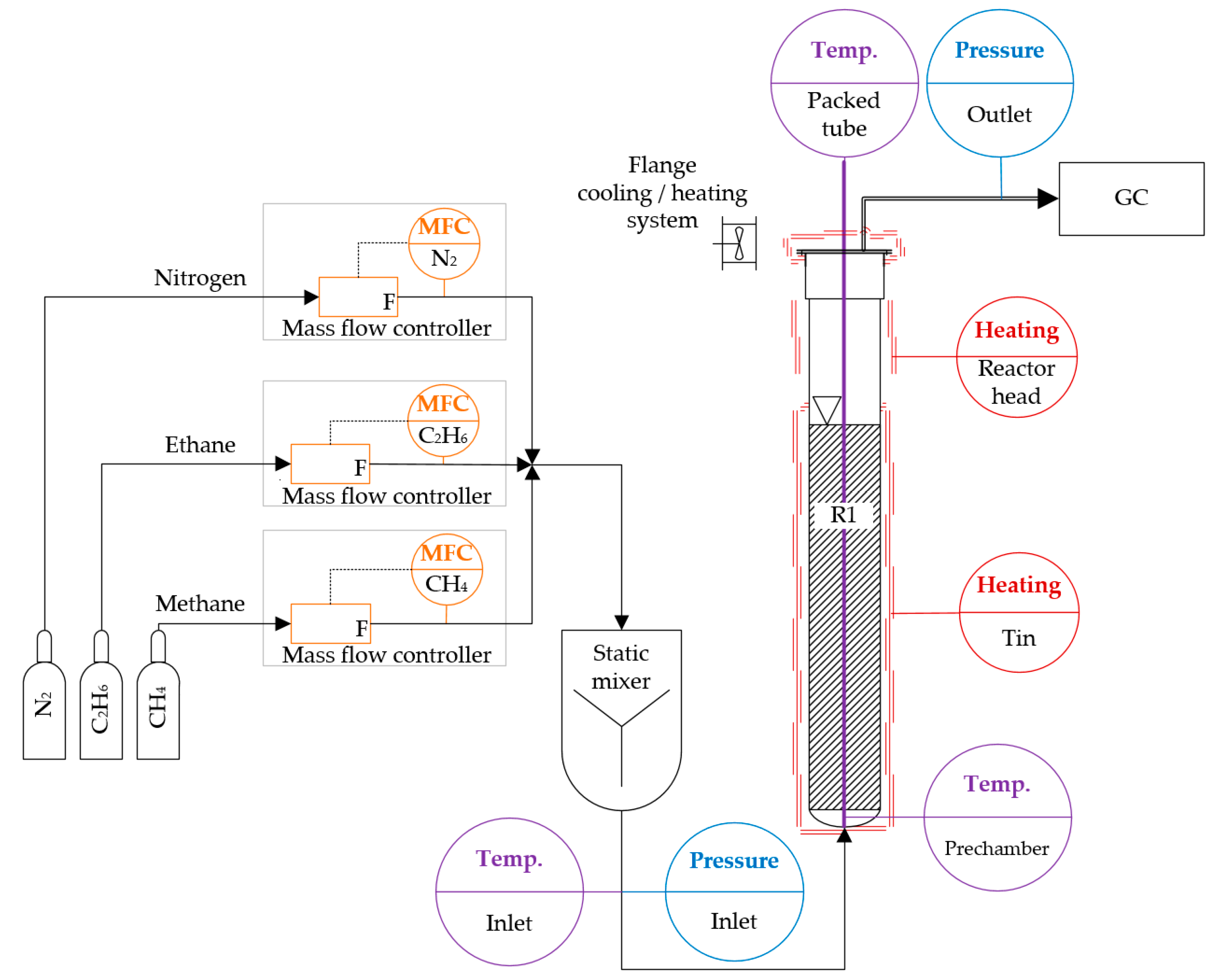
2. Experimental Setup
2.1. Gas Supply
2.2. Reactor
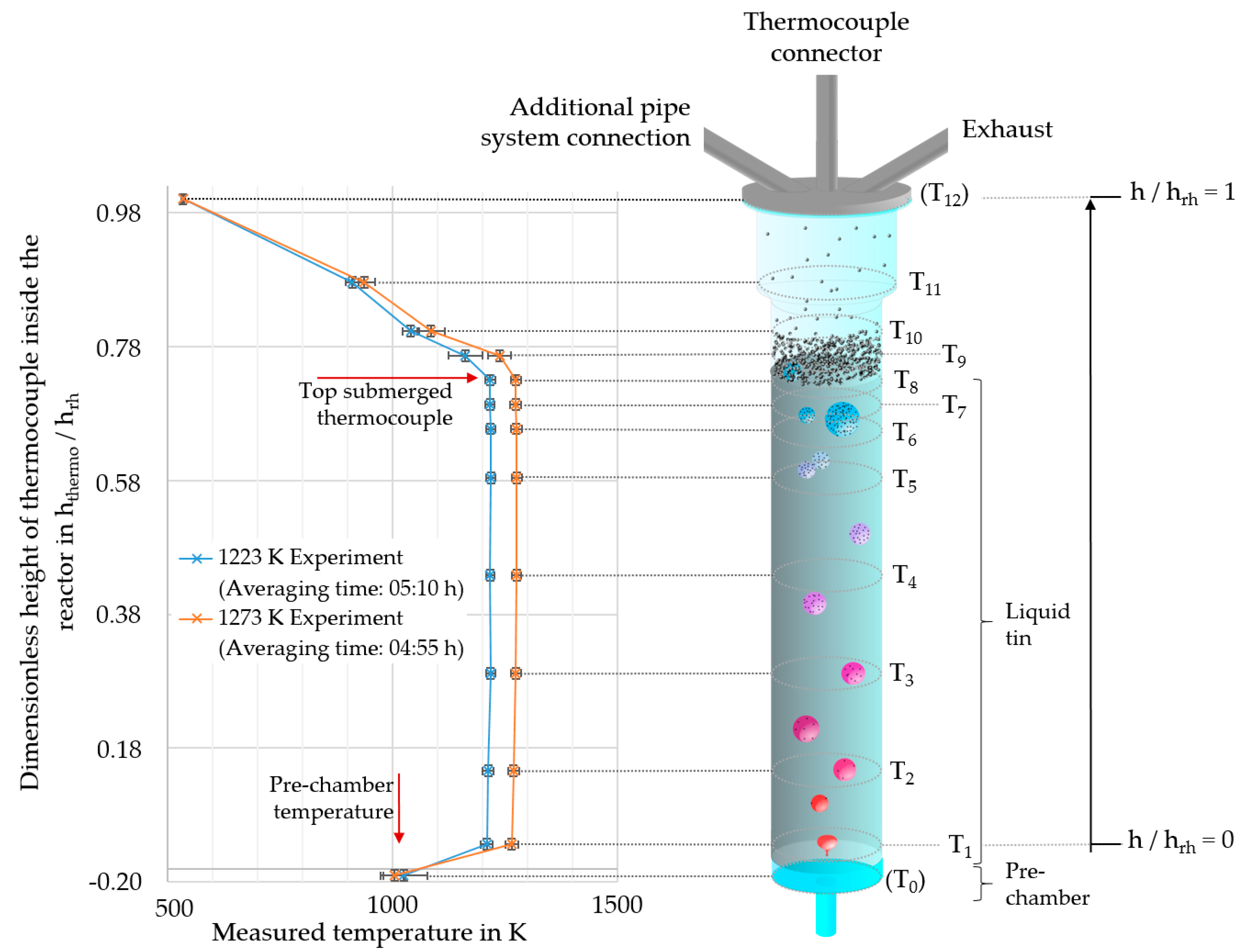
2.3. Temperature Evaluation
2.4. Pressure Evaluation
2.5. Gas Composition Evaluation
2.5.1. System of Equations for PM Pyrolysis
- = hydrogen yield with regard to methane
- = ethane yield with regard to methane
- = ethene yield with regard to methane
- = mole fraction of component
2.5.2. System of Equations for MEM and nGH Pyrolysis
- = mole fraction of component () in the feed gas flow
- = overall conversion rate of ethane
- = hydrogen yield with regard to methane
- = ethene yield with regard to methane
- = molar fraction of component
- Accuracy of the calibration gases (manufacturer’s specification, VDI 3490-2);
- Maximum standard uncertainty of multiple determination of each calibrated gas (four-fold determinations for each calibration point);
- Standard uncertainty of each multiple determination of the product-gas during the experiments.
2.6. Conducted Experiments
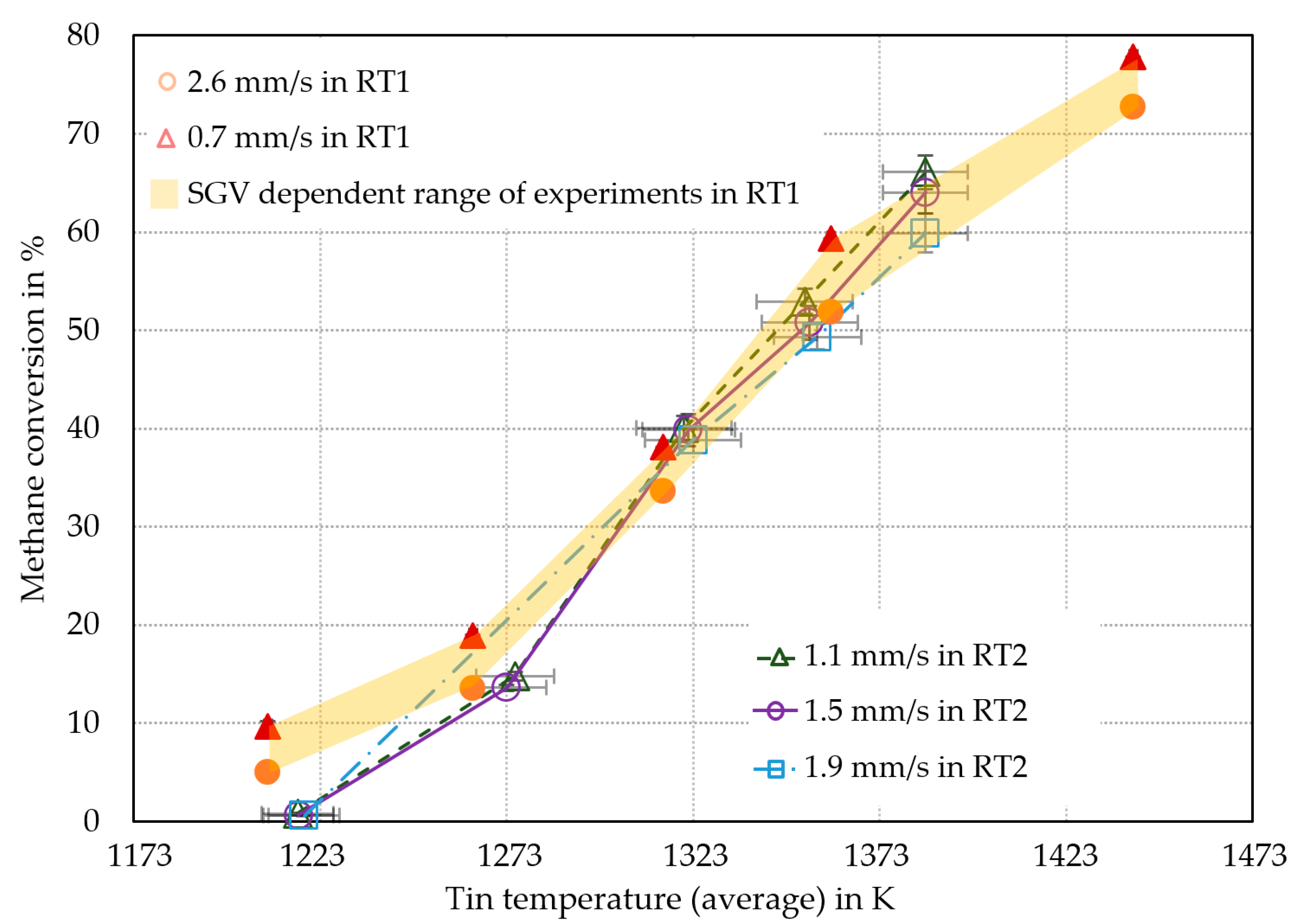
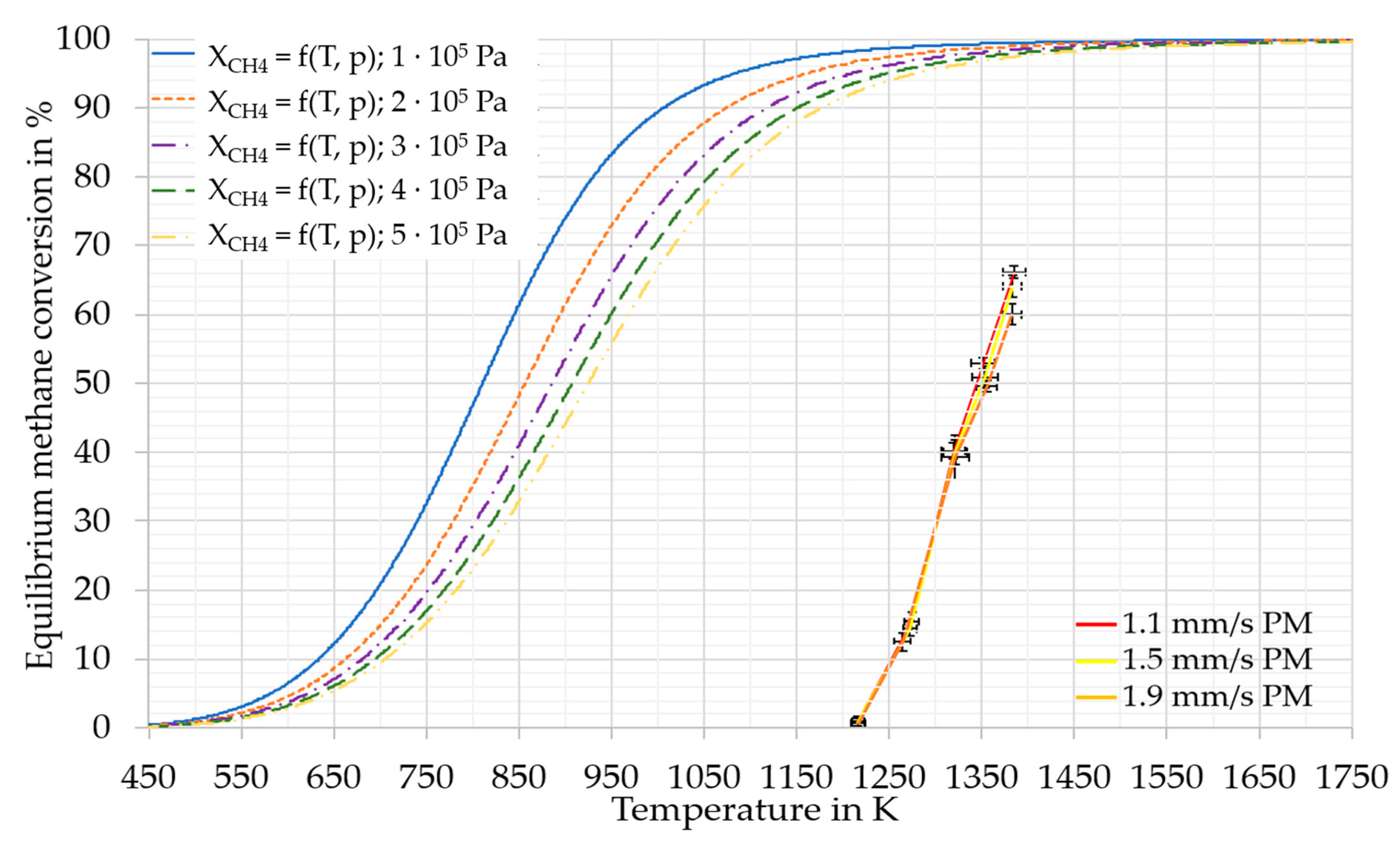
3. Experimental Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| RT1/2/3 | Reactor type 1/2/3 |
| PM | Pure methane |
| MEM | Methane-ethane mixture |
| nGH | High calorific natural gas |
| SGV | Superficial gas velocity |
| GC | Gas chromatograph |
| MFC | Mass flow controller |
| TCD | Thermal conductivity detector |
| hthermo | Height of thermocouple |
| hrh | Reactor height |
| hSn | Tin filling height |
| hpch | Prechamber height |
References
- Lambert, M. EU Hydrogen Strategy: A Case for Urgent Action towards Implementation; Oxford Institute for Energy Studies: Oxford, UK, 2020. [Google Scholar]
- Da Silva Veras, T.; Mozer, T.S.; Da Silva César, A. Hydrogen: Trends, production and characterization of the main process worldwide. Int. J. Hydrog. Energy 2017, 42, 2018–2033. [Google Scholar] [CrossRef]
- Ramachandran, R.; Menon, R.K. An overview of industrial uses of hydrogen. Int. J. Hydrog. Energy 1998, 23, 593–598. [Google Scholar] [CrossRef]
- De Mattos, M.; Souza, V.M. Processos Inorgânicos; SYNERGIA: Roßdorf, Germany, 2012; ISBN 10: 856132581X. [Google Scholar]
- Wasserstoff-Farbenlehre. 2020. Available online: https://usercontent.one/wp/www.ikem.de/wp-content/uploads/2021/03/IKEM_Kurzstudie_Wasserstoff_Farbenlehre.pdf?media=1667839188 (accessed on 19 December 2022).
- Muradov, N. Hydrogen via methane decomposition: An application for decarbonization of fossil fuels. Int. J. Hydrog. Energy 2001, 26, 1165–1175. [Google Scholar] [CrossRef]
- Lemus, R.G.; Duart, J.M. Updated hydrogen production costs and parities for conventional and renewable technologies. Int. J. Hydrog. Energy 2010, 35, 3929–3936. [Google Scholar] [CrossRef]
- Geißler, T.; Abánades, A.; Heinzel, A.; Mehravaran, K.; Müller, G.; Rathnam, R.; Rubbia, C.; Salmieri, D.; Stoppel, L.; Stückrad, S.; et al. Hydrogen production via methane pyrolysis in a liquid metal bubble column reactor with a packed bed. Chem. Eng. J. 2016, 299, 192–200. [Google Scholar] [CrossRef]
- Muradov, N.; Smith, F.; Huang, C.; Ali, T. Autothermal catalytic pyrolysis of methane as a new route to hydrogen production with reduced CO2 emissions. Catal. Today 2006, 116, 281–288. [Google Scholar] [CrossRef]
- Guéret, C.; Daroux, M.; Billaud, F. Methane pyrolysis: Thermodynamics. Chem. Eng. Sci. 1997, 52, 815–827. [Google Scholar] [CrossRef]
- Geißler, T.; Plevan, M.; Abánades, A.; Heinzel, A.; Mehravaran, K.; Rathnam, R.; Rubbia, C.; Salmieri, D.; Stoppel, L.; Stückrad, S.; et al. Experimental investigation and thermo-chemical modeling of methane pyrolysis in a liquid metal bubble column reactor with a packed bed. Int. J. Hydrogen Energy 2015, 40, 14134–14146. [Google Scholar] [CrossRef]
- Abánades, A.; Rathnam, R.K.; Geißler, T.; Heinzel, A.; Mehravaran, K.; Müller, G.; Plevan, M.; Rubbia, C.; Salmieri, D.; Stoppel, L.; et al. Development of methane decarbonisation based on liquid metal technology for CO2-free production of hydrogen. Int. J. Hydrog. Energy 2016, 41, 8159–8167. [Google Scholar] [CrossRef]
- Abánades, A.; Ruiz, E.; Ferruelo, E.M.; Hernández, F.; Cabanillas, A.; Martínez-Val, J.M.; Rubio, J.A.; López, C.; Gavela, R.; Barrera, G.; et al. Experimental analysis of direct thermal methane cracking. Int. J. Hydrog. Energy 2011, 36, 12877–12886. [Google Scholar] [CrossRef]
- Steinberg, M. Fossil fuel decarbonization technology for mitigating global warming. Int. J. Hydrog. Energy 1999, 24, 771–777. [Google Scholar] [CrossRef]
- Serban, M.; Lewis, M.A.; Marshall, C.L.; Doctor, R.D. Hydrogen Production by Direct Contact Pyrolysis of Natural Gas. Energy Fuels 2003, 17, 705–713. [Google Scholar] [CrossRef]
- Geißler, T.G. Methanpyrolyse in einem Flüssigmetall-Blasensäulenreaktor; Verlag Dr. Hut: Karlsruhe, Germany, 2017. [Google Scholar]
- Plevan, M. Entwicklung eines Verfahrens zur Thermischen Zerlegung von Methan zu Wasserstoff und Kohlenstoff unter Nutzung Flüssiger Metalle als Wärmeübertragungsmedium. Ph.D. Dissertation, Karlsruher Institut für Technologie (KIT), Karlsruhe, Germany, 2017. [Google Scholar]
- Von Wald, G.A.; Masnadi, M.S.; Upham, D.C.; Brandt, A.R. Optimization-based technoeconomic analysis of molten-media methane pyrolysis for reducing industrial sector CO2 emissions. Sustain. Energy Fuels 2020, 4, 4598–4613. [Google Scholar] [CrossRef]
- Thomas, L.; Gunther, M.; Uwe, S. Inviscid bubble formation on porous plates and sieve plates. Chem. Eng. Sci. 2004, 59, 809–818. [Google Scholar]
- Kulkarni, A.A.; Joshi, J.B. Bubble formation and bubble rise velocity in gas− liquid systems: A review. Ind. Eng. Chem. Res. 2005, 44, 5873–5931. [Google Scholar] [CrossRef]
- Giordanengo, B.; Benazzi, N.; Vinckel, J.; Gasser, J.G.; Roubi, L. Thermal conductivity of liquid metals and metallic alloys. J. Non-Cryst. Solids 1999, 250–252, 377–383. [Google Scholar] [CrossRef]
- Assael, M.J.; Kalyva, A.E.; Antoniadis, K.D.; Michael Banish, R.; Egry, I.; Wu, J.; Kaschnitz, E.; Wakeham, W.A. Reference data for the density and viscosity of liquid copper and liquid tin. J. Phys. Chem. Ref. Data 2010, 39, 33105. [Google Scholar] [CrossRef]
- Nauman, E.B. Residence Time Theory. Ind. Eng. Chem. Res. 2008, 47, 3752–3766. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- SciPy: Open Source Scientific Tools for Python. 2001. Available online: https://scipy.org/ (accessed on 22 December 2022).
- Clift, R.; Grace, J.R.; Weber, M.E. Bubbles, Drops, and Particles. Dover Publications: Mineola, NY, USA, 2005. [Google Scholar]
- Sano, M.; Mori, K. Bubble formation from single nozzles in liquid metals. Trans. Jpn. Inst. Met. 1976, 17, 344–352. [Google Scholar] [CrossRef]
- Fau, G.; Gascoin, N.; Gillard, P.; Steelant, J. Methane pyrolysis: Literature survey and comparisons of available data for use in numerical simulations. J. Anal. Appl. Pyrolysis 2013, 104, 1–9. [Google Scholar] [CrossRef]
- Atkins, P.W.; De Paula, J. Physikalische Chemie; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Schaber, K.; Stephan, K.; Mayinger, F. Thermodynamik. Grundlagen und Technische Anwendungen: Band 1: Einstoffsysteme; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Moldoveanu, S.C. Pyrolysis of Hydrocarbons. Pyrolysis Org. Mol. Appl. Health Environ. 2019, 2, 35–161. [Google Scholar]
- Grigull, U. Das Prinzip von Le Chatelier und Braun. Int. J. Heat Mass Transf. 1964, 7, 23–31. [Google Scholar] [CrossRef]
- Levenspiel, O. Chemical Reaction Engineering; John Wiley & Sons: Hoboken, NJ, USA, 1998. [Google Scholar]
- Arutyunov, V.S.; I Vedeneev, V. Pyrolysis of methane in the temperature range 1000–1700 K. Russ. Chem. Rev. 1991, 60, 1384–1397. [Google Scholar] [CrossRef]
- Stewart, P.H.; Smith, G.P.; Golden, D.M. The pressure and temperature dependence of methane decomposition. Int. J. Chem. Kinet. 1989, 21, 923–945. [Google Scholar] [CrossRef]
| Reactor Type (RT) | Reactor to Prechamber Ratio hrh/hpch | Single Orifice Diameter in mm | Reactor Volume in L | Publication Part |
|---|---|---|---|---|
| 1 | - | 0.5 ± 0.1 mm | 1.6 | - |
| 2 | 39 | 0.6 ± 0.1 mm | 6 | I and II |
| 3 | - | 0.6 ± 0.1 mm | 6 | II |
| Reactor Type (RT) | Pyrolyzed Gases | SGVs in mm/s | Overall Inlet Pressure Range in 105 Pa (a) | Overall Outlet Pressure Range in 105 Pa (a) |
|---|---|---|---|---|
| 1 | PM | 0.6 1.3 1.9 2.6 | 1.68–2.46 | 1.01–1.34 |
| 2 | PM MEM | 1.1 1.5 1.9 | 1.63–2.95 | 0.95–1.37 |
| 3 | nGH | 1.1 1.5 1.9 | 1.73–2.74 | 0.97–1.54 |
| Component | Calibration Range in mol% | Correlation Coefficient |
|---|---|---|
| Methane (CH4) | 0.1–99.995 | >0.9999 |
| Ethane (C2H6) | 0.1–10 | >0.9996 |
| Ethene (C2H4) | 0.1–10 | >0.9996 |
| Ethyne (C2H2) | 0.1–10 | >0.9998 |
| Nitrogen (N2) | 20–99.9999 | >0.9999 |
| Hydrogen (H2) | 0.1–99.9995 | >0.9995 |
| Reactor Type (RT) | SGVs in mm/s | Temperatures in K | Feed |
|---|---|---|---|
| 1 | 0.6 & 1.3 & 1.9 & 2.6 for all temperatures | 1209 ± 16 1264 ± 15 1315 ± 16 1360 ± 15 1441 ± 4 | PM PM PM PM PM |
| 2 | 1.1 & 1.5 & 1.9 for all temperatures | 1210 to 1220 ± 6 1264 to 1276 ± 13 1316 to 1325 ± 14 1347 to 1356 ± 11 1383 to 1388 ± 10 | PM PM PM PM PM |
| 1.1 & 1.5 & 1.9 1.1 & 1.5 & 1.9 1.5 & 1.9 | 1217 to 1220 ± 8 1264 to 1275 ± 9 1314 to 1328 ± 9 | MEM MEM MEM | |
| 3 | 1.1 & 1.5 & 1.9 for all temperatures | 1222 to 1226 ± 5 1326 to 1332 ± 7 1423 to 1430 ± 8 | nGH nGH nGH |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hofberger, C.M.; Dietrich, B.; Durán Vera, I.; Krumholz, R.; Stoppel, L.; Uhlenbruck, N.; Wetzel, T. Natural Gas Pyrolysis in a Liquid Metal Bubble Column Reaction System—Part I: Experimental Setup and Methods. Hydrogen 2023, 4, 295-306. https://doi.org/10.3390/hydrogen4020021
Hofberger CM, Dietrich B, Durán Vera I, Krumholz R, Stoppel L, Uhlenbruck N, Wetzel T. Natural Gas Pyrolysis in a Liquid Metal Bubble Column Reaction System—Part I: Experimental Setup and Methods. Hydrogen. 2023; 4(2):295-306. https://doi.org/10.3390/hydrogen4020021
Chicago/Turabian StyleHofberger, Christoph Michael, Benjamin Dietrich, Inés Durán Vera, Ralf Krumholz, Leonid Stoppel, Neele Uhlenbruck, and Thomas Wetzel. 2023. "Natural Gas Pyrolysis in a Liquid Metal Bubble Column Reaction System—Part I: Experimental Setup and Methods" Hydrogen 4, no. 2: 295-306. https://doi.org/10.3390/hydrogen4020021
APA StyleHofberger, C. M., Dietrich, B., Durán Vera, I., Krumholz, R., Stoppel, L., Uhlenbruck, N., & Wetzel, T. (2023). Natural Gas Pyrolysis in a Liquid Metal Bubble Column Reaction System—Part I: Experimental Setup and Methods. Hydrogen, 4(2), 295-306. https://doi.org/10.3390/hydrogen4020021









