Abstract
The concept of classical nuclear motion is extremely successful in describing motion at the atomic scale. In describing chemical reactions, it is even far more convincing than the picture obtained by using the Schrödinger equation for time development. However, this theory must be subject to critical tests. In particular, it must be checked if vibrational and rotational spectra are obtained correctly. Particularly critical are the spectra of small molecules containing the light hydrogen atom, since they have a distinctive rotational structure. The present study presents computations of the spectra of ammonia and hydrogen chloride using ab initio molecular dynamics, that is, by describing nuclear motion classically.
1. Introduction
All kind of matter is quantized in the sense that everything consists of atoms. Any system consisting of atoms can be reliably modelled with modern quantum mechanical codes. Essentially all these codes describe the electronic structure quantum-mechanically using the time-independent Schrödinger equation. This works extremely well and explains the rich variety of chemical structures. Hence, there is no doubt that, for describing the electronic structure, Schrödinger’s picture of quantum mechanics is needed and is also sufficient. (Let us, for the moment, ignore the need of relativity for inner electrons of heavy nuclei. Relativity does not affect the point that is made here, because nuclei normally move at the velocity of sound, not at the velocity of light.) Any classical description of molecular structure would lead to nonsense. This is also true for extreme conditions; hence, there is no transition to the classical picture—bound electrons must always be described with the Schrödinger equation.
So much about the electronic structure. What about nuclear structure? Nuclei are tiny objects compared to electronic orbitals; while the latter have a typical extension of about 0.1 to 1 nm, nuclei are just 10 fm in size. They have an inner structure consisting of protons and neutrons. Nuclei may undergo nuclear fission and fusion. They have properties such as spin. However, all these properties are not relevant for the description of chemical reactivity, because, for chemical reactions, only the motion of the nuclei, not their inner structure matters. Hence, in all practical applications of quantum chemistry, nuclei are described without inner structure and without the possibility of undergoing nuclear fission and fusion. We assume perfectly stable objects right from the beginning. Within this numerically successful picture, there is no point in using quantum field theory in practical calculations even if we are convinced that quantum field theory is the basis of everything. The time-independent Schrödinger equation is perfect in describing electronic wave functions and this is what it was made for. For the motion of the nuclei, and respectively for the motion of whole atoms, Newtonian dynamics are perfect. Trial and error, or also an ingenious guess, is what led to the development of ab initio molecular dynamics (AIMD) [1,2], which is presently the most widely used approach for the description of chemical dynamics. ‘Ab initio’ means that density-functional theory (DFT) is applied to the electrons. DFT is a very successful approximation to the time-independent Schrödinger equation in order to tackle the electronic problem. Note that all important density functionals have a semi-empirical character, because information from experiment is used. For chemical applications, it is not attractive to lose accuracy by sticking to the ‘exact’ theory. Hence, DFT using modern functionals is still called ab initio or also first-principles theory. ‘Molecular dynamics’ means that Newtonian dynamics is used for the atomic, and respectively nuclear, motion. Remarkably, it turns out that one directly arrives at the AIMD equations if one starts from the assumption that nuclear motion is classical [3,4,5,6]. Hereby, we use the general idea of Roberto Car and Michele Parrinello to derive both the ionic and electronic equations from one single Lagrangian, respectively Hamiltonian [1]. A separation of nuclear and electronic variables as in the Born–Oppenheimer approximation is not needed and no coupling terms arise.
Claiming that nuclear motion is classical means that there is no zero-point energy in nuclear vibration. This presents no problem: the rotational problem has no zero-point energy either, while the electronic problem has infinite zero-point energy. Quantum chemists were computing vibrational zero-point energies for a long time; however, with the advent of density functional theory, the community mainly ‘forgot’ to add these corrections. It seems after all, that zero-point energies corrected the error of Moeller–Plesset second-order perturbation theory (MP2), while for density functional theory, such an error compensation is not needed. Actually, meanwhile, these two directions, post-Hartree–Fock and DFT, are reconciled in the double-hybrid B2PLYP functional.
All this is not yet sufficient for proving the hypothesis that nuclear motion is classical. It turns out that this proof is difficult, because people are used to accepting the Copenhagen interpretation with all its strange phenomena and paradoxes. The only way is comparison to experiment for as many properties as possible. In the present study this is undertaken for the rovibrational spectra of ammonia and hydrogen chloride.
Using the Born–Oppenheimer approximation, the spectrum of ammonia has been described before on the basis of coupled-cluster potential energy surfaces or also fitted potential energy surfaces [7,8,9]. These studies demonstrate the significant effort that is necessary to do such calculations and also the limitations in comparison with the experimental spectra. With our ‘on-the-fly’ simulations, in which only those points of the potential energy surface are computed which are reached during the dynamics, it is much easier to go to larger systems. Simulations are feasible for 100 atoms, or for up to 1000 atoms if supercomputer facilities are available.
The result of our simulations is a very trivial picture of the structure and dynamics of matter—quantum mechanics just describes mathematically what is observed in high-resolution microscopy experiments.
2. Methods
In all practical applications, we employ Car–Parrinello molecular dynamics (CPMD), which is probably still the AIMD approach with the best cost-value ratio. Car–Parrinello molecular dynamics simulations [1,2,10] have been performed in the NVE ensemble using the Becke–Lee–Yang–Parr (BLYP) functional in connection with the Grimme dispersion correction [11]. Unless otherwise noted, the time step was chosen as 1 a.u. (0.0242 fs) and the fictitious electron mass as 100 a.u. Troullier–Martins pseudopotentials, as optimized for the BLYP functional, were employed for describing the core electrons [12,13]. The plane-wave cutoff, which determines the size of the basis set, was set to 70.0 Rydberg which corresponds to a very large basis set. The simulation cell size was 16 × 16 × 16 a.u. (8.5 × 8.5 × 8.5 Angstrom). This value is very large for the small molecules investigated. The aim is not to lose accuracy through limited basis sets and cell sizes. After geometry optimization, simulation runs were performed with initial kinetic energies of 100, 200, 250, 260, 270, 280, 290, 300, 310, 320, 330, 340, 350, 400, 450, 500, 550, 600, 700, 800, and 900 K, in order to model a Maxwell–Boltzmann distribution. Trajectories were determined for 1,000,000 steps per simulation run, that is, for 24 ps. The TRAVIS program [14,15] was used to compute the spectra from the trajectories. The TRAVIS code computes the spectra from the autocorrelation of the dipole moments [16,17]. Both the contributions of nuclei and orbitals to the dipole moment are taken into account. The orbital contribution is included via localized Wannier orbitals, as obtained from AIMD simulations [18,19,20]. For the computation of the dipole moments, only the centers of these localized orbitals are needed.
For comparison, Gaussian calculations [21] were performed using BLYP, BLYP-D3, the hybrid functionals B3LYP and B3LYP-D3, and the double-hybrid functionals B2PLYP and B2PLYP-D3 [21,22,23,24,25]. The basis set was chosen to be 6-311G(d,p). Standard frequency calculations were performed using the freq keyword in order to obtain the infrared spectra.
3. Results and Discussion
3.1. Ammonia
The spectrum of ammonia, as obtained from the ab initio simulations using the TRAVIS program, agrees well with experiment [26] (Figure 1). All relevant features are described correctly, namely N-H stretching (about 3300 cm), H-N-H scissoring (about 1700 cm), and N-H wagging (about 1000 cm). The experimental lines are observed at 3337 cm, 3444 cm, 1627 cm, and 950 cm. Below 1000 cm, mainly rotational bands are observed. The dispersion correction has little effect.
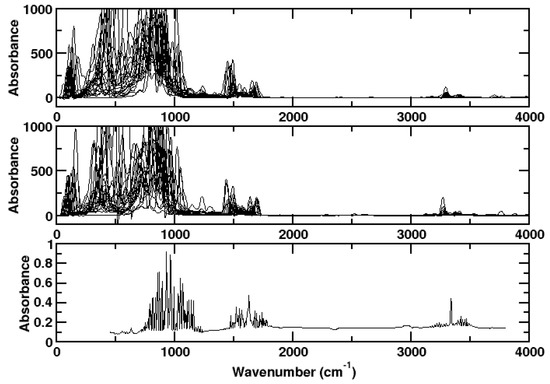
Figure 1.
Upper panel: Spectrum of ammonia as computed for a single molecule at different kinetic energies without dispersion correction using CPMD/BLYP. Medium panel: With dispersion correction. Lower panel: Experimental spectrum.
The spectrum of ammonia as computed for a single optimized molecule using the Gaussian program package [21] is only in moderate agreement with experiment (Figure 2). The vibrational modes are in essence obtained correctly, while the rotational structure is lacking completely. Of course, this comes as no surprise because the frequency calculation of Gaussian yields vibrations only. In Figure 2, the Gaussian result is compared to the result of the AIMD simulations when rotation is frozen. The resulting picture resembles more closely the picture obtained from Gaussian calculations. In the Supplementary Materials, the spectra are computed from one large trajectory file concatenated from the trajectory files at different temperatures. The result is less structured spectra (Figures S1 and S2).
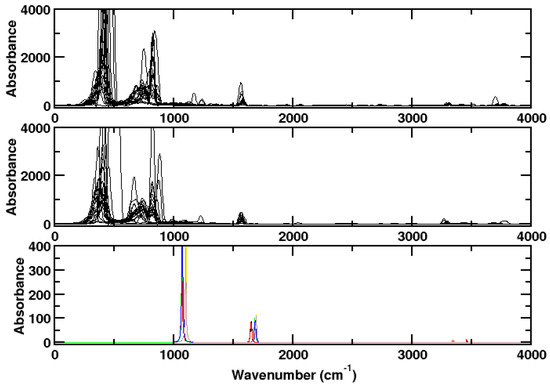
Figure 2.
Upper panel: Spectrum of ammonia as computed for a single molecule at different kinetic energies without dispersion correction using CPMD/BLYP. The rotational degrees of freedom are frozen. Medium panel: With dispersion correction. Lower panel: Spectrum of ammonia as computed for a single NH molecule with Gaussian. Black: BLYP, red: B3LYP, green: BLYP-D3, blue: B3LYP-D3, yellow: B2PLYP, brown: B2PLYP-D3. The choice of the functional has little influence on the result. In particular the dispersion correction makes hardly a difference.
3.2. Hydrogen Chloride
It is not so easy to obtain the hydrogen chloride spectrum with its characteristic form that can be attributed to the Maxwell–Boltzmann distribution. We model this Maxwell–Boltzmann distribution by using a distribution of initial kinetic energies in our simulations. The result is not the same as for running our simulations for a very long time or for putting several molecules in one simulation cell. In the first case, the exchange of energy with other molecules is lacking; hence, we get just two sharp peaks. In the latter case, we have way shorter mean free paths than in experiment. That is, we have a problem with ergodicity and our simulations are too few and too short to obtain a perfect picture. The red lines in Figure 3 show that our Maxwell–Boltzmann distribution is not perfect. What is important to note is the fact that, as in experiment, the distances between the peaks increase with decreasing wave number.
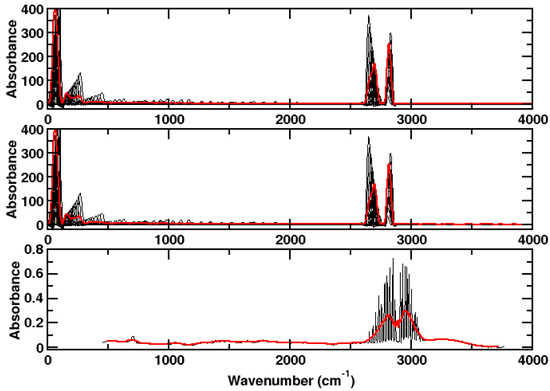
Figure 3.
Upper panel: Spectrum of hydrogen chloride as computed for a single molecule at different kinetic energies without dispersion correction using CPMD/BLYP. Medium panel: With dispersion correction. Lower panel: Experimental spectrum. Red: Sum over computed peaks, respectively, average of the experimental spectrum.
In Figure 4, it is shown that, if the rotation is frozen, only single peaks are observed. All of them have about the same wave number and shape. The result agrees well with Gaussian frequency calculations. Again, in the Supplementary Materials, one big trajectory file, stemming from concatenating all trajectory files, is evaluated. Like for ammonia, this leads to a less structured spectrum (Figures S3 and S4).
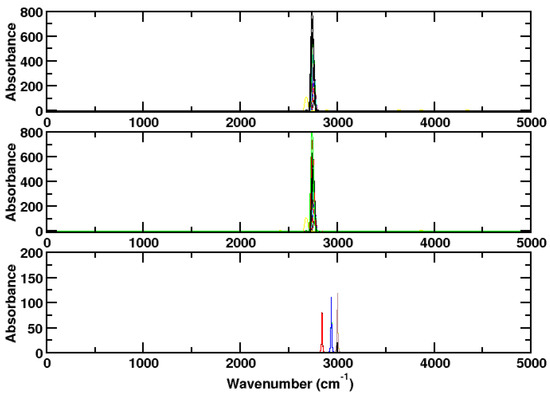
Figure 4.
Upper panel: Spectrum of hydrogen chloride as computed for a single molecule at different kinetic energies without dispersion correction using CPMD/BLYP. The rotational degrees of freedom are frozen. Medium panel: With dispersion correction. Lower panel: Spectrum of ammonia as computed for a single NH molecule with Gaussian. Black: BLYP, red: BLYP-D3, green: B3LYP, blue: B3LYP-D3, yellow: B2PLYP, brown: B2PLYP-D3. The choice of the functional has little influence on the result. In particular, the dispersion correction makes hardly a difference; hence, the graphs without dispersion correction are hardly visible.
Figure 5 illustrates what can go wrong when simulating rotational spectra: In the upper panel, the spectra of ammonia molecules at two different temperatures are shown. Both spectra exhibit two peaks in the region of the H-Cl vibration. Raising the temperature leads to a higher distance of the two peaks and to a red shift. It is not clear what leads to the fact that the peaks obtained for the higher temperature (green) are larger than those obtained for the lower temperature (red).
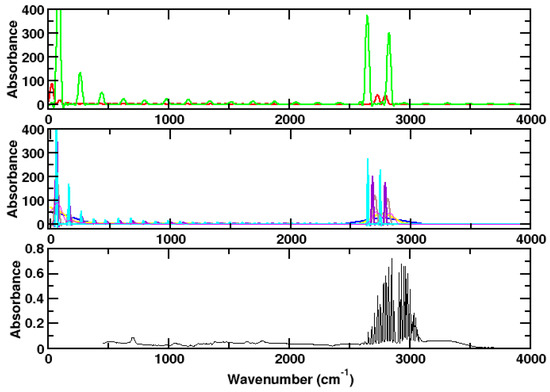
Figure 5.
Upper panel: Resulting spectrum of two single simulations (red: 100 K, green: 900 K) for hydrogen chloride. Medium panel: Result obtained by using different time steps and electronic masses. This affects mainly the rotational structure. Blue: lowest time step (0.1 a.u resp. 0.0024 fs, corresponding to a simulation time of 2.4 ps), cyan: highest time step (4.0 a.u. resp. 0.096 fs, corresponding to a simulation time of 96.0 ps). Lower panel: Experimental spectrum. For describing the experimental spectrum, it is necessary to perform many simulations at different kinetic energies.
Slighty different conditions may lead to strongly different single peaks. This phenomenon is investigated in Figure 5, medium panel. Several different time steps (in the range of 0.1–4.0 a.u.) and different electronic masses (in the range of 10–400 a.u.) were used in simulations with 1,000,000 time steps, resulting in different total simulation times (Figure 5).
Finally, simulations were performed optimizing the wave function in every time step. This yields nothing new, see the Supplementary Materials, Figure S5.
4. Conclusions
AIMD simulations are able to describe vibrational and rotational spectra. While this has been known for quite some time for vibrational spectra, the situation was not so clear for rovibrational spectra. It turns out that simulating rotational spectra is not straightforward. This is particularly true for the gas-phase spectra of small molecules containing hydrogen. It must be emphasized that a single simulation run yields random numbers. Instead, a Maxwell–Boltzmann distribution of kinetic energies must be modelled; that is, several individual molecules must be simulated at different kinetic energies for some time and the complete result must be evaluated. The result of several individual simulation runs at different kinetic energies is not the same as the result of many molecules in one simulation cell. This is due to the fact that the mean free path is larger than in experiment by about two orders of magnitude.
We clearly have a problem with ergodicity stemming from limited CPU time. However, the classical description of nuclear motion is in nice agreement with the experimental findings: The observed bands are clearly in the correct region of the spectrum, the Maxwell–Boltzmann distribution explains the shape of the bands, and the peaks at the red end of the bands have larger distances than those at the blue end. Again, the conclusion is that nuclear motion is well described by a classical approach. Incidentally, this fits to the observation that ammonia in its stable ground state has symmetry, not , as it would have if nuclear tunneling in the ammonia double-well potential were allowed. Experimentally, ammonia has a non-zero dipole moment, which confirms the classical picture.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/hydrogen4020020/s1, Figure S1: Summarized spectrum of ammonia, Figure S2: Summarized spectrum of ammonia with frozen rotation, Figure S3: Summarized spectrum of hydrogen chloride, Figure S4: Summarized spectrum of hydrogen chloride with frozen rotation, Figure S5: Spectrum of hydrogen chloride computed without dispersion correction. The wavefunction was optimized in every time step.
Funding
Part of the calculations were performed on the local cluster of the Leibniz University of Hannover at the LUIS.
Data Availability Statement
Input files for CPMD version 4.3 are available on demand from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AIMD | Ab Initio Molecular Dynamics |
| BLYP | Becke–Lee–Yang–Parr density functional |
| B3LYP | Hybrid functional based on BLYP |
| B2PLYP | Double-hybrid functional based on B3LYP and MP2 |
| CPMD | Car–Parrinello Molecular Dynamics |
| -D3: | With dispersion correction |
| DFT | Density functional theory |
| MP2 | Moeller–Plesset second-order perturbation theory |
References
- Car, R.; Parrinello, M. Unified Approach for Molecular Dynamics and Density-Functional Theory. Phys. Rev. Lett. 1985, 55, 2471–2474. [Google Scholar] [CrossRef] [PubMed]
- Marx, D.; Hutter, J. Ab Initio Molecular Dynamics: Basic Theory and Advanced Methods; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Frank, I.; Genuit, S.; Matz, F.; Oschinski, H. Ammonia, water, and hydrogen: Can nuclear motion be described classically? Int. J. Quantum Chem. 2020, 120, e26142. [Google Scholar] [CrossRef]
- Frank, I. Classical motion of the nuclei in a molecule: A concept without alternatives. Chem. Select 2020, 5, 1872. [Google Scholar] [CrossRef]
- Büchel, R.C.; Rudolph, D.A.; Frank, I. Deterministic quantum mechanics: The role of the Maxwell-Boltzmann distribution. Int. J. Quantum Chem. 2021, 121, e26555. [Google Scholar] [CrossRef]
- Frank, I. Classical nuclear motion: Comparison to approaches with quantum mechanical nuclear motion. Hydrogen 2023, 4, 11–21. [Google Scholar] [CrossRef]
- Yurchenko, S.N.; Barber, R.J.; Tennyson, J.; Thiel, W.; Jensen, P. Towards efficient refinement of molecular potential energy surfaces: Ammonia as a case study. J. Mol. Spectrosc. 2011, 268, 123. [Google Scholar] [CrossRef]
- Marquardt, R.; Sagui, K.; Zheng, J.; Thiel, W.; Luckhaus, D.; Yurchenko, S.N.; Mariotti, F.; Quack, M. Global analytical potential energy surface for the electronic ground state of NH3 from high level ab initio calculations. J. Phys. Chem. A 2013, 117, 7502. [Google Scholar] [CrossRef]
- Fabri, C.; Marquardt, R.; Csaszar, A.G.; Quack, M. Controlling tunneling in ammonia isotopomers. J. Chem. Phys. 2019, 150, 014102. [Google Scholar] [CrossRef]
- Hutter, J.; Alavi, A.; Deutsch, T.; Bernasconi, M.; Goedecker, S.; Marx, D.; Tuckerman, M.; Parrinello, M. CPMD Version 4.3. Copyright IBM Corp 1990–2015. Copyright MPI für Festkörperforschung Stuttgart 1997–2001. Available online: https://github.com/CPMD-code/CPMD/releases/tag/4.3 (accessed on 11 May 2023).
- Grimme, S. Accurate Description of van der Waals Complexes by Density Functional Theory Including Empirical Corrections. J. Comput. Chem. 2004, 25, 1463. [Google Scholar] [CrossRef] [PubMed]
- Troullier, N.; Martins, J.L. Efficient Pseudopotentials for Plane-Wave Calculations. Phys. Rev. B 1991, 43, 1993. [Google Scholar] [CrossRef]
- Boero, M.; Parrinello, M.; Terakura, K.; Weiss, H. Car-Parrinello study of Ziegler-Natta heterogeneous catalysis: Stability and destabilization problems of the active site models. Mol. Phys. 2002, 100, 2935–2940. [Google Scholar] [CrossRef]
- Brehm, M.; Kirchner, B. TRAVIS—A free analyzer and visualizer for monte carlo and molecular dynamics trajectories. J. Chem. Inf. Model. 2011, 51, 2007. [Google Scholar] [CrossRef] [PubMed]
- Brehm, M.; Thomas, M.; Gehrke, S.; Kirchner, B. TRAVIS—A free analyzer for trajectories from molecular simulation. J. Chem. Phys. 2020, 152, 164105. [Google Scholar] [CrossRef] [PubMed]
- Thomas, M.; Brehm, M.; Fligg, R.; Vöhringer, P.; Kirchner, B. Computing vibrational spectra from ab initio molecular dynamics. Phys. Chem. Chem. Phys. 2013, 15, 6608. [Google Scholar] [CrossRef] [PubMed]
- Thomas, M.; Brehm, M.; Kirchner, B. Voronoi dipole moments for the simulation of bulk phase vibrational spectra. Phys. Chem. Chem. Phys. 2015, 17, 3207. [Google Scholar] [CrossRef] [PubMed]
- Marzari, N.; Vanderbilt, D. Maximally localized generalized Wannier functions for composite energy bands. Phys. Rev. B 1997, 56, 12847. [Google Scholar] [CrossRef]
- Ikeda, T.; Boero, M. Role of van der Waals corrections in first principles simulations of alkali metal ions in aqueous solutions. J. Chem. Phys. 2015, 143, 194510. [Google Scholar] [CrossRef] [PubMed]
- Silvestrelli, P.L.; Ambrosetti, A. Van der Waals interactions in DFT using Wannier functions without empirical parameters. J. Chem. Phys. 2019, 150, 164109. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian~16 Revision A.03; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Becke, A. Density-Functional Exchange-Energy Approximation with Correct Asymptotic Behavior. Phys. Rev. A 1988, 38, 3098. [Google Scholar] [CrossRef] [PubMed]
- Becke, A. A New Mixing of Hartree-Fock and Local-Density Functional Theories. J. Chem. Phys. 1993, 98, 1372. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S. Semiempirical hybrid density functional with perturbative second-order correlation. J. Chem. Phys. 2006, 124, 034108. [Google Scholar] [CrossRef] [PubMed]
- NIST Chemistry WebBook. Available online: https://webbook.nist.gov/ (accessed on 30 December 2022).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).