Constant-pH Simulations of a Coarse-Grained Model of Polyfunctional Weak Charged Biopolymers
Abstract
1. Introduction
2. Results and Discussion
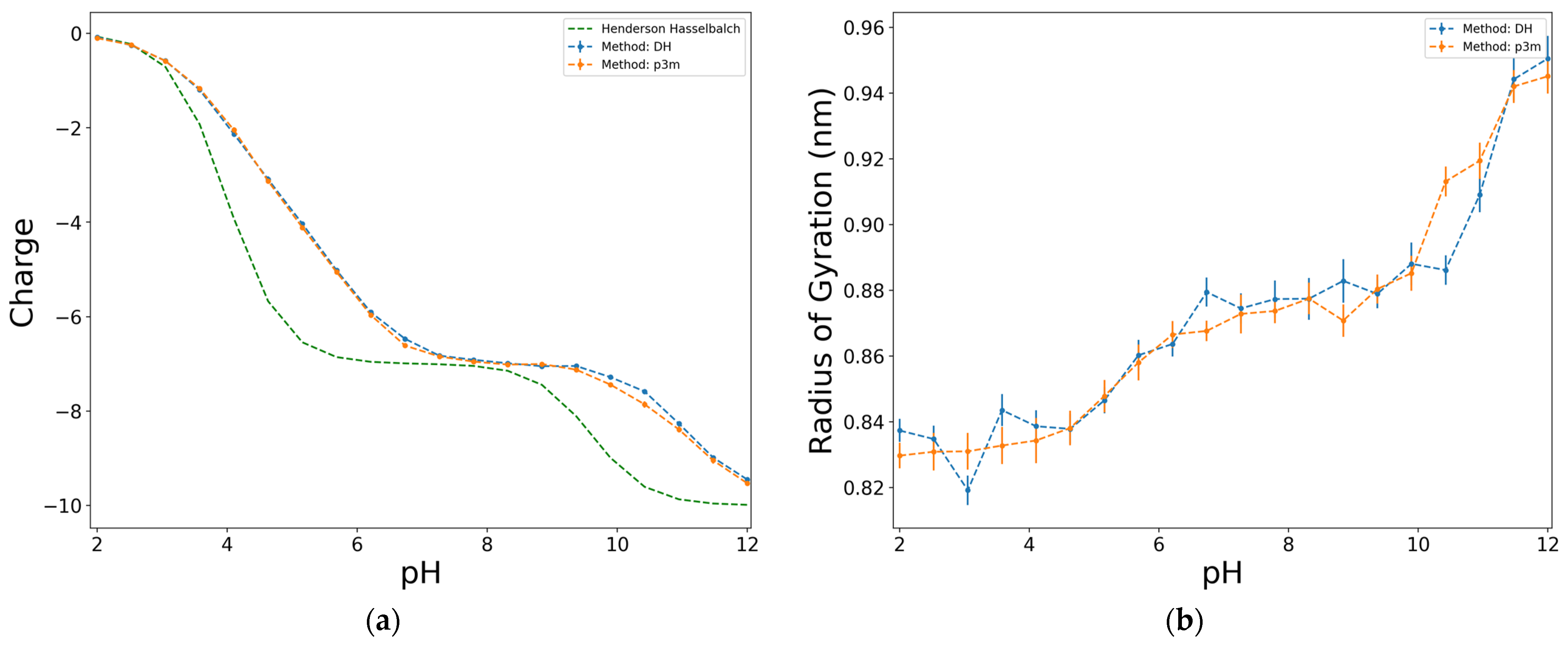
2.1. Effect of the Electrostatic Interaction Methodology
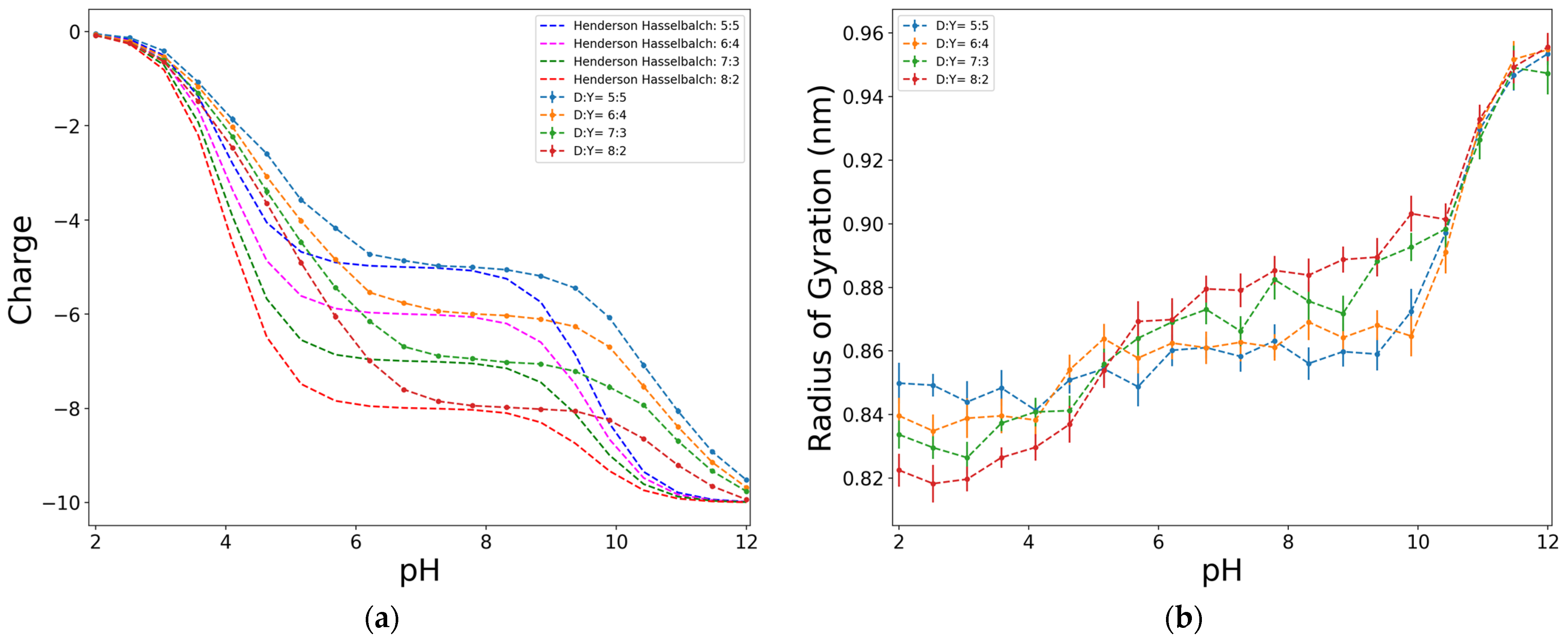
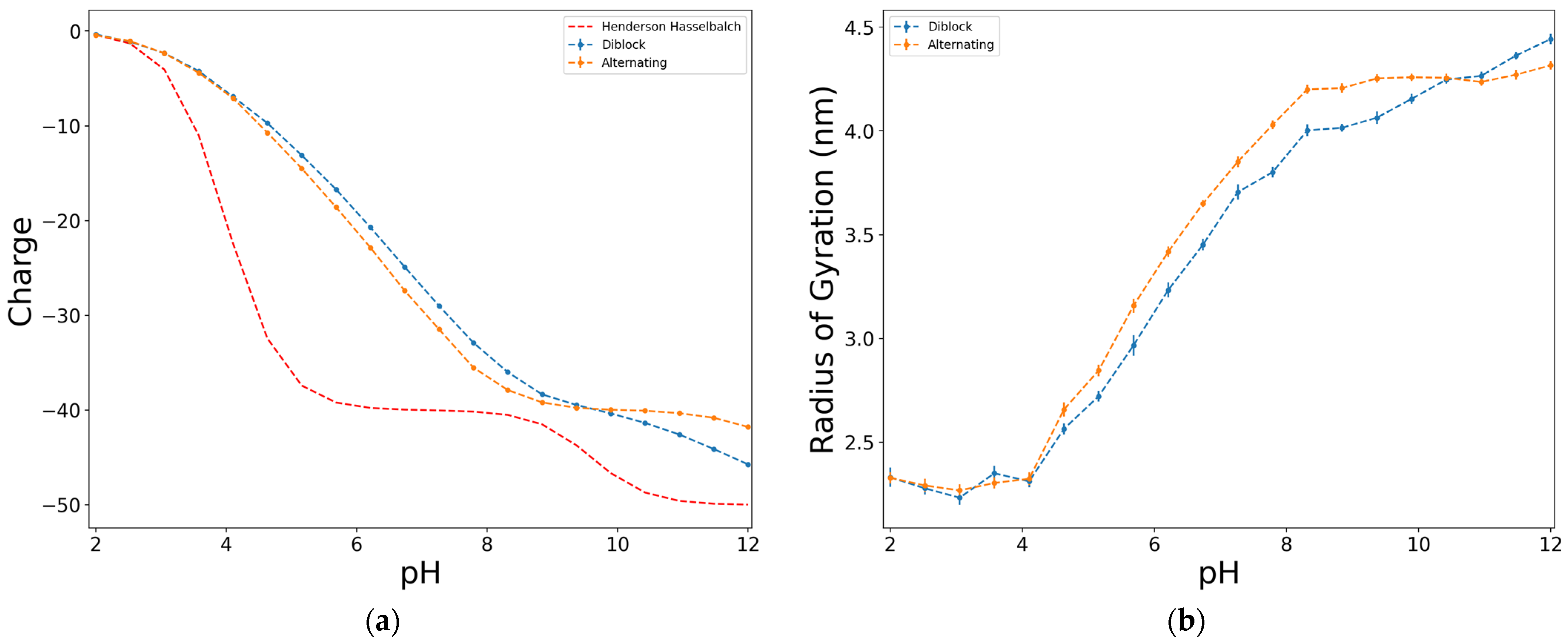
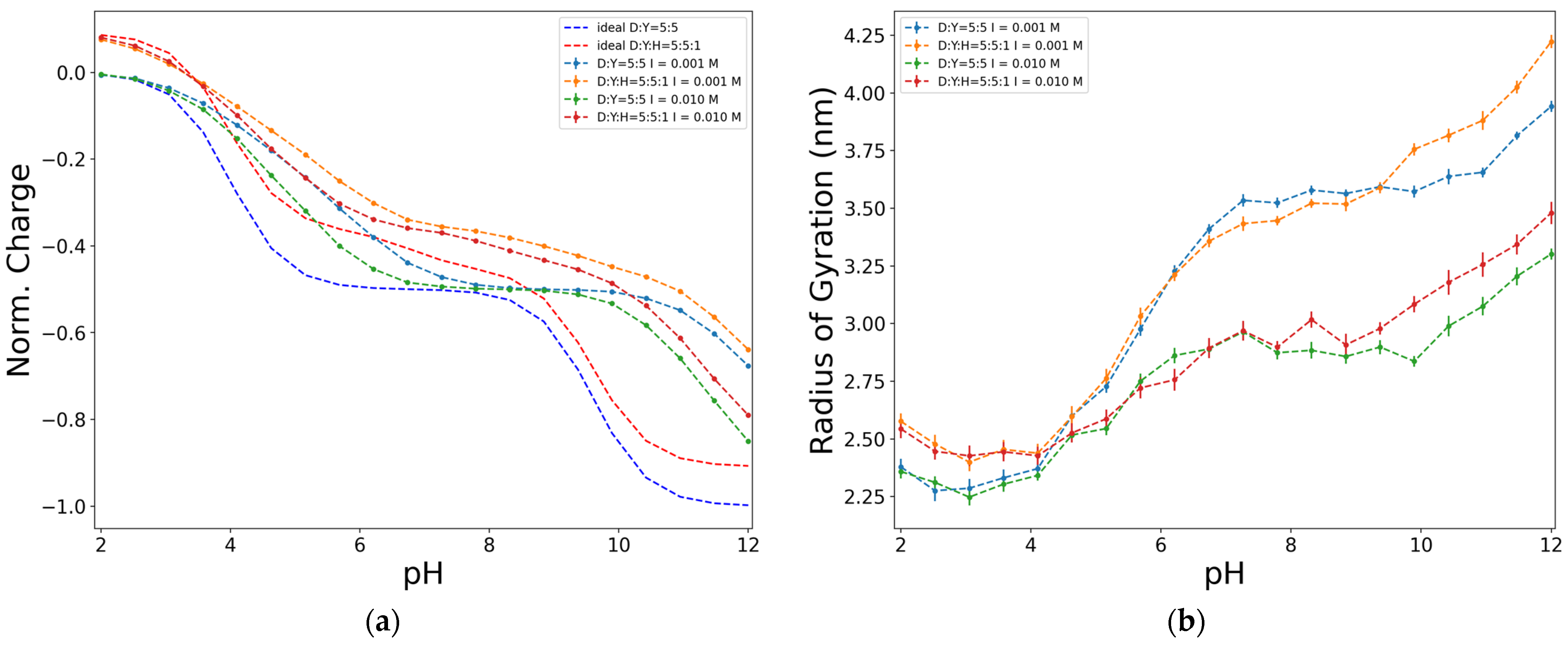
2.2. Effect of the Size, Proportion, and Distribution of D:Y Functional Groups
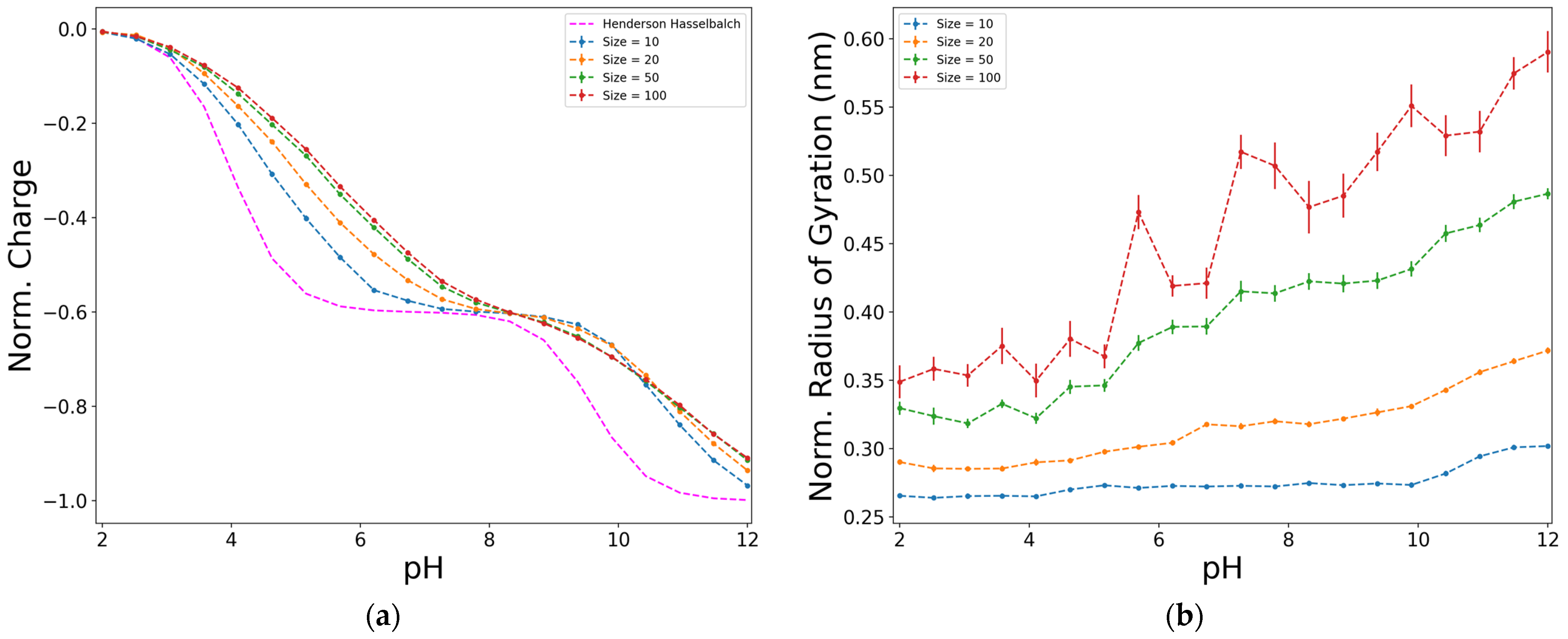
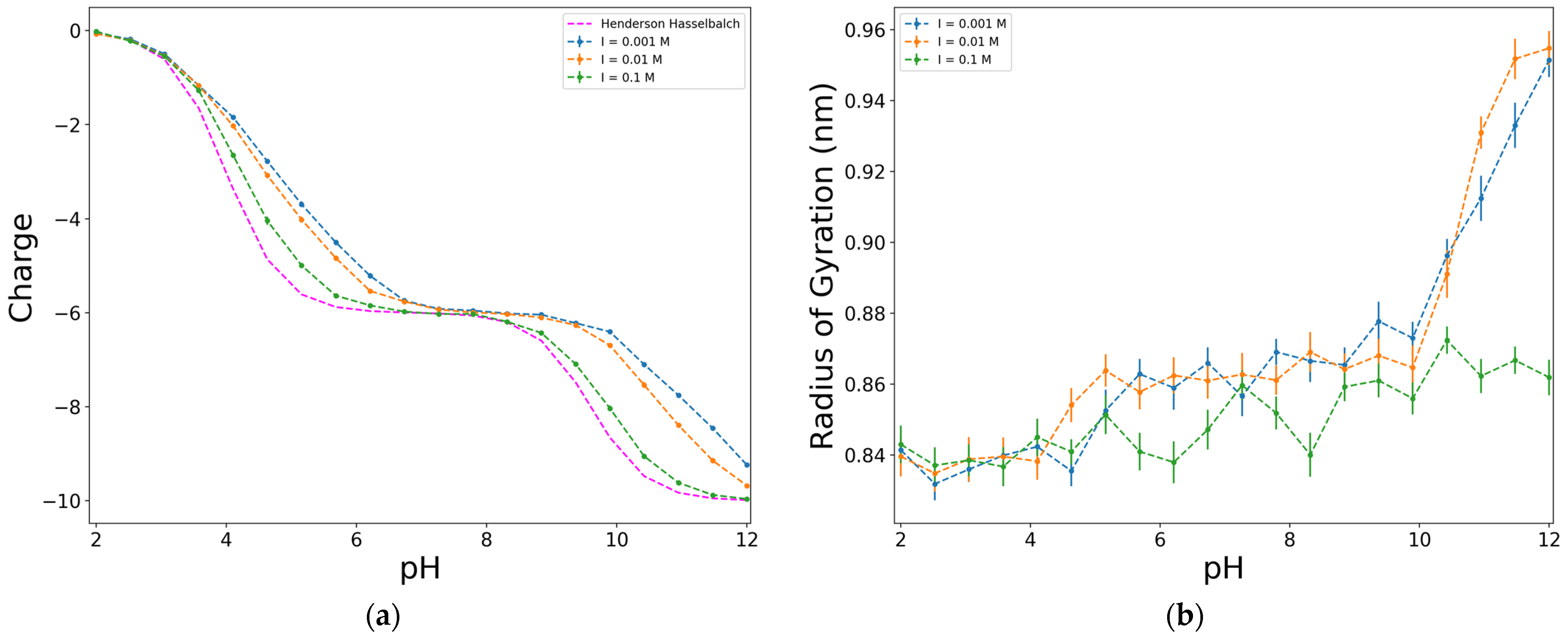
2.3. Effect of the Ionic Strength
2.4. Effect of a Third Functional Group Associated with Nitrogen (H)
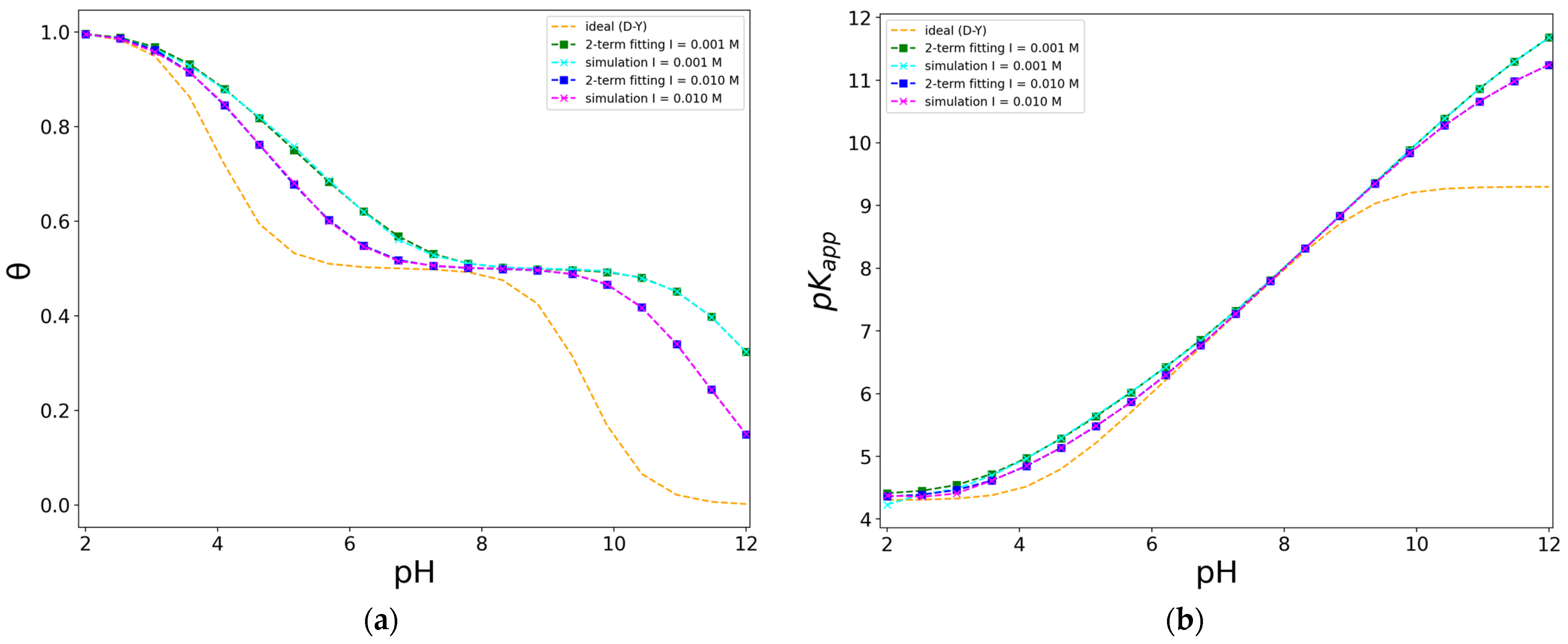
2.5. Description of the Protonation Process Using a Frumkin Isotherm
3. Methodology
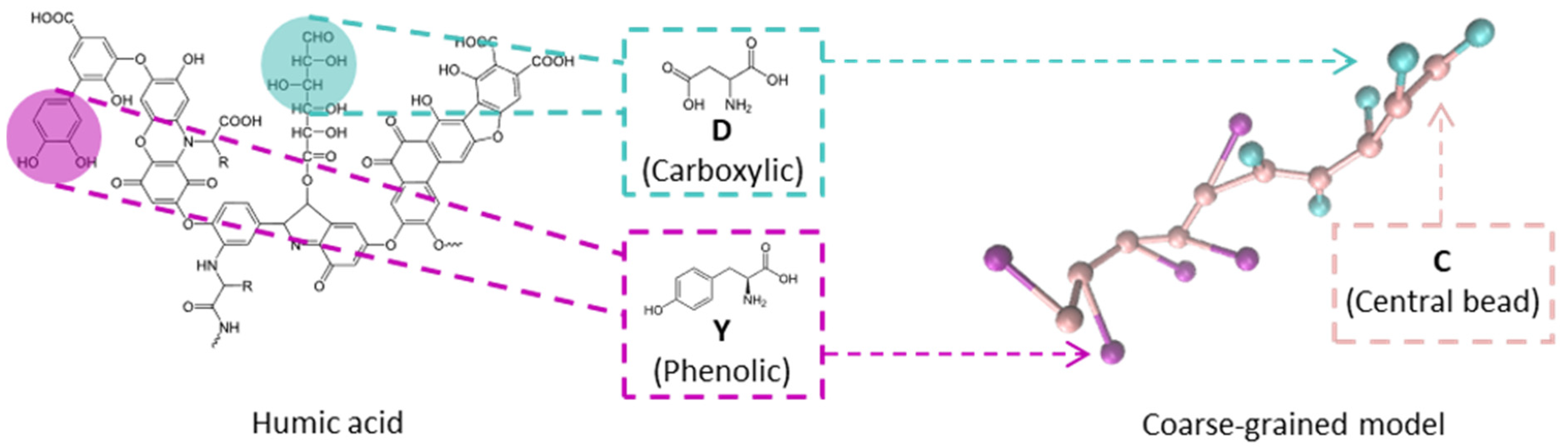
3.1. The Model
| Bead | Functional Group | Diameter (nm) | C-Bond Length (nm) | pki |
|---|---|---|---|---|
| D | Carboxylic | 0.35 | 0.329 | 4.0 |
| Y | Phenolic | 0.35 | 0.648 | 9.6 |
| H | Other associated with N | 0.35 | 0.452 | 6.8 |
| C | Central bead | 0.35 | 0.382 | - |
| Na | Cation | 0.35 | - | - |
| Cl | Anion | 0.35 | - | - |
3.2. Electrostatic Interactions
3.2.1. P3M Method
3.2.2. Debye–Hückel Potential
3.3. Computational Details
3.4. Magnitudes
3.5. Fitting Procedure
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Holm, C.; Joanny, J.F.; Kremer, K.; Netz, R.R.; Reineker, P.; Seidel, C.; Vilgis, T.A.; Winkler, R.G. Polyelectrolyte Theory. In Advances in Polymer Science; Springer: Berlin/Heidelberg, Germany, 2004; pp. 67–111. [Google Scholar] [CrossRef]
- Muthukumar, M. 50th Anniversary Perspective: A Perspective on Polyelectrolyte Solutions. Macromolecules 2017, 50, 9528–9560. [Google Scholar] [CrossRef]
- Landsgesell, J.; Nová, L.; Rud, O.; Uhlík, F.; Sean, D.; Hebbeker, P.; Holm, C.; Košovan, P. Simulations of ionization equilibria in weak polyelectrolyte solutions and gels. Soft Matter 2019, 15, 1155–1185. [Google Scholar] [CrossRef]
- Blanco, P.M.; Narambuena, C.F.; Madurga, S.; Mas, F.; Garcés, J.L. Unusual Aspects of Charge Regulation in Flexible Weak Polyelectrolytes. Polymers 2023, 15, 2680. [Google Scholar] [CrossRef]
- Liu, S.; Ghosh, K.; Muthukumar, M. Polyelectrolyte Solutions with Added Salt: A Simulation Study. J. Chem. Phys. 2003, 119, 1813–1823. [Google Scholar] [CrossRef]
- Koper, G.J.; Borkovec, M. Proton binding by linear, branched, and hyperbranched polyelectrolytes. Polymer 2010, 51, 5649–5662. [Google Scholar] [CrossRef]
- Blanco, P.M.; Madurga, S.; Narambuena, C.F.; Mas, F.; Garcés, J.L. Role of Charge Regulation and Fluctuations in the Conformational and Mechanical Properties of Weak Flexible Polyelectrolytes. Polymers 2019, 11, 1962. [Google Scholar] [CrossRef]
- Lyulin, A.V.; Dünweg, B.; Borisov, O.V.; Darinskii, A.A. Computer Simulation Studies of a Single Polyelectrolyte Chain in Poor Solvent. Macromolecules 1999, 32, 3264. [Google Scholar] [CrossRef]
- Udayakumar, G.P.; Muthusamy, S.; Selvaganesh, B.; Sivarajasekar, N.; Rambabu, K.; Sivamani, S.; Sivakumar, N.; Maran, J.P.; Hosseini-Bandegharaei, A. Ecofriendly biopolymers and composites: Preparation and their applications in water-treatment. Biotech. Adv. 2021, 52, 107815. [Google Scholar] [CrossRef]
- Baranwal, J.; Barse, B.; Fais, A.; Delogu, G.L.; Kumar, A. Biopolymer: A Sustainable Material for Food and Medical Applications. Polymers 2022, 14, 983. [Google Scholar] [CrossRef]
- Perera, K.Y.; Jaiswal, A.K.; Jaiswal, S. Biopolymer-Based Sustainable Food Packaging Materials: Challenges, Solutions, and Applications. Foods 2023, 12, 2422. [Google Scholar] [CrossRef]
- Buffle, J. Complexation Reactions in Aquatic Systems: An Analytical Approach; Ellis Horwood Ltd.: Chichester, UK, 1988. [Google Scholar]
- Stumm, W.; Morgan, J.J. Aquatic Chemistry: Chemical Equilibria and Rates in Natural Waters; Wiley: Hoboken, NJ, USA, 1996. [Google Scholar]
- Inselsbacher, E. Recovery of Individual Soil Nitrogen Forms after Sieving and Extraction. Soil Biol. Biochem. 2014, 71, 76–86. [Google Scholar] [CrossRef]
- Peña-Méndez, E.M.; Havel, J.; Patočka, J. Humic substances-compounds of still unknown structure: Applications in agriculture, industry, environment, and biomedicine. J. Appl. Biomed. 2005, 3, 13–24. [Google Scholar] [CrossRef]
- de Melo, B.A.G.; Motta, F.L.; Santana, M.H.A. Humic acids: Structural properties and multiple functionalities for novel technological developments. Mater. Sci. Eng. C 2016, 62, 967–974. [Google Scholar] [CrossRef] [PubMed]
- Bezuglova, O.; Klimenko, A. Application of Humic Substances in Agricultural Industry. Agronomy 2022, 12, 584. [Google Scholar] [CrossRef]
- Yikrazuul. Hypothetical Chemical Structure of an Imaginary Humic Acid. Wikimedia Commons. 2009. Available online: https://commons.wikimedia.org/wiki/File:Humic_acid.svg (accessed on 15 December 2023).
- Pernet-Coudrier, B.; Companys, E.; Galceran, J.; Morey, M.; Mouchel, J.M.; Puy, J.; Ruiz, N.; Varrault, G. Pb-Binding to Various Dissolved Organic Matter in Urban Aquatic Systems: Key Role of the Most Hydrophilic Fraction. Geochim. Cosmochim. Acta 2011, 75, 4005–4019. [Google Scholar] [CrossRef]
- Petrov, D.; Tunega, D.; Gerzabek, M.H.; Oostenbrink, C. Molecular Dynamics Simulations of the Standard Leonardite Humic Acid: Microscopic Analysis of the Structure and Dynamics. Environ. Sci. Technol. 2017, 51, 5414–5424. [Google Scholar] [CrossRef] [PubMed]
- Lunkad, R.; Murmiliuk, A.; Tošner, Z.; Štěpánek, M.; Košovan, P. Role of pKA in Charge Regulation and Conformation of Various Peptide Sequences. Polymers 2021, 13, 214. [Google Scholar] [CrossRef]
- Lunkad, R.; Murmiliuk, A.; Hebbeker, P.; Boublík, M.; Tošner, Z.; Štěpánek, M.; Košovan, P. Quantitative Prediction of Charge Regulation in Oligopeptides. Mol. Syst. Des. Eng. 2021, 6, 122–131. [Google Scholar] [CrossRef]
- Lunkad, R.; Biehl, P.; Murmiliuk, A.; Blanco, P.M.; Mons, P.; Štěpánek, M.; Schacher, F.H.; Košovan, P. Simulations and Potentiometric Titrations Enable Reliable Determination of Effective pKa Values of Various Polyzwitterions. Macromolecules 2022, 55, 7775–7784. [Google Scholar] [CrossRef]
- Garcés, J.L.; Mas, F.; Cecília, J.; Companys, E.; Galceran, J.; Salvador, J.; Puy, J.; Galceran, J. Complexation isotherms in metal speciation studies at trace concentration levels. Voltammetric techniques in environmental samples. Phys. Chem. Chem. Phys. 2002, 4, 3764–3773. [Google Scholar] [CrossRef]
- Nagasawa, M.; Murase, T.; Kondo, K. Potentiometric titration of stereoregular polyelectrolytes. J. Phys. Chem. 1965, 69, 4005–4012. [Google Scholar] [CrossRef]
- Companys, E.; Garcés, J.L.; Salvador, J.; Galceran, J.; Puy, J.; Mas, F. Electrostatic and specific binding to macromolecular ligands A general analytical expression for the Donnan volume. Coll. Surf. A Physicochem. Eng. Asp. 2007, 306, 2–13. [Google Scholar] [CrossRef]
- Goli, E.; Hiemstra, T.; Rahnemaie, R. Interaction of Boron with Humic Acid and Natural Organic Matter: Experiments and Modeling. Chem. Geol. 2019, 515, 1–8. [Google Scholar] [CrossRef]
- Liu, S.; Muthukumar, M. Langevin Dynamics Simulation of Counterion Distribution around Isolated Flexible Polyelectrolyte Chains. J. Chem. Phys. 2002, 116, 9975–9982. [Google Scholar] [CrossRef]
- Borkovec, M.; Jönsson, B.; Koper, G.J.M. Ionization Processes and Proton Binding in Polyprotic Systems: Small Molecules, Proteins, Interfaces, and Polyelectrolytes. In Surface and Colloid Science; Matijevic, E., Ed.; Springer: Boston, MA, USA, 2001; pp. 99–339. [Google Scholar] [CrossRef]
- Jusufi, A.; Likos, C.N.; Löwen, H. Conformations and Interactions of Star-Branched Polyelectrolytes. Phys. Rev. Lett. 2002, 88, 018301. [Google Scholar] [CrossRef]
- Dobrynin, A.V.; Rubinstein, M. Theory of polyelectrolytes in solutions and at surfaces. Prog. Polym. Sci. 2005, 30, 1049–1118. [Google Scholar] [CrossRef]
- Hofzumahaus, C.; Hebbeker, P.; Schneider, S. Monte Carlo simulations of weak polyelectrolyte microgels: pH-dependence of conformation and ionization. Soft Matter 2018, 14, 4087–4100. [Google Scholar] [CrossRef] [PubMed]
- Hofzumahaus, C.; Strauch, C.; Schneider, S. Monte Carlo simulations of weak polyampholyte microgels: pH-dependence of conformation an ionization. Soft Matter 2021, 17, 6029–6043. [Google Scholar] [CrossRef]
- Strauch, C.; Schneider, S. Ionisation and swelling behaviour of weak polyampholyte core–shell networks–a Monte Carlo study. Soft Matter 2023, 19, 938–950. [Google Scholar] [CrossRef]
- Diallo, M.S.; Simpson, A.; Gassman, P.; Faulon, J.L.; Johnson, J.H.; Goddard, W.A.; Hatcher, P.G. 3-D Structural Modeling of Humic Acids through Experimental Characterization, Computer Assisted Structure Elucidation and Atomistic Simulations. 1. Chelsea Soil Humic Acid. Environ. Sci. Technol. 2003, 37, 1783–1793. [Google Scholar] [CrossRef]
- Albers, C.N.; Banta, G.T.; Jacobsen, O.S.; Hansen, P.E. Characterization and Structural Modelling of Humic Substances in Field Soil Displaying Significant Differences from Previously Proposed Structures. Eur. J. Soil. Sci. 2008, 59, 693–705. [Google Scholar] [CrossRef]
- Feng, H.; Zhang, H.; Cao, H.; Sun, Y.; Zhang, A.; Fu, J. Application of a Novel Coarse-Grained Soil Organic Matter Model in the Environment. Environ. Sci. Technol. 2018, 52, 14228–14234. [Google Scholar] [CrossRef] [PubMed]
- Weik, F.; Weeber, R.; Szuttor, K.; Breitsprecher, K.; deGraaf, J.; Kuron, M.; Landsgesell, J.; Menke, H.; Sean, D.; Holm, C. ESPResSo 4.0—An extensible software package for simulating soft matter systems. Eur. Phys. J. Spec. Top. 2019, 227, 1789–1816. [Google Scholar] [CrossRef]
- Weeber, R.; Grad, J.N.; Beyer, D.; Blanco, P.M.; Kreissl, P.; Reinauer, A.; Tischler, I.; Košovan, P.; Holm, C. ESPResSo, a Versatile Open-Source Software Package for Simulating Soft Matter Systems. In “ESPResSo, a Versatile Open-Source Software Package for Simulating Soft Matter Systems,” in Comprehensive Computational Chemistry, 1st ed.; Yáñez, M., Boyd, R.J., Eds.; Elsevier: Oxford, UK, 2024; pp. 578–601. [Google Scholar] [CrossRef]
- Beyer, D.; Torres, P.B.; Pineda, S.P.; Narambuena, C.F.; Grad, J.N.; Košovan, P.; Blanco, P.M. pyMBE: The Python-based Molecule Builder for ESPResSo. arXiv preprint. arXiv 2024, arXiv:2401.14954. [Google Scholar] [CrossRef]
- Barr, S.A.; Panagiotopoulos, A.Z. Conformational Transitions of Weak Polyacids Grafted to Nanoparticles. J. Chem. Phys. 2012, 137, 144704. [Google Scholar] [CrossRef] [PubMed]
- Ullner, M.; Woodward, C.E. Simulations of the Titration of Linear Polyelectrolytes with Explicit Simple Ions: Comparisons with Screened Coulomb Models and Experiments. Macromolecules 2000, 33, 7144–7156. [Google Scholar] [CrossRef]
- Tanford, C. Physical Chemistry of Macromolecules; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1961. [Google Scholar]
- Burak, Y.; Netz, R.R. Charge Regulation of Interacting Weak Polyelectrolytes. J. Phys. Chem. B 2004, 108, 4840–4849. [Google Scholar] [CrossRef]
- Payamyar, P.; King, B.T.; Öttinger, H.C.; Schlüter, A.D. Two-Dimensional Polymers: Concepts and Perspectives. Chem. Commun. 2016, 52, 18–34. [Google Scholar] [CrossRef]
- Kozynchenko, A.I.; Kozynchenko, S.A. About Improving Efficiency of the P3M Algorithms When Computing the Inter-Particle Forces in Beam Dynamics. Comput. Phys. Commun. 2017, 212, 47–54. [Google Scholar] [CrossRef]
- Pollock, E.L.; Glosli, J. Comments on P3M, FMM, and the Ewald Method for Large Periodic Coulombic Systems. Comp. Phys. Commun. 1996, 95, 93–110. [Google Scholar] [CrossRef]
- Reed, C.E.; Reed, W.F. Monte Carlo study of titration of linear polyelectrolytes. J. Chem. Phys. 1992, 96, 1609. [Google Scholar] [CrossRef]
- Janke, W. Statistical Analysis of Simulations: Data Correlations and Error Estimation. In Quantum Simulations of Complex Many-Body Systems: From Theory to Algorithms; Grotendorst, J., Marx, D., Muramatsu, A., Eds.; Lecture Notes: Jülich, Germany, 2002; Volume 10, pp. 423–445. [Google Scholar]
- Labbez, C.; Jönsson, B. Applied Parallel Computing. State of the Art in Scientific Computing; Kågström, B., Elmroth, E., Dongarra, J., Waśniewski, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; Volume 4699, pp. 66–72. [Google Scholar]
- Košovan, P.; Landsgesell, J.; Nová, L.; Uhlík, F.; Beyer, D.; Blanco, P.M.; Staňo, R.; Holm, C. Reply to the ‘Comment on “Simulations of ionization equilibria in weak polyelectrolyte solutions and gels” by J. Landsgesell, L. Nová, O. Rud, F. Uhlík, D. Sean, P. Hebbeker, C. Holm and P. Košovan, Soft Matter, 2019, 15, 1155–1185’. Soft Matter 2023, 19, 3522–3525. [Google Scholar] [CrossRef]
- Levenberg, K. A Method for the Solution of Certain Problems in Least Squares. Q. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef]
- Marquardt, D. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. SIAM J. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]


| Units/pi | I (mol/L) | βδ | pkD | pkY | pD | |
|---|---|---|---|---|---|---|
| 25:25 (0.5:0.5) | 0.001 | 4.78 ± 0.15 | 4.12 ± 0.04 | 9.53 ± 0.08 | 0.499 ± 0.002 | 2.4 × 10−5 |
| 0.01 | 2.70 ± 0.11 | 4.11 ± 0.03 | 9.70 ± 0.07 | 0.497 ± 0.002 | 2.3 × 10−5 | |
| 30:20 (0.6:0.4) | 0.001 | 4.85 ± 0.10 | 4.15 ± 0.03 | 9.38 ± 0.06 | 0.601 ± 0.002 | 1.8 × 10−5 |
| 0.01 | 3.17 ± 0.09 | 4.05 ± 0.03 | 9.34 ± 0.06 | 0.598 ± 0.002 | 2.1 × 10−5 | |
| 35:15 (0.7:0.3) | 0.001 | 4.52 ± 0.11 | 4.18 ± 0.04 | 9.66 ± 0.10 | 0.702 ± 0.003 | 4.3 × 10−5 |
| 0.01 | 3.05 ± 0.07 | 4.07 ± 0.02 | 9.48 ± 0.05 | 0.699 ± 0.002 | 1.9 × 10−5 | |
| 40:10 (0.8:0.2) | 0.001 | 4.54 ± 0.09 | 4.23 ± 0.04 | 9.45 ± 0.15 | 0.804 ± 0.004 | 4.7 × 10−5 |
| 0.01 | 3.07 ± 0.06 | 4.09 ± 0.02 | 9.37 ± 0.06 | 0.802 ± 0.002 | 2.5 × 10−5 |
| Units/pi | I (mol/L) | βδ | pkD | pkY | pD | |
|---|---|---|---|---|---|---|
| 25:25:5 (0.455:0.455:0.090) | 0.001 | 6.6 ± 0.3 | 3.39 ± 0.07 | 7.9 ± 0.2 | 0.480 ± 0.005 | 8.0 × 10−5 |
| 0.01 | 4.2 ± 0.3 | 3.60 ± 0.07 | 8.4 ± 0.2 | 0.481 ± 0.006 | 1.4 × 10−4 | |
| 30:20:5 (0.545:0.364:0.091) | 0.001 | 6.3 ± 0.2 | 3.45 ± 0.06 | 7.9 ± 0.1 | 0.577 ± 0.005 | 7.8 × 10−5 |
| 0.01 | 4.2 ± 0.3 | 3.61 ± 0.07 | 8.3 ± 0.2 | 0.577 ± 0.006 | 1.3 × 10−4 | |
| 35:15:5 (0.636:0.273:0.091) | 0.001 | 5.8 ± 0.2 | 3.50 ± 0.07 | 8.1 ± 0.2 | 0.668 ± 0.006 | 1.2 × 10−4 |
| 0.01 | 3.9 ± 0.2 | 3.62 ± 0.07 | 8.4 ± 0.2 | 0.672± 0.006 | 1.5 × 10−4 | |
| 40:10:5 (0.727:0.182:0.091) | 0.001 | 5.6 ± 0.2 | 3.58 ± 0.06 | 7.8 ± 0.2 | 0.763 ± 0.007 | 1.2 × 10−4 |
| 0.01 | 3.9 ± 0.2 | 3.65 ± 0.06 | 8.3 ± 0.1 | 0.765 ± 0.006 | 1.4 × 10−4 |
| Units/pi | I (mol/L) | βδ | pkD | pkY | pkH | pD | pY | |
|---|---|---|---|---|---|---|---|---|
| 25:25:5 (0.455:0.455:0.090) | 0.001 | 5.8 ± 0.3 | 3.80 ± 0.08 | 8.8 ± 0.2 | 6.6 ± 0.3 | 0.456 ± 0.007 | 0.482 ± 0.012 | 3.5 × 10−5 |
| 0.01 | 3.2 ± 0.2 | 3.91 ± 0.04 | 9.4 ± 0.1 | 6.7 ± 0.2 | 0.445 ± 0.006 | 0.479 ± 0.007 | 3.3 × 10−5 | |
| 30:20:5 (0.545:0.364:0.091) | 0.001 | 5.8 ± 0.2 | 3.88 ± 0.06 | 8.8 ± 0.1 | 6.7 ± 0.3 | 0.552 ± 0.006 | 0.377 ± 0.011 | 2.1 × 10−5 |
| 0.01 | 3.4 ± 0.2 | 3.93 ± 0.04 | 9.2 ± 0.1 | 6.8 ± 0.2 | 0.545 ± 0.006 | 0.382 ± 0.008 | 3.1 × 10−5 | |
| 35:15:5 (0.636:0.273:0.091) | 0.001 | 5.5 ± 0.2 | 3.94 ± 0.08 | 9.1 ± 0.2 | 7.0 ± 0.3 | 0.645 ± 0.007 | 0.27 ± 0.02 | 4.1 × 10−5 |
| 0.01 | 3.4 ± 0.1 | 3.92 ± 0.03 | 9.2 ± 0.1 | 7.0 ± 0.1 | 0.640 ± 0.004 | 0.284 ± 0.006 | 1.4 × 10−5 | |
| 40:10:5 (0.727:0.182:0.091) | 0.001 | 5.4± 0.1 | 4.06 ± 0.14 | 9.3 ± 0.8 | 7.2 ± 0.5 | 0.745 ± 0.008 | 0.16 ± 0.03 | 5.8 × 10−5 |
| 0.01 | 3.5 ± 0.1 | 3.95 ± 0.03 | 9.1 ± 0.1 | 7.0 ± 0.1 | 0.734 ± 0.004 | 0.186 ± 0.006 | 1.5 × 10−5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naranjo, D.; Blanco, P.M.; Garcés, J.L.; Madurga, S.; Mas, F. Constant-pH Simulations of a Coarse-Grained Model of Polyfunctional Weak Charged Biopolymers. Biophysica 2024, 4, 107-127. https://doi.org/10.3390/biophysica4010008
Naranjo D, Blanco PM, Garcés JL, Madurga S, Mas F. Constant-pH Simulations of a Coarse-Grained Model of Polyfunctional Weak Charged Biopolymers. Biophysica. 2024; 4(1):107-127. https://doi.org/10.3390/biophysica4010008
Chicago/Turabian StyleNaranjo, David, Pablo M. Blanco, Josep L. Garcés, Sergio Madurga, and Francesc Mas. 2024. "Constant-pH Simulations of a Coarse-Grained Model of Polyfunctional Weak Charged Biopolymers" Biophysica 4, no. 1: 107-127. https://doi.org/10.3390/biophysica4010008
APA StyleNaranjo, D., Blanco, P. M., Garcés, J. L., Madurga, S., & Mas, F. (2024). Constant-pH Simulations of a Coarse-Grained Model of Polyfunctional Weak Charged Biopolymers. Biophysica, 4(1), 107-127. https://doi.org/10.3390/biophysica4010008







