Abstract
As the water molecules found at the interface of lipid bilayers exhibit distinct structural and reorientation dynamics compared to water molecules found in bulk, the fluctuations in their hydrogen bond (HB) network are expected to be different from those generated by the bulk water molecules. The research presented here aims to gain an insight into temperature-dependent fluctuations of a HB network of water molecules found in an interfacial layer of multilamellar liposomes (MLVs) composed of anionic 1,2-dimyristoyl-sn-glycero-3-phospho-L-serine (DMPS) lipids. Besides suspending DMPS lipids in phosphate buffer saline (PBS) of different pH values (6.0, 7.4, and 8.0), the changes in HB network fluctuations were altered by the incorporation of a non-polar flavonoid molecule myricetin (MCE) within the hydrocarbon chain region. By performing a multivariate analysis on the water combination band observed in temperature-dependent FTIR spectra, the results of which were further mathematically analyzed, the temperature-dependent fluctuations of interfacial water molecules were captured; the latter were the greatest for DMPS in PBS with a pH value of 7.4 and in general were greater for DMPS multibilayers in the absence of MCE. The presence of MCE made DMPS lipids more separated, allowing deeper penetration of water molecules towards the non-polar region and their restricted motion that resulted in decreased fluctuations. The experimentally observed results were supported by MD simulations of DMPS (+MCE) lipid bilayers.
1. Introduction
Fundamental biological phenomena such as enzyme activity [1,2], cell adhesion [3], membrane fusion [4], and lipid diffusion [5] are intimately related to the structural features and reorientation dynamics of the water molecules found at the biomembrane interface. In exclusively lipid membranes, often investigated with the aim of simplifying and understanding events on the surface of biomembranes, the arrangement and orientation of water molecules within the interfacial aqueous layer are primarily a function of the magnitude and of the charge distribution on lipid molecule polar head-groups [6,7]. In bulk water, a single water molecule is hydrogen-bonded to tetrahedrally surrounded water molecules from the first solvation shell that can be exchanged with those from a second solvation shell owing to the concerted reorientation and cleavage of the existing hydrogen bond (HB) [8]. However, a disruption of the tetrahedral ordering of water molecules due to the proximity of the lipid membrane interface [9] imposes significant limitations on water reorientation dynamics.
The investigation of structural and reorientation dynamics of interfacial water usually involves ultrafast vibrational spectroscopic techniques such as vibrational sum frequency generation (VSFG) and two-dimensional IR spectroscopy (2D-IR) [10,11,12,13]. Despite the inherent limitation of its application to exclusively lipid monolayers, VSFG showed that H-atoms of water molecules near choline (positive) [14] and phosphate (negative) [15,16] moieties are oppositely oriented, and these findings are further corroborated by independent computational studies [17,18,19]. Besides identifying differently oriented H-atoms, VSFG showed that oppositely oriented water molecules in the vicinity of choline (positive) and phosphate (negative) groups obey different HB dynamics [20]. Specifically, as water molecules near positively charged functional groups display the maintenance of tetrahedral arrangement, their reorientation dynamics resemble those of bulk water [14], whereas near negatively charged functional groups the opposite scenario is found; the loss of the tetrahedral ordering of water molecules [9] is accompanied by the retardation of HB exchange dynamics due to the reduced number of partners in a HB arrangement [9,13,21,22,23,24,25,26]. Unlike VSFG, 2D IR is not an intrinsically surface-sensitive technique, but nevertheless it allows distinguishing the events that occur at different time scales [27]; in particular, by using the appropriate vibrational echo pulse sequence it becomes possible to decipher the position of the oscillator, commonly of an environmentally sensitive C=O moiety, within the heterogeneous sample such as a hydrated bilayer [28].
Along with the mentioned and briefly introduced state-of-the-art spectroscopic techniques, whose main disadvantage is the price, limiting their use to a small number of laboratories in the world, the use of widely available conventional linear FTIR spectroscopy [29] occasionally produces a spark of progress in the characterization of water-based HB systems. Although it contains the averaged signal of all water molecules present in the lipid suspension (bulk and interfacial water), the analysis of the band(s) loaded with water HB network fingerprints [30,31], as well as defining/introducing an arbitrary metric, can enable the expression of the acquired spectroscopic data in terms of water HB network fluctuations [32].
Accordingly, Tong et al. managed to distinguish bulk water molecules from those at the air–water interface by inspecting water librations (δL), i.e., intermolecular vibrations between water molecules, the existence of which is the result of HBs [31]. Further, Verma et al. conducted a comprehensive concentration and temperature study of aqueous solutions of various salts in order to elucidate the impact of a particular anion/cation on the water combination band (usually centered at about 2130 cm−1) that originates from the fundamental transition of water bending (δHOH) and ρL [30]. Because the direction and the magnitude of the water combination band maximum displacement to higher/lower frequencies in the presence of ions coincided with their position in a Hoffmeister series, this approach provided a platform for monitoring both local and global water dynamics through the impact of kosmotropes/chaotropes on a HB network.
The quantification of temperature-dependent fluctuations in a water-molecule-based HB network in the presence of anions of Na+ and K+ salts (Cl−, Br−, I−, CH3COO−, NO3−, NO2−) was presented for the first time in the study conducted by Brkljača et al. [32]. Briefly, the water combination band was subjected to a multivariate analysis in which the response of water molecules in a certain temperature range (25–75 °C) was divided into two contributions: the one produced by low-temperature (high-density) water and the other produced by high-temperature (low-density) water [33,34]. The observed hysteresis between the responses of these two kinds of water, expressed in terms of mathematical quantities that reflect HB-network-associated phenomena, showed that temperature-dependent fluctuations in a HB network are actually ion-invariant. The validity of the obtained results was confirmed by independent study conducted on equivalent systems investigated using a femtosecond elastic second harmonic scattering (fs-ESHS) technique that produced analogous findings [35].
As the synergy of linear FTIR spectroscopy and multivariate analysis managed to provide an insight into the fluctuations in the water HB network in the presence of anions, this study aimed to apply the same approach in characterizing the fluctuations in the HB network of water molecules found at the interface of negatively charged supramolecular aggregates. Accordingly, multilamellar liposomes (MLVs) of 1,2-dimyristoyl-sn-glycero-3-phospho-L-serine (DMPS) were prepared in a phosphate buffer saline (PBS) and examined by FTIR spectroscopy in a temperature range that spanned about ±10 °C around their melting point (Tm). The latter is the temperature at which van der Waals interactions between hydrocarbon chains are reduced, causing lipids to transition from a more ordered gel (Lβ) phase to a disordered fluid (Lα) phase, and which for DMPS lipids is reported to be between 37 and 39 °C [36,37]. Overall, this Lβ→Lα transition is accompanied by thinning of the lipid bilayer, loss of lipid lateral arrangement, and consequently greater hydration of polar groups and the glycerol backbone that encompasses the HB network between the water molecules in the interfacial layer [38].
By knowing that negatively charged phosphatidylserine (PS) lipids are generally very unstable in terms of curvature variations and local pH change [39], especially in the form of large unilamellar liposomes (LUVs) [40], the presumed fluctuations in the interfacial HB network of DMPS in the Lβ and in Lα phase were enhanced in two ways: (i) MLVs of DMPS were prepared in PBS with three pH values: 6.0, 7.4, and 8.0, at which all DMPS lipids are negatively charged; (ii) the incorporation of flavonoid myricetin (MCE), a non-polar molecule that prefers accommodation in a hydrocarbon chain region [41], which should induce the separation of lipid molecules and provide deeper penetration of interfacial water that consequently modulates fluctuations in their HB network (structural formulas are displayed in Figure 1). The results obtained in this study are aimed to be applied in further studies addressing the fluctuations in the interfacial water layer of other supramolecular aggregates carrying the charges of different magnitudes and distributions.
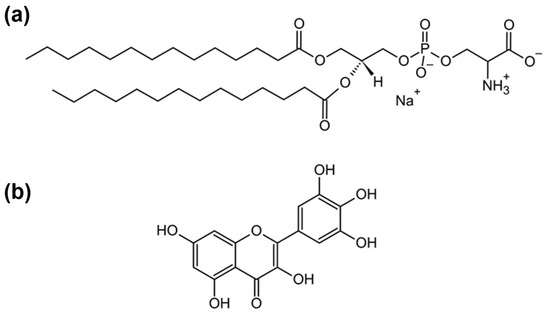
Figure 1.
Structural formulas of (a) 1,2-dimyristoyl-sn-glycero-3-phospho-L-serine (sodium salt) (DMPS); (b) myricetin (MCE).
2. Materials and Methods
2.1. Chemical and Suspension Preparations
Commercially available 1,2-dimyristoyl-sn-glycero-3-phospho-L-serine (sodium salt) (DMPS; M = 679.9 gmol−1, white powder, Avanti, Alabaster, AL, United States, ≥99%); myricetin (MCE; M = 318.2 gmol−1, yellow powder, Sigma-Aldrich, Burlington, MA, United States, ≥96%); chloroform (CHCl3; Merck, Darmstadt, Germany, p. a.); methanol (MeOH, Merck, Darmstadt, Germany ≥98%); and powders used for phosphate buffer saline (PBS) preparation (dissolution of NaCl, KCl, Na2HPO4, KH2PO4 (Kemika, Zagreb, Croatia, p. a. grade) in milli-Q water®) of ionic strength I = 100 mM and pH 6.0, 7.4, and 8.0 were used as received. The stock solutions of DMPS/MCE in CHCl3/MeOH were prepared by weighing DMPS (≈90 mg)/MCE (≈6 mg) that were dissolved in 6 mL CHCl3/0.9 mL MeOH. In six/three round-bottom flasks, 1 mL of DMPS stock solution (in CHCl3)/0.3 mL of MCE stock solution (in MeOH) was added. In this way, in 6/3 flasks there was about 15 mg of DMPS/2 mg of MCE, so that the mole ratio of MCE in DMPS lipid bilayers was x(MCE) ≈ 0.3. Films of DMPS (+MCE) were obtained upon evaporating CHCl3 (+MeOH) on a rotary evaporator, and, after drying with N2(g), the films were suspended in PBS with pH values of 6.0, 7.4, and 8.0. The suspensions of multilamellar liposomes (MLVs) of DMPS were made by successive heating (~80 °C), vortexing (RT), and cooling (~4 °C) cycles, where each step lasted about one minute. The suspensions prepared were milky white (DMPS only) or slightly yellow (DMPS + MCE).
2.2. FT-IR Spectroscopy
2.2.1. FT-IR Spectra Acquisition
FT-IR spectra were measured on an ABB Bomem MB102 spectrometer (ABB Bomem factory, Québec, QC, Canada), equipped with CsI optics and a DTGS detector in a transmission. FT-IR spectra of DMPS (+MCE) lipid suspensions in PBS of three different pH values (6.0, 7.4, and 8.0) were acquired in a sealed cell equipped with CaF2 windows with the path length of the cell d = 27.37 μm [42]. Temperature was regulated by a Specac 3000 Series high-stability temperature controller with heating jacket (Specac, Kent, UK). The spectra of all suspensions were acquired as duplicates in the temperature range 30–50 °C using a heating rate of 1 °C min−1, at nominal resolution of 2 cm−1 and 10 scans.
2.2.2. FT-IR Spectra Analysis
After measuring FT-IR spectra of DMPS (+MCE) suspensions in PBS with three pH values, the obtained spectra were divided into two separate spectral regions (D1, D2): (i) 2980–2820 cm−1, displaying the bands originated from the (anti)symmetric stretching of methylene (CH2) groups of hydrocarbon chains (ν(a)sCH2), and (ii) 2650–1800 cm−1 where only water absorbs (a combination band that originates from water bending (δHOH) and water libration (ρLH2O); H2O comb). The analysis of spectral region D1 is thoroughly presented in Supplementary Materials, Section S1 (Figure S1), and here the analysis of D2 spectral region is presented. Two-point baseline correction at the band minima in spectral region D2 was followed after smoothing (Savitzky–Golay; polynomial of 3rd degree through 50 points [43]). Additionally, the spectral range 2650–2300 cm−1 was eliminated from the analysis because the band originated from νasCO2, the amount of which varies during the measurement, obscures the results [32]. The information obtained by analyzing the first spectral region (D1) concerned the determination of the melting temperature (Tm) [44,45]—i.e., the temperature at which van der Waals interactions between hydrocarbon chains are weakened—and its change in the presence of MCE (Table S1 in Supplementary Materials), whereas the second one addressed temperature-dependent fluctuations in a HB network formed by water molecules, both bulk ones and those that are found in the interfacial water layers [32].
The prepared spectra underwent further analysis using the Multivariate Curve Resolution-Alternating Least Squares (MCR-ALS) method. This mathematical method examines a data set for main sources of variation and, when applied to spectroscopic data, identifies the spectra of system components with no prior knowledge of their identity, position, or signal shape [46,47]. The requirements of MCR-ALS are for data to be structured as a two-way matrix, and for that matrix to be bilinear (i.e., a product of two matrices). In the case of FTIR spectra in this study, raw data form a matrix describing signal intensity at particular temperatures and wavenumbers. The matrix is the result of contributions of smaller matrices describing individual species and their concentrations. This relationship is described mathematically as
where D is the raw data matrix, ST is a spectral matrix of individual components, C is the concentration matrix of those components, and E is the matrix of unexplained residuals.
D = CST + E
Before starting the MCR-ALS analysis, initial guesses of contributions are required. First, the Singular Value Decomposition (SVD) method was applied to estimate the number of components. As Libnau et al. demonstrated [33], the spectral evolution of the water signals as a function of temperature can be presented in the form of a matrix whose rank is two; in other words, two components contain all the information about the system under investigation. Thus, two components were expected to meaningfully contribute to our spectral data [48]. Evolving Factor Analysis (EFA) was then utilized to obtain initial guesses of the concentration profiles of those components [46,47]. Subsequently, the MCR-ALS equation with the provided initial estimates can be solved iteratively to produce the final ST and C. The MCR-ALS procedure with EFA is publicly available and implemented in MATLAB [49], and further explanations of the theory may be found elsewhere [46,50,51]. It is important to note that constraints need to be applied when analyzing FTIR data: all spectral profiles and concentration values must be kept positive (non-negativity constraint), and the individual pure spectra are regarded as unimodal (unimodality constraint).
The spectral and concentration profiles obtained will depend on the examined spectral region and the nature of the chemical species producing signals. Since the examined system contained species that undergo a phase transition in the explored temperature range, a sigmoid profile was expected, with the inflection point around the transition temperature [48]. Thus, the contributions of the species existing below Tm will be referred to as the low-temperature component (LTC), and those above Tm will be referred to as the high-temperature component (HTC).
The concentration profiles generated by MCR-ALS were of sigmoid character for the D1 spectral range (examined in Supplementary Materials, Figure S2), and of polynomial for the spectral range D2. The obtained curves in spectral range D2 were fitted on a 2nd-degree polynomial (parabolic fit; R2 (DMPS/DMPS + MCE) ≥ 0.998/0.999) expressed in the form . In a mathematical context, the obtained coefficients (dimensionless quantity), (in °C−1), and (in °C−2) indicate relative concentrations of the particular component (LTC or HTC) at 0 °C, the rate of a decrease in LTC/HTC in favor of an increase in HTC/LTC, and a profile curvature, respectively. As thoroughly described in a previous paper [32], values obtained for LTC and HTC reflect the hysteresis between the temperature-dependent fluctuations in a HB network meshed by water molecules.
2.3. Molecular Dynamics Simulations
Simulations of DMPS bilayers with and without the presence of MCE were conducted using classical molecular dynamics (MD). Homogeneous DMPS bilayers were prepared with the CHARMM-GUI Membrane Builder module [52] and consisted of 200 lipid molecules. DMPS + MCE bilayers were generated by randomly adding 60 MCE molecules to the bilayer (MCE-to-lipid ratio: 0.3). Bilayers were solvated with 50 water molecules per bilayer component. We added 21 Na+ and Cl− ions to achieve the experimental ion concentration of 100 mM, along with an additional 200 Na+ ions to neutralize the bilayer charge. All simulations were conducted using the GROMACS 2020.0 software [53], CHARMM36m force field [54], and TIP3P water model [55]. MCE was parametrized using CGenFF [56]. NBFIX corrections for Na-carbonyl interactions have been included in all simulations, as provided in the July 2021 version of the CHARMM36m force field [57]. The systems underwent energy minimization followed by 200 ps of equilibration in the NVT ensemble with the V-rescale algorithm. The production run was conducted for 300 ns in the NpT ensemble using the Nosé–Hoover thermostat [58] with a time constant of 1 ps and the Parrinello–Rahman barostat [59] with semi-isotropic pressure coupling and a time constant of 2 ps (target pressure: 1 bar). When conducting the trajectory analysis, the first half of the production run was discarded as equilibration time, and only the last 150 ns were examined. In all simulations, the cutoff for short-range Coulomb interactions and van der Waals interactions was set to 1.2 nm with a switching function turned on after 1 nm. The Particle Mesh Ewald (PME) procedure [60] was used to handle long-range Coulomb interactions. The LINCS algorithm was employed to constrain bonds involving hydrogen. Three-dimensional periodic boundary conditions were used throughout for all systems. And the time step was 2 fs. Visualization and analysis were conducted with Gromacs modules and Visual Molecular Dynamics (VMD) [61].
3. Results and Discussion
The multivariate analysis of the D2 spectral region (Figure 2) produced spectral (Figure 2, dotted curves) and, more importantly, concentration profiles of the LTC and HTC (Figure 3). The expected low-frequency shift of the combination band maximum upon heating was found in all systems (~2131 cm−1 at 30 °C and ~2117 cm−1 at 50 °C), regardless of the absence/presence of MCE or the pH (see Table 1). However, it appears that for the DMPS suspension in the absence of MCE there is a slightly greater shift in the band maximum than in its presence, especially for the pH value of 7.4 (2130 cm−1 at 30 °C and 2114 cm−1 at 50 °C), which is the closest to the physiologically relevant pH value.
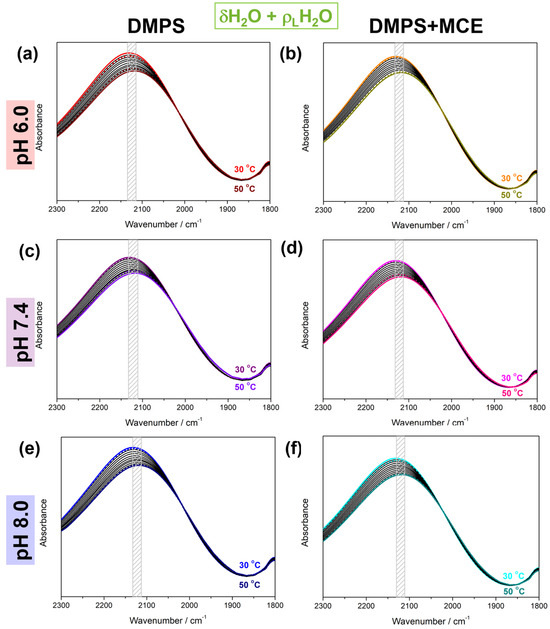
Figure 2.
Baseline-corrected and Savitzky–Golay-smoothed, temperature-dependent FT-IR spectra of DMPS in the absence (a,c,e) and the presence of MCE (b,d,f) suspended in PBS at pH 6.0 (a,b), 7.4 (c,d), and 8.0 (e,f). The lowest/highest (30 °C/50 °C) temperatures are highlighted in red/wine (DMPS, pH 6.0, 30 °C/50 °C), orange/dark yellow (DMPS + MCE, pH 6.0, 30 °C/50 °C), purple/violet (DMPS, pH 7.4, 30 °C/50 °C), purple/pink (DMPS + MCE, pH 7.4, 30 °C/50 °C), blue/navy (DMPS, pH 8.0, 30 °C/50 °C), and cyan/dark cyan (DMPS + MCE, pH 8.0, 30 °C/50 °C). The temperature-dependent FTIR spectra are represented by solid curves and the spectral profiles of low- and high-temperature components obtained from MCR-ALS with EFA by dotted curves. Grey rectangles emphasize the temperature-dependent displacement of the band maximum.
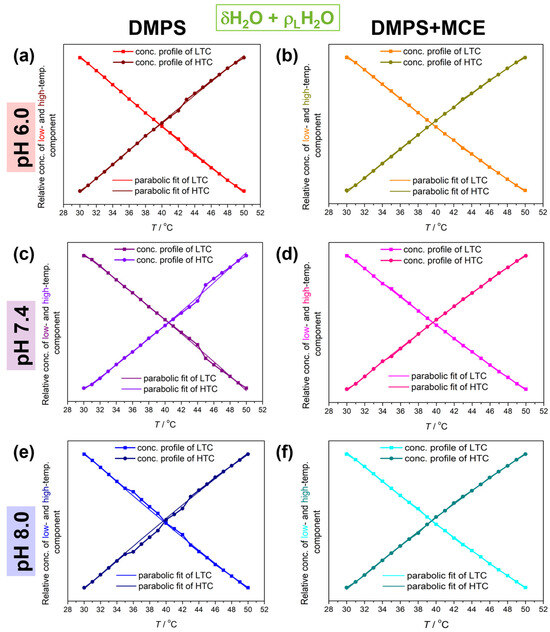
Figure 3.
The concentration profiles of low- and high-temperature component of DMPS in the absence (a,c,e) and the presence of MCE (b,d,f) suspended in PBS at pH 6.0 (a,b), 7.4 (c,d), and 8.0 (e,f). Experimentally obtained low- and high-temperature components are represented by solid curves colored red/wine (DMPS, pH 6.0), orange/dark yellow (DMPS + MCE, pH 6.0), purple/violet (DMPS, pH 7.4), purple/pink (DMPS + MCE, pH 7.4), blue/navy (DMPS, pH 8.0), and cyan/dark cyan (DMPS + MCE, pH 8.0). Their fit on a polynomial of 2nd degree is represented by dotted curves of the corresponding color.

Table 1.
Parameters obtained from polynomial regression (B0, B1, B2) of the results produced by multivariate analysis conducted on spectral range 2300–1800 cm−1.
Following the analogy developed in a previous study, these results can be examined in the context of a decrease in temperature-dependent fluctuations in the water HB network when it surrounds MLVs of DMPC+MCE suspensions, which is not the case for pure DMPS lipids. As this approach catches the response of all water molecules, i.e., both bulk (the contribution of which is dominant) and interfacial ones, it seems reasonable to assume that the bulk water contribution is nearly the same for all suspensions, regardless of the pH value or the presence of MCE. The major variable that changes in this consideration is the amount of interfacial HB water and how its HB pattern is changed when MCE is inserted into the DMPS lipids. A potential explanation for this phenomenon is that the motions (primarily librations) of water molecules in the interfacial regions are more restricted when MCE is incorporated in MLVs. If the DMPS lipids are more separated even at lower temperatures (due to the inclusion of MCE), then more water will be able to penetrate into the interfacial region, that is, it will penetrate deeper into the liposome itself and will certainly show different dynamics compared to interfacial water which does not penetrate so deeply into the lipid double layer (as with DMPS itself).
At first glance, polynomial fits of the LTC and HTC (Figure 3) reveal deviations from the experimental values for DMPS suspensions in the absence of MCE. Although the deviations are observed at all pH values, for the DMPS suspension in PBS of pH 6.0, 7.4, and 8.0 they are the most significant in the temperature range 43–45 °C, 42–48 °C, and 37–44 °C, respectively. Interestingly, this is not observed for DMPS + MCE suspensions, regardless of the pH value of PBS.
Another interesting phenomenon observed from the FTIR data of the DMPS suspensions concerns the difference in absolute values of B1 (Δ|B1|) and especially of B2 (Δ|B2|) coefficients of the LTC and HTC (Table 1); Δ|B1| values for the DMPS in PBS with pH values of 6.0, 7.4, and 8.0 are about 0.003 C−1, 0.009 C−1, and 0.002 C−1, whereas for the DMPS + MCE in PBS with pH values of 6.0, 7.4, and 8.0 they are about 0.003 C−1, 0.001 C−1, and 0.002 C−1. Regarding Δ|B2| values, for the DMPS in PBS of pH 6.0, 7.4, and 8.0 they are about 0.3–0.5 C−2, 1 C−2, and 0.1 C−2, whereas for the DMPS + MCE in PBS of pH 6.0, 7.4, and 8.0 they are about 0.3 C−2, 0.1 C−2, and 0.3 C−2. When the uncertainty is taken into consideration, it can be seen that Δ|B1| and Δ|B2| for all suspensions are the same value. However, it cannot be ignored that dissipation in Δ|B1| and especially in Δ|B2| is much larger for DMPS only, which contrasts the situation when MCE is incorporated in the bilayers.
Finally, it should be noted that the incorporation of MCE, in addition to affecting the change in the dynamics of the interfacial layer of water molecules, also affects the separation of or interaction between lipid molecules both in the gel phase and in the fluid phase. The most obvious indicators of the consequences of incorporating MCE into the DMPS lipid bilayer are changes in the lipid Tm and the cooperativity of the phase transition [38], both of which are available and can be determined from the temperature-dependent FTIR spectra in the spectral region D1 (Figures S1 and S2 and Table S1) [48,62]. Although the reduction in Tm due to the incorporation of MCE was observed only in the DMPS lipid bilayers hydrated with PBS of pH 8.0 (Table S1, Figure S2), which might be associated with greater rigidity and compactness of anionic lipid bilayers in comparison with zwitterionic ones [40,41,44,63,64], in all three lipid suspensions (i.e., at all three pH values) it is evident that the melting is not characterized by such a steep sigmoidal transition in the presence of MCE as it is in its absence, which is a clear indication of a decrease in the cooperativity of the transition [62,65].
The structure and hydration of DMPS bilayers at different temperatures with or without MCE were also examined using MD simulations. Examination of bilayer structural parameters revealed larger spatial separation of DMPS lipids following MCE inclusion, as demonstrated in Table 2. Additional information on the structural analysis can be found in Supplementary Materials. APL and membrane thickness are common parameters describing lipid organization: smaller APLs indicate tighter packing, while larger thicknesses are due to ordered lipid acyl chains with less interdigitation. Thus, the values obtained for pure DMPS bilayers reflect the tendency of lipids to pack more tightly at lower temperatures (gel phase) compared to higher temperatures (fluid phase) [66,67], and are consistent with reports in the literature for similar systems. Wide-angle X-ray scattering data on DMPS at 30 °C pointed to an APL of 0.415 nm2 [68], which is close to the calculated figure. Also, pressure isotherm studies have shown that DMPS monolayers collapse at an APL of ~0.40 nm2 [69]. Computational studies provided estimations of 47.6 nm2 in the gel (30 °C) and 55.6 nm2 in the fluid phase (60 °C) for pure bilayers or ~0.60 nm2 for bilayers containing small molecules [70]. The respective studies also provided bilayer thickness estimates of 4.0–4.4 nm, or ~3.5 nm. Experimental data on DMPS bilayer thicknesses are lacking. X-ray diffraction of DMPS MLVs showed the lamellar repeat distance in phosphate buffer to decrease from 6.2 nm to 5.2 nm following an increase in temperature from 20 °C to 53 °C; however, those values include the layer of interlamellar water [71].

Table 2.
Structural parameters of DMPS and DMPS + MCE bilayers obtained from molecular dynamics simulations.
MCE addition disrupted the ability of DMPS to pack tightly and interfered with the close interactions between lipid chains that are crucial for bilayer organization, resulting in significant APL increase and a decrease in thickness. Greater fluidity of acyl chains is shown by analyzing acyl chain order parameters (Figure S3 in Supplementary Materials), which are significantly decreased in DMPS + MCE systems. Notably, the effect of MCE is larger at 30 °C, where structural parameters are changed enough to be consistent with the fluid phase despite the low temperature, thus confirming membrane disruption. Even visually, the equilibrated DMPS + MCE system at 30 °C is more like the fluid phase of pure DMPS (Figure S4 in Supplementary Materials), and the distribution of chain tilt angles is broadened (Figure S5 in Supplementary Materials). The change in structural parameters followed the same trend in the simulations of MCE + 1,2-dimyristoyl-sn-glycerol-phosphocholine by Sadžak et al. [41]. Other bioflavonoids such as quercetin, genistein, or daidzein were also shown to raise APL and lower bilayer thickness [72,73]. However, the existence of a fluid phase at 30 °C is in contrast with the experimental results, which have not suggested a meaningful reduction in Tm. Still, some changes in the transition process were noted, and it is known from the literature that hydrophobic flavonoids may influence the melting [41,74,75,76]. Considering the relatively small gap of ~8 °C between the simulation temperature and Tm, and the known tendency of simulated membranes to melt at temperatures up to 5 °C below experimental values [66], this discrepancy is not unusual. Nevertheless, since the gel phase was not successfully achieved in the DMPS + MCE systems, the comparison of DMPS and DMPS + MCE at 30 °C is considered unreliable.
Since bilayer disruption may lead to changes in water penetration and interfacial interactions, membrane hydration was examined. Density profiles of water (Figure 4) were used to visualize the presence of water molecules in the bilayer.
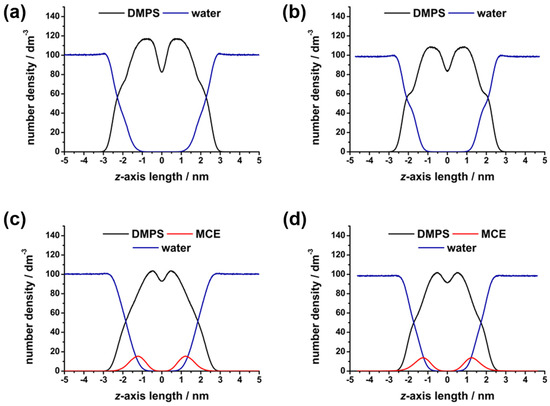
Figure 4.
Number density profiles of DMPS, MCE, and water molecules along the z axis of the simulation box, obtained from molecular dynamics simulations: (a) DMPS at 30 °C, (b) DMPS at 50 °C, (c) DMPS + MCE at 30 °C, and (d) DMPS + MCE at 50 °C.
Water was able to penetrate the surface of the bilayers in all cases, showing some presence among the polar headgroups oriented outwards. In the center of the bilayer, water was excluded due to the hydrophobicity of the acyl chains. Then, the HB network was analyzed in order to confirm lipid–water interactions. As expected, MD simulations showed better hydration and more HBs established in the fluid-phase systems (Table 3), since the separation of lipids due to the expanding surface area allowed for more water to penetrate and bind to the lipids. The impact was notably greater for the DMPS functional groups that are situated deeper in the bilayer, in accordance with findings showing solvent accessibility to be the greatest barrier to lipid group hydration [17]. Thus, the COO− group, which sits at the bilayer surface exposed to water, showed no major change in H-bonding, while PO2− and carbonyl C=O were significantly better hydrated in the fluid phase. Considering the aforementioned unreliability of the DMPS + MCE results at lower temperatures, we cannot draw conclusions on the MCE impact. However, the comparison of higher-temperature simulations with and without MCE suggests an effect of increased water interactions, particularly with the deeply situated C=O group.

Table 3.
Average number of hydrogen bonds (HBs) between select molecules or functional groups for DMPS and DMPS + MCE systems at 30 °C and 50 °C.
A deeper analysis of the HB networks examined the average number of HBs an interfacial water molecule may form with lipids and surrounding water molecules. The DMPS–water binding patterns (Table S2) show that most water molecules establish 1 HB with 1 DMPS molecule (1-1 pattern), but 15–20% of the water molecules form “bridges”, linking 2 lipids together (1-2 pattern). There is also a small amount of water molecules that establish two HBs with a single lipid, while other patterns are negligibly rare. When comparing the systems, it is notable that gel-to-fluid transition increases the percentage of 1-1 patterns from 75.8 ± 1.9% to 80.1 ± 1.9%, which is accompanied by a reduction in 1-2 patterns from 20.1 ± 1.2% to 16.0 ± 1.0%. On the other hand, the water–water binding patterns revealed the amount of additional water–water HBs that each lipid-bound water may establish (Table S3). In all systems, the majority of bonded water molecules at the interface established one or two more HBs with other water molecules, with less than 10% fulfilling their maximum of three additional HBs. Roughly a quarter of water molecules were not bonded to any other water molecules, having been isolated within the bilayer, with all donor or acceptor sites occupied by DMPS or MCE. This is consistent with observations of the loss of the tetrahedral HB network in interfacial water [77]. However, the fluctuations in the water network appeared to be insignificant between the systems. There is a small trend of a decreasing number of isolated water molecules (zero extra HBs), accompanied by a small increase in water molecules with three extra HBs when going from gel to fluid. Again, MCE effects at lower temperatures must be dismissed as unreliable. Thus, DMPS–water and to a lesser extent water–water networks show some changes as a consequence of increased water penetration, though the MCE effect is inconclusive.
Despite the small scale of the effects on the simulated bilayer segments, in combination with the experimental work they serve to confirm the temperature-dependent change in water behavior at the interface exacerbated by the presence of MCE. Ultimately, as demonstrated by Schönfeldová et al. [36], the melting itself induces redistribution of water molecules in the interfacial water layer. As this feature is changed upon the presence of MCE, as well as the characteristics of the melting itself (see Figure S2), it is somewhat expected that the water HB network features are changed in DMPS ± MCE situations. In the approach applied in this study, this reflects the difference in the fluctuations of a water HB network. Due to the great potential of the former, further development of its methodology is underway.
4. Conclusions
The research presented in this paper tackles the characterization of the fluctuations of a HB network of water molecules found in the interfacial region of liposomes constituted by negative DMPS lipids. Using the presented multivariate-based approach, two important fluctuation-related findings were discovered: (i) when the pH value of PBS is changed, it appears that for pH 7.4 the fluctuations are slightly larger than for pH values of 6.0 or 8.0; (ii) when MCE, a non-polar flavonoid molecule, is inserted in the hydrocarbon region of DMPS multibilayers, the fluctuations are significantly reduced. The suggested increase in the number of water molecules in the interfacial region upon incorporation of MCE is also suggested by the MD simulations, as well as a perturbation of the membrane ordering.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/biophysica4010007/s1. Figure S1. Baseline-corrected temperature-dependent FT-IR spectra of DMPS in the absence (left column) and the presence of MCE (right column) suspended in PBS at pH 6.0 (upper row), 7.4 (middle row), and 8.0 (bottom row). The lowest/highest (30 °C/50 °C) temperatures were highlighted with red/wine (DMPS, pH 6.0), orange/dark yellow (DMPS + MCE, pH 6.0), purple/violet (DMPS, pH 7.4), purple/pink (DMPS + MCE, pH 7.4), blue/navy (DMPS, pH 8.0) and cyan/dark cyan (DMPS + MCE, pH 8.0). The temperature-dependent FTIR spectra are designated with solid curves, whereas spectral profiles of low- and high-temperature components obtained from MCR-ALS with EFA using dotted curves; Figure S2. The concentrational profiles of low- and high-temperature component of DMPS in the absence (left column) and the presence of MCE (right column) suspended in PBS at pH 6.0 (upper row), 7.4 (middle row), and 8.0 (bottom row). Experimentally obtained low- and high-temperature components were labeled with solid curves colored red/wine (DMPS, pH 6.0), orange/dark yellow (DMPS + MCE, pH 6.0), purple/violet (DMPS, pH 7.4), purple/pink (DMPS + MCE, pH 7.4), blue/navy (DMPS, pH 8.0) and cyan/dark cyan (DMPS + MCE, pH 8.0). Their fit on a single Boltzmann profile is designated with dotted curves of the corresponding color; Figure S3. Order parameters of acyl chains for DMPS and DMPS + MCE systems at 30 °C and 50 °C, obtained from molecular dynamics simulations; Figure S4. Representative snapshots of lipid bilayers in the production runs of molecular dynamics simulations: (a) DMPS at 30 °C, (b) DMPS at 50 °C, (c) DMPS + MCE at 30 °C and (d) DMPS + MCE at 50 °C. Lipids are shown in Line mode with the acyl chains painted in gray. Phosphorus atoms are shown as gold spheres. MCE is shown in Licorice mode in violet, and water molecules as cyan dots. Black outlines represent the edges of the simulation boxes; Figure S5. The histograms showing the distribution of chain tilt angles of DMPS and DMPS + MCE systems for sn-1 chain (a) and sn-2 chain (b).; Table S1. Tm values (Tm,1 and Tm,2) obtained from fitting LTC (Tm,1) and HTC (Tm,2) on a single Boltzmann profile and from the intersection point (Tm,i); Table S2. The percentage of H-bonded water molecules that form a particular bonding pattern with DMPS lipids, for studied systems. Pattern 1-1 indicates one water molecule bound to one lipid. Pattern 1-2 indicates one water molecule bound to two different lipids. Pattern 1-3 indicates one water molecule bound to three lipids. Pattern 1=1 indicates one water molecule forming two bonds with the same lipid molecule. Pattern 1-12 indicates one water molecule bound to one lipid through one bond, and to one another lipid through two bonds; Table S3. The percentage of water molecules bonded to DMPS lipids, that also establish additional HBs with other waters. References [36,37,38,48,62,63,65,70,78] are cited in the supplementary materials.
Author Contributions
Conceptualization, B.P. and D.B.; methodology, D.B.; software, B.P.; formal analysis, D.B.; investigation, A.-M.P.; resources, D.B.; data curation, B.P.; writing—original draft preparation, B.P. and D.B.; writing—review and editing, B.P. and D.B.; supervision, D.B.; project administration, D.B.; funding acquisition, D.B. All authors have read and agreed to the published version of the manuscript.
Funding
This paper was supported by the Croatian Science Foundation through financing of project UIP-2020-02-7669 (“Model of demyelination on a molecular scale at physiological and pathological conditions”, DEMYMOLSCALE).
Data Availability Statement
Data will be available upon request.
Acknowledgments
The authors gratefully acknowledge Suzana Šegota (Laboratory for biocolloids and surface chemistry, Division of Physical Chemistry, Ruđer Bošković Institute) and retired Goran Baranović (Laboratory for molecular spectroscopy, Division of Organic Chemistry and Biochemistry, Ruđer Bošković Institute) for their generosity in purchasing required chemicals (DMPS and MCE).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Kamenac, A.; Obser, T.; Wixforth, A.; Schneider, M.F.; Westerhausen, C. The Activity of the Intrinsically Water-Soluble Enzyme ADAMTS13 Correlates with the Membrane State When Bound to a Phospholipid Bilayer. Sci. Rep. 2021, 11, 24476. [Google Scholar] [CrossRef] [PubMed]
- Damodaran, S. Water at Biological Phase Boundaries: Lts Role in Interfacial Activation of Enzymes and Metabolic Pathways. In Membrane Hydration; Disalvo, E.A., Ed.; Springer: Cham, Switzerland, 2015; Volume 71, pp. 233–261. ISBN 9783319190600. [Google Scholar]
- Schneck, E.; Sedlmeier, F.; Netz, R.R. Hydration Repulsion between Biomembranes Results from an Interplay of Dehydration and Depolarization. Proc. Natl. Acad. Sci. USA 2012, 109, 14405–14409. [Google Scholar] [CrossRef] [PubMed]
- Kasson, P.M.; Lindahl, E.; Pande, V.S. Water Ordering at Membrane Interfaces Controls Fusion Dynamics. J. Am. Chem. Soc. 2011, 133, 3812–3815. [Google Scholar] [CrossRef] [PubMed]
- Chattopadhyay, M.; Krok, E.; Orlikowska, H.; Schwille, P.; Franquelim, H.G.; Piatkowski, L. Hydration Layer of Only a Few Molecules Controls Lipid Mobility in Biomimetic Membranes. J. Am. Chem. Soc. 2021, 143, 14551–14562. [Google Scholar] [CrossRef]
- Saak, C.M.; Dreier, L.B.; Machel, K.; Bonn, M.; Backus, E.H.G. Biological Lipid Hydration: Distinct Mechanisms of Interfacial Water Alignment and Charge Screening for Model Lipid Membranes. Faraday Discuss. 2024, 249, 317–333. [Google Scholar] [CrossRef] [PubMed]
- Dreier, L.B.; Nagata, Y.; Lutz, H.; Gonella, G.; Hunger, J.; Backus, E.H.G.; Bonn, M. Saturation of Charge-Induced Water Alignment at Model Membrane Surfaces. Sci. Adv. 2018, 4, eaap7415. [Google Scholar] [CrossRef]
- Laage, D.; Hynes, J.T. A Molecular Jump Mechanism of Water Reorientation. Science 2006, 311, 832–835. [Google Scholar] [CrossRef]
- Stirnemann, G.; Rossky, P.J.; Hynes, J.T.; Laage, D. Water Reorientation, Hydrogen-Bond Dynamics and 2D-IR Spectroscopy next to an Extended Hydrophobic Surface. Faraday Discuss. 2010, 146, 263–281. [Google Scholar] [CrossRef]
- Re, S.; Nishima, W.; Tahara, T.; Sugita, Y. Mosaic of Water Orientation Structures at a Neutral Zwitterionic Lipid/Water Interface Revealed by Molecular Dynamics Simulations. J. Phys. Chem. Lett. 2014, 5, 4343–4348. [Google Scholar] [CrossRef]
- Kundu, A.; Kwak, K.; Cho, M. Water Structure at the Lipid Multibilayer Surface: Anionic Versus Cationic Head Group Effects. J. Phys. Chem. B 2016, 120, 5002–5007. [Google Scholar] [CrossRef]
- Singh, P.C.; Inoue, K.I.; Nihonyanagi, S.; Yamaguchi, S.; Tahara, T. Femtosecond Hydrogen Bond Dynamics of Bulk-like and Bound Water at Positively and Negatively Charged Lipid Interfaces Revealed by 2D HD-VSFG Spectroscopy. Angew. Chem. Int. Ed. 2016, 55, 10621–10625. [Google Scholar] [CrossRef]
- Flanagan, J.C.; Valentine, M.L.; Baiz, C.R. Ultrafast Dynamics at Lipid-Water Interfaces. Acc. Chem. Res. 2020, 53, 1860–1868. [Google Scholar] [CrossRef]
- Livingstone, R.A.; Zhang, Z.; Piatkowski, L.; Bakker, H.J.; Hunger, J.; Bonn, M.; Backus, E.H.G. Water in Contact with a Cationic Lipid Exhibits Bulklike Vibrational Dynamics. J. Phys. Chem. B 2016, 120, 10069–10078. [Google Scholar] [CrossRef] [PubMed]
- Ohto, T.; Backus, E.H.G.; Hsieh, C.S.; Sulpizi, M.; Bonn, M.; Nagata, Y. Lipid Carbonyl Groups Terminate the Hydrogen Bond Network of Membrane-Bound Water. J. Phys. Chem. Lett. 2015, 6, 4499–4503. [Google Scholar] [CrossRef] [PubMed]
- Livingstone, R.A.; Nagata, Y.; Bonn, M.; Backus, E.H.G. Two Types of Water at the Water-Surfactant Interface Revealed by Time-Resolved Vibrational Spectroscopy. J. Am. Chem. Soc. 2015, 137, 14912–14919. [Google Scholar] [CrossRef] [PubMed]
- Lopez, C.F.; Nielsen, S.O.; Klein, M.L.; Moore, P.B. Hydrogen Bonding Structure and Dynamics of Water at the Dimyristoylphosphatidylcholine Lipid Bilayer Surface from a Molecular Dynamics Simulation. J. Phys. Chem. B 2004, 108, 6603–6610. [Google Scholar] [CrossRef]
- Shen, H.; Wu, Z.; Zou, X. Interfacial Water Structure at Zwitterionic Membrane/Water Interface: The Importance of Interactions between Water and Lipid Carbonyl Groups. ACS Omega 2020, 5, 18080–18090. [Google Scholar] [CrossRef] [PubMed]
- Karathanou, K.; Bondar, A.N. Dynamic Water Hydrogen-Bond Networks at the Interface of a Lipid Membrane Containing Palmitoyl-Oleoyl Phosphatidylglycerol. J. Membr. Biol. 2018, 251, 461–473. [Google Scholar] [CrossRef]
- Inoue, K.I.; Singh, P.C.; Nihonyanagi, S.; Yamaguchi, S.; Tahara, T. Cooperative Hydrogen-Bond Dynamics at a Zwitterionic Lipid/Water Interface Revealed by 2D HD-VSFG Spectroscopy. J. Phys. Chem. Lett. 2017, 8, 5160–5165. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, A.; Malik, S.; Debnath, A. Heterogeneity in Structure and Dynamics of Water near Bilayers Using TIP3P and TIP4P/2005 Water Models. Chem. Phys. 2019, 525, 110396. [Google Scholar] [CrossRef]
- Calero, C.; Stanley, H.E.; Franzese, G. Structural Interpretation of the Large Slowdown of Water Dynamics at Stacked Phospholipid Membranes for Decreasing Hydration Level: All-Atom Molecular Dynamics. Materials 2016, 9, 319. [Google Scholar] [CrossRef]
- Zhao, L.; Ma, K.; Yang, Z. Changes of Water Hydrogen Bond Network with Different Externalities. Int. J. Mol. Sci. 2015, 16, 8454–8489. [Google Scholar] [CrossRef]
- Fayer, M.D. Dynamics of Water Interacting with Interfaces, Molecules, and Ions. Acc. Chem. Res. 2012, 45, 3–14. [Google Scholar] [CrossRef]
- Piskulich, Z.A.; Laage, D.; Thompson, W.H. On the Role of Hydrogen-Bond Exchanges in the Spectral Diffusion of Water. J. Chem. Phys. 2021, 154, 064501. [Google Scholar] [CrossRef]
- Gruenbaum, S.M.; Skinner, J.L. Vibrational Spectroscopy of Water in Hydrated Lipid Multi-Bilayers. I. Infrared Spectra and Ultrafast Pump-Probe Observables. J. Chem. Phys. 2011, 135, 075101. [Google Scholar] [CrossRef]
- Valentine, M.L.; Waterland, M.K.; Fathizadeh, A.; Elber, R.; Baiz, C.R. Interfacial Dynamics in Lipid Membranes: The Effects of Headgroup Structures. J. Phys. Chem. B 2021, 125, 1343–1350. [Google Scholar] [CrossRef] [PubMed]
- Flanagan, J.C.; Cardenas, A.E.; Baiz, C.R. Ultrafast Spectroscopy of Lipid-Water Interfaces: Transmembrane Crowding Drives H-Bond Dynamics. J. Phys. Chem. Lett. 2020, 11, 4093–4098. [Google Scholar] [CrossRef] [PubMed]
- Maréchal, Y. The H2O Molecules in Liquid Water. In The Hydrogen Bond and the Water Molecule; Elsevier Ltd.: Amsterdam, The Netherlands, 2007; pp. 215–248. [Google Scholar]
- Verma, P.K.; Kundu, A.; Puretz, M.S.; Dhoonmoon, C.; Chegwidden, O.S.; Londergan, C.H.; Cho, M. The Bend+Libration Combination Band Is an Intrinsic, Collective, and Strongly Solute-Dependent Reporter on the Hydrogen Bonding Network of Liquid Water. J. Phys. Chem. B 2018, 122, 2587–2599. [Google Scholar] [CrossRef] [PubMed]
- Tong, Y.; Kampfrath, T.; Campen, R.K. Experimentally Probing the Libration of Interfacial Water: The Rotational Potential of Water Is Stiffer at the Air/Water Interface than in Bulk Liquid. Phys. Chem. Chem. Phys. 2016, 18, 18424–18430. [Google Scholar] [CrossRef] [PubMed]
- Brkljača, Z.; Butumović, M.; Bakarić, D. Water Does Not Dance as Ions Sing: A New Approach in Elucidation of Ion-Invariant Water Fluctuation. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2022, 271, 120907. [Google Scholar] [CrossRef] [PubMed]
- Libnau, F.O.; Toft, J.; Christy, A.A.; Kvalheim, O.M. Structure of Liquid Water Determined from Infrared Temperature Profiling and Evolutionary Curve Resolution. J. Am. Chem. Soc. 1994, 116, 8311–8316. [Google Scholar] [CrossRef]
- Czarnik-Matusewicz, B.; Pilorz, S.; Hawranek, J.P. Temperature-Dependent Water Structural Transitions Examined by near-IR and Mid-IR Spectra Analyzed by Multivariate Curve Resolution and Two-Dimensional Correlation Spectroscopy. Anal. Chim. Acta 2005, 544, 15–25. [Google Scholar] [CrossRef]
- Chen, Y.; Dupertuis, N.; Okur, H.I.; Roke, S. Temperature Dependence of Water-Water and Ion-Water Correlations in Bulk Water and Electrolyte Solutions Probed by Femtosecond Elastic Second Harmonic Scattering. J. Chem. Phys. 2018, 148, 222835. [Google Scholar] [CrossRef] [PubMed]
- Schönfeldová, T.; Piller, P.; Kovacik, F.; Pabst, G.; Okur, H.I.; Roke, S. Lipid Melting Transitions Involve Structural Redistribution of Interfacial Water. J. Phys. Chem. B 2021, 125, 12457–12465. [Google Scholar] [CrossRef] [PubMed]
- Bach, D.; Miller, I.R. Hydration of Phospholipid Bilayers in the Presence and Absence of Cholesterol. Biochim. Biophys. Acta 1998, 1368, 216–224. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Heimburg, T. Thermal Biophysics of Membranes; Wiley-VCH Verlag GmbH: Weinheim, Germany, 2007; ISBN 9783527404711. [Google Scholar]
- May, S. Curvature Elasticity and Thermodynamic Stability of Electrically Charged Membranes. J. Chem. Phys. 1996, 105, 8314–8323. [Google Scholar] [CrossRef]
- Pašalić, L.; Pem, B.; Bakarić, D. Lamellarity-Driven Differences in Surface Structural Features of DPPS Lipids: Spectroscopic, Calorimetric and Computational Study. Membranes 2023, 13, 83. [Google Scholar] [CrossRef] [PubMed]
- Sadžak, A.; Brkljača, Z.; Crnolatac, I.; Baranović, G.; Šegota, S. Flavonol Clustering in Model Lipid Membranes: DSC, AFM, Force Spectroscopy and MD Simulations Study. Colloids Surf. B Biointerfaces 2020, 193, 111147. [Google Scholar] [CrossRef]
- Dale Keefe, C. Computer Programs for the Determination of Optical Constants from Transmission Spectra and the Study of Absolute Absorption Intensities. J. Mol. Struct. 2002, 641, 165–173. [Google Scholar] [CrossRef]
- Menges, F. Spectragryph—Optical Spectroscopy Software. Available online: https://www.effemm2.de/spectragryph/ (accessed on 3 January 2024).
- Cevc, G.; Watts, A.; Marsh, D. Titration of the Phase Transition of Phosphatidylserine Bilayer Membranes. Effects of pH, Surface Electrostatics, Ion Binding, and Head-Group Hydration. Biochemistry 1981, 20, 4955–4965. [Google Scholar] [CrossRef]
- Lewis, R.N.A.H.; McElhaney, R.N. Calorimetric and Spectroscopic Studies of the Thermotropic Phase Behavior of Lipid Bilayer Model Membranes Composed of a Homologous Series of Linear Saturated Phosphatidylserines. Biophys. J. 2000, 79, 2043–2055. [Google Scholar] [CrossRef]
- Maeder, M.; de Juan, A. Two-Way Data Analysis: Evolving Factor Analysis. Compr. Chemom. 2009, 2, 261–274. [Google Scholar] [CrossRef]
- Keller, H.R.; Massart, D.L. Evolving Factor Analysis. Chemom. Intell. Lab. Syst. 1991, 12, 209–224. [Google Scholar] [CrossRef]
- Maleš, P.; Brkljača, Z.; Crnolatac, I.; Bakarić, D. Application of MCR-ALS with EFA on FT-IR Spectra of Lipid Bilayers in the Assessment of Phase Transition Temperatures: Potential for Discernment of Coupled Events. Colloids Surf. B Biointerfaces 2021, 201, 111645. [Google Scholar] [CrossRef] [PubMed]
- Jaumot, J.; Gargallo, R.; De Juan, A.; Tauler, R. A Graphical User-Friendly Interface for MCR-ALS: A New Tool for Multivariate Curve Resolution in MATLAB. Chemom. Intell. Lab. Syst. 2005, 76, 101–110. [Google Scholar] [CrossRef]
- De Juan, A.; Jaumot, J.; Tauler, R. Multivariate Curve Resolution (MCR). Solving the Mixture Analysis Problem. Anal. Methods 2014, 6, 4964–4976. [Google Scholar] [CrossRef]
- Fega, K.R.; Wilcox, D.S.; Ben-Amotz, D. Application of Raman Multivariate Curve Resolution to Solvation-Shell Spectroscopy. Appl. Spectrosc. 2012, 66, 282–288. [Google Scholar] [CrossRef] [PubMed]
- Jo, S.; Kim, T.; Iyer, V.G.; Im, W. CHARMM-GUI: A Web-Based Graphical User Interface for CHARMM. J. Comput. Chem. 2008, 29, 1859–1865. [Google Scholar] [CrossRef] [PubMed]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindah, E. Gromacs: High Performance Molecular Simulations through Multi-Level Parallelism from Laptops to Supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef]
- Klauda, J.B.; Venable, R.M.; Freites, J.A.; O’Connor, J.W.; Tobias, D.J.; Mondragon-Ramirez, C.; Vorobyov, I.; MacKerell, A.D., Jr.; Pastor, R.W. Update of the CHARMM All-Atom Additive Force Field for Lipids: Validation on Six Lipid Types. J. Phys. Chem. B 2010, 114, 7830–7843. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Vanommeslaeghe, K.; Hatcher, E.; Acharya, C.; Kundu, S.; Zhong, S.; Shim, J.; Darian, E.; Guvench, O.; Lopes, P.; Vorobyov, I.; et al. CHARMM General Force Field: A Force Field for Drug-Like Molecules Compatible with the CHARMM All-Atom Additive Biological Force Fields. J. Comput. Chem. 2010, 31, 671–690. [Google Scholar] [CrossRef] [PubMed]
- MacKerell Lab. Available online: http://mackerell.umaryland.edu/charmm_ff.shtml#gromacs (accessed on 12 February 2024).
- Nosé, S. A Molecular Dynamics Method for Simulations in the Canonical Ensemble. Mol. Phys. Int. J. Interface Between Chem. Phys. 1984, 52, 255–268. [Google Scholar] [CrossRef]
- Parrinello, M.; Rahman, A. Polymorphic Transitions in Single Crystals: A New Molecular Dynamics Method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Essmann, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L.G. A Smooth Particle Mesh Ewald Method. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Lewis, R.N.A.H.; McElhaney, R.N. Membrane Lipid Phase Transitions and Phase Organization Studied by Fourier Transform Infrared Spectroscopy. Biochim. Biophys. Acta-Biomembr. 2013, 1828, 2347–2358. [Google Scholar] [CrossRef]
- Browning, J.L.; Seelig, J. Bilayers of Phosphatidylserine: A Deuterium and Phosphorus Nuclear Magnetic Resonance Study. Biochemistry 1980, 19, 1262–1270. [Google Scholar] [CrossRef]
- Ge, M.; Freed, J.H. Hydration, Structure, and Molecular Interactions in the Headgroup Region of Dioleoylphosphatidylcholine Bilayers: An Electron Spin Resonance Study. Biophys. J. 2003, 85, 4023–4040. [Google Scholar] [CrossRef]
- Šegota, S.; Vojta, D.; Kendziora, D.; Ahmed, I.; Fruk, L.; Baranović, G. Ligand-Dependent Nanoparticle Clustering within Lipid Membranes Induced by Surrounding Medium. J. Phys. Chem. B 2015, 119, 5208–5219. [Google Scholar] [CrossRef]
- Khakbaz, P.; Klauda, J.B. Investigation of Phase Transitions of Saturated Phosphocholine Lipid Bilayers via Molecular Dynamics Simulations. Biochim. Biophys. Acta-Biomembr. 2018, 1860, 1489–1501. [Google Scholar] [CrossRef] [PubMed]
- Moradi, S.; Nowroozi, A.; Shahlaei, M. Shedding Light on the Structural Properties of Lipid Bilayers Using Molecular Dynamics Simulation: A Review Study. RSC Adv. 2019, 9, 4644–4658. [Google Scholar] [CrossRef]
- Hishida, M.; Endo, A.; Nakazawa, K.; Yamamura, Y.; Saito, K. Effect of N-Alkanes on Lipid Bilayers Depending on Headgroups. Chem. Phys. Lipids 2015, 188, 61–67. [Google Scholar] [CrossRef] [PubMed]
- Korchowiec, B.; Gorczyca, M.; Rogalska, E.; Regnouf-De-Vains, J.B.; Mourer, M.; Korchowiec, J. The Selective Interactions of Cationic Tetra-p-Guanidinoethylcalix[4]Arene with Lipid Membranes: Theoretical and Experimental Model Studies. Soft Matter 2015, 12, 181–190. [Google Scholar] [CrossRef] [PubMed]
- Yousefpour, A.; Amjad-Iranagh, S.; Goharpey, F.; Modarress, H. Effect of Drug Amlodipine on the Charged Lipid Bilayer Cell Membranes DMPS and DMPS + DMPC: A Molecular Dynamics Simulation Study. Eur. Biophys. J. 2018, 47, 939–950. [Google Scholar] [CrossRef] [PubMed]
- Hauser, H.; Paltauf, F.; Shipley, G.G. Structure and Thermotropic Behavior of Phosphatidylserine Bilayer Membranes. Biochemistry 1982, 21, 1061–1067. [Google Scholar] [CrossRef] [PubMed]
- Eid, J.; Jraij, A.; Greige-Gerges, H.; Monticelli, L. Effect of Quercetin on Lipid Membrane Rigidity: Assessment by Atomic Force Microscopy and Molecular Dynamics Simulations. BBA Adv. 2021, 1, 100018. [Google Scholar] [CrossRef] [PubMed]
- Raghunathan, M.; Zubovski, Y.; Venable, R.M.; Pastor, R.W.; Nagle, J.F.; Tristram-Nagle, S. Structure and Elasticity of Lipid Membranes with Genistein and Daidzein Bioflavinoids Using X-Ray Scattering and MD Simulations. J. Phys. Chem. B 2012, 116, 3918–3927. [Google Scholar] [CrossRef]
- Selvaraj, S.; Krishnaswamy, S.; Devashya, V.; Sethuraman, S.; Krishnan, U.M. Influence of Membrane Lipid Composition on Flavonoid-Membrane Interactions: Implications on Their Biological Activity. Prog. Lipid Res. 2015, 58, 1–13. [Google Scholar] [CrossRef]
- Abram, V.; Berlec, B.; Ota, A.; Šentjurc, M.; Blatnik, P.; Ulrih, N.P. Effect of Flavonoid Structure on the Fluidity of Model Lipid Membranes. Food Chem. 2013, 139, 804–813. [Google Scholar] [CrossRef]
- Altunayar-Unsalan, C.; Unsalan, O.; Mavromoustakos, T. Insights into Molecular Mechanism of Action of Citrus Flavonoids Hesperidin and Naringin on Lipid Bilayers Using Spectroscopic, Calorimetric, Microscopic and Theoretical Studies. J. Mol. Liq. 2022, 347, 118411. [Google Scholar] [CrossRef]
- Srivastava, A.; Debnath, A. Hydration Dynamics of a Lipid Membrane: Hydrogen Bond Networks and Lipid-Lipid Associations. J. Chem. Phys. 2018, 148, 094901. [Google Scholar] [CrossRef]
- Boughter, C.T.; Monje-Galvan, V.; Im, W.; Klauda, J.B. Influence of Cholesterol on Phospholipid Bilayer Structure and Dynamics. J. Phys. Chem. B 2016, 120, 11761–11772. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).