Heat Transfer Analysis in a Channel Mounted with In-Line Downward-Facing and Staggered Downward-Facing Notched Baffles
Abstract
1. Introduction
2. Theoretical Aspects
3. Experimental Facility Setup
- •
- Reynolds number (Re)
- •
- Nusselt number (Nu)
- •
- Friction factor (f)
4. Experimental Results
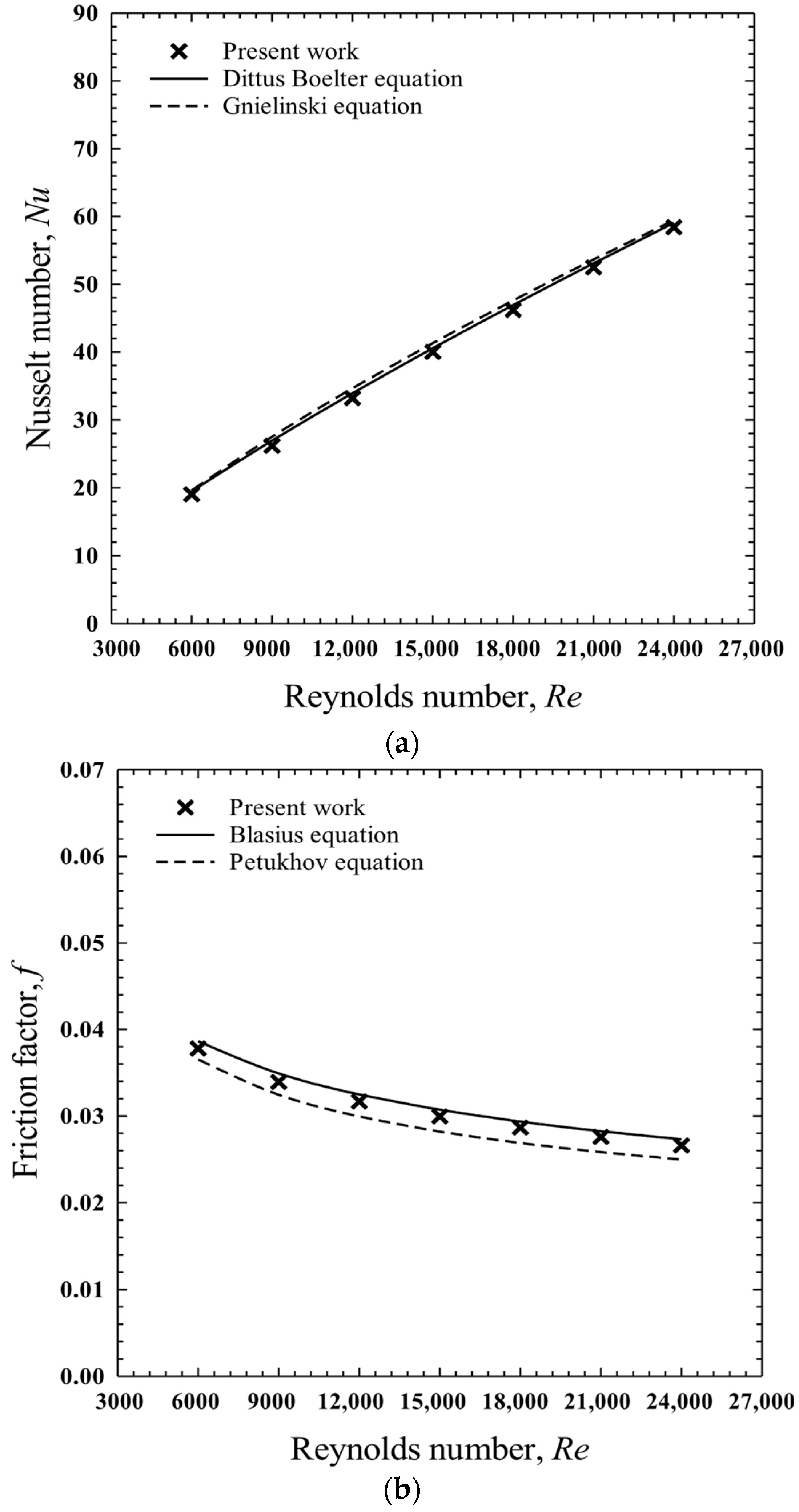
4.1. Validation of Flow and Heat Transfer Characteristics in a Smooth Channel
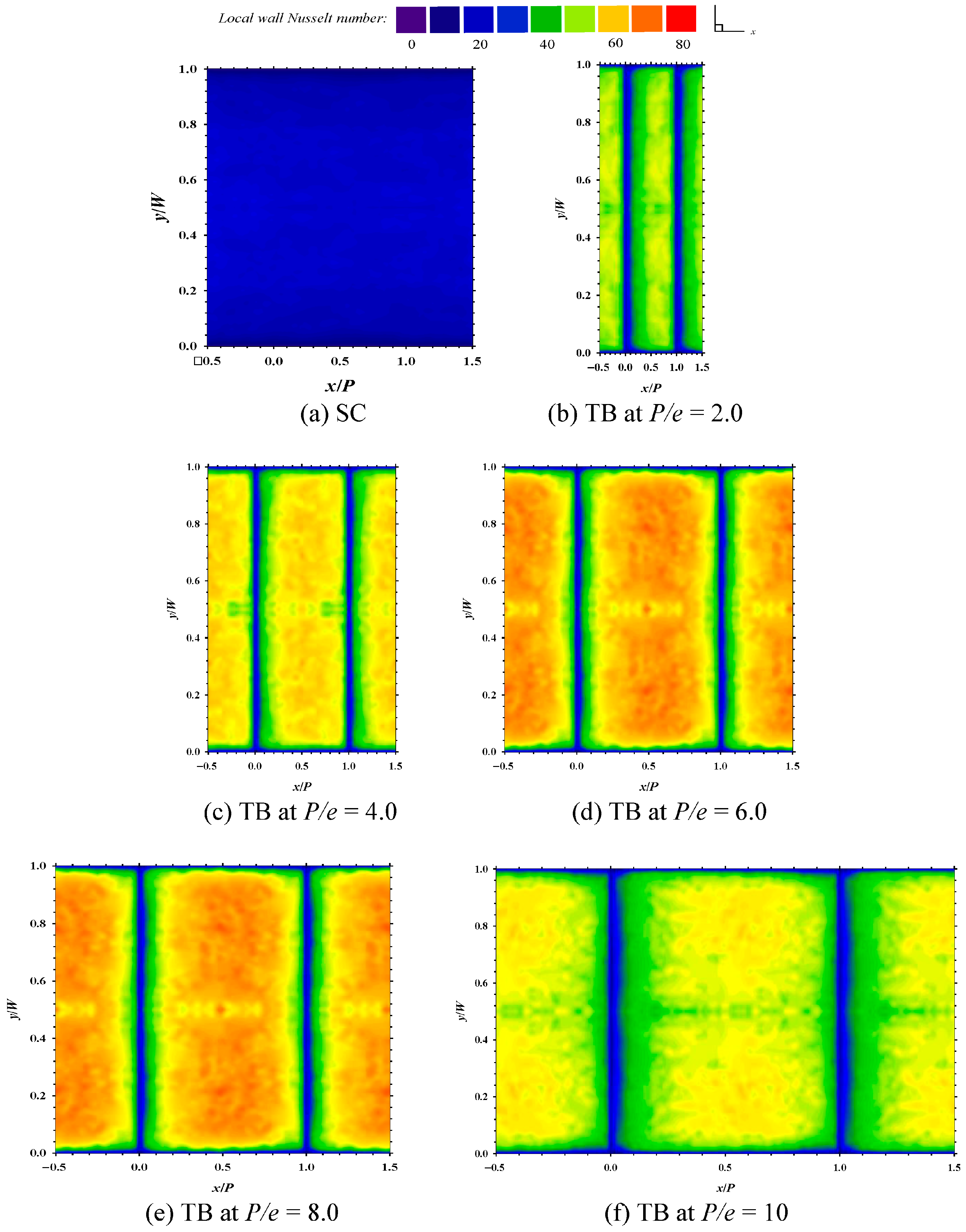
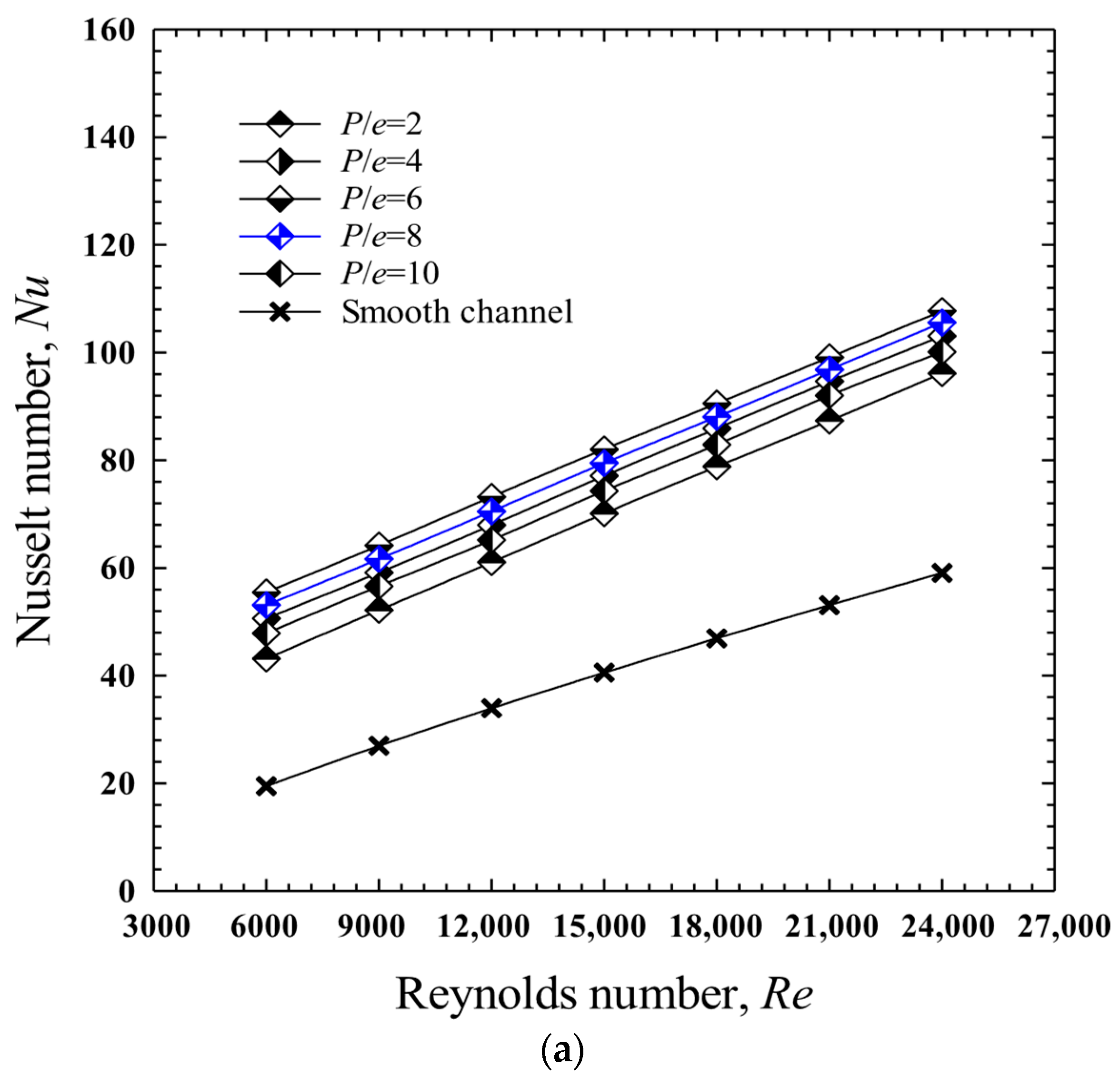
4.2. Effect of Baffle Pitch to Baffle Height Ratio, (P/e): Case I: Conventional Transverse Baffles (TBs)
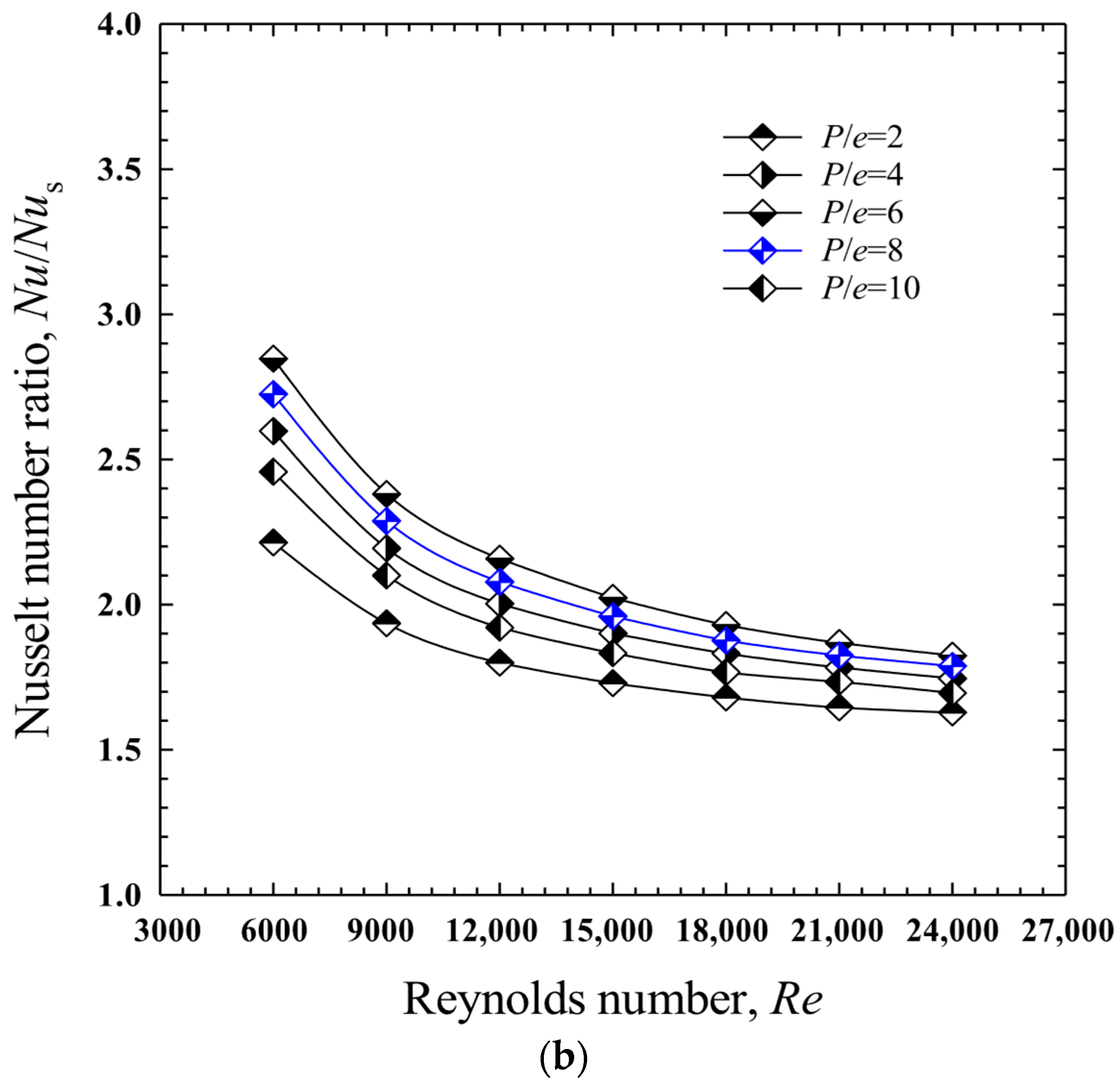
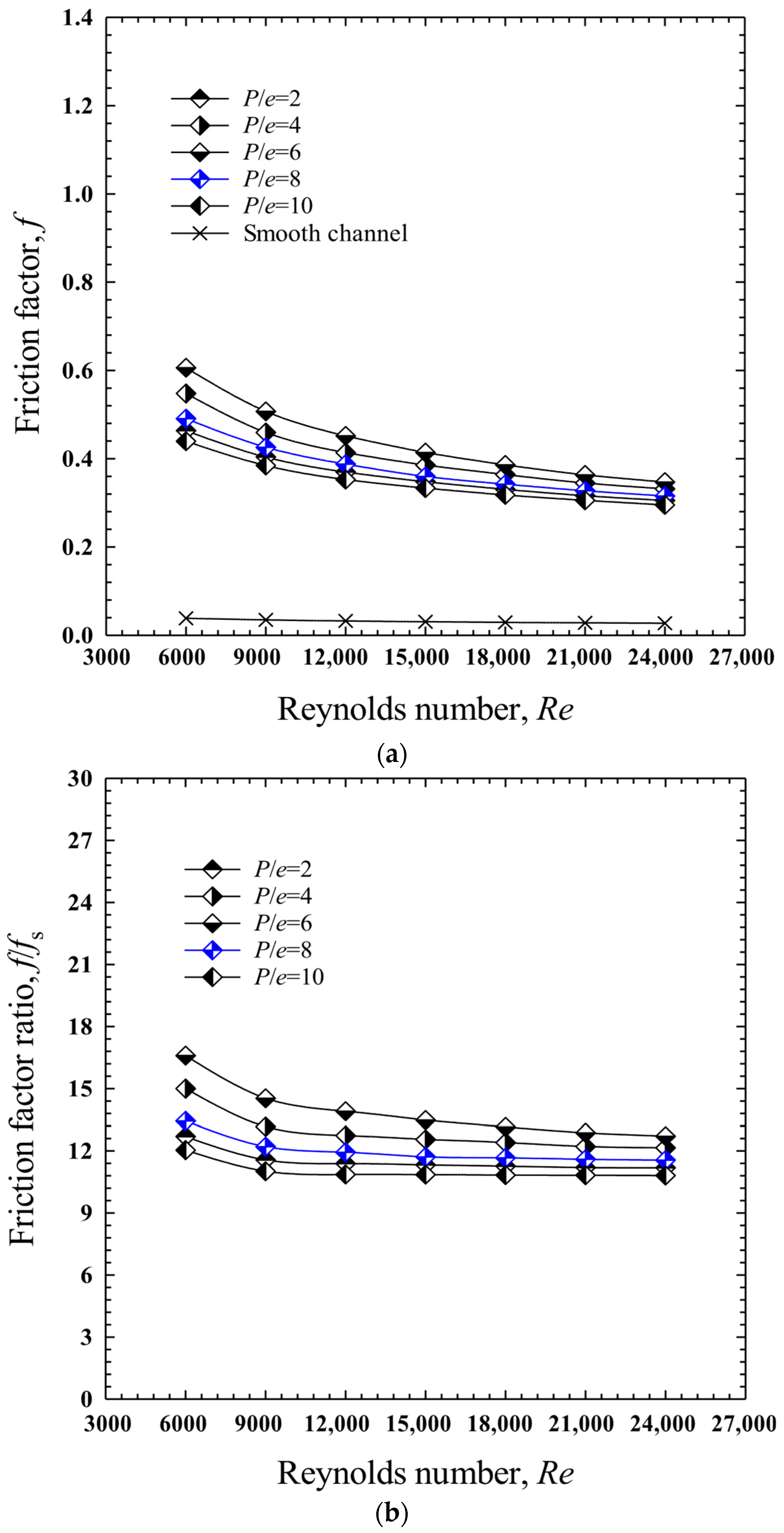
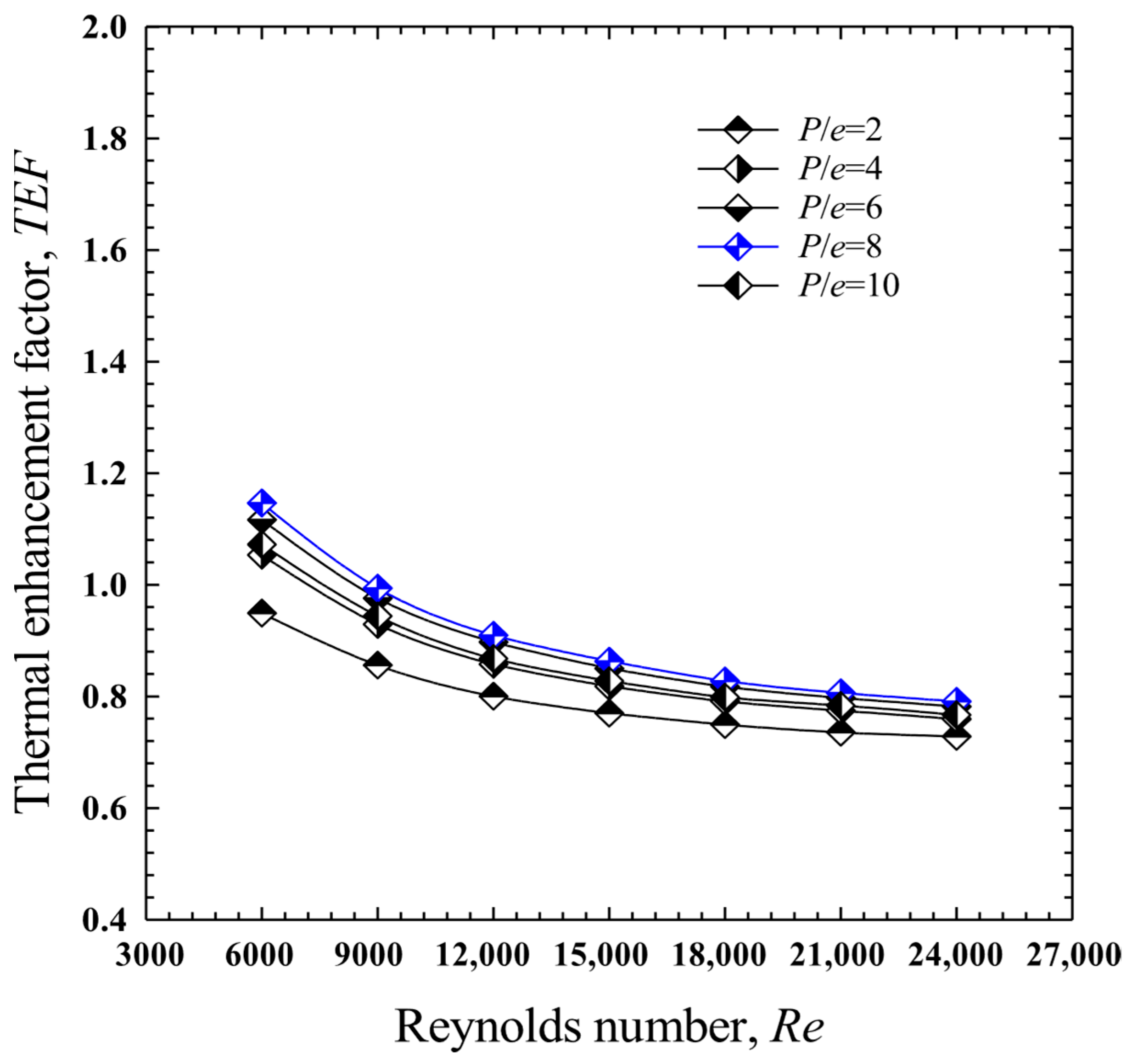
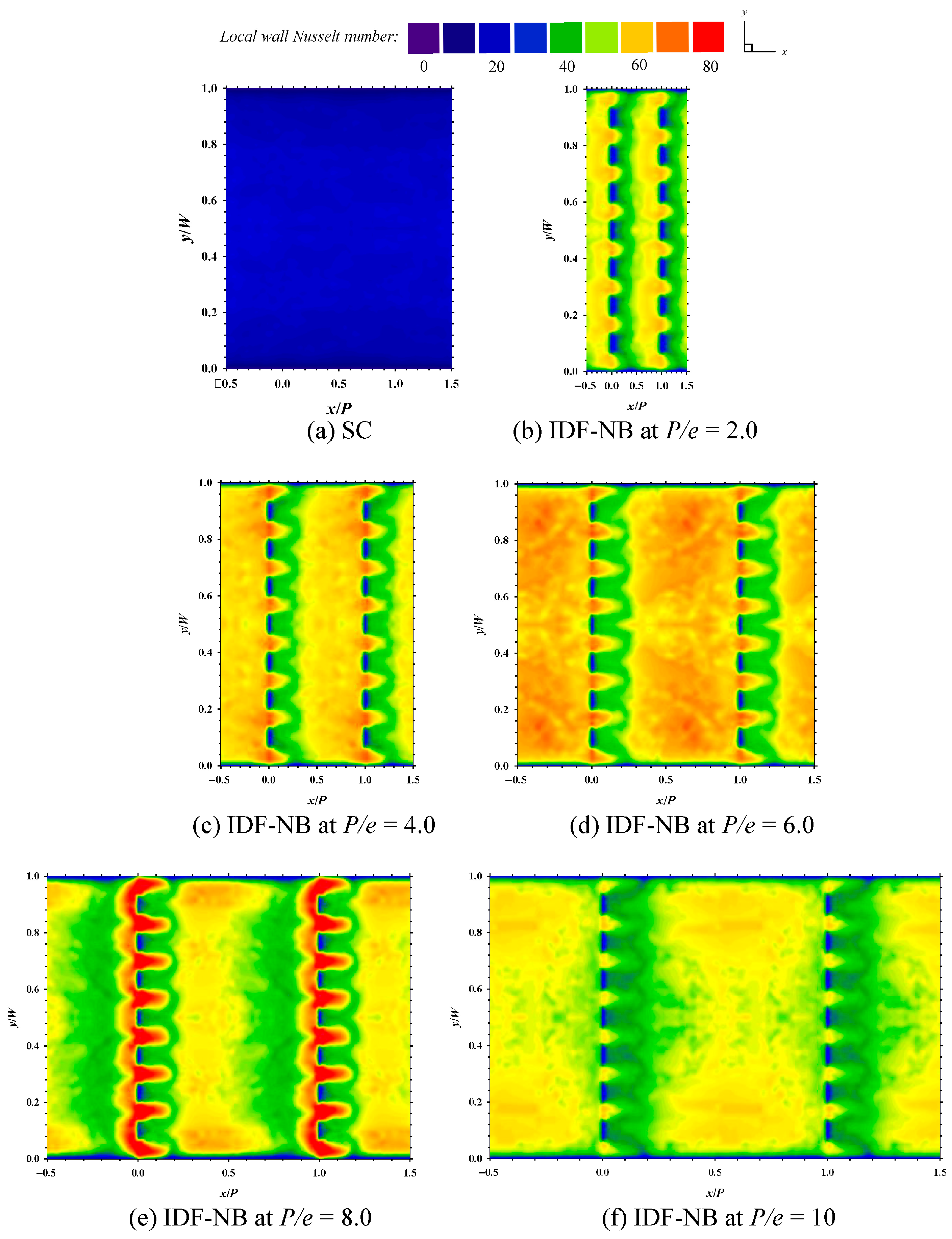
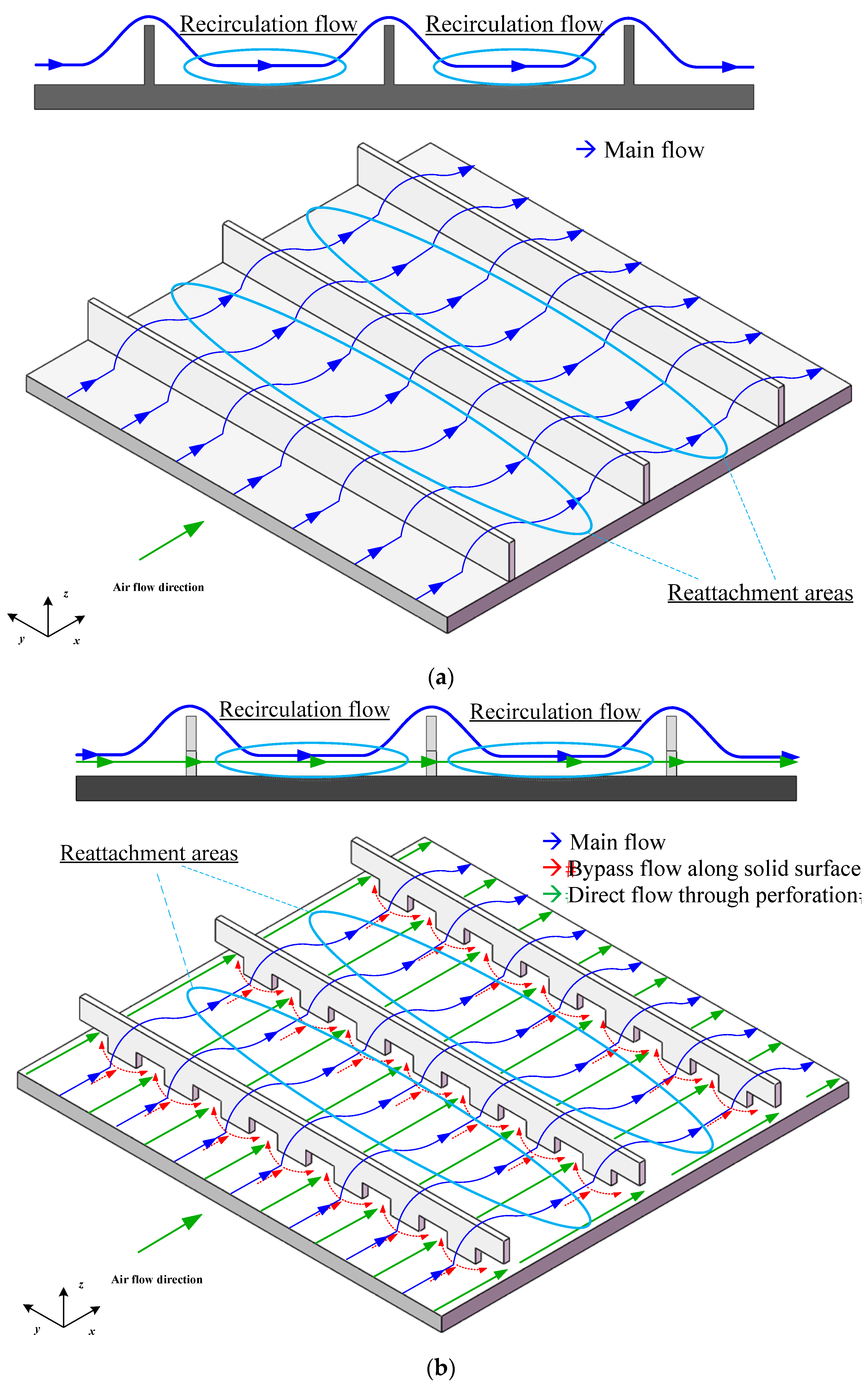
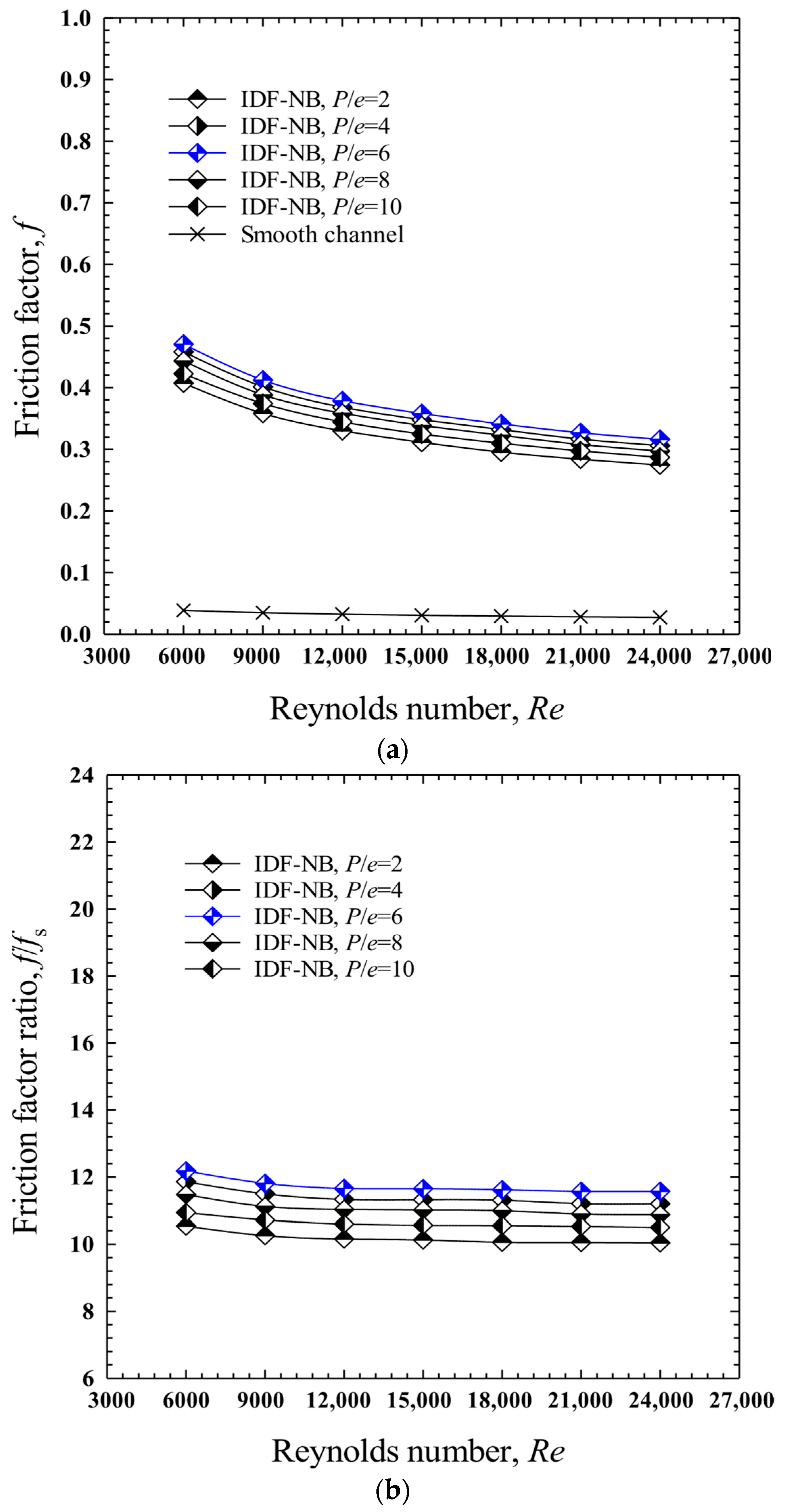
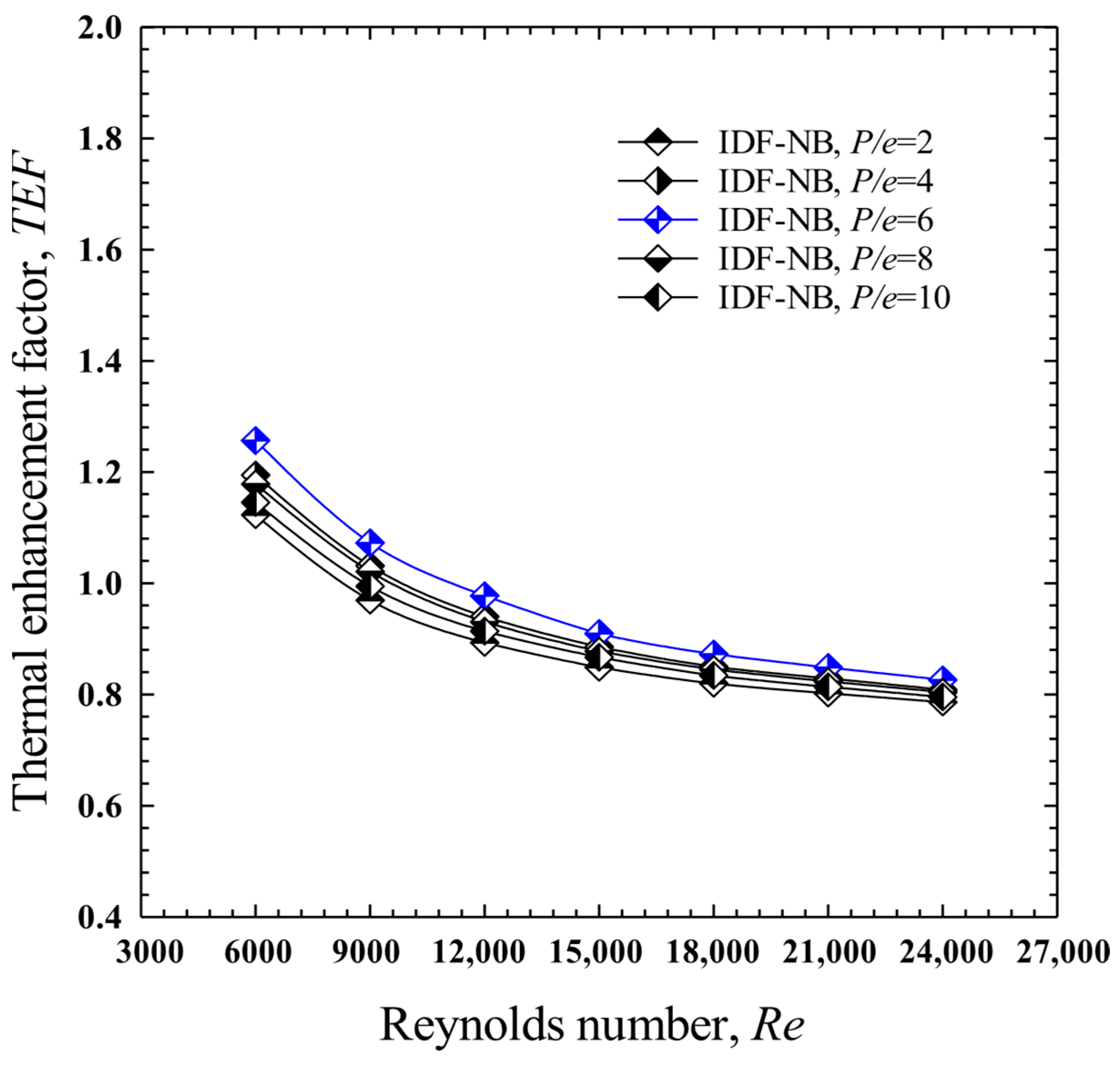
4.3. Effect of Baffle Pitch to Baffle Height Ratio, (P/e): Case II: In-Line Downward-Facing Notched Baffles (IDF-NB)
- Main flow (blue arrows): This portion represents the primary airflow that travels along the channel and experiences flow separation and reattachment upon encountering the baffles.
- Direct flow through perforation (green arrows): This airflow passes directly through the notches (perforations) in the baffles, providing an alternate path.
- Bypass flow along solid surface (red arrows): This portion strikes the solid area adjacent to the perforations and is redirected along the baffle surface, sweeping the dead zone in front of the baffle before entering through the perforation.
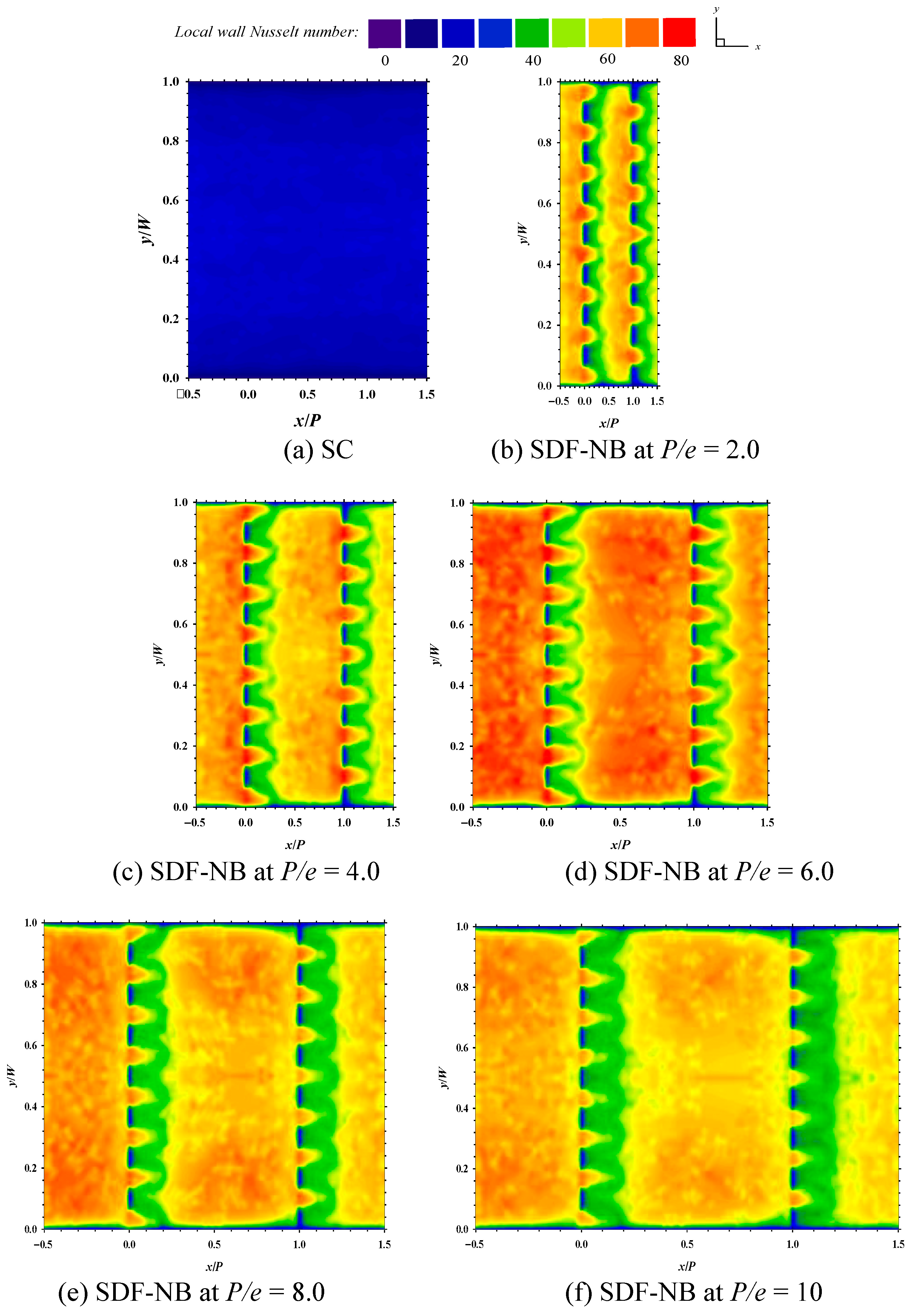
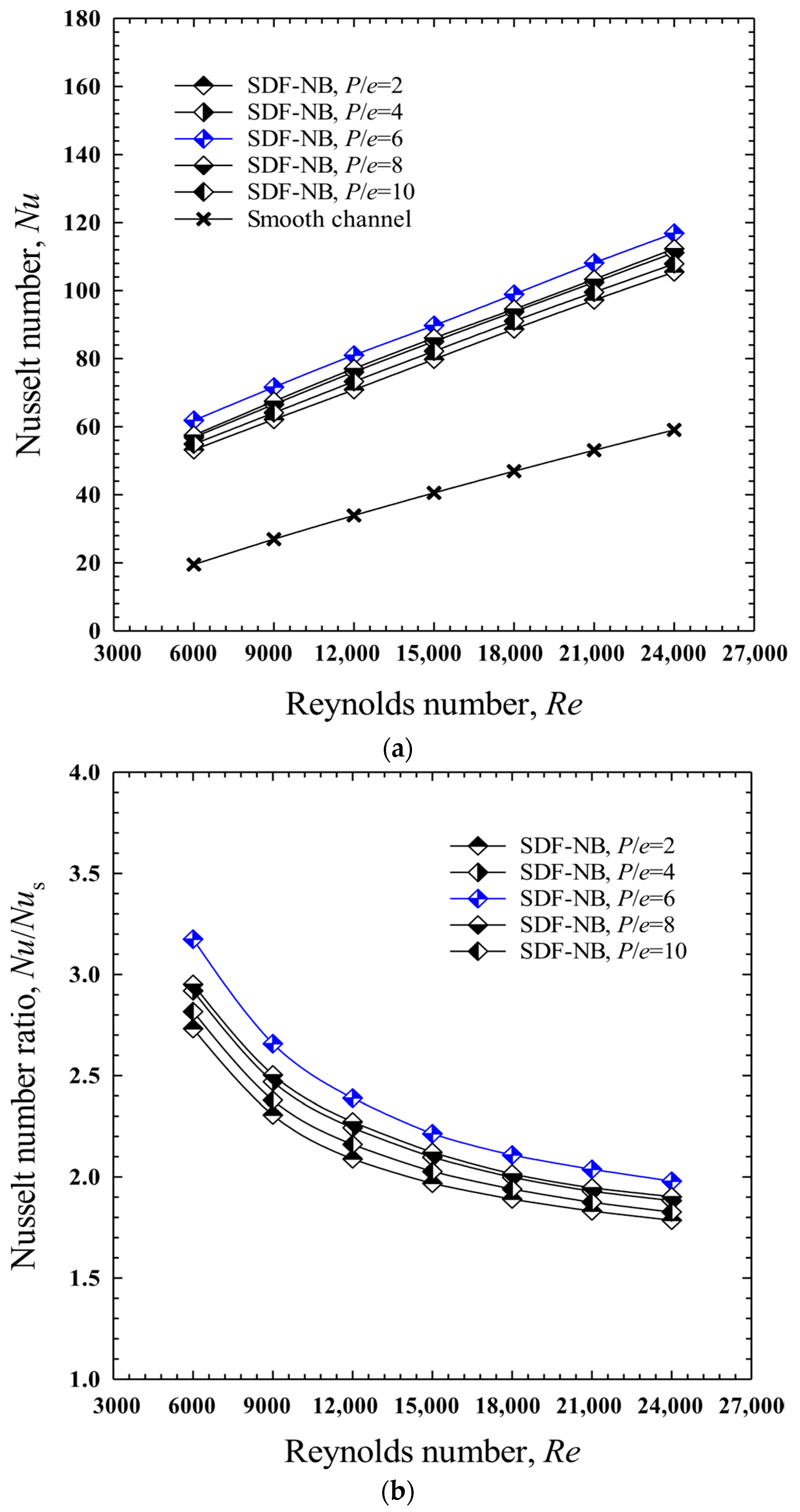
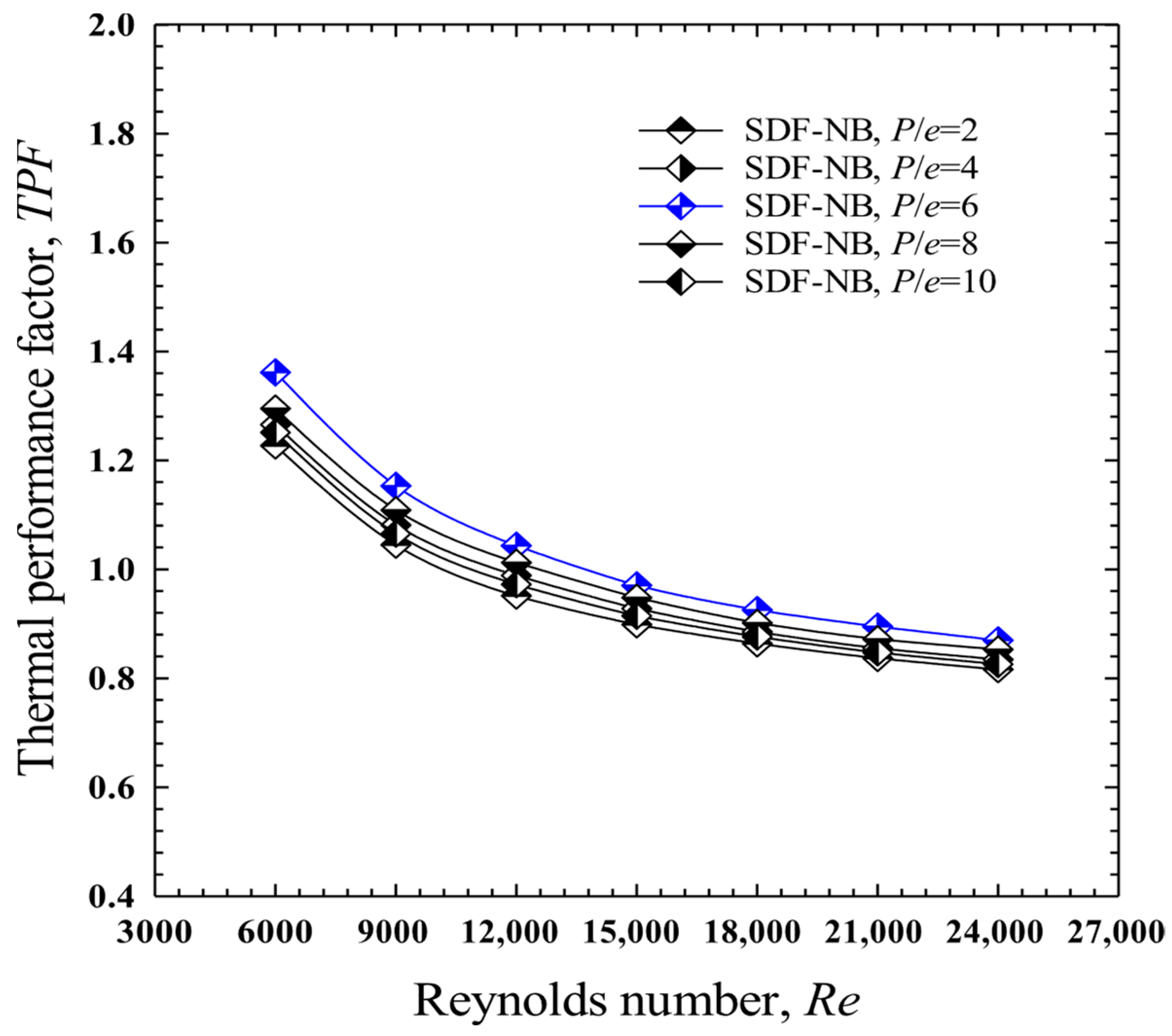
4.4. Effect of Baffle Pitch to Baffle Height Ratio, (P/e): Case III: Staggered Downward-Facing Notched Baffles (SDF-NB)
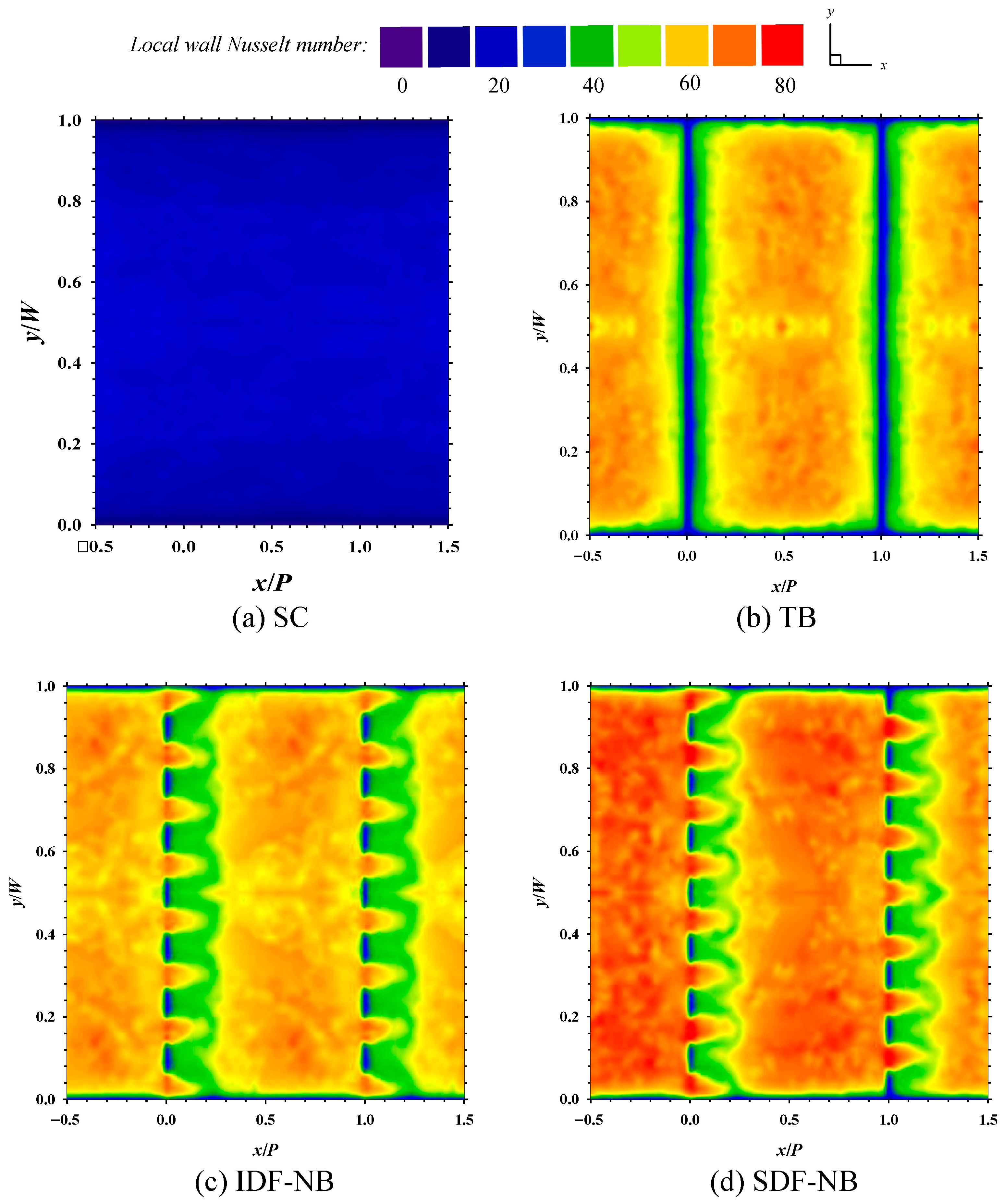
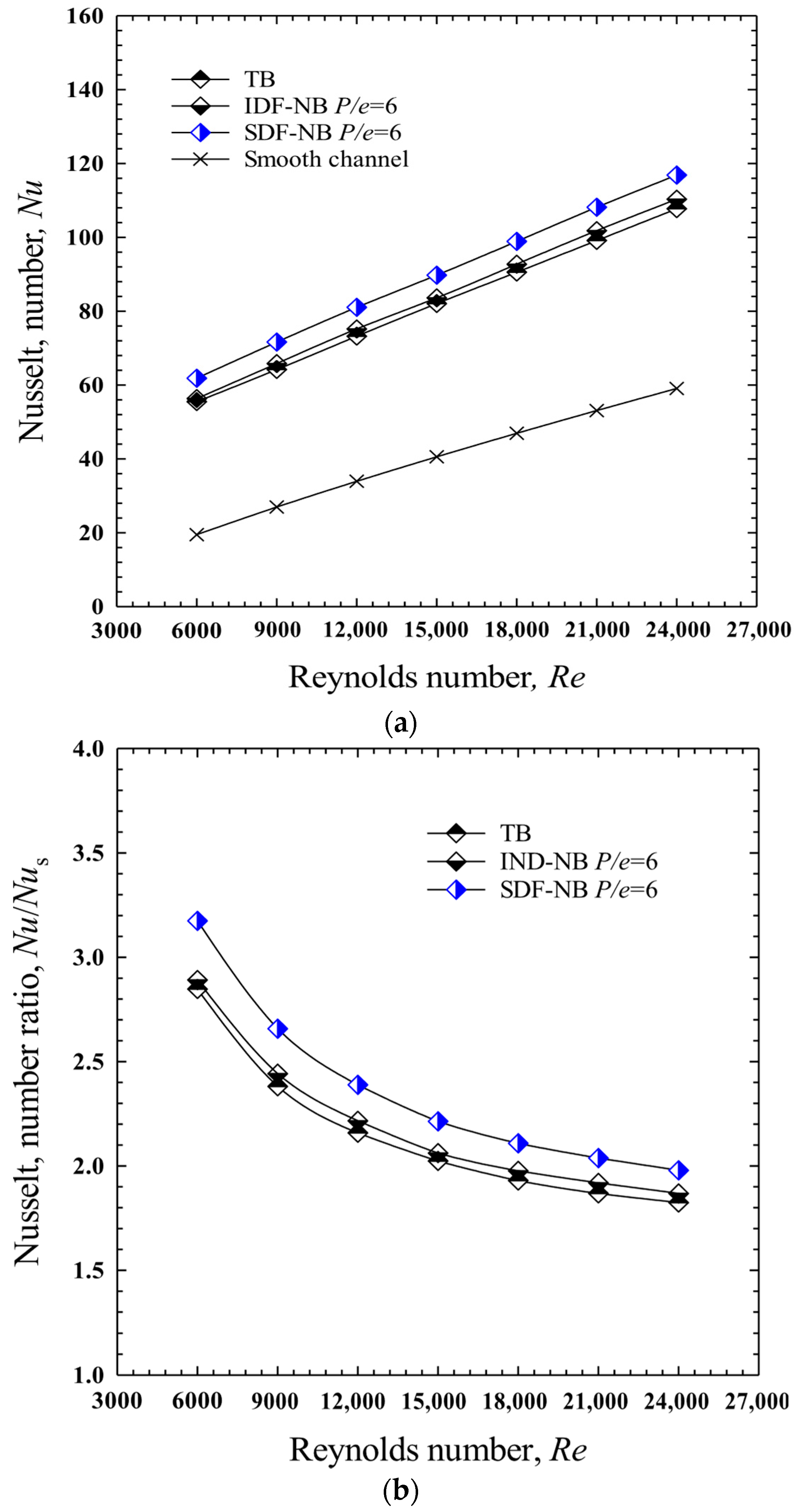
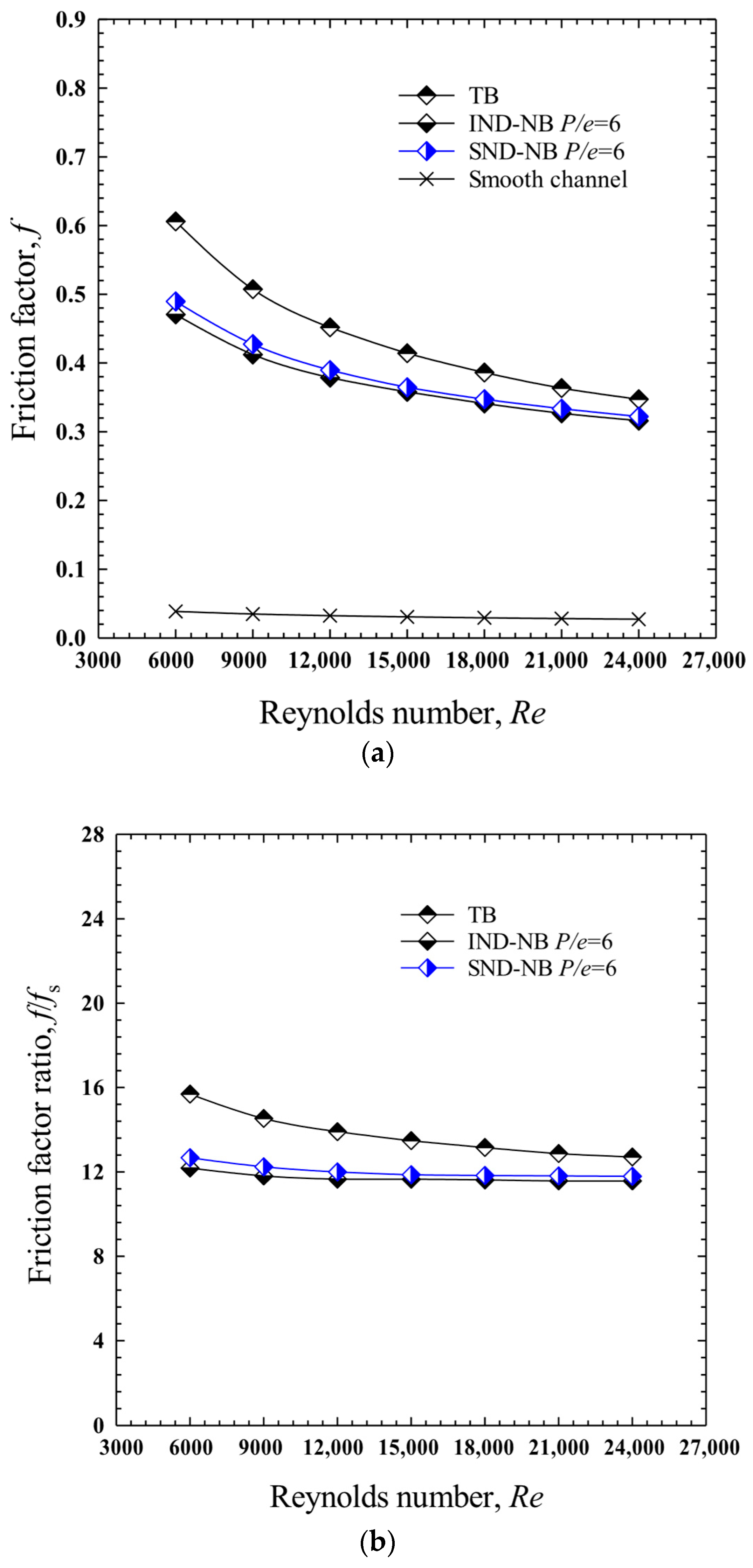
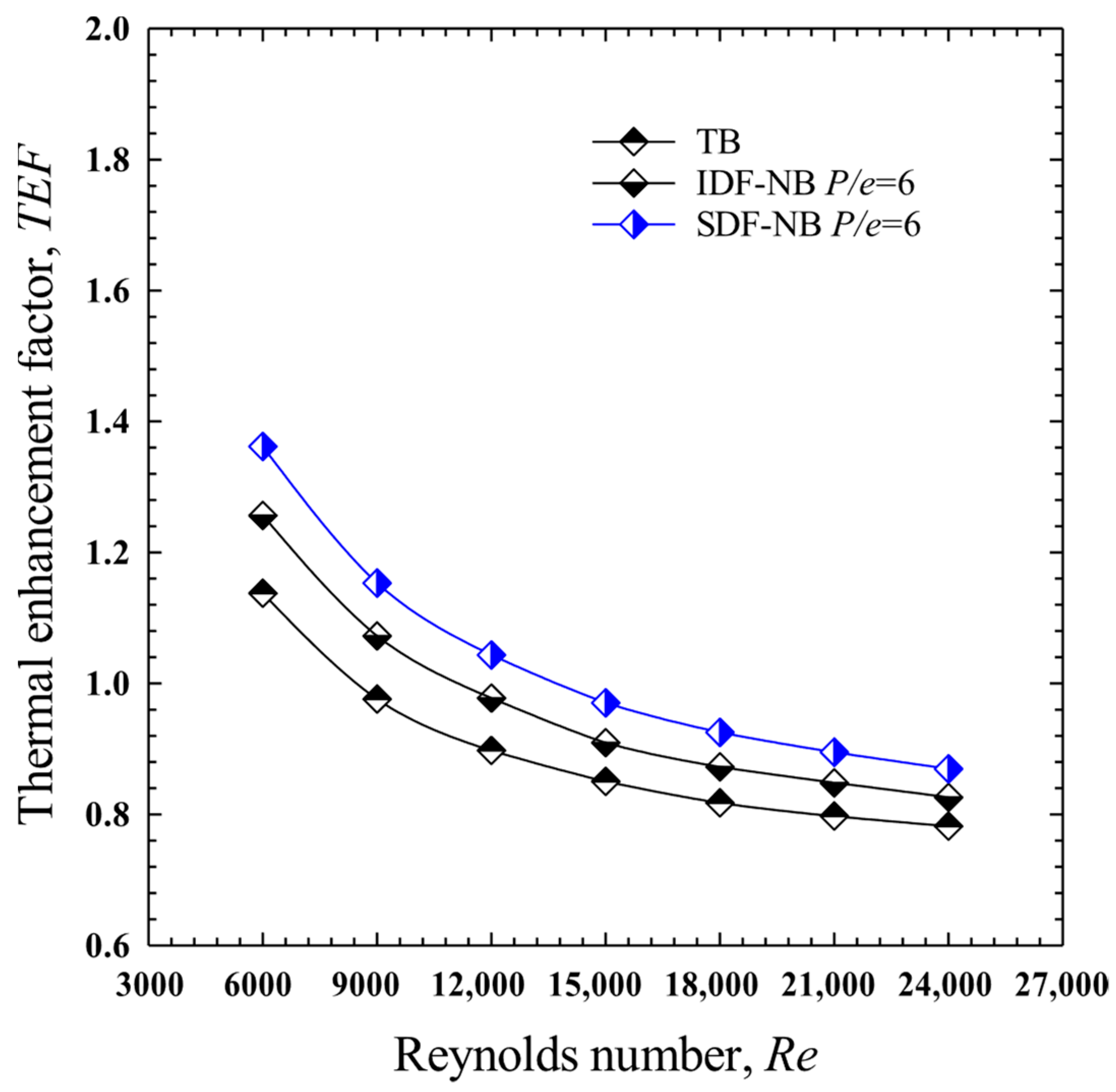
4.5. Effect of Baffle Design
5. Summary
- Across all configurations, a P/e ratio of 6.0 consistently yielded the highest Nusselt numbers, indicating the most effective convective heat transfer.
- For the conventional transverse baffle (TB) configuration, the highest heat transfer occurred at P/e = 6.0 (Nu = 107.8, Nu/Nus = 2.848), but with a high friction penalty (f/fs = 15.686). The optimal thermal performance, considering pressure loss, was achieved at P/e = 8.0, where the TEF reached 1.168.
- For the in-line downward-facing notched baffle (IDF-NB), P/e = 6.0 provided the best balance between heat transfer and pressure drop, with a maximum Nu of 110.4, Nu/Nus = 2.891, f/fs = 12.18, and the highest TEF of 1.257.
- The staggered downward-facing notched baffles (SDF-NBs) achieved the most efficient performance at P/e = 6.0, with the highest Nu of 116.886, Nu/Nus = 3.175, f/fs = 12.669, and a peak TEF of 1.362, making it the most effective configuration overall.
- Notched baffles (IDF-NBs and SDF-NBs) significantly reduced dead zones via perforation-induced reattachment and improved flow uniformity compared to conventional transverse baffles (TBs).
- The staggered arrangement (SDF-NB) facilitated more vigorous redirected flow behind the baffles, leading to the highest overall thermal performance.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | Cross-sectional area of testing section (m2) |
| b | The spacing between adjacent notches |
| Cp | Specific heat capacity (J/K⋅kg) |
| Dh | Channel hydraulic diameter (m) |
| e | Baffle height (m) |
| f | Friction factor |
| h | Convective heat transfer coefficient (W/m2K) or notch height (m) |
| H | Channel height (m) |
| k | Conductivity of air, (W/m2K) |
| L | Channel length (m) |
| m | Mass flow rate (kg/s) |
| N | Notch height (mm) |
| Nu | Nusselt number |
| P | Baffle pitch length (m) |
| Pe | Perimeter (m) |
| P/e | Baffle pitch length to baffle height ratio |
| Δp | Pressure loss (Pa) |
| Q | Heat transfer (W) |
| Re | Reynolds number |
| T | Temperature (K) |
| U | Velocity (m/s) |
| Volumetric flow rate (m3/s) | |
| W | Channel width (m) |
| Greek letters | |
| ν | kinematic viscosity (m2/s) |
| ρ | Fluid density (kg/m3) |
| Subscripts | |
| a | air |
| b | Bulk |
| conv | convection |
| h | Equivalent channel height |
| i | Inlet |
| I | Electric current (A) |
| o | Outlet |
| S | Smooth channel |
| V | Voltage (V) |
| w | Wall |
| Abbreviation | |
| IDF-NB | In-line downward-facing notched-baffle |
| SDF-NB | Staggered downward-facing notched-baffle |
| TB | Conventional Transverse baffle |
| TEF | Thermal enhancement factor |
| TLC | Thermochromic liquid crystal |
References
- Joo, H.J.; Kwak, H.Y.; Kong, M. Effect of twisted tape inserts on thermal performance of heat pipe evacuated-tube solar thermal collector. Energy 2022, 254, 124307. [Google Scholar] [CrossRef]
- Jaisankar, S.; Radhakrishnan, T.K.; Sheeba, K.N. Studies on heat transfer and friction factor characteristics of thermosyphon solar water heating system with helical twisted tapes. Energy 2009, 34, 1054–1064. [Google Scholar] [CrossRef]
- Göksu, T.T. Energy, exergy analysis, and RSM modeling of different designed twisted tapes in placed PV/T systems. Energy 2024, 304, 132041. [Google Scholar] [CrossRef]
- Yang, W.; Jin, C.; Zhu, W.; Xie, C.; Huang, L.; Li, Y.; Xiong, B. Innovative design for thermoelectric power generation: Two-stage thermoelectric generator with variable twist ratio twisted tapes optimizing maximum output. Appl. Energy 2024, 363, 123047. [Google Scholar] [CrossRef]
- Abajja, K.M.A.; Selimli, S.; Shaneb, A.M.A.; Eljetlawi, I.A.M. Enhancing Heat Transfer for Laminar Flow in Heat Pipes Using Perforated and Jagged-Edged Twisted Tapes: An experimental study. Energy 2025, 325, 136141. [Google Scholar] [CrossRef]
- Kouidri, I.; Dahmani, A.; Furizal, F.; Ma’arif, A.A.; Amrane, A.; Mouni, L.; Sharkawy, A.N. Artificial intelligence-based techniques for fouling resistance estimation of shell-and-tube heat exchanger: Cascaded forward and recurrent models. Eng 2025, 6, 85. [Google Scholar] [CrossRef]
- Ko, K.H.; Anand, N.K. Use of porous baffles to enhance heat transfer in a rectangular channel. Int. J. Heat Mass Tran. 2003, 46, 4191–4199. [Google Scholar] [CrossRef]
- Huang, K.D.; Tzeng, S.C.; Jeng, T.M.; Wang, J.R.; Cheng, S.Y.; Tseng, K.T. Experimental study of fluid flow and heat transfer characteristics in the square channel with a perforation baffle. Int. Commun. Heat Mass Transf. 2008, 35, 1106–1112. [Google Scholar] [CrossRef]
- Ary, B.K.P.; Lee, M.S.; Ahn, S.W.; Lee, D.H. The effect of the inclined perforated baffle on heat transfer and flow patterns in the channel. Int. Commun. Heat Mass Transf. 2012, 39, 1578–1583. [Google Scholar] [CrossRef]
- Chompookham, T.; Eiamsa-ard, S.; Promvonge, P. Heat transfer enhancement of turbulent channel flow by baffles with rectangular, triangular and trapezoidal upper edges. J. Engine. Thermo Phys. 2015, 24, 296–304. [Google Scholar] [CrossRef]
- Sahel, D.; Ameur, H.; Benzeguir, R.; Kamla, Y. Enhancement of heat transfer in a rectangular channel with perforated baffles. Appl. Therm. Eng. 2016, 101, 156–164. [Google Scholar] [CrossRef]
- Mashaei, P.R.; Taheri-Ghazvini, M.; Moghadam, R.S.; Madani, S. Smart role of Al2O3 -water suspension on laminar heat transfer in entrance region of a channel with transverse in-line baffles. Appl. Therm. Eng. 2016, 112, 450–463. [Google Scholar] [CrossRef]
- Habet, M.E.; Ahmed, S.A.; Saleh, M.A. Thermal/hydraulic characteristics of a rectangular channel with inline/staggered perforated baffles. Int. Commun. Heat Mass Transf. 2021, 128, 105591. [Google Scholar] [CrossRef]
- Habet, M.A.E.; Ahmed, S.A.; Saleh, M.A. The effect of using staggered and partially tilted perforated baffles on heat transfer and flow characteristics in a rectangular channel. Int. J. Therm. Sci. 2021, 174, 107422. [Google Scholar] [CrossRef]
- Eiamsa-ard, S.; Sripattanapipat, S.; Saysroy, A.; Promvonge, P.; Maruyama, N.; Hirota, M. Heat transfer distribution and flow characteristics in a channel with perforated-baffles. Energy Rep. 2022, 8, 420–426. [Google Scholar] [CrossRef]
- Karabulut, K. Heat transfer and thermal–hydraulic evaluations of cross-circular grooved rectangular flow ducts depending on rectangular baffle design parameters. Eur. Phys. J. Plus. 2024, 139, 227. [Google Scholar] [CrossRef]
- Jamal, I.; Barhdadi, F.Z.; Amghar, K.; Daoudi, S.; Yahiaoui, R.; Ghoumid, K. Enhancing performance in solar air channels: A numerical analysis of turbulent flow and heat transfer with novel shaped baffles. Appl. Therm. Eng. 2024, 251, 123561. [Google Scholar] [CrossRef]
- Alwatban, A.; Aljabr, A. Thermo-flow behavior of air-channel heat exchanger with nonidentical baffle lengths: Computa-tional analysis. J. Therm. Anal. Calorim. 2024, 149, 3593–3603. [Google Scholar] [CrossRef]
- Biswas, R.; Tripathy, P.P. Finite element based computational analysis to study the effects of baffle and fin on the perfor-mance assessment of solar collector. Therm. Sci. Eng. Prog. 2024, 49, 102431. [Google Scholar] [CrossRef]
- Jamal, I.; Barhdadi, F.Z.; Daoudi, S.; Kaouachi, A. Numerical analysis of the effect of baffle length and arrangement on the thermal performance of solar air channels. Int. Commun. Heat Mass Transf. 2024, 161, 108458. [Google Scholar] [CrossRef]
- Suri, A.R.S.; Kumar, A.; Maithani, R. Experimental determination of enhancement of heat transfer in a multiple square perforated twisted tape inserts heat exchanger tube. Exp Heat Transfer. 2018, 31, 85–105. [Google Scholar] [CrossRef]
- Coleman, H.W.; Steele, W.G. Experimentation, Validation, and Uncertainty Analysis for Engineers, 3rd ed.; John Wiley and Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Toriyama, K.; Tada, S.; Ichimiya, K.; Funatani, S.; Tomita, Y. A new method of temperature measurement using thermo-chromic liquid crystals (extension of measurable range based on spectral intensity in the narrow-band wavelength). Int. J. Heat Mass Transf. 2016, 92, 483–489. [Google Scholar] [CrossRef]
- Abdullah, N.A.; Talib, R.A.; Jaafer, A.A.; Salleh, M.A.M.; Chong, W.T. The basics and issues of thermochromic liquid crystal calibrations. Exp. Therm. Fluid Sci. 2010, 34, 1089–1121. [Google Scholar] [CrossRef]
- Kline, S.J.; McClintock, F.A. Describing uncertainties in single sample experi-ments. Mech. Eng. 1953, 75, 3–8. [Google Scholar]


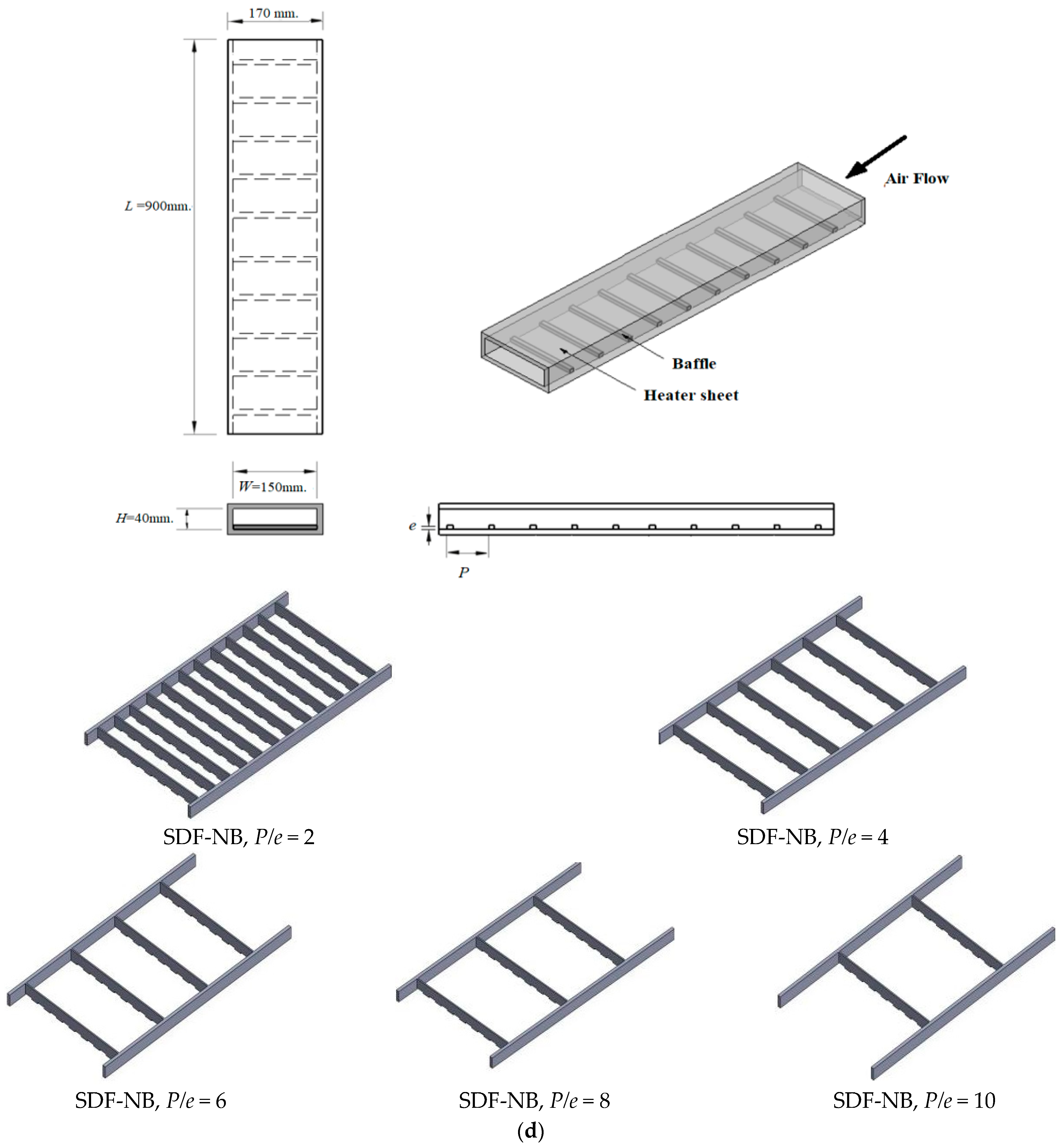



| Test Channel (Height, Width, Length; H × W × L) | 40 mm × 150 mm × 900 mm |
| Channel aspect ratio (W/H) | 3.75 |
| Baffle material | Polylactic acid plastic (PLA) |
| Space between adjacent notches (b) | 10 |
| Roughness pitch ratio (P/e) | 2.0, 4.0, 6.0, 8.0, and 10 |
| notch height-to-baffle height ratio (N/e) | 0.125 for Case II and Case III |
| Working fluid | Air |
| Reynolds number | 6000–24,000 |
| Prandtl number | 0.7 |
| Item | Description | Specification |
|---|---|---|
| Camera Type SLR-like | take TLC (Surface pictures) | Effective Pixel 24.93 megapixels (4928 × 3264 pixels for large size) |
| Liquid Crystal Coated sheet (TLC) | Temperature indicating sheet (Heating surface) | accuracy: ±0.1 °C, 40–45 °C (104–113 °F) |
| Fluke 922 thermo-anemometer | Air velocity (Measurement airflow) | accuracy: ±2.5% for reading (±0.015 m/s), range: 1–80 m/s resolution: 0.01 m/s |
| Dwyer MS2 | Differential pressure sensor (Orifice section) | accuracy: ±1% for 250 Pa, ±1% for 250–1250 Pa |
| Dwyer DM-2005-LCD | Differential pressure sensor (Test section) | accuracy: ±1% full scale at 70 °C |
| HIOKI data logger | Temperature recorder (Display show temperature) | 10 ms high-speed sampling (30-channel as standard) |
| RTD Pt100 | Temperature sensor (Inlet and outlet temperature) | accuracy: ±0.001 Ω at 0 °C (−130 to 95 ±0.05 °C) |
| Variable | Uncertainty |
|---|---|
| Air temperature (T) | ±0.1% |
| Surface temperature (Ts) | ±0.1% |
| Air velocity (U) | ±2.5% |
| Differential pressure (ΔP) | ±1.0% |
| Duct diameter/length (D, L) | ±0.5% |
| Cross-section area (A) | ±0.5% |
| Density (ρ) | ±1.5% |
| Viscosity (μ) | ±2.0% |
| Thermal conductivity (k) | ±3.0% |
| Power input (Q) | ±0.5% |
| Parameter | Uncertainty (%) |
|---|---|
| Reynolds number (Re) | ±3.54% |
| Nusselt number (Nu) | ±3.10% |
| Friction factor (f) | ±5.34% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Phila, A.; Keaitnukul, W.; Kumar, M.; Pimsarn, M.; Chokphoemphun, S.; Eiamsa-Ard, S. Heat Transfer Analysis in a Channel Mounted with In-Line Downward-Facing and Staggered Downward-Facing Notched Baffles. Eng 2025, 6, 229. https://doi.org/10.3390/eng6090229
Phila A, Keaitnukul W, Kumar M, Pimsarn M, Chokphoemphun S, Eiamsa-Ard S. Heat Transfer Analysis in a Channel Mounted with In-Line Downward-Facing and Staggered Downward-Facing Notched Baffles. Eng. 2025; 6(9):229. https://doi.org/10.3390/eng6090229
Chicago/Turabian StylePhila, A., W. Keaitnukul, M. Kumar, M. Pimsarn, S. Chokphoemphun, and S. Eiamsa-Ard. 2025. "Heat Transfer Analysis in a Channel Mounted with In-Line Downward-Facing and Staggered Downward-Facing Notched Baffles" Eng 6, no. 9: 229. https://doi.org/10.3390/eng6090229
APA StylePhila, A., Keaitnukul, W., Kumar, M., Pimsarn, M., Chokphoemphun, S., & Eiamsa-Ard, S. (2025). Heat Transfer Analysis in a Channel Mounted with In-Line Downward-Facing and Staggered Downward-Facing Notched Baffles. Eng, 6(9), 229. https://doi.org/10.3390/eng6090229







