A Novel Condition Monitoring Technique for Mining Ground Engagement Tools via Modal Analysis
Abstract
1. Introduction
2. Methodology
2.1. Principle of Vibration-Based Damage Identification
2.2. Mass Loss Detection with the Vibration-Based Method
2.2.1. Cantilever Beam—FEA
Model Description
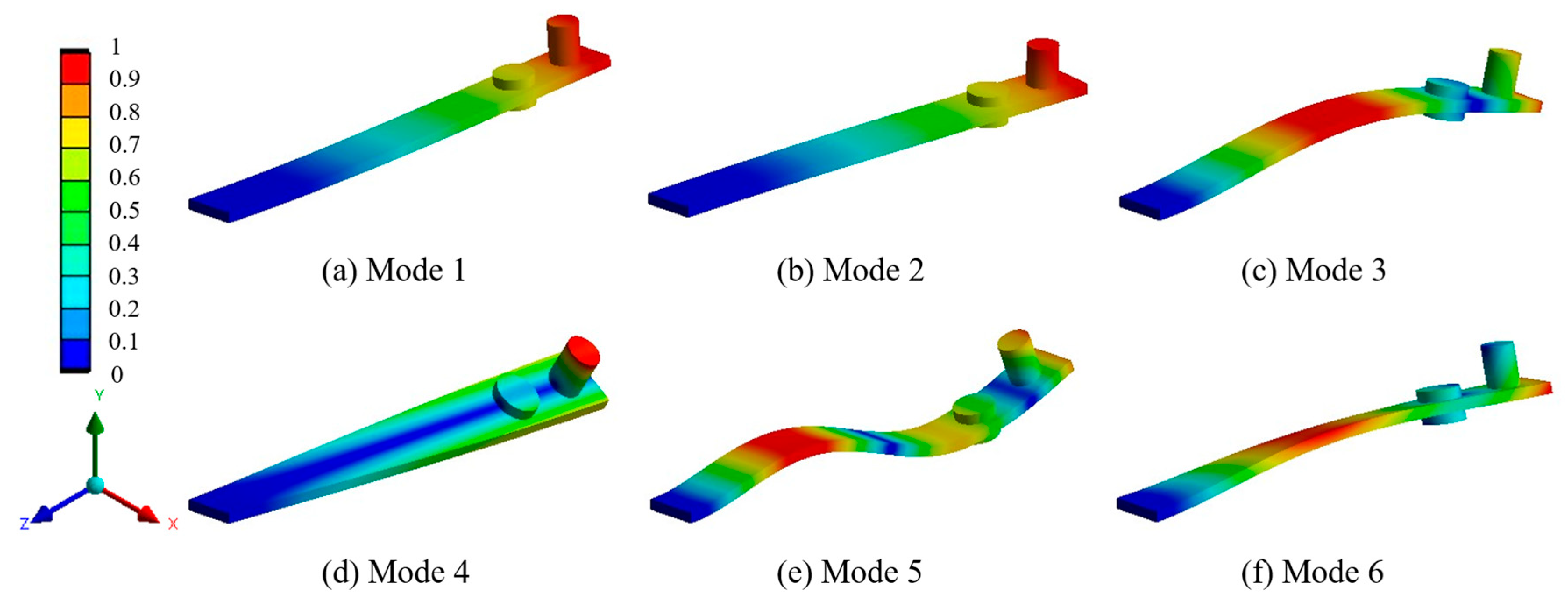
Modal Analysis
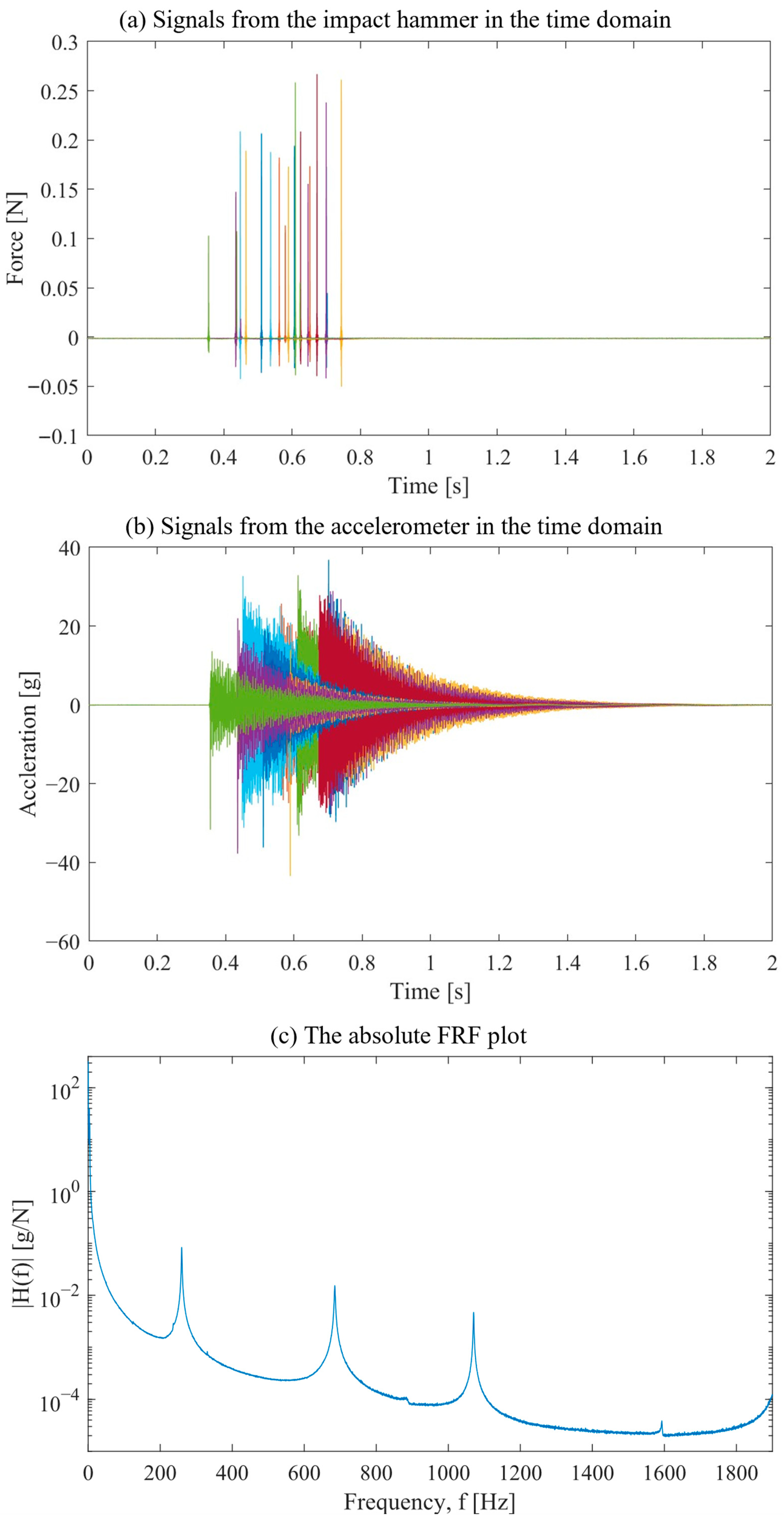
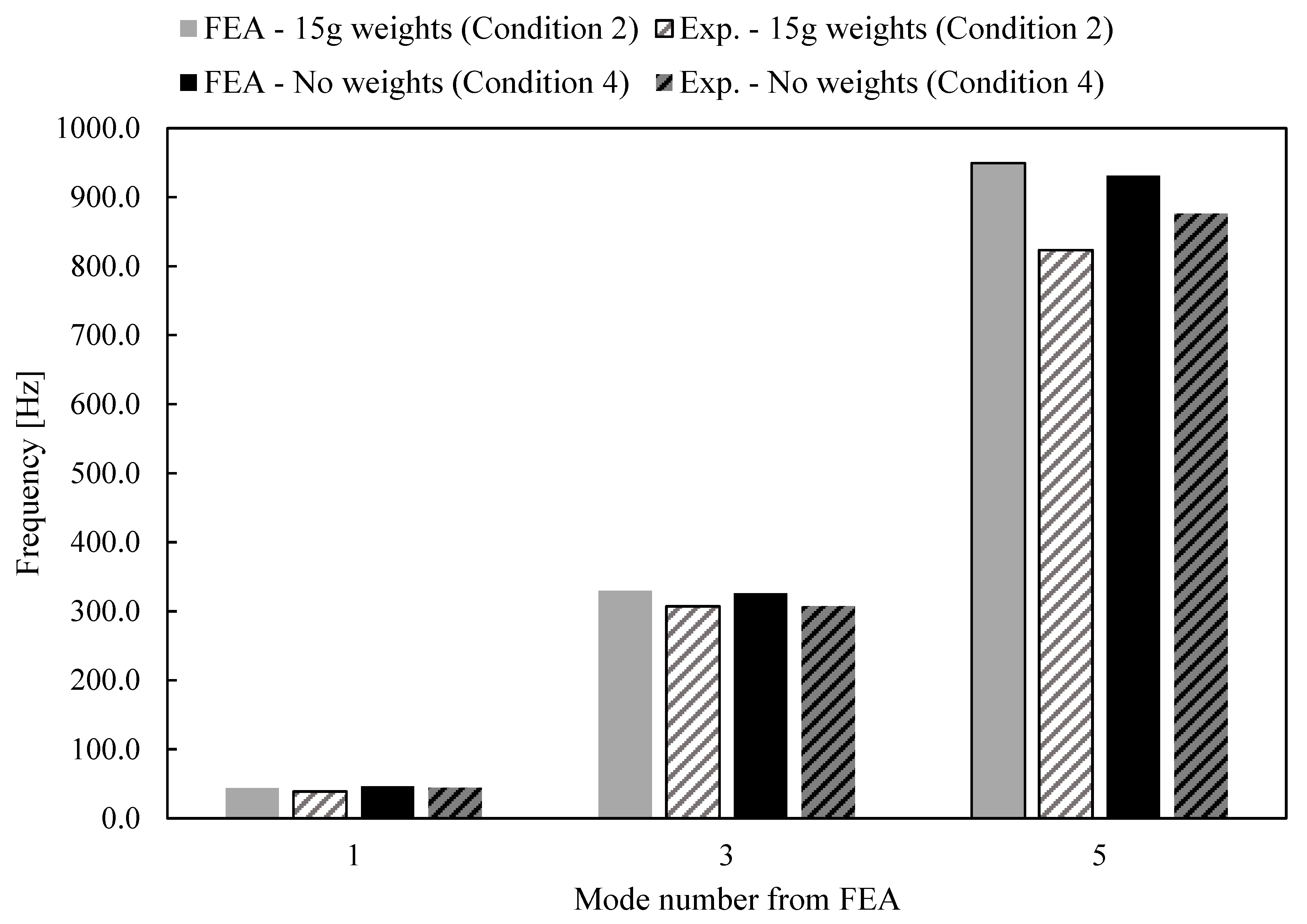
2.2.2. Cantilever Beam—Experiments
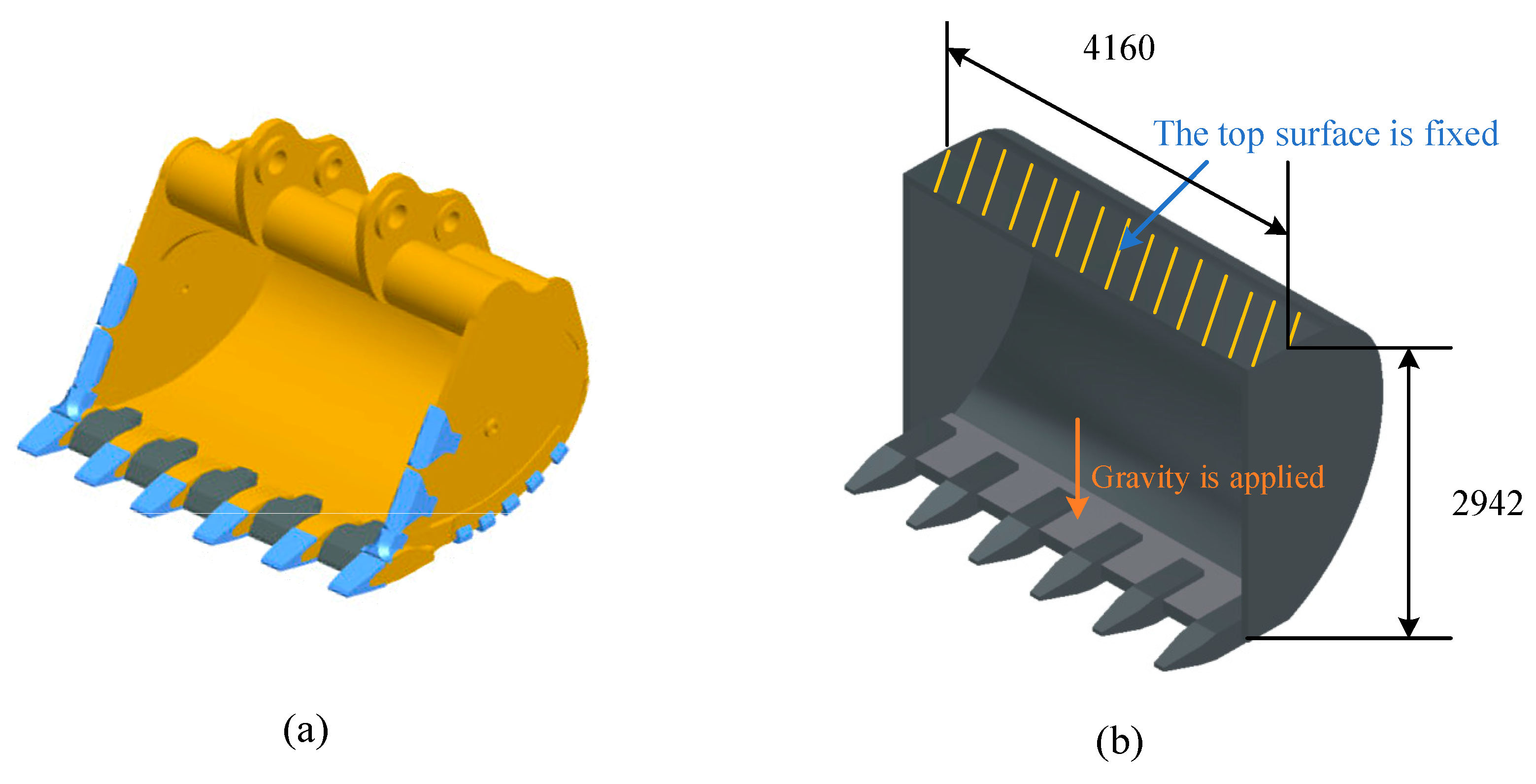
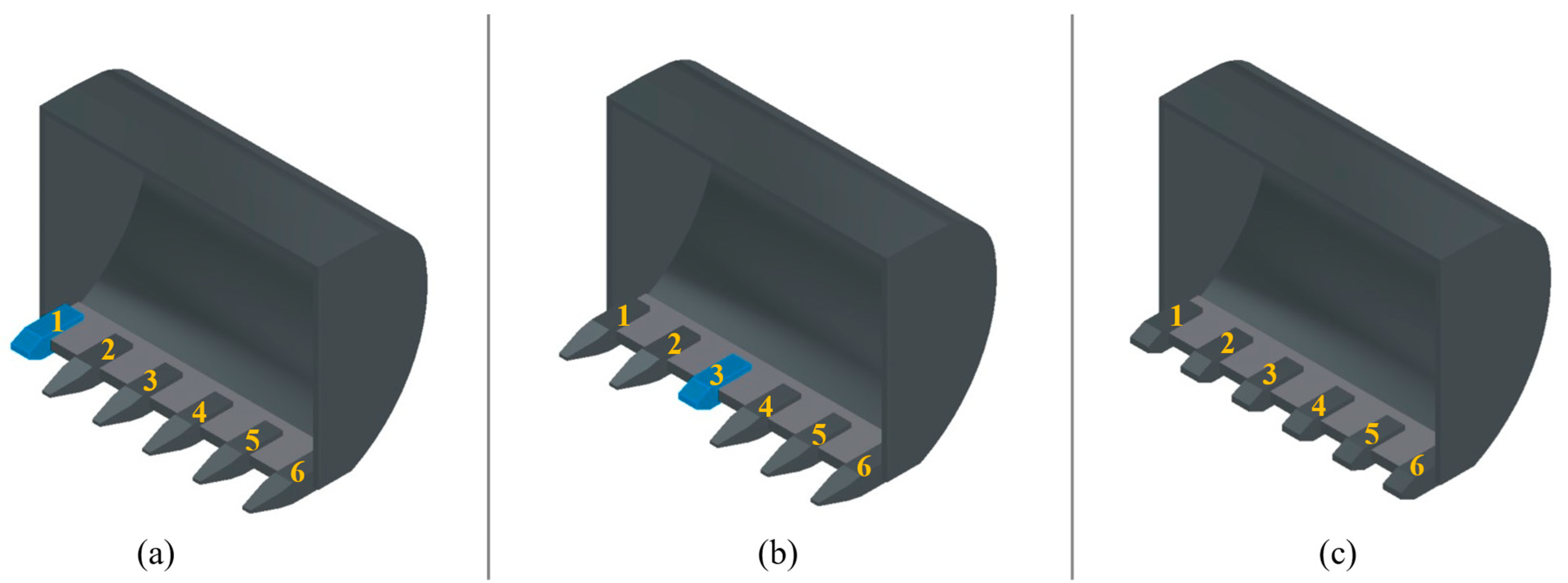
2.2.3. Mining Bucket with GETs—FEA
Model Description
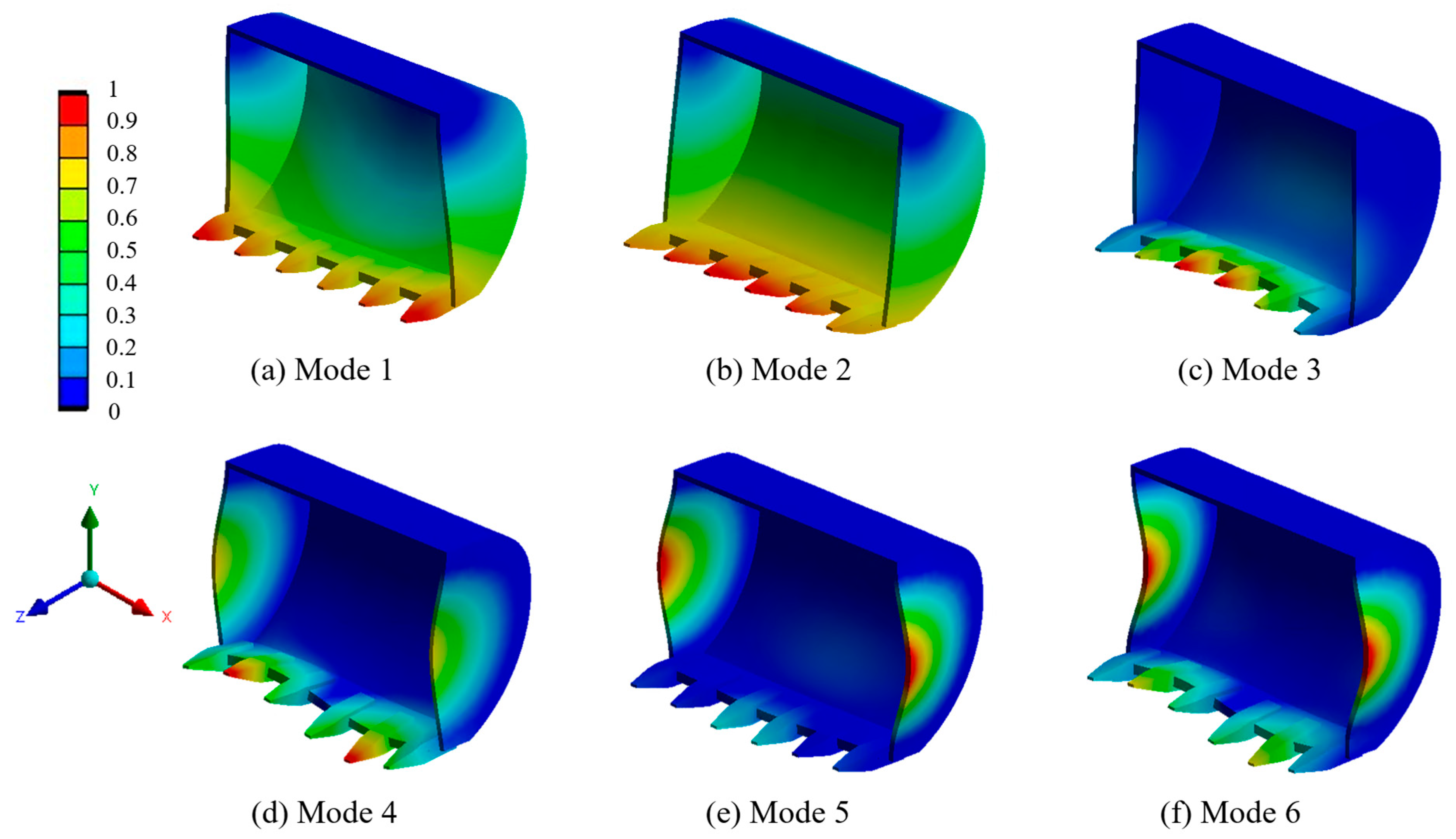
Modal Analysis
Dynamic Analysis
3. Results and Discussion
3.1. Cantilever Beam
3.1.1. FEA Modal Analysis
3.1.2. Experimental Impact Vibration Tests
3.2. Excavator Bucket
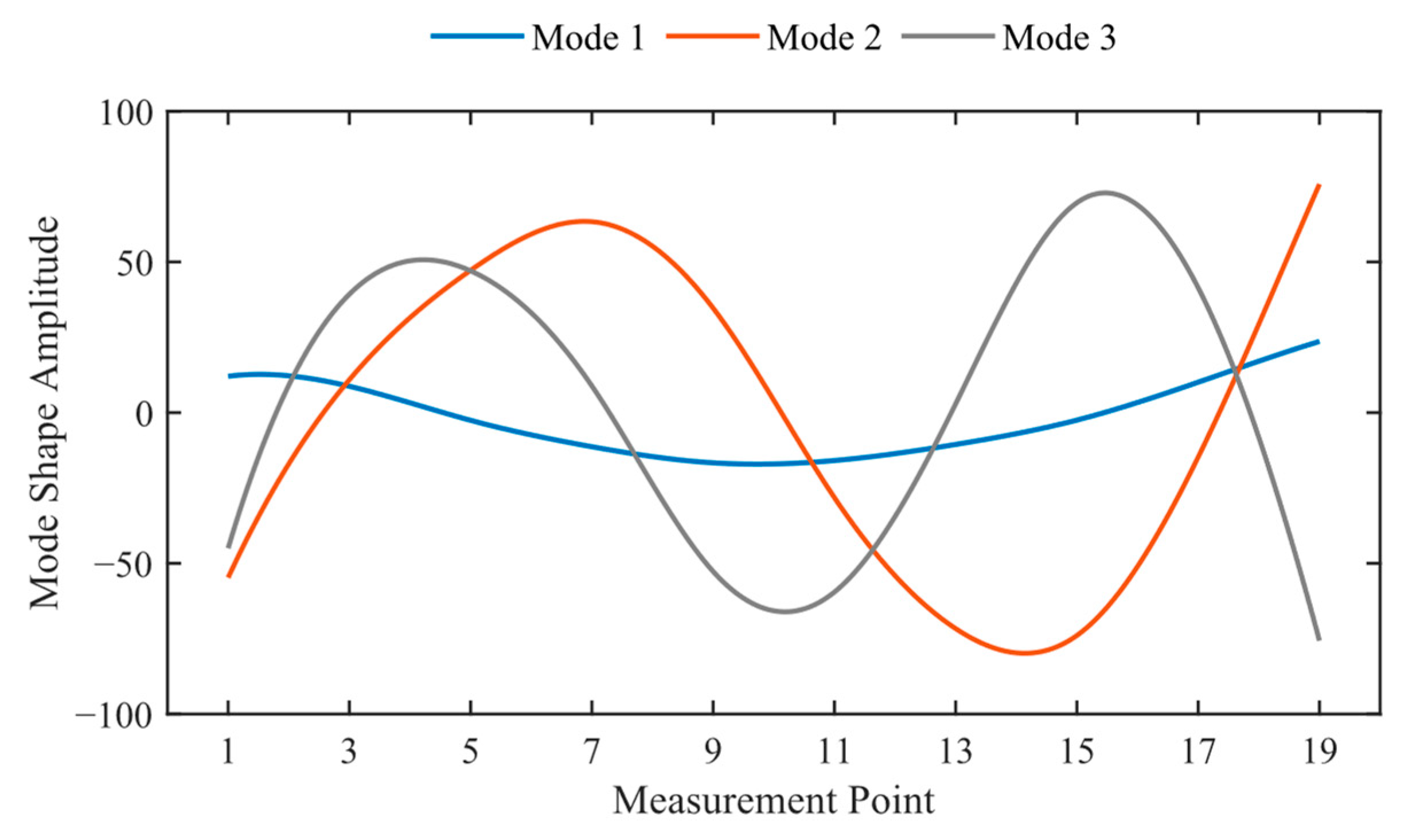
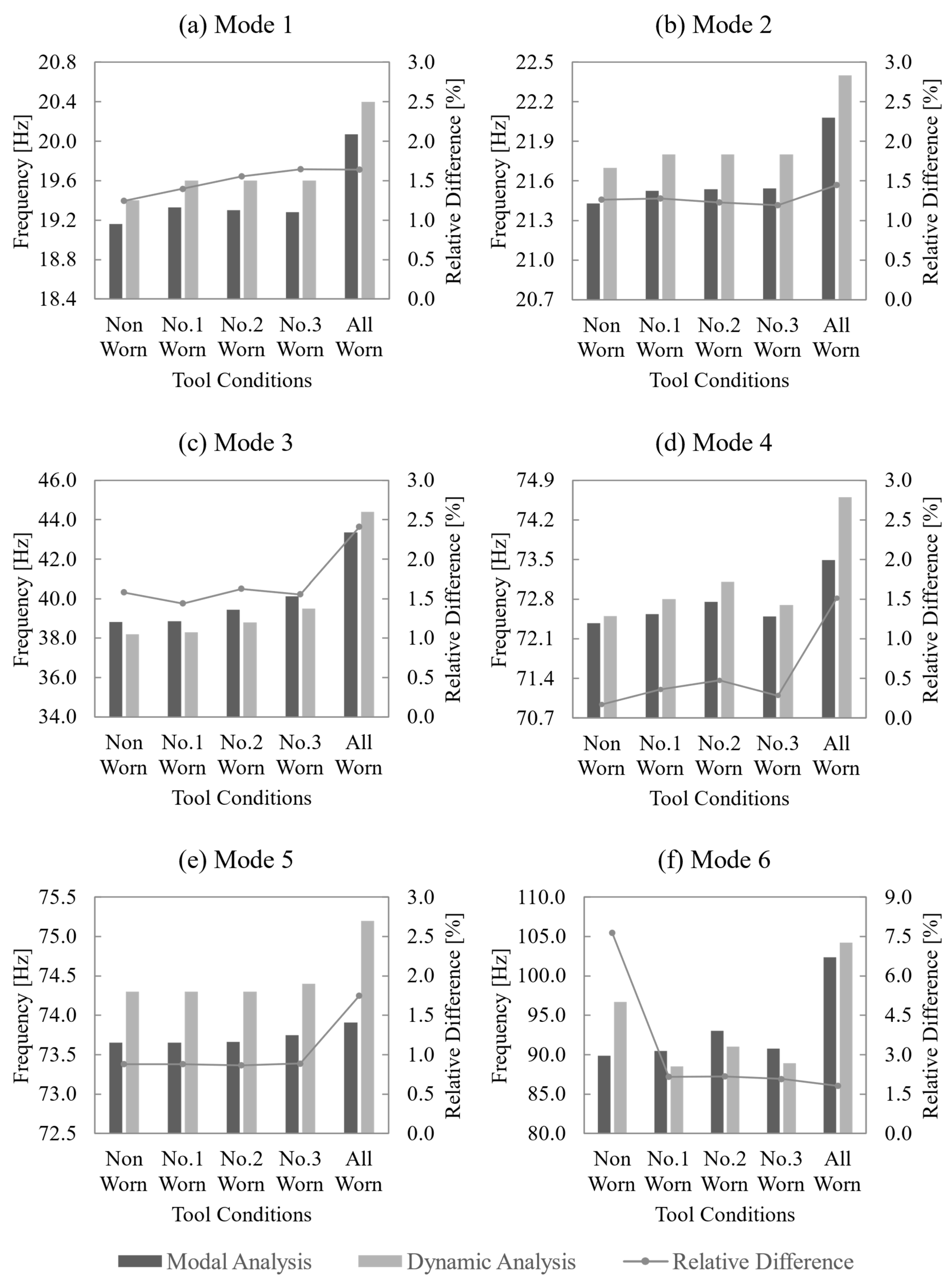
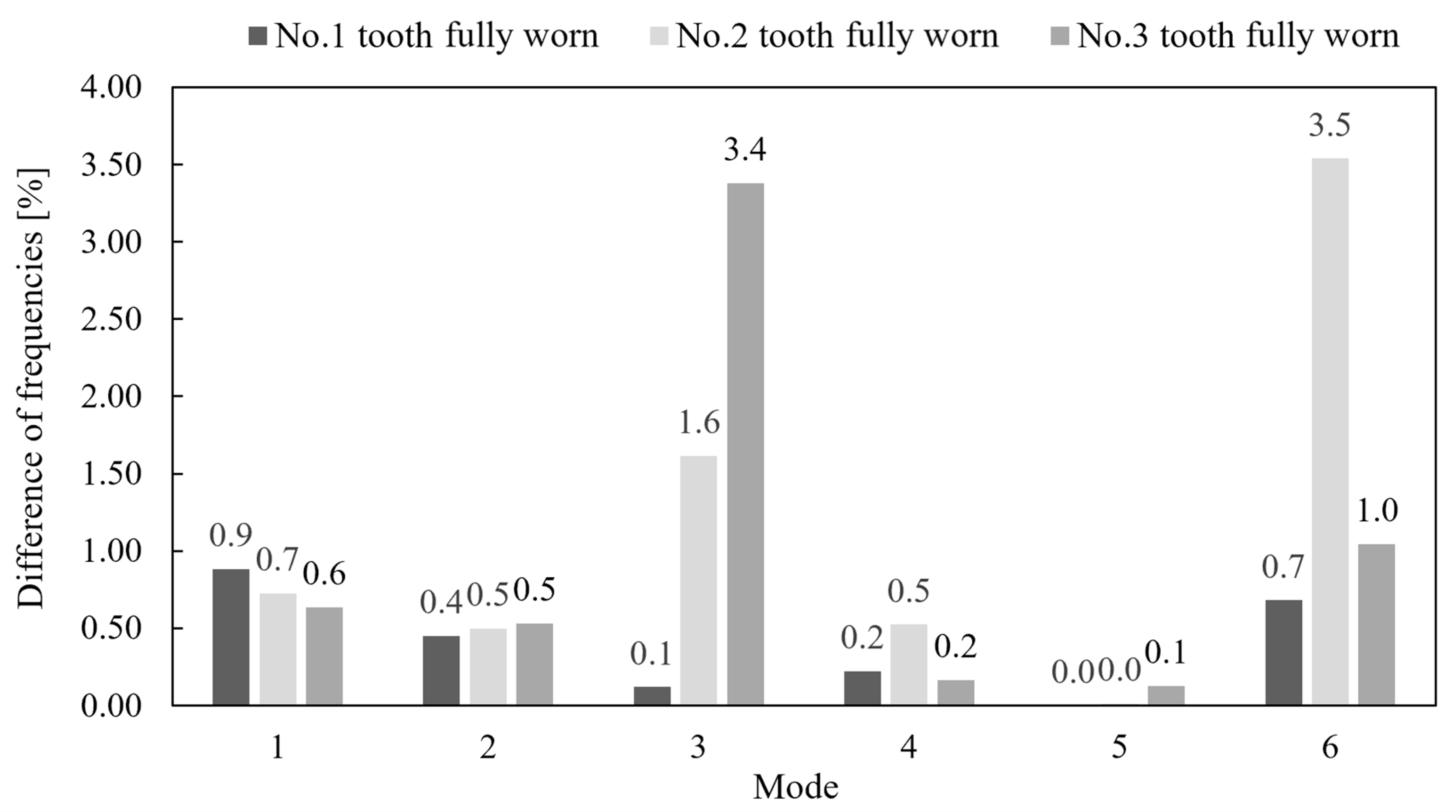
3.2.1. Modal Analysis
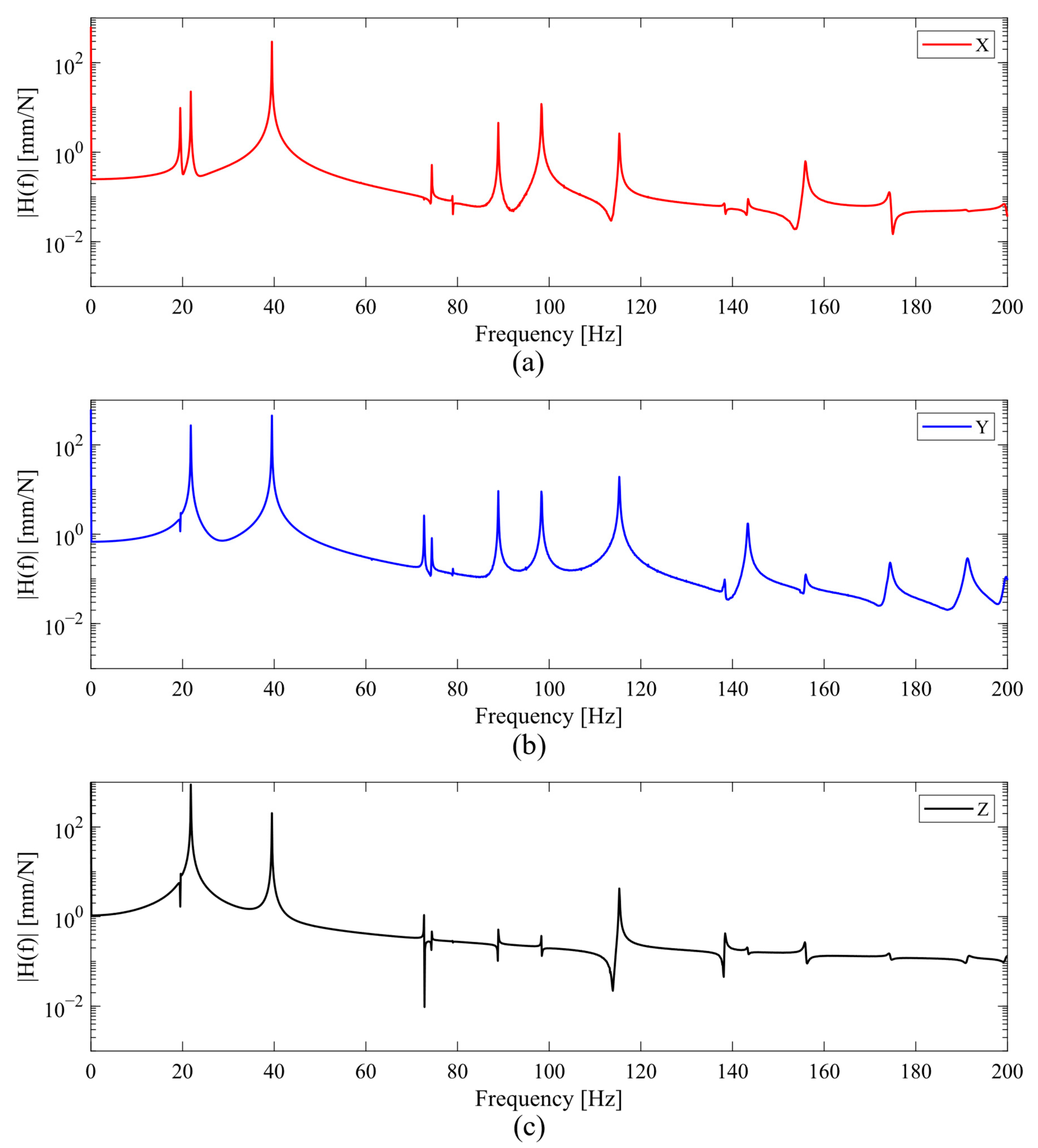
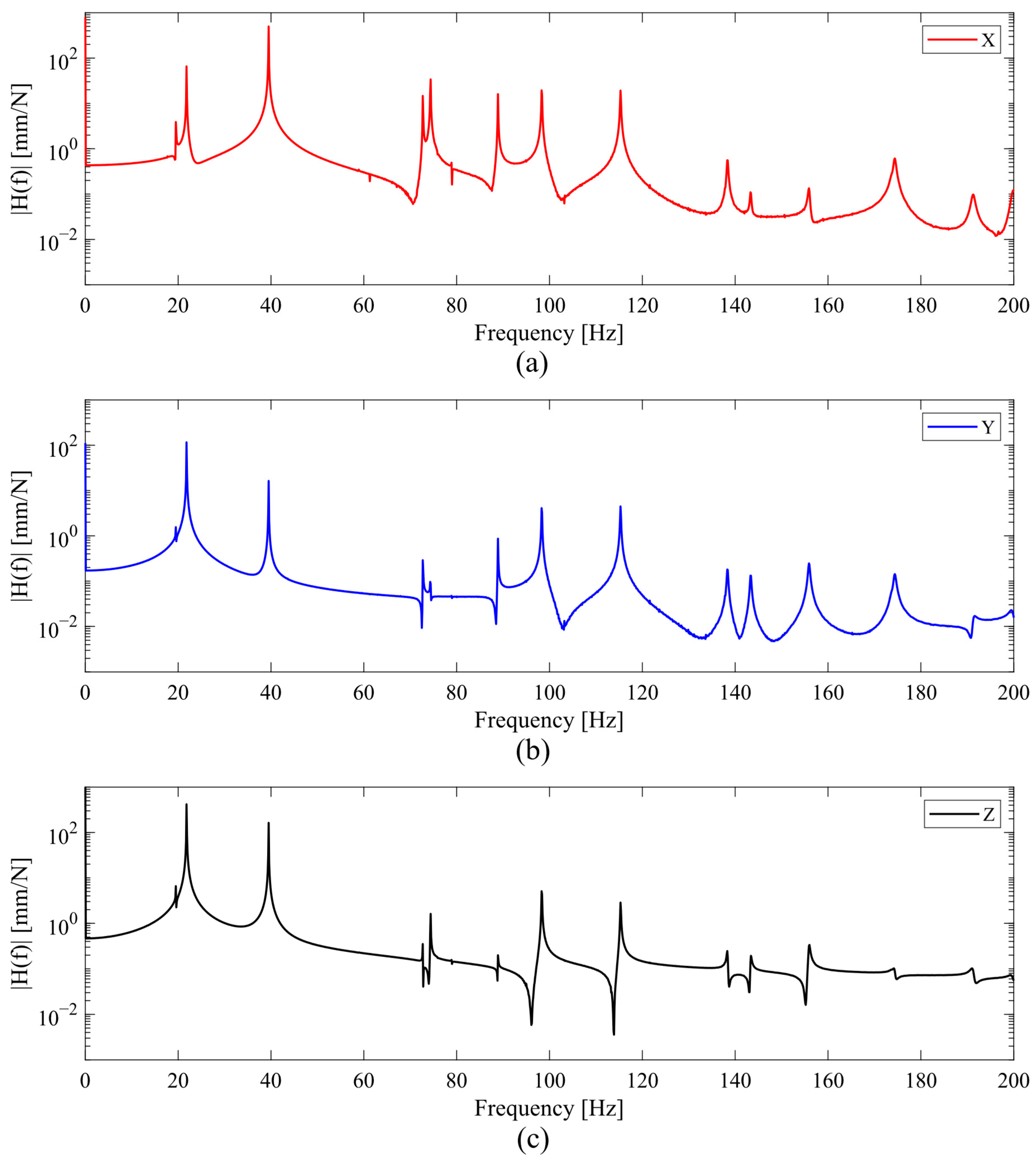
3.2.2. Dynamic Analysis
- (1)
- Allows the prediction of dynamic response behaviours of the system under specific impact magnitudes and locations, which is useful for designing the experimental verification.
- (2)
- Can be used to evaluate optimal sensor locations to capture maximum signal, which can be achieved by analysing the amplitude in the FFT plots.
- (3)
- Can assist the choice of sensor placement to capture frequencies of targeted modes. The locations and orientations of the sensors can be informed by dynamic analysis and mode shapes in the modal analysis.
4. Conclusions
- (1)
- Numerical modal analysis for the cantilever beam specimen proves that natural frequencies change with mass loss, specifically increasing as the mass loss increases. The vibration tests with an impact hammer verify the numerical predictions with acceptable differences, also demonstrating the ability for such changes in modal frequencies to be measured.
- (2)
- For the industrial excavator bucket scenario, the natural frequency changes as the conditions of the GETs vary. The maximum increase in natural frequency observed was 13.9% at mode 6, for the scenario when all teeth are fully worn to the non-worn/intact condition. The patterns of the frequency changes for the worn teeth at different positions were observed in this paper.
- (3)
- For the finite element model predictions, the dynamic analysis results closely align with the modal analysis results, with minimal differences. This consistency builds confidence in assessing tool conditions by experimental measurements of natural frequencies, while also guiding the design of impact and sensor locations and orientations for experimental verification.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
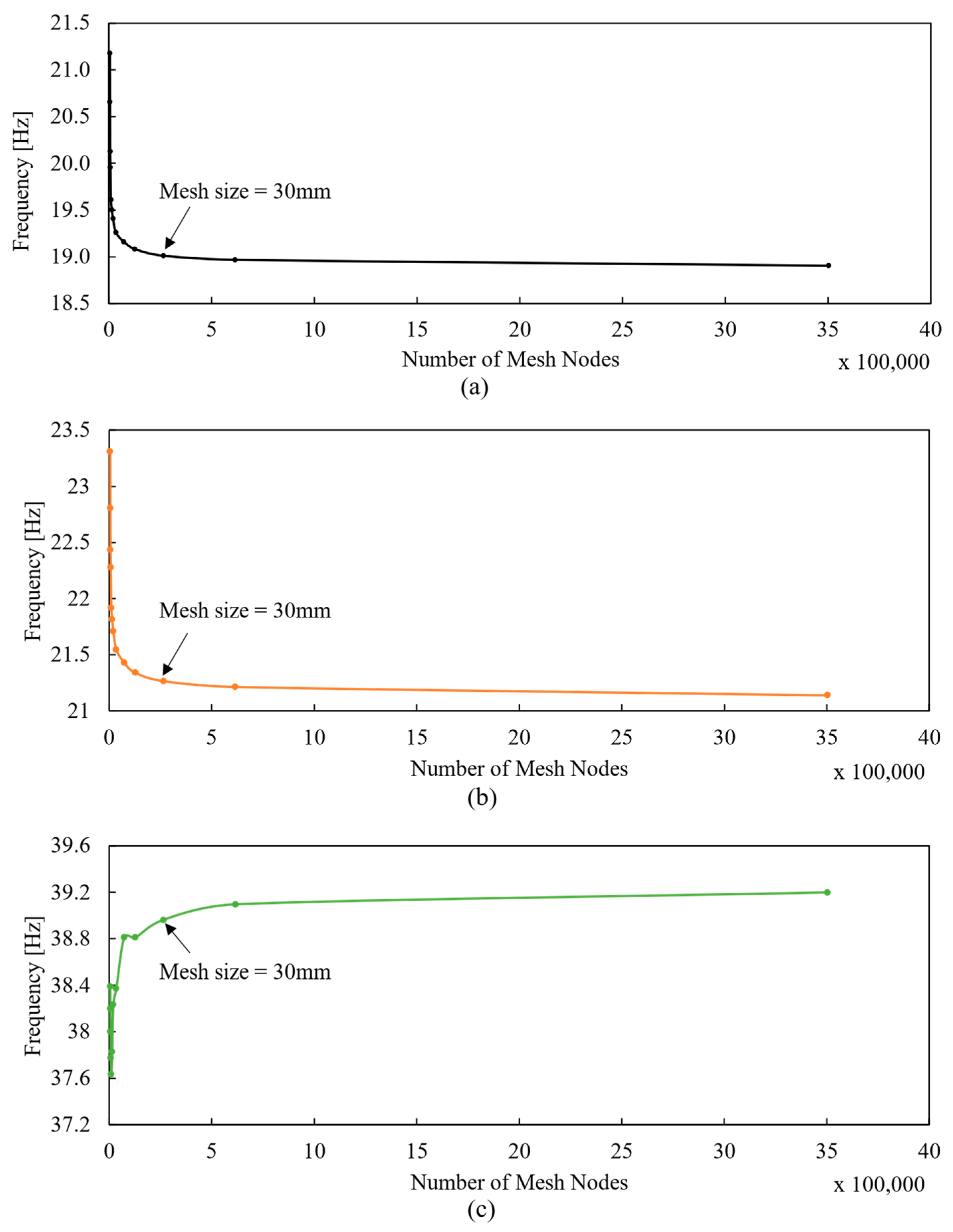
Appendix A. Mesh Convergence Analysis
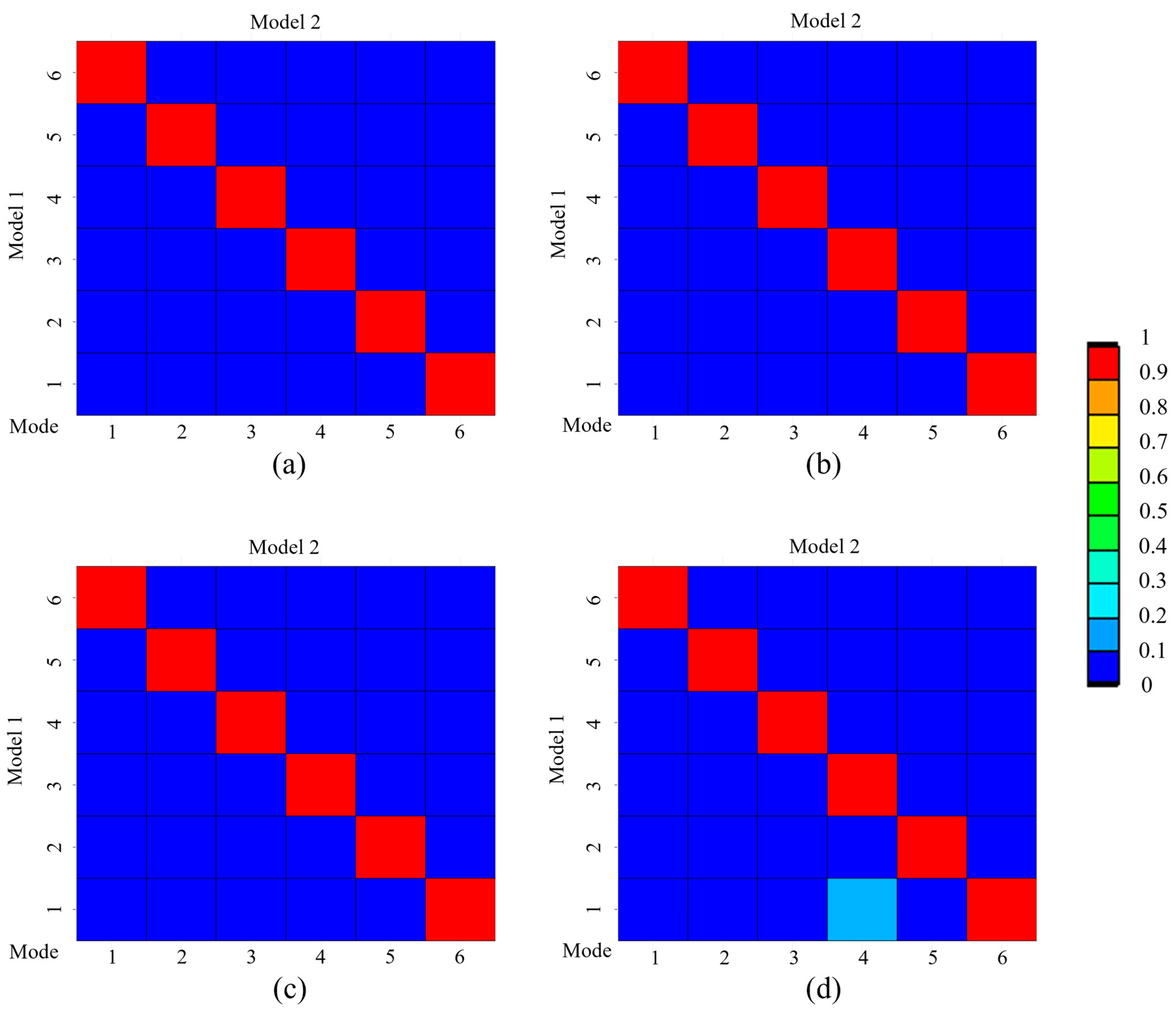
Appendix B. MAC of the Bucket Under Different Conditions
References
- Holmberg, K.; Kivikytö-Reponen, P.; Härkisaari, P.; Valtonen, K.; Erdemir, A. Global energy consumption due to friction and wear in the mining industry. Tribol. Int. 2017, 115, 116–139. [Google Scholar] [CrossRef]
- Ibrahim, M.A.; Hassan, G.; Hassanein, H.S.; Obaia, K. Wireless Sensing for Ground Engaging Tools. In Proceedings of the GLOBECOM 2020—2020 IEEE Global Communications Conference, Taipei, Taiwan, 7–11 December 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Saha, G. Abrasive Wear of Alloys for Ground Engaging Tools. Ph.D. Thesis, Deakin University, Burwood, VIC, Australia, 2017. [Google Scholar]
- Liu, X.; Qi, X.; Jiang, Y. Electric Shovel Teeth Missing Detection Method Based on Deep Learning. Comput. Intell. Neurosci. 2021, 2021, 6503029. [Google Scholar] [CrossRef]
- Lu, J.; Liu, Y. A real-time and accurate detection approach for bucket teeth falling off based on improved YOLOX. Mech. Sci. 2022, 13, 979–990. [Google Scholar] [CrossRef]
- Rafezi, H.; Hassani, F. Drill bit wear monitoring and failure prediction for mining automation. Int. J. Min. Sci. Technol. 2023, 33, 289–296. [Google Scholar] [CrossRef]
- Rafezi, H.; Hassani, F. Drilling signals analysis for tricone bit condition monitoring. Int. J. Min. Sci. Technol. 2021, 31, 187–195. [Google Scholar] [CrossRef]
- Radziszewski, P.; Martins, S.; Benson, C. Method and Device for Sensing Wear. US7677079B2, 16 March 2010. Available online: https://patents.google.com/patent/US7677079B2/en (accessed on 27 September 2023).
- Nicoson, R.; Popp, J.R.; Schlegel, D.; Pomerenke, K. Methods and Systems for Detecting Heavy Machine Wear. US10024034B2, 17 July 2018. Available online: https://patents.google.com/patent/US10024034B2/en (accessed on 27 September 2023).
- Steed, D.J.; Poulsen, S.D. Wear Indication Devices, and Related Assemblies and Methods. US9724697B2, 8 August 2017. Available online: https://patents.google.com/patent/US9724697B2/en (accessed on 27 September 2023).
- Davies, B. Wear Sensor. 20120043980, 23 February 2012. Available online: https://www.freepatentsonline.com/y2012/0043980.html (accessed on 27 September 2023).
- Motion Metrics® ShovelMetricsTM | Weir, (n.d.). Available online: https://www.global.weir/product-catalogue/motion-metrics-shovelmetrics/ (accessed on 27 September 2023).
- Finley, T.M.; Carpenter, C.M.; Wilkinson, E.E. Ground Engaging Tool Management. 20170352199, 7 December 2017. Available online: https://www.freepatentsonline.com/y2017/0352199.html (accessed on 27 September 2023).
- Ridley, R.K.; Kazmierczak, T.; Cai, L.; Johnston, P.C.; Pinto, H.; Sun, J.; Provencher, M.; Woolley, J.H.; Cardinal, G. System and a Method for Detecting a Damaged or Missing Machine Part. 8411930, 2 April 2013. Available online: https://www.freepatentsonline.com/8411930.html (accessed on 27 September 2023).
- Hamilton, I.H. Detection System. 2012. Available online: https://patentscope.wipo.int/search/en/detail.jsf?docId=WO2012116408 (accessed on 27 September 2023).
- Darlington, B.; Knowles, B.; Schild, P.; Dallard, B. Attachment Status Monitoring of Ground Engaging Tools (GET) at Heavy Machinery. US11280067B2, 22 March 2022. Available online: https://patents.google.com/patent/US11280067B2/en (accessed on 27 September 2023).
- Betournay, J.W.; Carpenter, C.M.; Hyde, S.D.; Lander, J.; Zuendel, K.D. Monitoring Ground-Engaging Products from Earth Working Equipment. AU2020264339B2, 24 March 2022. Available online: https://patents.google.com/patent/AU2020264339B2/en?q=(Monitoring+Gound-Engaging+Products+Earth+Working+Equipment)&oq=Monitoring+Gound-Engaging+Products+for+Earth+Working+Equipment (accessed on 27 September 2023).
- Nguyen, Q.-B.; Nguyen, H.-H. An Efficient Approach for Damage Identification of Beams Using Mid-Span Static Deflection Changes. Eng 2024, 5, 895–917. [Google Scholar] [CrossRef]
- Iliopoulos, A.; Shirzadeh, R.; Weijtjens, W.; Guillaume, P.; Hemelrijck, D.; Devriendt, C. A modal decomposition and expansion approach for prediction of dynamic responses on a monopile offshore wind turbine using a limited number of vibration sensors. Mech. Syst. Signal Process. 2015, 68, 84–104. [Google Scholar] [CrossRef]
- Li, W.; Huang, Y. A method for damage detection of a jacket platform under random wave excitations using cross correlation analysis and PCA-based method. Ocean. Eng. 2020, 214, 107734. [Google Scholar] [CrossRef]
- Zhang, K.; Yan, X. Multi-cracks identification method for cantilever beam structure with variable cross-sections based on measured natural frequency changes. J. Sound Vib. 2017, 387, 53–65. [Google Scholar] [CrossRef]
- Loutas, T.H.; Sotiriades, G.; Kalaitzoglou, I.; Kostopoulos, V. Condition monitoring of a single-stage gearbox with artificially induced gear cracks utilizing on-line vibration and acoustic emission measurements. Appl. Acoust. 2009, 70, 1148–1159. [Google Scholar] [CrossRef]
- Kouhpangi, M.Z.; Yaghoubi, S.; Torabipour, A. Improved Structural Health Monitoring Using Mode Shapes: An Enhanced Framework for Damage Detection in 2D and 3D Structures. Eng 2023, 4, 1742–1760. [Google Scholar] [CrossRef]
- Fan, W.; Qiao, P. Vibration-based Damage Identification Methods: A Review and Comparative Study. Struct. Health Monit. 2011, 10, 83–111. [Google Scholar] [CrossRef]
- Salawu, O.S. Detection of structural damage through changes in frequency: A review. Eng. Struct. 1997, 19, 718–723. [Google Scholar] [CrossRef]
- Sha, G.; Radzieński, M.; Cao, M.; Ostachowicz, W. A novel method for single and multiple damage detection in beams using relative natural frequency changes. Mech. Syst. Signal Process. 2019, 132, 335–352. [Google Scholar] [CrossRef]
- Patil, D.P.; Maiti, S.K. Experimental verification of a method of detection of multiple cracks in beams based on frequency measurements. J. Sound Vib. 2005, 281, 439–451. [Google Scholar] [CrossRef]
- Wang, J.; Guo, T.; Wang, Z.; Liu, W.; Yu, T.; Zhang, Y. Simulation and experimental research on vibration response of microcracked compressor blades under variable working conditions. Appl. Acoust. 2024, 216, 109766. [Google Scholar] [CrossRef]
- Wang, H. Study on natural-frequency-based structural damage identification of steel transmission tower. In Proceedings of the 2011 International Conference on Transportation, Mechanical, and Electrical Engineering (TMEE), Changchun, China, 16–18 December 2011; pp. 1382–1385. [Google Scholar] [CrossRef]
- Popescu, F.D.; Radu, S.M.; Andraș, A.; Kertesz, I. Simulation of the frequency response of the ERC 1400 Bucket Wheel Excavator boom, during the excavation process. New Trends Prod. Eng. 2019, 2, 153–167. [Google Scholar] [CrossRef]
- Jiang, Y.Z.; Liu, C.J.; Li, X.J.; He, K.F.; Xiao, D.M. Low-Frequency Vibration Testing of Huge Bucket Wheel Excavator Based on Step-Decay Signals. Shock. Vib. 2018, 2018, 6182156. [Google Scholar] [CrossRef]
- Li, T.; Liu, F.; Li, Z.; Lu, M.; He, Q. Analysis and Experimental Investigation of Vibration Characteristics of Rotary Platform of Hydraulic Excavator under Complex Working Conditions. Shock. Vib. 2021, 2021, 4469251. [Google Scholar] [CrossRef]
- Fu, Z.-F.; He, J. Modal Analysis; Elsevier: Amsterdam, The Netherlands, 2001. [Google Scholar]
- Avitabile, P. Experimental modal analysis. Sound Vib. 2001, 35, 20–31. [Google Scholar]
- Chandra, C.A.; Samal, P.K. Experimental determination of mode shapes of beams by roving impact test. Mater. Today Proc. 2021, 46, 9159–9163. [Google Scholar] [CrossRef]
- Alma’aitah, A.; Hassanein, H.S. Utilizing Sprouts WSN platform for equipment detection and localization in harsh environments. In Proceedings of the 39th Annual IEEE Conference on Local Computer Networks Workshops, Edmonton, AB, Canada, 8–11 September 2014; pp. 777–783. [Google Scholar] [CrossRef]
- KOMATSU. Hydraulic Excavator, KOMATSU (n.d.). Available online: https://cdn.machine.market/specifications/komatsu-mining-shovel-excavators-spec-0cf49e.pdf (accessed on 5 July 2024).
- Gao, S.; Liu, F.; Jiang, C. Improvement study of modal analysis for offshore structures based on reconstructed displacements. Appl. Ocean. Res. 2021, 110, 102596. [Google Scholar] [CrossRef]
- Bendat, J.S.; Piersol, A.G. Random Data: Analysis and Measurement Procedures; John Wiley & Sons: Hoboken, NJ, USA, 2011; Available online: https://books.google.com.au/books?hl=zh-CN&lr=&id=qYSViFRNMlwC&oi=fnd&pg=PT20&dq=random+data+analysis+and+measurement+procedures+4th+edition&ots=Ud-LRIISwh&sig=XUjH74pV2r_Ex5R6_yBgufBuEv4 (accessed on 10 August 2025).
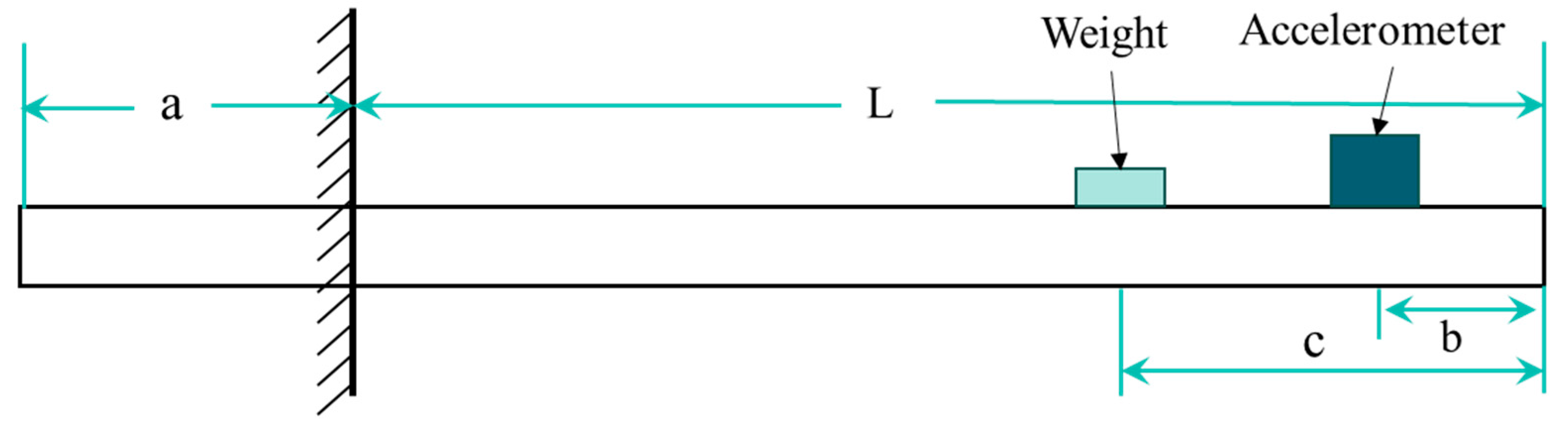



| Condition | L—Free end Length [mm] | a—Length of Fixing [mm] | b—Distance of Accelerometer [mm] | c—Distance of Weight [mm] | Weight [g] | Boundary Condition | Mass Loss [%] |
|---|---|---|---|---|---|---|---|
| 1 | 400 | 0 | 100 | - | 0 | Free-free | - |
| 2 | 300 | 100 | 20 | 60 | 15 | Fixed-free | - |
| 3 | 300 | 100 | 20 | 60 | 7.5 | Fixed-free | 3.7 |
| 4 | 300 | 100 | 20 | - | 0 | Fixed-free | 7.3 |
| 5 | 240 | 160 | 20 | 60 | 15 | Fixed-free | 15.9 |
| Modes | Frequencies Under Free-Free Condition [Hz] | Frequencies Under Fixed-Free Conditions [Hz] | |||
|---|---|---|---|---|---|
| 400 mm Beam | 300 mm Beam with 15 g Weights (Intact) | 300 mm Beam with 7.5 g Weights | 300 mm Beam | 240 mm Beam with 15 g Weights | |
| 1 | 206.8 | 44.0 | 45.2 | 46.6 | 66.7 |
| 2 | 546.5 | 216.0 | 221.7 | 228.4 | 323.8 |
| 3 | 1010.1 | 329.6 | 329.0 | 326.1 | 512.4 |
| 4 | 1068.3 | 693.1 | 718.1 | 714.1 | 850.8 |
| 5 | 1270.1 | 949.0 | 951.0 | 931.3 | 1457.5 |
| 6 | 1768.8 | 1605.5 | 1607.0 | 1609.4 | 2413.6 |
| Mode Number from FEA | FEA Frequencies [Hz] | Exp. Frequencies [Hz] | Relative Difference = (FEA − Exp.)/Exp. [%] |
|---|---|---|---|
| 1 | 206.8 | 208.5 | 0.8 |
| 3 | 546.5 | 540.0 | 1.2 |
| 5 | 1068.3 | 1061.3 | 0.7 |
| Scenario | Mode 3 Frequency [Hz] | Absolute Difference Compared to Intact Case [Hz] | Relative Difference Compared to Intact Case [%] |
|---|---|---|---|
| Intact | 38.8 | - | - |
| No. 1 tooth fully worn | 38.9 | 0.1 | 0.1 |
| No. 2 tooth fully worn | 39.4 | 0.6 | 1.6 |
| No. 3 tooth fully worn | 40.1 | 1.3 | 3.4 |
| All teeth fully worn | 43.4 | 4.5 | 11.7 |
| Sensor Location | Mode 1 | Mode 2 | Mode 3 | Mode 4 | Mode 5 | Mode 6 |
|---|---|---|---|---|---|---|
| A (Tooth 1) | x | x | x | x | x | |
| y | y | y | y | y | ||
| z | z | |||||
| B (Tooth 2) | x | x | x | x | x | |
| y | y | y | y | |||
| z | z | z | ||||
| C (Tooth 3) | x | x | x | x | x | |
| y | y | y | ||||
| z | z | |||||
| G (Midpoint of the right-side wall edge) | x | x | x | x | x | x |
| y | y | y | y | |||
| z | z | z |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.; Rolfe, B.F.; Griffin, J.; Delli Carri, A.; Lu, P.; Pereira, M.P. A Novel Condition Monitoring Technique for Mining Ground Engagement Tools via Modal Analysis. Eng 2025, 6, 220. https://doi.org/10.3390/eng6090220
Chen S, Rolfe BF, Griffin J, Delli Carri A, Lu P, Pereira MP. A Novel Condition Monitoring Technique for Mining Ground Engagement Tools via Modal Analysis. Eng. 2025; 6(9):220. https://doi.org/10.3390/eng6090220
Chicago/Turabian StyleChen, Shasha, Bernard F. Rolfe, James Griffin, Arnaldo Delli Carri, Ping Lu, and Michael P. Pereira. 2025. "A Novel Condition Monitoring Technique for Mining Ground Engagement Tools via Modal Analysis" Eng 6, no. 9: 220. https://doi.org/10.3390/eng6090220
APA StyleChen, S., Rolfe, B. F., Griffin, J., Delli Carri, A., Lu, P., & Pereira, M. P. (2025). A Novel Condition Monitoring Technique for Mining Ground Engagement Tools via Modal Analysis. Eng, 6(9), 220. https://doi.org/10.3390/eng6090220








