Explainable Machine Learning-Based Estimation of Labor Productivity in Rebar-Fixing Tasks
Abstract
1. Introduction
- Addressing a research gap: Introducing a predictive approach tailored specifically to rebar-fixing productivity, an area with limited previous investigation.
- Practical benefits: Providing an objective and accurate tool to support scheduling, resource allocation, and risk management in construction projects.
- Enhanced interpretability: Using SHAP to make model predictions transparent and actionable, encouraging wider adoption of AI-based tools in construction management.
2. Materials and Methods
2.1. Research Methodology
2.2. ML Model Theory
2.2.1. Support Vector Regression (SVR)
2.2.2. Random Forest Regression (RF)
2.2.3. K-Nearest Neighbors (KNN)
2.2.4. Extreme Gradient Boosting (XGBoost)
2.3. Performance Measures
2.4. SHAP Interpretation of the Developed Model
3. Database Used
4. Model Results
4.1. Optimal Model Results
4.2. Regression Slope Analysis
4.3. Statistical Analysis
4.4. Comparison with Traditional ML Models
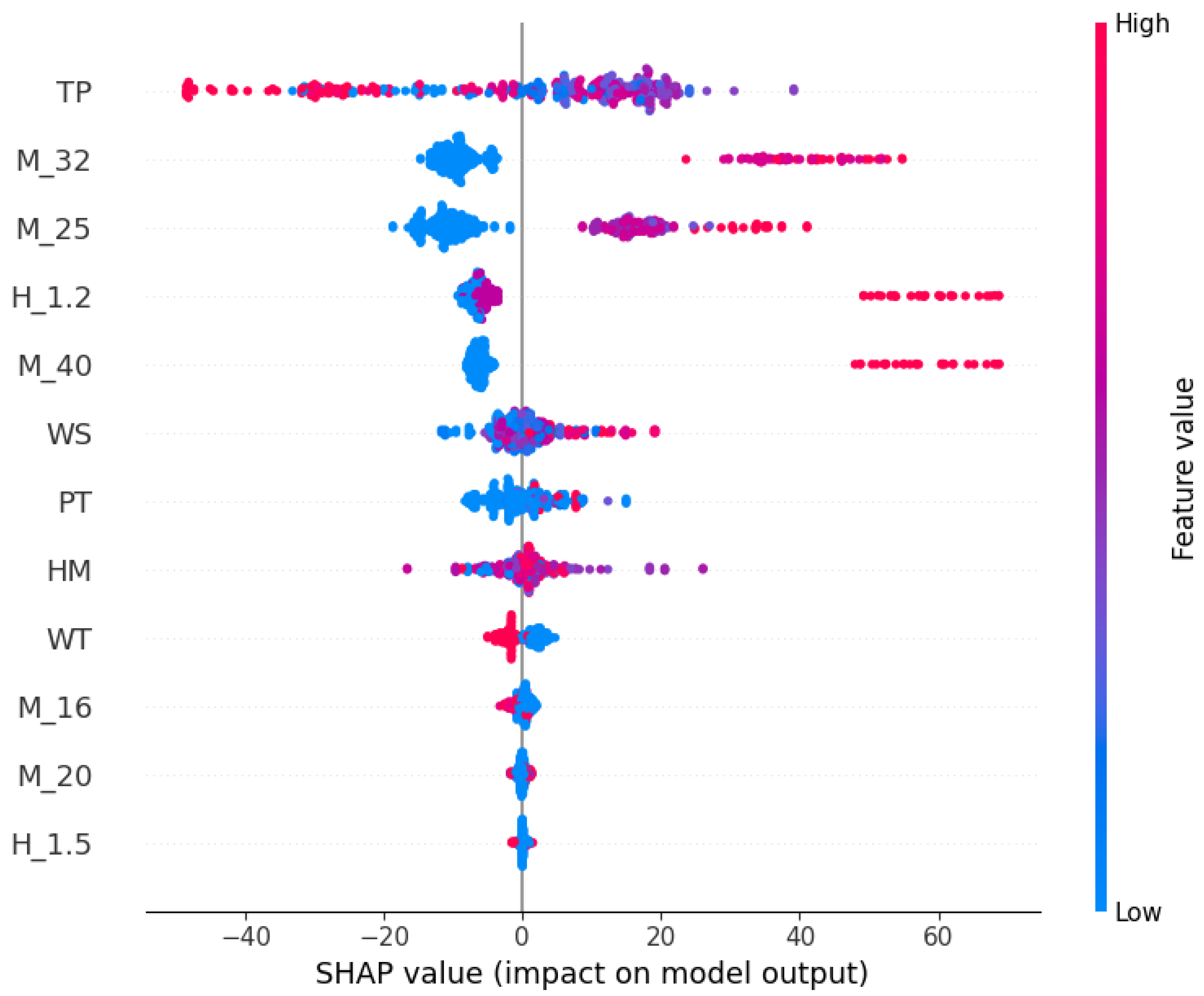
4.5. Feature Importance Analysis
5. Practical Application of Research
6. Limitations and Future Research
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ML | machine learning |
| AI | artificial intelligence |
| SVM | Support Vector Machine |
| SVR | Support Vector Regression |
| KNN | k-Nearest Neighbor |
| RF | Random Forest |
| RMSE | root mean square error |
| MAPE | mean absolute percentage error |
| MAE | mean absolute error |
| R | coefficient of determination |
| SHAP | SHapley Additive exPlanations |
| LASSO | Least Absolute Shrinkage and Selection Operator |
References
- El-Gohary, K.M.; Aziz, R.F.; Abdel-Khalek, H.A. Engineering approach using ANN to improve and predict construction labor productivity under different influences. J. Constr. Eng. Manag. 2017, 143, 04017045. [Google Scholar] [CrossRef]
- Dixit, S.; Mandal, S.N.; Thanikal, J.V.; Saurabh, K. Evolution of studies in construction productivity: A systematic literature review (2006–2017). Ain Shams Eng. J. 2019, 10, 555–564. [Google Scholar] [CrossRef]
- Dixit, S.; Mandal, S.N.; Sawhney, A.; Singh, S. Relationship between skill development and productivity in construction sector: A literature review. Int. J. Civ. Eng. Technol. 2017, 8, 649–665. [Google Scholar]
- Duncan, J.R. Innovation in the Building Sector: Trends and New Technologies; Building Research Association of New Zealand (BRANZ): Porirua, New Zealand, 2002. [Google Scholar]
- Gomar, J.E.; Haas, C.T.; Morton, D.P. Assignment and allocation optimization of partially multiskilled workforce. J. Constr. Eng. Manag. 2002, 128, 103–109. [Google Scholar] [CrossRef]
- Hanna, A.S.; Peterson, P.; Lee, M.J. Benchmarking productivity indicators for electrical/mechanical projects. J. Constr. Eng. Manag. 2002, 128, 331–337. [Google Scholar] [CrossRef]
- Allen, S.G. Why construction industry productivity is declining. Rev. Econ. Stat. 1985, LXVII, 661–669. [Google Scholar] [CrossRef]
- Grau, D.; Caldas, C.H.; Haas, C.T.; Goodrum, P.M.; Gong, J. Assessing the impact of materials tracking technologies on construction craft productivity. Autom. Constr. 2009, 18, 903–911. [Google Scholar] [CrossRef]
- Al-Zwainy, F.M.S.; Rasheed, H.A.; Ibraheem, H.F. Development of the construction productivity estimation model using artificial neural network for finishing works for floors with marble. ARPN J. Eng. Appl. Sci. 2012, 7, 714–722. [Google Scholar]
- Thomas, H.R. Quantification of losses of labor efficiencies: Innovations in and improvements to the measured mile. J. Leg. Aff. Disput. Resolut. Eng. Constr. 2010, 2, 106–112. [Google Scholar] [CrossRef]
- Song, L.; AbouRizk, S.M. Measuring and modeling labor productivity using historical data. J. Constr. Eng. Manag. 2008, 134, 786–794. [Google Scholar] [CrossRef]
- Elshaboury, N.; Al-Sakkaf, A.; Alfalah, G.; Abdelkader, E.M. Improved adaptive neuro-fuzzy inference system based on particle swarm optimization algorithm for predicting labor productivity. In Proceedings of the 2nd International Conference on Civil Engineering Fundamentals and Applications (ICCEFA’21), Virtual, 21–23 November 2021; pp. 21–23. [Google Scholar]
- Cheng, M.Y.; Cao, M.T.; Wu, Y.W. Predicting equilibrium scour depth at bridge piers using evolutionary radial basis function neural network. J. Comput. Civ. Eng. 2015, 29, 04014070. [Google Scholar] [CrossRef]
- Truong, T.T.; Dinh-Cong, D.; Lee, J.; Nguyen-Thoi, T. An effective deep feedforward neural networks (DFNN) method for damage identification of truss structures using noisy incomplete modal data. J. Build. Eng. 2020, 30, 101244. [Google Scholar] [CrossRef]
- Cheng, M.Y.; Wibowo, D.K.; Prayogo, D.; Roy, A.F. Predicting productivity loss caused by change orders using the evolutionary fuzzy support vector machine inference model. J. Civ. Eng. Manag. 2015, 21, 881–892. [Google Scholar] [CrossRef]
- Gong, M.; Bai, Y.; Qin, J.; Wang, J.; Yang, P.; Wang, S. Gradient boosting machine for predicting return temperature of district heating system: A case study for residential buildings in Tianjin. J. Build. Eng. 2020, 27, 100950. [Google Scholar] [CrossRef]
- Saleem, M. Assessing the load carrying capacity of concrete anchor bolts using non-destructive tests and artificial multilayer neural network. J. Build. Eng. 2020, 30, 101260. [Google Scholar] [CrossRef]
- Bilal, M.; Oyedele, L.O.; Qadir, J.; Munir, K.; Ajayi, S.O.; Akinade, O.O.; Owolabi, H.A.; Alaka, H.A.; Pasha, M. Big Data in the construction industry: A review of present status, opportunities, and future trends. Adv. Eng. Inform. 2016, 30, 500–521. [Google Scholar] [CrossRef]
- You, Z.; Wu, C. A framework for data-driven informatization of the construction company. Adv. Eng. Inform. 2019, 39, 269–277. [Google Scholar] [CrossRef]
- Cheng, M.Y.; Cao, M.T.; Mendrofa, A.Y.J. Dynamic feature selection for accurately predicting construction productivity using symbiotic organisms search-optimized least square support vector machine. J. Build. Eng. 2021, 35, 101973. [Google Scholar] [CrossRef]
- Pan, Y.; Zhang, L. Roles of artificial intelligence in construction engineering and management: A critical review and future trends. Autom. Constr. 2021, 122, 103517. [Google Scholar] [CrossRef]
- Fu, J.; Tian, H.; Song, L.; Li, M.; Bai, S.; Ren, Q. Productivity estimation of cutter suction dredger operation through data mining and learning from real-time big data. Eng. Constr. Archit. Manag. 2021, 28, 2023–2041. [Google Scholar] [CrossRef]
- Bzdok, D.; Altman, N.; Krzywinski, M. Points of significance: Statistics versus machine learning. Nat. Methods 2018, 15, 233–234. [Google Scholar] [CrossRef]
- Han, T.; Jiang, D.; Zhao, Q.; Wang, L.; Yin, K. Comparison of random forest, artificial neural networks and support vector machine for intelligent diagnosis of rotating machinery. Trans. Inst. Meas. Control 2018, 40, 2681–2693. [Google Scholar] [CrossRef]
- Ezeldin, A.S.; Sharara, L.M. Neural networks for estimating the productivity of concreting activities. J. Constr. Eng. Manag. 2006, 132, 650–656. [Google Scholar] [CrossRef]
- Kassem, M.; Mahamedi, E.; Rogage, K.; Duffy, K.; Huntingdon, J. Measuring and benchmarking the productivity of excavators in infrastructure projects: A deep neural network approach. Autom. Constr. 2021, 124, 103532. [Google Scholar] [CrossRef]
- Jeong, J.; Jeong, J.; Lee, J.; Kim, D.; Son, J. Learning-driven construction productivity prediction for prefabricated external insulation wall system. Autom. Constr. 2022, 141, 104441. [Google Scholar] [CrossRef]
- Gurmu, A.T.; Ongkowijoyo, C.S. Predicting construction labor productivity based on implementation levels of human resource management practices. J. Constr. Eng. Manag. 2020, 146, 04019115. [Google Scholar] [CrossRef]
- Mahfouz, T. A productivity decision support system for construction projects through machine learning (ml). In Proceedings of the CIB W78 2012: 29th International Conference, Beirut, Lebanon, 17–19 October 2012; Volume 78, p. 2012. [Google Scholar]
- Mady, M. Prediction Model of Construction Labor Production Rates in Gaza Strip Using Artificial Neural Network. Unpublished. Master’s Thesis, The Islamic University of Gaza (IUG), Gaza, Palestine, 2013. [Google Scholar]
- Al-Zwainy, F.M.S.; Abdulmajeed, M.H.; Aljumaily, H.S.M. Using multivariable linear regression technique for modeling productivity construction in Iraq. Open J. Civ. Eng. 2013, 3, 127–135. [Google Scholar] [CrossRef]
- Kaya, M.; Keleş, A.E.; Oral, E.L. Construction crew productivity prediction by using data mining methods. Procedia-Soc. Behav. Sci. 2014, 141, 1249–1253. [Google Scholar] [CrossRef]
- Heravi, G.; Eslamdoost, E. Applying artificial neural networks for measuring and predicting construction-labor productivity. J. Constr. Eng. Manag. 2015, 141, 04015032. [Google Scholar] [CrossRef]
- Ok, S.C.; Sinha, S.K. Construction equipment productivity estimation using artificial neural network model. Constr. Manag. Econ. 2006, 24, 1029–1044. [Google Scholar] [CrossRef]
- Mirahadi, F.; Zayed, T. Simulation-based construction productivity forecast using neural-network-driven fuzzy reasoning. Autom. Constr. 2016, 65, 102–115. [Google Scholar] [CrossRef]
- Nasirzadeh, F.; Kabir, H.D.; Akbari, M.; Khosravi, A.; Nahavandi, S.; Carmichael, D.G. ANN-based prediction intervals to forecast labour productivity. Eng. Constr. Archit. Manag. 2020, 27, 2335–2351. [Google Scholar] [CrossRef]
- Golnaraghi, S.; Zangenehmadar, Z.; Moselhi, O.; Alkass, S. Application of artificial neural network (s) in predicting formwork labour productivity. Adv. Civ. Eng. 2019, 2019, 5972620. [Google Scholar] [CrossRef]
- Jiang, C. Measurement and Estimation of Labor Productivity in Hong Kong Public Rental Housing Projects. Master’s Thesis, The Hong Kong Polytechnic University, Hong Kong, China, 2014. [Google Scholar]
- Bansal, A.; Garg, C.; Hariri, E.; Kassis, N.; Mentias, A.; Krishnaswamy, A.; Kapadia, S.R. Machine learning models predict total charges and drivers of cost for transcatheter aortic valve replacement. Cardiovasc. Diagn. Ther. 2022, 12, 464. [Google Scholar] [CrossRef]
- Fang, C.; Pan, Y.; Zhao, L.; Niu, Z.; Guo, Q.; Zhao, B. A machine learning-based approach to predict prognosis and length of hospital stay in adults and children with traumatic brain injury: Retrospective cohort study. J. Med Internet Res. 2022, 24, e41819. [Google Scholar] [CrossRef]
- Anker, M.; Borsum, C.; Zhang, Y.; Zhang, Y.; Krupitzer, C. Using a machine learning regression approach to predict the aroma partitioning in dairy matrices. Processes 2024, 12, 266. [Google Scholar] [CrossRef]
- Guimarães, T.T.; Veronez, M.R.; Koste, E.C.; Souza, E.M.; Brum, D.; Gonzaga, L., Jr.; Mauad, F.F. Evaluation of regression analysis and neural networks to predict total suspended solids in water bodies from unmanned aerial vehicle images. Sustainability 2019, 11, 2580. [Google Scholar] [CrossRef]
- Wang, B.; Liu, F.; Deveaux, L.; Ash, A.; Gerber, B.; Allison, J.; Herbert, C.; Poitier, M.; MacDonell, K.; Li, X.; et al. Predicting adolescent intervention non-responsiveness for precision hiv prevention using machine learning. AIDS Behav. 2023, 27, 1392–1402. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Sun, J.; Zhang, J.; Gu, Y.; Huang, Y.; Sun, Y.; Ma, G. Prediction of permeability and unconfined compressive strength of pervious concrete using evolved support vector regression. Constr. Build. Mater. 2019, 207, 440–449. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Farhadi, Z.; Bevrani, H.; Feizi-Derakhshi, M.R.; Kim, W.; Ijaz, M.F. An ensemble framework to improve the accuracy of prediction using clustered random-forest and shrinkage methods. Appl. Sci. 2022, 12, 10608. [Google Scholar] [CrossRef]
- Hastie, T. The elements of statistical learning: Data mining, inference, and prediction. J. R. Stat. Soc. Ser. A Stat. Soc. 2009, 173, 693–694. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. Adv. Neural Inf. Process. Syst. 2017, 30. Available online: https://proceedings.neurips.cc/paper_files/paper/2017/file/8a20a8621978632d76c43dfd28b67767-Paper.pdf (accessed on 12 August 2025).
- Li, X.; Chow, K.H.; Zhu, Y.; Lin, Y. Evaluating the impacts of high-temperature outdoor working environments on construction labor productivity in China: A case study of rebar workers. Build. Environ. 2016, 95, 42–52. [Google Scholar] [CrossRef]
- Aldahash, M.; Alshamrani, O.S. Factors Affecting Construction Productivity for Steel Rebar Work in Hot Climate Country. Open Constr. Build. Technol. J. 2022, 16, e187483682206272. [Google Scholar] [CrossRef]
- Jarkas, A.M. The influence of buildability factors on rebar fixing labour productivity of beams. Constr. Manag. Econ. 2010, 28, 527–543. [Google Scholar] [CrossRef]
- Puth, M.T.; Neuhäuser, M.; Ruxton, G.D. Effective use of Pearson’s product–moment correlation coefficient. Anim. Behav. 2014, 93, 183–189. [Google Scholar] [CrossRef]
- Pearson, K.X. On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1900, 50, 157–175. [Google Scholar] [CrossRef]
- Gravier, J.; Vignal, V.; Bissey-Breton, S.; Farre, J. The use of linear regression methods and Pearson’s correlation matrix to identify mechanical–physical–chemical parameters controlling the micro-electrochemical behaviour of machined copper. Corros. Sci. 2008, 50, 2885–2894. [Google Scholar] [CrossRef]
- Iqbal, M.F.; Javed, M.F.; Rauf, M.; Azim, I.; Ashraf, M.; Yang, J.; Liu, Q.f. Sustainable utilization of foundry waste: Forecasting mechanical properties of foundry sand based concrete using multi-expression programming. Sci. Total Environ. 2021, 780, 146524. [Google Scholar] [CrossRef]
- Azim, I.; Yang, J.; Iqbal, M.F.; Mahmood, Z.; Javed, M.F.; Wang, F.; Liu, Q.F. Prediction of catenary action capacity of RC beam-column substructures under a missing column scenario using evolutionary algorithm. KSCE J. Civ. Eng. 2021, 25, 891–905. [Google Scholar] [CrossRef]
- Jalal, F.E.; Xu, Y.; Iqbal, M.; Jamhiri, B.; Javed, M.F. Predicting the compaction characteristics of expansive soils using two genetic programming-based algorithms. Transp. Geotech. 2021, 30, 100608. [Google Scholar] [CrossRef]
- Smith, G.N. Probability and statistics in civil engineering. In Collins Professional and Technical Books; Nichols Publishing Company: New York, NY, USA, 1986; Volume 244. [Google Scholar]
- Sharma, C.; Ojha, C. Statistical parameters of hydrometeorological variables: Standard deviation, SNR, skewness and kurtosis. In Advances in Water Resources Engineering and Management: Select Proceedings of TRACE 2018; Springer: Singapore, 2019; pp. 59–70. [Google Scholar]
- Brown, S.C.; Greene, J.A. The wisdom development scale: Translating the conceptual to the concrete. J. Coll. Stud. Dev. 2006, 47, 1–19. [Google Scholar] [CrossRef]
- Kjellstrom, T.; Holmer, I.; Lemke, B. Workplace heat stress, health and productivity–an increasing challenge for low and middle-income countries during climate change. Glob. Health Action 2009, 2, 2047. [Google Scholar] [CrossRef]
- Sahu, S.; Sett, M.; Kjellstrom, T. Heat exposure, cardiovascular stress and work productivity in rice harvesters in India: Implications for a climate change future. Ind. Health 2013, 51, 424–431. [Google Scholar] [CrossRef]





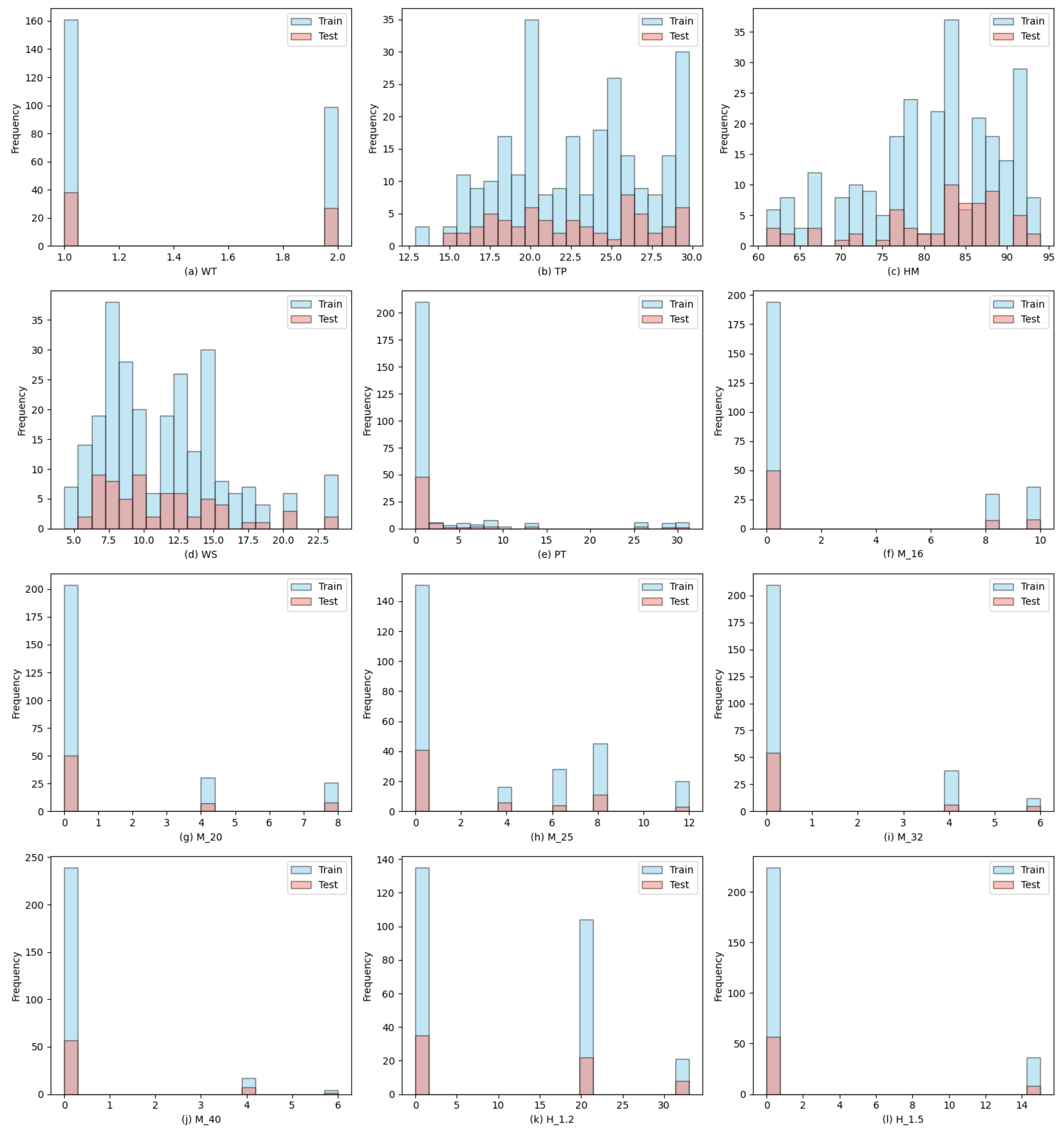



| Variable | Mode | Kurtosis | Min | Max | Mean | Median | Skewness | Range | Std Dev | Std Error |
|---|---|---|---|---|---|---|---|---|---|---|
| WT | 1.00 | −1.79 | 1.00 | 2.00 | 1.39 | 1.00 | 0.46 | 1.00 | 0.49 | 0.03 |
| TP | 20.40 | −1.01 | 12.90 | 29.80 | 22.90 | 22.90 | −0.08 | 16.90 | 4.29 | 0.24 |
| HM | 84.00 | −0.34 | 61.00 | 94.00 | 81.11 | 83.00 | −0.71 | 33.00 | 8.52 | 0.47 |
| WS | 14.60 | 0.36 | 4.30 | 23.90 | 11.36 | 10.90 | 0.82 | 19.60 | 4.25 | 0.24 |
| PT | 0.00 | 7.67 | 0.00 | 31.30 | 2.99 | 0.00 | 2.95 | 31.30 | 7.34 | 0.41 |
| M_16 | 0.00 | −0.45 | 0.00 | 10.00 | 2.26 | 0.00 | 1.21 | 10.00 | 3.97 | 0.22 |
| M_20 | 0.00 | 1.69 | 0.00 | 8.00 | 1.29 | 0.00 | 1.79 | 8.00 | 2.62 | 0.15 |
| M_25 | 0.00 | −0.72 | 0.00 | 12.00 | 3.09 | 0.00 | 0.84 | 12.00 | 4.04 | 0.22 |
| M_32 | 0.00 | 1.57 | 0.00 | 6.00 | 0.86 | 0.00 | 1.79 | 6.00 | 1.82 | 0.10 |
| M_40 | 0.00 | 8.09 | 0.00 | 6.00 | 0.39 | 0.00 | 3.08 | 6.00 | 1.26 | 0.07 |
| H_1.2 | 0.00 | −1.32 | 0.00 | 33.00 | 10.70 | 0.00 | 0.41 | 33.00 | 11.76 | 0.65 |
| H_1.5 | 0.00 | 2.54 | 0.00 | 15.00 | 2.03 | 0.00 | 2.13 | 15.00 | 5.14 | 0.29 |
| LP | 119.19 | 0.40 | 56.66 | 360.60 | 164.75 | 159.16 | 0.74 | 303.94 | 63.71 | 3.53 |
| Model | Hyperparameter | Grid Search Range | Selected Value |
|---|---|---|---|
| Random Forest | (50, 100) | 100 | |
| (None, 10, 20) | 10 | ||
| XGBoost | (50, 100) | 50 | |
| (0.01, 0.1, 0.2) | 0.1 | ||
| (3, 6, 10) | 3 | ||
| SVR | {rbf, linear} | linear | |
| C | (0.1, 1, 10) | 10 | |
| (0.01, 0.1, 0.5) | 0.5 | ||
| KNN | (3, 5, 7) | 3 | |
| {uniform, distance} | uniform | ||
| {minkowski, euclidean, manhattan} | minkowski |
| Indicator | RF | XGBoost | SVR | KNN |
|---|---|---|---|---|
| Training | ||||
| MAE | 12.494 | 18.538 | 26.073 | 17.928 |
| RMSE | 19.943 | 26.881 | 37.355 | 26.265 |
| 0.901 | 0.821 | 0.654 | 0.829 | |
| MAPE | 9.12% | 13.96% | 18.37% | 13.81% |
| A20-index | 0.8615 | 0.7769 | 0.7000 | 0.8192 |
| Testing | ||||
| MAE | 16.654 | 17.422 | 21.814 | 18.840 |
| RMSE | 22.260 | 22.472 | 28.706 | 24.938 |
| 0.874 | 0.872 | 0.791 | 0.842 | |
| MAPE | 10.98% | 11.68% | 13.57% | 12.11% |
| A20-index | 0.8308 | 0.8308 | 0.7692 | 0.8000 |
| Indicator | Lasso | Decision Tree | Random Forest |
|---|---|---|---|
| MAE | 22.557 | 21.237 | 16.696 |
| RMSE | 28.233 | 28.019 | 22.501 |
| 0.798 | 0.801 | 0.872 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taha, F.F.; Ahmed, M.A.; Aldhamad, S.H.R.; Imran, H.; Bernardo, L.F.A.; Nepomuceno, M.C.S. Explainable Machine Learning-Based Estimation of Labor Productivity in Rebar-Fixing Tasks. Eng 2025, 6, 219. https://doi.org/10.3390/eng6090219
Taha FF, Ahmed MA, Aldhamad SHR, Imran H, Bernardo LFA, Nepomuceno MCS. Explainable Machine Learning-Based Estimation of Labor Productivity in Rebar-Fixing Tasks. Eng. 2025; 6(9):219. https://doi.org/10.3390/eng6090219
Chicago/Turabian StyleTaha, Farah Faaq, Mohammed Ali Ahmed, Saja Hadi Raheem Aldhamad, Hamza Imran, Luís Filipe Almeida Bernardo, and Miguel C. S. Nepomuceno. 2025. "Explainable Machine Learning-Based Estimation of Labor Productivity in Rebar-Fixing Tasks" Eng 6, no. 9: 219. https://doi.org/10.3390/eng6090219
APA StyleTaha, F. F., Ahmed, M. A., Aldhamad, S. H. R., Imran, H., Bernardo, L. F. A., & Nepomuceno, M. C. S. (2025). Explainable Machine Learning-Based Estimation of Labor Productivity in Rebar-Fixing Tasks. Eng, 6(9), 219. https://doi.org/10.3390/eng6090219









