Abstract
An Analog-to-Digital Converter (ADC) is an indispensable part of image sensor systems. This paper presents a silicon-based 13-bit 100 kS/s two-step single-slope analog-to-digital converter (TS-SS ADC) for infrared image sensors with a frame rate of 100 Hz. For the charge leakage and offset voltage issues inherent in conventional TS-SS ADC, a four-terminal comparator was employed to resolve the fine ramp voltage offset caused by charge redistribution in storage and parasitic capacitors. In addition, a current-steering digital-to-analog converter (DAC) was adopted to calibrate the voltage reference of the dynamic comparator and mitigate differential nonlinearity (DNL)/integral nonlinearity (INL). To eliminate quantization dead zones, a 1-bit redundancy was incorporated into the fine quantization circuit. Finally, the quantization scheme consisted of 7-bit coarse quantization followed by 7-bit fine quantization. The ADC was implemented using an SMIC 55 nm processSemiconductor Manufacturing International Corporation, Shanghai, China. The post-simulation results show that when the power supply is 3.3 V, the ADC achieves a quantization range of 1.3 V–3 V. Operating at a 100 kS/s sampling rate, the proposed ADC exhibits an effective number of bits (ENOBs) of 11.86, a spurious-free dynamic range (SFDR) of 97.45 dB, and a signal-to-noise-and-distortion ratio (SNDR) of 73.13 dB. The power consumption of the ADC was 22.18 mW.
1. Introduction
The primary function of an image sensor is to convert the captured scene into storable electrical signals. Its operation consists of two main phases: photoelectric conversion and ADC quantization. Based on the intensity of incident light, the optical signal collected on the photosensitive surface is converted into a corresponding voltage signal. This voltage is then processed through correlated double sampling (CDS) to produce a refined analog signal, which is subsequently quantized by the ADC to generate discrete digital output. In infrared image systems, ADC serves as a key component for digitizing photoelectric signals. Its conversion accuracy and efficiency have a direct impact on the data acquisition speed and the quality of image reconstruction. Currently, image sensors primarily adopt three kinds of ADC structures: single-channel ADC, column-parallel ADC and pixel-level ADC [1]. The parallel structure of column-parallel ADC makes its speed superior to single-channel ADC and enables multi-channel parallel analog-to-digital conversion across the pixel array. The off-pixel quantization structure of the column-parallel ADC makes its design complexity lower than the pixel-level ADC. A column-parallel ADC becomes the mainstream structure in modern image sensor applications. Column-parallel ADC contains various structures, and the structures applied to image sensors are successive approximation register (SAR) ADC, cyclic ADC, and single-slope (SS) ADC. The SAR ADC features a simple structure and low power consumption. It completes an N-bit quantization in N clock cycles [2]. However, increasing the resolution by one bit doubles the number of switches and capacitors required, which results in a significant area overhead. The cyclic ADC, similar to the SAR ADC, also requires N clock cycles for N-bit quantization. Without large capacitors, the cyclic ADC occupies less area [3]. However, the high-gain operational amplifiers of cyclic ADC lead to higher power consumption. Compared with cyclic ADC and SAR ADC, the SS ADC benefits from its simple structure, low power consumption, small area, and the ability of the slope generator to generate high-resolution and high-linearity ramp signals. However, it requires 2N clock cycles to complete N-bit quantization, which significantly limits its conversion speed [4].
To address the limited conversion speed of SS ADC, two-step structures based on a single slope have been proposed. The most common include multiple-ramp single-slope (MRSS) ADC and two-step single-slope (TS-SS) ADC. Reference [5] proposed an MRSS ADC that utilizes a coarse ramp generator to perform high 3-bit quantization and fine ramp generators operating at different voltage to perform low 8-bit quantization. Although this structure significantly improves conversion speed, there are issues with voltage range misalignment and power consumption. Reference [6] introduced a TS-SS ADC that integrates coarse and fine quantization, which utilizes a sample-and-hold capacitor to store coarse quantization results. This structure implements 5-bit quantization with a coarse ramp generator and a 6-bit quantization with fine ramp generator. An additional redundant bit is included. This design addresses the power issue of MRSS ADC but remains sensitive to parasitic capacitance, which may lead to voltage shifting during fine quantization and create quantization dead zones. Reference [7] employed a four-input comparator in TS-SS ADC to separate the high 7-bit coarse quantization and low 8-bit fine quantization. This structure avoids signal mismatch between coarse and fine ramps and prevents degradation of the fine ramp slope. Despite these advantages, the resolution remains a major limitation. Reference [8] applied the Look-Up-Table (LUT) calibration technique to TS-SS ADC. This approach corrects parasitic capacitance errors and improves linearity. After calibration, the ENOB of SS ADC improves from 6-bit to 11.77-bit. Reference [9] applied a multi-column shared capacitor DAC to TS-SS ADC, which significantly reduces the area constraints imposed by column pitch. However, this structure still faces limitations in speed and increased control complexity. Reference [10] proposed a TS-SS ADC with a detachable DAC. A high-linearity coarse ramp signal is generated by the DAC, and this design achieves an INL of −0.89/+1.04 LSB and a DNL of −0.67/+0.91 LSB. Nevertheless, it still suffers from charge injection errors and limited system integration. Reference [11] implemented 14-bit quantization using a two-step ADC based on a 7-bit capacitor array. DAC is employed to adjust the reference voltage, which can enhance resolution. After calibration, the SNDR improved from 73.41 dB to 81.52 dB. However, the increase in resolution came at the cost of higher circuit complexity and reduced stability. Reference [12] integrated a variable gain amplifier (VGA) into a hybrid SAR-SS ADC. In this design, the SS ADC performs 3-bit quantization, and only 8-bit SAR ADC is required to achieve an ENOB of 11-bit. Unfortunately, the introduction of redundant bits leads to an inherent error of 1.5 LSB, and the D-flip-flop scanning scheme accounts for 45% of the total power consumption. Moreover, the dynamic range is limited to 58.3 dB. Reference [13] eliminated the use of the hold capacitor to reduce the load on ramp generators, which minimizes errors caused by mismatch and offset between fine ramps. During the coarse quantization phase, the coarse quantization switch is immediately turned off once the comparator completes the comparison of the 4-bit counter. As a result, the power consumption is only 90 μW, whereas the resolution is 12-bit. However, gain mismatch between the coarse and fine ramps leads to periodic fluctuations in DNL, and the area of the control logic limits the scalability of the coarse quantization resolution. Reference [14] introduced error feedback into noise-shaping ADC. This design uses a second-order switched-capacitor FIR filter and a charge-sharing technique to achieve optimized complex zeros and robust second-order noise shaping. Although it attains an ENOB of 12.83, the design also faces challenges such as increased design complexity and limited system flexibility. Reference [15] proposed a multi-slope column-parallel ADC that enhances conversion speed and introduces compression characteristics through multiple reference slopes. This structure significantly improves the performance-to-power ratio of CMOS image sensors but also presents challenges in control complexity and slope error management. Reference [16] proposed a high-precision, low-area-overhead calibration circuit to address the current ratio mismatch in Dual-Ramp Single Slope (DRSS) ADC. Through structural optimizations, such as the reset scheme, switch isolation, and auto-zero comparator, the design significantly enhances DNL performance. However, the calibration logic falls under foreground calibration, which lacks the ability to dynamically adapt online. As a result, it exhibits limited real-time adaptability to variations caused by temperature drift, aging, or bias drift. Reference [17] employed a pre-comparator to divide pixel signals into small- and large-signal regions. When quantizing large pixel signals, the TS-SS ADC enters an accelerated mode and significantly enhances conversion speed through differential ramping. However, this approach incurs additional circuit area and power consumption, which may constrain large-scale integration in high-resolution arrays.
Compared with MRSS ADC, TS-SS ADC stores the intermediate voltage of coarse quantization by sample capacitors and implements low-bit conversion with a single fine ramp generator. This optimized design preserves the accuracy advantages of multi-level quantization and addresses the issues of area and power consumption. However, charge leakage through the coarse ramp switch during quantization can cause errors on the storage capacitor plate, thus affecting fine quantization. However, the coarse ramp switch will cause charge leakage during quantization. Charge leakage can introduce errors on the storage capacitor plate and consequently affect fine quantization. To address this issue, this paper grounds the bottom plate of the storage capacitor to prevent quantization errors caused by charge leakage. Compared with a traditional two-step ADC that requires an exponentially increasing number of parallel comparators or capacitor arrays in coarse quantization, the proposed TS-SS ADC employs two structurally similar ramp generators for coarse and fine quantization separately, which effectively reduces area and power consumption.
Infrared image sensors are widely employed in applications such as night vision imaging, thermal monitoring, medical diagnostics, and environmental perception. The output signals from these sensors typically exhibit low signal-to-noise ratios, small amplitudes, and significant temperature drift, which impose more stringent requirements on ADC in terms of resolution, linearity, and offset tolerance. Particularly in long-range detection or weak signal imaging scenarios, enhanced ADC resolution contributes to a broader grayscale dynamic range and significantly improves the visibility of subtle targets and the robustness of subsequent image recognition. To address the high-precision sampling demands in infrared imaging, this paper presents a design of ADC based on a Two-Step Signal-Slope structure. The proposed ADC is implemented using the SMIC 55 nm process. It employs a four-terminal comparator instead of the conventional differential comparator to enable the separation of coarse and fine quantization stages. This structure effectively mitigates the issue of fine ramp voltage offset caused by charge redistribution between sample capacitors and parasitic capacitances. In addition, a current-steering DAC is integrated to dynamically calibrate the reference voltage of the dynamic comparator. This calibration approach helps to suppress the offset voltages induced by switch nonlinearity and device mismatches, while simultaneously improving the overall performance by reducing both DNL and INL errors.
2. Circuit Design
The proposed TS-SS ADC targets a 13-bit + 1-bit quantization resolution and features three distinct quantization schemes, as detailed in Table 1. When the “7 + 7” quantization scheme is selected, it achieves the minimal cycle count and optimal conversion speed.

Table 1.
Comparison of cycle numbers for different quantization schemes.
The block diagram of the proposed TS-SS ADC is shown in Figure 1. The ADC mainly consists of the following blocks: a sample-and-hold circuit, coarse/fine ramp generators, the DAC, a four-input comparator, and digital logic units. The operational principle is that the sample-and-hold circuit converts analog signal into a sampled VS and applies it to the negative input of comparator VIN. The coarse ramp generator produces a coarse ramp voltage VRAMP_C, stores it in CH, and applies it to the positive input of comparator VCIP. The comparator compares VIN and VCIP. When VCIP exceeds VIN, the comparator inverts and the coarse quantization is completed. The coarse quantization result is stored in latch. Then, the fine ramp generator produces a fine ramp voltage VRAMP_F and applies it to the positive input of comparator VFIP. The comparator compares VIN and VFIP and the result is also stored in latch. Finally, the quantization results are output through the digital logic circuit.
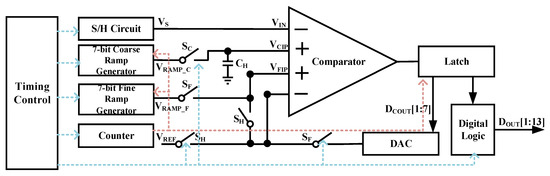
Figure 1.
The structure of the proposed TS-SS ADC.
2.1. Quantization Scheme
Sampling reset phase: Switches SC and SH are turned on. The coarse ramp voltage VRAMP_C is connected to VCIP through switch SC and serves as the initial quantization voltage. The reference VREF is connected to VFIP through switch SH. At this time, the comparator output is low, and the input VIN is as follows:
Coarse quantization phase: The states of switches remain unchanged. The sampled voltage VS and coarse ramp voltage VRAMP_C are fed into the comparator for comparison. At this time, VRAMP_C jumps in steps of value I, with each step corresponding to a voltage VRAMP_C[i]. The input of the comparator is as follows:
When VIN > 0, the comparator output switches from low to high, and the switch SC turns off. The latch stores the binary code from the coarse quantization counter. Irrespective of the parasitic effect in the storage capacitor and charge injection from the coarse quantization switch SC, the voltage across CH is as follows:
where m is the step of the coarse ramp, M is the coarse quantization resolution, and VFS is the full-scale voltage.
Fine quantization phase: Switches SC and SH turn off. Switch SF turns on. Each step of the fine ramp corresponds to a voltage of VRAMP_F[i], as follows:
As step i increases, VIN increases. When VIN > 0, the comparator flips. The binary code of the counter is taken as the fine quantization result.
Output results: Due to the inclusion of the redundancy bit, the coarse and fine quantization results cannot be directly added together. Instead, the results need to be processed through addition and subtraction. As shown in Figure 2, the coarse and fine quantization results are transferred from latches to an adder for summation. The first bit of coarse quantization and the seventh bit of fine quantization are added to obtain DOUT [1:13]. Since fine quantization has been extended from 6-bit to 7-bit, a fixed offset of 27 must be subtracted by a subtractor to obtain the final binary code DOUT [1:13] corresponding to the analog signal.

Figure 2.
Quantization data processing of the proposed TS-SS ADC.
Error analysis and improvement: As observed in the coarse quantization phase, parasitic effects in the storage capacitor CH and the charge injection caused by SC will change the voltage across CH, which results in deviation of the coarse quantization result. Assuming W and L are the width and length of switch SC, m is the coarse quantization result, δ is the proportion of charge injected into the capacitor, and the amount of charge injected into CH by switch SC is as follows:
The voltage variation across CH caused by the charge is as follows:
To ensure the performance of the proposed ADC, must be less than 0.5 LSB.
Combining with Equation (3), the voltage of the storage capacitor CH increases from to . It can be seen that is related to m. Taking the derivative with respect to m, we obtain the following:
According to Equation (8), and m have a linear relationship. To mitigate the impact caused by the charge injection of , a current-steering DAC is designed to dynamically compensate for the variation of . After considering the error introduced by SC, the input of the comparator during the fine quantization phase can be corrected as follows:
To ensure that the input of the comparator during the fine quantization phase matches the ideal condition,
This paper employs three DACs to achieve the elimination of . The specific structure is shown in Figure 3. The top DAC and the bottom DAC receive a 6-bit binary code to generate VH and VL, respectively, which serve as the voltage inputs of 7-bit DACs. The coarse quantization binary code DCOUT [1:7] is input into the 7-bit DAC, and the calibrated VDAC is finally obtained.
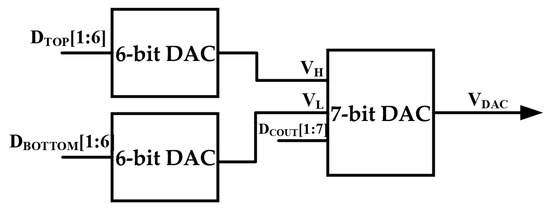
Figure 3.
The structure of the current-steering DAC.
Assuming N is the number of DAC bits, that is, the number of coarse quantization bits, and D is the decimal value corresponding to the DAC input binary code, then the DAC output expression is as follows:
The output expression of the top DAC is as follows:
Then:
Therefore, the DAC output expression can also be written as follows:
Combining with Equation (10), it only requires the following:
When DTOP and DBOTTOM are in the default state of 100,000, VDAC = VREF. During circuit operation, the offset can be eliminated by adjusting the code values of DTOP and DBOTTOM.
2.2. Sample-and-Hold Circuit
The structure of the sample-and-hold circuit is shown in Figure 4. This structure mainly consists of a gate-boosted switch, a sampling capacitor, an operational amplifier, and other switches. The operation is divided into two main phases: the sampling phase and the hold phase.
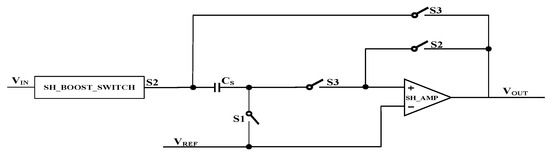
Figure 4.
The structure of the sample-and-hold circuit.
Sampling phase: Switches S1 and S2 are turned on, while S3 is turned off. The circuit is equivalent to a first-order RC circuit. The voltage across the sampling capacitor is VIN, and the charge stored on CS is as follows:
Hold phase: Switches S1 and S2 are turned off, and S3 is turned on. The left plate of the sampling capacitor CS is connected to the output of the operational amplifier, and node X is the positive input of the amplifier. According to charge conservation, we obtain the following:
The output voltage of the hold phase is as follows:
2.3. Coarse Ramp Generator
The coarse ramp generator is shown in Figure 5. It mainly consists of top and bottom clamp amplifiers, a resistor array, a decoder, and an output buffer. The two clamp amplifiers are used to define the top and bottom voltages of the ramp generator, corresponding to VH_3 and VL_1.3. The resistor array divides the voltage, whereas the output buffer enhances the driving capability. The decoder outputs different logic states, resulting in different voltage outputs from the resistor array.
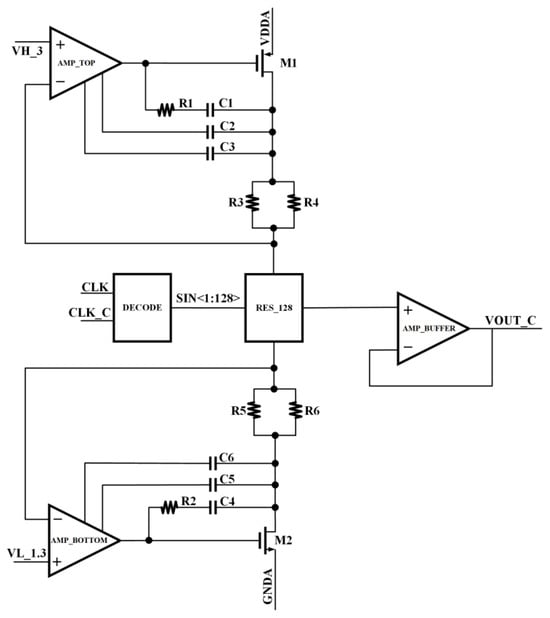
Figure 5.
The structure of the coarse ramp generator.
The top and bottom clamp amplifiers and their respective output transistors form a three-pole system. To ensure that the output ramp signal remains free of oscillation, the stability of both the top and bottom feedback loops must be maintained. Taking the top loop as an example, the system adopts a nested Miller compensation scheme. The unity-gain bandwidth and the second and third pole frequencies are, respectively:
To ensure sufficient phase margin of the loop, the second and third pole frequencies should be placed as far away from the GBW (Gain Bandwidth) as possible. The second pole is set at four times the GBW, whereas the third pole is set at eight times the GBW, as follows:
Since the dominant pole located at the GBW already contributes 90° of phase shift, the phase margin (PM) can be expressed as follows:
Combining Equations (23) and (24), the phase margin is approximately 69°, which meets the stability requirements.
2.4. Fine Ramp Generator
The structure of the fine ramp generator is shown in Figure 6. Considering the redundancy bit, the quantization resolution of the fine ramp generator is also 7-bit. Its structure is similar to the coarse ramp generator and includes top and bottom clamp amplifiers, a resistor array, a decoder, and an output buffer.
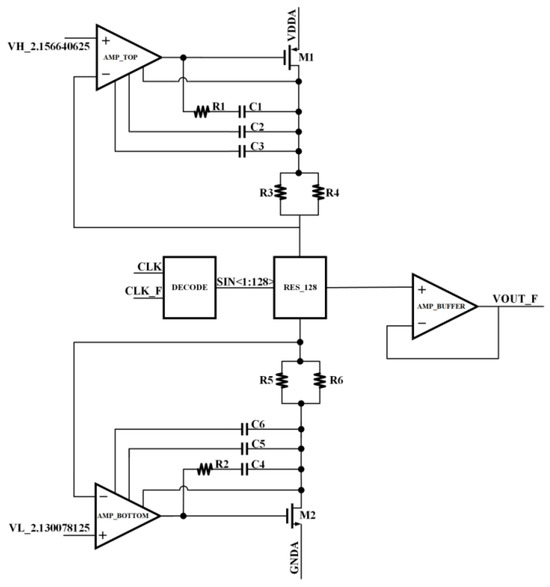
Figure 6.
The structure of the fine ramp generator.
The voltage quantization range of the fine ramp is 2ΔVC. With VREF = 2.15 V, the quantization interval was determined to range from 2.130078125 V to 2.156640625 V. The small quantization voltage implies that the current flowing through transistors M1 and M2 is small and results in low transconductance in the top and bottom clamp amplifiers, which does not meet the stability of the upper and lower feedback loops. Therefore, compared to the coarse ramp generator, an additional current source was added inside each clamping amplifier in the fine ramp generator and was connected to the external path to improve stability.
2.5. Comparator
The proposed TS-SS ADC performs two comparison operations in each quantization cycle, corresponding to the coarse and fine quantization phases. The structure of the four-input comparator is shown in Figure 7, which consists of a preamplifier, a dynamic comparator, and an output buffer. The two-stage preamplifier amplifies the input and reduces the impact of latch offset. The dynamic comparator carries out the comparison operation. The output buffer enhances driving capability and isolates load interference to ensure reliable output.

Figure 7.
The structure of the four-input comparator.
To reduce the impact of comparator offset and suppress kickback noise, a two-stage cascaded preamplifier structure was adopted. The first-stage preamplifier is shown in Figure 8.
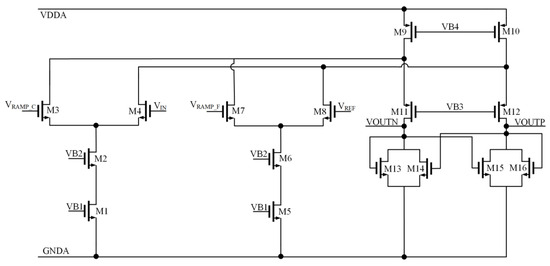
Figure 8.
The structure of the first-stage preamplifier.
The preamplifier splits the differential input pair into two paths. During the first comparison, only the coarse ramp voltage VRAMP_C and the input voltage VIN are processed by the first-stage preamplifier. The output voltage of the first-stage preamplifier is as follows:
During the second comparison, only the fine ramp voltage VRAMP_F and the reference voltage VREF are fed into the first-stage preamplifier. The output voltage of the first-stage preamplifier is as follows:
where m is the coarse quantization result and ΔVC is the voltage corresponding to each step of coarse quantization.
As shown in Figure 8, the folded input structure achieves a wide input common-mode range. A constant bias provides the tail current to ensure stable operation with different inputs. The cross-coupled structure forms positive feedback to increase transconductance. The gain of the first-stage preamplifier is as follows:
The second-stage preamplifier consists of a differential operational amplifier with cross-coupled PMOS transistors as the load. The total gain of the preamplifiers is the product of the gains of the two stage preamplifiers.
The dynamic comparator is shown in Figure 9. Controlled by the clock signal CLK, the operation of the dynamic comparator is divided into a reset and comparison phase. When CLK is low, the comparator is in the reset state. M6 and M9 are turned on, pulling VOUTP and VOUTN up to VDDA. When M1 is off, there is no current path from the power supply to ground and this results in no power consumption. When CLK is high, the comparator is in the comparison state. M6 and M9 are turned off, and the currents in the M2 and M3 branches are determined by the input voltages VIP and VIN. When VIP is greater than VIN, the current in branch M2 exceeds that in branch M3. As a result, the source voltage of M4 drops faster than that of M5 and creates a voltage difference ΔV. This voltage difference is continuously amplified by the positive feedback formed by the cross-coupled inverters. When the VOUTN is eventually pulled to GNDA and VOUTP is pulled to VDDA, the comparison completes. When VIN is greater than VIP, the current in branch M3 exceeds that in M2. A voltage difference of -ΔV is formed between the source of M4 and M5. This voltage difference is continuously amplified by positive feedback. Finally, the VOUTN is pulled to GNDA and VOUTP is pulled to VDDA.
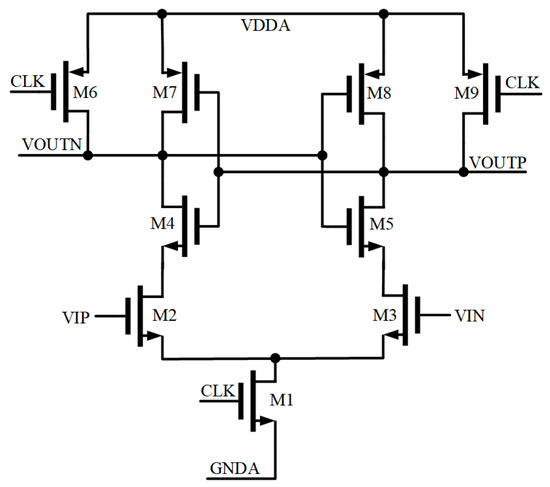
Figure 9.
The structure of the dynamic latch comparator.
3. Post-Simulation Results
The proposed design is implemented using the SMIC 55 nm process. The layout of the TS-SS ADC is shown in Figure 10, with an overall area of 0.942 mm2.

Figure 10.
Layout of the TS-SS ADC.
To eliminate the influence of non-ideal factors, an ideal DAC was connected to the output of the TS-SS ADC during simulation. The ideal DAC restores the quantized binary code of ADC to analog signals. Under the typical–typical (TT) process corner, with a full-scale input amplitude of 1.7 V, Fast Fourier Transforms (FFTs) are performed on the output of the proposed TS-SS ADC. The output spectrum is shown in Figure 11 and is based on 4096 sampling points. The results show that the proposed TS-SS ADC achieves an ENOB of 11.86 bits, an SNDR of 73.13 dB, and an SFDR of 97.45 dB with different input frequencies.
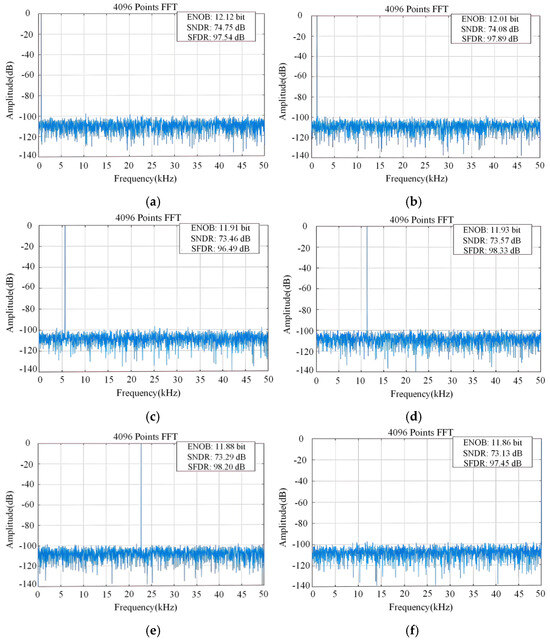
Figure 11.
Output signal spectrum diagram. (a) fin = 610 Hz; (b) fin = 1.19 kHz; (c) fin = 5.59 kHz; (d) fin = 11.3 kHz; (e) fin = 23.1 kHz; and (f) fin = 49.6 kHz.
As shown in Figure 12, under the TT process corner and with an input frequency of 25 kHz, the performance at different input amplitudes was evaluated. The input amplitude started at 0 dBFS and decreased in steps of 10 dBFS. The results show that as the input amplitude decreases, the signal power Psignal also decreases, which leads to a reduction in both SNDR and SFDR. Since ENOB is proportional to SNDR, when SDNR decreases, ENOB decreases accordingly.
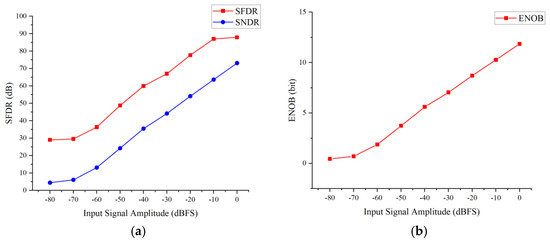
Figure 12.
Performance comparison of the proposed TS-SS ADC at different input amplitudes. (a) The relationship between SFDR/SNDR and input amplitude; (b) the relationship between ENOB and input amplitude.
As shown in Figure 13, under the TT process corner and with a full-scale input amplitude of 1.7 V, the performance of the proposed TS-SS ADC at different input frequencies was evaluated. The results indicate that as the input signal frequency increases, the ENOB, SNDR, and SFDR show a general downward trend, and the decline is relatively small. The primary reason for this degradation is the limited bandwidth of operational amplifiers in the sample-and-hold circuit, ramp generators, and the comparator. As the input frequency increases, the gain of amplifiers decreases, which degrades signal settling accuracy and ultimately reduces SFDR. High-frequency signals exhibit rapid variations and sampling errors, and hold clamping errors are induced in the sample-and-hold circuit. These errors will cause deviation in the sampled value and a reduction in both SNDR and ENOB. The reason for small performance degradation is that the TS-SS ADC provides sufficient bandwidth to ensure adequate charge and discharge time even at higher input frequencies. Furthermore, a dynamic comparator with an adequate margin was adopted, which prevents erroneous comparisons even under faster input frequencies.
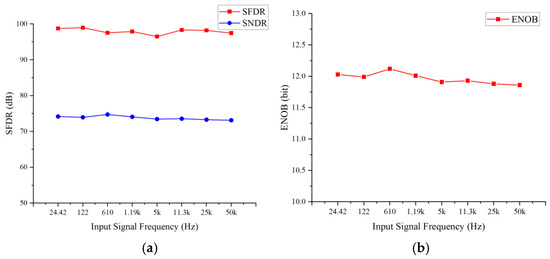
Figure 13.
Performance comparison of the proposed TS-SS ADC at different input frequencies. (a) The relationship between SFDR/SNDR and input frequency; (b) the relationship between ENOB and input frequency.
As shown in Figure 14, the performance under different process corners was evaluated, with an input amplitude of 1.7 V and a frequency of 25 kHz. The results indicate that under the FF process corner, the proposed TS-SS ADC exhibits lower ENOB, SNDR, and SFDR. This degradation is attributed to the reduced threshold voltage and increased carrier mobility of MOS transistors in the FF corner, which results in faster switching and a higher current, thereby intensifying kickback noise. Kickback noise interferes with the analog voltage held on the sampling capacitor, which may introduce errors and reduce SNDR and ENOB. Furthermore, kickback noise may cause nonlinear charge injection, which leads to increased higher-order harmonics and reduced SFDR.
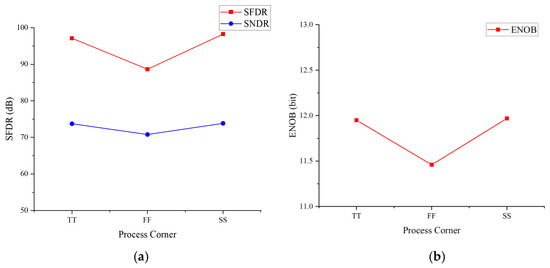
Figure 14.
Dynamic performance of the proposed TS-SS ADC under different process corners: (a) the relationship between SFDR/SNDR and the process corners; (b) the relationship between ENOB and the process corners.
The comparison results with others are shown in Table 2. The proposed design achieves higher resolution, which enhances the system’s dynamic range and noise immunity. In addition, this design offers a wider quantization range and faster conversion speed, which can better meet the requirements of the front-end readout circuit for full well capacity and support high bandwidth, high dynamic range, and low latency signal processing. However, the use of a four-terminal comparator in this paper results in relatively high power consumption, which in turn leads to a Figure of Merit (FoM) significantly larger than other designs.

Table 2.
Performance comparison.
4. Conclusions
To ensure high performance of infrared image sensors, it is critical to develop high resolution and low power ADCs. Among various column-parallel ADC structures, the SS ADC has been widely adopted due to its simple structure, low power consumption, and small area. However, the conversion speed of the SS ADC is fundamentally limited by the exponential growth of clock cycles (2N), which makes them unsuitable for high-frame-rate applications. The TS-SS ADC improves conversion speed by dividing the quantization process into coarse and fine phases. This structure reduces the scale of the capacitor array and switching energy to reduce both power consumption and area overhead. The TS-SS ADC demonstrates strong advantages in large-scale pixel arrays.
In this paper, a column-parallel TS-SS ADC was proposed for infrared image sensors with a frame rate of 100 Hz. This ADC was realized using the SMIC 55 nm process with a supply voltage of 3.3 V. The post-simulation results show that with a full-scale amplitude of 1.7 V, the proposed TS-SS ADC achieves an ENOB of 11.86-bit, an SNDR of 73.13 dB, and an SFDR of 97.45 dB at the Nyquist frequency. Although the proposed TS-SS ADC exhibits relatively high power consumption, it remains suitable for infrared imaging sensor systems that demand both high speed and high precision. Moreover, it provides a feasible solution for the future design of high-performance column-level ADCs.
Author Contributions
Conceptualization, Q.G. and W.L.; software simulation and parameter optimization, Q.G., W.L., W.Z., E.Y. and Z.C.; data processing, E.Y. and Z.C.; writing—original draft preparation, Q.G., W.L. and W.Z.; writing—review and editing, C.C.; Supervision, C.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Foundation of Fujian Province (2023H0052), major science and technology projects of Xiamen (3502Z20221022), and the National Natural Science Foundation of China (6247011759).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Lyu, T.; Yao, S.; Nie, K.; Xu, J. A 12-Bit High-Speed Column-Parallel Two-Step Single-Slope Analog-to-Digital Converter (ADC) for CMOS Image Sensors. Sensors 2014, 14, 21603–21625. [Google Scholar] [CrossRef] [PubMed]
- McCreary, J.L.; Gray, P.R. All-MOS charge redistribution analog-to-digital conversion techniques. I. IEEE J. Solid-State Circuits 1975, 10, 371–379. [Google Scholar] [CrossRef]
- Decker, S.; McGrath, D.; Brehmer, K.; Sodini, C.G. A 256/spl times/256 CMOS imaging array with wide dynamic range pixels and column-parallel digital output. IEEE J. Solid-State Circuits 1998, 33, 2081–2091. [Google Scholar] [CrossRef]
- Allen, P.E.; Holberg, D.R. CMOS Analog Circuit Design; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- Snoeij, M.F.; Theuwissen, A.J.P.; Huijsing, J.H.; Makinwa, K.A.A. Power and Area Efficient Column-Parallel ADC Architectures for CMOS Image Sensors. In Proceedings of the 2007 IEEE Sensors, Atlanta, GA, USA, 28–31 October 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 523–526. [Google Scholar] [CrossRef]
- Lim, S.; Lee, J.; Kim, D.; Han, G. A High-Speed CMOS Image Sensor with Column-Parallel Two-Step Single-Slope ADCs. IEEE Trans. Electron Devices 2009, 56, 393–398. [Google Scholar] [CrossRef]
- Bae, J.; Kim, D.; Ham, S.; Chae, Y.; Song, M. A Two-Step A/D Conversion and Column Self-Calibration Technique for Low Noise CMOS Image Sensors. Sensors 2014, 14, 11825–11843. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.; Zhang, Q.; Li, J.; Zhang, Z.; Deng, H.; Ning, N.; Yu, Q. A Calibration Technique for Two-Step Single-Slope Analog-to-Digital Converter. In Proceedings of the 2019 IEEE 13th International Conference on ASIC (ASICON), Chongqing, China, 29 October–1 November 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Zhang, H.; Fang, Z.; Yu, N.; Lv, N.; Guo, Z. A Column-parallel SAR/SS ADC with Multi-Column Shared Capacitor DAC for CMOS Image Sensor. In Proceedings of the 2022 IEEE 16th International Conference on Solid-State & Integrated Circuit Technology (ICSICT), Nangjing, China, 25–28 October 2022; pp. 1–3. [Google Scholar] [CrossRef]
- Park, W.; Piao, C.; Lee, H.; Choi, J. CMOS Image Sensor with Two-Step Single-Slope ADCs and a Detachable Super Capacitive DAC. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 849–853. [Google Scholar] [CrossRef]
- Shin, M.-S.; Kwon, O.-K. 14-bit two-step successive approximation ADC with calibration circuit for high-resolution CMOS imagers. Electron. Lett. 2011, 47, 790–791. [Google Scholar] [CrossRef]
- Tang, F.; Chen, D.G.; Wang, B.; Bermak, A. Low-Power CMOS Image Sensor Based on Column-Parallel Single-Slope/SAR Quantization Scheme. IEEE Trans. Electron Devices 2013, 60, 2561–2566. [Google Scholar] [CrossRef]
- Lee, J.; Park, H.; Song, B.; Kim, K.; Eom, J.; Kim, K.; Burm, J. High Frame-Rate VGA CMOS Image Sensor Using Non-Memory Capacitor Two-Step Single-Slope ADCs. IEEE Trans. Circuits Syst. I Regul. Pap. 2015, 62, 2147–2155. [Google Scholar] [CrossRef]
- Li, S.; Qiao, B.; Gandara, M.; Pan, D.Z.; Sun, N. A 13-ENOB Second-Order Noise-Shaping SAR ADC Realizing Optimized NTF Zeros Using the Error-Feedback Structure. IEEE J. Solid-State Circuits 2018, 53, 3484–3496. [Google Scholar] [CrossRef]
- Snoeij, M.F.; Theuwissen, A.J.P.; Makinwa, K.A.A.; Huijsing, J.H. Multiple-Ramp Column-Parallel ADC Architectures for CMOS Image Sensors. IEEE J. Solid-State Circuits 2007, 42, 2968–2977. [Google Scholar] [CrossRef]
- Nuzumlalı, O.L.; Karalar, T.C. A Current Calibration Circuit for a 14-Bit Column-Parallel Dual-Ramp Single-Slope ADC in Infrared Image Sensors. IEEE Trans. Circuits Syst. II Express Briefs 2024, 71, 4824–4828. [Google Scholar] [CrossRef]
- Fang, D.; Nie, K.; Zhang, Z.; Xu, J. Two-Step Single-Slope ADC Utilizing Differential Ramps for CMOS Image Sensors. Circuits Syst. Signal Process 2024, 43, 6097–6114. [Google Scholar] [CrossRef]
- Zhang, B.; Yang, C.; Chen, N.; Chen, J.; Hu, Z.; Wang, G.; Feng, P.; Liu, J.; Wu, N.; Liu, L. A Novel Hybrid Dual Ramp Generator for Two-Step Single-Slope ADCs in CMOS Image Sensors. In Proceedings of the 2024 6th International Conference on Circuits and Systems (ICCS), Chengdu, China, 20–23 September 2024; pp. 185–188. [Google Scholar] [CrossRef]
- Xu, R.; Guo, Z.; Cheng, X.; Su, C.; Li, C.; Wang, Y. A 13-Bit High Speed Two-Step Single Slope ADC Design Method for Hundreds of Mpxiel CMOS Image Sensors. In Proceedings of the 2022 IEEE 5th International Conference on Electronics Technology (ICET), Chengdu, China, 13–16 May 2022; pp. 147–151. [Google Scholar] [CrossRef]
- Zhang, Q.; Ning, N.; Li, J.; Yu, Q.; Wu, K.; Zhang, Z. A 12-Bit Column-Parallel Two-Step Single-Slope ADC With a Foreground Calibration for CMOS Image Sensors. IEEE Access 2020, 8, 172467–172480. [Google Scholar] [CrossRef]
- Park, H.; Yu, C.; Kim, H.; Roh, Y.; Burm, J. Low Power CMOS Image Sensors Using Two Step Single Slope ADC With Bandwidth-Limited Comparators & Voltage Range Extended Ramp Generator for Battery-Limited Application. IEEE Sens. J. 2020, 20, 2831–2838. [Google Scholar] [CrossRef]
- Nie, K.; Zha, W.; Shi, X.; Li, J.; Xu, J.; Ma, J. A Single Slope ADC With Row-Wise Noise Reduction Technique for CMOS Image Sensor. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 2873–2882. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).