Sensitivity Analysis and Optimization of Urban Roundabout Road Design Parameters Based on CFD

Abstract

With the rapid advancement of urbanization, urban transportation systems are facing increasingly severe congestion challenges, especially at traditional roundabouts. The rapid increase in vehicles has led to a sharp increase in pressure at roundabouts. In order to alleviate the traffic pressure in the roundabout, this paper changes the road design parameters of the roundabout, uses a CFD method combined with sensitivity analysis to study the influence of different inlet angles, lane numbers, and the outer radius on the pressure, and seeks the road design parameter scheme with the optimal mitigation effect. Firstly, the full factorial experimental design method is used to select the sample points in the design sample space, and the response values of each sample matrix are obtained by CFD. Secondly, the response surface model between the road design parameters of the roundabout and the pressure in the ring is constructed. The single-factor analysis method and the multi-factor analysis method are used to analyze the influence of the road parameters on the pressure of each feature point, and then the moment-independent sensitivity analysis method based on the response surface model is used to solve the sensitivity distribution characteristics of the road design parameters of the roundabout. Finally, the Kriging surrogate model is constructed, and the NSGA-II is used to solve the multi-objective optimization problem to obtain the optimal solution set of road parameters. The results show that there are significant differences in the mechanism of action of different road geometric parameters on the pressure of each feature point of the roundabout, and it shows obvious spatial heterogeneity of parameter sensitivity. The pressure changes in the two feature points at the entrance conflict area and the inner ring weaving area are significantly correlated with the lane number parameters. There is a strong coupling relationship between the pressure of the maximum pressure extreme point in the ring and the radius parameters of the outer ring. According to the optimal scheme of road parameters, that is, when the parameter set (inlet angle/°, number of lanes, outer radius/m) meets (35.4, 5, 65), the pressures of the feature points decrease by 34.1%, 38.3%, and 20.7%, respectively, which has a significant effect on alleviating the pressure in the intersection. This study optimizes the geometric parameters of roundabouts through multidisciplinary methods, provides a data-driven congestion reduction strategy for the urban sustainable development framework, and significantly improves road traffic efficiency, which is crucial for building an efficient traffic network and promoting urban sustainable development.

1. Introduction

With the coordinated evolution of urbanization and the road traffic system, the problem of traffic congestion has become increasingly prominent. Solving this problem is crucial for the normal operation of the city [1]. In the topology of the road network, the intersection is a typical traffic conflict node, and its traffic efficiency directly restricts the overall efficiency of the road network. Facts have proved that the congestion at urban road intersections is the most serious, and more than 80% of delays are concentrated at intersections [2]. Their traffic bottleneck effect has become a major obstacle to the improvement of road network carrying capacity. Intersections without signal control, especially roundabouts, are more congested. Therefore, alleviating congestion at roundabouts is considered to be an important issue.

The congestion problem of roundabouts can be studied through the application of intelligent transportation technology or infrastructure transformation. The former traffic management system based on intelligent connected technology explores and develops technologies such as intelligent connected vehicles, vehicle–road coordination, and automatic driving by constructing traffic flow models and digital simulation platforms [3,4,5,6], which can significantly increase the number of passing vehicles and reduce control delays [7,8,9]. However, its technical framework still has systematic limitations--it has not broken through the structural capacity bottleneck of the physical road network, and it is difficult to cope with the commuting rigid demand in the saturated state of the road network during peak hours. In addition, equipping a signal [10,11] at the roundabout changes the operating mode from decentralized rule control to centralized control, which may reduce safety and effectiveness. The latter mainly breaks through the structural limitations from the perspective of physical space optimization. The geometric structure of the roundabout is the main determinant of the capacity and performance of the roundabout [12,13,14,15,16]. In the practical process of dealing with the bottleneck of urban traffic space, the optimization of physical space forms a dual technical path. On the one hand, innovative designs based on geometric reconstruction, such as the double-layer roundabout designed by alternative roundabouts, provide solutions for urban and suburban areas with limited space. It has unique advantages in capacity and safety [17,18], but this method ignores the problems of large engineering volume and high costs. On the other hand, it focuses on the refinement of existing facilities. Studies have confirmed that the optimization of the geometric parameters of conventional plane roundabouts also has significant benefits [17], such as the diameter of the inscribed circle and the angle of the vehicle entrance. These parameters directly affect the deflection angle, which in turn affects the speed control and traffic efficiency of the roundabout [19,20]. In this regard, the traffic flow characteristics of plane roundabouts are studied, the main bottleneck areas of traffic congestion are found, and the parameters affecting traffic congestion at roundabouts are optimized [21,22,23,24,25], which has a significant effect on alleviating traffic congestion at intersections.

The main bottleneck area of traffic congestion can be determined and analyzed by using the dynamic characteristics of fluid flow in CFD [26,27,28,29,30]. As an advanced numerical simulation technology, CFD provides a multi-dimensional analysis perspective and quantitative research tool for solving complex traffic flow problems such as traffic congestion. CFD can effectively give insight into the formation and propagation of congestion and can visually display the size of each point of the pressure field. It has a stronger visualization function so as to facilitate the study of the impact of queue distribution on congestion formation [31,32]. However, its limitation is based on a specific continuity assumption, and discrete traffic flow cannot be studied at present. It is worth noting that the road geometric parameters have different effects on the distribution of the traffic pressure field in different areas of the roundabout (such as the inner and outer ring roads) [33]. It is necessary to establish a parameter sensitivity analysis model to quantify the influence weight of key design parameters and provide a theoretical basis for the optimal design of transportation infrastructure [34]. Optimizing the design of roundabouts requires an in-depth understanding of traffic dynamics and the interaction between various design parameters and traffic behavior. Multi-objective optimization modeling can be applied to the optimization process of roundabout design, and algorithms are used to effectively balance these objectives to ensure that the roundabout design achieves the optimal balance between capacity and traffic efficiency [35].

In summary, based on the previous research theories, this paper further uses the theory of fluid mechanics to analyze the congestion pressure of urban roundabouts. In particular, the sensitivity of three key parameters (entrance angle, number of lanes, and outer radius) and synchronous multi-objective optimization are studied and quantified by CFD-derived pressure distribution. This paper uses Fluent (2018) software of CFD to study the congestion problem of roundabouts. Firstly, the key parameters affecting the road in the congested area are determined. The experimental design method is used to simulate each model, and the response surface model between the key parameters of the road and the pressure in the ring is constructed to reveal the influence of single factors and interaction effects on the pressure field. Then, the sensitivity analysis of key parameters is carried out to identify the parameters that have a significant impact on traffic pressure. Finally, the Kriging surrogate model is constructed, and the multi-objective genetic algorithm is used to optimize the road parameters of the roundabout to determine the optimal parameter combination.

2. Road Parameter Setting and Test Design of Roundabout

2.1. Geometric Model

The plane geometric parameter model of the roundabout takes the central island as the core and constructs a multi-lane circular traffic system through the geometric relationship of concentric circles. The core parameters include the following: central island diameter $d=65\mathrm{m}$, outer ring diameter $D=100\mathrm{m}$, total ring width $w=\left(D-d\right)/2=17.5\mathrm{m}$ (corresponding to a four-lane ring road, right single-lane width $w_1=4.3\mathrm{m}$); the total width of the single entrance and exit $l=7.5\mathrm{m}$ (including two lanes, single-lane width $w_2=3.75\mathrm{m}$); the entrance tangential angle $\theta =30°$ and the transition curve of the connecting section adopt an arc with a radius of $r=15\mathrm{m}$ to realize the curvature adaptation between the ring road and the entrance lane. In order to ensure the universality and statistical typicality of the selected values, the geometric model parameters are based on the ‘Urban Road Intersection Design Specification’ [36]. This size is suitable for conventional roundabouts and covers common urban traffic scenarios. Through the geometric data analysis of typical roundabouts in China [37,38,39,40,41], the median diameter of the central island is 65 m (IQR: 50–80 m) and the number of lanes accounts for 78%, indicating that the selected value is located in the mainstream distribution interval. According to the design specification, the design speed of the intersection is the basis for calculating the geometric design index of the intersection. The design speed of the road section can be 0.5 to 0.7 times the design speed of the road section. The upper limit can be taken when designing the straight lane, and the lower limit can be taken when designing the turning lane. The design speed of the main road in the urban area is generally 60 km/h. If the value is 0.5 times, the design speed is about 30 km/h, and the minimum radius of the central island is 35 m. The specific geometric model is shown in Figure 1.

In order to better analyze the pressure characteristics around the roundabout, the intersection point located at the center line of the entrance lane and the edge line of the outer ring lane is selected, and the initial merging position of the vehicle and the pressure statistical benchmark are calibrated, which is the feature point A. The point is set based on the concept of the “conflict point” in traffic flow theory, which can capture the initial interaction between the vehicle entering the ring road and the original traffic flow in the ring. From point A along the extension line of the entrance lane to the center line of the inner ring lane, the geometric mapping relationship between the entrance and the inner ring lane is characterized, that is, feature point B, which is located in the vehicle weaving zone. Monitoring its pressure value can provide key data support for geometric parameter optimization and traffic efficiency improvement. Based on the traffic density–velocity dynamic model, the maximum traffic pressure value of the loop is monitored, which is the characteristic point P_max. The spatial position is dynamically determined by the extreme condition of the pressure field gradient, and its purpose is to quantify the bottleneck effect intensity. The positions of feature points A and B are shown in Figure 1. The three feature points constitute a collaborative analysis framework, which supports the multi-dimensional evaluation of traffic efficiency and pressure at roundabouts.

2.2. Data Acquisition

Now taking Dalian Digital Plaza in China as an example, through video playback and manual counting, the time spent by vehicles passing through the entrance and exit and the specific range of the weaving area is recorded so as to calculate the vehicle speed data at the entrance of the roundabout and the ring road during the peak period. After processing, the average speed of each entrance area during the peak period is as shown in

Table 1. Statistical value of entrance speed.

Intersection	North Entrance	South Entrance	East Entrance	West Entrance
Average speed (km/h)	35.095	31.350	27.560	26.522
Median speed (km/h)	35.031	32.512	28.409	27.311
Standard deviation	3.32	5.53	7.21	3.35

.

Through the speed survey, the speed distribution of each entrance at the intersection is obtained. According to the above table, the speed of the north and south entrances during the morning rush hour is mostly 30–35 km/h, while the speed of the east and west entrances is about 25–30 km/h. It is observed that pedestrians will choose to pass when there is no car, which will hardly affect the change in vehicle speed. At the same time, the average speed range of the entrance vehicle is 25–35 km/h in the 5 min interval of the morning and evening peak hours. Therefore, 30 km/h is taken as the input velocity parameter for numerical simulation.

2.3. CFD Numerical Method

Traffic flow pressure is an important parameter to characterize the interaction between vehicles and traffic congestion. Based on the numerical simulation method of CFD, the traffic flow is compared to fluid, and a two-dimensional control equation is established to model the vehicle flow. With the help of the Lighthill–Whitham–Richards (LWR) theory, a traffic flow control system including the continuity equation, momentum equation, and state equation is constructed. It is worth noting that the LWR model [27] is a classical traffic flow model. Its core is the continuity equation combined with the velocity–density relationship, that is, the state equation, ignoring the inertia term in the momentum equation. In this study, the standard k-ε (2 equation) turbulence model was used, and its core parameters were systematically adjusted. The calibration of benchmark data is mainly based on the design specification of urban road roundabouts [36], and the optimization of calibration indicators is designed to minimize the difference between the simulation results and the benchmark data. Moreover, the key solution variables reach the asymptotic convergence range, and the discrete error estimates are also acceptable for engineering applications [32,33]. The numerical solution uses the finite volume method to discretize the computational domain, sets the inlet/outlet boundary conditions and the initial density field, and iterates through the pressure–velocity coupling algorithm. The simulation results can quantitatively show the pressure distribution in the road network. The high-pressure area corresponds to the congested road section with the frequent acceleration and deceleration of vehicles, and the low-pressure area represents the free flow state. The specific control equation is as follows.

(1) Continuity equation:

$${\displaystyle \frac{\partial \rho }{\partial t}}+{\displaystyle \frac{\partial \left(\rho u\right)}{\partial x}}+{\displaystyle \frac{\partial \left(\rho v\right)}{\partial y}}=0,$$

(1)

where $\rho$ is the density, $t$ is the time, $u$ and $v$ are the components of the velocity vector in the x and y directions.

Because the simulation selects the steady-state environment, the density $\rho$ does not change with time, and Equation (1) can be expressed as

$${\displaystyle \frac{\partial \left(\rho u\right)}{\partial x}}+{\displaystyle \frac{\partial \left(\rho v\right)}{\partial y}}=0.$$

(2)

(2) Turbulent Kinetic Energy Equation:

The turbulent viscosity governing equations in this study are calculated using the standard $k-\epsilon$ (2 equation) model as follows.

$${\displaystyle \frac{\partial }{\partial t}}\left(\rho k\right)+{\displaystyle \frac{\partial }{\partial x_i}}\left(\rho k{u}_i\right)={\displaystyle \frac{\partial }{\partial x_j}}\left[\left(\mu +{\displaystyle \frac{{\mu }_t}{{\sigma }_k}}\right){\displaystyle \frac{\partial k}{\partial x_j}}\right]+G_k+G_b-\rho \epsilon -Y_M+S_k,$$

(3)

$${\displaystyle \frac{\partial }{\partial t}}\left(\rho k\right)+{\displaystyle \frac{\partial }{\partial x_i}}\left(\rho k{u}_i\right)={\displaystyle \frac{\partial }{\partial x_j}}\left[\left(\mu +{\displaystyle \frac{{\mu }_t}{{\sigma }_{\epsilon }}}\right){\displaystyle \frac{\partial \epsilon }{\partial x_j}}\right]+C_{1\epsilon }{\displaystyle \frac{\epsilon }{k}}\left(G_k+G_{3\epsilon }{G}_b\right)-C_{2\epsilon }\rho {\displaystyle \frac{{\epsilon }^2}{k}}+S\epsilon .$$

(4)

where $G_k$ is the generation term for turbulent energy $k$ due to the mean velocity gradient, $G_b$ is the generation term for turbulent energy $k$ due to buoyancy, and $Y_M$ represents the contribution of pulsation expansion in compressible turbulence; $C_{1\epsilon }$, $C_{2\epsilon }$, and $C_{3\epsilon }$ are empirical constants, $C_{3\epsilon }$ = 0 when the main flow direction is perpendicular to the direction of gravity, and the default constants are $C_{1\epsilon }$ = 1.44, $C_{2\epsilon }$ = 1.92, $C_{\mu }$ = 0.09, ${\sigma }_k$ = 1.0, and ${\sigma }_{\epsilon }$ = 1.3.

When the flow is unpressurized and no user-defined source terms are considered, $G_b=0$, $Y_M=0$, $S_k=0$, and $S_{\epsilon }=0$. At this time, the standard $k-\epsilon$ model becomes as follows:

$${\displaystyle \frac{\partial \left(\rho k\right)}{\partial t}}+{\displaystyle \frac{\partial \left(\rho k{u}_i\right)}{\partial x_i}}={\displaystyle \frac{\partial }{\partial x_j}}\left[\left(\mu +{\displaystyle \frac{{\mu }_t}{{\sigma }_k}}\right){\displaystyle \frac{\partial k}{\partial x_j}}\right]+G_k-\rho \epsilon ,$$

(5)

$${\displaystyle \frac{\partial \left(\rho \epsilon \right)}{\partial t}}+{\displaystyle \frac{\partial \left(\rho \epsilon u_i\right)}{\partial x_i}}={\displaystyle \frac{\partial }{\partial x_j}}\left[\left(\mu +{\displaystyle \frac{{\mu }_t}{{\sigma }_{\epsilon }}}\right){\displaystyle \frac{\partial \epsilon }{\partial x_j}}\right]+{\displaystyle \frac{C_{1\epsilon }\epsilon }{k}}{G}_k-C_{2\epsilon }\rho {\displaystyle \frac{{\epsilon }^2}{k}}.$$

(6)

2.4. Road Parameter Test Design

The geometric parameter design of the road is the main determinant of the capacity and performance of the roundabout. For example, the diameter of the roundabout directly affects the smoothness of the vehicle’s roundabout trajectory. If the diameter is too small, it will lead to frequent vehicle interweaving and increase conflict points. An insufficient number and width of lanes may limit the parallel capacity of vehicles and aggravate congestion. An insufficient number of import lanes or unreasonable channelization will reduce traffic efficiency. Therefore, this paper considers optimizing the geometric design of the road from three parameters: the inlet angle of the roundabout, the number of lanes, and the outer radius.

The inlet angle refers to the angle between the center line of the entrance lane and the tangent line of the outer edge of the circular lane when the vehicle enters the roundabout from the entrance lane. The number of lanes refers to the number of independent lanes available for vehicles to drive around the island in the roundabout ring. The outer radius refers to the radius of curvature of the center line of the outermost lane at the roundabout (the distance from the center of the roundabout to the center line of the outer edge lane). The range of each parameter is shown in

Table 2. Variation ranges of roundabout design parameters.

Parameter	Inlet Angle	Number of Lanes	Outer Radius
Minimum	15°	2	42.5 m
Maximum	45°	5	65 m

.

The Full Factorial Design (FFD) method was used to comprehensively analyze all combinations of all independent variables at all levels, and the inlet angle was used as a gradient every 5°. The number of lanes per unit 1 is expressed as a gradient; the radius of the outer ring is taken as a gradient every 7.5 m, and a total of 112 sample matrices are obtained. Then, the pressure response values of the characteristic points A, B, and P_max are obtained by Fluent software simulation calculation due to the large number of design sample matrix data. In view of the integrity requirements and space limitations of data presentation, only a few representative sample matrix response values are listed, as shown in

Table 3. FFD matrix and response values.

NO.	Inlet Angle (°)	Number of Lanes	Outer Radius (m)	Point A Pressure (Pa)	Point B Pressure (Pa)	Point Pmax Pressure (Pa)
1	15	2	42.5	−7882.5	−11,833.1	15,571.6
2	15	3	42.5	−10,104	−21,082.8	14,383.2
3	15	4	42.5	−12,274	−23,143	15,966.3
4	15	5	42.5	−15,309.7	−28,458.1	14,991.7
5	15	2	50	−9933.3	−11,500.1	22,138.3
……
108	45	5	57.5	−10,180.1	−20,688.1	23,993.1
109	45	2	65	−3111.9	−5998.8	26,981.3
110	45	3	65	−6838.81	−7233.62	28,432.2
111	45	4	65	−10,339.9	−14,334.3	27,489.2
112	45	5	65	−14,736.7	−16,732.3	27,583.6

.

From the values of the three input factors given in Table 3, it can be seen that there are great differences in the values of the three input factors, such as the inlet angle of the roundabout and the number of lanes. In order to avoid the influence of the difference in the value of the three input factors on the response target y(x), the values of the three input factors are normalized by the formula.

$$M_i={\displaystyle \frac{2x_i-x_{\max }-x_{\min }}{x_{\max }-x_{\min }}}.$$

(7)

where $M_i$ is the normalized parameter of different input variables, $x_i$ is the $i$-th input variable, and $x_{\max }$ and $x_{\min }$ are the maximum and minimum values of the input variables, respectively.

3. Sensitivity Analysis of Road Parameters at Roundabouts

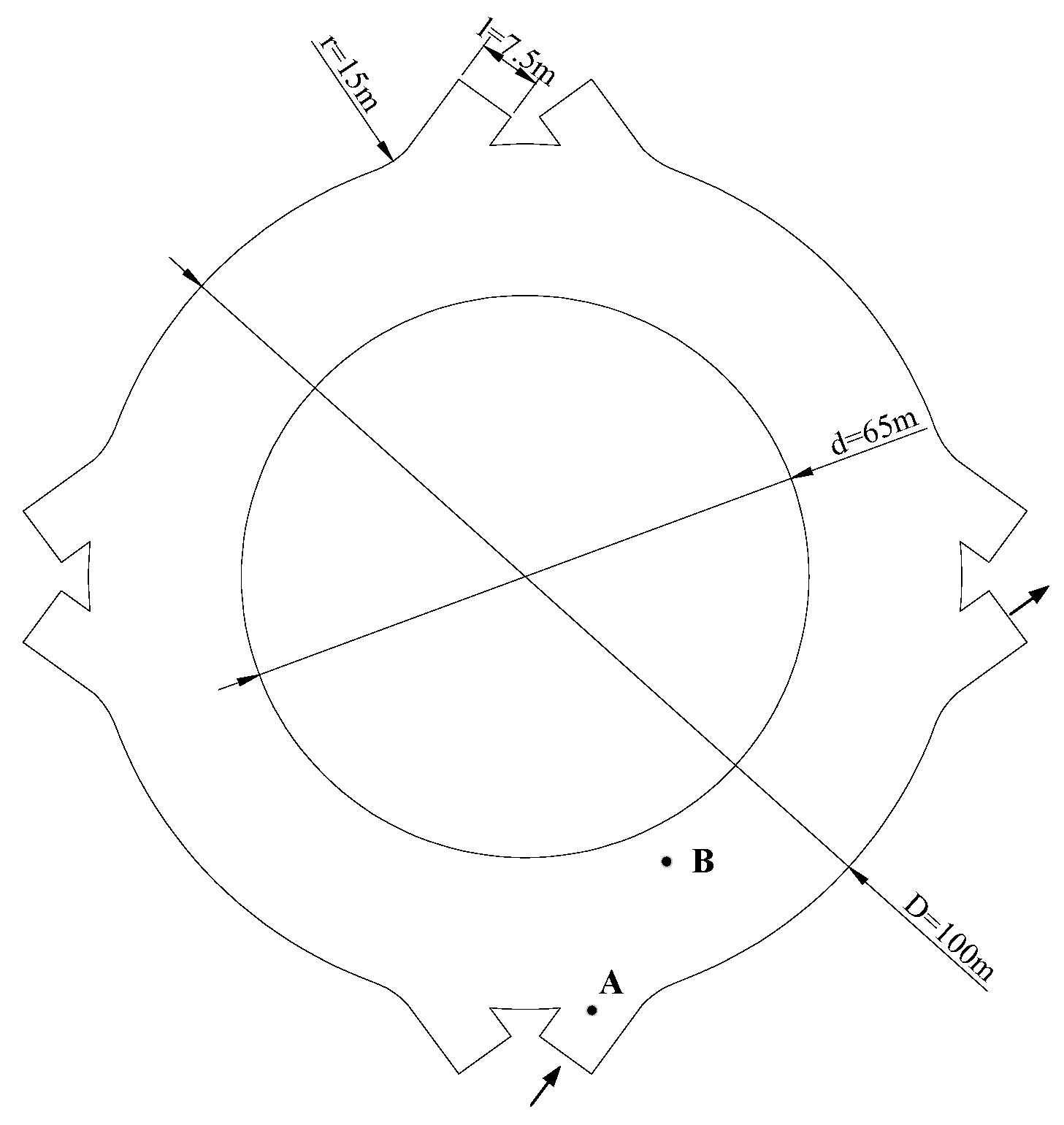
3.1. Response Surface Model Construction

The Response Surface Method (RSM) is a method to establish a one-to-one mathematical relationship between the selected road design parameters and the pressure of each feature point based on the experimental design results. For the n-dimensional input factor $x={\left[x_1,\cdots ,x_n\right]}^T$, the response target is $y={\left[y_1,\cdots ,y_n\right]}^T$. The function expression between the input factor x and the response objective y is

$$y\left(x\right)=\widehat{y}\left(x\right)+\epsilon ={\displaystyle \sum _{i=0}^{n-1}{\alpha }_i}{\phi }_i\left(x\right)+\epsilon .$$

(8)

where $\phi \left(x\right)$ is the sub-item of the fitting polynomial with order $m$ of x, ${\alpha }_i$ is the coefficient of each item, which is fitted by the least squares method from the response target $y\left(x\right)$, and $n$ is the number of items of the fitting polynomial.

Based on FFD, 112 sample point matrices were generated to construct a response surface approximation model. Then, the significant p-value analysis of each sub-item of the constructed response surface approximation model is carried out.

Table 4. Analysis of p-values for the response surface surrogate model.

Fitting Term	${\mathit{x}}_{\mathbf{1}}$	${\mathit{x}}_{\mathbf{2}}$	${\mathit{x}}_{\mathbf{3}}$	${\mathit{x}}_{\mathbf{1}}^{\mathbf{2}}$	${\mathit{x}}_{\mathbf{2}}^{\mathbf{2}}$	${\mathit{x}}_{\mathbf{3}}^{\mathbf{2}}$	${\mathit{x}}_{\mathbf{1}}{\mathit{x}}_{\mathbf{2}}$	${\mathit{x}}_{\mathbf{1}}{\mathit{x}}_{\mathbf{3}}$	${\mathit{x}}_{\mathbf{2}}{\mathit{x}}_{\mathbf{3}}$
Point A	0.012	0.001	0.021	0.009	0.003	0.188	0.037	0.054	0.047
Point B	0.027	0.001	0.018	0.162	0.001	0.047	0.084	0.091	0.023
Point Pmax	0.008	0.001	0.010	0.042	0.001	0.034	0.052	0.028	0.019

gives the significant p-values of each sub-item of the A point, B point, and P_max response surface model under different parameters. In the response surface polynomial, $x_1$ represents the inlet angle; $x_2$ represents the number of lanes; $x_3$ represents the outer radius of the intersection.

For the A point response surface model, the significance p-values of the polynomial sub-items $x_1$, $x_2$, $x_3$, $x_1^2$, $x_2^2$, $x_1{x}_2$, and $x_2{x}_3$ are less than 0.05, indicating that the above sub-items have significant effects. For the B-point response surface model, the polynomial sub-terms $x_1$, $x_2$, $x_3$, $x_2^2$, $x_3^2$, and $x_2{x}_3$ have a significant effect. For the P_max response surface model, the polynomial sub-formulas $x_1$, $x_2$, $x_3$, $x_1^2$, $x_2^2$, $x_3^2$, $x_1{x}_3$, and $x_2{x}_3$ have a significant effect.

According to the significance p-value analysis results of each sub-item of the polynomial response surface of point A, point B, and P_max, combined with the significance p-value analysis evaluation criteria, the sub-items with significant influence are retained, and the sub-items with insignificant influence are removed. Finally, the polynomial response surface approximation model is obtained, and the mathematical relationship is as follows.

$$Y_A=-9258.6+1487.4x_1-1886.1x_2+945.2x_3-146.5x_1^2-948.7x_2^2-400.1x_1{x}_2-481.4x_2{x}_3,$$

(9)

$$Y_B=-15720.5-610.5x_1-2958.7x_2-1277.1x_3-1163.8x_2^2-538.9x_3^2+746.2x_2{x}_3,$$

(10)

$$Y_{\max }=19974.5+1976x_1-2232.9x_2-2126.7x_3-705x_1^2-1031.4x_2^2-602x_3^2-764.8x_1{x}_3+971x_2{x}_3.$$

(11)

The polynomial response surface model is gradually approaching the actual value through the approximate value, so there is a random error in the process of fitting the polynomial response surface model. In order to ensure the accuracy of the fitted response surface approximation model, it is necessary to analyze the error of the fitted response surface approximation model. The commonly used error evaluation criteria are Maximum Error (ME), Root Mean Square Error (RMSE), Average Error (AE), and Coefficient of Determination (R²). As shown in Table 4, the 1–3 order error values of the polynomial response surface approximation model of point A, point B, and P_max are given.

From

Table 5. Error analysis of the response surface surrogate model.

Target Response	Order	AE	ME	RMSE	R2
Point A	1	1176.49	4235.19	1586.03	0.712
	2	892.35	2963.93	1244.71	0.884
	3	745.87	2624.45	997.30	0.891
Point B	1	2457.88	8912.37	3880.19	0.653
	2	1542.70	6210.57	2654.35	0.852
	3	1321.42	5347.86	2216.23	0.867
Point Pmax	1	1623.53	5874.29	2649.61	0.785
	2	1085.75	4123.84	1483.42	0.897
	3	942.86	3752.12	1297.57	0.913

, it can be found that with the gradual increase in the fitting order of the polynomial response surface approximation model of A point, B point, and P_max, the values of the polynomial function ME, AE, and RMSE show a decreasing trend. On the contrary, the value of R² gradually increases with the increase in the polynomial function fitting order, and the value gradually approaches 1. For the second-order and third-order polynomial response surface, the error of each polynomial response surface approximation model is relatively close, which indicates that the accuracy of the second-order polynomial response surface approximation model is sufficient to meet the design requirements. Therefore, this paper chooses the second-order polynomial to fit the A point, B point, and P_max polynomial response surface approximation model.

3.2. Single-Parameter Influence Analysis

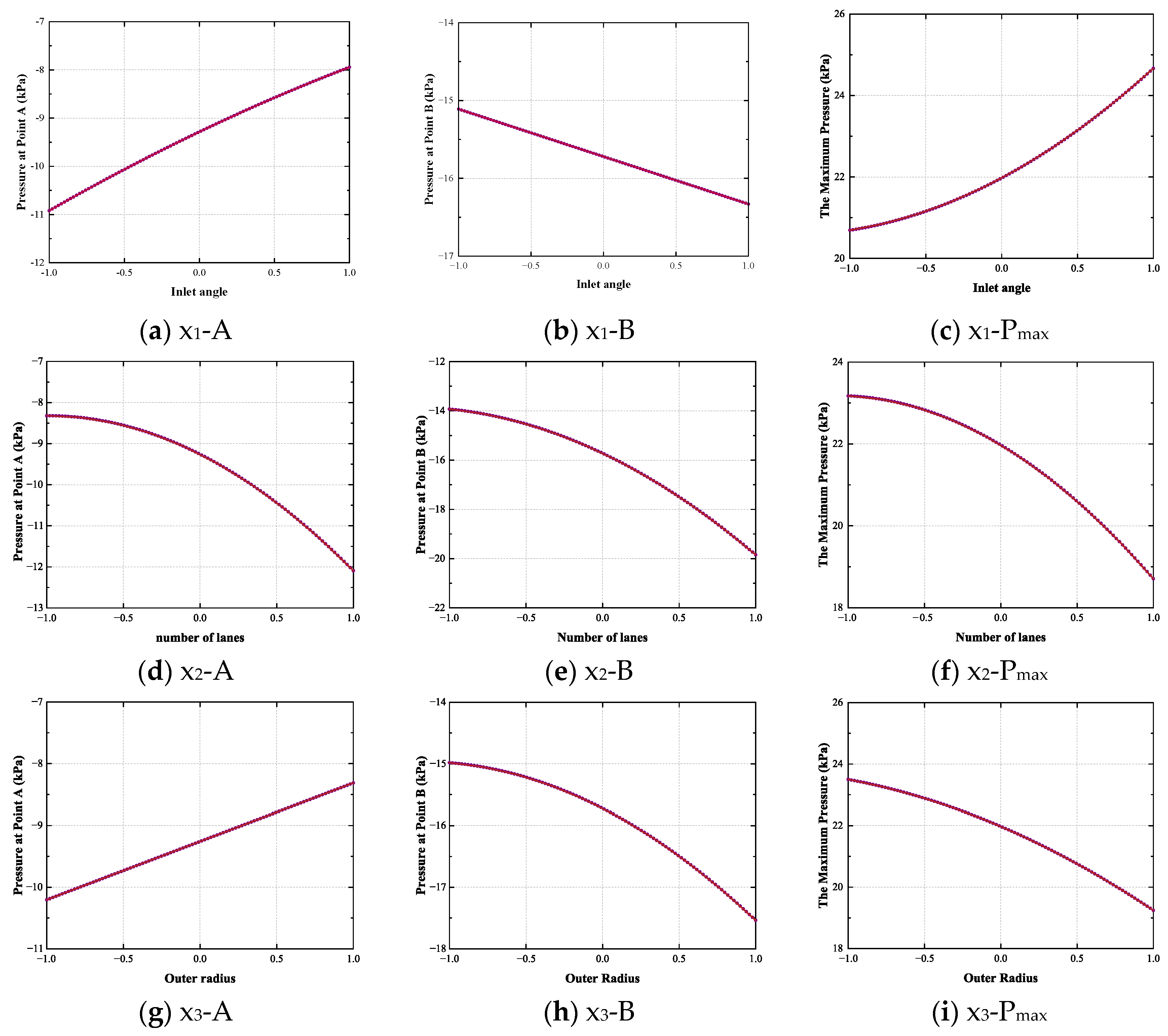
Using the obtained response surface approximation model and the single-factor analysis method, the independent influence of the inlet angle (x₁), the number of lanes (x₂), and the outer radius (x₃) on the A point, B point, and P_max are analyzed, respectively. The influence of specific parameters is shown in Figure 2.

Figure 2a–c are the curves of point A, point B, and P_max pressure at different inlet angles. It can be seen that with the increase in the inlet angle, the pressure of point A and P_max is positively correlated, and the pressure of point B is negatively correlated. The reason is that as the entrance angle increases, the weaving angle between the vehicle trajectory entering the loop and the vehicle in the loop becomes larger, and the relative speed and conflict degree between the vehicles will also increase accordingly, resulting in a rapid increase in vehicle density and delay at point A and P_max. However, the increase in the entrance angle reduces the speed when the vehicle enters the inner loop, thereby reducing the interference with the inner loop traffic flow and reducing the pressure on the traffic flow at point B of the inner loop.

Figure 2d–f are the pressure change curves of each feature point when setting different numbers of lanes. It can be seen that the pressure of point A, point B, and P_max shows a strong negative correlation with the increase in the number of lanes, indicating that the more lanes set within a certain range, the better the pressure relief effect in the ring. The reason is that with the increase in the number of lanes at the roundabout, the traffic capacity is correspondingly improved, and the vehicles can be more orderly shunted into the roundabout, which reduces the frequency of interweaving and conflict of vehicles in the ring, thus effectively alleviating the traffic pressure in the ring.

Figure 2g–i are the pressure curves of each feature point when the outer radius is different. It can be seen that with the increase in the outer radius, the pressure at point A is positively correlated, and the pressure at point B and P_max is negatively correlated. The reason is that the increase in the outer ring radius of the roundabout leads to the increase in the length of the interweaving area in the ring, and the distribution of the conflict points tends to be dispersed, which reduces the interaction strength and delay within the traffic flow and reduces the pressure of point B and P_max. However, with the increase in the traffic capacity of the ring road, the traffic volume of the intersection also increases accordingly, which leads to the increase in the vehicle interweaving conflict in the interweaving section, and the length of the interweaving section and the vehicle interweaving gap are difficult to adjust and match, which makes the traffic pressure at point A increase.

3.3. Two-Parameter Impact Analysis

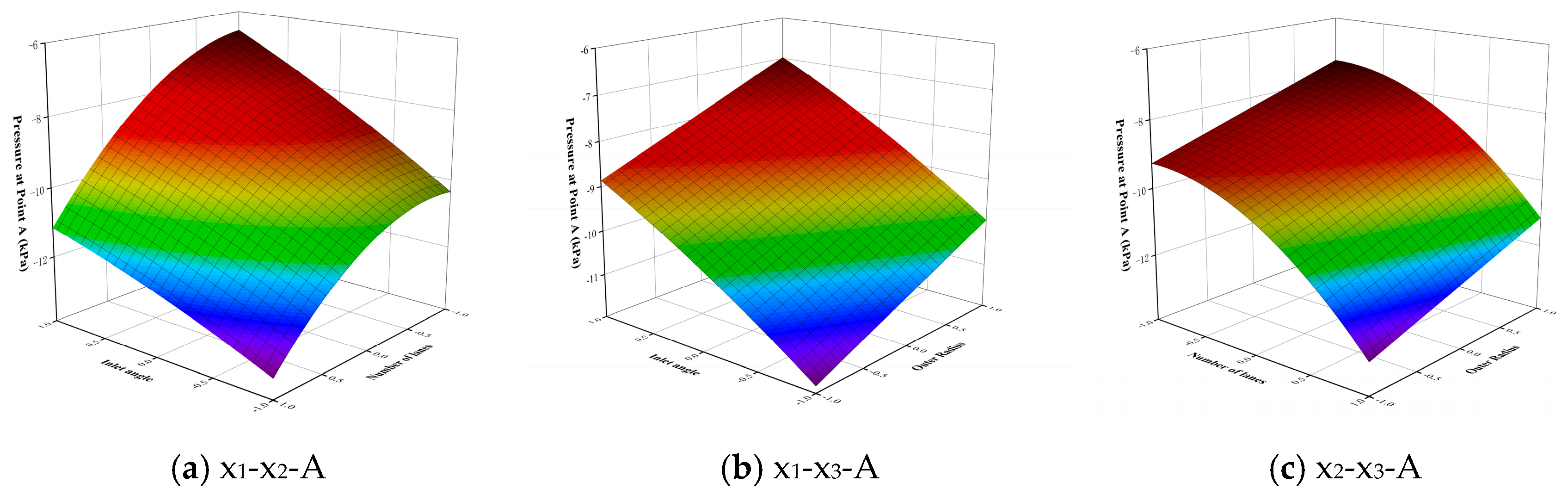
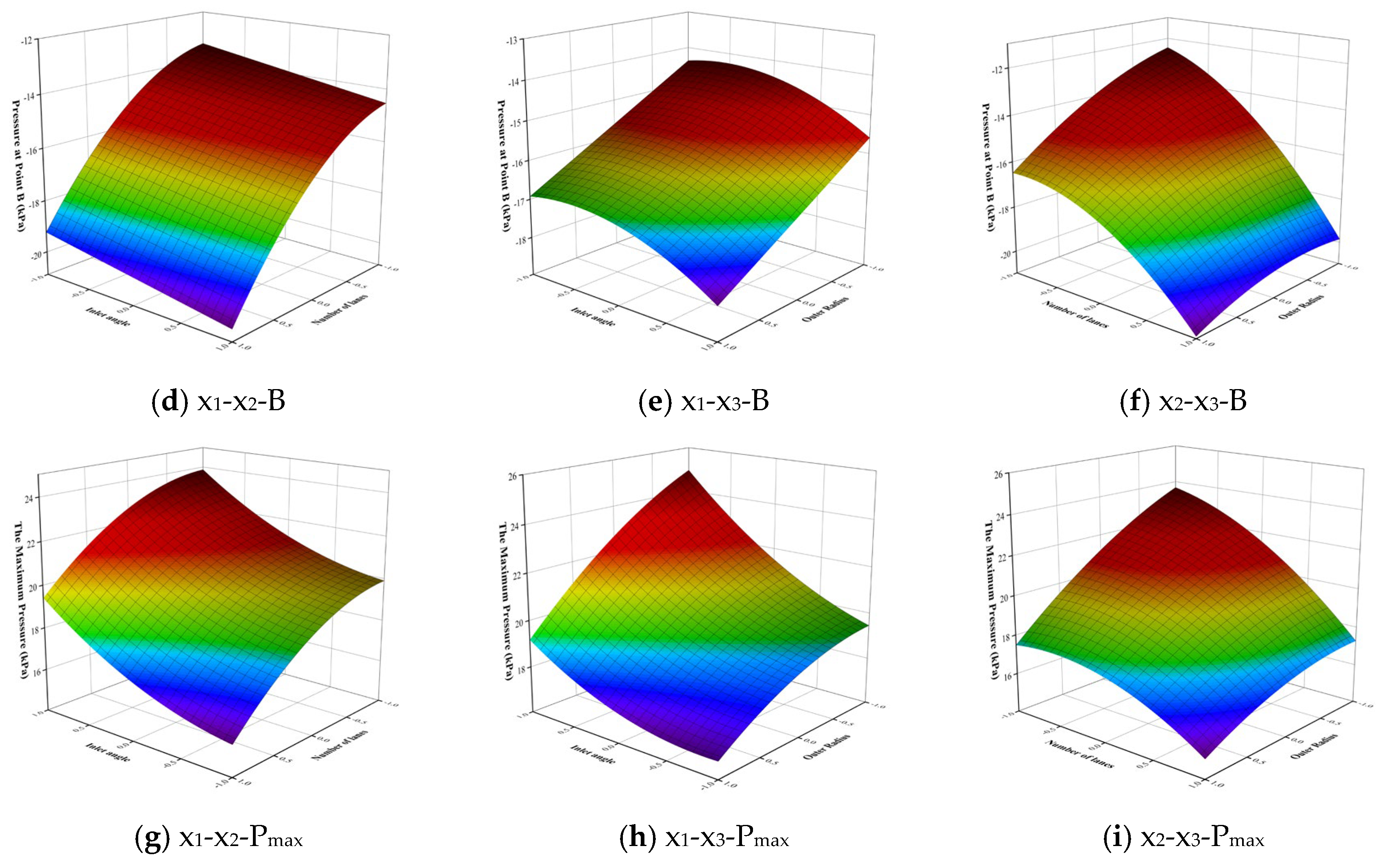
The multi-factor and multi-crossover analysis method was used to explore the influence of different key parameters of the roundabout on the pressure of point A, point B, and P_max under the interaction of two. The results of the influence of the three key road parameters of the roundabout on the pressure of each feature point are shown in Figure 3.

The following two conclusions can be obtained from Figure 3. First, it can be determined whether the interaction between the three key parameters is significant. For example, the interaction between the inlet angle and the number of lanes in Figure 3a has a significant effect on point A. Figure 3b: The interaction between the inlet angle and the outer ring radius is relatively not significant. Secondly, the distribution law of the parameters when the pressure of each feature point is the smallest can be obtained from the results of the interaction of the three key parameters in the above figure. For example, when the number of lanes at the roundabout in Figure 3c is five lanes, the pressure at point A is the smallest when the radius of the outer ring is 42.5 m.

In addition, in the actual optimization of the roundabout, some key parameters (such as the number of roundabout lanes) may not be adjusted due to physical space constraints, existing structural constraints, high transformation costs, or regulations and policies. When faced with such fixed parameter constraints, the two-parameter influence analysis can provide an alternative optimization approach for road designers.

3.4. Full Parameter Impact Analysis

In the global sensitivity analysis [42] (GSA) method, the moment-independent sensitivity analysis method is selected to quantitatively analyze the influence of different parameters of the roundabout road design. According to the above, FFD is used to construct the response surface model of A point, B point, and P_max, respectively, and the statistics of the response surface approximation model $\widehat{K}S$ of each feature point can be obtained. The moment-independent sensitivity analysis method is applied to the sensitivity analysis of the key parameters of different roads at roundabouts through Python (3.13).

$$\widehat{K}S(x_i)=\underset{y}{\max }\left|{\widehat{F}}_y(f(x_i))-{\widehat{F}}_{\left.y\right|x_i}(f(x_i))\right|,$$

(12)

where ${\stackrel{⌢}{F}}_y\left(\cdot \right)$ and ${\stackrel{⌢}{F}}_{\left.y\right|x_i}\left(\cdot \right)$ are the empirical unconditional cumulative distribution function and the conditional cumulative distribution function, respectively.

Then the sensitivity index ${\widehat{T}}_i$ of the point A, point B, and P_max response surface model can be calculated:

$${\widehat{T}}_i=\underset{x_i}{stat}\left[\widehat{K}S\left(x_i\right)\right],$$

(13)

The main geometric parameters affecting the internal pressure of the ring at the roundabout include the vehicle entrance angle $\left(x_1\right)$, the number of lanes $\left(x_2\right)$, and the outer ring radius $\left(x_3\right)$, which are defined as the following unified form:

$$y=\left(x_1,x_2,x_3\right).$$

(14)

3.4.1. Sensitivity Analysis Results of Different Parameters at Point A

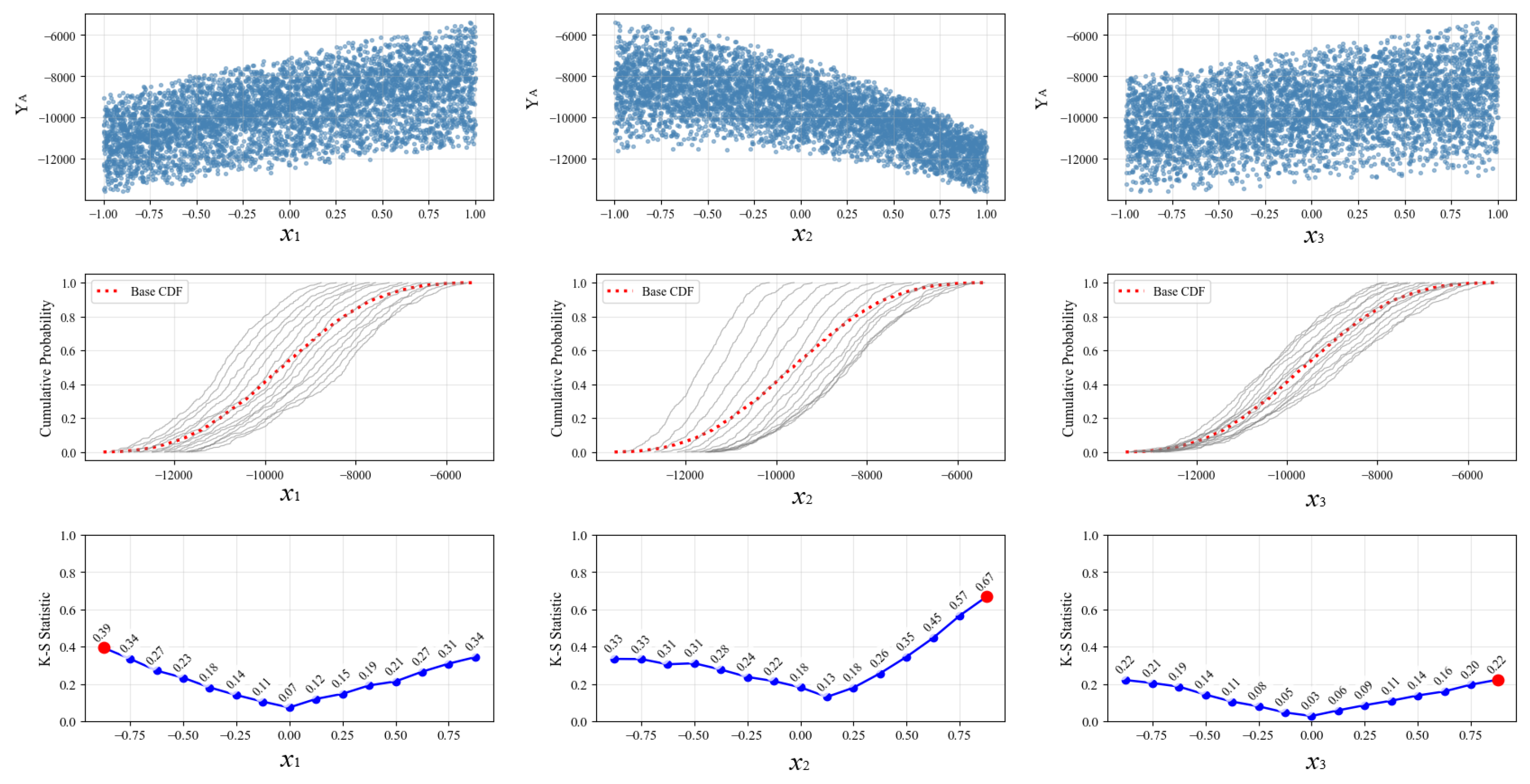
Based on the existing response surface approximation model of point A, the sensitivity analysis of different key parameters of the road is carried out by using the moment-independent sensitivity analysis method so as to obtain the quantitative influence degree of different parameters on the pressure of point A. The results of K-S statistical distribution and the cumulative distribution function (CDF) of different parameters are shown in Figure 4.

Through Formula (13), the sensitivity index $T_i$ of the different parameters of roundabout road design can be obtained. However, since the expected value is very sensitive to the extreme value of K-S, for some specific conditional values $x_i$, the median is used as the summary statistic, supplemented by the maximum value [43]. The sensitivity index $T_i$ is shown in Table 5.

Based on the sensitivity indicators given in Figure 4 and

Table 6. Sensitivity indices of parameter effects on pressure at point A.

$\mathbf{Sensitivity}\mathbf{Index}{\mathit{T}}_{\mathit{i}}$	${\mathit{x}}_{\mathbf{1}}$	${\mathit{x}}_{\mathbf{2}}$	${\mathit{x}}_{\mathbf{3}}$
Median	0.21	0.31	0.14
Maximum	0.39	0.67	0.22

, the following rules can be summarized:

(1) According to the relevant content of CDF, if the distance between the conditional CDF $F_{\left.y\right|x_i}\left(y\right)$ (gray solid line) and the unconditional CDF $F_y\left(y\right)$ (red dotted line) is larger, or the conditional CDF $F_{\left.y\right|x_i}\left(y\right)$ is more dispersed around the unconditional cumulative distribution function $F_y\left(y\right)$, then this parameter has a greater impact on the output response. From the distribution results of CDF with different parameters in Figure 4, it can be found that the design parameters $x_1$ and $x_2$ of the roundabout road have a great influence on the pressure in the ring, and $x_3$ has the least influence on the pressure in the ring.

(2) According to the relevant content of the statistical sensitivity index, it can be concluded that the larger the value of the sensitivity index is, the greater the influence of the parameter on the response value $y$ is. According to the sensitivity index given in Table 6, it can be seen that the design parameters $x_1$ and $x_2$ of the roundabout road have a great influence on the pressure in the ring, and $x_3$ has the least influence.

(3) In general, the order of the influence of different parameters on the pressure in the ring is: $x_2$ > $x_1$ > $x_3$, that is, number of lanes > inlet angle > outer radius.

3.4.2. The Sensitivity Analysis Results of Different Parameters of B Point

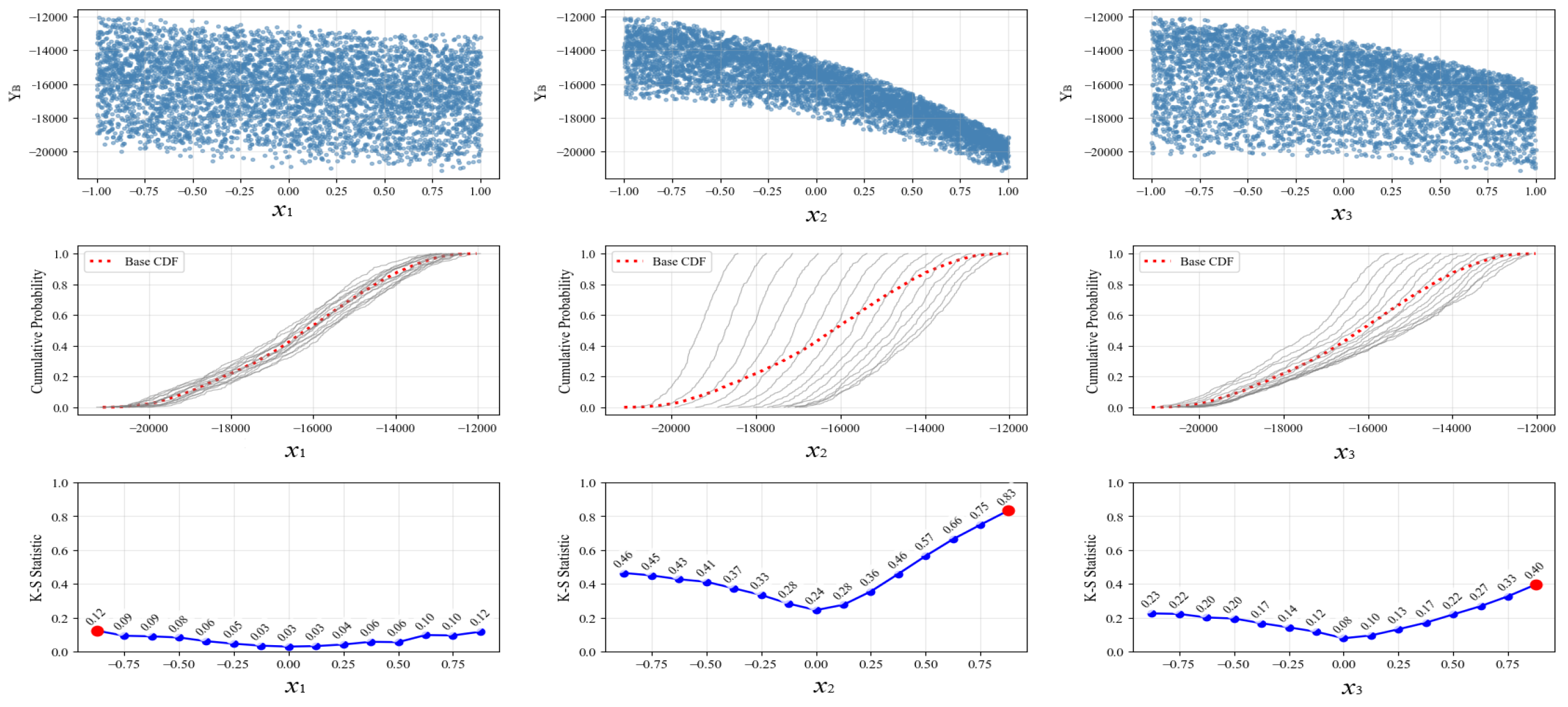
Combining the second-order polynomial response surface approximation model of B point fitted by experimental design with the sensitivity analysis method, the sensitivity analysis of different key parameters is carried out so as to obtain the quantitative influence degree of different road geometric parameters on B point pressure. The statistical distribution of different parameters and the results of the CDF are shown in Figure 5.

According to Formula (13), the sensitivity indexes of different parameters for point B pressure can be obtained. The specific values are shown in

Table 7. Sensitivity indices of parameter effects on pressure at point B.

$\mathrm{Sensitivity}\mathrm{Index}{\mathit{T}}_{\mathit{i}}$	${\mathit{x}}_{\mathbf{1}}$	${\mathit{x}}_{\mathbf{2}}$	${\mathit{x}}_{\mathbf{3}}$
Median	0.06	0.43	0.20
Maximum	0.12	0.83	0.40

.

Based on the sensitivity index $T_i$ for the different parameters of point B pressure given in Figure 5 and Table 7, the following rules can be summarized:

(1) From the distribution results of different parameters of CDF in Figure 5, it can be found that for parameter $x_2$, a significant deviation is observed between the conditional CDF $F_{\left.y\right|x_i}\left(y\right)$ and the unconditional CDF $F_y\left(y\right)$, indicating that $x_2$ has the most pronounced influence on the output response. Parameter $x_3$ also exhibits a moderate impact on the in-ring pressure.

(2) According to the K-S statistical sensitivity index $T_i$ of the different parameters given in Table 7, it can be seen that the value of the $x_2$ sensitivity index is the largest, which indicates that the road design parameter $x_2$ has the greatest influence on the response output value.

(3) It is found that the influence of different road design parameters on the pressure of point B in the ring is sorted from large to small as follows: $x_2$ > $x_3$ > $x_1$, that is, the number of lanes > outer radius > inlet angle.

3.4.3. Sensitivity Analysis Results of Different Parameters of P_max

The sensitivity analysis of different parameters is also carried out. The sensitivity analysis of different key parameters is carried out by the moment-independent sensitivity analysis method combined with the P_max response surface approximation model. The statistical distribution and CDF results of different parameters are shown in Figure 6.

The sensitivity indexes of different parameters are shown in

Table 8. Sensitivity indices of parameter effects on pressure at point P_max.

$\mathbf{Sensitivity}\mathbf{Index}{\mathit{T}}_{\mathit{i}}$	${\mathit{x}}_{\mathbf{1}}$	${\mathit{x}}_{\mathbf{2}}$	${\mathit{x}}_{\mathbf{3}}$
Median	0.18	0.23	0.25
Maximum	0.39	0.48	0.56

.

From the sensitivity index $T_i$ of the different parameters listed in Figure 6 and Table 8, the following rules can be obtained:

(1) From the distribution results of the different parameters of the CDF in Figure 6, it can be seen that the difference between the conditional CDF $F_{\left.y\right|x_i}\left(y\right)$ and the unconditional CDF $F_y\left(y\right)$ of parameter $x_3$ is the largest, indicating that $x_3$ has the most significant influence on the output response. $x_2$ exhibits a secondary influence, while $x_1$ has a minimal impact.

(2) From the K-S statistical sensitivity index $T_i$ of the different parameters given in Table 8, parameter $x_3$ shows the largest maximum and median values of the sensitivity index $T_i$, further confirming its dominant effect on the target response.

(3) Based on the above conclusions, the quantified influence of parameters on the in-ring P_max follows the order $x_3$ > $x_2$ > $x_1$, corresponding to outer radius > number of lanes > inlet angle.

4. Road Parameter Optimization and Optimal Scheme Analysis of Roundabout

4.1. Multi-Objective Optimization Model and Approximate Model Construction

Multi-objective optimization can be understood as the process of optimizing multiple independent variables at the same time. The multi-objective optimization problem can be expressed in the following form:

$$\begin{array}{c}\min f_m\left(x\right)m=1,2\cdots ,M\\ s.t. g_j\left(x\right)\le 0j=1,2\cdots ,J\\ h_k\left(x\right)\le 0k=1,2\cdots ,K\\ x_i^L\le x\le x_i^{U}i=1,2\cdots ,N\end{array},$$

(15)

where $x_i$ is the $i$-th design variable; $f_m\left(x\right)$ is the $m$-th objective function; $g_j\left(x\right)$ is the $j$-th constraint condition; $h_k\left(x\right)$ is the $k$-th constraint condition; $x_i^L$ and $x_i^U$ are the upper and lower limits of the $i$-th variable range.

Due to the large difference in the flow field structure around each feature point area, the pressure at each point is also different. Therefore, starting from the principle of relieving the pressure in the ring to the greatest extent, the pressure minimization of feature points A, B, and P_max is taken as the optimization objective, and a multi-objective optimization mathematical model with different parameters under constraint conditions is established. The formula is as follows:

$$\begin{array}{c}\min \left[Y_A\left(x_i\right),Y_B\left({x_i}^{\prime }\right),Y_{\max }\left({x_i}^{″}\right)\right],i=1,2,3\\ s.t.15°\le x_1\le 45°\\ 2\le x_2\le 5\\ 85m\le x_3\le 130m\end{array}.$$

(16)

where $x_1$, $x_2$, and $x_3$ are used as the optimization variables, which represent the entrance angle, the number of lanes, and the radius of the outer ring, respectively.

The RSM used in the previous article is used for preliminary model development and verification. The purpose is to quickly obtain an acceptable approximate model, understand the basic trends of the problem, and provide a benchmark for subsequent and more refined models. However, its ability to fit complex and highly nonlinear systems is limited. When the nonlinearity of the problem exceeds a range that can be effectively captured by the selected polynomial order, the prediction accuracy of RSM will decrease significantly. The Kriging model is a non-parametric interpolation method. It accurately captures the complex nonlinear relationship and spatial variability between input variables and responses by introducing spatial correlation functions. This allows Kriging to fit the highly nonlinear function response surface more accurately and can provide more reliable predictions even in areas with sparse sample points. In multi-objective optimization, an independent Kriging model can be constructed for each objective function to improve the efficiency of solving complex multi-objective problems. In multi-objective optimization, an independent Kriging model can be constructed for each objective function to improve the efficiency of solving complex multi-objective problems. The Kriging model consists of a local deviation surrogate model and a global approximation surrogate model. The expression is as follows [44]:

$$y\left(x\right)=F\left(\widehat{\beta },x\right)+Z\left(x\right),$$

(17)

where $x$ is the variable of the Kriging model, $F\left(\widehat{\beta },x\right)$ is the regression model found according to the known function group dependent on $x$, $Z\left(x\right)$ is the error of the random process, and its mean value is 0. The regression model can be calculated in the following ways:

$$F\left(\widehat{\beta },x\right)={\widehat{\beta }}_1{f}_1\left(x\right)+{\widehat{\beta }}_2{f}_2\left(x\right)+\cdots +{\widehat{\beta }}_n{f}_n\left(x\right)=\widehat{\beta }{f}^T\left(x\right),$$

(18)

where $\widehat{\beta }$ is the regression coefficient, $f_i\left(x\right)$ is the predetermined basis function, $n$ is the number of sample points in the training sample, $f$ is the unit column vector. In addition, the covariance between any two points is as follows:

$$\mathrm{cov}\left[Z\left(x_i\right),Z\left(x_j\right)\right]={\sigma }^{2}R\left[R\left(x_i,x_j\right)\right],$$

(19)

where ${\sigma }^2$ is the variance of the random process, $R$ is an $n\times n$-dimensional symmetric positive-definite diagonal matrix, and $R\left(x_i,x_j\right)$ is the spatial correlation function between any two points $x_i$ and $x_j$ in the sample. The spatial correlation function is usually described by the Gaussian correlation function, as stipulated in engineering [45]:

$$R\left(x_i,x_j\right)=\exp \left\{-{{\displaystyle \sum _{k=1}^m{\theta }_k\left|x_{ik}-x_{jk}\right|}}^2\right\}.$$

(20)

where $m$ is the number of optimization variables and ${\theta }_k$ is the correlation coefficient of the approximate model.

The Kriging model is used to fit the nonlinear characteristics of the pressure of each feature point. The inlet angle, the number of lanes and the radius of the outer ring of the roundabout are used as the independent variables of the Kriging approximation model. The sample matrix of the design sample space is selected by DOE, and then the response values of each feature point are obtained by numerical calculation. The Kriging surrogate model also uses a step-by-step approximation method to fit the sample point matrix, so there are also random errors. In order to ensure the accuracy of the Kriging approximation model, the error of the Kriging approximation model must be analyzed.

The error analysis of the Kriging surrogate model constructed by A point, B point, and P_max is carried out, respectively. The values of the four error evaluation criteria of the Kriging surrogate model are shown in

Table 9. Error analysis of the Kriging model.

Target Response	AE	ME	RMSE	R2
Point A	<0.001	<0.001	<0.001	1
Point B	<0.001	<0.001	<0.001	1
Point Pmax	<0.001	<0.001	<0.001	1

.

The values of the ME, AE, and RMSE of the Kriging surrogate model constructed by each feature point are relatively small, and the value of R² is equal to 1. This shows that the accuracy of the constructed Kriging approximation model can meet the design requirements, so the Kriging approximation model selected in this study is feasible.

4.2. Road Parameter Optimization

The NSGA-II genetic algorithm is an optimized version of the existing NSGA algorithm proposed by Deb et al. [46] in 2000. It introduces a fast non-decision sorting algorithm, which further reduces the computational complexity of the optimized NSGA-II genetic algorithm. At the same time, the crowding degree comparison operator is also introduced, so the shared radius does not need to be specified. In the same level comparison, sorting is used as the preferred criterion, which can ensure that one of the solutions in the quasi-Pareto domain is evenly distributed in the entire Pareto solution set domain. The method of elite strategy is used to expand the sample space, avoid the lack of optimal solutions, and improve the robustness control and calculation speed of the NSGA-II genetic algorithm. The simulation results of difficult test problems show that NSGA-II can find better solution distribution and convergence close to the real Pareto optimal frontier on most problems compared with the Pareto archived evolution strategy and strength Pareto evolution strategy. In order to obtain the Pareto frontier optimal solution set with the minimum pressure of each feature point in the ring, the Kriging approximation model is used, and the multi-objective optimization of road design parameters is carried out with NSGA-II. The specific parameter settings of NSGA-II in the optimization process are shown in

Table 10. Parameter settings for the NSGA-II genetic algorithm.

Parameter	Value
Population size	100
Number of generations	100
Crossover probability	0.9
Crossover distribution index	15
Mutation distribution index	20

.

After multi-objective optimization using NSGA-II, a total of 100 Pareto front solutions are obtained, which constitute the optimal solution set of the pressure in the ring. The three-dimensional Pareto front cloud map composed of the optimal solution set obtained by the pressure optimization of each feature point is shown in Figure 7.

The dynamic balance mechanism of pressure in the ring is revealed by NSGA-II multi-objective collaborative optimization. Because the inlet angle, the number of lanes, and the outer radius have directional conflicts with the pressure of each feature point, the Pareto frontier is irregularly distributed, and the optimal interval of the comprehensive pressure drop needs to be determined by non-dominated sorting and crowding distance calculation. The enhanced Pareto front is visualized by a blue highlight and white edge enhancement. In this paper, the “shortest distance method” standard is used to select a relatively optimal solution from the frontier solution set obtained by optimization. The calculation formula of the “shortest distance method” standard is as follows:

$$\min D=\sqrt{\left({\displaystyle {\sum }_{\tau =1}^n{\left(\frac{f_{c\tau }}{\min \left(f_{\tau }\left(x\right)\right)}-1\right)}^2}\right)}.$$

(21)

where $n$ is the number of optimization objectives, $f_{c\tau }$ is the value of the c-th Pareto solution of the $\tau$-th optimization objective in the Pareto frontier optimization solution set, and $D$ is the distance between the selected Pareto frontier optimal solution and the origin.

In this paper, the pressure of point A in the optimized frontier solution set is-11,253.86 Pa by the “shortest distance method” standard. B point pressure—21,134.30 Pa; the non-dominated solution of P_max pressure is 15,488.49 Pa. The design variables of the road parameters of the roundabout corresponding to the above optimization results are as follows: the inlet angle is 35.4°; the number of lanes is 5 lanes; the outer radius is 65 m. The comparison of optimization results and simulation results is shown in

Table 11. Comparison of optimization and simulation results.

Target Variable	Simulation Value (Pa)	Optimized Value (Pa)	Relative Error (%)
$Y_A$	−11,940.15	−11,253.86	5.74
$Y_B$	−20,281.52	−21,134.30	4.20
$Y_{\max }$	16,748.34	15,488.49	7.52

.

Through numerical verification, the error between the genetic algorithm optimization solution set and the simulation results is within an acceptable range, which verifies the reliability of the Pareto front solution. It should be noted that the typical solution obtained in this study is based on the shortest distance method. In practical engineering, the optimization scheme can be dynamically selected in combination with multi-criteria decision-making. If the inlet congestion needs to be alleviated first, the solution set with the minimum pressure of feature point A can be selected, and then the changed parameters can be selected according to the actual situation.

4.3. Analysis of Optimal Scheme

The geometric model is established by using the optimization scheme obtained by the shortest distance method, and the numerical solution is based on the standard $k-\epsilon$ (2 equation) model. The pressure cloud diagram of the roundabout before and after optimization is shown in Figure 8.

Compared with the original roundabout, the pressure of each region of the optimized intersection is effectively alleviated. For the ① and ② regions in Figure 8, the significant pressure at the entrance of the roundabout is mainly due to the interlaced area formed by the incoming traffic flow and the circulating traffic flow in the roundabout, which leads to the discontinuity of the velocity field and induces the vehicle to slow down or even stop waiting. By adding the number of lanes, the degree of mutual interference between traffic flows can be effectively reduced. It is worth noting that the pressure field is characterized by a banded distribution with the red high-pressure area as the core and wrapped by the yellow sub-high-pressure area, rather than discrete node congestion. For regions ③ and ④ in Figure 8, the reason for the high pressure in the inner ring road is that the inner ring vehicles need to change lanes continuously to reach the exit, and frequent lane changes cause conflicts and deceleration. By increasing the number of lanes and the outer radius, the vehicle has enough time and space to complete the adjustment of speed and lane.

In summary, this scheme mainly increases the number of lanes from four to five and expands the outer radius from 50 m to 65 m, so that the weaving angle of the weaving area decreases, and the decrease in the weaving angle will reduce the lane-changing weaving conflict of the vehicle, thereby increasing the driving speed of the vehicle when merging and diverging to relieve the pressure. The pressure of quantitative index feature points A, B, and P_max is reduced by 34.1%, 38.3%, and 20.7%, respectively, which has a significant effect on alleviating congestion at intersections. The appropriate inlet angle also ensures the fluency of vehicle inflow and the balance of sight distance, avoiding conflicts caused by sharp turns or insufficient sight distance.

5. Conclusions

In this study, the sample matrix of the inlet angle, the number of lanes, and the outer radius of the roundabout was constructed by CFD numerical simulation, and the response surface models of feature points A (entrance conflict zone), B (inner ring weaving zone), and P_max (pressure extreme point in the ring) were established. The influence mechanism of parameters is revealed by single factors, interaction effects, and global sensitivity analysis. Finally, the multi-objective optimization of road design parameters is carried out by NSGA-II with the pressure drop in the ring as the optimization objective. The main conclusions are as follows:

(1) The influence of independence and interaction of road design parameters on pressure. Under the influence of a single factor, the increase in lane number significantly alleviates the pressure in the ring. The inlet angle is positively correlated with point A and P_max pressure and negatively correlated with point B. The increase in the outer radius leads to the increase in point A pressure and the decrease in point B and P_max. In the interaction effect, the influence of different parameters on the pressure of each point is obtained, respectively. For example, the interaction between the inlet angle and the number of lanes has a significant effect on the pressure of point A, while the interaction between the inlet angle and the outer radius has a weak effect on point A. The nonlinear coupling mechanism between parameters is quantitatively revealed.

(2) There are regional differences in the sensitivity of road design parameters. By constructing the feature point response surface model and the moment-independent global sensitivity analysis method, the influence weight of the design parameters of the roundabout on the pressure in the ring is quantitatively evaluated. According to the distribution of the CDF and K-S statistical sensitivity index $T_i$, the results show that for point A, the influence of different parameters on the pressure in the ring is ranked from large to small as the number of lanes > inlet angle > outer radius. For point B, it is the number of lanes > outer radius > inlet angle. For P_max, it is the outer radius > the number of lanes > inlet angle.

(3) The optimization scheme of road design parameters can effectively alleviate the pressure in the ring. By constructing the Kriging surrogate model of the roundabout and carrying out multi-objective collaborative optimization based on NSGA-II, the Pareto optimal solution set of the pressure of the feature points is obtained, that is, the combination scheme of the road parameters to minimize the pressure in the ring. For example, the inlet angle is changed to 35.4°, the number of lanes is increased from four to five, and the outer radius is widened from 50 m to 65 m. Compared with the original scheme, the pressure of feature points A, B, and P_max is reduced by 34.1%, 38.3%, and 20.7%, respectively, which significantly improves the traffic pressure at the roundabout.