Review: Axial Motion of Material in Rotary Kilns
Abstract
1. Introduction
- Key Concepts—defines the terminology and core phenomena needed for the rest of the review;
- Experimental Data—surveys laboratory and pilot-scale studies on axial transport in rotating cylinders;
- Mathematical Models—compares analytical, empirical, and numerical approaches for predicting axial flow parameters;
- Conclusions—summarizes the main findings and proposes priority directions for future research.
2. Key Concepts
2.1. Axial Motion
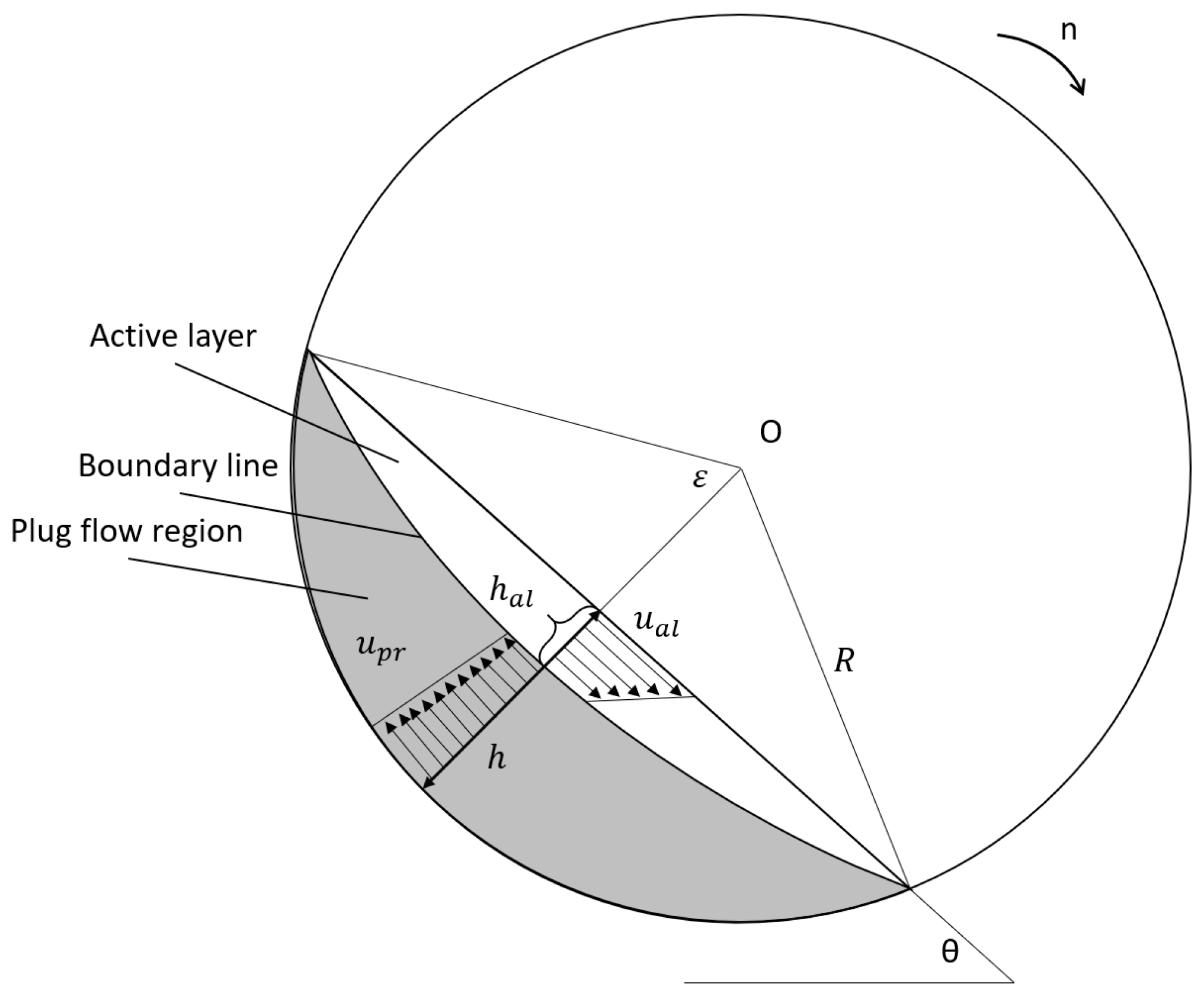
2.2. Transverse Motion
Rolling Regime
2.3. Angle of Repose
2.3.1. Dynamic Angle of Repose
2.3.2. Static Angle of Repose
2.4. Filling Degree
3. Experimental Data
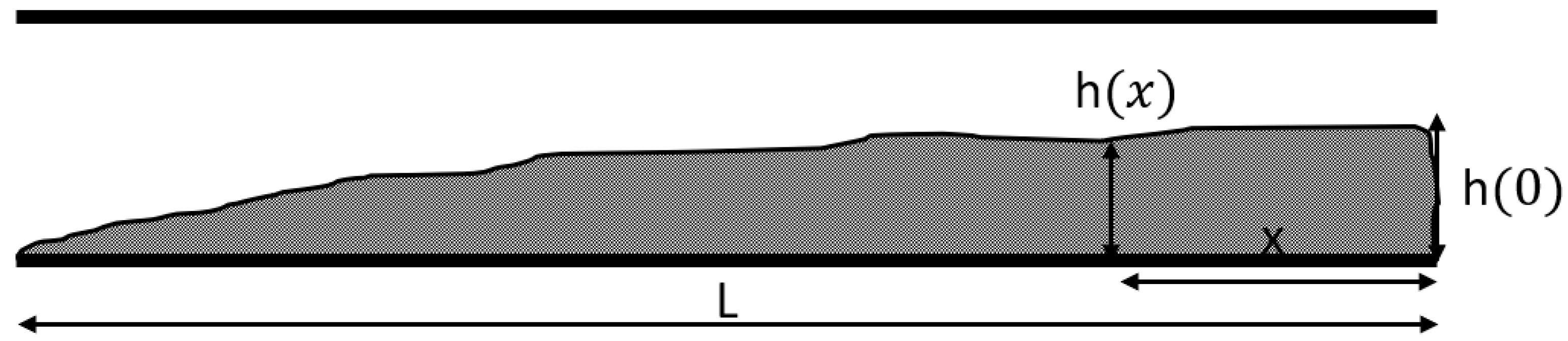
3.1. Material Bed Height
3.1.1. Laboratory Studies Without Internal Structures
3.1.2. Laboratory Studies with Internal Structures
3.1.3. Industrial Experiments
3.2. Axial Velocity of Material
3.2.1. Laboratory Studies Without Internal Structures
| № | Material | Particle Size (mm) | Particle Density (kg/m³) | Bulk Density (kg/m³) | Static Angle of Repose (°) | Dynamic Angle of Repose (°) | Length (m) | Diameter (m) | Rotational Speed (rpm) | Inclination Angle (°) | Filling Degree | Flow Rate | Special Conditions |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [12] | Sand | 0.5 | - | - | - | 34.95 | 2.13 | 0.152 | 2.5 | 2 | 25 | 0.0144 m3/h | - |
| [17] | Sand | 0.2–1 | - | 1490 | 33 | - | 0.65 | 0.11 | 10–50 | 0 | 20–40 | - | - |
| [17] | Rye | 7×2 | - | 710 | 40 | - | 0.65 | 0.11 | 10–50 | 0 | 20–40 | - | - |
| [23] | Cement raw mix | - | - | - | - | - | 79.25 | 2.5 | 0.91 | 2.29 | - | 7.95 m3/h | REAL Chains |
| [23] | Cement raw mix | - | - | - | - | - | 99.06 | 2.5 | 0.91 | 2.29 | - | 7.95 m3/h | REAL Chains |
| [23] | Cement raw mix | - | - | - | - | - | 109.73 | 3.4 | 1 | 2.29 | - | 14.56 m3/h | REAL Chains |
| [23] | Cement raw mix | - | - | - | - | - | 112.78 | 3.4 | 0.86 | 2.29 | - | 16.58 m3/h | REAL Chains |
| [24] | Clinker | 3.5–5 | - | 1550 | 37 | 46.1 | 2.7 | 0.5–0.3 | 1.05–3.47 | 1–4.5 | 5–10 | - | |
| [24] | Clinker | 2–3.5 | - | 1518 | 38.4 | 47.5 | 2.7 | 0.5–0.3 | 1.05–3.47 | 1–4.5 | 5–10 | - | |
| [24] | Clinker | 0.6–2 | - | 1570 | 38.2 | 47.5 | 2.7 | 0.5–0.3 | 1.05–3.47 | 1–4.5 | 5–10 | - | |
| [24] | Red brick | 3.5–5 | - | 915 | 42.0 | 53.2 | 2.7 | 0.5–0.3 | 1.05–3.47 | 1–4.5 | 5–10 | - | |
| [24] | Red brick | 2–3.5 | - | 915 | 39.4 | 52 | 2.7 | 0.5–0.3 | 1.05–3.47 | 1–4.5 | 5–10 | - | |
| [24] | Red brick | 0.6–2 | - | 945 | 39.3 | 51.4 | 2.7 | 0.5–0.3 | 1.05–3.47 | 1–4.5 | 5–10 | - | |
| [24] | Limestone | 3.5–5 | - | 1340 | 39.4 | 44.5 | 2.7 | 0.5–0.3 | 1.05–3.47 | 1–4.5 | 5–10 | - | |
| [24] | Limestone | 2–3.5 | - | 1245 | 40 | 47.35 | 2.7 | 0.5–0.3 | 1.05–3.47 | 1–4.5 | 5–10 | - | |
| [24] | Limestone | 0.6–2 | - | 1230 | 40 | 48.5 | 2.7 | 0.5–0.3 | 1.05–3.47 | 1–4.5 | 5–10 | - | |
| [24] | Marl | 0.2–2 | - | 1265 | 45 | 50 | 2.7 | 0.5–0.3 | 1.05–3.47 | 1–4.5 | 5–10 | - | |
| [24] | Shale | 0.2–2 | - | 777 | 40 | 44.3 | 2.7 | 0.5–0.3 | 1.05–3.47 | 1–4.5 | 5–10 | - | |
| [24] | Sand | 0.2–2 | - | 2650 | 33.25 | 37.4 | 2.7 | 0.5–0.3 | 1.05–3.47 | 1–4.5 | 5–10 | - | |
| [24] | Cement raw mix | - | - | 1155 | 43.18 | 49.48 | 45 | 2.7 | 1.07 | 2.18 | - | 6.19 t/h | REAL |
| [25] | Cement raw mix | - | - | - | - | - | 150 | 3 | - | - | - | - | REAL Chains |
| [25] | Cement raw mix | - | - | - | - | - | 150 | 4 | - | - | - | - | REAL Chains |
| [37] | Cement raw mix | - | - | - | - | - | 150 | 4 | 1.07 | 4 | - | 40.5 t/h | REAL |
| [37] | Cement raw mix | - | - | - | - | - | 150 | 4 | 1.07 | 4 | - | 40.5 t/h | REAL R |
| [37] | Cement raw mix | - | - | - | - | - | 50 | 3.2 | 0.79–1.17 | 5 | - | - | REAL |
| [37] | Cement raw mix | - | - | - | - | - | 50.4 | 3.1 | 0.8 | 3.5 | - | - | REAL |
| [37] | Cement raw mix | - | - | - | - | - | 85.5 | 2.9 | - | 3.5 | - | - | REAL |
| [37] | Cement raw mix | - | - | - | - | - | 85.5 | 2.9 | - | 3.5 | - | - | REAL R |
| [38] | Sand | 1–2 | 2660 | 1342 | 29.7 | - | 1.8 | 0.3 | 0.5–10 | 0–5 | - | - | DH R |
| [38] | Wood chips Paper Rubber | 777.6 | 225 | 48.5 | - | 1.8 | 0.3 | 0.5–10 | 0–5 | - | - | DH R | |
| [29] | Coal | 5–20 | 1240 | 750 | 47 | 37 | 6 | 0.6 | 2–4 | 1 | 8–23 | 0.424–0.835 m3/h | - |
| [29] | Coke | 5–20 | 720 | 480 | 47 | 37 | 6 | 0.6 | 2–4 | 1 | 8–23 | 0.424–0.835 m3/h | - |
| [30] | Sand | 0.49 | - | 1600 | 32 | - | 1 | 0.0515 | 3–7.5 | 0–5 | 5–25 | - | - |
| [30] | Sand | 0.49 | - | 1600 | 32 | - | 1 | 0.119 | 3–7.5 | 0–5 | 5–25 | - | - |
| [19] | Cement raw mix | - | - | - | - | - | 185 | 5 | 0.93 | - | - | - | REAL Chains |
| [19] | Cement raw mix | - | - | - | - | - | 185 | 5 | 0.918 | - | - | - | REAL Chains |
| [19] | Cement raw mix | - | - | - | - | - | 185 | 5 | 1.2 | - | - | - | REAL Chains |
| [39] | Coke | 3.5 | - | 755 | 34 | - | 3 | 0.45 | 1–8 | 1.74–3.76 | - | - | DH |
| [39] | Coke | 3.5 | - | 755 | 34 | - | 3 | 0.554 | 1–8 | 1.74–3.76 | - | - | DH |
| [32] | Granulated concrete | 0.40 | - | 1360 | 32 | - | 16 | 4.096 | 0.267–0.89 | 1–2.2 | 3.67–12.24 | - | - |
| [34] | Cement raw mix | - | 948 | - | 35 | - | 55 | 2.3 | 0–3.57 | 1.72 | - | 0–24 t/h | REAL |
| [40] | Nepheline Limestone | 0.5–10 | - | - | - | - | 23 out of 150 | 3.4 | 1.8 | 1°43′ | - | 44 m3/h | REAL Chains |
3.2.2. Laboratory Studies with Internal Structures
3.2.3. Industrial Experiments
3.3. Mean Residence Time
3.3.1. Laboratory Studies Without Internal Structures
| № | Material | Particle Size (mm) | Particle Density (kg/m³) | Bulk Density (kg/m³) | Static Angle of Repose (°) | Dynamic Angle of Repose (°) | Length (m) | Diameter (m) | Rotational Speed (rpm) | Inclination Angle (°) | Filling Degree | Flow Rate | Special Conditions |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [12] | Sand | 0.5 | - | - | - | 34.95 | 2.13 | 0.152 | 2.5 | 2 | 25 | 0.0144 m3/h | - |
| [17] | Sand | 0.2–1 | - | 1490 | 33 | - | 0.65 | 0.11 | 10–50 | 0 | 20–40 | - | - |
| [17] | Rye | 7×2 | - | 710 | 40 | - | 0.65 | 0.11 | 10–50 | 0 | 20–40 | - | - |
| [23] | Cement raw mix | - | - | - | - | - | 79.25 | 2.5 | 0.91 | 2.29 | - | 7.95 m3/h | REAL Chains |
| [23] | Cement raw mix | - | - | - | - | - | 99.06 | 2.5 | 0.91 | 2.29 | - | 7.95 m3/h | REAL Chains |
| [23] | Cement raw mix | - | - | - | - | - | 109.73 | 3.4 | 1 | 2.29 | - | 14.56 m3/h | REAL Chains |
| [23] | Cement raw mix | - | - | - | - | - | 112.78 | 3.4 | 0.86 | 2.29 | - | 16.58 m3/h | REAL Chains |
| [24] | Clinker | 3.5–5 | - | 1550 | 37 | 46.1 | 2.7 | 0.5–0.3 | 1.05–3.47 | 1–4.5 | 5–10 | - | |
| [24] | Clinker | 2–3.5 | - | 1518 | 38.4 | 47.5 | 2.7 | 0.5–0.3 | 1.05–3.47 | 1–4.5 | 5–10 | - | |
| [24] | Clinker | 0.6–2 | - | 1570 | 38.2 | 47.5 | 2.7 | 0.5–0.3 | 1.05–3.47 | 1–4.5 | 5–10 | - | |
| [24] | Red brick | 3.5–5 | - | 915 | 42.0 | 53.2 | 2.7 | 0.5–0.3 | 1.05–3.47 | 1–4.5 | 5–10 | - | |
| [24] | Red brick | 2–3.5 | - | 915 | 39.4 | 52 | 2.7 | 0.5–0.3 | 1.05–3.47 | 1–4.5 | 5–10 | - | |
| [24] | Red brick | 0.6–2 | - | 945 | 39.3 | 51.4 | 2.7 | 0.5–0.3 | 1.05–3.47 | 1–4.5 | 5–10 | - | |
| [24] | Limestone | 3.5–5 | - | 1340 | 39.4 | 44.5 | 2.7 | 0.5–0.3 | 1.05–3.47 | 1–4.5 | 5–10 | - | |
| [24] | Limestone | 2–3.5 | - | 1245 | 40 | 47.35 | 2.7 | 0.5–0.3 | 1.05–3.47 | 1–4.5 | 5–10 | - | |
| [24] | Limestone | 0.6–2 | - | 1230 | 40 | 48.5 | 2.7 | 0.5–0.3 | 1.05–3.47 | 1–4.5 | 5–10 | - | |
| [24] | Marl | 0.2–2 | - | 1265 | 45 | 50 | 2.7 | 0.5–0.3 | 1.05–3.47 | 1–4.5 | 5–10 | - | |
| [24] | Shale | 0.2–2 | - | 777 | 40 | 44.3 | 2.7 | 0.5–0.3 | 1.05–3.47 | 1–4.5 | 5–10 | - | |
| [24] | Sand | 0.2–2 | - | 2650 | 33.25 | 37.4 | 2.7 | 0.5–0.3 | 1.05–3.47 | 1–4.5 | 5–10 | - | |
| [24] | Cement raw mix | - | - | 1155 | 43.18 | 49.48 | 45 | 2.7 | 1.07 | 2.18 | - | 6.19 t/h | REAL |
| [25] | Cement raw mix | - | - | - | - | - | 150 | 3 | - | - | - | - | REAL Chains |
| [25] | Cement raw mix | - | - | - | - | - | 150 | 4 | - | - | - | - | REAL Chains |
| [45] | Dolomite | 28×35, 35×48, 48×65–TS * | - | - | - | - | 0.24 | 0.08 | 20–80 | 0–3 | - | 1.8–8.64 kg/h | - |
| [37] | Cement raw mix | - | - | - | - | - | 150 | 4 | 1.07 | 4 | - | 40.5 t/h | REAL |
| [37] | Cement raw mix | - | - | - | - | - | 150 | 4 | 1.07 | 4 | - | 40.5 t/h | REAL R |
| [37] | Cement raw mix | - | - | - | - | - | 50 | 3.2 | 0.79–1.17 | 5 | - | - | REAL |
| [37] | Cement raw mix | - | - | - | - | - | 50.4 | 3.1 | 0.8 | 3.5 | - | - | REAL |
| [37] | Cement raw mix | - | - | - | - | - | 85.5 | 2.9 | - | 3.5 | - | - | REAL |
| [37] | Cement raw mix | - | - | - | - | - | 85.5 | 2.9 | - | 3.5 | - | - | REAL R |
| [46] | Sodium carbonate | 0.137 | 2530 | - | - | - | 0.6 | 0.25 | 1–10 | 0 | 16–40 | 0.0025–0.0102 m3/h | - |
| [26] | Iron ore | 3–6 | - | - | - | - | 2 | 0.3 | 0.3–0.7 | 1–3 | - | 30 kg/h | DH- |
| [27] | Iron ore | - | - | 1600 | 35 | - | 2 | 0.2–0.6 | 0.6 | 1.5 | - | 0.25–1.25 kg/h | - |
| [27] | Iron ore | - | - | 1600 | 35 | - | 2–4.8 | 0.3 | 0.6 | 1.5 | - | 0.25–1.25 kg/h | - |
| [26] | Iron ore | 3–6 | - | - | - | - | 2 | 0.3 | 0.3–0.7 | 1–3 | - | 30 kg/h | DH |
| [27] | Iron ore | - | - | 1600 | 35 | - | 2 | 0.2–0.6 | 0.6 | 1.5 | - | 0.25–1.25 kg/h | DH |
| [27] | Iron ore | - | - | 1600 | 35 | - | 2–4.8 | 0.3 | 0.6 | 1.5 | - | 0.25–1.25 kg/h | DH |
| [14] | Iron ore | 3–6 | - | - | - | - | 2 | 0.3 | 0.3–0.7 | 1.5 | - | 0.5 kg/h | CL |
| [14] | Iron ore | 3–6 | - | - | - | - | 4.8 | 0.3 | 0.3–0.7 | 1.5 | - | 0.5 kg/h | CL |
| [28] | Ilmenite | 0.1–0.3 | 4200 | - | 27.4 | - | 5.9 | 0.147 | 1–3 | 0.78–1.37 | - | - | DH |
| [28] | Ilmenite | 0.1–0.3 | 4200 | - | 27.4 | - | 5.9 | 0.147 | 1–3 | 0.78–1.37 | - | - | - |
| [47] | Sand | 2.02 | 2630 | 1640 | 36 | - | 1.05 | 0.192 | 0–100 | 0 | - | 22.68–109.08 kg/h | DH LIF |
| [38] | Sand | 1–2 | 2660 | 1342 | 29.7 | - | 1.8 | 0.3 | 0.5–10 | 0–5 | - | - | DH R |
| [38] | Wood chips Paper Rubber | 777.6 | 225 | 48.5 | - | 1.8 | 0.3 | 0.5–10 | 0–5 | - | - | DH R | |
| [29] | Coal | 5–20 | 1240 | 750 | 47 | 37 | 6 | 0.6 | 2–4 | 1 | 8–23 | 0.424–0.835 m3/h | - |
| [29] | Coke | 5–20 | 720 | 480 | 47 | 37 | 6 | 0.6 | 2–4 | 1 | 8–23 | 0.424–0.835 m3/h | - |
| [48] | Sand | 0.366 | - | 1370 | - | 33 | 4.635 | 0.4 | 1–3 | 3 | 2–11 | 59.9–149.536 kg/h | DH |
| [39] | Coke | 3.5 | - | 755 | 34 | - | 3 | 0.45 | 1–8 | 1.74–3.76 | - | - | DH |
| [39] | Coke | 3.5 | - | 755 | 34 | - | 3 | 0.554 | 1–8 | 1.74–3.76 | - | - | DH |
| [32] | Granulated concrete | 0.40 | - | 1360 | 32 | - | 16 | 4.096 | 0.267–0.89 | 1–2.2 | 3.67–12.24 | - | - |
| [35] | Raw wood chips | 5–15× 2–7× 1–3 | - | 280 | - | 42 | 4.2 | 0.21 | 2–4 | 1–2 | 5.2–18.1 | 4–8 kg/h | - |
| [49] | Sand | 0.55 | 1422 | 39 | - | 1.95 | 0.101 | 2–12 | 2–5 | - | 0.68–2.5 kg/h | DH LIF | |
| [49] | Rice | 3.8×1.9 | - | 889 | 36 | - | 1.95 | 0.101 | 2–12 | 2–5 | - | 0.68–2.5 kg/h | DH LIF |
| [34] | Cement raw mix | - | 948 | - | 35 | - | 55 | 2.3 | 0–3.57 | 1.72 | - | 0–24 t/h | REAL |
| [50] | Wood chips | 5–17× 2–8× 1–4 | 1506 | 260 | 42 | - | 4.2 | 0.21 | 0.5–21 | 1–3 | 8–10 | 2.5–7.5 kg/h | R LIF |
| [51] | Quartz sand | 1.25–2 | 2650 | - | - | - | 1.2 | 0.1 | 1–3 | 0.5–3 | 15 | 18–36 kg/h | - |
| [51] | Quartz sand | 3–3.75 | 2650 | - | - | - | 1.2 | 0.1 | 1–3 | 0.5–3 | 15 | 18–36 kg/h | - |
| [52] | Coal | 0.053–0.579 | - | 530 | - | 29.2 | 1 | 0.095 | 1.5–10 | 1.1–2 | 2.8–13 | 0.2–2.3 kg/h | - |
| [52] | Olive pits | 1.144–3.624 | - | 790 | - | 38.0 | 1 | 0.095 | 1.5–10 | 1.1–2 | 2.8–13 | 0.2–2.3 kg/h | - |
| [52] | Sand | 0.257–0.416 | - | 1470 | - | 34.0 | 1 | 0.095 | 1.5–10 | 1.1–2 | 2.8–13 | 0.2–2.3 kg/h | - |
| [53] | Aluminum hydroxide | - | - | - | - | - | 51 | 2.56 | 1.98 | 1.43 | 2.1 | 2640 m3/s | REAL |
| [53] | Aluminum hydroxide | - | - | - | - | - | 51 | 2.56 | 1.98 | 1.43 | 2 | 2640 m3/s | REAL |
| [53] | Aluminum hydroxide | - | - | - | - | - | 60 | 2.84 | 1.98 | 1.43 | 2.4 | 3140 m3/s | REAL |
| [53] | Aluminum hydroxide | - | - | - | - | - | 50 | 2.24 | 1.04 | 1.43 | 2.1 | 1830 m3/s | REAL |
| [53] | Aluminum hydroxide | - | - | - | - | - | 50 | 2.42 | 1.35 | 1.43 | 1.5 | 1970 m3/s | REAL |
| [53] | Aluminum hydroxide | - | - | - | - | - | 50 | 2.05 | 1.182 | 1.43 | 1.7 | 1750 m3/s | REAL |
| [53] | Aluminum hydroxide | - | - | - | - | - | 60 | 2.84 | 1.8 | 1.15 | 2 | 3060 m3/s | REAL |
| [53] | Aluminum hydroxide | - | - | - | - | - | 60 | 2.84 | 1.98 | 1.72 | 1.8 | 3400 m3/s | REAL |
| [53] | Aluminum hydroxide | - | - | - | - | - | 60 | 2.584 | 1.8 | 1.72 | 1.8 | 3350 m3/s | REAL |
3.3.2. Laboratory Studies with Internal Structures
3.3.3. Industrial Experiments
4. Mathematical Models
4.1. Material Bed Height
4.2. Axial Velocity of Material
4.3. Mean Residence Time
4.4. Modern Approaches to the Modeling of Rotary Kilns
4.4.1. Numerical Modeling Methods
4.4.2. Neural Networks and Machine Learning Methods
5. Conclusions
Funding
Conflicts of Interest
Nomenclature
| h | Material bed height, m |
| hbf | Material bed height outside the retaining ring influence area, m |
| F | Half the chord of the segment occupied by the material, m |
| x | Axial coordinate, m |
| θ | Dynamic angle of repose, degree |
| σ | Dynamic angle of repose, rad |
| s | Static angle of repose, degree |
| κ | Static angle of repose, rad |
| χ | Difference between the dynamic and static angles of repose of the material, rad |
| M | Material mass flow rate, kg/s |
| Mh | Material mass flow rate, kg/h |
| n | Rotational speed, rev/s |
| w | Rotational speed, rev/m |
| f | Rotational speed, rad/s |
| ρ | Bulk density of material, kg/m3 |
| ρtapped | Tapped material density, kg/m3 |
| R | Internal radius of the kiln (cylinder), m |
| D | Internal diameter of the kiln (cylinder), m |
| L | Kiln length, m |
| β | Cylinder inclination angle, degree |
| δ | Cylinder inclination angle, rad |
| i | Cylinder inclination angle, % |
| h0 | Retaining ring height at the kiln outlet, m |
| dp | Particle diameter, m |
| mp | Particle mass, kg |
| BDN | Boundary condition |
| Q | Material volumetric flow rate, m3/s |
| Qm | Material volumetric flow rate, m3/min |
| Qh | Material volumetric flow rate, m3/h |
| Ri | Radius of the i-th internal structure, m |
| Rdam | Radius of the internal partition, m |
| Ddam | Diameter of the retaining ring opening, m |
| CQ | Power coefficient for volumetric flow |
| Cw | Power coefficient for rotational speed |
| Cβ | Power coefficient for kiln inclination angle |
| H | Dimensionless coefficient |
| a | Dimensionless coefficient |
| b | Dimensionless coefficient |
| ε | Fill angle, degree |
| ε0 | Fill angle at the kiln outlet, degree |
| φ | Fill angle, rad |
| Z | Degree of filling |
| ri | i-th root of the cubic equation |
| u | Axial velocity of material, m/s |
| ual | Velocity of material in the active layer, m/s |
| upr | Velocity of material in the passive region, m/s |
| Uc.z. | Axial velocity of material in the chain curtain zone, m/min |
| Ud.z. | Axial velocity of material in the decarbonization zone, m/min |
| Us.z. | Axial velocity of material in the sintering zone, m/min |
| Umax | Maximum axial velocity of material, m/min |
| λ | Angle between kiln axis and material surface, rad |
| µ | Angle between kiln axis and material surface, degree |
| K | Dimensionless coefficient |
| e | Dimensionless coefficient |
| A | Dimensionless coefficient |
| α | Inclination angle of material to the horizon in a plane perpendicular to the kiln axis, rad |
| k1 | Dimensionless coefficient accounting for dynamic conditions |
| k2 | Dimensionless coefficient characterizing internal resistance |
| B | Proportionality coefficient |
| k3 | Dimensionless coefficient of material properties |
| Y | Angle between chain direction and kiln axis, degree |
| Dimensionless parameter characterizing chain curtain density | |
| H1 | Enthalpy of feed at the kiln inlet, J |
| H2 | Enthalpy of feed at the point of interest, J |
| k4 | Dimensionless empirical coefficient |
| Te.g., | Exhaust gas temperature, ℃ |
| P | Draft behind the kiln, kgf/cm2 |
| Mm | Kiln throughput, t/h |
| Lc | Length of the chain curtain, m |
| Tc.z. | Temperature of the calcination zone, ℃ |
| Gc | Mass of the chain curtain, t |
| Tm | Clinker temperature at the kiln outlet, ℃ |
| Ta | Secondary air temperature, ℃ |
| S | Cross-sectional area of material in the kiln, m2 |
| Sc | Chain surface area, m2 |
| MRT | Mean residence time, min |
| Sb | Backflow as a fraction of total output |
| k5 | Correction coefficient for mean residence time |
| k6 | Dimensionless coefficient |
| g | Acceleration due to gravity, m/s2 |
| k7 | Power coefficient |
| k8 | Power coefficient |
| k9 | Power coefficient |
| k10 | Power coefficient |
| k11 | Power coefficient |
| k12 | Power coefficient |
| k13 | Power coefficient |
| k14 | Coefficient that accounts for the material’s properties |
| Dex | Effective outlet diameter, m |
| Slift | Area covered by solid particles in a lifter at horizontal position, m2 |
| hal | Active layer thickness, m |
| hpr | Passive region thickness, m |
| lal | Chord length at half the active layer height, m |
| lpr | Chord length at half the passive layer height, m |
| j | Particle acceleration in the active layer, m/s2 |
| z | |
| С | Equation coefficient |
| E | Equation coefficient |
| y | Conical section angle of the kiln, degree |
| N | Factor accounting for retaining ring influence |
| V | Material volume, m3 |
| v | Kiln volume, m3 |
References
- Zanoli, S.M.; Pepe, C.; Astolfi, G. Advanced Process Control for Clinker Rotary Kiln and Grate Cooler. Sensors 2023, 23, 2805. [Google Scholar] [CrossRef]
- Singh, A.P.; Ghoshdastidar, P.S. Computer Simulation of Heat Transfer in Alumina and Cement Rotary Kilns. J. Therm. Sci. Eng. Appl. 2022, 14, 031001. [Google Scholar] [CrossRef]
- Mungyeko Bisulandu, B.J.R.; Marias, F. Modeling of the Thermochemical Conversion of Biomass in Cement Rotary Kiln. Waste Biomass Valoriz. 2021, 12, 1005–1024. [Google Scholar] [CrossRef]
- Machalek, D.; Powell, K.M. Model predictive control of a rotary kiln for fast electric demand response. Miner. Eng. 2019, 144, 106021. [Google Scholar] [CrossRef]
- Zhukovsky, Y.; Suslikov, P. Assessment of the potential effect of applying demand management technology at mining enterprises. Sustain. Dev. Mt. Territ. 2024, 16, 895–908. [Google Scholar] [CrossRef]
- Khamidov, O.U.; Shibanov, D.A.; Shishkin, P.V.; Kolpakov, V.O. Efficiency of excavators application in open pit mines of Uzbekistan. Min. Ind. J. 2024, 5, 135–142. [Google Scholar] [CrossRef]
- Navatskaya, V.A.; Neyrus, S.K.; Skorobogatova, M.A.; Afanasiev, M.P. Systematic study of structural divisions of industrial enterprise using queuing systems. J. Technol. Manag. Innov. 2023, 18, 51–59. [Google Scholar] [CrossRef]
- Korshunov, G.I.; Nikulin, A.N.; Krasnoukhova, D.Y. Development of recommendations for professional risk management of employees of the mining and processing plant. Min. Informational Anal. Bull. 2023, 9-1, 199–214. [Google Scholar] [CrossRef]
- Petrov, P.A.; Shestakov, A.K.; Nikolaev, M.Y. Use of multifunctional crust breaker and machine vision system for acquisition and processing of aluminium reduction cell data. Tsvetnye Met. 2023, 4, 45–53. [Google Scholar] [CrossRef]
- Gendler, S.G.; Bratskih, A.S. Actual problems of coal accumulations ignition in rock dumps. Min. Ind. J. 2024, 5, 71–77. [Google Scholar] [CrossRef]
- Oksengoyt, E.A.; Kunitskiy, N.A.; Petrov, P.A.; Shestakov, A.K. Modern equipment by Soyuztsvetmetavtomatika for detecting aerosols and spills of harmful pollutants. Tsvetnye Met. 2023, 4, 61–65. [Google Scholar] [CrossRef]
- Sullivan, J.D.; Maier, C.G.; Ralston, O.C. Passage of Solid Particles Through Rotary Cylindrical Kilns; Technical Papers; U.S. Government Printing Office: Washington, DC, USA, 1927; pp. 1–42. [Google Scholar]
- Mellmann, J. The transverse motion of solids in rotating cylinders-forms of motion and transition behavior. Powder Technol. 2001, 118, 251–270. [Google Scholar] [CrossRef]
- Chatterjee, A.; Mukhopadhyay, P.K. Flow of materials in rotary kilns used for sponge iron manufacture: Part III. Effect of ring formation within the kiln. Metall. Trans. B 1983, 14, 393–399. [Google Scholar] [CrossRef]
- Jie, H.; Herz, F. The influence of operational parameters on the axial transport behavior of a bidisperse particle assembly of spherical particles in rotary kilns. Powder Technol. 2025, 454, 120739. [Google Scholar] [CrossRef]
- Henein, H.; Brimacombe, J.K.; Watkinson, A.P. The modeling of transverse solids motion in rotary kilns. Metall. Trans. B 1983, 14, 207–220. [Google Scholar] [CrossRef]
- Vàhl, L.; Kingma, W.G. Transport of solids through horizontal rotary cylinders. Chem. Eng. Sci. 1952, 1, 253–258. [Google Scholar] [CrossRef]
- Khodorov, E.I. Cement Industry Furnaces, 2nd ed.; Stroyizdat: Leningrad, Russia, 1968. [Google Scholar]
- Besedin, P.V.; Trubaev, P.A. Research and Optimization of Processes in Cement Clinker Technology; Publishing House BelGTASM, BIEI: Belgorod, Russia, 2004; ISBN 2013206534. [Google Scholar]
- Litvinova, T.E.; Gerasev, S.A. Behaviour of cerium(III) phosphate in a carbonate-alkaline medium. J. Min. Inst. 2024, 271, 181–188. [Google Scholar]
- Bolshunov, A.V.; Vasilev, D.A.; Dmitriev, A.N.; Ignatev, S.A.; Kadochnikov, V.G.; Krikun, N.S.; Serbin, D.V.; Shadrin, V.S. Results of complex experimental studies at Vostok station in Antarctica. J. Min. Inst. 2023, 263, 724–741. [Google Scholar]
- Kholodilov, A.N.; Istomin, R.S.; Kirilenko, V.I. Improvement technique for manufacturing equivalent materials for modeling nonlinear geomechanical processes in underground mineral mining. MIAB. Mining Inf. Anal. Bull. 2024, 10, 108–122. [Google Scholar] [CrossRef]
- Rutle, J. Investigation of material transport in wet-process rotatory kilns by radio isotopes. Pit Quarry 1955, 48, 120–136. [Google Scholar] [CrossRef]
- Khodorov, E.I. Material Movement in a Rotary Kiln; State Publishing House of Literature on Building Materials: Moscow, Russia, 1957. [Google Scholar]
- Kichkina, E.S.; Abramson, I.G.; Bednyakov, F.I.; Katyshev, Y.; Klimov, V.V.; Chebotarev, V.L. Study of material movement and dust formation in rotary kilns by the labeled atom method. Cement 1967, 4, 6–8. [Google Scholar]
- Chatterjee, A.; Sathe, A.V.; Srivastava, M.P.; Mukhopadhyay, P.K. Flow of materials in rotary kilns used for sponge iron manufacture: Part I. Effect of some operational variables. Metall. Trans. B 1983, 14, 375–381. [Google Scholar] [CrossRef]
- Chatterjee, A.; Sathe, A.V.; Mukhopadhyay, P.K. Flow of materials in rotary kilns used for sponge iron manufacture: Part II. Effect of kiln geometry. Metall. Trans. B 1983, 14, 383–392. [Google Scholar] [CrossRef]
- Sai, P.S.T.; Surender, G.D.; Damodaran, A.D.; Suresh, V.; Philip, Z.G.; Sankaran, K. Residence time distribution and material flow studies in a rotary kiln. Metall. Trans. B 1990, 21, 1005–1011. [Google Scholar] [CrossRef]
- Lebas, E.; Hanrot, F.; Ablitzer, D.; Houzelot, J.-L. Experimental study of residence time, particle movement and bed depth profile in rotary kilns. Can. J. Chem. Eng. 1995, 73, 173–180. [Google Scholar] [CrossRef]
- Spurling, R.J.; Davidson, J.F.; Scott, D.M. The transient response of granular flows in an inclined rotating cylinder. Chem. Eng. Res. Des. 2001, 79, 51–61. [Google Scholar] [CrossRef]
- Scott, D.M.; Davidson, J.F.; Lim, S.-Y.; Spurling, R.J. Flow of granular material through an inclined, rotating cylinder fitted with a dam. Powder Technol. 2008, 182, 466–473. [Google Scholar] [CrossRef]
- Ndiaye, L.G.; Caillat, S.; Chinnayya, A.; Gambier, D.; Baudoin, B. Application of the dynamic model of Saeman to an industrial rotary kiln incinerator: Numerical and experimental results. Waste Manag. 2010, 30, 1188–1195. [Google Scholar] [CrossRef]
- Specht, E.; Shi, Y.C.; Woche, H.; Knabbe, J.; Sprinz, U. Experimental investigation of solid bed depth at the discharge end of rotary kilns. Powder Technol. 2010, 197, 17–24. [Google Scholar] [CrossRef]
- Ngako, S.; Mouangue, R.; Caillat, S.; Kuitche, A.; Saragba, E. Numerical investigation of bed depth height, axial velocity and mean residence time of inert particles in steady state industrial cement rotary kiln: Case of Figuil Plant in Cameroon. Powder Technol. 2015, 271, 221–227. [Google Scholar] [CrossRef]
- Colin, B.; Dirion, J.L.; Arlabosse, P.; Salvador, S. Wood chips flow in a rotary kiln: Experiments and modeling. Chem. Eng. Res. Des. 2015, 98, 179–187. [Google Scholar] [CrossRef]
- Perron, J.; Bui, R.T. Rotary cylinders: Solid transport prediction by dimensional and rheological analysis. Can. J. Chem. Eng. 1990, 68, 61–68. [Google Scholar] [CrossRef]
- Zabolotny, V.; Vish, Z. Application of radioactive materials in the study of material velocity in a furnace. Cement 1975, 4, 21–23. [Google Scholar]
- Murphy, N.; Palmer, C. Axial transport and residence time of MSW in rotary kilns Part I. Experimenta. Foot 1993, 3, 205–206. [Google Scholar] [CrossRef]
- Chen, W.Z.; Wang, C.H.; Liu, T.; Zuo, C.Y.; Tian, Y.H.; Gao, T.T. Residence time and mass flow rate of particles in carbon rotary kilns. Chem. Eng. Process. Process Intensif. 2009, 48, 955–960. [Google Scholar] [CrossRef]
- Abramov, V.Y. Research of Regularities of Work of Chain Heat Exchangers; Stroiizdat: Leningrad, Russia, 1966. [Google Scholar]
- Wu, W.N.; Liu, X.Y.; Hu, Z.; Herz, F.; Specht, E. Measurement of the local material depth in a directly-heated pilot rotary kiln based on temperature fields. Powder Technol. 2018, 330, 12–18. [Google Scholar] [CrossRef]
- Cheremisina, O.V.; Balandinsky, D.A.; Gorbacheva, A.A.; Lysenko, M.R.; Yinzhou, L. Physicochemical features of action of ethoxylated esters of phosphoric acid with different degree of ethoxylation in conditions of froth flotation of apatite. Colloids Surf. A Physicochem. Eng. Asp. 2025, 708, 135974. [Google Scholar] [CrossRef]
- Lebedev, A.B.; Noah, H.L.; Martines, K.Y.; Balandinsky, D.A. The influence of a mixture of nepheline, red mud and calcinated coke on the strength of iron ore pellets. Chernye Met. 2024, 10–18. [Google Scholar] [CrossRef]
- Aleksandrova, T.N.; Lushina, E.A. Influence of an ionic composition of a sludge liquid phase on technological parameters of beneficiation. Tsvetnye Met. 2024, 13–20. [Google Scholar] [CrossRef]
- Abouzeid, A.Z.M.A.; Mika, T.S.; Sastry, K.V.; Fuerstenau, D.W. The influence of operating variables on the residence time distribution for material transport in a continuous rotary drum. Powder Technol. 1974, 10, 273–288. [Google Scholar] [CrossRef]
- Hehl, M.; Kröger, H.; Helmrich, H.; Schügerl, K. Longitudinal mixing in horizontal rotary drum reactors. Powder Technol. 1978, 20, 29–37. [Google Scholar] [CrossRef]
- Afacan, A.; Masliyah, J.H. Solids hold-up in rotary drums. Powder Technol. 1990, 61, 179–184. [Google Scholar] [CrossRef]
- Liu, X.Y.; Specht, E. Mean residence time and hold-up of solids in rotary kilns. Chem. Eng. Sci. 2006, 61, 5176–5181. [Google Scholar] [CrossRef]
- Bongo Njeng, A.S.; Vitu, S.; Clausse, M.; Dirion, J.L.; Debacq, M. Effect of lifter shape and operating parameters on the flow of materials in a pilot rotary kiln: Part I. Experimental RTD and axial dispersion study. Powder Technol. 2015, 269, 554–565. [Google Scholar] [CrossRef]
- Paredes, I.J.; Yohannes, B.; Emady, H.N.; Muzzio, F.J.; Maglio, A.; Borghard, W.G.; Glasser, B.J.; Cuitiño, A.M. Measurement of the residence time distribution of a cohesive powder in a flighted rotary kiln. Chem. Eng. Sci. 2018, 191, 56–66. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, Y.; Li, H.; Li, X.; Gao, X. A simple step-change method to determine mean residence time in rotary kiln and a predictive model at low inclination. Powder Technol. 2018, 333, 30–37. [Google Scholar] [CrossRef]
- Haeldermans, T.; Lataf, M.A.; Vanroelen, G.; Samyn, P.; Vandamme, D.; Cuypers, A.; Vanreppelen, K.; Schreurs, S. Numerical prediction of the mean residence time of solid materials in a pilot-scale rotary kiln. Powder Technol. 2019, 354, 392–401. [Google Scholar] [CrossRef]
- Ryvkin, V.D. Improving the Quality of Products in Pyrometallurgical Processes During the Integrated Processing of Alkaline Aluminosilicates in Alumina Production; Stroiizdat: Leningrad, Russia, 1991. [Google Scholar]
- Wirtz, S.; Pieper, C.; Buss, F.; Schiemann, M.; Schaefer, S.; Scherer, V. Impact of coating layers in rotary cement kilns: Numerical investigation with a blocked-off region approach for radiation and momentum. Therm. Sci. Eng. Prog. 2020, 15, 100429. [Google Scholar] [CrossRef]
- Berta, R.; Lukáč, L. Ash Ring Formation in Lime Rotary Kilns. Adv. Therm. Process. Energy Transform. 2018, 1, 1–4. [Google Scholar] [CrossRef]
- Rippon, L.; Hirtz, B.; Sheehan, C.; Reinheimer, T.; Loewen, P.; Gopaluni, B. Visualization of multiscale ring formation in a rotary kiln. Nord. Pulp Pap. Res. J. 2021, 36, 549–558. [Google Scholar] [CrossRef]
- Saeman, W.C. Passage of solids through rotary kilns: Factors affecting time passage. Chem. Eng. Prog. 1951, 47, 508–514. [Google Scholar]
- Danish, M.; Kumar, S.; Kumar, S. Exact analytical solution for the bed depth profile of solids flowing in a rotary kiln. Powder Technol. 2012, 230, 29–35. [Google Scholar] [CrossRef]
- Parveen, N.; Zaidi, S.; Danish, M. Development and analyses of data-driven models for predicting the bed depth profile of solids flowing in a rotary kiln. Adv. Powder Technol. 2020, 31, 678–694. [Google Scholar] [CrossRef]
- Kramers, H.; Croockewit, P. The passage of granular solids through inclined rotary kilns. Chem. Eng. Sci. 1952, 1, 259–265. [Google Scholar] [CrossRef]
- Ronco, J.J. Tecnologia de las operaciones y 10s procesos de la industria quimica. Ind. y Quim. 1965, 20, 605–614. [Google Scholar]
- Khodorov, E.I. Cement Industry Kilns; Stroiizdat: Leningrad, Russia, 1968. [Google Scholar]
- Aronzon, V.L.; Khodorov, E.I. Calculation of material movement in a rotary kiln using a digital computer. Proc. VAMI 1969, 65–66, 112–120. [Google Scholar]
- Aronzon, V.L.; Khodorov, E.I. Nomograms for calculating material movement in rotary kilns. Proc. VAMI 1969, 65–66, 105–112. [Google Scholar]
- Scribner, N.G. Material movement in rotary drums. Proc. VAMI 1976, 94, 49–55. [Google Scholar]
- Voroshilov, A.P. Modern Problems of Drying Mechanics; Gosenergoizdat: Moscow, Russia, 1938. [Google Scholar]
- Bayard, R.A. New Formula Developed for Kiln Time. Chem Met. 1945, 52, 100–102. [Google Scholar]
- Saeman, W.C. Passage of solids through rotary kilns: Factors affecting time passage. Pit Quarr. 1952, 45, 97–104. [Google Scholar]
- Sai, P.S.T.; Surender, G.D.; Damodaran, A.D. Prediction of axial velocity profiles and solids hold-up in a rotary kiln. Can. J. Chem. Eng. 1992, 70, 438–443. [Google Scholar] [CrossRef]
- Friedman, E.; Marshall, A. Studies in Rotary Drying. Chem. Eng. Prog. 1949, 45, 482–588. [Google Scholar]
- Perry, R.H.; Chilton, C.G.; Kirkpatrick, S.D. Chemical Engineers’ Handbook; McGraw-Hill: New York, NY, USA, 1961. [Google Scholar]
- Zablotny, W.W. The Movement of the Charge in Rotary Kilns. Int. Chem. Eng. 1965, 5, 360–366. [Google Scholar]
- Heiligenstaedt, W. Thermique Appliquee Aux Fours Industriels, 2nd ed.; Dunod: Paris, France, 1971. [Google Scholar]
- Guigui, G.; Huy, F. Thermodynamics of a cement kiln. Third Int. Congr. Cem. Chem. 1958, 346–370. [Google Scholar]
- Mazurov, D.Y. Thermal Engineering Equipment of Binder Plants, 2nd ed.; Stroyizdat: Moscow, Russia, 1982. [Google Scholar]
- Lee, C.C.; Lin, S.D. Handbook of Environmental Engineering Calculations, 2nd ed.; McGraw-Hill: New York, NY, USA, 2007; ISBN 0071475834. [Google Scholar]
- Besedin, P.V.; Klassen, V.K.; Litvinov, A.I.; Sharipov, I.K.; Vasiliev, V.P. Influence of firing process parameters on the material velocity in the kiln. Cement 1978, 10, 21–23. [Google Scholar]
- Perry, J.H. Chemical engineers’ handbook. J. Chem. Educ. 1950, 27, 533. [Google Scholar] [CrossRef]
- Li, S.Q.; Chi, Y.; Li, R.D.; Yan, J.H.; Cen, K.F. Axial transport and residence time of MSW in rotary kilns: Part II. Theoretical and optimal analyses. Powder Technol. 2002, 126, 228–240. [Google Scholar] [CrossRef]
- Bongo Njeng, A.S.; Vitu, S.; Clausse, M.; Dirion, J.L.; Debacq, M. Effect of lifter shape and operating parameters on the flow of materials in a pilot rotary kiln: Part III. Up-scaling considerations and segregation analysis. Powder Technol. 2016, 297, 415–428. [Google Scholar] [CrossRef]
- Yin, H.; Zhang, M.; Liu, H. Numerical simulation of three-dimensional unsteady granular flows in rotary kiln. Powder Technol. 2014, 253, 138–145. [Google Scholar] [CrossRef]
- Moghaddam, S.; Orouji, P.; Mirshams, A.M.; Roomizadeh, E.; Ali, Y.H.E.; Hamzehloo, N. Investigating the potentials to improve the energy consumption of a lime rotary kiln using measurement and CFD simulation. Heat Mass Transf. Und Stoffuebertragung 2022, 59, 949–970. [Google Scholar] [CrossRef]
- Mujumdar, K.S.; Ranade, V.V. CFD modeling of rotary cement kilns. Asia-Pac. J. Chem. Eng. 2008, 3, 106–118. [Google Scholar] [CrossRef]
- Pichler, M.; Haddadi, B.; Jordan, C.; Norouzi, H.; Harasek, M. Influence of particle residence time distribution on the biomass pyrolysis in a rotary kiln. J. Anal. Appl. Pyrolysis 2021, 158, 105171. [Google Scholar] [CrossRef]
- Baba, T.; Nakamura, H.; Takimoto, H.; Ohsaki, S.; Watano, S.; Takehara, K.; Higuchi, T.; Hirosawa, T.; Yamamoto, T. DEM–PBM coupling method for the layering granulation of iron ore. Powder Technol. 2021, 378, 40–50. [Google Scholar] [CrossRef]
- Oschmann, T.; Kruggel-Emden, H. A novel method for the calculation of particle heat conduction and resolved 3D wall heat transfer for the CFD/DEM approach. Powder Technol. 2018, 338, 289–303. [Google Scholar] [CrossRef]
- Witt, P.J.; Sinnott, M.D.; Cleary, P.W.; Schwarz, M.P. A hierarchical simulation methodology for rotary kilns including granular flow and heat transfer. Miner. Eng. 2018, 119, 244–262. [Google Scholar] [CrossRef]
- Wu, W.; Chen, K.; Tsotsas, E. Prediction of rod-like particle mixing in rotary drums by three machine learning methods based on DEM simulation data. Powder Technol. 2024, 448, 120307. [Google Scholar] [CrossRef]
| Slipping Motion | |
| The regimes in this group are primarily characterized by the absence of material mixing, caused by extremely low wall roughness of the cylinder. | |
| Sliding | Occurs in cylinders with smooth walls. It is characterized by the material resting at a certain angle and simply sliding along the rotating wall of the cylinder. Material mixing is practically absent. |
| Surging | Compared to the sliding regime, the material still does not mix. However, due to the less smooth wall surface, the material adheres to the wall and moves with it for some time before sliding back to its initial position after covering a certain distance. |
| Cascading motion | |
| The regimes in this group are primarily characterized by good material mixing and occur when the cylinder wall has sufficiently high friction. The specific regime within this group depends on the following factors: degree of filling, rotational speed, and particle size. | |
| Slumping | Unlike the surging regime, the material does not slide back after traveling a certain distance along the cylinder wall. Instead, it cascades in an avalanche-like manner, creating a sort of discrete process where the motion alternates between the entire mass moving with the wall and subsequently tumbling downward. |
| Rolling | This type of motion is considered the most desirable in rotary kilns, as it provides optimal conditions for heat transfer and chemical reactions. It can be described as follows: In the cross-section, the material is divided into two zones: a stagnant zone and an active zone. In the stagnant zone, mixing is virtually absent, while in the active zone, intensive mixing occurs. At the same time, the surface of the material layer usually remains smooth. |
| Cascading | In this regime, the layer “rolls over”, its height increases, and it ceases to remain smooth. |
| Cataracting motion | |
| The regimes in this group are primarily characterized by the detachment of individual particles from the bulk material and their ejection into the kiln space. These regimes are achieved due to the high rotational speed of the drum. | |
| Cataracting | This regime is characterized by the ejection of particles into the kiln space, which intensifies with an increase in rotational speed. |
| Centrifuging | This regime is achieved at an even higher rotational speed and is characterized by the adhesion of particles ejected from the bulk material to the drum’s surface. |
| № | Material | Particle Size (mm) | Particle Density (kg/m³) | Bulk Density (kg/m³) | Static Angle of Repose (°) | Dynamic Angle of Repose (°) | Length (m) | Diameter (m) | Rotational Speed (rpm) | Inclination Angle (°) | Filling Degree | Flow Rate | Special Conditions |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [12] | Sand | 0.5 | - | - | - | 34.96 | 2.13 | 0.152 | 2.5 | 2 | 25 | 0.0144 m3/h | - |
| [23] | Cement raw mix | - | - | - | - | - | 79.25 | 2.5 | 0.91 | 2.29 | - | 7.95 m3/h | REAL Chains |
| [23] | Cement raw mix | - | - | - | - | - | 99.06 | 2.5 | 0.91 | 2.29 | - | 7.95 m3/h | REAL Chains |
| [23] | Cement raw mix | - | - | - | - | - | 109.73 | 3.4 | 1 | 2.29 | - | 14.56 m3/h | REAL Chains |
| [23] | Cement raw mix | - | - | - | - | - | 112.78 | 3.4 | 0.86 | 2.29 | - | 16.58 m3/h | REAL Chains |
| [24] | Clinker | 3.5–5 | - | 1550 | 37 | 46.1 | 2.7 | 0.5–0.3 | 1.05–3.47 | 1–4.5 | 5–10 | - | |
| [24] | Clinker | 2–3.5 | - | 1518 | 38.4 | 47.5 | 2.7 | 0.5–0.3 | 1.05–3.47 | 1–4.5 | 5–10 | - | |
| [24] | Clinker | 0.6–2 | - | 1570 | 38.2 | 47.5 | 2.7 | 0.5–0.3 | 1.05–3.47 | 1–4.5 | 5–10 | - | |
| [24] | Red brick | 3.5–5 | - | 915 | 42.0 | 53.2 | 2.7 | 0.5–0.3 | 1.05–3.47 | 1–4.5 | 5–10 | - | |
| [24] | Red brick | 2–3.5 | - | 915 | 39.4 | 52 | 2.7 | 0.5–0.3 | 1.05–3.47 | 1–4.5 | 5–10 | - | |
| [24] | Red brick | 0.6–2 | - | 945 | 39.3 | 51.4 | 2.7 | 0.5–0.3 | 1.05–3.47 | 1–4.5 | 5–10 | - | |
| [24] | Limestone | 3.5–5 | - | 1340 | 39.4 | 44.5 | 2.7 | 0.5–0.3 | 1.05–3.47 | 1–4.5 | 5–10 | - | |
| [24] | Limestone | 2–3.5 | - | 1245 | 40 | 47.35 | 2.7 | 0.5–0.3 | 1.05–3.47 | 1–4.5 | 5–10 | - | |
| [24] | Limestone | 0.6–2 | - | 1230 | 40 | 48.5 | 2.7 | 0.5–0.3 | 1.05–3.47 | 1–4.5 | 5–10 | - | |
| [24] | Marl | 0.2–2 | - | 1265 | 45 | 50 | 2.7 | 0.5–0.3 | 1.05–3.47 | 1–4.5 | 5–10 | - | |
| [24] | Shale | 0.2–2 | - | 777 | 40 | 44.3 | 2.7 | 0.5–0.3 | 1.05–3.47 | 1–4.5 | 5–10 | - | |
| [24] | Sand | 0.2–2 | - | 2650 | 33.25 | 37.4 | 2.7 | 0.5–0.3 | 1.05–3.47 | 1–4.5 | 5–10 | - | |
| [24] | Cement raw mix | - | - | 1155 | 43.18 | 49.48 | 45 | 2.7 | 1.07 | 2.18 | - | 6.19 t/h | REAL |
| [25] | Cement raw mix | - | - | - | - | - | 150 | 3 | - | - | - | - | REAL Chains |
| [26] | Iron ore | 3–6 | - | - | - | - | 2 | 0.3 | 0.3–0.7 | 1–3 | - | 30 kg/h | DH- |
| [26] | Iron ore | 3–6 | - | - | - | - | 2 | 0.3 | 0.3–0.7 | 1–3 | - | 30 kg/h | DH |
| [27] | Iron ore | - | - | 1600 | 35 | - | 2 | 0.2–0.6 | 0.6 | 1.5 | - | 0.25–1.25 kg/h | - |
| [27] | Iron ore | - | - | 1600 | 35 | - | 2–4.8 | 0.3 | 0.6 | 1.5 | - | 0.25–1.25 kg/h | - |
| [27] | Iron ore | - | - | 1600 | 35 | - | 2 | 0.2–0.6 | 0.6 | 1.5 | - | 0.25–1.25 kg/h | DH |
| [27] | Iron ore | - | - | 1600 | 35 | - | 2–4.8 | 0.3 | 0.6 | 1.5 | - | 0.25–1.25 kg/h | DH |
| [14] | Iron ore | 3–6 | - | - | - | - | 2 | 0.3 | 0.3–0.7 | 1.5 | - | 0.5 kg/h | CL |
| [14] | Iron ore | 3–6 | - | - | - | - | 4.8 | 0.3 | 0.3–0.7 | 1.5 | - | 0.5 kg/h | CL |
| [28] | Ilmenite | 0.1–0.3 | 4200 | - | 27.4 | - | 5.9 | 0.147 | 1–3 | 0.78–1.37 | - | 6.8–36 kg/h | DH |
| [29] | Coal | 5–20 | 1240 | 750 | 47 | 37 | 6 | 0.6 | 2–4 | 1 | 8–23 | 0.424–0.835 m3/h | - |
| [29] | Coke | 5–20 | 720 | 480 | 47 | 37 | 6 | 0.6 | 2–4 | 1 | 8–23 | 0.424–0.835 m3/h | - |
| [30] | Sand | 0.49 | - | 1600 | 32 | - | 1 | 0.119 | 3–7.5 | 0–5 | 5–25 | - | - |
| [30] | Sand | 0.49 | - | 1600 | 32 | - | 1 | 0.0515 | 3–7.5 | 0–5 | 5–25 | - | - |
| [31] | Sand | 0.46 | - | 1600 | 32 | - | 1 | 0.0515 | 5.6–7.5 | 0–5 | 2–25 | - | DH |
| [31] | Sand | 0.46 | - | 1600 | 32 | - | 1 | 0.053 | 5.6–7.5 | 0–5 | 2–25 | - | DH |
| [32] | Granulated concrete | 0.40 | - | 1360 | 32 | - | 16 | 4.096 | 0.267–0.89 | 1–2.2 | 3.67–12.24 | - | - |
| [32] | Granulated concrete | 0.40 | - | 1360 | 32 | - | 16 | 4.096 | 0.267–0.89 | 1–2.2 | 3.67–12.24 | - | DH |
| [33] | Quartz sand | 0.1–0.4 | - | 1570 | - | 32 | 5 | 0.4 | 1–8 | 1–5 | - | 45–440 kg/h | DH |
| [33] | Clinker | 1–12 | - | 1410 | - | 31 | 5 | 0.4 | 1–8 | 1–5 | - | 45–440 kg/h | DH |
| [33] | Glass beads | 0.4–0.84 | - | 1560 | - | 21 | 5 | 0.4 | 1–8 | 1–5 | - | 45–440 kg/h | DH |
| [33] | Quartz sand | 0.1–0.4 | - | 1570 | - | 32 | 6.7 | 0.25 | 3.5 | 1–2 | - | 25–90 kg/h | - |
| [33] | Clinker | 1–12 | - | 1410 | - | 31 | 6.7 | 0.25 | 3.5 | 1–2 | - | 25–90 kg/h | - |
| [33] | Glass beads | 0.4–0.84 | - | 1560 | - | 28 | 6.7 | 0.25 | 3.5 | 1–2 | - | 25–90 kg/h | - |
| [34] | Cement raw mix | - | 948 | - | 35 | - | 55 | 2.3 | 0–3.57 | 1.72 | - | 0–24 t/h | REAL |
| [35] | Raw wood chips | 5–15x 2–7x 1–3 | - | 280 | - | 42 | 4.2 | 0.21 | 2–4 | 1–2 | 5.2–18.1 | 4–8 kg/h | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fedorova, E.; Morgunov, V.; Lobko, K.; Pupysheva, E. Review: Axial Motion of Material in Rotary Kilns. Eng 2025, 6, 106. https://doi.org/10.3390/eng6060106
Fedorova E, Morgunov V, Lobko K, Pupysheva E. Review: Axial Motion of Material in Rotary Kilns. Eng. 2025; 6(6):106. https://doi.org/10.3390/eng6060106
Chicago/Turabian StyleFedorova, Elmira, Vladimir Morgunov, Kirill Lobko, and Elena Pupysheva. 2025. "Review: Axial Motion of Material in Rotary Kilns" Eng 6, no. 6: 106. https://doi.org/10.3390/eng6060106
APA StyleFedorova, E., Morgunov, V., Lobko, K., & Pupysheva, E. (2025). Review: Axial Motion of Material in Rotary Kilns. Eng, 6(6), 106. https://doi.org/10.3390/eng6060106








