Observer-Based Robust Containment Control of Multi-Agent Systems with Structural Uncertainties and Multiple Delays
Abstract
1. Introduction
2. Preliminaries and Problem Formulation
2.1. Preliminaries and Notations
2.2. Problem Formulation
3. Robust Containment Control Design Condition
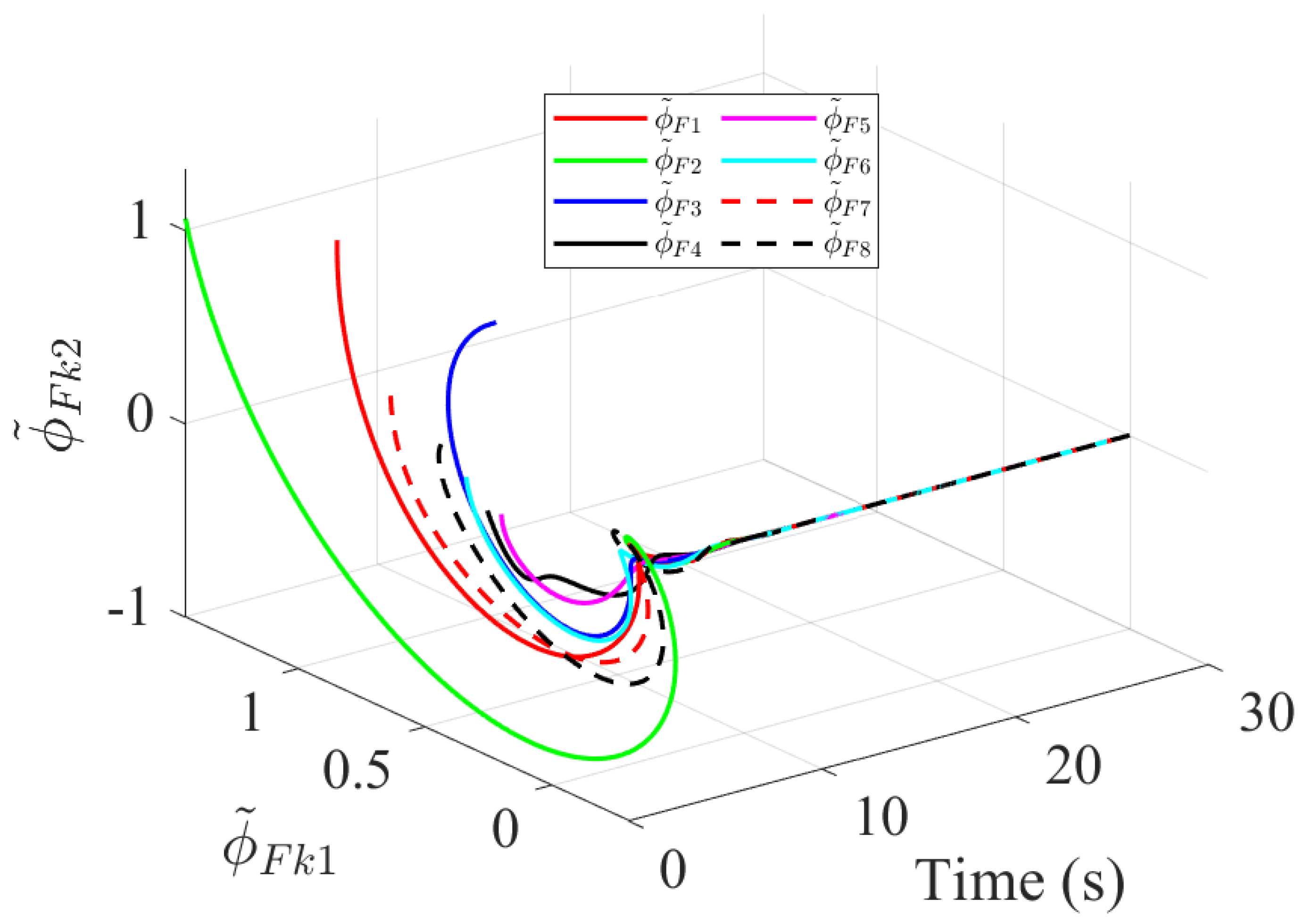
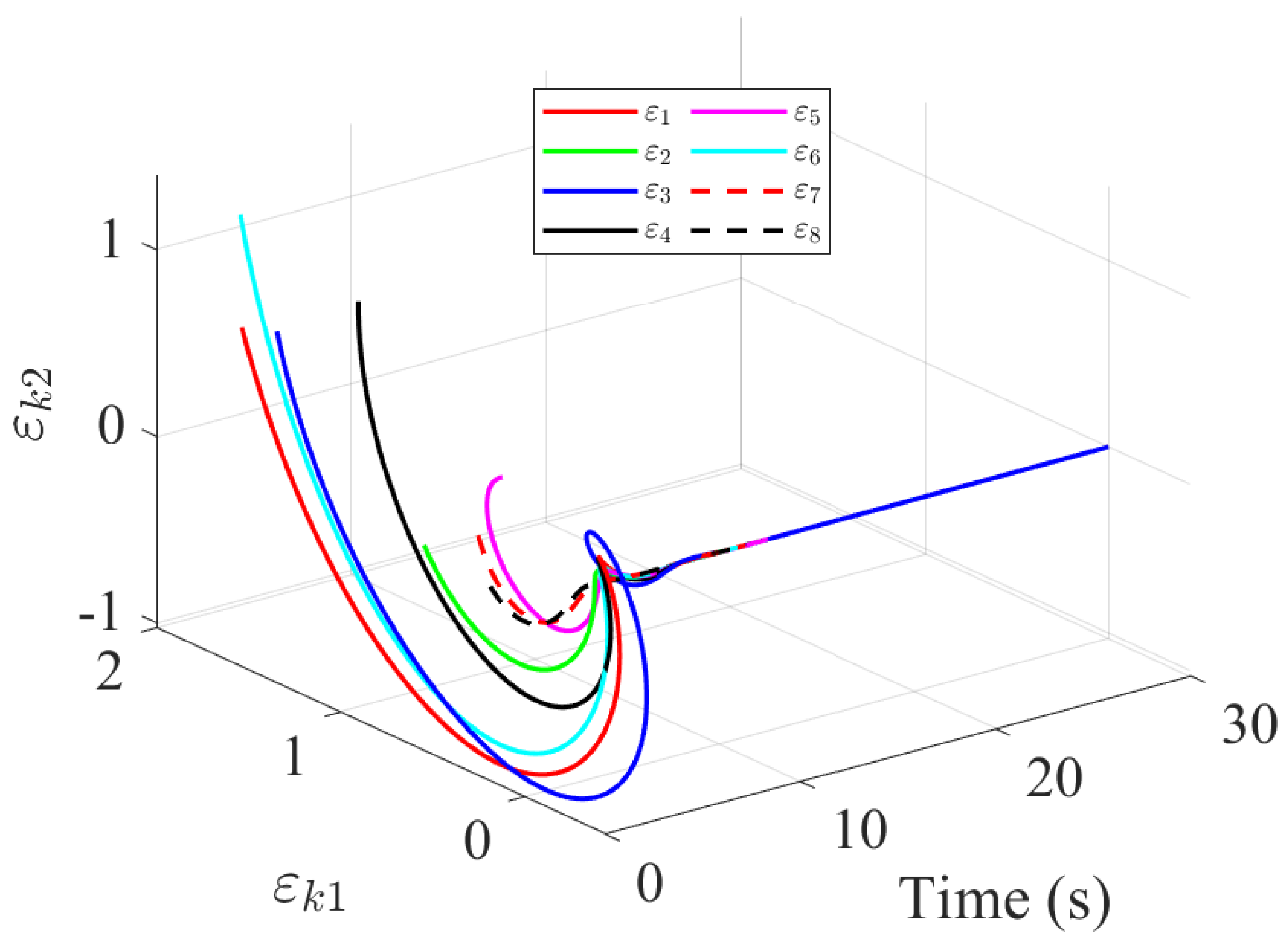
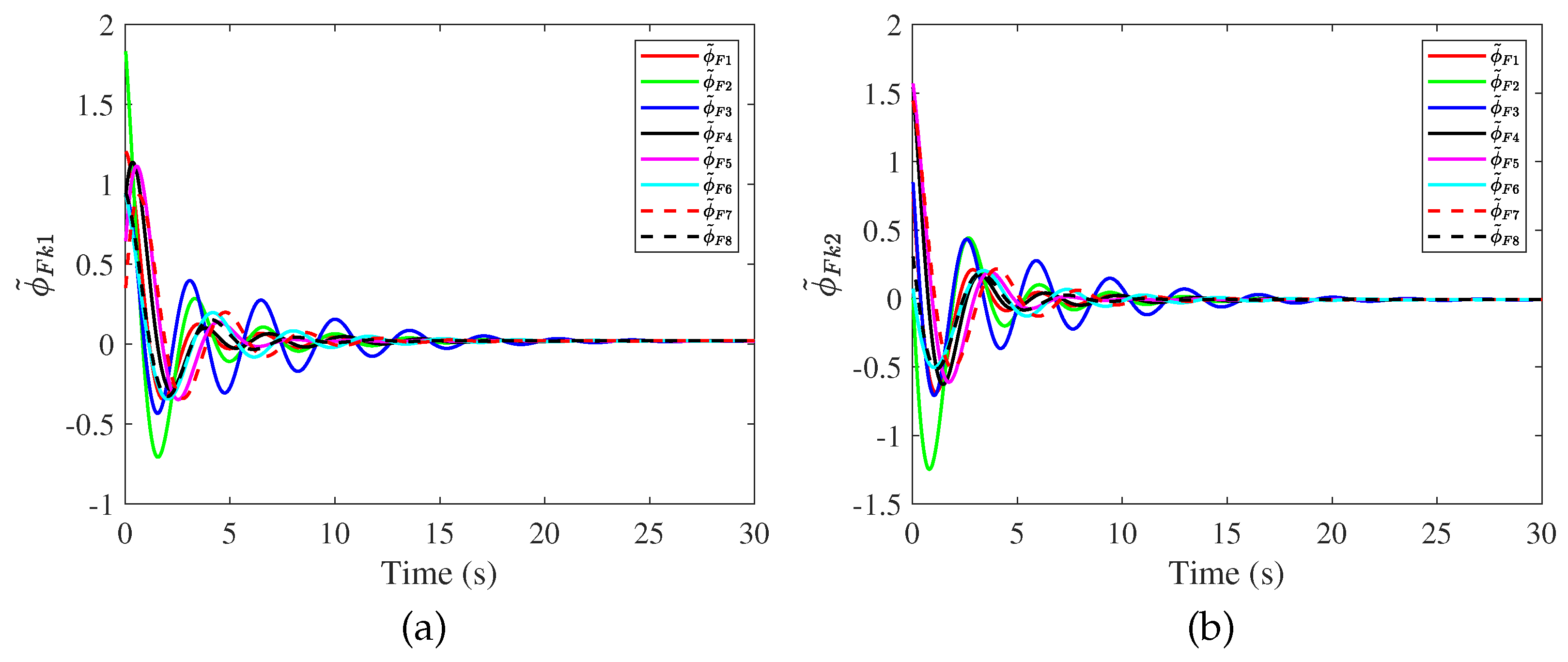
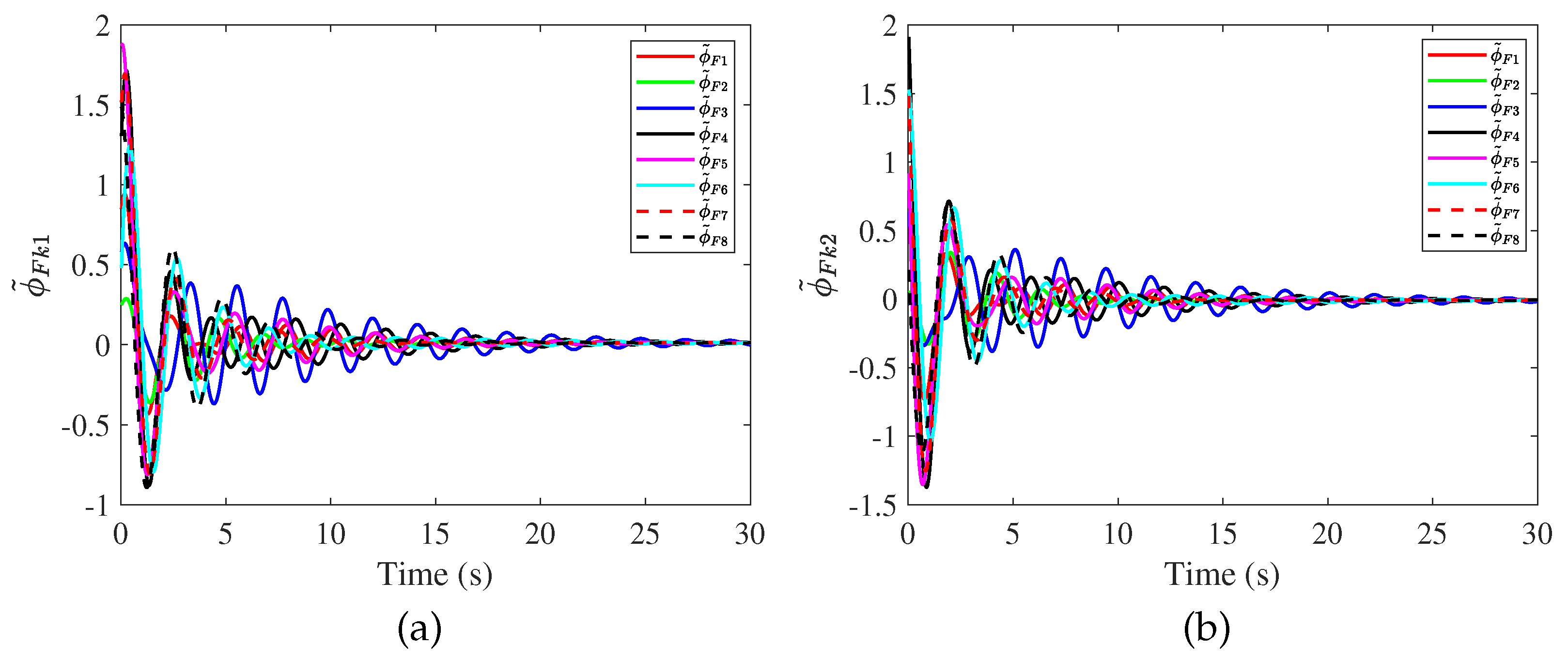
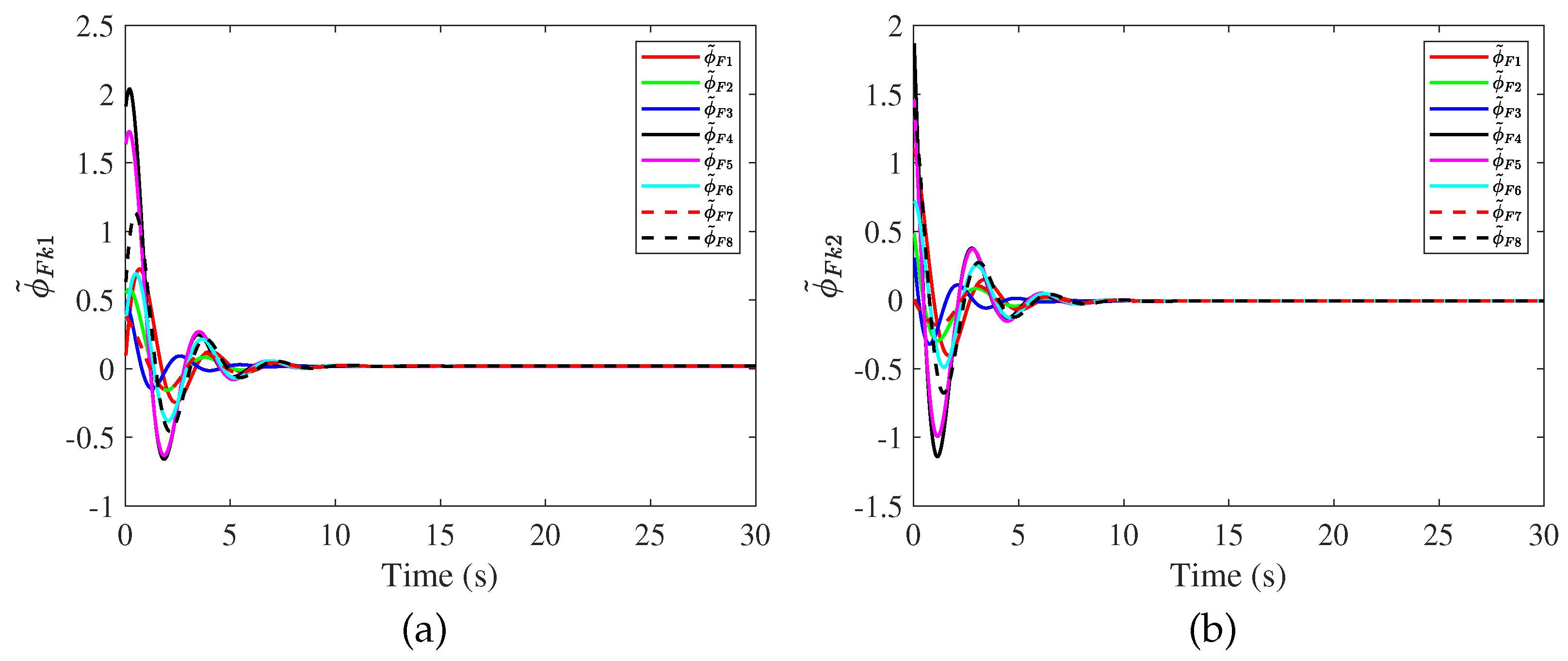
4. Simulation Results
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yuan, C.; Du, Y.; Huangfu, Y.; Gong, C.; Gao, F.; Li, Z. Consensus-based powered cruise and yaw controls for unmanned aerial vehicle with distributed electric propulsion system. IEEE J. Emerg. Sel. Top. Power Electron. 2025, 13, 1769–1782. [Google Scholar] [CrossRef]
- Wu, W.; Lu, Z.; Sun, Y.; Ang, M.; Gong, C. Dynamic task assignment of multiple heterogeneous unmanned aerial vehicles based on consensus with uncertainties. IEEE Aerosp. Electron. Syst. Mag. 2025, 40, 48–60. [Google Scholar] [CrossRef]
- Gao, J.; Manogaran, G.; Nguyen, T.; Kadry, S.; Hsu, C.; Kumar, P. A vehicle-consensus information exchange scheme for traffic management in vehicular ad-hoc networks. IEEE Trans. Intell. Transp. Syst. 2022, 23, 19602–19612. [Google Scholar] [CrossRef]
- Guo, J.; Ding, X.; Wu, W. Reliable traffic monitoring mechanisms based on blockchain in vehicular networks. IEEE Trans. Reliab. 2021, 71, 1219–1229. [Google Scholar] [CrossRef]
- Zhou, Y.; Liu, J. Advances in emerging digital technologies for energy efficiency and energy integration in smart cities. Energy Build. 2024, 315, 114289. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, Y.; Chen, Z.; Soares, J. Multi-agent system consistency-based cooperative scheduling strategy of regional integrated energy system. Energy 2024, 295, 130904. [Google Scholar] [CrossRef]
- Pan, J.; Zhou, G.; Gong, M.; Li, B.; Gao, F.; Tian, G. Estimation and correction of azimuth and attitude errors of attitude tracking for vehicular spacecraft. IEEE Trans. Instrum. Meas. 2023, 72, 1–10. [Google Scholar] [CrossRef]
- Liu, C.; Loxton, R.; Lin, Q.; Teo, K. Dynamic optimization for switched time-delay systems with state-dependent switching conditions. Siam J. Control Optim. 2018, 56, 3499–3523. [Google Scholar] [CrossRef]
- Liu, C.; Loxton, R.; Teo, K.; Wang, S. Optimal state-delay control in nonlinear dynamic systems. Automatica 2022, 135, 109981. [Google Scholar] [CrossRef]
- Wang, J.; Li, Y.; Duan, Z.; Zeng, J. A fully distributed robust secure consensus protocol for linear multi-agent systems. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 3264–3268. [Google Scholar] [CrossRef]
- Zhou, Y.; Wen, G.; Zhou, J.; Liu, H.; Lü, J. Data-driven output consensus tracking control for heterogeneous multi-agent systems with a dynamic leader. IEEE Trans. Control Netw. Syst. 2025, 12, 2029–2039. [Google Scholar] [CrossRef]
- Wang, D.; Huang, Y.; Guo, S.; Wang, W. Distributed h∞ containment control of multiagent systems over switching topologies with communication time delay. Int. J. Robust Nonlinear Control 2020, 30, 5221–5232. [Google Scholar] [CrossRef]
- Zhou, T.; Liu, Q.; Wang, W. Nonfragile containment control of nonlinear multi-agent systems via a disturbance observer-based approach. Int. J. Robust Nonlinear Control 2024, 34, 3726–3741. [Google Scholar] [CrossRef]
- Zhou, T.; Liu, C.; Wang, W. Nonfragile robust H∞ containment control for multi-agent systems with a time-varying delay. J. Frankl. Inst. 2024, 361, 106732. [Google Scholar] [CrossRef]
- Lu, Y.; Dong, X.; Li, Q.; Lü, J.; Ren, Z. Time-varying group formation-containment tracking control for general linear multiagent systems with unknown inputs. IEEE Trans. Cybern. 2022, 52, 11055–11067. [Google Scholar] [CrossRef]
- Feng, L.; Huang, B.; Sun, J.; Sun, Q.; Xie, X. Adaptive event-triggered time-varying output group formation containment control of heterogeneous multiagent systems. IEEE/CAA J. Autom. Sin. 2024, 11, 1398–1409. [Google Scholar] [CrossRef]
- Wang, P.; Jia, Y. Robust h∞ containment control for uncertain multi-agent systems with inherent nonlinear dynamics. Int. J. Syst. Sci. 2016, 47, 1073–1083. [Google Scholar] [CrossRef]
- Han, D.; Chesi, G.; Hung, Y. Robust consensus for a class of uncertain multi-agent dynamical systems. IEEE Trans. Ind. Inform. 2013, 9, 306–312. [Google Scholar] [CrossRef]
- Wang, P.; Jia, Y. Robust h∞ containment control for second-order multi-agent systems with nonlinear dynamics in directed networks. Neurocomputing 2015, 153, 235–241. [Google Scholar] [CrossRef]
- Li, Z.; Duan, Z.; Lewis, F. Distributed robust consensus control of multi-agent systems with heterogeneous matching uncertainties. Automatica 2014, 50, 883–889. [Google Scholar] [CrossRef]
- Wen, G.; Wang, P.; Huang, T.; Yu, W.; Sun, J. Robust neuro-adaptive containment of multileader multiagent systems with uncertain dynamics. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 406–417. [Google Scholar] [CrossRef]
- Zhang, S.; Li, Z.; Wang, X. Robust h2 consensus for multi-agent systems with parametric uncertainties. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 2473–2477. [Google Scholar]
- Hu, Y.; Yan, H.; Zhang, H.; Wang, M.; Zeng, L. Robust adaptive fixed-time sliding-mode control for uncertain robotic systems with input saturation. IEEE Trans. Cybern. 2023, 53, 2636–2646. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, X.; Chang, X.; Zhao, N. Adaptive fault-tolerant control-based real-time reachable set synthesis of heterogeneous nonlinear singular multiagent systems with uncertain parameters. IEEE Trans. Autom. Sci. Eng. 2024, 21, 4526–4535. [Google Scholar] [CrossRef]
- Huang, W.; Liu, H.; Huang, J. Distributed robust containment control of linear heterogeneous multi-agent systems: An output regulation approach. IEEE/CAA J. Autom. Sin. 2022, 9, 864–877. [Google Scholar] [CrossRef]
- Atrianfar, H.; Karimi, A. Robust containment control of heterogeneous multi-agent systems with structured uncertainty and external disturbances. Int. J. Robust Nonlinear Control 2022, 32, 698–714. [Google Scholar] [CrossRef]
- Wang, Q.; Shu, P.; Yan, B.; Shi, Z.; Hua, Y.; Lü, J. Robust predefined output containment for heterogeneous nonlinear multiagent systems under unknown nonidentical leaders’ dynamics. IEEE Trans. Cybern. 2024, 54, 5770–5780. [Google Scholar] [CrossRef] [PubMed]
- Tian, B.; Zhang, H.; Cui, P.; Wang, Z.; Yan, H. Robust finite-time containment of networked heterogeneous nonlinear systems with intermittent measurement only. IEEE Trans. Netw. Sci. Eng. 2025, 12, 2823–2834. [Google Scholar] [CrossRef]
- Xiao, W.; Cao, L.; Li, H.; Lu, R. Observer-based adaptive consensus control for nonlinear multi-agent systems with time-delay. Sci. China Inf. Sci. 2020, 63, 1–17. [Google Scholar] [CrossRef]
- Zhou, X.; Wang, H.; Tian, Y.; Dai, X. Consensus tracking via quantized iterative learning control for singular nonlinear multi-agent systems with state time-delay and initial state error. Nonlinear Dyn. 2021, 103, 2701–2719. [Google Scholar] [CrossRef]
- Shi, L.; Li, W.; Shi, M.; Lin, B. Event-based bipartite containment control for multi-agent networks subject to communication delay. IEEE Trans. Netw. Sci. Eng. 2024, 11, 2024–2033. [Google Scholar] [CrossRef]
- Li, H.; Zhang, C.; Liu, S.; Zhang, X. A dynamic gain approach to consensus control of nonlinear multiagent systems with time delays. IEEE Trans. Cybern. 2022, 52, 6993–7001. [Google Scholar] [CrossRef]
- Zhang, H.; Ren, H.; Mu, Y.; Han, J. Optimal consensus control design for multiagent systems with multiple time delay using adaptive dynamic programming. IEEE Trans. Cybern. 2022, 52, 12832–12842. [Google Scholar] [CrossRef] [PubMed]
- Sun, H.; Yang, H.; Han, H.; Sun, J.; Qiao, J. Consensus of mass with input and communication delays by predictor-based protocol. IEEE Trans. Cybern. 2023, 11, 7126–7135. [Google Scholar] [CrossRef]
- Zhang, K.; Zhou, B.; Duan, G. Leader-following consensus of multi-agent systems with time delays by fully distributed protocols. Syst. Control Lett. 2023, 178, 105582. [Google Scholar] [CrossRef]
- Hua, C.; Feng, S.; Zhang, L. Output-feedback control of interconnected nonlinear systems with both state and input delays based on truncated prediction. IEEE Trans. Circuits Syst. II Express Briefs 2023, 70, 4108–4112. [Google Scholar] [CrossRef]
- Koru, A.; Ramírez, A.; Sarsılmaz, S.; Sipahi, R.; Yucelen, T.; Dogan, K. Containment control of multi-human multi-agent systems under time delays. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 3344–3356. [Google Scholar] [CrossRef]
- Yang, R.; Liu, S.; Li, X. Observer-based bipartite containment control of fractional multi-agent systems with mixed delays. Inf. Sci. 2023, 626, 204–222. [Google Scholar] [CrossRef]
- Chen, L.; Liu, C.; Chu, Z.; Lopes, A.; Chen, Y. Leader follower weighted consensus of nonlinear fractional-order multiagent systems using current and time delay state information. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 5814–5823. [Google Scholar] [CrossRef]
- Shariati, A.; Tavakoli, M. A descriptor approach to robust leader-following output consensus of uncertain multi-agent systems with delay. IEEE Trans. Autom. Control 2017, 62, 5310–5317. [Google Scholar] [CrossRef]
- Parsa, M.; Danesh, M. Robust containment control of uncertain multi-agent systems with time-delay and heterogeneous lipschitz nonlinearity. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 2312–2321. [Google Scholar] [CrossRef]
- Mesbahi, M.; Egerstedt, M. Graph Theoretic Methods in Multiagent Networks; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Gu, K.; Chen, J.; Kharitonov, V. Stability of Time-Delay Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2003. [Google Scholar]

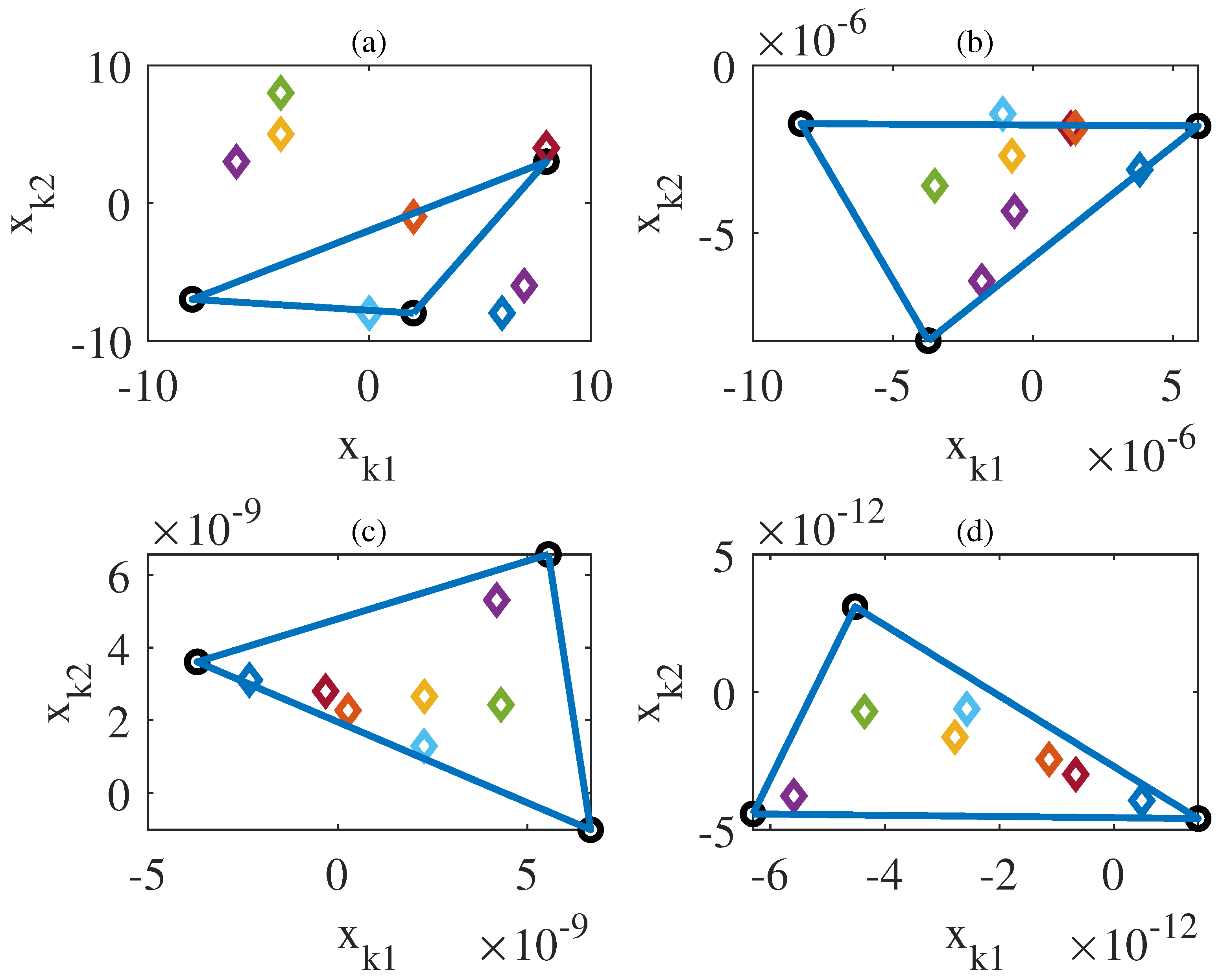
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, T. Observer-Based Robust Containment Control of Multi-Agent Systems with Structural Uncertainties and Multiple Delays. Eng 2025, 6, 336. https://doi.org/10.3390/eng6120336
Zhou T. Observer-Based Robust Containment Control of Multi-Agent Systems with Structural Uncertainties and Multiple Delays. Eng. 2025; 6(12):336. https://doi.org/10.3390/eng6120336
Chicago/Turabian StyleZhou, Tuo. 2025. "Observer-Based Robust Containment Control of Multi-Agent Systems with Structural Uncertainties and Multiple Delays" Eng 6, no. 12: 336. https://doi.org/10.3390/eng6120336
APA StyleZhou, T. (2025). Observer-Based Robust Containment Control of Multi-Agent Systems with Structural Uncertainties and Multiple Delays. Eng, 6(12), 336. https://doi.org/10.3390/eng6120336








