A Practical Tutorial on Spiking Neural Networks: Comprehensive Review, Models, Experiments, Software Tools, and Implementation Guidelines

Abstract

Spiking neural networks (SNNs) provide a biologically inspired, event-driven alternative to artificial neural networks (ANNs), potentially delivering competitive accuracy at substantially lower energy. This tutorial-study offers a unified, practice-oriented assessment that combines critical review and standardized experiments. We benchmark a shallow fully connected network (FCN) on MNIST and a deeper VGG7 architecture on CIFAR-10 across multiple neuron models (leaky integrate-and-fire (LIF), sigma–delta, etc.) and input encodings (direct, rate, temporal, etc.), using supervised surrogate-gradient training implemented in Intel Lava, SLAYER, SpikingJelly, Norse, and PyTorch. Empirically, we observe a consistent but tunable trade-off between accuracy and energy. On MNIST, sigma–delta neurons with rate or sigma–delta encodings achieve 98.1% accuracy (ANN baseline: 98.23%). On CIFAR-10, sigma–delta neurons with direct input reach 83.0% accuracy at just two time steps (ANN baseline: 83.6%). A GPU-based operation-count energy proxy indicates that many SNN configurations operate below the ANN energy baseline; some frugal codes minimize energy at the cost of accuracy, whereas accuracy-oriented settings (e.g., sigma–delta with direct or rate coding) narrow the performance gap while remaining energy-conscious—yielding up to threefold efficiency compared with matched ANNs in our setup. Thresholds and the number of time steps are decisive factors: intermediate thresholds and the minimal time window that still meets accuracy targets typically maximize efficiency per joule. We distill actionable design rules—choose the neuron–encoding pair according to the application goal (accuracy-critical vs. energy-constrained) and co-tune thresholds and time steps. Finally, we outline how event-driven neuromorphic hardware can amplify these savings through sparse, local, asynchronous computation, providing a practical playbook for embedded, real-time, and sustainable AI deployments.

1. Introduction

Modern AI systems—particularly deep neural networks—have achieved remarkable accuracy across vision, language, and control tasks, but at rapidly growing computational and energy costs [1,2]. Mitigation strategies such as pruning and quantization can reduce multiply-accumulate (MAC) counts and memory traffic [3,4,5]. Yet, the overall footprint of state-of-the-art models continues to raise sustainability concerns [6]. This tension motivates the exploration of approaches that are both accurate and power-aware. Recent studies demonstrate that conventional machine learning techniques are increasingly being applied to embedded and industrial tasks under tight resource and latency constraints [7,8,9], underscoring the need for more event-driven, energy-efficient paradigms.

Spiking neural networks (SNNs) offer a biologically inspired, event-driven paradigm in which discrete spikes convey information over time [10,11]. Their sparse, asynchronous computation and temporal coding can translate into lower energy consumption on neuromorphic substrates while naturally capturing temporal structure [12,13,14,15]. At the same time, practical deployment remains challenging; spikes are non-differentiable, complicating gradient-based optimization [16,17,18]; performance depends critically on the choice of encoding scheme [19,20]; and toolchains and benchmarks for fair SNN–ANN comparisons are still maturing.

Gap. The key gap lies in the lack of a unified, practice-oriented analysis. Existing surveys often treat neuron models, encodings, learning rules, and software stacks in isolation, providing limited apples-to-apples evidence on accuracy–energy trade-offs against equivalent ANN baselines across both shallow and deep regimes. A comprehensive perspective that links design choices to measurable performance and energy efficiency remains scarce [18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33].

This work. We address this gap by combining a comprehensive, critical review with a hands-on tutorial and standardized benchmarking:

• We systematize SNN components, as follows: neuron models (integrate-and-fire (IF)/leaky integrate-and-fire (LIF), adaptive leaky integrate-and-fire (ALIF), exponential integrate-and-fire/adaptive exponential integrate-and-fire (EIF/AdEx), resonate-and-fire (RF), Hodgkin–Huxley (HH), Izhikevich (IZH), resonate-and-fire–Izhikevich (RF–IZH) hybrid, current-based neuron (CUBA), sigma–delta ($\mathsf{\Sigma }\mathsf{\Delta }$)); neural encodings (direct/single-value encoding, rate coding, temporal variants including time-to-first-spike (TTFS), rank-order with number-of-spikes (R–NoM), population coding, phase-of-firing coding (PoFC), burst coding, sigma–delta encoding ($\mathsf{\Sigma }\mathsf{\Delta }$)); and learning paradigms: supervised (backpropagation-through-time (BPTT) with surrogate gradients, e.g., SLAYER, SuperSpike, EventProp), unsupervised (spike-timing–dependent plasticity (STDP) and variants), reinforcement (reward-modulated STDP (R-STDP), e-prop), hybrid supervised STDP (SSTDP), and ANN→SNN conversion. The practical pipeline used in this study relies on supervised training via BPTT with surrogate gradients (aTan by default; SLAYER/SuperSpike-style updates) for the tutorial and benchmark experiments [16,17,18,19].
• We provide a practical tutorial (with reference to a representative neuromorphic software stack, e.g., Intel Lava) covering model construction, encoding choices, and training–inference workflows suitable for resource-constrained deployment.
• We establish a side-by-side evaluation protocol that compares SNNs with architecturally matched ANNs on a shallow setting (MNIST) and a deeper convolutional setting (CIFAR-10 with VGG-style backbones [34]). Metrics include task accuracy, time steps, spike activity, and power-oriented proxies to highlight accuracy–efficiency trade-offs.
• We distill design guidelines that map application goals—accuracy targets and per-inference energy budgets—onto actionable choices of neuron model, encoding scheme, number of time steps, and supervised surrogate-gradient training (e.g., SLAYER, SuperSpike, aTan).

Scope and structure. Section 2 reviews the fundamentals of SNNs, including encoding strategies, neuron models, and learning paradigms. Section 3 presents the datasets, experimental setup, model architectures, and software tools. Section 4 reports the comparative performance and energy analyses on MNIST and CIFAR-10 and provides an integrated discussion of accuracy–energy trade-offs and design implications. Finally, Section 5 summarizes the key findings and offers recommendations for future research. Our aim is to provide a coherent pathway from principles to practice, guiding the design of SNNs that balance accuracy with energy efficiency in real-world deployments. An overview of the article’s logical flow and interconnections among its main sections is illustrated in Figure 1.

2. Background of Spiking Neural Networks

SNNs are widely regarded as the “third generation” of neural models, narrowing the gap between ANNs and biological computation by representing information through discrete spike events over time [10,35]. Whereas ANNs operate with continuous activations and synchronous MAC operations [36], SNNs exploit sparse, event-driven accumulation updates. This temporal, asynchronous processing aligns with neural physiology and can yield substantial energy savings—particularly on neuromorphic hardware—while natively handling time-dependent signals.

2.1. Key Aspects of Spiking Neural Networks

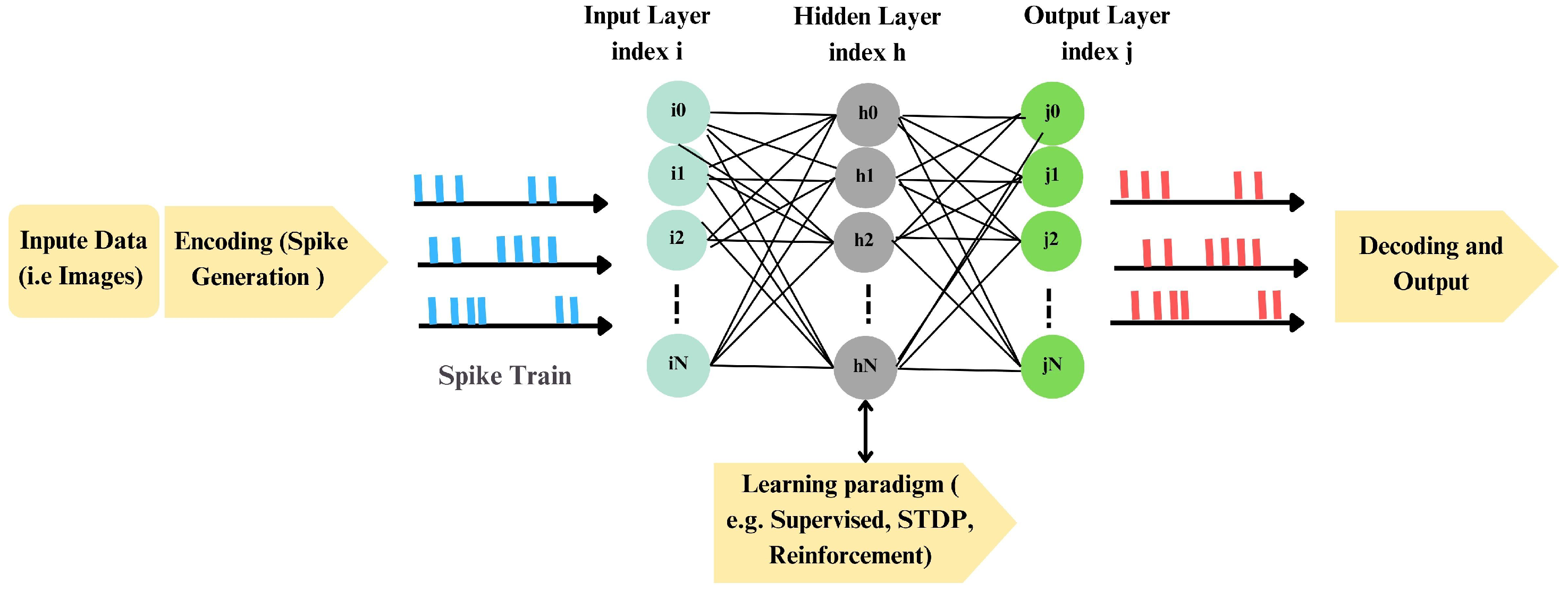
2.1.1. Processing Pipeline

Figure 2 outlines a generic SNN workflow comprising encoding, network processing, decoding, and learning. In the encoding stage, external signals are transformed into spike trains. Common strategies include rate codes, time-based codes (e.g., TTFS or inter-spike intervals), and population codes, selected according to signal statistics and latency–energy constraints. For instance, image intensities can be converted into Poisson spike trains whose rates are proportional to pixel values [37]. During network processing, spikes propagate through layers of model neurons—e.g., LIF, AdEx, IZH, or HH—whose subthreshold dynamics and thresholds determine temporal integration and spike generation [38,39]. Decoding then maps output spike activity to decisions using spike counts (rate-based), precise timing (temporal), or pooled population activity, depending on the task requirements [37]. Learning rules—supervised, unsupervised, reinforcement, or hybrid—adjust synapses to meet specific behavioral or optimization goals.

2.1.2. Power Efficiency: Mechanisms and Practice

The energy efficiency of SNNs stems from sparsity (computation occurs only upon spike events), lower-cost accumulate (AC) updates in place of dense MACs, and event-driven memory traffic, which reduces data movement—often the dominant energy term in modern systems [40,41]. On neuromorphic substrates (e.g., Intel Loihi, IBM TrueNorth, SpiNNaker), these properties translate into significant system-level gains through fine-grained parallelism, on-chip spike routing, and local memory near compute units [42,43,44,45,46,47]. Empirically, energy per inference scales with the total number of synaptic events and the average firing rate. Consequently, design parameters—encoding sparsity (e.g., TTFS, $\mathsf{\Sigma }\mathsf{\Delta }$), neuron/leak constants, thresholds, rate regularizers, and time-window length—directly trade accuracy for energy [28,37,48]. Comparative studies report multi× efficiency improvements for SNNs in event-rich settings and on dedicated hardware [42,45,49], while highlighting the importance of maintaining low spike rates and co-optimizing algorithms with hardware constraints.

2.1.3. Advantages and Challenges

By design, SNNs capture temporal dependencies with high timing resolution. They can compute efficiently in sparse regimes, enabling low-latency, low-power inference in settings such as event-based sensing and edge computing [25,28,48]. However, three obstacles hinder their widespread adoption. First, spike non-differentiability complicates gradient-based training; practical solutions rely on surrogate gradients, exact adjoints, local plasticity, or ANN-to-SNN conversion, each with trade-offs in accuracy, stability, or hardware compatibility [16,17,18]. Second, performance can lag ANN baselines if encoders, decoders, and neuron models are not co-designed for the specific task [50]. Third, software and hardware ecosystems for SNNs are still maturing, and standardized, energy-aware benchmarks remain limited.

2.1.4. Learning and Encoding

Unsupervised learning in SNNs often relies on STDP to uncover structure from temporal correlations [51]. Supervised training employs BPTT with surrogate gradients to approximate spike derivatives, enabling deep SNN optimization [16]. Reinforcement learning adjusts synaptic weights based on reward signals, supporting closed-loop control and robotics [52]. Encoding strategies strongly influence latency and energy—rate codes are robust but can be spike-heavy; time-based codes reduce spikes and latency but demand precise timing; and population codes improve separability and noise tolerance at the expense of added computational cost.

2.1.5. Real-World Applications

SNNs have been validated across multiple domains where temporal precision and energy constraints are critical. In event-based vision, SNNs implemented on neuromorphic hardware achieve real-time gesture recognition on Dynamic Vision Sensor (DVS) datasets with milliwatt-scale power budgets [42,53], demonstrate robust object and gesture processing on mobile platforms [54,55], and enable low-latency tracking and control [56,57]. Beyond human-centric vision, embedded deep models are applied to animal affect recognition [9], where SNNs offer low-latency, low-power inference for on-animal or field-deployed sensors. In robotics and closed-loop control, while conventional ANN-based controllers remain prevalent in practice [58,59], spike-based policies can operate on-chip, enabling responsive and power-aware navigation and manipulation [53,56]. In biomedical signal processing, SNNs support wearable ECG/EEG analytics and brain–computer interfaces under stringent energy and latency constraints [60,61,62,63]. In industrial monitoring and tribology, neural models estimate lubrication parameters from sensor data [7], where event-driven SNN inference can reduce both power consumption and latency at the edge. For time-series forecasting, SNNs model nonstationary environmental and energy signals, with traditional ML baselines from subsurface and energy domains providing context for accuracy–efficiency comparisons [8] (e.g., wind and solar forecasting), while maintaining low inference costs [64,65,66,67,68]. In finance and IoT/edge analytics, event-driven SNNs process sparse, asynchronous streams for anomaly detection and prediction under tight power budgets [69,70,71,72]. These applications underscore SNNs’ ability to transform biological inspiration into practical, energy-efficient intelligence—particularly when learning rules, encoding schemes, and neuron models are co-optimized with the target hardware and workload.

2.2. Encoding in SNNs

Encoding is a pivotal process in SNNs, transforming continuous-valued inputs into discrete spike events and thereby bridging the gap between external stimuli and spike-based information processing [73]. This transformation is central to leveraging the distinctive advantages of SNNs, including temporal dynamics, event-driven computation, and energy efficiency [74]. The choice of encoding strategy directly determines how effectively information is represented, how temporal patterns are captured, and how power-efficiently the network operates—properties that are crucial for real-time processing and deployment on neuromorphic hardware [75].

Despite their importance, encoding schemes face several design challenges. These include balancing representational accuracy with computational complexity, maintaining biological plausibility, and ensuring compatibility with neuromorphic circuits [76,77]. Furthermore, encoding decisions strongly influence system robustness, as some strategies offer greater resilience to noise or adversarial perturbations than others [78]. Consequently, research on encoding has increasingly focused on systematically exploring and optimizing strategies to enhance scalability and efficiency, thereby positioning SNNs as viable alternatives to traditional ANNs in energy-constrained and real-time environments [79].

This subsection reviews the main categories of encoding schemes employed in SNNs, emphasizing their respective strengths and limitations.

Table 1. Summary Of SNN encoding schemes reflecting the critical analysis in Section 2.2. Figure 3 and Figure 4 illustrate representative examples.

Encoding Type	Main Applications	Complexity	Biological Plausibility	Advantages	Challenges
Rate Coding [38,75,78]	Image and signal processing; ANN-to-SNN conversion; resource-constrained inference	Low	High	Simple implementation; noise–adversarial robustness; hardware-friendly mapping from activations	Loses fine temporal structure; window-length–latency sensitivity; can require high spike counts that raise energy [80]
Direct Input Encoding [73,74,76,78,81]	Deep vision and real-time pipelines with large datasets; accuracy/ latency–critical use	Moderate–high	Low	Fewer time steps; preserves input fidelity; simplifies front end; fast inference	Not event driven; multi-bit input raises compute–energy; lower biological realism
Temporal Coding [14,24,38,76,82]	Rapid sensory processing; real-time decisions; fine temporal discrimination–patterns	High	High	High information per spike; low-latency responses; potentially energy efficient with sparse spiking	Sensitive to jitter/noise; complex decoding; training with precise timings is challenging
Population Coding [83,84]	Speech–audio; noisy environments; improving separability with simple classifiers	High	High	Noise robustness via redundancy; improved linear separability	More neurons increase energy; decoding large populations adds computational overhead
$\mathsf{\Sigma }\mathsf{\Delta }$ Encoding [74,78,85,86,87,88]	Dynamic signals (wearables, biomedical, streaming sensors); energy-aware neuromorphic platforms	Moderate–high	Moderate	Encodes changes (fewer spikes) with good fidelity; noise shaping; strong energy savings	Requires feedback-loop–circuit tuning; trade-offs among fidelity, latency, and energy
Burst Coding [13,75,89,90]	Biologically realistic simulations; temporally complex signals; long-activity tasks	Moderate–high	High	Rapid information transfer in spike packets; can be energy saving when bursts are well managed	Synchronizing bursts complicates decoding; scalability and parameter tuning on hardware
PoFC [87,91,92,93]	Spatial navigation/sensory processing with oscillations; high-fidelity temporal representation	High	High	Dense information per spike via phase; strong discriminability; potential spike-count/energy reduction	Requires precise global phase reference; sensitive to timing noise; complex decoding and STDP integration

provides a comparative overview, while Figure 3 and Figure 4 illustrate representative examples. The first figure highlights three fundamental approaches—rate, TTFS, and burst coding—while the second figure expands the view to include inter-spike interval, N-of-M, population, and PoFC coding. Together, these visualizations and the summary table offer an integrated perspective on how information can be encoded in SNNs.

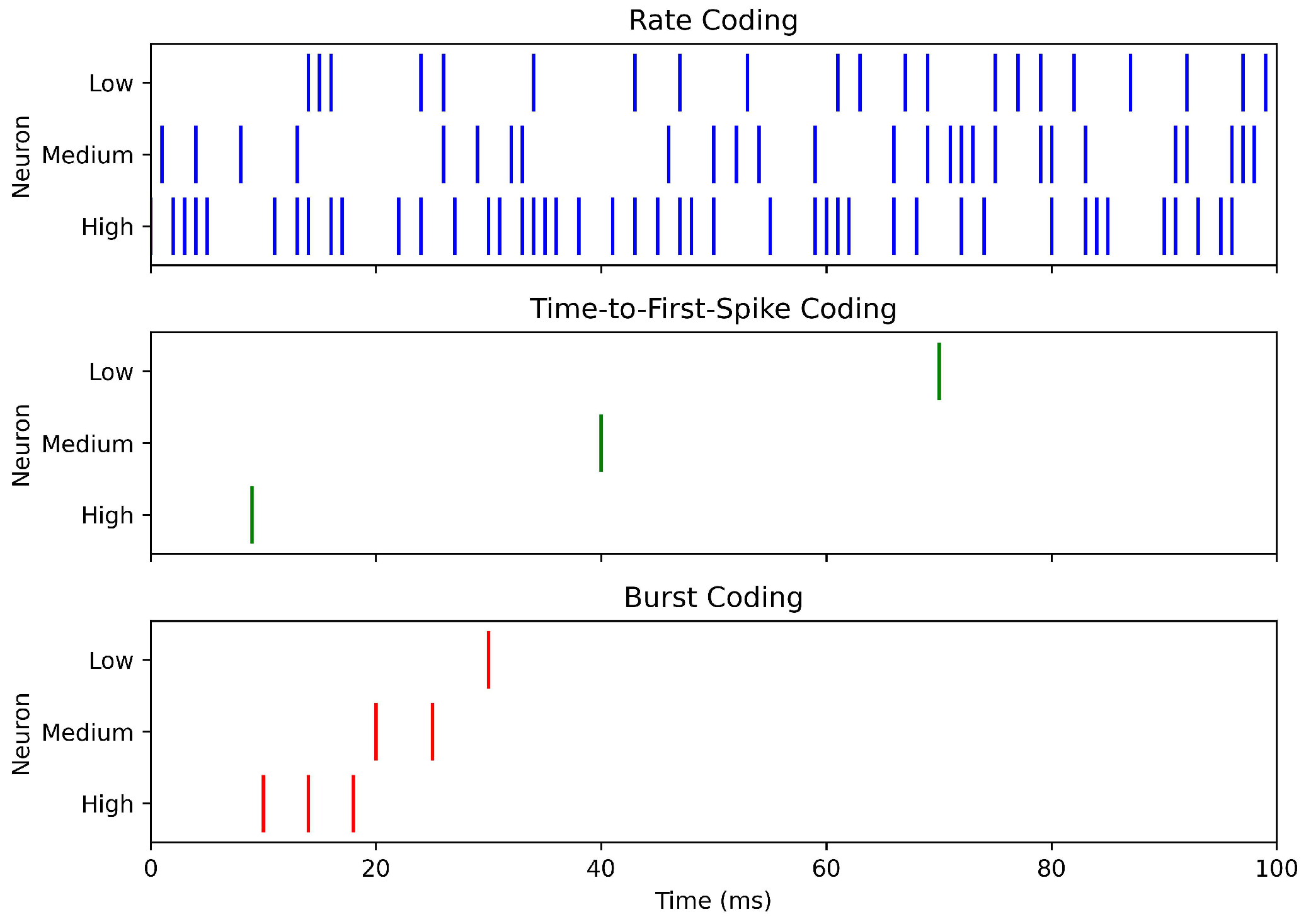
2.2.1. Rate Coding

Rate coding represents stimulus intensity by the number of spikes emitted within a time window:

$$V={\displaystyle \frac{N_{\mathrm{spike}}}{T}}.$$

(1)

Its simplicity, biological plausibility, and the clear correspondence between firing rates and ANN activations make it a common choice for image and signal processing, as well as for embedded deployments where robustness and ease of implementation are priorities [78]. Because it averages activity over a window T, it discards fine timing information. Consequently, achieving high accuracy often requires longer windows or higher spike counts, which increases latency and energy consumption, making this method less suitable for rapid, event-driven scenarios [78,80].

2.2.2. Direct Input Encoding

Direct input encoding feeds continuous-valued signals (e.g., pixel intensities) directly into the input layer without converting them into spike trains [74,78]. By bypassing stochastic spike generation, it can reduce the number of time steps and improve latency and accuracy—making it useful for deep architectures, large-scale vision applications, and real-time decision tasks—while preserving input fidelity and simplifying the preprocessing stage [76]. However, this convenience comes at the cost of event-driven sparsity: multi-bit input activity increases computational load and energy consumption compared to spike-based schemes and reduces biological plausibility, making it a weaker fit for resource- or power-constrained neuromorphic deployments [73,74,78,81].

2.2.3. Temporal Coding

Temporal coding emphasizes the precise timing of spikes rather than their average rate, aligning with biological evidence that spike timing conveys rich and rapidly accessible information [24,38,75]. By leveraging the timing of spikes, this family of methods offers faster and potentially more energy-efficient information transmission than rate coding. Several variants exist:

• Time-to-first-spike (TTFS): Encodes stimulus strength in the latency of the first spike:

  $$t_{\mathrm{spike}}=t_{\mathrm{onset}}+\mathsf{\Delta }t,$$

  (2)

  where $t_{\mathrm{onset}}$ is the stimulus onset time and $\mathsf{\Delta }t$ the delay before firing [14]. TTFS is highly power-efficient, as minimal spiking activity can support rapid decisions, although it requires precise timing and complicates learning.
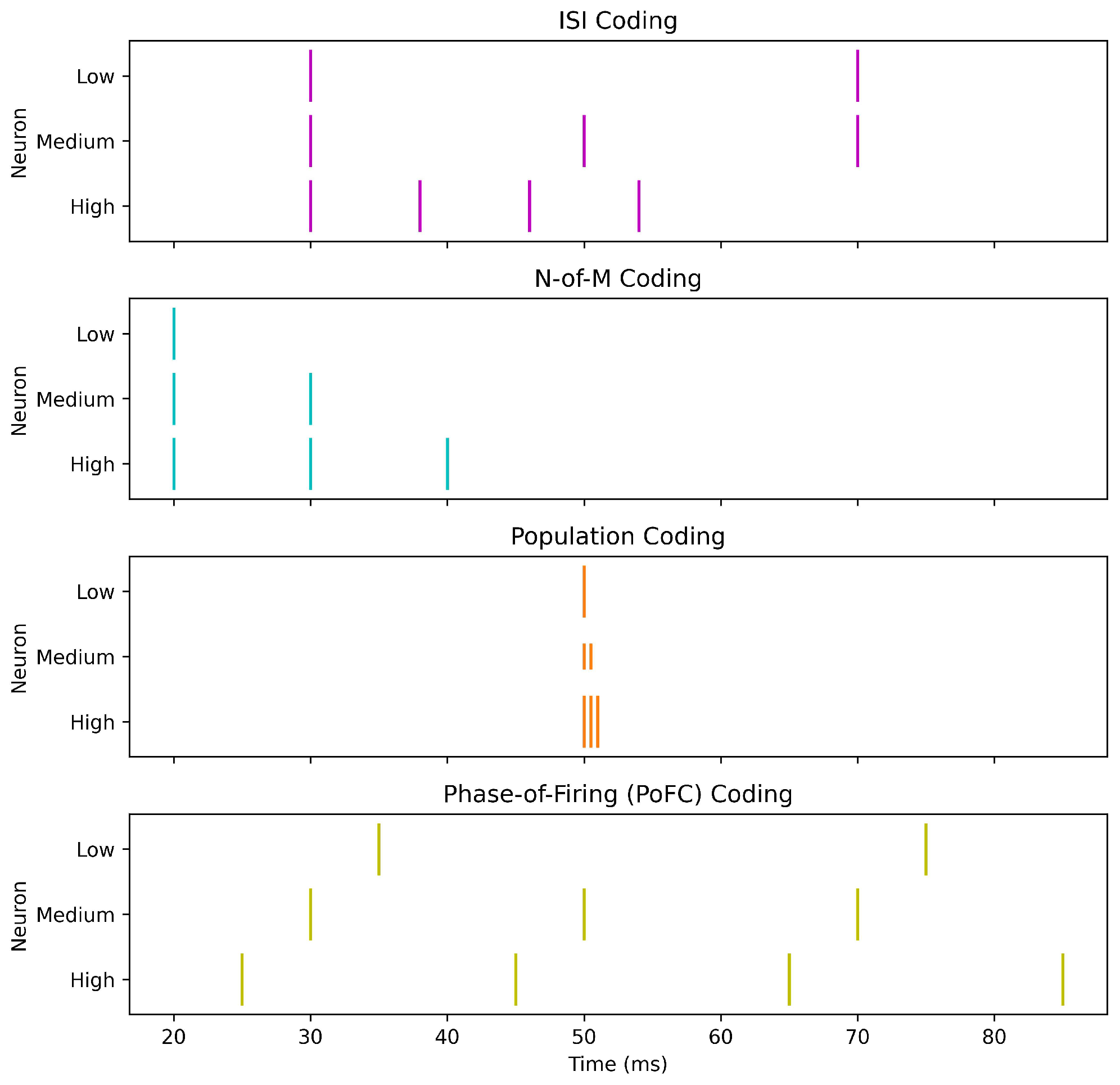
• Inter-spike interval (ISI): Encodes information in the time gap between consecutive spikes:

  $$IS{I}_i=t_{i+1}-t_i,$$

  (3)

  providing richer temporal detail at the cost of increased spiking and energy use [14].
• N-of-M (NoM) coding: Transmits only the first N out of M possible spikes, improving hardware efficiency but discarding spike-order information [82].
• Rank order coding (ROC): Utilizes the sequence of spike arrivals according to synaptic weights, providing high discriminability but at the cost of computational intensity and sensitivity to precise timing [24].
• Ranked-N-of-M (R-NoM): Combines ROC and NoM by propagating the first N spikes while weighting their order:

  $$\mathrm{Activation}=\sum _{i=1}^N{\mathrm{Weight}}_i\times f\left(i\right)\times {\mathrm{Spike}}_i,$$

  (4)

  where $f\left(i\right)$ is a decreasing modulation function with spike order [82].

Temporal coding can yield more information per spike and support low-latency decision-making, potentially reducing overall energy consumption if efficiently implemented. However, it also introduces challenges in robustness: decoding can be complex, the schemes are sensitive to noise and spike-timing variability, and training deep SNNs with precise temporal codes remains difficult [76]. These trade-offs position temporal coding as a powerful yet demanding alternative, best suited for applications where rapid response and high temporal precision outweigh implementation simplicity and energy stability.

2.2.4. Population Coding

Population coding distributes information across an ensemble of neurons, enhancing robustness and separability—useful for noisy, time-varying signals such as speech, audio, or sensor fusion—but at the cost of greater neuron count, decoding overhead, and increased energy and memory traffic [83,84]. A common readout is the weighted population response:

$$R=\sum _{i=1}^n{w}_i{r}_i,$$

where $w_i$ and $r_i$ denote the weight and firing rate of the i-th neuron, respectively. This approach complements latency- and phase-based schemes by pooling precise temporal cues, thereby trading efficiency for improved reliability [83,84].

2.2.5. $\mathsf{\Sigma }\mathsf{\Delta }$ Encoding

$\mathsf{\Sigma }\mathsf{\Delta }$ encoding transmits changes rather than absolute values through a simple feedback loop:

$$\mathsf{\Delta }{x}_t=x_t-x_{t-1},$$

(5)

$$y_t=\mathrm{Threshold}\left({\mathsf{\Sigma }}_t+\mathsf{\Delta }{x}_t\right),$$

(6)

$${\mathsf{\Sigma }}_{t+1}={\mathsf{\Sigma }}_t+\mathsf{\Delta }{x}_t-y_t,$$

(7)

where $x_t$ is the input, $\mathsf{\Delta }{x}_t$ the change in input, $y_t$ the emitted spike, and ${\mathsf{\Sigma }}_t$ an accumulated reconstruction error. By encoding differences instead of absolute values, $\mathsf{\Sigma }\mathsf{\Delta }$ encoding produces sparse spike trains with high temporal fidelity and reduced energy consumption, making it particularly effective for dynamic, streaming signals on neuromorphic and wearable/biomedical platforms [74,78]. Noise shaping supports robust signal reconstruction [85,86,87], though effective deployment requires careful tuning of thresholds and feedback parameters, as well as circuit-aware trade-offs among fidelity, latency, and power [88].

2.2.6. Burst Coding

Burst coding represents information using short, high-frequency spike packets, mirroring rhythmic firing patterns observed in cortical and subcortical regions [13,75,89,90]. A burst for neuron i over a window $[t_{\mathrm{start}},t_{\mathrm{end}}]$ can be expressed as

$$B_i=\sum _{t=t_{\mathrm{start}}}^{t_{\mathrm{end}}}{s}_i\left(t\right),$$

(8)

where $s_i\left(t\right)\in \{0,1\}$ indicates a spike at time t. Grouping spikes into short, dense packets facilitates rapid information transfer and provides strong temporal cues with fewer decision windows—an advantage for event-rich sensing and closed-loop control. However, synchronizing burst onset and network-wide timing increases decoding complexity and hardware demands, while poorly tuned burst parameters may negate energy savings [13,75,89,90]. In practice, burst coding is most effective when biological realism and efficient processing of temporally complex signals are priorities, provided that synchronization and parameter tuning are carefully managed.

2.2.7. PoFC Coding

Phase-of-firing coding (PoFC) encodes information through the phase of each spike relative to an ongoing oscillation (e.g., theta or gamma rhythms) [87,91,92,93]. The phase of the i-th spike is computed as

$${\varphi }_i=mod\left(t_{{\mathrm{spike}}_i}-t_{\mathrm{osc}},T_{\mathrm{osc}}\right),$$

(9)

where $t_{\mathrm{osc}}$ is the oscillation reference time and $T_{\mathrm{osc}}$ its period. By exploiting phase locking observed in the hippocampus and other brain regions, PoFC can encode more information per spike than rate coding—yielding rich, low-count representations and potentially lower energy consumption. However, it requires precise synchronization and is sensitive to timing jitter; accurate phase extraction and integration with plasticity mechanisms (e.g., STDP) further increase implementation complexity [91,92,93]. PoFC is most effective for high-fidelity temporal discrimination and navigation or sensory tasks shaped by oscillatory dynamics, though resource-constrained neuromorphic deployments must balance its representational richness against robustness and hardware simplicity [87].

2.2.8. Impact of Encoding Schemes on SNN Performance and Power Efficiency

Encoding serves as a primary lever shaping both information representation and the computational or energy footprint of SNNs. Foundational work includes $\mathsf{\Sigma }\mathsf{\Delta }$ modulation for efficient analog-to-spike conversion [85] and temporally rich schemes such as rank-order coding [24]. Subsequent surveys emphasize that the “best” encoding scheme is application-dependent, balancing accuracy, latency, energy, robustness, and hardware constraints [73].

Recent developments highlight several trends: (i) $\mathsf{\Sigma }\mathsf{\Delta }$ interfaces adapted to SNNs maintain signal fidelity over wide dynamic ranges while reducing spike counts, though they require careful feedback tuning and add circuit complexity [86,87]; (ii) unified analyses of TTFS, ROC, NoM, and R–NoM clarify discriminability under realistic noise and timing variability, and differentiable training methods help narrow the gap with gradient-based optimization [76,82]; and (iii) hybrid or dynamic approaches—such as layer-wise burst+phase schemes or attention-gated temporal encodings—enhance throughput-per-watt without sacrificing accuracy [13,94,95].

Comparative trends across studies remain consistent: Direct-input (analog) encoding reduces time steps and can improve accuracy and latency for deep architectures but sacrifices event-driven sparsity at the input stage [74]; rate coding is simple, conversion-friendly, and robust but loses fine temporal resolution and may require longer windows or higher spike counts [78]; temporal encodings (TTFS/ISI) provide high information density and fast decision-making yet are sensitive to jitter and more challenging to train or deserialize at scale [14,82]; and population coding improves separability and noise tolerance in temporally rich signals but increases neuron count and decoding cost [84]. Table 1 and Figure 3, Figure 4 and Figure 5 summarize these trade-offs.

Guidelines for Selecting an Encoding Scheme

• Primary objective: For latency-critical workloads, prefer TTFS, ROC, or layer-wise hybrids that emphasize fast temporal cues [13,14]. For energy-constrained continuous sensing, use $\mathsf{\Sigma }\mathsf{\Delta }$ or sparse rate coding [78,86,87].
• Noise and non-idealities: In noisy sensors or non-ideal hardware, population or burst coding can enhance robustness. Fine temporal encodings, however, may require precise clocking or signal filtering [13,84].
• Model and hardware complexity: Choose rate or direct-input encoding for simplicity, ANN→SNN conversion, or resource-limited devices. Reserve $\mathsf{\Sigma }\mathsf{\Delta }$ and temporal hybrid schemes for platforms that support feedback loops or high-precision timing [74,78,87].
• Scalability and training: When end-to-end gradient optimization is essential, select encodings with proven surrogate-gradient compatibility (rate, TTFS, or selected hybrids) and validated noise tolerance [76,82].

In summary, no single encoding scheme dominates across all use cases. Effective designs tailor—and often hybridize—encodings according to the target application’s accuracy–latency–energy requirements and the hardware’s timing and circuit capabilities. These relationships are visualized in Figure 3, Figure 4 and Figure 5, and summarized in Table 1.

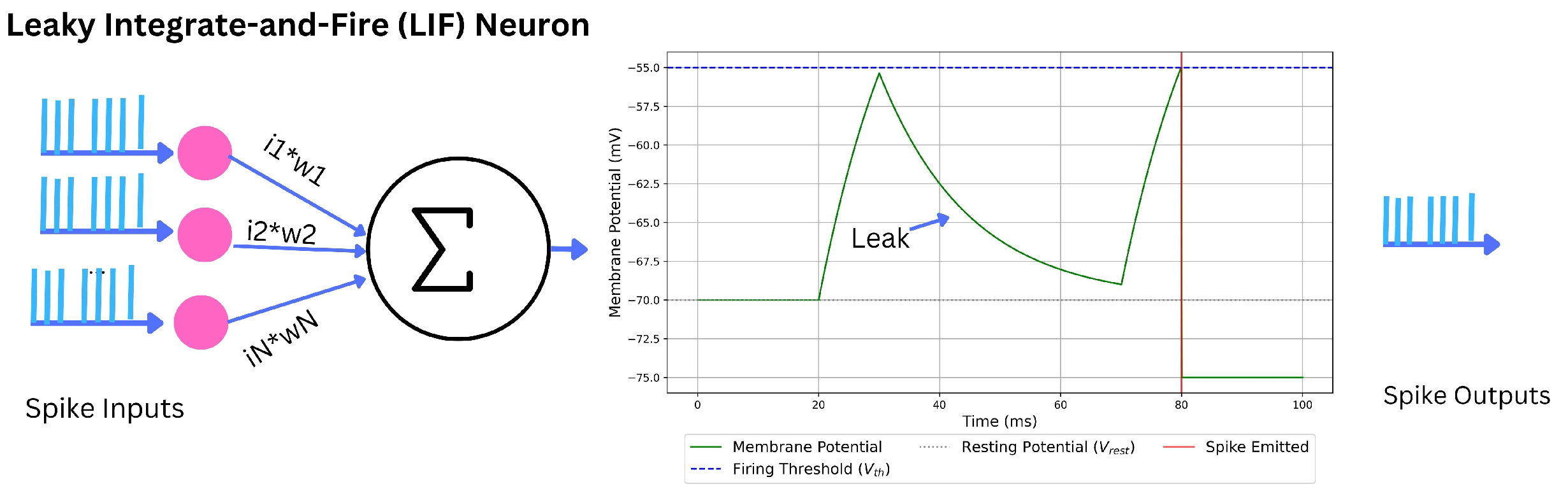
2.3. Spiking Neuron Models

Neuron models are the computational primitives of SNNs: they define how synaptic events are integrated, how spikes are generated, and how signals propagate through a network. The choice of model governs representational power, energy consumption, latency, and hardware suitability [10,38,96]. Broadly, neuron models lie on a spectrum that trades biological fidelity for computational efficiency. At one end, biophysical formulations such as HH accurately reproduce membrane dynamics but are computationally expensive at scale [97,98]. At the other end, families of integrate-and-fire models (IF, LIF, and extensions such as ALIF, QIF/EIF, SRM) abstract spiking as filtered integration followed by thresholding, enabling large networks and low-power deployment [38]. Intermediate phenomenological models (IZH, AdEx, RF) capture rich firing behaviors with moderate cost, offering a pragmatic balance for many practical applications [39,99].

Selecting a neuron model is, therefore, an application-driven decision that weighs fidelity, efficiency, and implementation complexity. Detailed conductance-based models can be advantageous for tasks requiring precise subthreshold or adaptive dynamics, while simplified IF variants often suffice for rate-based processing and fast, energy-efficient inference. Intermediate models are attractive when diverse temporal patterns are important, but computational resources are limited. Additional factors include the availability of stable learning rules (e.g., surrogate-gradient training for LIF/AdEx/IZH), robustness to noise and device non-idealities, and the target hardware’s support for state variables and synaptic dynamics [96,98,99]. A concise, per-model summary of mechanisms, advantages, and challenges is provided in Table 2.

2.3.1. Spike Response Neuron (SRM)

The SRM provides a compact, kernel-based description of a spiking neuron, in which the membrane potential is modeled as the superposition of postsynaptic response kernels and a spike-triggered afterpotential [38,100]:

$$V\left(t\right)=\eta (t-\widehat{t})+{\int }_{-\infty }^t\kappa (t-\widehat{t},s)I(t-s)ds,$$

(10)

where $\widehat{t}$ denotes the last spike time, $\eta (·)$ is a refractory/after-spike kernel, $\kappa (·,·)$ is a synaptic filter, and $I(·)$ represents the input drive. A spike is generated when $V\left(t\right)$ exceeds a dynamic threshold:

$$\theta (t-\widehat{t})=\left\{\begin{array}{cc}\infty ,\hfill & t-\widehat{t}\le {\gamma }_{\mathrm{ref}},\hfill \\ {\theta }_0+{\theta }_1{e}^{-(t-\widehat{t})/{\tau }_{\theta }},\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

(11)

where ${\gamma }_{\mathrm{ref}}$ is the absolute refractory period and the threshold decays exponentially back to ${\theta }_0$. The SRM encompasses fixed-kernel variants (SRM₀) and forms with spike-triggered threshold adaptation or state-dependent kernels (SRM⁺), unifying integrate-and-fire dynamics while remaining analytically tractable and efficient for event-driven simulation. This separation of synaptic and refractory effects makes SRM convenient for modeling STDP, analyzing computational properties, and hardware-efficient implementations. Being phenomenological, however, it lacks rich subthreshold biophysics (e.g., voltage-gated conductances or resonance) unless extended, and practical use requires careful calibration of $\eta$, $\kappa$, and $\theta (·)$ [38].

2.3.2. Integrate-and-Fire Neuron Family (IF, LIF)

The integrate-and-fire family models a neuron as a linear integrator with threshold-and-reset dynamics [35,38,101,102,103]. When $V\left(t\right)$ crosses $\vartheta$ from below, a spike is emitted and $V\leftarrow V_{\mathrm{reset}}$ (optionally followed by a refractory period). Their minimal state, analytical tractability, and event-driven nature make IF/LIF models a cornerstone for large-scale SNNs and neuromorphic hardware deployment.

Perfect IF (PIF)

The ideal, non-leaky integrator accumulates input without passive decay:

$$C{\displaystyle \frac{dV\left(t\right)}{dt}}=I\left(t\right),$$

(12)

where C is the membrane capacitance and $I\left(t\right)$ is the input current. When $V\left(t\right)\ge \vartheta$, the neuron emits a spike and resets to $V_{\mathrm{reset}}$. PIF is computationally minimal but overestimates temporal integration by neglecting leak effects.

Leaky IF (LIF)

Illustrated in Figure 6, the LIF model incorporates passive membrane leakage:

$${\tau }_m{\displaystyle \frac{dV\left(t\right)}{dt}}=-\left(V\left(t\right)-V_{\mathrm{rest}}\right)+RI\left(t\right),$$

(13)

where ${\tau }_m=RC$ is the membrane time constant, R the membrane resistance, and $V_{\mathrm{rest}}$ the resting potential. The LIF model captures membrane decay, supports stochastic analysis, and enables efficient event-driven updates [38,102].

Both IF and LIF provide simplicity, stability, and compatibility with surrogate-gradient training, but their linear subthreshold dynamics lack conductance-based nonlinearities such as adaptation or resonance. They are frequently extended with adaptive mechanisms (ALIF) or nonlinear thresholds (EIF/AdEx) when richer temporal behavior is required.

2.3.3. Adaptive Leaky Integrate-and-Fire Neuron (ALIF)

ALIF augments LIF with spike-frequency adaptation, reproducing reduced firing under sustained drive via either a dynamic threshold or a spike-triggered hyperpolarizing current [38,100,104]. This adds history dependence while retaining efficient, event-driven simulation and surrogate-gradient trainability.

Dynamic-Threshold ALIF

$${\tau }_m{\displaystyle \frac{dv\left(t\right)}{dt}}=-\left(v\left(t\right)-V_{\mathrm{rest}}\right)+RI\left(t\right),\mathrm{spike}\mathrm{if}v\left(t\right)\ge \theta \left(t\right),$$

(14)

$$\theta \left(t\right)={\theta }_0+\beta \sum _{t_s<t}exp\left(-(t-t_s)/{\tau }_{\theta }\right),$$

(15)

where ${\tau }_m=RC$, ${\theta }_0$ is the baseline threshold, $\beta$ the adaptation strength, and ${\tau }_{\theta }$ its decay constant. On a spike at $t_s$, $v\left(t_s^{+}\right)=V_{\mathrm{reset}}$.

Current-Based ALIF

$${\tau }_m{\displaystyle \frac{dv\left(t\right)}{dt}}=-\left(v\left(t\right)-V_{\mathrm{rest}}\right)+RI\left(t\right)-w\left(t\right),\mathrm{spike}\mathrm{if}v\left(t\right)\ge \vartheta ,$$

(16)

$${\tau }_w{\displaystyle \frac{dw\left(t\right)}{dt}}=-w\left(t\right)+b\sum _{t_s<t}\delta (t-t_s),$$

(17)

with adaptation current $w\left(t\right)$, jump b per spike, and decay ${\tau }_w$. After a spike, $v\left(t_s^{+}\right)=V_{\mathrm{reset}}$ and $w\left(t_s^{+}\right)\leftarrow w\left(t_s^{-}\right)+b$.

ALIF improves sequence processing and temporal credit assignment with modest overhead but introduces additional state variables and parameters that require calibration. Very slow or multi-timescale adaptation may call for extended variants (e.g., AdEx or multi-${\tau }_w$ ALIF) [35,102].

2.3.4. Exponential Integrate-and-Fire Neuron (EIF)

The EIF neuron sharpens spike initiation by adding an exponential term to the leaky membrane dynamics, providing a smooth, biophysically motivated threshold [38,105]. In current-based form,

$${\tau }_m{\displaystyle \frac{dV\left(t\right)}{dt}}=-\left(V\left(t\right)-V_{\mathrm{rest}}\right)+{\mathsf{\Delta }}_{T}exp\left({\displaystyle \frac{V\left(t\right)-V_T}{{\mathsf{\Delta }}_T}}\right)+RI\left(t\right),$$

(18)

where $V_{\mathrm{rest}}$ is the resting potential, $V_T$ the rheobase (effective spike-initiation) voltage, ${\mathsf{\Delta }}_T$ the slope factor controlling onset sharpness, and $I\left(t\right)$ the input current. A spike is emitted when $V\left(t\right)$ diverges past a set peak (e.g., $V_{\mathrm{spike}}$), after which $V\leftarrow V_{\mathrm{reset}}$ and an absolute refractory period ${\tau }_{\mathrm{ref}}$ may be imposed.

Compared with LIF, EIF reproduces the rapid upstroke of action potentials and more accurate responses to fast, fluctuating inputs (gain, phase response, and f–I curves) while remaining far cheaper than conductance-based models [103,105]. The added nonlinearity and parameters improve fidelity but require calibration (notably ${\mathsf{\Delta }}_T$ and $V_T$) and can stiffen numerical integration near threshold. EIF serves as a practical compromise for studies of high-frequency synaptic integration, spike initiation, and neuromorphic implementations that need a smooth, differentiable surrogate of threshold dynamics [38].

2.3.5. Adaptive Exponential Integrate-and-Fire Neuron (AdEx)

AdEx extends LIF with an exponential spike-initiation term and a spike-triggered adaptation variable, yielding a compact neuron that reproduces regular/fast-spiking, adapting, and bursting behaviors [106]:

$$C_m{\displaystyle \frac{d{V}_m}{dt}}=-G_L(V_m-E_L)+G_L{\mathsf{\Delta }}_{T}exp\left({\displaystyle \frac{V_m-V_T}{{\mathsf{\Delta }}_T}}\right)-w+I_{\mathrm{syn}},$$

(19)

$${\tau }_w{\displaystyle \frac{dw}{dt}}=a(V_m-E_L)-w,$$

(20)

where $V_m$ is membrane potential, $C_m$ capacitance, $G_L$ leak conductance, $E_L$ leak reversal, $V_T$ spike-initiation voltage, ${\mathsf{\Delta }}_T$ slope factor, w the adaptation current, a subthreshold adaptation, ${\tau }_w$ its time constant, and $I_{\mathrm{syn}}$ synaptic current. A spike is registered when $V_m$ exceeds $V_{\mathrm{spike}}$, after which $V_m\leftarrow V_{\mathrm{reset}}$ and $w\leftarrow w+b$ (optional absolute refractory).

EIF-like sharp onset supports realistic spike initiation, while $(a,{\tau }_w,b)$ captures spike-frequency adaptation and bursting at modest cost, enabling efficient numerical integration and event-driven simulation. Hardware-oriented variants (fixed-point/high-accuracy arithmetic, power-of-two linearizations, and CORDIC exponentials) further reduce runtime without sacrificing fidelity [107,108,109]. Careful calibration of ${\mathsf{\Delta }}_T$, $V_T$, and adaptation parameters is essential; near-threshold stiffness may require smaller steps or dedicated solvers. In practice, AdEx is a good default when richer dynamics than LIF are needed with only a slight complexity increase.

2.3.6. Resonate-and-Fire Neuron (RF)

The RF neuron captures subthreshold oscillations and frequency selectivity—complementing integrator-style IF/LIF models—via a complex state with linear dynamics [110]:

$${\dot{z}}_i\left(t\right)=\left(b_i+i{\omega }_i\right)z_i\left(t\right)+\sum _{j=1}^n{c}_{ij}\delta \left(t-t_j^{\prime }\right),$$

(21)

where $z_i\in \mathbb{C}$ encodes the oscillatory state, ${\omega }_i$ is the intrinsic angular frequency, $b_i<0$ sets damping (stability requires $\mathrm{Re}\left\{b_i\right\}<0$), $c_{ij}$ are synaptic couplings, and $\delta (·)$ are presynaptic spike impulses at times $t_j^{\prime }$. A spike is emitted when a readout (e.g., $\mathrm{Im}\left\{z_i\right\}$ or a linear projection of $(\mathrm{Re}\left\{z_i\right\},\mathrm{Im}\left\{z_i\right\})$) crosses threshold ${\vartheta }_{\mathrm{RF}}$ from below, followed by a reset $z_i\leftarrow z_{\mathrm{reset}}$. Writing $z_i=x_i+i{y}_i$ reveals a damped resonator with eigenvalues $b_i\pm i{\omega }_i$, producing natural selectivity to inputs near ${\omega }_i$ and to spike phase—useful for tasks rich in temporal structure, resonance, and phase/PoFC-style coding.

In practice, RF offers lightweight oscillatory dynamics that simulate efficiently and admit analysis; balanced RF (BRF) improves stability in recurrent SNNs by regulating excitation–inhibition [111], and analog realizations demonstrate direct signal-to-spike conversion for edge sensing without explicit A/D front ends [112]. As a phenomenological model, however, spiking is threshold-based (not biophysical), channel nonlinearities are implicit, parameters (frequency, damping, reset) require calibration, and the second-order state increases per-neuron cost versus IF/LIF; for strongly nonlinear spiking such as complex bursting, AdEx or IZH variants can be preferable.

2.3.7. Hodgkin–Huxley Neuron (HH)

The HH model gives a biophysical account of spike generation via voltage-gated ${\mathrm{Na}}^{+}$ and ${\mathrm{K}}^{+}$ channels plus leak, fit to voltage-clamp data from squid axon [97]. The membrane equation balances capacitive and ionic currents:

$$C_m{\displaystyle \frac{dV}{dt}}=-g_L(V-E_L)-g_{\mathrm{Na}}{m}^{3}h(V-E_{\mathrm{Na}})-g_{\mathrm{K}}{n}^4(V-E_{\mathrm{K}})+I_{\mathrm{syn}}+I_{\mathrm{ext}},$$

(22)

with gating kinetics

$$\dot{x}={\alpha }_x\left(V\right)\left(1-x\right)-{\beta }_x\left(V\right)x,x\in \{m,h,n\}.$$

(23)

As the gold standard for single-cell fidelity, HH reproduces subthreshold dynamics, spike upstroke, refractoriness, and pharmacological effects, making it ideal for mechanism studies and validating reduced models. Its computational cost (stiff ODEs, many parameters) limits large network use, so EIF/AdEx/LIF variants are typically preferred for SNN simulation [38]. Hardware-aware implementations (e.g., CORDIC-based exponentials/fractions on FPGAs) improve tractability [113], and conductance-based synapse extensions clarify information transfer under realistic inputs [114].

Table 2. Summary of spiking neuron models: key mechanisms, advantages, and limitations. Complexity and plausibility are qualitative: very low (V. Low), low, moderate (Mod.), moderate–high (Mod.–High), high, very high (V. High).

Neuron Model	Main Applications	Complexity	Biological Plausibility	Advantages	Challenges
SRM [38,100]	STDP studies; analytical probes of SNNs; event-driven/hardware simulation	Low	Mod.	Kernel-based, tractable; separates synaptic and refractory effects; efficient	Limited subthreshold nonlinearities; requires kernel/threshold calibration
IF [101,103]	Baselines; large-scale SNNs; theoretical analysis	V. Low	Low	Extremely simple; fast; closed-form insights	Unrealistic integration (no leak); no adaptation/resonance
LIF [38,102]	Neuromorphic inference; brain–computer interfaces; large-scale simulations	Low	Mod.	Good accuracy–efficiency balance; event-driven; well-studied statistics	No intrinsic adaptation/bursting; linear subthreshold
ALIF [100,104]	Temporal/sequential tasks; speech-like streams; robotics control	Mod.	Mod.	Spike-frequency adaptation; better temporal credit assignment	Extra state and parameters; tuning sensitivity
EIF [103,105]	Fast fluctuating inputs; spike initiation studies; neuromorphic surrogates	Mod.	High	Sharp, smooth onset; improved gain/phase vs. LIF	Parameter calibration; stiffer near threshold
AdEx [106]	Cortical pattern repertoire; adapting/bursting cells; efficient yet rich neurons	Mod.–High	High	Diverse firing patterns with compact model; efficient integration	More parameters; careful numerical and hardware calibration
RF [110]	Resonance/phase codes; frequency-selective processing; edge sensing prototypes	Mod.	High	Captures subthreshold oscillations and resonance; phase selectivity	Phenomenological spike; added second-order state; parameter tuning
HH [97]	Biophysical mechanism studies; channelopathies; pharmacology; single-cell fidelity	V. High	V. High	Gold-standard fidelity; reproduces ionic mechanisms and refractoriness	Computationally expensive; stiff; many parameters
IZH [39,89]	Large-scale networks with rich firing; cortical microcircuits; plasticity studies	Mod.	High	Wide repertoire at low cost; simple 2D form with reset	Lower biophysical interpretability; heuristic fitting
RF–IZH [110,115]	Phase-aware resonance with lightweight reset; recurrent SNNs; neuromorphic stacks	Mod.	High	Preserves phase; efficient event rules; toolchain support (Lava)	Phenomenological; calibration of $(\omega ,b,\vartheta )$; still > IF/LIF cost
CUBA [98]	Large-scale SNNs; theory; fast prototyping; hardware with current-mode synapses	Low	Low	Very fast; analytically convenient; event-driven synapses independent of V	Ignores reversal/shunt; biases in high-conductance regimes vs. COBA
$\mathsf{\Sigma }\mathsf{\Delta }$ [88,115,116]	Energy-constrained streaming (audio/vision); edge sensing; $\mathsf{\Sigma }\mathsf{\Delta }$–LIF layers	Mod.	Mod.	Sparse, error-driven spikes; low switching energy; good reconstruction	Feedback/threshold tuning; integration details for stability and latency

Table 2. Summary of spiking neuron models: key mechanisms, advantages, and limitations. Complexity and plausibility are qualitative: very low (V. Low), low, moderate (Mod.), moderate–high (Mod.–High), high, very high (V. High).

Neuron Model	Main Applications	Complexity	Biological Plausibility	Advantages	Challenges
SRM [38,100]	STDP studies; analytical probes of SNNs; event-driven/hardware simulation	Low	Mod.	Kernel-based, tractable; separates synaptic and refractory effects; efficient	Limited subthreshold nonlinearities; requires kernel/threshold calibration
IF [101,103]	Baselines; large-scale SNNs; theoretical analysis	V. Low	Low	Extremely simple; fast; closed-form insights	Unrealistic integration (no leak); no adaptation/resonance
LIF [38,102]	Neuromorphic inference; brain–computer interfaces; large-scale simulations	Low	Mod.	Good accuracy–efficiency balance; event-driven; well-studied statistics	No intrinsic adaptation/bursting; linear subthreshold
ALIF [100,104]	Temporal/sequential tasks; speech-like streams; robotics control	Mod.	Mod.	Spike-frequency adaptation; better temporal credit assignment	Extra state and parameters; tuning sensitivity
EIF [103,105]	Fast fluctuating inputs; spike initiation studies; neuromorphic surrogates	Mod.	High	Sharp, smooth onset; improved gain/phase vs. LIF	Parameter calibration; stiffer near threshold
AdEx [106]	Cortical pattern repertoire; adapting/bursting cells; efficient yet rich neurons	Mod.–High	High	Diverse firing patterns with compact model; efficient integration	More parameters; careful numerical and hardware calibration
RF [110]	Resonance/phase codes; frequency-selective processing; edge sensing prototypes	Mod.	High	Captures subthreshold oscillations and resonance; phase selectivity	Phenomenological spike; added second-order state; parameter tuning
HH [97]	Biophysical mechanism studies; channelopathies; pharmacology; single-cell fidelity	V. High	V. High	Gold-standard fidelity; reproduces ionic mechanisms and refractoriness	Computationally expensive; stiff; many parameters
IZH [39,89]	Large-scale networks with rich firing; cortical microcircuits; plasticity studies	Mod.	High	Wide repertoire at low cost; simple 2D form with reset	Lower biophysical interpretability; heuristic fitting
RF–IZH [110,115]	Phase-aware resonance with lightweight reset; recurrent SNNs; neuromorphic stacks	Mod.	High	Preserves phase; efficient event rules; toolchain support (Lava)	Phenomenological; calibration of $(\omega ,b,\vartheta )$; still > IF/LIF cost
CUBA [98]	Large-scale SNNs; theory; fast prototyping; hardware with current-mode synapses	Low	Low	Very fast; analytically convenient; event-driven synapses independent of V	Ignores reversal/shunt; biases in high-conductance regimes vs. COBA
$\mathsf{\Sigma }\mathsf{\Delta }$ [88,115,116]	Energy-constrained streaming (audio/vision); edge sensing; $\mathsf{\Sigma }\mathsf{\Delta }$–LIF layers	Mod.	Mod.	Sparse, error-driven spikes; low switching energy; good reconstruction	Feedback/threshold tuning; integration details for stability and latency

2.3.8. Izhikevich Neuron (IZH)

The IZH neuron is a two-state hybrid model reproducing a wide repertoire of cortical firing patterns at very low computational cost [39,89]. With membrane potential V and recovery variable U,

$$\begin{array}{cc}\hfill {\displaystyle \frac{dV}{dt}}& =0.04V^2+5V+140-U+I\left(t\right),\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill {\displaystyle \frac{dU}{dt}}& =a\left(bV-U\right),\hfill \end{array}$$

(25)

and after-spike reset

$$\mathrm{if}V\ge V_{\mathrm{peak}}\left(\mathrm{typically}30\mathrm{mV}\right),V\leftarrow c,U\leftarrow U+d.$$

(26)

Here $I\left(t\right)$ is the synaptic/injected current; $a,b,c,d$ control time scale, sensitivity, and reset. Proper tuning yields tonic/fast spiking, bursting, chattering, rebound, and Class I/II excitability while avoiding explicit action-potential integration, thus enabling large-scale simulations and neuromorphic emulation with good accuracy–efficiency trade-offs [39,89]. As a phenomenological model, parameters have limited biophysical interpretability and often require heuristic fitting; numerical care near $V_{\mathrm{peak}}$ is useful. In practice, it serves as a pragmatic middle ground—richer dynamics than IF/LIF at modest cost, though for detailed channel mechanisms HH/AdEx may be preferred, and for strict minimalism or gradient training pipelines LIF/ALIF remain common [38].

2.3.9. Resonate-and-Fire Izhikevich Neuron (RF–IZH)

RF–IZH augments the RF oscillator with a minimal hybrid spike/reset that preserves phase while simplifying post-spike dynamics [110]. The subthreshold state follows RF (cf. (21)):

$$\dot{z}\left(t\right)=\left(b+i\omega \right)z\left(t\right)+\sum _j{c}_j\delta \left(t-t_j^{\prime }\right),$$

(27)

with $z\in \mathbb{C}$ the oscillatory state, $\omega$ preferred frequency, $b<0$ damping, and $c_j$ synaptic couplings. Spiking is phase-sensitive, with a lightweight reset that retains the imaginary (phase) component:

$$\begin{array}{cc}\hfill & \mathrm{spike}\mathrm{if}Im\left\{z\right(t\left)\right\}\ge \vartheta ,\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill & \mathrm{after}\mathrm{spike}:Re\left\{z\right(t\left)\right\}\leftarrow 0,z\left(t\right)\leftarrow iIm\left\{z\right(t\left)\right\},\hfill \end{array}$$

(29)

optionally followed by an absolute refractory period. This preserves resonance and phase continuity, yielding low-cost frequency selectivity and PoFC-style coding that is more faithful to oscillatory timing than IF/LIF yet far cheaper than conductance-based neurons. As a phenomenological model, spike generation is thresholded and channel nonlinearities are implicit; parameters $(\omega ,b,\vartheta )$ require calibration, and for complex bursting, AdEx/IZH or HH may be preferable. Efficient discrete-time updates with event-driven checks are available in neuromorphic toolchains (e.g., Lava) for large-scale simulation and deployment [115].

2.3.10. Current-Based Neuron (CUBA)

In the current-based (CUBA) formulation, synaptic events enter the membrane equation as additive currents independent of voltage, in contrast to conductance-based (COBA) synapses that scale with the driving force [98]. The membrane potential obeys

$${\displaystyle \frac{dV\left(t\right)}{dt}}=-{\displaystyle \frac{V\left(t\right)-V_{\mathrm{rest}}}{{\tau }_m}}+I_{\mathrm{syn}}\left(t\right),$$

(30)

with resting potential $V_{\mathrm{rest}}$, membrane time constant ${\tau }_m$, and total synaptic current $I_{\mathrm{syn}}\left(t\right)$ (typically a weighted sum of presynaptic spike kernels). A spike is emitted when $V\left(t\right)\ge V_{\mathrm{thresh}}$, followed by a reset $V\leftarrow V_{\mathrm{reset}}$ and an optional absolute refractory period.

CUBA is computationally efficient and analytically convenient for large-scale SNNs because synaptic drive does not depend on V. Its main limitation is reduced biological realism relative to COBA (e.g., no reversal potentials or shunting), which can bias gain and dynamics in high-conductance regimes [98].

2.3.11. Sigma–Delta Neuron ($\mathsf{\Sigma }\mathsf{\Delta }$)

The $\mathsf{\Sigma }\mathsf{\Delta }$ neuron realizes asynchronous pulsed $\mathsf{\Sigma }\mathsf{\Delta }$ modulation (APSDM), emitting spikes only when the discrepancy between the instantaneous drive $S\left(t\right)$ (e.g., filtered synaptic current) and its internal reconstruction $\widehat{S}\left(t\right)$ exceeds a dynamic threshold [116]. With the error variable

$$u\left(t\right)=S\left(t\right)-\widehat{S}\left(t\right),$$

(31)

a spike is produced when

$$\left|u\left(t\right)\right|\ge \vartheta \left(t\right)\Rightarrow y\left(t\right)\in \{-1,+1\},\widehat{S}\left(t^{+}\right)\leftarrow \widehat{S}\left(t^{-}\right)+y\left(t\right)\vartheta \left(t\right),$$

(32)

and the adaptive threshold evolves via

$$\vartheta \left(t\right)={\vartheta }_0+\sum _{t_i<t}\beta exp\left(-(t-t_i)/{\tau }_{\vartheta }\right).$$

(33)

Thus, spikes convey only significant changes, yielding sparse activity and low switching energy.

A practical discrete-time form (common in neuromorphic stacks) uses a dead-zone delta encoder with sigma reconstruction [115]:

$$\mathsf{\Delta }{x}_t=x_t-{\widehat{x}}_{t-1},y_t=sgn\left(\mathsf{\Delta }{x}_t\right)⊮\{\left|\mathsf{\Delta }{x}_t\right|>\theta \},{\widehat{x}}_t={\widehat{x}}_{t-1}+y_t\theta ,$$

(34)

optionally combined with LIF subthreshold dynamics (“$\mathsf{\Sigma }\mathsf{\Delta }$–LIF”). In dynamic sensing (audio/vision streams), this event-driven compressor achieves high-fidelity reconstructions with few spikes and strong energy efficiency [88,116].

Effective use hinges on feedback/threshold tuning and stability of the reconstruction. Poorly chosen $\theta$ or kernels can increase quantization noise or latency, and deployment may require careful calibration (step sizes, refractory handling). Reference implementations and layer abstractions are available in Lava for large-scale simulation and deployment [115].

2.3.12. Trade-Offs in Neuron Model Selection for SNNs

Model choice balances biological fidelity, compute–energy, trainability, and hardware fit (see Table 2).

• IF/LIF—Minimal state and event-driven efficiency make them defaults for large, low-power systems; linear subthreshold dynamics limit adaptation and resonance [38,101,102,103].
• ALIF—Adds spike-frequency adaptation (dynamic threshold or current) for better sequence processing with modest overhead; extra parameters require calibration [100,104].
• EIF/AdEx—Smooth spike onset (exponential term) and adaptation reproduce diverse cortical patterns at moderate cost; accuracy depends on careful tuning of ${\mathsf{\Delta }}_T,V_T,a,b,{\tau }_w$ and numerics can stiffen near threshold [105,106].
• SRM—Kernel superposition with spike-triggered refractoriness is analytically tractable and efficient; phenomenological nature limits rich subthreshold nonlinearities unless extended [38,100].
• IZH—Two-dimensional hybrid yields rich firing at low cost; parameters are less biophysically interpretable and typically fit heuristically [39,89].
• RF/RF–IZH—Resonator neurons capture phase/resonance for PoFC-like codes; lightweight but with added second-order state and calibration; BRF improves recurrent stability [110,111].
• HH—Gold-standard ion-channel fidelity for mechanism studies; too costly/stiff for large or ultra-low-power networks; useful as a reference [97].
• CUBA—Current-based synapses are simple and fast for scaling and analysis; reduced realism vs. COBA grows in high-conductance regimes [98].
• $\mathsf{\Sigma }\mathsf{\Delta }$ neuron—Event-driven, error-based spiking transmits only significant changes for sparse, energy-efficient operation; performance hinges on feedback/threshold tuning; supported in Lava and low-power circuits [88,115,116].

Practical Guidelines

• Energy/scale: LIF/ALIF or $\mathsf{\Sigma }\mathsf{\Delta }$; use CUBA when speed > realism.
• Temporal richness: ALIF, EIF/AdEx, or RF/RF–IZH for adaptation, resonance, or phase coding.
• Mechanistic fidelity: HH for channel-level questions; validate reduced models against HH.
• Trainability: Prefer models with robust surrogate-gradient practice; constrain parameters to avoid stiffness/instability.
• Hardware fit: Match state and nonlinearities to the target fabric (fixed-point, exponentials/CORDIC, event-driven kernels); layer-wise hybrids (e.g., LIF front ends + AdEx/ALIF deeper) often optimize accuracy–efficiency.

Overall, no single model is optimal; combine or stack models to meet the task’s accuracy–latency–energy envelope and hardware constraints.

2.4. Learning Paradigms in SNNs

Learning endows SNNs with the capacity to adapt and generalize while exploiting event-driven, temporally precise computation—an advantage over ANNs with static, continuous activations [18]. The same spiking discreteness, however, introduces two central challenges: (i) the non-differentiability of spikes, which complicates gradient-based optimization, and (ii) temporal credit assignment across membrane dynamics and spike times [16,17]. Contemporary training strategies address these challenges through several complementary paradigms.

Supervised methods treat SNNs as recurrent dynamical systems and apply BPTT, typically using surrogate gradients that replace the intractable spike derivative with smooth approximations. Recent extensions learn surrogate shapes or widths to mitigate gradient vanishing and instability while improving convergence [117,118,119,120].

Unsupervised methods—most prominently STDP—implement biologically plausible synaptic adaptation driven by spike-timing correlations, though they often require additional supervisory or architectural signals to reach competitive accuracy [51,121].

Reinforcement learning leverages reward signals to optimize spiking policies in interactive or sequential tasks, whereas hybrid approaches combine supervision, self-organization, and reward modulation to exploit their respective strengths.

Finally, ANN-to-SNN conversion transfers pre-trained ANN weights to spiking equivalents, circumventing non-differentiability during training and enabling efficient deployment on neuromorphic hardware [16,18].

No single paradigm dominates across all applications; the optimal choice depends on the target task’s accuracy–latency–energy trade-offs, biological plausibility, data regime, and hardware constraints. A consolidated summary of representative algorithms, their mechanisms, advantages, and limitations is presented in Table 3.

2.4.1. Supervised Learning

Supervised learning trains SNNs on labeled datasets by associating each input with a desired output (e.g., class labels or target spike statistics). Because spikes are discrete events, standard backpropagation is hindered by the non-differentiability of spike generation. Therefore, practical methods unroll the network in time—analogous to recurrent neural networks—and optimize losses defined on spike-based readouts, such as spike counts, rates, or latencies, while replacing the non-differentiable spike function with a smooth surrogate gradient [16].

This approach enables gradient-based optimization using BPTT and its variants, achieving high accuracy on both classification and regression tasks. However, it incurs increased memory and computational demands from temporal unrolling and requires careful tuning of surrogate functions, membrane time constants, and firing thresholds.

• SpikeProp

SpikeProp [122] was one of the earliest backpropagation-style algorithms for SNNs, extending temporal error backpropagation to learn precise spike times—particularly useful for temporal pattern recognition. The synaptic update is

$$\mathsf{\Delta }{w}_{ij}=-\eta \sum _d{\displaystyle \frac{\partial E}{\partial t_i^d}}{\displaystyle \frac{\partial t_i^d}{\partial w_{ij}}},$$

(35)

where $\eta$ is the learning rate, E measures the mismatch between actual and desired spike times $t_i^d$, and $\partial t_i^d/\partial w_{ij}$ is the spike-time sensitivity. SpikeProp showed that backpropagation concepts can be carried into the temporal domain, enabling accurate nonlinear classification with fewer units than purely rate-based networks and foreshadowing modern surrogate-gradient and locality-aware rules.

• SuperSpike

SuperSpike [123] generalizes SpikeProp by introducing surrogate gradients and eligibility traces for deep, multilayer SNNs trained on spatiotemporal inputs. The update takes the form

$$\mathsf{\Delta }{w}_{ij}=\eta {\int }_{t_b}^{t_{b+1}}{e}_i\left(t\right)\left[\alpha \ast \left({\sigma }^{\prime }\left(U_i\left(t\right)\right)·(ϵ\ast S_j)\left(t\right)\right)\right]dt,$$

(36)

with error signal $e_i\left(t\right)$, surrogate derivative ${\sigma }^{\prime }\left(U_i\left(t\right)\right)$ of the spike function, and presynaptic trace $(ϵ\ast S_j)\left(t\right)$. SuperSpike enables end-to-end training despite spike non-differentiability by combining gradient approximation with local eligibility.

• SLAYER

SLAYER (Spike Layer Error Reassignment in Time) [119] tackles temporal credit assignment by backpropagating errors through time and reassigning them to causal spike events. The generic update is

$$\mathsf{\Delta }w=-\eta \sum _t{\displaystyle \frac{\partial E}{\partial s\left(t\right)}}{\displaystyle \frac{\partial s\left(t\right)}{\partial w}},$$

(37)

where $\partial s\left(t\right)/\partial w$ is a surrogate gradient of the spike train concerning the weight. SLAYER is effective for tasks that hinge on precise spike timing, such as sequence prediction and temporal classification.

• EventProp

EventProp [124] computes exact gradients by explicitly handling derivative discontinuities at spike times via an adjoint method, avoiding surrogate approximations. The loss is

$$L=l_p\left(t_{\mathrm{post}}\right)+{\int }_0^T{l}_V(V\left(t\right),t)dt,$$

(38)

and its gradient w.r.t. a synapse $w_{ji}$ is

$${\displaystyle \frac{dL}{d{w}_{ji}}}=-{\tau }_{\mathrm{syn}}\sum _{\mathrm{spikes}\mathrm{from}i}{\left({\lambda }_I\right)}_j,$$

(39)

where ${\left({\lambda }_I\right)}_j$ is the adjoint for the synaptic current and ${\tau }_{\mathrm{syn}}$ a synaptic constant. The event-driven treatment lowers memory and compute overheads, making EventProp appealing for neuromorphic execution.

2.4.2. Unsupervised Learning in SNNs

Unsupervised learning discovers structure without labels, typically through local rules that exploit spike timing. The most prominent is STDP, with numerous extensions improving stability, hardware efficiency, and biological plausibility.

• STDP

Classical STDP [51,121] modifies synapses by the relative timing of pre/post-spikes:

$$\mathsf{\Delta }w=\left\{\begin{array}{cc}{A}^{+}exp\left(\frac{t_{\mathrm{pre}}-t_{\mathrm{post}}}{{\tau }^{+}}\right),\hfill & t_{\mathrm{pre}}\le t_{\mathrm{post}},\hfill \\ A^{-}exp\left(-\frac{t_{\mathrm{pre}}-t_{\mathrm{post}}}{{\tau }^{-}}\right),\hfill & t_{\mathrm{pre}}>t_{\mathrm{post}},\hfill \end{array}\right.$$

(40)

with $(A^{+},A^{-})$ the potentiation/depression amplitudes and $({\tau }^{+},{\tau }^{-})$ the time constants.

• Adaptive STDP (aSTDP)

aSTDP extends classical STDP by dynamically adjusting the parameters governing synaptic updates, thereby improving stability and robustness—particularly in neuromorphic hardware with limited synaptic resolution [125]. The variant proposed by Gautam and Kohno simplifies the exponential weight-update function into a rectangular learning window, improving hardware efficiency. The update rule is as follows:

$$\mathsf{\Delta }{w}_j=\left\{\begin{array}{cc}+1\mathrm{bit},\hfill & \mathrm{if}{t}_j\le t_i\mathrm{and}{t}_i-t_j<t_{\mathrm{pre}}\left(\mathrm{LTP}\right),\hfill \\ -1\mathrm{bit},\hfill & \mathrm{if}{t}_j>t_i\mathrm{and}{t}_j-t_i<t_{\mathrm{post}}\left(\mathrm{LTD}\right),\hfill \end{array}\right.$$

(41)

where $t_{\mathrm{pre}}$ is the maximum delay between a presynaptic spike followed by a postsynaptic spike that induces long-term potentiation (LTP); $t_{\mathrm{post}}$ maximum delay between a postsynapticsynaptic spike followed by a presynaptic spike that induces long-term depression (LTD); adaptively increased during learning, $t_i$ and $t_j$ postsynaptic and presynaptic spike times, respectively.

Alternative aSTDP formulations, such as that proposed by Li et al. [126], enhance biological plausibility using perturbation-based approximations of postsynaptic derivatives. These approaches facilitate biologically realistic, local unsupervised learning without global supervision.

• Multiplicative STDP

Multiplicative STDP [127] incorporates the current synaptic weight into the learning rule, improving biological plausibility and preventing unbounded weight growth or decay. The update dynamics are as follows:

$$\mathsf{\Delta }w=A^{+}·x_{\mathrm{pre}}·{\delta }_{\mathrm{post}}-A^{-}·x_{\mathrm{post}}·{\delta }_{\mathrm{pre}},$$

(42)

$${\displaystyle \frac{d{x}_{\mathrm{pre}}}{dt}}=-{\displaystyle \frac{x_{\mathrm{pre}}\left(t\right)}{{\tau }^{+}}}+\delta \left(t\right),$$

(43)

$${\displaystyle \frac{d{x}_{\mathrm{post}}}{dt}}=-{\displaystyle \frac{x_{\mathrm{post}}\left(t\right)}{{\tau }^{-}}}+\delta \left(t\right),$$

(44)

where $A^{+}$ and $A^{-}$ Learning rate parameters for potentiation and depression, $x_{\mathrm{pre}}$ and $x_{\mathrm{post}}$ Pre- and postsynaptic spike traces, ${\delta }_{\mathrm{pre}}$ and ${\delta }_{\mathrm{post}}$ Indicators for pre- and postsynaptic spike events, ${\tau }^{+}$ and ${\tau }^{-}$ Time constants governing trace decay.

• Triplet STDP

Triplet STDP [128] extends pair-based STDP by incorporating triplet interactions, such as two presynaptic spikes and one postsynaptic spike or vice versa. This extension accounts for the frequency dependence of synaptic changes, where high-frequency spiking produces stronger potentiation or depression due to cumulative intracellular calcium effects. The update rule is as follows:

$$\mathsf{\Delta }w=\eta (x_{\mathrm{pre}}-x_{\mathrm{tar}})(w_{\max }-w)u,$$

(45)

where $\eta$ learning rate, $x_{\mathrm{pre}}$ is the presynaptic trace value, and $x_{\mathrm{tar}}$ is the target presynaptic trace at the time of a postsynaptic spike. $w_{\max }$ Maximum allowable synaptic weight, w current synaptic weight, u modulation term controlling dependence on the current weight. By integrating multi-spike interactions, triplet STDP captures nonlinear dependencies and better reflects the complexity of biological synaptic plasticity.

2.4.3. Reinforcement Learning in SNNs

Reinforcement Learning modulates plasticity with evaluative feedback, enabling SNNs to learn action policies from rewards—well-suited to closed-loop, real-time settings.

• R-STDP

R-STDP [52] extends classical STDP by incorporating a reward signal $R\left(t\right)$ that modulates synaptic weight changes according to whether the received feedback is positive or negative. The weight update rule is as follows:

$$\mathsf{\Delta }w=R\left(t\right)·\left\{\begin{array}{cc}{A}^{+}exp\left({\displaystyle \frac{-\mathsf{\Delta }t}{{\tau }^{+}}}\right),\hfill & \mathrm{if}\mathsf{\Delta }t>0,\hfill \\ A^{-}exp\left({\displaystyle \frac{\mathsf{\Delta }t}{{\tau }^{-}}}\right),\hfill & \mathrm{if}\mathsf{\Delta }t<0,\hfill \end{array}\right.$$

(46)

where $R\left(t\right)$ Reward signal at time t, $\mathsf{\Delta }w$ Change in synaptic weight, $A^{+}$ and $A^{-}$ Learning rates for potentiation and depression, respectively, $\mathsf{\Delta }t=t_{\mathrm{post}}-t_{\mathrm{pre}}$ Time difference between postsynaptic and presynaptic spikes, ${\tau }^{+}$ and ${\tau }^{-}$ Time constants defining the potentiation and depression windows.

By integrating temporal spike relationships with reward feedback, R-STDP enables adaptive learning in environments where the network’s behavior must evolve based on environmental cues, such as maze navigation or game playing, where purely supervised or unsupervised methods may be less effective.

• ReSuMe (Rewarded Subspace Method)

ReSuMe [129] combines supervised learning principles with reinforcement signals, enabling synaptic weight adjustments that align target outputs with environmental rewards. The update rule is as follows:

$$\mathsf{\Delta }w=\eta ·(r-y)·x$$

(47)

where $\mathsf{\Delta }w$ change in synaptic weight, $\eta$ learning rate, r reward signal, y actual neuron output, and x input signal.

By leveraging reinforcement-modulated weight updates, ReSuMe bridges the gap between biologically inspired learning and computational efficiency, making it suitable for tasks requiring both supervised target guidance and environmental adaptation.

• Eligibility Propagation (e-prop)

e-prop [130] provides a biologically plausible alternative to backpropagation by using eligibility traces to capture the influence of past synaptic activity on current outputs. This approach is particularly effective for tasks involving long temporal dependencies. The eligibility trace is updated according to the following:

$$E_{t+1}=\lambda E_t+{\displaystyle \frac{\partial y_t}{\partial w}}$$

(48)

where $E_t$ Eligibility trace at time t, $\lambda$ trace decay factor, $y_t$ output at time t, and w synaptic weight.

e-prop allows error information to propagate backward through time without storing the entire history of network states, significantly reducing memory requirements while maintaining the ability to learn both synaptic weights and temporal dependencies in parallel.

2.4.4. Hybrid Learning Paradigms

Hybrid schemes combine global error signals with local spike-based plasticity or reward, aiming for better accuracy–efficiency trade-offs and hardware compatibility.

• (SSTDP)

SSTDP [131] is a supervised learning rule designed to enhance training efficiency and accuracy in SNNs by uniting backpropagation-based global optimization with the local temporal dynamics of STDP. This hybrid approach bridges the gap between gradient-based learning and biologically plausible spike-based plasticity.

The synaptic weight update is as follows:

$$\mathsf{\Delta }{w}_{ij}^l=-\alpha {\displaystyle \frac{\partial E}{\partial w_{ij}^l}},\mathrm{where}{\displaystyle \frac{\partial E}{\partial w_{ij}^l}}={\displaystyle \frac{\partial E}{\partial t_j^l}}{\displaystyle \frac{\partial t_j^l}{\partial w_{ij}^l}},$$

(49)

where $\alpha$ Learning rate, ${\displaystyle \frac{\partial E}{\partial t_j^l}}$ Error signal propagated back to the firing time of the postsynaptic neuron, ${\displaystyle \frac{\partial t_j^l}{\partial w_{ij}^l}}$ Partial derivative of postsynaptic firing time with respect to the synaptic weight.

The derivative ${\displaystyle \frac{\partial t_j^l}{\partial w_{ij}^l}}$ is defined as:

$${\displaystyle \frac{\partial t_j^l}{\partial w_{ij}^l}}=\left\{\begin{array}{cc}{ϵ}_1\left(e^{-{\displaystyle \frac{t_{\mathrm{post}}-t_{\mathrm{pre}}}{\tau }}}-\delta \right){(w_{\max }-w)}^{\mu },\hfill & t_{\mathrm{post}}>t_{\mathrm{pre}},\hfill \\ {ϵ}_2\left(e^{-{\displaystyle \frac{t_{\mathrm{pre}}-t_{\mathrm{post}}}{\tau }}}-\delta \right){(w_{\max }-w)}^{\mu },\hfill & t_{\mathrm{post}}<t_{\mathrm{pre}},\hfill \end{array}\right.$$

(50)

where $t_{\mathrm{pre}}$, $t_{\mathrm{post}}$ Pre- and postsynaptic firing times, ${ϵ}_1,{ϵ}_2$ Scaling factors for potentiation and depression, $\tau$ Time constant for exponential decay of STDP effects, $\delta$ Temporal window parameter defining effective STDP update intervals, $w_{\max }$ Maximum allowable synaptic weight, w Current synaptic weight, $\mu$ Weight-dependence factor controlling the influence of $w_{\max }$ on update magnitude.

SSTDP achieves reduced inference latency, lower computational overhead, and improved energy efficiency for neuromorphic deployment by combining global error feedback with local spike-timing-based plasticity.

• ANN-to-SNN Conversion

ANN-to-SNN conversion reduces the need to train SNNs from scratch by transforming pre-trained ANNs into equivalent spiking architectures [132,133]. This approach maps continuous neuron activations and synaptic weights to spike-based counterparts, minimizing performance degradation while preserving learned representations [31,134,135,136,137].

The general process involves:

• Training a conventional ANN using backpropagation.
• Converting neuron activations to spike rates or spike times.
• Adjusting weights, thresholds, and normalization parameters to match the target SNN framework.

Two main strategies exist:

• Rate-based conversion: Maps ANN activations to SNN firing rates using normalization and threshold adaptation, ensuring the spike rate approximates the ANN output [132,133].
• Temporal coding conversion: Encodes information in spike timing to capture temporal patterns, reducing latency and improving performance on dynamic datasets [89].

Enhancements such as Max Normalization for pooling layers and reset-by-subtraction mechanisms further mitigate performance loss, maintaining high accuracy on datasets like MNIST [138] and CIFAR-10 [139] while improving energy efficiency [136,140]. ANN-to-SNN conversion thus combines the mature training capabilities of ANNs with the deployment advantages of SNNs on neuromorphic hardware.

Table 3. Overview of learning algorithms in SNNs, summarizing their paradigms, typical applications, computational complexity, biological plausibility, key advantages, and main challenges.

Algorithm Name	Learning Paradigm	Main Applications	Complexity	Biological Plausibility	Advantages	Challenges
SpikeProp [122]	Supervised	Temporal pattern recognition	Low	Low	Enables precise spike timing learning; first event-based backpropagation for SNNs	Limited to shallow networks; affected by spike non-differentiability
SuperSpike [123]	Supervised	Temporal pattern recognition; deep SNN training	Medium	Medium	Uses surrogate gradients; enables multilayer training	Requires careful surrogate design; added computational cost
SLAYER [119]	Supervised	Complex temporal data; sequence prediction	High	Medium	Addresses temporal credit assignment; handles sequences well	Computationally intensive; complex to implement
EventProp [124]	Supervised	Exact gradient computation; neuromorphic hardware	High	High	Computes exact gradients; efficient for event-driven processing	Complex discontinuity handling; implementation challenges
STDP [51,121]	Unsupervised	Pattern recognition; feature extraction	Low	High	Biologically plausible; local weight updates	Limited scalability; lower accuracy for large-scale tasks
aSTDP [125,126]	Unsupervised	Adaptive feature learning	Medium	High	Dynamically adapts learning parameters; robust	Parameter tuning complexity; additional computation
Multiplicative STDP [127]	Unsupervised	Weight updates scaled by current weight; prevents unbounded growth/decay	High	Medium	Improves biological plausibility; stabilizes learning	Requires careful parameter tuning
Triplet-STDP [128]	Unsupervised	Frequency-dependent learning	Medium	Medium	Captures multi-spike interactions; models frequency effects	Complex spike attribution; higher computation
R-STDP [52]	RL	Adaptive learning; decision making	Medium	High	Integrates reward signals; adaptive to reinforcement tasks	Requires carefully designed reward schemes
ReSuMe [141]	RL	Temporal precision learning	Medium	High	Combines supervised targets with reinforcement feedback	Dependent on reward design; non-gradient-based
e-prop [130]	RL	Temporal dependencies; complex dynamics	High	High	Tracks synaptic influence with eligibility traces	Computationally intensive; eligibility tracking complexity
SSTDP [131]	Hybrid	High temporal precision; visual recognition	Medium	High	Merges backpropagation and STDP; energy-efficient	Requires precise timing data; integration complexity
ANN-to-SNN Conversion [134,135]	Hybrid	Neuromorphic deployment	Medium	Low	Leverages pre-trained ANNs; fast deployment	Accuracy loss in conversion; parameter mapping issues

Table 3. Overview of learning algorithms in SNNs, summarizing their paradigms, typical applications, computational complexity, biological plausibility, key advantages, and main challenges.

Algorithm Name	Learning Paradigm	Main Applications	Complexity	Biological Plausibility	Advantages	Challenges
SpikeProp [122]	Supervised	Temporal pattern recognition	Low	Low	Enables precise spike timing learning; first event-based backpropagation for SNNs	Limited to shallow networks; affected by spike non-differentiability
SuperSpike [123]	Supervised	Temporal pattern recognition; deep SNN training	Medium	Medium	Uses surrogate gradients; enables multilayer training	Requires careful surrogate design; added computational cost
SLAYER [119]	Supervised	Complex temporal data; sequence prediction	High	Medium	Addresses temporal credit assignment; handles sequences well	Computationally intensive; complex to implement
EventProp [124]	Supervised	Exact gradient computation; neuromorphic hardware	High	High	Computes exact gradients; efficient for event-driven processing	Complex discontinuity handling; implementation challenges
STDP [51,121]	Unsupervised	Pattern recognition; feature extraction	Low	High	Biologically plausible; local weight updates	Limited scalability; lower accuracy for large-scale tasks
aSTDP [125,126]	Unsupervised	Adaptive feature learning	Medium	High	Dynamically adapts learning parameters; robust	Parameter tuning complexity; additional computation
Multiplicative STDP [127]	Unsupervised	Weight updates scaled by current weight; prevents unbounded growth/decay	High	Medium	Improves biological plausibility; stabilizes learning	Requires careful parameter tuning
Triplet-STDP [128]	Unsupervised	Frequency-dependent learning	Medium	Medium	Captures multi-spike interactions; models frequency effects	Complex spike attribution; higher computation
R-STDP [52]	RL	Adaptive learning; decision making	Medium	High	Integrates reward signals; adaptive to reinforcement tasks	Requires carefully designed reward schemes
ReSuMe [141]	RL	Temporal precision learning	Medium	High	Combines supervised targets with reinforcement feedback	Dependent on reward design; non-gradient-based
e-prop [130]	RL	Temporal dependencies; complex dynamics	High	High	Tracks synaptic influence with eligibility traces	Computationally intensive; eligibility tracking complexity
SSTDP [131]	Hybrid	High temporal precision; visual recognition	Medium	High	Merges backpropagation and STDP; energy-efficient	Requires precise timing data; integration complexity
ANN-to-SNN Conversion [134,135]	Hybrid	Neuromorphic deployment	Medium	Low	Leverages pre-trained ANNs; fast deployment	Accuracy loss in conversion; parameter mapping issues

2.5. Evolution of Supervised Learning in SNNs and Broader Context

Supervised training for SNNs has evolved from early adaptations of backpropagation to methods that explicitly handle spike timing and discontinuities. Initial work by [142] applied backpropagation-like updates with adaptive learning rates, demonstrating viability on small datasets (e.g., Iris) but highlighting the difficulty of optimizing through non-differentiable spikes. ReSuMe [143] bridged supervised objectives with STDP-like timing rules, while perceptron-style temporal learners [144] and multi-spike gradient approaches [145] improved efficiency and supported richer temporal patterns. Meta-heuristic variants—such as SpikeProp with PSO [146]—achieved gains in accuracy and convergence, and biologically inspired models like the tempotron [147] underscored the utility of precise temporal coding.

A major inflection point came with surrogate gradients, which replace the intractable spike derivative with smooth approximations, enabling BPTT in deep SNNs [16,148]. Temporal-coding supervision via direct gradient descent [76] aligned learning with event-driven dynamics; SuperSpike [123] combined surrogate gradients with eligibility traces for multilayer training; and SLAYER [119] reassigned errors across space and time to address temporal credit assignment. EventProp [124] later introduced exact gradients for continuous-time SNNs using an adjoint-state formulation, eliminating the need for surrogates. Hybrid rules such as SSTDP [131] merged global error signals with local timing windows, while system-level innovations—including single-spike hybrid input encodings [149], threshold-dependent batch normalization for deep SNNs [150], and spiking Transformers [151,152]—expanded the accuracy–latency–efficiency frontier on large-scale benchmarks.

In parallel, unsupervised and reinforcement-based paradigms emphasize locality and energy efficiency. Classical and adaptive STDP variants [51,121,125,126] excel at feature discovery but typically benefit from auxiliary supervision to achieve state-of-the-art accuracy. R-STDP and e-prop [52,130] enable closed-loop learning with reduced memory requirements. ANN-to-SNN conversion [31,132,133,134,135,136,137] leverages mature ANN training pipelines, mapping activation rates or spike timings to spiking equivalents for neuromorphic deployment. These methods sustain strong performance on MNIST [138] and CIFAR-10 [139] while achieving improved efficiency [18,140]. Energy-aware objectives and normalization techniques (e.g., Spike-Norm, rate normalization) further stabilize training and reduce power consumption [153,154].

Overall, supervised approaches deliver the highest accuracy but at increased computational and energy cost; unsupervised and reinforcement learning methods prioritize locality and efficiency, often at the expense of scalability; and hybrid or conversion-based frameworks increasingly reconcile these objectives. Continued progress will depend on integrating temporal coding, normalization, and hardware-aware optimization to achieve energy-efficient, high-performance SNNs at scale.

The preceding sections reviewed encoding strategies, neuron models, and learning paradigms that distinguish SNNs from ANNs, emphasizing their potential for event-driven efficiency alongside persistent challenges of trainability, robustness, and hardware compatibility. Building on these foundations, the following section presents a controlled empirical study that couples matched SNN and ANN architectures with standardized encodings and training procedures. The aim is to quantify accuracy–energy trade-offs under comparable conditions and to derive actionable design guidelines. Accordingly, the next section details the datasets, model backbones, encoding and neuron configurations, training setup, and evaluation metrics used in our analysis.

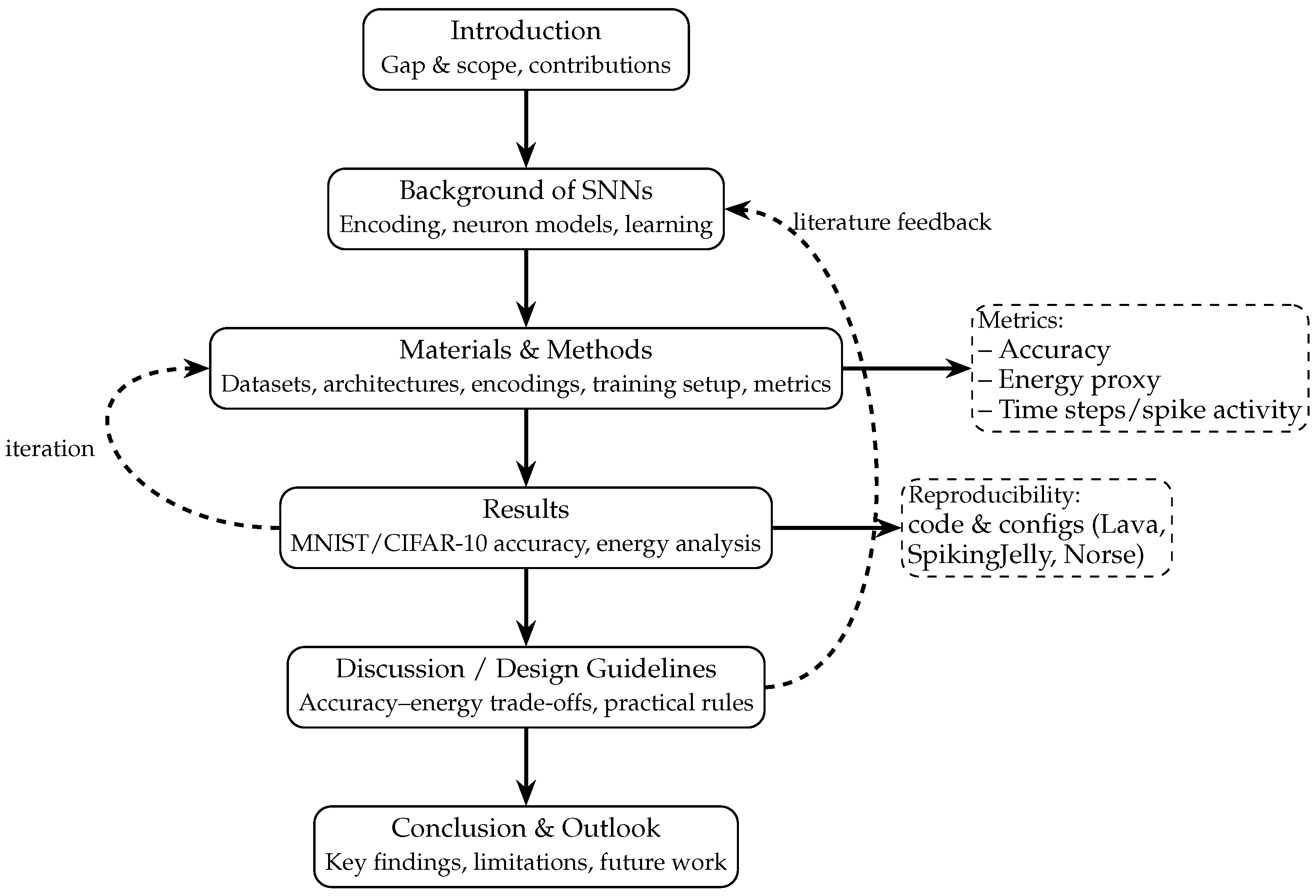
3. Materials and Methods

This section describes the datasets and preprocessing steps, model architectures and spiking configurations, training and inference procedures, and evaluation metrics used in the comparative study.

3.1. Experimental Design

Objective. The goal is to evaluate the predictive efficacy (accuracy) and energy efficiency (power consumption) of SNNs relative to architecturally matched ANNs for image classification tasks. To ensure fair comparison, each SNN is paired with an ANN using the same network backbone. Experiments are conducted on two standard benchmarks—MNIST and CIFAR-10. SNN variants span multiple combinations of encoding schemes and neuron models under supervised learning, along with different surrogate-gradient functions. Energy per inference is estimated following [155] using the KerasSpiking framework [156].

We design and train both shallow and deep architectures suited to MNIST and CIFAR-10:

• Fully connected network (FCN): two hidden fully connected layers and a classification head, applied to MNIST; approximately 118,288 trainable parameters.
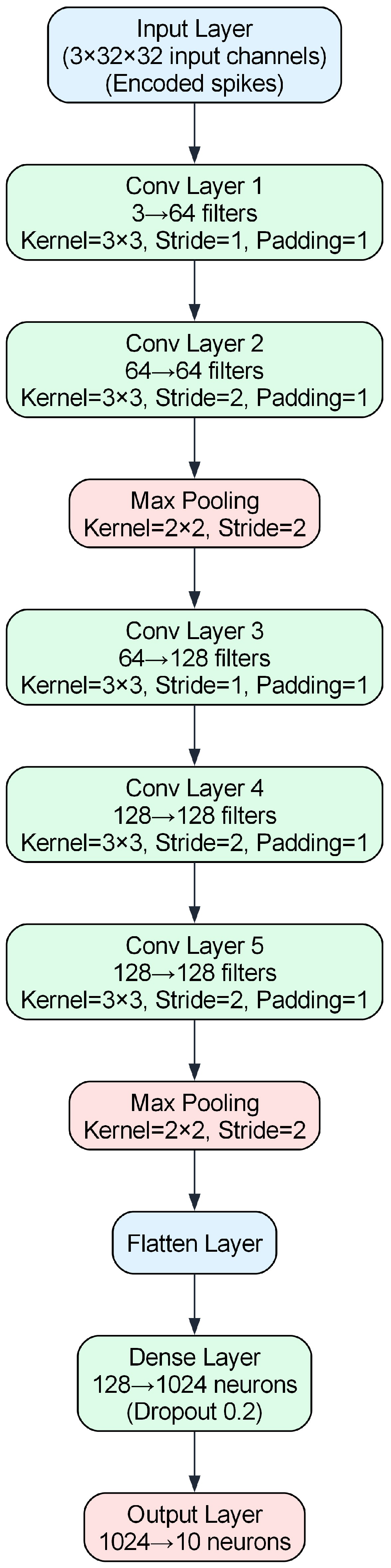
• Deep convolutional network (VGG7): five convolutional layers, two max-pooling layers, one hidden fully connected layer, and a classifier, applied to CIFAR-10; approximately 548,554 trainable parameters.

Each architecture is instantiated with diverse neuron models and encoding schemes to generate spike trains from input data. The encoding and neuron model details are summarized in Table 1 and Table 2.

• Neuron models: IF, LIF, ALIF, CUBA, $\mathsf{\Sigma }\mathsf{\Delta }$, RF, RF–IZH, EIF, and AdEx.
• Encoding schemes: Direct encoding, rate encoding, temporal TTFS, sigma–delta ($\mathsf{\Sigma }\mathsf{\Delta }$) encoding, burst coding, PoFC, and R–NoM. Each method transforms continuous pixel intensities into discrete spike trains distributed across specific time steps.

The number of time steps is limited to maintain tractable inference: $T\in \{4,6,8\}$ for MNIST and $T\in \{2,4,6\}$ for CIFAR-10, given the latter’s higher complexity and computational cost. Every SNN variant is trained and evaluated across these configurations, and performance is assessed using two primary metrics:

• Predictive efficacy (accuracy): proportion of correctly classified samples.
• Energy efficiency (power consumption): theoretical power usage estimated per inference.

The evaluation procedure includes:

• Training models on MNIST and CIFAR-10 under varying time-step configurations;
• Encoding input images using the predefined schemes;
• Measuring predictive accuracy and estimating energy consumption; and
• Comparing SNN performance against equivalent ANN baselines to quantify accuracy–energy trade-offs.

These experiments identify SNN configurations that best balance accuracy and energy consumption, providing insights for both research and neuromorphic deployment.

3.2. Data Collection and Preprocessing

The evaluation uses MNIST [138] and CIFAR-10 [139]. MNIST contains 70,000 grayscale images ($28\times 28$ pixels) of handwritten digits (60,000 for training and 10,000 for testing across ten classes). Images are normalized to mean $0.5$, standard deviation $0.5$, and range $[-1,1]$, then converted into spike trains using multiple encoding schemes with time steps $T\in \{4,6,8\}$. CIFAR-10 comprises 60,000 RGB images ($32\times 32$ pixels) across ten classes (50,000 training and 10,000 testing). Data augmentation includes random cropping (padding of four) and horizontal flipping, followed by per-channel normalization with means $[0.4914,0.4822,0.4465]$ and standard deviations $[0.2023,0.1994,0.2010]$. Normalized images are encoded as spike trains with $T\in \{2,4,6\}$. Encoding methods follow Table 1, and neuron models (IF, LIF, ALIF, CUBA, $\mathsf{\Sigma }\mathsf{\Delta }$, RF, RF–IZH, EIF, AdEx) are implemented as listed in Table 2.

3.3. Implementation Frameworks and Tools

All preprocessing, encoding, and model development were implemented in Python using specialized SNN frameworks—Lava [115], SpikingJelly [157], and Norse [158]—integrated within the PyTorch environment. These toolchains supported both MNIST (FCN) and CIFAR-10 (VGG7) experiments.

3.3.1. Lava

Intel’s neuromorphic framework provides modular neuron and synapse models, learning rules, and deployment utilities. The Lava-DL module includes SLAYER 2.0 for efficient surrogate-gradient training, while NetX facilitates compilation to neuromorphic targets such as Loihi [42]. It supports rate and temporal coding, ANN→SNN conversion (e.g., Bootstrap), PyTorch interoperability, and HDF5-based, platform-independent model exchange [115].

3.3.2. SpikingJelly

A PyTorch-native SNN library offering IF/LIF neurons, advanced surrogate gradients (e.g., ATan), and multiple encoding options (rate, temporal, and phase). CuPy-based GPU acceleration enables efficient large-scale training [157].

3.3.3. Norse

A lightweight PyTorch extension emphasizing biologically realistic neuron models (e.g., AdEx) and efficient simulation. It supports surrogate-gradient training (e.g., SuperSpike), just-in-time compilation, and GPU acceleration [158].

3.3.4. PyTorch

Used to construct both ANN and SNN backbones, manage training loops, and optimize parameters (Adam optimizer). It provides standard deep-learning infrastructure while integrating seamlessly with SNN-specific modules.

Together, these frameworks enabled efficient experimentation, reproducibility, and fair comparison across ANN and SNN configurations incorporating diverse neuron models and encoding strategies.

3.4. Neural Network Architectures

In this study, both ANNs and SNNs were employed on the MNIST and CIFAR-10 datasets to enable direct, architecture-level comparisons. The ANN models were implemented in PyTorch, using an FCN (two fully connected layers with 128 units, 5% dropout, and ReLU activations) for MNIST, and a VGG7-inspired convolutional network (multiple convolutional layers interleaved with batch normalization, ReLU, max-pooling, and a 1024-unit fully connected layer with 20% dropout) for CIFAR-10. MNIST images were normalized to a mean of 0.5 and a standard deviation of 0.5. CIFAR-10 images underwent data augmentation—random cropping with 4-pixel padding and horizontal flipping—followed by per-channel normalization using dataset-specific statistics.

The SNN counterparts were developed using the Lava, SpikingJelly, and Norse frameworks integrated with PyTorch. These models adopted the same architectural depth and width as their ANN equivalents to ensure a fair comparison. Each SNN variant incorporated a specific neuron model and encoding scheme as described in Section 3.1. The detailed configurations of the two architectures are summarized in

Table 4. ANN and SNN architectures for FCN and VGG7.

Layer	FCN Architecture	VGG7 Architecture
Input Layer	784 input neurons	3 channels, $32\times 32$ pixels
Layer 1	Dense, 128 neurons, $\mathrm{Dropout}(p=0.05)$	Conv, 64 filters, $3\times 3$ kernel, stride 1, padding 1
Layer 2	Dense, 128 neurons, $\mathrm{Dropout}(p=0.05)$	Conv, 64 filters, $3\times 3$ kernel, stride 2, padding 1
–	Output, 10 neurons	Max Pooling, $2\times 2$ kernel, stride 2
Layer 3	—	Conv, 128 filters, $3\times 3$ kernel, stride 1, padding 1
Layer 4	—	Conv, 128 filters, $3\times 3$ kernel, stride 2, padding 1
Layer 5	—	Conv, 128 filters, $3\times 3$ kernel, stride 2, padding 1
–	—	Max Pooling, $2\times 2$ kernel, stride 2
Flatten Layer	—	Flatten feature maps
Layer 6	—	Dense, 1024 neurons, $\mathrm{Dropout}(p=0.2)$
Layer 7	Output, 10 neurons	Output, 10 neurons
Special Components	Weight Normalization, Weight Scaling	Weight Normalization, Weight Scaling
Total Parameters	∼118,016	∼548,554
Frameworks Used	PyTorch for ANNs; Lava, Norse, SpikingJelly for SNNs	PyTorch for ANNs; Lava, Norse, SpikingJelly for SNNs

, and their structural overviews are illustrated in Figure 7 and Figure 8.

FCN architecture. This shallow network, containing approximately 118,288 parameters, processes spike trains derived from the 784 input pixels of MNIST. It consists of two fully connected layers with 128 spiking neurons each (5% dropout), followed by an output layer of ten neurons corresponding to the digit classes.

VGG7 architecture. This deeper network, with a total of approximately 548,554 parameters, is based on the VGG family design and operates on CIFAR-10 images of size $32\times 32$ pixels in RGB format. It comprises sequential convolutional layers with varying strides and 64 or 128 filters, interspersed with max-pooling operations. The extracted feature maps are flattened and passed through a 1024-neuron fully connected layer (20% dropout) before the final output layer of ten neurons corresponding to the image classes.

3.5. Training Configuration and Procedures

All experiments were conducted on Google Colab with GPU acceleration. ANNs were implemented in PyTorch, while SNNs were trained using PyTorch in conjunction with the Lava, SpikingJelly, and Norse frameworks, employing surrogate-gradient backpropagation through time (BPTT). A consistent training–validation split and identical data loaders were used across all models, encoding schemes, and neuron types to ensure fair, reproducible comparisons for both the FCN and VGG7 architectures.

Hyperparameters: Unless stated otherwise, all models used the Adam optimizer (learning rate $0.001$, weight decay $1\times {10}^{-5}$) with CrossEntropyLoss. FCN models were trained for 100 epochs, and VGG7 models for 150 epochs, with a batch size of 64 in all cases. Dropout was 5% for FCN and 20% for VGG7, with batch normalization applied where appropriate. ANNs used ReLU activations and the default PyTorch weight initialization. SNNs relied on spiking activations, with neuron parameters matched across datasets except for threshold voltage: FCN used $V_{\mathrm{th}}=1.25$, and VGG7 used $V_{\mathrm{th}}=0.5$. Shared SNN settings were as follows: current decay $0.25$, voltage decay $0.03$, tau gradient $0.03$, scale gradient 3, and refractory decay 1. A consolidated summary of parameters is provided in

Table 5. Hyperparameters for ANN and SNN models on FCN and VGG7 architectures.

Parameter	ANN (FCN/VGG7)	SNN (FCN)	SNN (VGG7)
Optimizer	Adam	Adam	Adam
Learning rate	0.001	0.001	0.001
Weight decay	$1\times {10}^{-5}$	$1\times {10}^{-5}$	$1\times {10}^{-5}$
Loss function	Cross-Entropy	CrossEntropyLoss	CrossEntropyLoss
Number of epochs	FCN: 100; VGG7: 150	100	150
Batch size	64	64	64
Dropout rate	FCN: 5%; VGG7: 20%	5%	20%
Activation function	ReLU	—	—
Weight initialization	PyTorch defaults	—	—
Neuron parameters	—	Threshold ($V_{\mathrm{th}}$): 1.25 Current decay: 0.25 Voltage decay: 0.03 Tau gradient: 0.03 Scale gradient: 3 Refractory decay: 1	Threshold ($V_{\mathrm{th}}$): 0.5 Current decay: 0.25 Voltage decay: 0.03 Tau gradient: 0.03 Scale gradient: 3 Refractory decay: 1

.

Preprocessing and encoding: ANN pipelines applied standard normalization (and augmentation for CIFAR-10). For SNNs, inputs were converted into spike trains using the evaluated encoding schemes (e.g., rate, temporal, and $\mathsf{\Sigma }\mathsf{\Delta }$) and processed by the selected neuron models.

Training loop: Each iteration comprised a forward pass, temporal aggregation of SNN outputs (time-averaged logits or readouts), computation of cross-entropy loss, gradient backpropagation (BPTT with surrogate gradients for SNNs, standard backpropagation for ANNs), and parameter updates using Adam. This unified training procedure ensured consistent optimization across all ANN and SNN configurations.

3.6. Evaluation Metrics

Two metrics were used for evaluation: (i) classification accuracy and (ii) a per-inference energy estimate.

Accuracy: The fraction of correctly classified test samples (single-label, top-1), computed from logits using CrossEntropyLoss. For SNNs, outputs were temporally aggregated (e.g., time-averaged logits or spike counts across T steps) before applying the final argmax. Identical data splits, preprocessing, batch size, and, for SNNs, time step settings were used across FCN and VGG7 models to ensure fairness.

Energy estimate: The energy per inference was estimated using the KerasSpiking methodology [155,156], which models total energy as the sum of synaptic (multiply-accumulate, MAC) operations and neuron-state updates:

$$\begin{array}{cc}\hfill E_S& =E_{o}S,\hfill \end{array}$$

(51)

$$\begin{array}{cc}\hfill E_N& =E_{u}U,\hfill \end{array}$$

(52)

$$\begin{array}{cc}\hfill E_{\mathrm{total}}& =E_S+E_N,\hfill \end{array}$$

(53)

where $E_o$ and $E_u$ are hardware-dependent energy constants, and S and U represent operation counts collected during inference. For ANNs, S is the number of MACs and U the number of activation evaluations; for SNNs, S counts synaptic events (spike transmissions) and U counts membrane or state updates across T time steps. Constants $E_o$ and $E_u$ were instantiated using published hardware values (e.g., GPU figures reported in [155], with typical Titan-class estimates $E_o\approx E_u\approx 0.3\mathrm{nJ}$), and $E_{\mathrm{total}}$ is reported in nJ/inference.

Rationale and limitations of KerasSpiking: KerasSpiking integrates with TensorFlow/Keras to provide energy estimates by pairing measured or literature-based device constants with operation counts [156]. Prior studies have applied this approach to benchmark SNNs against ANNs [155,159,160]. However, these constants represent generalized device characteristics rather than chip-specific, peer-validated calibrations; thus, they serve as approximations sensitive to architecture, memory traffic, and data movement. In this work, KerasSpiking is used as a transparent, hardware-pluggable proxy—appropriate for relative comparisons and adaptable to other platforms (e.g., neuromorphic chips such as Intel Loihi)—by substituting platform-specific per-operation constants. It should not be regarded as a definitive measure of absolute energy consumption.

3.7. Algorithms

This subsection enumerates the exact encodings, neuron models, and learning rules used in the experiments. Unless otherwise specified, SNNs employed surrogate-gradient BPTT. Time steps were set to $T\in \{4,6,8\}$ for FCN and $T\in \{2,4,6\}$ for VGG7, as shown in Algorithm 1.

Encodings used:

• Direct input: the image is duplicated across T time steps without spike synthesis.
• Rate (Poisson): intensities $\in [0,1]$ mapped to firing rates (maximum 100 Hz); Bernoulli sampling applied at each step.
• TTFS: a single spike latency monotonically mapped from intensity across T bins.
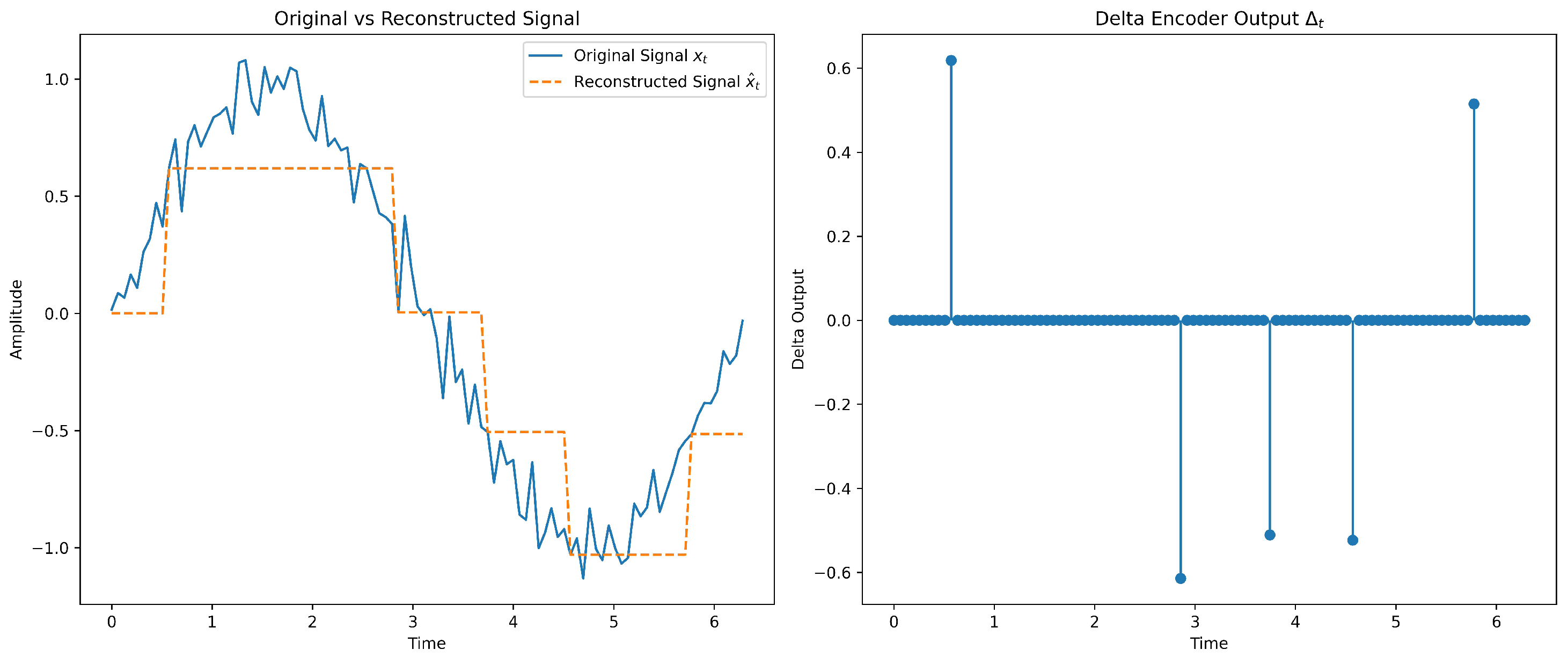
• $\mathsf{\Sigma }\mathsf{\Delta }$: dead-zone delta encoder with feedback; spikes emitted when $\left|\mathsf{\Delta }x\right|>\theta$ (here $\theta =0.5$), reconstructed by $\pm \theta$.
• R–NoM: rank-modulated top-N spiking from sorted intensities; N tuned by validation.
• PoFC: phase derived from normalized intensity over a $T_{\mathrm{osc}}=T$ cycle.
• Burst: intensity-dependent bursts capped at $B_{max}$ (selected via validation) within T.

Neuron models instantiated:

• IF and LIF (SpikingJelly; ATan surrogate gradient).
• ALIF (Lava; dynamic threshold or current adaptation).
• CUBA (Lava; current-based neuron).
• $\mathsf{\Sigma }\mathsf{\Delta }$ neuron (Lava; event-driven, error-based spiking).
• RF and RF–IZH (Lava; resonance and phase sensitivity).
• EIF and AdEx (Norse; exponential onset and adaptive dynamics).

Learning rules:

• SLAYER surrogate gradient (Lava/SLAYER 2.0).
• SuperSpike surrogate gradient (Norse).
• ATan surrogate function (SpikingJelly).

Algorithm 1: Training/evaluation for VGG7 on CIFAR-10 and FCN on MNIST with operation counting for energy estimation.
Notes: thresholds were dataset-specific ($V_{\mathrm{th}}=1.25$ for FCN/MNIST; $0.5$ for VGG7/CIFAR-10). Shared SNN settings: current decay $0.25$, voltage decay $0.03$, tau gradient $0.03$, scale gradient 3, refractory decay 1. Frameworks: PyTorch (ANNs); SpikingJelly/Lava/Norse (SNNs). Energy is reported via $E_{\mathrm{total}}=E_{o}S+E_{u}U$ using hardware constants cited in Section 3.6.

4. Results

This section presents the outcomes of the experiments conducted to evaluate the predictive performance and energy efficiency of all SNN configurations in comparison with their ANN counterparts. Experiments were performed on the MNIST and CIFAR-10 datasets using different network architectures, encoding schemes, and neuron models. The primary metrics include classification accuracy, inference energy consumption, and computational efficiency, quantified in terms of synaptic operations (SynOps) and event sparsity.

4.1. Performance on the MNIST Dataset

A shallow FCN consisting of two dense layers was used for the MNIST experiments, as described in Section 3.1. The objective was to assess the predictive performance of different SNN configurations relative to the baseline ANN model. Various encoding schemes and neuron models were tested to investigate their influence on classification accuracy. Furthermore, the models were evaluated at different numbers of time steps (4, 6, and 8) to examine the impact of temporal dynamics on performance.

4.1.1. Classification Accuracy Results

Table 6. Maximum classification accuracies (%) on the FCN with MNIST dataset.

Neuron Type	Time Steps	Rate Encoding	TTFS	$\mathsf{\Sigma }\mathsf{\Delta }$	Direct Coding	Burst Coding	PoFC	R-NoM
ANN (Baseline)	–	98.23%
IF	8	97.20	86.60	97.70	78.90	80.00	71.20	72.20
	6	97.10	90.00	97.60	88.10	91.00	78.50	74.00
	4	96.90	92.00	97.40	86.80	88.40	79.80	76.80
LIF	8	97.00	86.50	97.40	81.90	80.06	72.10	71.00
	6	96.90	90.00	97.50	90.00	91.10	77.70	73.00
	4	96.90	92.00	97.20	88.60	83.30	82.30	75.50
ALIF	8	97.30	96.40	96.50	97.10	97.14	92.70	58.00
	6	96.60	96.10	96.30	97.00	97.00	92.90	57.00
	4	96.40	96.70	96.30	97.00	96.90	93.00	46.00
CUBA	8	97.66	97.10	97.40	97.60	79.50	94.10	68.00
	6	97.56	97.00	97.18	97.50	79.30	94.10	66.50
	4	97.20	96.30	96.40	97.30	96.80	93.40	56.00
$\mathsf{\Sigma }\mathsf{\Delta }$	8	98.10	97.90	98.00	88.00	88.30	95.00	86.70
	6	97.80	97.50	98.00	88.50	97.90	87.40	86.00
	4	97.90	97.50	97.70	98.00	97.90	87.80	64.00
RF	8	93.00	86.80	90.05	97.20	92.20	85.80	52.00
	6	92.60	88.70	92.00	79.00	92.00	84.90	50.00
	4	93.00	88.00	91.60	53.00	91.70	83.90	47.70
RF-IZH	8	97.70	47.00	79.60	97.70	50.00	94.90	48.00
	6	97.55	87.70	97.40	97.70	97.40	94.80	69.70
	4	97.00	96.40	96.00	97.20	96.80	93.00	74.00
EIF	8	96.70	94.60	96.50	97.50	96.30	95.20	88.10
	6	96.20	94.90	96.20	97.60	96.00	94.50	86.70
	4	96.55	95.80	96.60	97.50	96.40	95.10	87.70
AdEx	8	96.50	94.70	96.50	97.40	96.70	95.40	89.50
	6	96.40	95.00	96.40	97.50	96.80	95.30	89.20
	4	96.00	95.90	96.44	97.39	96.80	95.20	88.50

and Figure 9 summarize the maximum MNIST classification accuracies (in percent) obtained across neuron models, encoding schemes, and time steps ($T=4,6,8$). The baseline ANN achieved an accuracy of 98.23%. For each neuron-encoding combination, the best-performing result is highlighted in the table. Figure 9 panels (a–c) present the corresponding bar plots for 4, 6, and 8 time steps, respectively.

Observation

The results indicate that SNNs can achieve classification accuracies comparable to traditional ANNs on the MNIST dataset. The choice of neuron model and encoding scheme significantly influences performance.

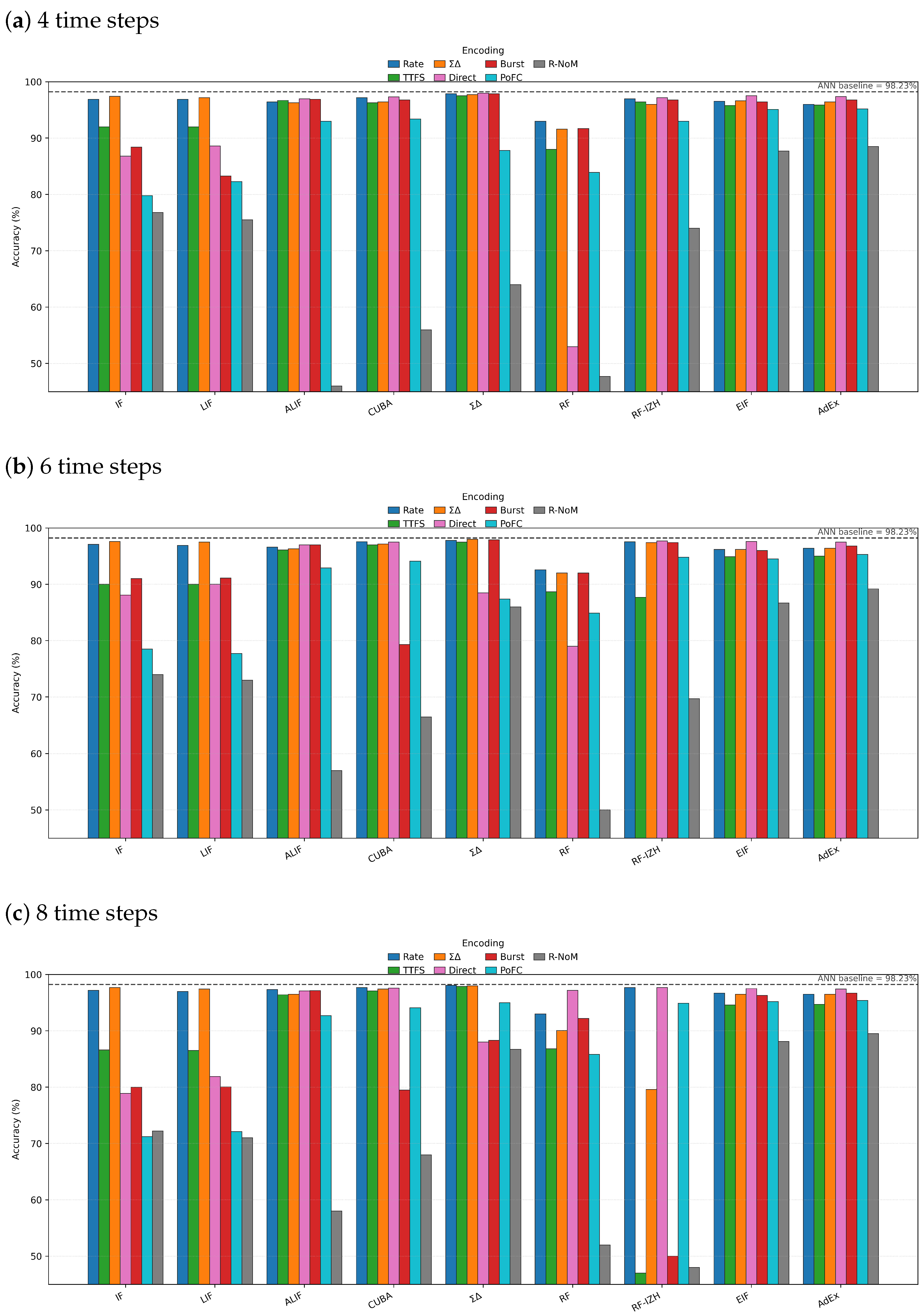
• $\mathsf{\Sigma }\mathsf{\Delta }$ neurons achieving the highest accuracy: $\mathsf{\Sigma }\mathsf{\Delta }$ neurons attained the highest accuracy of 98.10% using rate encoding at eight time steps. They also performed strongly across other encodings, reaching 98.00% with $\mathsf{\Sigma }\mathsf{\Delta }$ encoding at both eight and six time steps. These results highlight their effectiveness in precise spike-based computation and suitability for tasks requiring accurate temporal processing and efficient encoding.
• Adaptive neuron models showing competitive performance: Adaptive neuron models such as ALIF and AdEx achieved competitive accuracy, particularly with direct and burst encodings. ALIF reached a maximum of 97.30% with rate encoding at eight time steps, while AdEx achieved 97.50% with direct encoding at six time steps. Their adaptation mechanisms enable better capture of temporal dynamics, providing a favorable trade-off between accuracy and computational efficiency.
• Solid performance of simpler neuron models: Simpler models such as IF and LIF also demonstrated strong performance with rate and $\mathsf{\Sigma }\mathsf{\Delta }$ encodings. IF achieved 97.70% accuracy with $\mathsf{\Sigma }\mathsf{\Delta }$ encoding at eight time steps, while LIF reached 97.50% at six time steps. Although slightly below the ANN baseline of 98.23%, these results confirm that simpler neuron models can still perform effectively when combined with appropriate encoding schemes.
• Performance of RF neurons: The standard RF neuron achieved lower accuracies compared with other models, with a maximum of 97.20% using direct encoding at eight time steps. The RF–IZH variant performed better, reaching 97.70% with rate and direct encodings at eight time steps.
• Robustness of CUBA neurons: CUBA neurons achieved consistent results, with a maximum accuracy of 97.66% using rate encoding at eight time steps and 97.60% using direct encoding. Their stability across encoding schemes highlights robustness and adaptability.
• EIF neurons’ performance: EIF neurons achieved 97.60% accuracy using direct encoding at six time steps, reflecting their capability to process direct input representations efficiently. Models such as CUBA and EIF that perform well across multiple encoding strategies demonstrate strong generalization and are suitable for applications requiring flexibility in encoding.
• Effectiveness of encoding schemes: Direct and $\mathsf{\Sigma }\mathsf{\Delta }$ encodings emerged as the most effective across multiple neuron types, frequently producing the highest accuracies. Burst encoding also performed well, particularly when paired with adaptive neuron models such as ALIF and AdEx. Temporal encodings (TTFS and PoFC) improved with increasing time steps but generally did not surpass direct or $\mathsf{\Sigma }\mathsf{\Delta }$ encoding.
• Effect of time steps on accuracy: Increasing the number of time steps generally improved accuracy for most neuron and encoding combinations, especially for temporal encodings such as TTFS and PoFC. However, models such as ALIF and $\mathsf{\Sigma }\mathsf{\Delta }$ neurons maintained high accuracy even with fewer time steps, demonstrating their efficiency in capturing temporal dynamics while minimizing computational and energy costs.
• Advanced versus simpler neuron models: Advanced neuron models such as $\mathsf{\Sigma }\mathsf{\Delta }$, ALIF, and AdEx consistently achieved higher accuracies than simpler models like IF and LIF. This underscores the importance of mechanisms such as spike-frequency adaptation and precise spike timing in enhancing classification performance. Although some SNN configurations slightly lagged behind the ANN baseline, several achieved near-equivalent accuracy while maintaining superior energy efficiency and temporal processing capabilities.
• Variable performance of R–NoM encoding: R–NoM encoding showed variable performance across neuron models. ALIF neurons achieved a maximum of 58.00%, whereas EIF neurons reached 88.10%. This variability suggests that R–NoM’s effectiveness depends heavily on the underlying neuron dynamics.

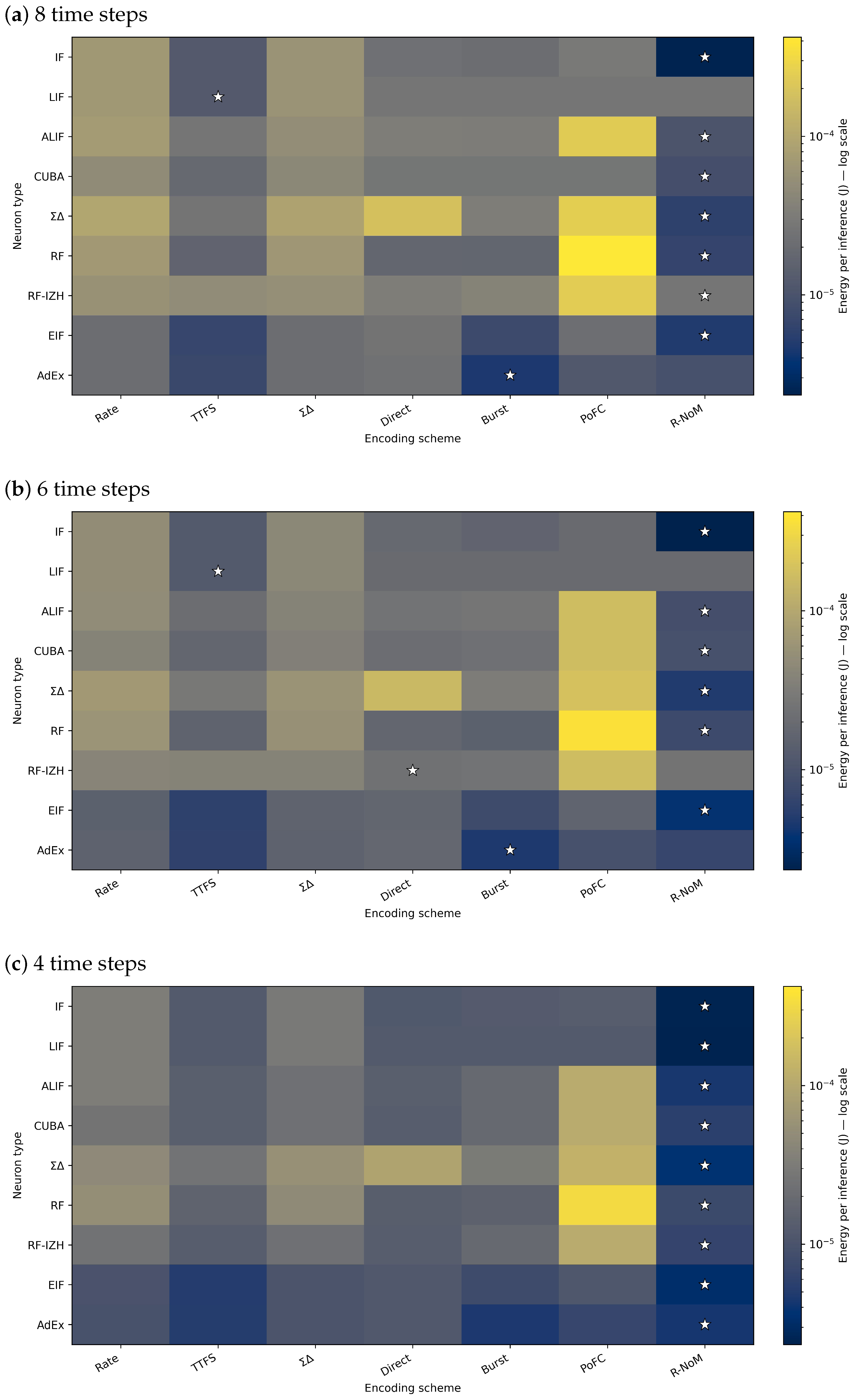
4.1.2. Energy Consumption

Table 7. Total energy consumption during inference on the MNIST dataset (joules per sample).

Neuron Type	Time Steps	Rate Encoding	TTFS	$\mathsf{\Sigma }\mathsf{\Delta }$	Direct Coding	Burst Coding	PoFC	R-NoM
IF	8	$6.69581\times {10}^{-5}$	$1.23361\times {10}^{-5}$	$5.99763\times {10}^{-5}$	$2.28804\times {10}^{-5}$	$2.12915\times {10}^{-5}$	$3.00687\times {10}^{-5}$	$2.40915\times {10}^{-6}$
	6	$5.02249\times {10}^{-5}$	$1.22764\times {10}^{-5}$	$4.48093\times {10}^{-5}$	$1.89740\times {10}^{-5}$	$1.66753\times {10}^{-5}$	$1.96420\times {10}^{-5}$	$2.33240\times {10}^{-6}$
	4	$3.34828\times {10}^{-5}$	$1.22051\times {10}^{-5}$	$2.95766\times {10}^{-5}$	$1.15835\times {10}^{-5}$	$1.27242\times {10}^{-5}$	$1.32330\times {10}^{-5}$	$2.50741\times {10}^{-6}$
LIF	8	$6.69782\times {10}^{-5}$	$1.23361\times {10}^{-5}$	$6.00020\times {10}^{-5}$	$2.69682\times {10}^{-5}$	$2.69682\times {10}^{-5}$	$2.69682\times {10}^{-5}$	$2.69682\times {10}^{-5}$
	6	$5.02339\times {10}^{-5}$	$1.22746\times {10}^{-5}$	$4.48206\times {10}^{-5}$	$1.94391\times {10}^{-5}$	$1.94391\times {10}^{-5}$	$1.94391\times {10}^{-5}$	$1.94391\times {10}^{-5}$
	4	$3.34905\times {10}^{-5}$	$1.22085\times {10}^{-5}$	$2.95881\times {10}^{-5}$	$1.23209\times {10}^{-5}$	$1.23209\times {10}^{-5}$	$1.23209\times {10}^{-5}$	$2.44273\times {10}^{-6}$
ALIF	8	$7.3510\times {10}^{-5}$	$2.6871\times {10}^{-5}$	$5.1945\times {10}^{-5}$	$3.40339\times {10}^{-5}$	$3.24837\times {10}^{-5}$	$2.33675\times {10}^{-4}$	$1.03986\times {10}^{-5}$
	6	$4.92296\times {10}^{-5}$	$2.10553\times {10}^{-5}$	$3.81021\times {10}^{-5}$	$2.50982\times {10}^{-5}$	$2.70057\times {10}^{-5}$	$1.72831\times {10}^{-4}$	$8.96057\times {10}^{-6}$
	4	$3.28536\times {10}^{-5}$	$1.44922\times {10}^{-5}$	$2.33582\times {10}^{-5}$	$1.41680\times {10}^{-5}$	$1.86396\times {10}^{-5}$	$1.10753\times {10}^{-4}$	$4.41252\times {10}^{-6}$
CUBA	8	$4.90000\times {10}^{-5}$	$1.90000\times {10}^{-5}$	$4.50000\times {10}^{-5}$	$2.64009\times {10}^{-5}$	$2.66573\times {10}^{-5}$	$2.66573\times {10}^{-5}$	$8.95950\times {10}^{-6}$
	6	$3.81410\times {10}^{-5}$	$1.74550\times {10}^{-5}$	$3.48430\times {10}^{-5}$	$2.17564\times {10}^{-5}$	$2.35472\times {10}^{-5}$	$1.69526\times {10}^{-4}$	$9.35265\times {10}^{-6}$
	4	$2.55850\times {10}^{-5}$	$1.43430\times {10}^{-5}$	$2.31800\times {10}^{-5}$	$1.33601\times {10}^{-5}$	$1.85833\times {10}^{-5}$	$1.11244\times {10}^{-4}$	$5.78706\times {10}^{-6}$
$\mathsf{\Sigma }\mathsf{\Delta }$	8	$9.57181\times {10}^{-5}$	$2.57815\times {10}^{-5}$	$8.88477\times {10}^{-5}$	$1.86487\times {10}^{-4}$	$3.38357\times {10}^{-5}$	$2.50818\times {10}^{-4}$	$5.86194\times {10}^{-6}$
	6	$6.94061\times {10}^{-5}$	$2.85522\times {10}^{-5}$	$6.02046\times {10}^{-5}$	$1.55357\times {10}^{-4}$	$3.23769\times {10}^{-5}$	$1.88630\times {10}^{-4}$	$5.02764\times {10}^{-6}$
	4	$4.70307\times {10}^{-5}$	$2.47350\times {10}^{-5}$	$5.58219\times {10}^{-5}$	$9.05406\times {10}^{-5}$	$3.03132\times {10}^{-5}$	$1.28965\times {10}^{-4}$	$3.66343\times {10}^{-6}$
RF	8	$7.04992\times {10}^{-5}$	$1.64224\times {10}^{-5}$	$6.49873\times {10}^{-5}$	$1.77361\times {10}^{-5}$	$1.71799\times {10}^{-5}$	$4.22585\times {10}^{-4}$	$6.52145\times {10}^{-6}$
	6	$6.15202\times {10}^{-5}$	$1.59444\times {10}^{-5}$	$5.60981\times {10}^{-5}$	$1.75526\times {10}^{-5}$	$1.49569\times {10}^{-5}$	$3.67283\times {10}^{-4}$	$7.72182\times {10}^{-6}$
	4	$5.28138\times {10}^{-5}$	$1.57942\times {10}^{-5}$	$4.79926\times {10}^{-5}$	$1.38899\times {10}^{-5}$	$1.52142\times {10}^{-5}$	$3.30481\times {10}^{-4}$	$7.46545\times {10}^{-6}$
RF-IZH	8	$5.74303\times {10}^{-5}$	$4.94997\times {10}^{-5}$	$5.39998\times {10}^{-5}$	$3.38775\times {10}^{-5}$	$3.84832\times {10}^{-5}$	$2.41357\times {10}^{-4}$	$2.69479\times {10}^{-5}$
	6	$4.09763\times {10}^{-5}$	$3.86407\times {10}^{-5}$	$3.84926\times {10}^{-5}$	$2.36274\times {10}^{-5}$	$2.48624\times {10}^{-5}$	$1.72002\times {10}^{-4}$	$2.54921\times {10}^{-5}$
	4	$2.43212\times {10}^{-5}$	$1.33653\times {10}^{-5}$	$2.27467\times {10}^{-5}$	$1.31812\times {10}^{-5}$	$1.88247\times {10}^{-5}$	$1.10943\times {10}^{-4}$	$6.54786\times {10}^{-6}$
EIF	8	$2.09544\times {10}^{-5}$	$6.89162\times {10}^{-6}$	$2.10879\times {10}^{-5}$	$2.54309\times {10}^{-5}$	$7.57636\times {10}^{-6}$	$2.18263\times {10}^{-5}$	$4.88905\times {10}^{-6}$
	6	$1.50407\times {10}^{-5}$	$5.82237\times {10}^{-6}$	$1.57690\times {10}^{-5}$	$1.73112\times {10}^{-5}$	$7.84863\times {10}^{-6}$	$1.61259\times {10}^{-5}$	$3.81949\times {10}^{-6}$
	4	$9.98311\times {10}^{-6}$	$5.11222\times {10}^{-6}$	$1.03737\times {10}^{-5}$	$1.17131\times {10}^{-5}$	$7.73232\times {10}^{-6}$	$1.11675\times {10}^{-5}$	$3.30303\times {10}^{-6}$
AdEx	8	$2.10624\times {10}^{-5}$	$7.36623\times {10}^{-6}$	$2.10755\times {10}^{-5}$	$2.37614\times {10}^{-5}$	$4.60625\times {10}^{-6}$	$1.17924\times {10}^{-5}$	$9.51151\times {10}^{-6}$
	6	$1.55792\times {10}^{-5}$	$6.13887\times {10}^{-6}$	$1.56530\times {10}^{-5}$	$1.81244\times {10}^{-5}$	$4.65618\times {10}^{-6}$	$9.51664\times {10}^{-6}$	$6.74905\times {10}^{-6}$
	4	$9.70576\times {10}^{-6}$	$5.24387\times {10}^{-6}$	$1.04670\times {10}^{-5}$	$1.17669\times {10}^{-5}$	$4.59669\times {10}^{-6}$	$6.84008\times {10}^{-6}$	$4.31047\times {10}^{-6}$

reports the total energy per inference (joules) on MNIST across SNN configurations, measured on a GPU, with the ANN baseline consuming $\mathbf{1}.\mathbf{1355}\times {\mathbf{10}}^{-\mathbf{3}}$ J per sample. The lower energy consumption for each neuron type and encoding are highlighted in bold Figure 10 complements the table with heatmaps for 8, 6, and 4 time steps (panels a–c), where rows are neuron types and columns are encoding schemes; color denotes energy on a logarithmic scale, and a star marks the lowest-energy encoding within each neuron type.

Trade-Off Between Accuracy and Power Consumption

As summarized in Table 7, R–NoM consistently yields the lowest energy consumption for most neuron types. However, Table 6 shows that its classification accuracy remains notably below that of the best-performing schemes such as $\mathsf{\Sigma }\mathsf{\Delta }$ and direct coding. Conversely, the highest-accuracy configurations (for example, $\mathsf{\Sigma }\mathsf{\Delta }$ neurons with rate or $\mathsf{\Sigma }\mathsf{\Delta }$ encoding) still operate at energy levels below the ANN baseline ($1.1355\times {10}^{-3}$ J), highlighting the ability of SNNs to outperform traditional ANNs in power efficiency without substantial loss in accuracy.

• R–NoM: minimal energy, lower accuracy. R–NoM encoding achieves exceptionally low power usage, for instance $2.33\times {10}^{-6}$ J for the IF neuron at six time steps. However, these configurations typically exhibit weaker accuracies (approximately 70–75% for IF and considerably lower for ALIF), illustrating a clear trade-off between energy savings and predictive performance.
• High-accuracy configurations remain energy-efficient. Several neuron types—including $\mathsf{\Sigma }\mathsf{\Delta }$, ALIF, and CUBA—achieve accuracies near or above 97–98% while consuming far less energy than the ANN baseline. For example, $\mathsf{\Sigma }\mathsf{\Delta }$ neurons with rate encoding at eight time steps yield 98.10% accuracy (Table 6) and require approximately $9.57\times {10}^{-5}$ J per inference (Table 7), representing about a tenfold improvement in energy efficiency relative to the ANN baseline.
• AdEx neurons: best energy with burst coding, highest accuracy with direct coding. AdEx neurons achieve their minimum energy consumption under burst coding (as reported in Table 7) but attain their best accuracy, around 97.4–97.5%, using direct coding (Table 6). This illustrates that the most energy-efficient configuration does not necessarily coincide with the highest-accuracy one, even within the same neuron model.
• Fewer time steps reduce energy but may lower accuracy. Most neuron types consume less power at four or six time steps than at eight. However, for temporal encodings such as TTFS and PoFC, reducing the number of steps can lower accuracy by several percentage points. Models with adaptive dynamics—ALIF, AdEx, and $\mathsf{\Sigma }\mathsf{\Delta }$—maintain relatively high accuracy at lower time steps, making them favorable for energy-constrained applications.
• Overall SNN advantage. Almost all SNN configurations, including those achieving 97–98% accuracy, consume substantially less energy than the ANN baseline. This confirms the suitability of SNNs for edge and low-power deployments, where minor accuracy losses may be acceptable in exchange for significant energy savings.
• Balancing encoding and neuron type. Although R–NoM leads in power reduction, it consistently trails in accuracy. Encodings such as $\mathsf{\Sigma }\mathsf{\Delta }$ or direct coding achieve near-ANN accuracy with only moderate energy overhead compared with R–NoM, while still maintaining far lower energy usage than ANNs. Selecting the optimal combination of a neuron model and encoding scheme, therefore, requires balancing accuracy requirements against available power budgets, as each pairing exhibits distinct performance–efficiency characteristics.

4.2. Performance on CIFAR-10 Dataset

In this subsection, we utilized a VGG7 network architecture as described in Section 3.1 and evaluated it on the CIFAR-10 dataset using various neuron models and encoding schemes to show classification accuracies achieved. We aimed to assess the performance of different SNN configurations compared to a baseline ANN. Additionally, we evaluated the models at varying time steps (2, 4, and 6) to evaluate the effect of temporal dynamics.

4.2.1. Classification Accuracy Results

Table 8. Maximum classification accuracies (%) on VGG7 with CIFAR-10 dataset.

Neuron Type	Time Steps	Rate Encoding	TTFS	$\mathsf{\Sigma }\mathsf{\Delta }$	Direct Coding	Burst Coding	PoFC	R-NoM
ANN (Baseline)	–	83.60%
IF	2	57.00	60.00	62.00	74.00	60.00	57.00	29.00
	4	56.50	62.00	65.00	74.50	64.00	65.00	27.00
	6	57.00	62.50	65.00	74.50	64.50	68.00	30.00
LIF	2	50.00	61.50	62.50	74.30	57.60	59.00	28.00
	4	51.00	62.00	64.50	74.50	61.00	63.00	23.00
	6	50.00	59.50	65.00	74.00	61.50	67.00	21.00
ALIF	2	10.00	10.00	10.00	10.00	10.00	10.00	10.00
	4	39.00	34.00	20.00	46.00	20.00	27.00	14.00
	6	51.00	38.00	28.00	49.00	27.00	29.00	24.00
CUBA	2	10.00	10.00	10.00	10.00	10.00	10.00	10.00
	4	34.00	50.00	33.50	40.00	30.00	24.00	25.00
	6	45.00	43.00	40.00	50.00	30.00	31.00	27.00
$\mathsf{\Sigma }\mathsf{\Delta }$	2	57.00	72.00	56.00	83.00	57.00	57.00	30.00
	4	61.00	72.00	66.00	78.00	66.00	62.00	27.00
	6	60.00	72.50	68.00	79.00	66.00	67.00	24.00
RF	2	10.00	10.00	10.00	10.00	10.00	10.00	10.00
	4	22.00	10.00	10.00	42.00	10.00	10.00	10.00
	6	37.00	36.00	32.00	47.00	39.00	37.00	31.00
RF-IZH	2	10.00	10.00	10.00	10.00	10.00	10.00	10.00
	4	10.00	10.00	10.00	33.00	10.00	10.00	10.00
	6	45.00	37.00	30.00	39.00	32.00	32.00	27.00
EIF	2	58.50	56.00	53.50	70.00	58.50	54.00	25.00
	4	59.50	64.00	60.00	69.00	57.00	57.00	22.50
	6	60.00	65.00	61.00	68.50	53.50	60.00	24.00
AdEx	2	59.00	55.50	60.00	69.50	58.50	54.00	27.00
	4	60.00	62.00	61.50	70.00	56.50	59.00	29.00
	6	60.50	63.00	60.50	70.10	52.00	61.00	25.50

and Figure 11 summarize the maximum classification accuracies (%) achieved by various neuron models, encoding schemes, and time steps on CIFAR-10. The dashed horizontal line in Figure 11 marks the ANN baseline (83.6%), and panels (a)–(c) correspond to 2, 4, and 6 time steps, respectively. Note that accuracies near 10% indicate ineffective learning at those settings (roughly random guessing over 10 classes). For clarity, the highest accuracies for each neuron type and encoding scheme are highlighted in bold in Table 8.

Observation

The results in Table 8 demonstrate that SNNs can approach the classification accuracy of traditional ANNs on complex datasets such as CIFAR-10. The choice of neuron model, encoding scheme, and number of time steps has a significant impact on performance.

• $\mathsf{\Sigma }\mathsf{\Delta }$ neurons achieving the highest accuracy. $\mathsf{\Sigma }\mathsf{\Delta }$ neurons attained the highest SNN accuracy of 83.00% with direct coding at two time steps, closely matching the ANN baseline of 83.60%. This strong performance with a minimal number of time steps highlights the efficiency of $\mathsf{\Sigma }\mathsf{\Delta }$ neurons in capturing complex spatial–temporal patterns. In addition, TTFS encoding with $\mathsf{\Sigma }\mathsf{\Delta }$ neurons achieved accuracies up to 72.50%, confirming their versatility across different encoding schemes.
• Performance of IF and LIF neurons. IF and LIF neurons achieved comparable performance, with maximum accuracies of 74.50% each using direct coding at four time steps. These findings suggest that even simpler neuron models can perform effectively on complex datasets when combined with appropriate encoding methods. Accuracy improved modestly with additional time steps, indicating that temporal dynamics contribute positively to their classification capability.
• Performance of ALIF neurons. The adaptive LIF (ALIF) model achieved a maximum accuracy of 51.00% with rate encoding at 6 time steps. The relatively lower accuracy compared with other neuron types suggests that ALIF may require further tuning or more advanced encoding strategies to fully exploit its adaptation mechanisms on CIFAR-10.
• Performance of CUBA neurons. CUBA neurons reached a peak accuracy of 50.00% with TTFS encoding at 4 time steps. Although this exceeds random performance, it indicates that CUBA neurons alone may not effectively capture the complex features in CIFAR-10 without additional optimization.
• Performance of RF and RF–IZH neurons. RF and its Izhikevich variant (RF–IZH) achieved peak accuracies of 47.00% and 45.00%, respectively. These results suggest that resonate-and-fire dynamics are less suited for complex vision tasks such as CIFAR-10 image classification.
• Performance of EIF and AdEx neurons. EIF neurons reached an accuracy of 70.00% with direct coding at 2 time steps, while AdEx achieved 70.10% with direct coding at 6 time steps. These findings suggest that exponential spike initiation and adaptive dynamics enhance the processing of complex input patterns.
• Effectiveness of direct coding and TTFS encoding. Across neuron models, direct coding proved the most effective scheme, consistently yielding higher accuracies. This is likely because it preserves detailed spatial information without depending heavily on temporal representation. TTFS also performed well, particularly with $\mathsf{\Sigma }\mathsf{\Delta }$ neurons, indicating that precise spike timing benefits certain configurations.
• Impact of time steps. The number of time steps affected performance, though less strongly than in the MNIST experiments. Some models, such as $\mathsf{\Sigma }\mathsf{\Delta }$, achieved high accuracy even at 2 time steps, highlighting computational efficiency. Increasing time steps generally provided modest accuracy gains, suggesting a balance between temporal resolution and computational cost.
• Comparison with ANN baseline. Although several SNN configurations approached the ANN baseline, many remained slightly below. Careful selection of neuron models and encoding schemes is, therefore, crucial to achieving high performance on complex datasets. In particular, $\mathsf{\Sigma }\mathsf{\Delta }$ neurons combined with direct coding exhibit strong potential, offering high accuracy at low time steps while maintaining energy and computational efficiency.

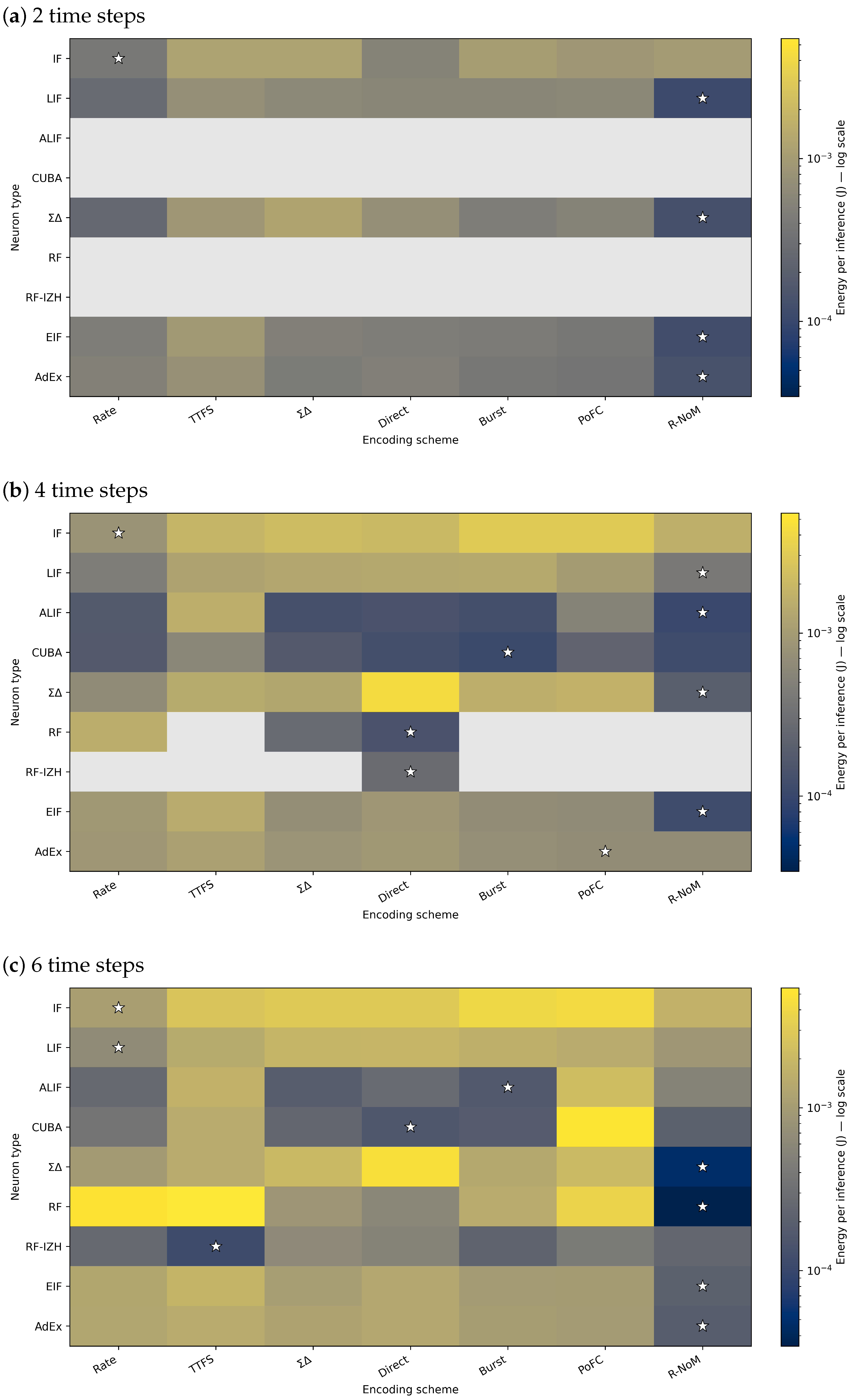
4.2.2. Energy Consumption on the CIFAR-10 Dataset

Table 9. Total energy consumption during inference on the CIFAR-10 dataset (joules per sample).

Neuron Type	Time Steps	Rate Encoding	TTFS	$\mathsf{\Sigma }\mathsf{\Delta }$	Direct Coding	Burst Coding	PoFC	R-NoM
IF	2	$\mathbf{3}.\mathbf{94852}\times {\mathbf{10}}^{-\mathbf{4}}$	$1.16663\times {10}^{-3}$	$1.17000\times {10}^{-3}$	$5.22092\times {10}^{-4}$	$1.04445\times {10}^{-3}$	$8.80562\times {10}^{-4}$	$9.83376\times {10}^{-4}$
	4	$8.27214\times {10}^{-4}$	$1.83994\times {10}^{-3}$	$2.20152\times {10}^{-3}$	$2.05982\times {10}^{-3}$	$3.00816\times {10}^{-3}$	$2.99366\times {10}^{-3}$	$1.63505\times {10}^{-3}$
	6	$1.08961\times {10}^{-3}$	$2.65824\times {10}^{-3}$	$2.94586\times {10}^{-3}$	$2.94252\times {10}^{-3}$	$4.02648\times {10}^{-3}$	$4.26378\times {10}^{-3}$	$1.70701\times {10}^{-3}$
LIF	2	$2.78448\times {10}^{-4}$	$7.26634\times {10}^{-4}$	$6.23768\times {10}^{-4}$	$5.80780\times {10}^{-4}$	$5.80780\times {10}^{-4}$	$6.11386\times {10}^{-4}$	$\mathbf{1}.\mathbf{08714}\times {\mathbf{10}}^{-\mathbf{4}}$
	4	$4.61336\times {10}^{-4}$	$1.20903\times {10}^{-3}$	$1.32926\times {10}^{-3}$	$1.38078\times {10}^{-3}$	$1.41197\times {10}^{-3}$	$1.01033\times {10}^{-3}$	$4.01296\times {10}^{-4}$
	6	$6.68692\times {10}^{-4}$	$1.42619\times {10}^{-3}$	$1.84539\times {10}^{-3}$	$1.90760\times {10}^{-3}$	$1.63428\times {10}^{-3}$	$1.50135\times {10}^{-3}$	$8.81364\times {10}^{-4}$
ALIF	2	0	0	0	0	0	0	0
	4	$1.74226\times {10}^{-4}$	$1.60722\times {10}^{-3}$	$1.29974\times {10}^{-4}$	$1.41245\times {10}^{-4}$	$1.25511\times {10}^{-4}$	$5.29554\times {10}^{-4}$	$\mathbf{1}.\mathbf{03862}\times {\mathbf{10}}^{-\mathbf{4}}$
	6	$2.60075\times {10}^{-4}$	$1.70157\times {10}^{-3}$	$1.85570\times {10}^{-4}$	$2.79213\times {10}^{-4}$	$1.70813\times {10}^{-4}$	$2.28347\times {10}^{-3}$	$5.30497\times {10}^{-4}$
CUBA	2	0	0	0	0	0	0	0
	4	$1.78050\times {10}^{-4}$	$6.03918\times {10}^{-4}$	$1.75168\times {10}^{-4}$	$1.26776\times {10}^{-4}$	$\mathbf{1}.\mathbf{07812}\times {\mathbf{10}}^{-\mathbf{4}}$	$2.34300\times {10}^{-4}$	$1.15656\times {10}^{-4}$
	6	$3.63035\times {10}^{-4}$	$1.46932\times {10}^{-3}$	$2.48938\times {10}^{-4}$	$1.60722\times {10}^{-4}$	$1.83053\times {10}^{-4}$	$5.15800\times {10}^{-3}$	$2.10588\times {10}^{-4}$
$\mathsf{\Sigma }\mathsf{\Delta }$	2	$2.56910\times {10}^{-4}$	$8.69356\times {10}^{-4}$	$1.23596\times {10}^{-3}$	$7.30794\times {10}^{-4}$	$4.56246\times {10}^{-4}$	$5.34300\times {10}^{-4}$	$1.30238\times {10}^{-4}$
	4	$6.60378\times {10}^{-4}$	$1.43843\times {10}^{-3}$	$1.29967\times {10}^{-3}$	$4.38806\times {10}^{-3}$	$1.60582\times {10}^{-3}$	$1.76199\times {10}^{-3}$	$1.96755\times {10}^{-4}$
	6	$9.75392\times {10}^{-4}$	$1.45020\times {10}^{-3}$	$2.06100\times {10}^{-3}$	$4.73134\times {10}^{-3}$	$1.37457\times {10}^{-3}$	$2.10540\times {10}^{-3}$	$\mathbf{4}.\mathbf{66853}\times {\mathbf{10}}^{-\mathbf{5}}$
RF	2	0	0	0	0	0	0	0
	4	$1.54216\times {10}^{-3}$	0	$2.75743\times {10}^{-4}$	$1.42578\times {10}^{-4}$	0	0	0
	6	$4.95305\times {10}^{-3}$	$5.45528\times {10}^{-3}$	$8.55122\times {10}^{-4}$	$5.99531\times {10}^{-4}$	$1.45782\times {10}^{-3}$	$3.74125\times {10}^{-3}$	$\mathbf{3}.\mathbf{45218}\times {\mathbf{10}}^{-\mathbf{5}}$
RF-IZH	2	0	0	0	0	0	0	0
	4	0	0	0	$\mathbf{2}.\mathbf{85883}\times {\mathbf{10}}^{-\mathbf{4}}$	0	0	0
	6	$2.60712\times {10}^{-4}$	$1.12258\times {10}^{-4}$	$6.43347\times {10}^{-4}$	$5.21456\times {10}^{-4}$	$2.23209\times {10}^{-4}$	$4.21825\times {10}^{-4}$	$2.45245\times {10}^{-4}$
EIF	2	$4.51992\times {10}^{-4}$	$9.22080\times {10}^{-4}$	$4.80420\times {10}^{-4}$	$4.62498\times {10}^{-4}$	$4.36462\times {10}^{-4}$	$3.92722\times {10}^{-4}$	$\mathbf{1}.\mathbf{18310}\times {\mathbf{10}}^{-\mathbf{4}}$
	4	$9.11080\times {10}^{-4}$	$1.45713\times {10}^{-3}$	$7.15536\times {10}^{-4}$	$8.86820\times {10}^{-4}$	$6.84824\times {10}^{-4}$	$6.64914\times {10}^{-4}$	$1.15656\times {10}^{-4}$
	6	$1.30268\times {10}^{-3}$	$1.81481\times {10}^{-3}$	$1.06204\times {10}^{-3}$	$1.34335\times {10}^{-3}$	$9.94740\times {10}^{-4}$	$1.01460\times {10}^{-3}$	$2.10588\times {10}^{-4}$
AdEx	2	$4.98822\times {10}^{-4}$	$7.65386\times {10}^{-4}$	$\mathbf{4}.\mathbf{27554}\times {\mathbf{10}}^{-\mathbf{4}}$	$4.79906\times {10}^{-4}$	$3.92988\times {10}^{-4}$	$3.56532\times {10}^{-4}$	$1.38236\times {10}^{-4}$
	4	$8.93400\times {10}^{-4}$	$1.12146\times {10}^{-3}$	$8.35974\times {10}^{-4}$	$9.07006\times {10}^{-4}$	$7.49690\times {10}^{-4}$	$6.93842\times {10}^{-4}$	$6.97172\times {10}^{-4}$
	6	$1.27278\times {10}^{-3}$	$1.45338\times {10}^{-3}$	$1.19859\times {10}^{-3}$	$1.36141\times {10}^{-3}$	$1.03748\times {10}^{-3}$	$9.92686\times {10}^{-4}$	$1.89960\times {10}^{-4}$

reports the total energy per inference (joules) on CIFAR-10 across all SNN configurations, measured on a GPU. The ANN baseline consumed $1.1355\times {10}^{-3}$ J per sample. For each neuron-encoding pair, the configuration with the lowest energy consumption is indicated in the table. Figure 12 complements these results with heatmaps for 6, 4, and 2 time steps (panels a–c), where rows correspond to neuron types and columns to encoding schemes. Color intensity represents energy consumption on a logarithmic scale, and a star denotes the lowest-energy encoding within each neuron category.

Observation

• Overall energy trends. SNNs consistently consume less energy than the baseline ANN across neuron types and encoding schemes. Models achieving higher classification accuracy—such as those using direct or temporal encodings—typically exhibit higher energy usage than simpler schemes. Nevertheless, even the most energy-demanding SNN configurations remain below the $1.1355\times {10}^{-3}$ J reference value set by the ANN. This finding reinforces SNNs’ potential for substantial energy savings in complex tasks such as CIFAR-10 classification.
• Influence of time steps. A consistent pattern emerges in which increasing the number of time steps leads to higher energy consumption. For example, IF neurons increase from $3.95\times {10}^{-4}$ J at two time steps to $1.09\times {10}^{-3}$ J at six time steps under rate encoding. Although additional time steps can enhance classification accuracy, they also raise energy cost. Consequently, applications requiring real-time performance or low power consumption may favor configurations with fewer time steps, provided accuracy remains within acceptable limits.
• Neuron models and encoding schemes. Simpler neuron models (e.g., IF, LIF) generally exhibit moderate energy usage, but their efficiency depends strongly on the encoding strategy. For instance, IF neurons with rate encoding at two time steps require as little as $3.95\times {10}^{-4}$ J, whereas LIF neurons combined with temporal encodings consume more energy but often achieve better accuracy. Advanced models such as ALIF and AdEx may improve classification performance but do not always minimize energy consumption. Their adaptive dynamics can reduce spike activity under certain conditions, although this benefit varies depending on the encoding scheme and the number of time steps.
• Balancing accuracy and efficiency. Encoding schemes with low energy requirements often exhibit lower accuracy. Thus, selecting an optimal combination of neuron model, encoding method, and time steps is essential for balancing performance and efficiency. Overall, the results confirm that SNNs consistently maintain lower energy consumption than conventional ANNs, even when configured for higher accuracy. This balance between accuracy and energy efficiency underscores SNNs’ suitability for edge devices and other power-sensitive applications.

4.3. Effect of Thresholding and Encoding Schemes on Model Performance and Energy Consumption

This subsection investigates how variations in neuronal firing threshold and encoding scheme influence both classification accuracy and energy consumption of SNNs. The analysis focuses on the EIF neuron model applied to the CIFAR-10 dataset. The experimental setup includes evaluation at time steps of 2, 4, and 6, threshold values of 0.1, 0.5, and 0.75, and a range of encoding schemes—rate encoding, TTFS, $\mathsf{\Sigma }\mathsf{\Delta }$, direct coding, burst coding, PoFC, and R–NoM. These experiments provide insight into how threshold tuning interacts with encoding dynamics to affect SNN performance and efficiency.

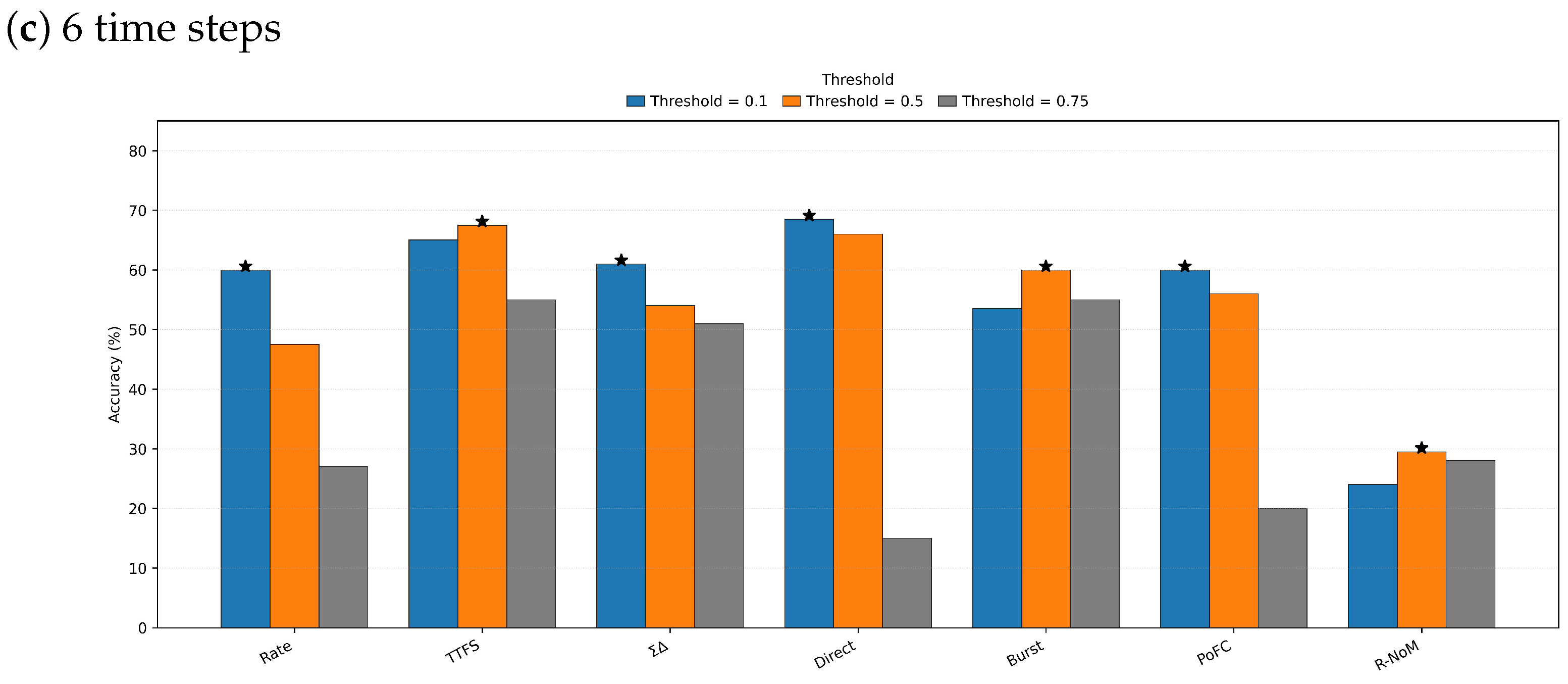
4.3.1. Impact of Threshold Values on Classification Accuracy

As summarized in

Table 10. Maximum classification accuracies (%) on CIFAR-10 dataset with varying thresholds. The highest accuracy for each encoding scheme is highlighted in bold.

Encoding Scheme	Threshold	2 Steps	4 Steps	6 Steps
Rate encoding	0.1	58.50	59.50	60.00
	0.5	47.00	53.00	47.50
	0.75	40.00	41.00	27.00
TTFS encoding	0.1	56.00	64.00	65.00
	0.5	57.00	65.50	67.50
	0.75	54.00	65.00	55.00
$\mathsf{\Sigma }\mathsf{\Delta }$ encoding	0.1	53.50	60.00	61.00
	0.5	39.00	38.50	54.00
	0.75	51.50	30.00	51.00
Direct coding	0.1	70.00	69.00	68.50
	0.5	68.00	67.50	66.00
	0.75	16.00	17.00	15.00
Burst Coding	0.1	58.50	57.00	53.50
	0.5	32.00	56.00	60.00
	0.75	51.00	57.00	55.00
PoFC	0.1	54.00	57.00	60.00
	0.5	42.50	53.50	56.00
	0.75	17.00	39.50	20.00
R-NoM	0.1	25.00	22.50	24.00
	0.5	28.00	28.00	29.50
	0.75	29.00	28.50	28.00

and visualized in Figure 13, the neuronal firing threshold across encoding schemes strongly influences classification accuracy. In Figure 13, a ★ marks the best threshold for each encoding at each time step. Lower thresholds, such as 0.1, tend to facilitate easier spiking and thus higher accuracy in schemes like Rate Encoding and Direct Coding, where performance noticeably declines as the threshold increases. In contrast, temporal TTFS encoding achieves optimal accuracy at an intermediate threshold of 0.5, which appears to balance the timing of the first spike effectively. $\mathsf{\Sigma }\mathsf{\Delta }$ encoding similarly benefits from lower thresholds, particularly at longer time steps, underscoring its sensitivity to threshold adjustments. Meanwhile, burst coding and PoFC exhibit variable performance across thresholds and time steps, indicating that their optimal operation requires careful tuning of threshold values. Finally, R-NoM consistently produces lower accuracy levels, with only marginal improvements at higher thresholds, suggesting that threshold variations limit its capability to capture complex patterns in the CIFAR-10 dataset.

4.3.2. Impact of Threshold Values on Energy Consumption

The results presented in

Table 11. Energy consumption (joules) on CIFAR-10 dataset with varying thresholds. The lowest energy consumption for each encoding scheme is highlighted in bold.

Encoding Scheme	Threshold	2 Steps	4 Steps	6 Steps
Rate encoding	0.1	$4.51992\times {10}^{-4}$	$9.11080\times {10}^{-4}$	$1.30268\times {10}^{-3}$
	0.5	$1.81350\times {10}^{-4}$	$4.17308\times {10}^{-4}$	$4.60568\times {10}^{-4}$
	0.75	$8.03670\times {10}^{-5}$	$1.67766\times {10}^{-4}$	$6.69786\times {10}^{-5}$
TTFS encoding	0.1	$9.22080\times {10}^{-4}$	$1.45713\times {10}^{-3}$	$1.81481\times {10}^{-3}$
	0.5	$2.55394\times {10}^{-4}$	$4.67294\times {10}^{-4}$	$6.54078\times {10}^{-4}$
	0.75	$1.78473\times {10}^{-4}$	$3.65690\times {10}^{-4}$	$2.76786\times {10}^{-4}$
$\mathsf{\Sigma }\mathsf{\Delta }$ encoding	0.1	$4.80420\times {10}^{-4}$	$7.15536\times {10}^{-4}$	$1.06204\times {10}^{-3}$
	0.5	$8.77776\times {10}^{-5}$	$1.77862\times {10}^{-4}$	$4.00548\times {10}^{-4}$
	0.75	$1.13804\times {10}^{-4}$	$7.55347\times {10}^{-5}$	$2.59425\times {10}^{-4}$
Direct coding	0.1	$4.62498\times {10}^{-4}$	$8.86820\times {10}^{-4}$	$1.34335\times {10}^{-3}$
	0.5	$3.14614\times {10}^{-4}$	$6.51242\times {10}^{-4}$	$9.66956\times {10}^{-4}$
	0.75	$9.16112\times {10}^{-6}$	$1.70082\times {10}^{-5}$	$3.43297\times {10}^{-5}$
Burst Coding	0.1	$4.36462\times {10}^{-4}$	$6.84824\times {10}^{-4}$	$9.94740\times {10}^{-4}$
	0.5	$9.06143\times {10}^{-5}$	$3.29403\times {10}^{-4}$	$3.35664\times {10}^{-4}$
	0.75	$1.68229\times {10}^{-4}$	$2.16433\times {10}^{-4}$	$2.27624\times {10}^{-4}$
PoFC	0.1	$3.92722\times {10}^{-4}$	$6.64914\times {10}^{-4}$	$1.01460\times {10}^{-3}$
	0.5	$1.51961\times {10}^{-4}$	$4.15849\times {10}^{-4}$	$5.35901\times {10}^{-4}$
	0.75	$2.53021\times {10}^{-5}$	$1.48193\times {10}^{-4}$	$4.42032\times {10}^{-5}$
R-NoM	0.1	$1.18310\times {10}^{-4}$	$1.15656\times {10}^{-4}$	$2.10588\times {10}^{-4}$
	0.5	$7.57243\times {10}^{-5}$	$7.66446\times {10}^{-5}$	$2.48482\times {10}^{-4}$
	0.75	$6.81089\times {10}^{-5}$	$5.90738\times {10}^{-5}$	$6.24119\times {10}^{-5}$

show that energy consumption generally decreases as the neuronal firing threshold increases from 0.1 to 0.75. This trend is consistent across most encoding schemes, reflecting the fact that higher thresholds reduce the number of spikes generated during inference and thereby lower the computational load. For example, both rate and TTFS encodings show substantial energy reductions at elevated thresholds, while direct coding exhibits a marked drop in energy usage at a threshold of 0.75—though at the expense of classification accuracy. $\mathsf{\Sigma }\mathsf{\Delta }$ encoding also benefits from higher thresholds, although the reduction in energy consumption is less pronounced, likely due to its inherent reliance on representing fine-grained variations in the input. Overall, these results highlight the delicate balance between minimizing energy consumption and maintaining predictive accuracy, as the threshold directly modulates the trade-off between energy efficiency and inference performance.

4.3.3. Trade-Off Between Accuracy and Energy Consumption

The analysis of Table 10 and Table 11 indicates that threshold values play a key role in determining the balance between classification accuracy and energy efficiency in SNNs. Lower thresholds increase neuronal activity and typically yield higher accuracy but result in greater energy consumption due to elevated spike rates. Conversely, higher thresholds suppress spiking activity and reduce energy use but may hinder the network’s ability to capture complex temporal or spatial patterns. Intermediate thresholds (e.g., 0.5) often provide a balanced compromise between accuracy and energy, as observed for TTFS and direct encodings. These findings emphasize the importance of optimal threshold selection, as it directly affects both network efficiency and representational fidelity. Moreover, the degree of threshold sensitivity varies among encoding schemes, underscoring the need for task-specific tuning of this hyperparameter to maximize the EIF model’s performance on complex datasets such as CIFAR-10.

4.3.4. Comparison with Related Studies

Recent studies have reached complementary conclusions. Takaghaj and Sampson (2024) introduced Rouser, a training method that adaptively learns neuronal thresholds, effectively mitigating the “dead neuron” problem and improving accuracy and convergence across neuromorphic datasets [161]. Their adaptive mechanism aligns with our observation that threshold optimization is crucial for performance stability. Similarly, Sengupta et al. [154] emphasized the importance of threshold balancing in ANN-to-SNN conversion for deep architectures (e.g., VGG and ResNet), showing that appropriate threshold tuning preserves accuracy and reduces hardware overhead by limiting redundant spiking. Diehl et al. [37] also demonstrated that optimal weight and threshold balancing minimizes performance degradation during ANN-to-SNN conversion, supporting our findings on the sensitivity of performance to threshold parameters.

4.4. Comparative Analysis and Discussion

Overall trade-off. Across all experimental conditions, a clear trade-off is evident: configurations optimized for maximum accuracy typically incur higher per-inference energy consumption and SynOps, whereas energy-efficient encodings achieve lower accuracy.

FCN (MNIST). From Table 6, $\mathsf{\Sigma }\mathsf{\Delta }$ neurons with rate encoding at eight time steps achieved an accuracy of 98.10%, closely matching the ANN baseline of 98.23%. However, Table 7 shows that this configuration consumes more energy than simpler IF/LIF models with energy-efficient encodings such as burst or R–NoM. ALIF and AdEx also performed competitively, while direct and $\mathsf{\Sigma }\mathsf{\Delta }$ encodings consistently yielded strong results across neuron types. Increasing the number of time steps generally improved accuracy—particularly for temporal encodings such as TTFS and PoFC—but at the cost of higher energy consumption.

VGG7 (CIFAR-10). From Table 8, $\mathsf{\Sigma }\mathsf{\Delta }$ neurons with direct coding achieved 83.00% accuracy at two time steps, close to the ANN baseline of 83.60%. This demonstrates effective temporal dynamics even at low T. However, this configuration required more energy than several lower-accuracy SNNs (Table 9). IF and LIF neurons with direct coding peaked at approximately 74.5%, whereas ALIF and CUBA underperformed without further tuning. Direct coding proved the most effective scheme overall for CIFAR-10, while TTFS paired particularly well with $\mathsf{\Sigma }\mathsf{\Delta }$ neurons.

Thresholds and time steps. Lower thresholds increased spike rates, typically improving accuracy but at the expense of higher energy usage. Higher thresholds reduced spiking and energy consumption but occasionally limited the model’s capacity to learn complex patterns. Intermediate thresholds offered the best trade-offs, especially for direct and TTFS encodings. Similarly, additional time steps improved accuracy in many cases yet also elevated energy demands, reinforcing the need for task-dependent tuning of T.

Energy. Across datasets, per-inference energy consumption is primarily influenced by encoding sparsity and the number of time steps. On MNIST, nearly all SNN configurations consumed less energy than the ANN baseline ($1.1355\times {10}^{-3}$ J); R–NoM yielded the lowest values (e.g., IF at $T=6$: $2.33\times {10}^{-6}$ J; LIF at $T=4$: $2.44\times {10}^{-6}$ J). Higher-accuracy configurations—such as $\mathsf{\Sigma }\mathsf{\Delta }$ neurons with rate or $\mathsf{\Sigma }\mathsf{\Delta }$ encoding—required more energy than R–NoM or burst but remained well below the ANN reference. On CIFAR-10, energy generally increased with T and denser encodings; several high-T configurations exceeded the ANN baseline, while low-T direct or rate encodings often remained below it. In practice, using fewer time steps and sparse encodings (R–NoM or burst) minimizes energy, whereas $\mathsf{\Sigma }\mathsf{\Delta }$ or direct coding improves accuracy with a moderate energy overhead.

Application guidance.

• Accuracy-critical tasks: $\mathsf{\Sigma }\mathsf{\Delta }$ neurons with direct (CIFAR-10) or rate/$\mathsf{\Sigma }\mathsf{\Delta }$ encodings (MNIST) achieve near-ANN accuracy, albeit with higher energy costs than ultra-sparse alternatives, yet still well below ANN levels.
• Energy-constrained or edge deployments: IF or LIF neurons combined with burst or R–NoM encoding and fewer time steps provide strong energy savings. Thresholds can be tuned to meet power constraints, accepting minor accuracy trade-offs.

Neuromorphic potential. Event-driven accelerators can leverage SNN properties such as data-dependent spiking, temporal asynchrony, and localized memory access to achieve system-level energy gains, reinforcing SNNs’ suitability for low-power and real-time applications.

Positioning in the literature. These findings are consistent with prior studies on the accuracy–efficiency trade-off and the challenges of training and converting deep spiking networks for complex vision tasks [133,153,154]. Our results highlight the promise of $\mathsf{\Sigma }\mathsf{\Delta }$ neurons for achieving high accuracy while confirming the substantial energy advantages of simpler neurons combined with sparse encodings.

Key takeaways. (i) $\mathsf{\Sigma }\mathsf{\Delta }$ neurons with suitable encodings achieve near-ANN accuracy on MNIST and reduce the performance gap on CIFAR-10; (ii) R–NoM and burst encodings minimize energy but lower accuracy; (iii) thresholds and time steps are the primary parameters governing the accuracy–energy balance; and (iv) direct and $\mathsf{\Sigma }\mathsf{\Delta }$ encodings are broadly effective, whereas temporal encodings benefit from larger T and careful tuning.

5. Conclusions and Outlook

This work paired a comprehensive review with a standardized, hands-on benchmarking of SNNs against architecturally matched ANNs on MNIST (shallow FCN) and CIFAR-10 (VGG7). We varied neuron models, input encodings, thresholds, and time steps, and we reported accuracy alongside a transparent per-inference energy proxy. Three consistent conclusions emerge:

(1)

Accuracy–energy trade-off is real but tunable.

Across both datasets, higher accuracy typically coincided with higher energy, yet many SNN settings still undercut the ANN energy baseline:

• MNIST (FCN): $\mathsf{\Sigma }\mathsf{\Delta }$ neurons with rate/$\mathsf{\Sigma }\mathsf{\Delta }$ encodings reached up to 98.1% (vs. 98.23% ANN) while remaining energetically below the ANN proxy. ALIF/AdEx and even LIF/IF also performed strongly when paired with effective encodings.
• CIFAR-10 (VGG7): $\mathsf{\Sigma }\mathsf{\Delta }$ neurons with Direct input achieved 83.0% at 2 time steps (vs. 83.6% ANN), indicating that well-chosen neuron–encoding pairs can approach ANN performance even on a deeper, more complex task.
• Encodings that are extremely frugal (e.g., R–NoM) minimized the energy proxy but incurred the largest accuracy drops; conversely, settings that closed the accuracy gap (e.g., $\mathsf{\Sigma }\mathsf{\Delta }$ with direct/rate) used more energy—but still generally below the ANN reference on our GPU-targeted model.

(2)

Practical configuration rules.

The most useful knobs in practice were the encoding, the neuron model, the threshold, and the number of time steps T:

• Accuracy-critical: Prefer $\mathsf{\Sigma }\mathsf{\Delta }$ neurons with Direct (CIFAR-10) or with Rate/$\mathsf{\Sigma }\mathsf{\Delta }$ (MNIST); AdEx/EIF are solid fallbacks. Keep T as low as possible once the accuracy target is met.
• Energy-constrained: Favor simpler neurons (IF/LIF) with burst or R–NoM encoding and small T; expect some accuracy loss. Intermediate thresholds typically balance activity with correctness better than very low or very high ones.
• General tip: Tune thresholds jointly with the encoding; moderate T and carefully chosen thresholds often deliver the best accuracy-per-joule.

(3)

Neuromorphic potential.

Event-driven accelerators can exploit data-dependent spiking, temporal asynchrony, and local memory access to translate our per-inference energy reductions into larger system-level savings, reinforcing SNNs’ suitability for edge and real-time deployments.

• Limitations

While this study provided a standardized comparative analysis of SNNs and ANNs, several limitations remain. First, energy efficiency was assessed through an operation-based GPU proxy using literature-derived constants rather than direct measurements on neuromorphic or low-power hardware, which may cause deviations from real device performance. Second, the experimental scope was restricted to two benchmark datasets (MNIST and CIFAR-10) and two network topologies (FCN and VGG7), leaving other domains—such as event-based vision or temporal signal processing—unexplored. Third, hyperparameter and threshold tuning were manually configured, limiting the exploration of automated optimization strategies that could further improve energy–accuracy balance. Finally, while surrogate-gradient training was applied effectively, cross-paradigm comparisons (e.g., hybrid STDP-supervised or reinforcement-based learning) were not systematically analyzed. These constraints outline important directions for expansion and validation.

• Future work

Future research should address the above limitations through specific methodological strategies: (i) Hardware-in-the-loop optimization: Incorporate direct power metering and latency profiling on neuromorphic and embedded devices (e.g., Loihi 2, SpiNNaker, TrueNorth, or Edge-TPUs) to calibrate theoretical energy models. (ii) Algorithm–hardware co-design: Develop reinforcement- or evolutionary-based search frameworks that jointly tune neuron thresholds, time windows, and precision levels to achieve optimal energy–accuracy trade-offs. (iii) Dynamic spiking policies: Introduce adaptive thresholding and time step schedules that adjust spiking activity in real time based on task difficulty or input sparsity. (iv) Architecture and encoding search: Employ automated architecture discovery (e.g., neural architecture search or Bayesian optimization) to identify optimal neuron-encoding pairs across tasks. (v) Cross-domain and on-device learning: Expand SNN applications to event-based sensors, biomedical, and audio datasets while investigating local plasticity and continual learning mechanisms for adaptive, low-power deployment. Collectively, these research pathways define a concrete roadmap toward robust, scalable, and energy-aware SNN systems that bridge algorithmic theory and neuromorphic practice.

• Distinct contribution and comparison with existing literature

Unlike previous surveys and reviews on spiking neural networks [19,20,21,22,23,27,28,29,30,33], which primarily focus on summarizing neuron models, encoding strategies, or learning algorithms in isolation, This article integrates both theoretical synthesis and experimental benchmarking into a unified, tutorial-style framework. Specifically, our study is the first to conduct a standardized, side-by-side evaluation of diverse neuron models (e.g., LIF, ALIF, AdEx, $\mathsf{\Sigma }\mathsf{\Delta }$, RF) and encoding schemes (direct, rate, temporal, $\mathsf{\Sigma }\mathsf{\Delta }$, burst, PoFC, R–NoM) on both shallow (MNIST/FCN) and deep (CIFAR-10/VGG7) architectures using common surrogate-gradient pipelines (SLAYER, SpikingJelly, Norse). While prior works such as [18,26,45] discuss energy efficiency conceptually, our contribution lies in providing a quantitative energy–accuracy analysis that links algorithmic parameters (thresholds, time steps, encodings) to measurable efficiency trends under reproducible experimental conditions. Furthermore, this article distills actionable design rules and optimization guidelines—bridging survey-style synthesis and empirical validation—thereby positioning it as a practical tutorial and benchmarking reference for new and advanced SNN researchers.

• Takeaway

With careful choices of neuron model, encoding, threshold, and time steps, SNNs can consistently approach ANN accuracy on both shallow and deep settings while offering meaningful energy advantages. The recipe is straightforward. Pick the encoding and neuron to match the task’s accuracy target, set T to the minimum that meets it, and calibrate thresholds for energy-aware operation—then map to event-driven hardware to compound the gains.