A Comparative Assessment of Regular and Spatial Cross-Validation in Subfield Machine Learning Prediction of Maize Yield from Sentinel-2 Phenology

Abstract

The aim of this study is to determine the reliability of regular and spatial cross-validation methods in predicting subfield-scale maize yields using phenological measures derived by Sentinel-2. Three maize fields from eastern Croatia were monitored during the 2023 growing season, with high-resolution ground truth yield data collected using combine harvester sensors. Sentinel-2 time series were used to compute two vegetation indices, Enhanced Vegetation Index (EVI) and Wide Dynamic Range Vegetation Index (WDRVI). These features served as inputs for three machine learning models, including Random Forest (RF) and Bayesian Generalized Linear Model (BGLM), which were trained and evaluated using both regular and spatial 10-fold cross-validation. Results showed that spatial cross-validation produced a more realistic and conservative estimate of the performance of the model, while regular cross-validation overestimated predictive accuracy systematically because of spatial dependence among the samples. EVI-based models were more reliable than WDRVI, generating more accurate phenomenological fits and yield predictions across parcels. These results emphasize the importance of spatially explicit validation for subfield yield modeling and suggest that overlooking spatial structure can lead to misleading conclusions about model accuracy and generalizability.

1. Introduction

Understanding and predicting crop yield variability at the subfield scale is a cornerstone of precision agriculture [1]. Subfield yield variability arises from spatial heterogeneity in complex biotic and abiotic factors, including soil properties, topography, drainage, fertility, and microclimate conditions [2,3]. Traditional field-scale yield assessments overlook this fine-scale variability, limiting the effectiveness of input management in precision agriculture [4]. Subfield-level yield prediction improves several aspects of site-specific management, including variable rate fertilization, hybrid selection, irrigation planning, and pest and disease control [5]. Yield maps derived from remote sensing can identify consistently high- or low-yielding zones within fields, allowing for more effective resource allocation and risk mitigation [6]. Over time, these predictive maps support adaptive management by informing decisions in subsequent seasons. As climate variability increases and input costs rise, yield prediction using free satellite imagery becomes an essential tool for optimizing productivity and sustainability across diverse agricultural systems [7].

While combine harvester yield monitors provide accurate, high-resolution yield data, their use is limited by high equipment costs, data inconsistencies, and restricted availability, particularly in smallholder or resource-limited farming systems [8]. These systems often lack access to the advanced machinery and technical infrastructure required to implement such monitoring, making widespread adoption challenging [9]. Furthermore, yield data collected from combine harvesters can be affected by calibration errors, mechanical delays, and incomplete spatial coverage, particularly at field edges or in irregularly shaped plots [10]. In contrast, satellite-based remote sensing missions, such as Sentinel-2, provide a globally consistent, freely accessible, and reliable source of high-resolution imagery [11,12]. Sentinel-2 delivers multispectral data at up to 10 m spatial resolution, with revisit frequencies of 5 days at the equator and even more frequent at higher latitudes when combined with both Sentinel-2A and 2B satellites [13]. This allows for regular and timely monitoring of crop development and spatial variability within and between fields over the entire growing season [6]. Previous studies observed that vegetation indices derived from Sentinel-2 imagery correlate with crop vigor, canopy structure, and biomass [14,15]. Nevertheless, vegetation indices from individual satellite observations tend to reflect only immediate canopy conditions. Crop phenology modeling has become a particularly effective approach to determine temporal dynamics by fitting smooth curves on vegetation index time series to derive important seasonal transition values [16,17]. It has been demonstrated that phenology-based indicators using MODIS, Landsat, and Sentinel-2 enhance the understanding of space and time variations in vegetation development and yield [18]. When combined with machine learning methods, these metrics can support yield prediction at the subfield scale [19]. Although these models may be less precise than direct yield measurements from harvester monitors, they offer a highly scalable and cost-effective alternative for monitoring large agricultural areas without requiring expensive machinery or dense ground-based observations. This approach also supports temporal analysis, allowing for yield monitoring over multiple seasons, which is critical for long-term agricultural planning and resilience due to climate variability [20].

Machine learning methods in previous studies enabled accurate modeling of the complex relationships between crop yield and various remote sensing, environmental, and management variables [21]. However, the validity of model performance assessments heavily depends on the choice of cross-validation approach used during model development [22]. A commonly applied approach is regular (random) cross-validation, where training and testing data are randomly split without considering the spatial structure of the dataset [23]. While this method is dominantly used even for geospatial predictions, it can produce overly optimistic accuracy estimates in geospatial modeling contexts, particularly in agricultural landscapes characterized by strong spatial autocorrelation and underlying heterogeneity in soil, topography, and plant growth conditions [24]. Especially in precision agriculture, which is based on geospatial variability in crop-growing conditions, using inappropriate validation methods can lead to misleading conclusions about the real-world performance of crop yield prediction models [25]. Regular cross-validation often results in spatial leakage, where training and test samples are drawn from nearby or overlapping locations, thus artificially inflating predictive accuracy [26]. This undermines the reliability of the models when applied to unseen areas, such as different fields or growing seasons [27]. Despite this, many existing yield prediction studies do not explicitly address the implications of spatial structure in their validation protocols. Even with technological advances in satellite-based phenological modeling, there remains a critical methodological issue, as the spatial autocorrelation of training data can skew the model validation results [28]. The standard (regular) cross-validation randomly partitions data without respect to spatial structure and can commonly lead to spatial leakage, whereby neighboring samples are observed in the training data and test data [29]. Spatial cross-validation techniques might be used to solve this problem by dividing data into geographically different folds, providing an improved generalization performance [23]. There is a research gap in understanding how the performance of crop yield prediction models changes when evaluated under spatial cross-validation, which partitions data to ensure spatial independence between training and test sets. Spatial cross-validation provides a more realistic assessment of generalization performance and is theoretically more suitable for geospatial applications [30,31].

The main aim of this study was to address this research gap by comparing the performance of machine learning yield prediction models under both regular and spatial cross-validation, highlighting the consequences for accuracy assessment and practical deployment in precision agriculture.

2. Materials and Methods

The workflow of the study included the following: (1) creation and preprocessing of ground truth maize yield samples from combine harvester yield mapping sensors; (2) creation of Sentinel-2 time series data for each yield sample and calculation of vegetation indices; (3) phenological modeling of vegetation index time series; (4) machine learning prediction of subfield maize yield based on phenological metrics as covariates; and (5) a comparison of accuracy assessment of evaluated yield prediction models according to regular and spatial cross-validation approaches.

2.1. Study Area and Ground Truth Maize Yield Data

The study area included three maize parcels located in the proximity of near Koška in Eastern Croatia (Figure 1). The Koška region in eastern Croatia is characterized by a continental climate with hot summers and moderately cold winters (Dfb according to Köppen climate classification), making it suitable for maize cultivation [32]. Annual precipitation averages 650–800 mm, with the majority occurring during the growing season (April–October) [33], while soils in the study area are predominantly clay loam [32]. Elevation ranges from 90 to 120 m above sea level, usually with minimal slope.

Maize yield samples were collected during harvest from 13 to 14 October 2023 using a Claas Lexion 6900 combine harvester (Harsewinkel, Germany) with a Quantimeter yield sensor and Claas Connect software v1.0 (Harsewinkel, Germany) [34], which was calibrated according to the standard procedure stated by the manufacturer. The maize yield was measured in t/ha. The combined area of the three analyzed parcels was 18.0 ha, with a total of 1566 collected georeferenced yield samples before preprocessing (

Table 1. Descriptive statistics of ground truth maize yield samples before and after preprocessing.

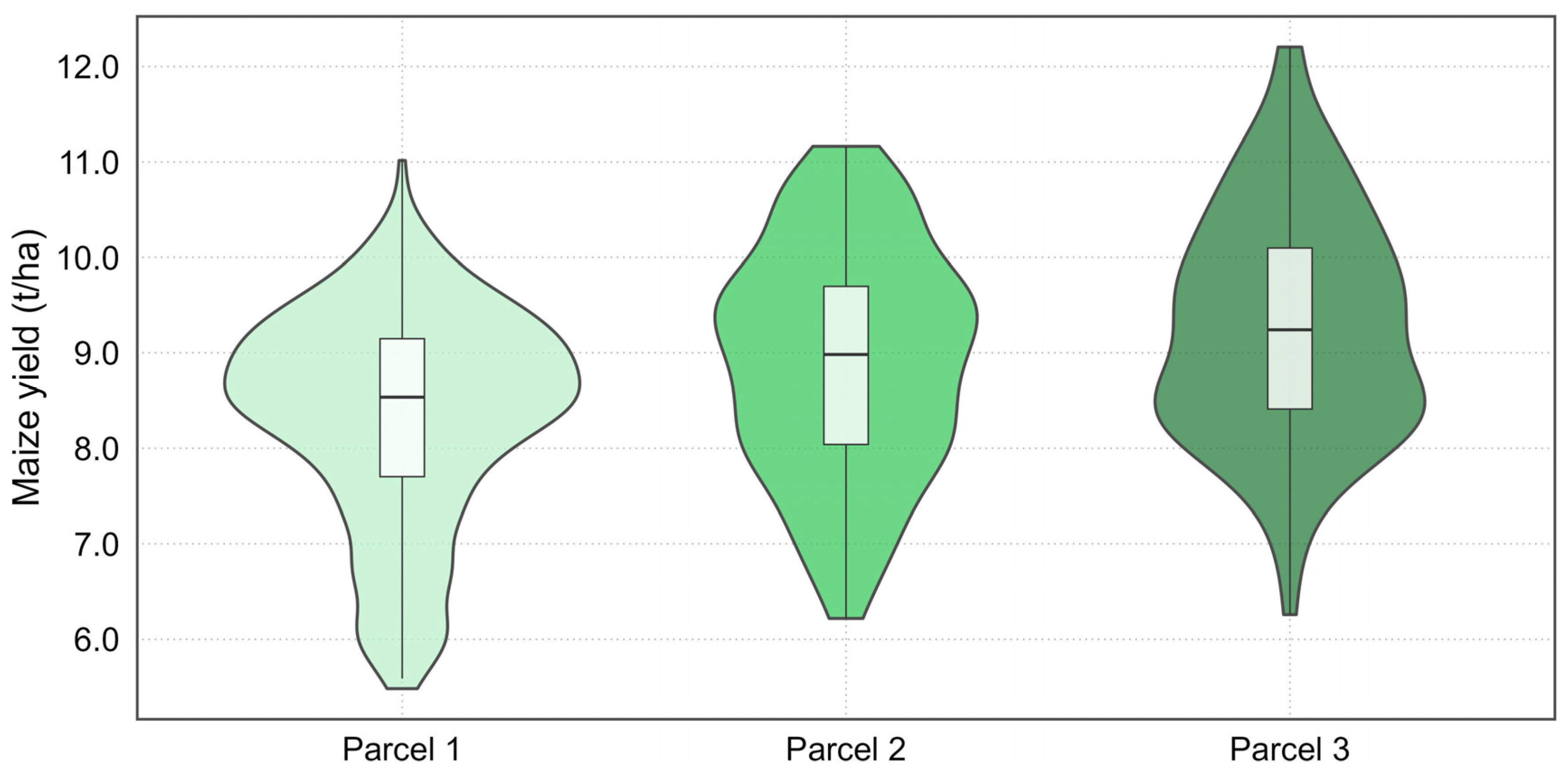
Parcel ID	Area	Preprocessing Stage	Sample Count	Mean	Median	CV	Shapiro–Wilk Test p-Value
Parcel 1	11.4 ha	Before preprocessing	1094	7.69	8.16	0.242	<0.0001
		After preprocessing	749	8.34	8.54	0.135	<0.0001
Parcel 2	4.4 ha	Before preprocessing	302	8.25	8.44	0.229	<0.0001
		After preprocessing	188	8.91	8.98	0.134	0.0217
Parcel 3	2.2 ha	Before preprocessing	170	8.20	8.46	0.275	<0.0001
		After preprocessing	94	9.27	9.24	0.129	0.4941

CV: coefficient of variation.

). The preprocessing was performed using the paar package in R v4.5.0 [35] according to procedure outlined by Paccioretti et al. [36]. It included spatial-statistical filtering in three steps: (1) edge removal, which excluded removing samples distanced 10 m or less from parcel boundaries to reduce border effects from mechanical operations; (2) outlier removal, which identified and removed extreme values outside three standard deviations from the mean yield value per parcel; and (3) inlier removal, which detected and excluded spatially inconsistent values that deviate from local trends quantified by the local Moran index. Additionally, the Shapiro–Wilk normality test was performed for all input samples, suggesting that only yield samples from Parcel 3 had normal distribution, while the coefficient of variation was notably lower for all three parcels after preprocessing.

2.2. Sentinel-2 Time Series Data and Vegetation Indices

Sentinel-2 bottom-of-atmosphere (BOA) Level-2A surface reflectance data [13] were acquired using Google Earth Engine to generate time series for maize yield samples between 1 January 2023 and 31 December 2023. Only scenes with less than 50% cloud cover were retained, while cloud, snow, shadow, and cirrus effects were mitigated using pixel-level quality information, including the MSK_CLDPRB, MSK_SNWPRB, and SCL bands. Pixels with cloud or snow probability higher than 5% or being classified as cloud shadow (SCL = 3) or cirrus (SCL = 10) were removed from the time series. The cleaned image collection was mapped to sample reflectance values for bands B1–B12 at a 10 m spatial resolution, with each observation being tagged with the acquisition date. After preprocessing, surface reflectance values from bands B2, B4, and B8 were used to compute the Enhanced Vegetation Index (EVI) and the Wide Dynamic Range Vegetation Index (WDRVI). Previous studies noted that EVI and WDRVI are well-suited for maize yield prediction due to their enhanced sensitivity to high-biomass conditions and improved performance in dense canopy environments typical of maize during peak growth [37]. EVI minimizes atmospheric and soil background effects [38], while WDRVI effectively distinguishes subtle changes in vegetation vigor during key phenological stages due to its increased resistance to saturation effect due to high biomass [39]. EVI and WDRVI were calculated according to Equations (1) and (2) as follows:

$$\mathrm{EVI}=2.5\times {\displaystyle \frac{\mathrm{NIR}-\mathrm{R}}{\mathrm{NIR}+6\mathrm{R}-7.5\mathrm{B}+1}},$$

(1)

$$\mathrm{WDRVI}={\displaystyle \frac{0.1\mathrm{NIR}-\mathrm{R}}{0.1\mathrm{NIR}+\mathrm{R}}},$$

(2)

where B—BOA surface reflectance in blue band (Band 2); R—BOA surface reflectance in red band (Band 4); and NIR—BOA surface reflectance in near-infrared band (Band 8).

2.3. Phenological Modeling

For each parcel and vegetation index, time series were separated by unique point identifiers and converted into daily observations. Phenological modeling was performed using the phenofit v0.3.10 R package [40], which provides a comprehensive framework for smoothing, fitting, and extracting seasonal dynamics from vegetation index time series. It supports multiple curve-fitting methods and is designed to handle irregular or noisy data, making it well-suited for remote sensing-based phenology analysis [41]. The workflow included temporal smoothing using the Whittaker smoother and phenological curve fitting using six methods, including Asymmetric Gaussian (AG), Beck, Elmore, Zhang, Klos, and Gu. The lambda parameter in the Whittaker smoother was calculated individually from cross-validation and differed for each sample, while the weight updating function used was the method used in TIMESAT, according to [40].

For each fitted curve, eleven phenological stages were extracted, including start of season, peak of season, end of season, greenup, maturity, senescence, dormancy, and transitional points, including upturn date, stabilization date, downturn date, and recession date. For each stage, the modeled vegetation index value and corresponding calendar date were calculated. The total number of Sentinel-2 observations per fit and goodness-of-fit metrics, including coefficient of determination, root mean square error, and Nash-Sutcliffe efficiency coefficient (NSE), were calculated for each model to assess fitting quality [41]. In cases of detection of multiple phenological cycles during 2023, the model with the longest vegetative period, quantified with the difference between the end of the season and the start of the season, was selected to ensure robust extraction of maize seasonal dynamics. In the study area, the maize growing season typically spans from April to October and thus covers most of the calendar year [42].

2.4. Machine Learning Prediction and Accuracy Assessment Using Regular and Spatial Cross-Validation

The evaluation of machine learning methods for subfield maize yield prediction based on phenological metrics was performed using the caret package in R [43]. The input dataset consisted of phenological metrics, which included transition dates converted to day of year (DOY) and corresponding vegetation index values, with a total of 22 covariates per model. For each combination of field parcel, vegetation index, and phenological fitting method, two machine learning methods were evaluated, including Random Forest (RF) from the ranger R package [44] and Bayesian Generalized Linear Model (BGLM) from the arm R package [45]. Before modeling, input data were cleaned to remove outliers in yield after phenological modeling and standardized. Hyperparameter tuning for each model was performed using a random search in 10 repetitions, and optimal hyperparameters were selected with the criterion of lowest root mean square error among repetitions. The hyperparameter ranges for random search during tuning were 2–22 for mtry, “variance” and “extratrees” for splitrule, and [1, 3, 5, 7, 10] for min.node.size for RF, while all hyperparameters for BGLM were selected from the prior scale and thus were not tuned.

Model training and accuracy assessment were performed using 10-fold cross-validation in five repetitions to reduce variance and improve model stability. To provide a comparative assessment for general and spatial aspects of data structure, both regular and spatial cross-validation were evaluated. Regular folds were determined randomly, while spatial folds were determined using the CAST R package [46], based on k-means clustering on E and N coordinates of yield samples in the Croatian Terrestrial Reference System (HTRS96/TM, EPSG: 3765), enabling evaluation across spatially distinct subfield sections (Figure 2). Input samples were clustered in 10 clusters to match the k-fold number of cross-validation, which was the sole parameter used for the creation of spatial folds. Wilcoxon tests were used to evaluate if there were significant differences in accuracy assessment metrics between regular and spatial cross-validation, using metrics from all calculated folds in the study.

Three accuracy assessment metrics were used for the evaluation of maize yield prediction using machine learning, including the coefficient of determination (R²), root-mean-square error (RMSE), and mean absolute error (MAE), which were calculated according to Equations (3)–(5) as follows:

$${\mathrm{R}}^2=1-{\displaystyle \frac{{\sum }_{i=1}^n{\left(y_i-\stackrel{\wedge }{y_i}\right)}^2}{{\sum }_{i=1}^n{\left(y_i-\overline{y}\right)}^2}},$$

(3)

$$\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=\sqrt{{\displaystyle \frac{{\sum }_{i=1}^n{\left(y_i-\stackrel{\wedge }{y_i}\right)}^2}{n}}},$$

(4)

$$\mathrm{M}\mathrm{A}\mathrm{E}={\displaystyle \frac{{\sum }_{i=1}^n\left|y_i-\stackrel{\wedge }{y_i}\right|}{n}},$$

(5)

where $y_i$—actual crop yield; ${\stackrel{\wedge }{y}}_i$—predicted crop yield; $\overline{y}$—mean of actual crop yield data; and n—sample count. The most accurate machine learning model for maize yield prediction had the highest R² and lowest RMSE and MAE per parcel, vegetation index and phenological fitting method.

3. Results

All three parcels in the study area had their median value in the range of 8.5–9.3 t/ha (Figure 3). Additionally, subfield variability in maize yield is notable, as collected maize yields across the study area ranged from 5.5 to 12.2 t/ha, with the highest frequency in yield samples of around 8.6 t/ha for Parcel 1, around 9.5 t/ha for Parcel 2, and 8.3 t/ha for Parcel 3.

The accuracy assessment of the evaluated fitting methods for phenological modeling varied significantly between parcels and vegetation indices (

Table 2. Accuracy assessment of evaluated fitting methods during phenological modeling per parcel and vegetation index.

Parcel ID	Fitting Method	EVI				WDRVI
		R2	RMSE	NSE	nfit	R2	RMSE	NSE	nfit
Parcel 1	AG	0.924	0.066	0.917	610	0.251	0.500	−0.941	35
	Beck	0.922	0.067	0.916	610	0.266	0.500	−0.939	35
	Elmore	0.921	0.067	0.915	610	0.265	0.500	−0.941	35
	Gu	0.928	0.064	0.922	259	0.160	0.488	−1.071	3
	Klos	0.928	0.064	0.923	259	0.160	0.490	−1.087	3
	Zhang	0.928	0.064	0.922	259	0.212	0.489	−1.078	3
Parcel 2	AG	0.603	0.284	0.582	146	0.258	0.491	−0.755	65
	Beck	0.599	0.284	0.582	146	0.284	0.491	−0.749	65
	Elmore	0.600	0.284	0.583	146	0.285	0.491	−0.755	65
	Gu	0.577	0.300	0.558	55	0.252	0.476	−0.700	10
	Klos	0.583	0.299	0.564	55	0.245	0.476	−0.702	10
	Zhang	0.577	0.300	0.559	55	0.265	0.477	−0.706	10
Parcel 3	AG	0.941	0.064	0.927	71	0.221	0.474	−0.927	28
	Beck	0.940	0.062	0.935	71	0.230	0.474	−0.928	28
	Elmore	0.939	0.062	0.935	71	0.237	0.473	−0.921	28
	Gu	0.938	0.064	0.934	14	0.203	0.473	−0.824	11
	Klos	0.941	0.062	0.937	14	0.275	0.472	−0.817	11
	Zhang	0.933	0.068	0.925	14	0.237	0.474	−0.836	11

n_fit—the number of successfully fitted samples during phenological modeling.

). EVI produced notably higher phenological fitting accuracy than WDRVI due to higher number of successfully fitted samples, particularly in Parcel 1 and Parcel 3. At these parcels, very high R² and NSE indicated high model agreement with observed data, with more than 0.92 and 0.91, respectively.

All six evaluated phenological fitting methods produced very similar fitting accuracy assessment metrics for both vegetation indices, with Gu, Klos, and Zhang being among the most accurate ones for Parcels 1 and 3 based on all three metrics. However, the main issue of these methods, in comparison to AG, Beck, and Elmore, was the number of successfully fitted samples during phenological modeling. For EVI, these three methods achieved percentages of successful fitting of 81.4%, 77.7%, and 75.5% in comparison to 34.6%, 29.3%, and 14.9% of Gu, Klos, and Zhang methods for Parcels 1, 2, and 3, respectively.

Table 3. Accuracy assessment of evaluated machine learning models for maize yield prediction per parcel and vegetation index according to regular and spatial cross-validation.

Parcel ID	Vegetation Index	Fitting Method	Cross-Validation Method	RF			BGLM			n
				R2	RMSE	MAE	R2	RMSE	MAE
Parcel 1	EVI	AG	regular	0.569	0.754	0.578	0.449	0.863	0.654	610
			spatial	0.134	0.902	0.720	0.149	0.916	0.706	610
		Beck	regular	0.571	0.749	0.564	0.457	0.841	0.651	608
			spatial	0.162	0.875	0.698	0.148	0.872	0.696	608
		Elmore	regular	0.505	0.801	0.611	0.329	0.932	0.740	606
			spatial	0.141	0.950	0.764	0.117	0.997	0.817	606
		Gu	regular	0.568	0.776	0.588	0.471	0.862	0.671	259
			spatial	0.172	0.920	0.762	0.250	0.943	0.776	259
		Klos	regular	0.498	0.839	0.642	0.360	0.964	0.724	258
			spatial	0.131	1.042	0.851	0.197	1.062	0.844	258
		Zhang	regular	0.576	0.772	0.582	0.450	0.884	0.683	259
			spatial	0.195	0.923	0.747	0.198	0.954	0.772	259
	WDRVI	AG	regular	0.461	0.433	0.387	0.551	0.596	0.528	34
			spatial	0.588	0.449	0.393	0.624	0.736	0.643	34
Parcel 2	EVI	AG	regular	0.309	1.023	0.823	0.362	1.008	0.800	146
			spatial	0.175	1.069	0.885	0.179	1.025	0.825	146
		Beck	regular	0.354	0.987	0.781	0.360	1.009	0.814	144
			spatial	0.160	1.035	0.844	0.173	1.013	0.833	144
		Elmore	regular	0.357	0.992	0.796	0.238	1.111	0.894	146
			spatial	0.251	1.025	0.845	0.200	1.197	0.988	146
		Gu	regular	0.677	0.897	0.767	0.700	0.837	0.724	55
			spatial	0.216	0.977	0.854	0.332	0.894	0.783	55
		Klos	regular	0.751	0.754	0.643	0.640	0.915	0.791	55
			spatial	0.356	0.833	0.737	0.329	1.041	0.878	55
		Zhang	regular	0.656	0.904	0.750	0.679	0.869	0.741	55
			spatial	0.180	1.087	0.937	0.319	1.078	0.912	55
	WDRVI	AG	regular	0.277	0.727	0.604	0.235	1.234	0.882	64
			spatial	0.240	0.740	0.647	0.203	1.267	0.900	64
Parcel 3	EVI	AG	regular	0.336	0.953	0.760	0.436	0.899	0.708	71
			spatial	0.150	1.135	0.937	0.282	1.000	0.810	71
		Beck	regular	0.397	0.925	0.749	0.395	1.004	0.806	71
			spatial	0.195	1.062	0.888	0.285	1.081	0.890	71
		Elmore	regular	0.298	1.043	0.842	0.237	1.135	0.896	71
			spatial	0.203	1.194	1.017	0.194	1.262	1.047	71
	WDRVI	AG	regular	0.594	1.044	0.865	0.598	1.650	1.357	28
			spatial	0.725	1.139	1.009	0.720	1.922	1.714	28

Accuracy assessment metrics indicating the most accurate prediction per parcel for both regular and spatial cross-validation are bolded.

presents the accuracy assessment metrics of the evaluated machine learning models for maize yield prediction across three parcels, vegetation indices, phenology fitting methods, and cross-validation approaches. The optimal hyperparameters for RF are presented in

Table A1. Optimal hyperparameters for all RF models used in the study.

Parcel ID	Vegetation Index	Fitting Method	Cross-Validation Method	RF Optimal Hyperparameters
Parcel 1	EVI	AG	regular	mtry = 15, splitrule = “extratrees”, min.node.size = 5
			spatial	mtry = 19, splitrule = “extratrees”, min.node.size = 5
		Beck	regular	mtry = 13, splitrule = “extratrees”, min.node.size = 5
			spatial	mtry = 4, splitrule = “extratrees”, min.node.size = 5
		Elmore	regular	mtry = 19, splitrule = “extratrees”, min.node.size = 5
			spatial	mtry = 22, splitrule = “extratrees”, min.node.size = 5
		Gu	regular	mtry = 22, splitrule = “extratrees”, min.node.size = 5
			spatial	mtry = 13, splitrule = “extratrees”, min.node.size = 5
		Klos	regular	mtry = 22, splitrule = “extratrees”, min.node.size = 5
			spatial	mtry = 19, splitrule = “extratrees”, min.node.size = 5
		Zhang	regular	mtry = 4, splitrule = “extratrees”, min.node.size = 5
			spatial	mtry = 6, splitrule = “extratrees”, min.node.size = 5
	WDRVI	AG	regular	mtry = 6, splitrule = “extratrees”, min.node.size = 5
			spatial	mtry = 10, splitrule = “extratrees”, min.node.size = 5
Parcel 2	EVI	AG	regular	mtry = 19, splitrule = “extratrees”, min.node.size = 5
			spatial	mtry = 13, splitrule = “extratrees”, min.node.size = 5
		Beck	regular	mtry = 6, splitrule = “extratrees”, min.node.size = 5
			spatial	mtry = 19, splitrule = “extratrees”, min.node.size = 5
		Elmore	regular	mtry = 22, splitrule = “extratrees”, min.node.size = 5
			spatial	mtry = 15, splitrule = “extratrees”, min.node.size = 5
		Gu	regular	mtry = 10, splitrule = “extratrees”, min.node.size = 5
			spatial	mtry = 15, splitrule = “extratrees”, min.node.size = 5
		Klos	regular	mtry = 13, splitrule = “extratrees”, min.node.size = 5
			spatial	mtry = 13, splitrule = “extratrees”, min.node.size = 5
		Zhang	regular	mtry = 13, splitrule = “extratrees”, min.node.size = 5
			spatial	mtry = 10, splitrule = “extratrees”, min.node.size = 5
	WDRVI	AG	regular	mtry = 4, splitrule = “extratrees”, min.node.size = 5
			spatial	mtry = 6, splitrule = “extratrees”, min.node.size = 5
Parcel 3	EVI	AG	regular	mtry = 22, splitrule = “extratrees”, min.node.size = 5
			spatial	mtry = 8, splitrule = “extratrees”, min.node.size = 5
		Beck	regular	mtry = 15, splitrule = “extratrees”, min.node.size = 5
			spatial	mtry = 13, splitrule = “extratrees”, min.node.size = 5
		Elmore	regular	mtry = 2, splitrule = “extratrees”, min.node.size = 5
			spatial	mtry = 6, splitrule = “extratrees”, min.node.size = 5
	WDRVI	AG	regular	mtry = 2, splitrule = “extratrees”, min.node.size = 5
			spatial	mtry = 2, splitrule = “extratrees”, min.node.size = 5

, while BGLM did not require hyperparameter tuning. Overall, the most accurate models according to regular cross-validation results indicated notably higher prediction accuracy than the most accurate models based on spatial cross-validation. This observation was the most pronounced for Parcel 1, but these results also might not be representative of maize yield value distribution for Parcels 1 and 2, in which machine learning models based on WDRVI produced the highest prediction accuracy but were trained on a very small number of available yield samples. Moreover, relative (R²) and absolute (RMSE, MAE) accuracy assessment metrics were dominantly in disagreement on the most accurate machine learning model per parcel. Wilcoxon tests comparing the accuracy assessment statistical metrics from regular and spatial cross-validation for evaluated machine learning models proved that there were significant differences in accuracy assessment metrics between regular and spatial cross-validation for all calculated folds (

Table 4. The results of Wilcoxon tests comparing the accuracy assessment statistical metrics from regular and spatial cross-validation for evaluated machine learning models.

Test Statistics	RF			BGLM
	R2	RMSE	MAE	R2	RMSE	MAE
p-value	<0.0001	<0.0001	<0.0001	<0.0001	<0.0001	<0.0001

).

As for machine learning methods, both RF and BGLM produced the most accurate prediction models in three instances, with RF producing higher prediction accuracy on Parcel 2 for both regular and spatial cross-validation, with the same being applicable for BGLM on Parcel 3. Among evaluated phenological fitting methods, AG most frequently produced the most accurate prediction model per parcel, also producing the highest number of samples with successfully fitted phenological models, slightly outperforming Beck and Elmore methods, whose sample counts were in some cases reduced after outlier removal prior to machine learning prediction.

Figure 4 presents value ranges of accuracy assessment metrics per fold in 10-fold cross-validation across all five repetitions, quantifying the effect of randomness in training and test data split during cross-validation on machine learning prediction accuracy. The robustness of predictions increased with the total number of available yield samples per parcel and vegetation index, with EVI in Parcel 1 producing the most stable prediction accuracy values. On the contrary, while WDRVI produced the most accurate prediction models for Parcels 1 and 2, very low sample counts produced very high ranges in resulting accuracy assessment metrics, which was the most pronounced for R².

4. Discussion

The smaller phenological fitting accuracy of Parcel 2 likely occurred not due to model inadequacy but to quality differences between data and local growing conditions. Local management variability in the form of hybrid type or variable nitrogen application could have changed canopy dynamics, weakening the temporal coherence of the vegetation index time series [47]. Moreover, sensor noise of yield monitors in this parcel might have added to the increased variance in the training data, as sampling density on Parcel 2 (42.7 samples per ha) was lower in comparison to Parcel 1 (65.7 samples per ha). This observation suggests that the additional property of input yield samples is a major determinant of phonological fitting accuracy and should be explored in future studies. The median yield of three parcels evaluated in the study is above the mean maize yield in the Pannonian biogeoregion of Croatia of 7.4 t/ha [48] but considerably below the maximum possible maize yield in the study area, which can reach up to 14 t/ha for some maize hybrids [33].

The inequality of evaluated phenological modeling methods in terms of fitting accuracy and the percentage of successfully fitted samples is a major observation on the future selection of fitting methods in crop yield prediction based on phenological metrics. AG, Beck, and Elmore methods ensured notably higher reliability in securing adequate yield sample count, thus providing more reliable options for yield prediction. Moreover, the potential trade-off of those methods against Gu, Klos, and Zhang’s methods in terms of fitting accuracy has only a minor effect, as it varied far less in comparison to the number of successfully fitted samples. While recent similar studies did not report phenological fitting accuracy per method, maximum achieved fitting accuracy was comparable [49] or slightly lower [18] than fitting results based on EVI time series from this study. The discrepancy between the fitting accuracy and amount of successfully fitted samples from the results of this study is disproportionate, suggesting that increased methods to variations in vegetation indices in time series data outweigh their slightly lower fitting accuracy. However, further studies based on increased ground truth data quantity and diverse study areas are required to confirm this observation.

The difference in predictive accuracy under regular cross-validation is attributable to spatial leakage [27], caused by the proximity of test samples relative to training samples, thus negating the assumption of independent and identically distributed data. In spatially structured environments, particularly in agricultural fields where soil and topographic characteristics typically vary gradually, neighboring samples tend to share similar phenological and yield characteristics [50]. Due to this occurrence, regular cross-validation was likely strongly affected by localized effects rather than generalized phenological maize properties, resulting in overestimated yield prediction accuracy. Due to the differences in prediction accuracy between regular and spatial cross-validation, it is very likely that these models exploited localized spatial effects caused by different micro-scale differences in soil management and microclimate that are correlated with maize yield. However, it does not demonstrate that evaluated machine learning models were incapable of learning the relationship between generalizable phenology and maize yield but that they are dependent on spatial dependence existing in the training data.

The previous studies dominantly focused on exploring the temporal component of cross-validation instead of the spatial, as a study by Croci et al. [51] emphasized temporal generalization using year-based splits, and, although their models showed good transferability across years, spatial heterogeneity was not accounted for. Moreover, Perich et al. [52] predicted winter wheat yields using Sentinel-2 time series and validated models using leave-one-year-out cross-validation, in which R² values resulted up to 0.88, but a lower prediction accuracy was noted in years with atypical weather. However, Fernando et al. [53], who applied leave-one-field-out cross-validation for canola yield prediction, reported a lower R² of 0.46, noting the possible magnitude in which regular cross-validation inflated metrics in spatially structured problems. Additionally, Crusiol et al. [54] compared different scales of model validation for soybean yield across 15 fields, reporting an R² of 0.82 under global validation but only 0.32 when using field-specific models. This observation reinforces the notion that models trained on aggregated data may exploit spatial dependencies rather than capturing physiologically meaningful responses to environmental variation. As was observed from the results presented in Table 3, spatial cross-validation indicated that prediction accuracy was actually lower than regular cross-validation results suggest, but the display of achieved value ranges of all three accuracy assessment metrics also indicates that prediction results are more affected by the randomness in training and test data split, which is especially apparent for smaller datasets [55].

Previous studies [56,57] demonstrated the predictive ability of phenological metrics derived from Sentinel-2, such as normalized difference vegetation index (NDVI), normalized difference red-edge index (NDRE), or EVI for yield estimation. The results from this study confirmed their effectiveness in crop yield prediction, while their prediction accuracy metrics heavily depended on the cross-validation approach. This was partially noted by Darra et al. [56], which utilized repeated 5-fold random cross-validation to predict tomato yield and reported high explained variance, but without a spatially blocked validation, the generalization of these results remains untested. Furthermore, while the inclusion of temporal metrics enhanced model performance under interpolation scenarios, their behavior under spatial extrapolation remains mixed [58].

The main limitations of this study were caused by the relatively short temporal span and restricted study area. Longer-term studies covering broader spatial gradients, including multiple agroclimatic zones, are needed for better understanding of the scalability of predictive models based on Sentinel-2 time series for crop yield prediction. Furthermore, more comprehensive evaluation of machine learning methods, especially deep learning or transfer learning, might further improve the understanding of the generalization gap observed under spatial cross-validation. Another important direction for future studies is the inclusion of ancillary data representing environmental covariates, such as climate, soil, and topography data, which may improve performance under spatial cross-validation by capturing site-specific effects that are otherwise contained in spatial autocorrelation [59]. However, climate and soil properties also pose a challenge to geospatial modeling at the subfield scale, as soil data are frequently insufficiently spatially resolved to resolve fine-scale variability in soil texture, organic matter, or nutrient levels in small parcels, and their extrapolation to sparse samples may lead to significant errors. Likewise, topography- or micro-management-motivated microclimatic gradients cannot be reliably captured by climate data based on meteorological stations or coarse-resolution gridded products, which could be improved in future studies. Given that the combination of EVI time series with more robust phenological fitting methods like AG, Beck, and Elmore enabled the most successful maize yield prediction in this study, the main challenge for practical use of the performed methodology is standardizing and validating this approach for crops with varying phenological dynamics, especially winter crops, which shall be evaluated in future studies.

5. Conclusions

This study aims to evaluate the predictive accuracy and reliability of regular and spatial cross-validation approaches in subfield-scale maize yield prediction using phenology-derived metrics from Sentinel-2 imagery. The results indicated that regular cross-validation overestimated model accuracy in comparison to the results of spatial cross-validation. Based on produced results, the main conclusions of this study are:

•

Spatial cross-validation likely captured the effects of spatial autocorrelation, unlike regular cross-validation, thus providing a more realistic and conservative estimate of model generalizability in geospatial applications. Cross-validation results were sensitive to training/test split randomness, especially under low sample counts, reinforcing the importance of repeated validation with sufficient sample size. Therefore, ignoring spatial structure during model evaluation can lead to misleading conclusions, which may negatively affect precision agriculture decision-making.

•

EVI consistently outperformed WDRVI in terms of phenological model fitting accuracy and yield prediction reliability. Most notably, EVI produced notably more samples whose time series data enabled successful phenological modeling, which produced more robust yield prediction in comparison to WDRVI. Yield prediction models based on WDRVI were occasionally more accurate but were highly unstable due to low sample sizes after phenology modeling.

•

Among phenological fitting methods, AG, Beck, and Elmore demonstrated higher robustness due to their greater number of successfully fitted samples, making them more suitable for subfield crop yield prediction. Conversely, despite small differences in fitting accuracy, Gu, Klos, and Zhang’s methods had poor reliability due to a high failure rate in curve fitting, limiting their applicability in real-world scenarios.

•

Machine learning model performance varied across parcels, with RF and BGLM producing similar predictive accuracy depending on the parcel and index used.

•

Future studies should include longer-term and broader spatial datasets and consider integrating environmental covariates, including climate, soil, and topography data, to improve spatial model generalization.