Improving Active Support Capability: Optimization and Scheduling of Village-Level Microgrid with Hybrid Energy Storage System Containing Supercapacitors

Abstract

With the rapid development of renewable energy and the continuous pursuit of efficient energy utilization, distributed photovoltaic power generation has been widely used in village-level microgrids. As a key platform connecting distributed photovoltaics with users, energy storage systems play an important role in alleviating the imbalance between supply and demand in VMG. However, current energy storage systems rely heavily on lithium batteries, and their frequent charging and discharging processes lead to rapid lifespan decay. To solve this problem, this study proposes a hybrid energy storage system combining supercapacitors and lithium batteries for VMG, and designs a hybrid energy storage scheduling strategy to coordinate the “source–load–storage” resources in the microgrid, effectively cope with power supply fluctuations and slow down the life degradation of lithium batteries. In order to give full play to the active support ability of supercapacitors in suppressing grid voltage and frequency fluctuations, the scheduling optimization goal is set to maximize the sum of the virtual inertia time constants of the supercapacitor. In addition, in order to efficiently solve the high-complexity model, the reason for choosing the snow goose algorithm is that compared with the traditional mathematical programming methods, which are difficult to deal with large-scale uncertain systems, particle swarm optimization, and other meta-heuristic algorithms have insufficient convergence stability in complex nonlinear problems, SGA can balance global exploration and local development capabilities by simulating the migration behavior of snow geese. By improving the convergence effect of SGA and constructing a multi-objective SGA, the effectiveness of the new algorithm, strategy and model is finally verified through three cases, and the loss is reduced by 58.09%, VMG carbon emissions are reduced by 45.56%, and the loss of lithium battery is reduced by 40.49% after active support optimization, and the virtual energy inertia obtained by VMG from supercapacitors during the scheduling cycle reaches a total of 0.1931 s.

1. Introduction

In microgrids (MGs), which typically include distributed photovoltaics, distributed wind power, and small hydropower, these renewable energies can sometimes operate independently [1,2,3]. However, renewable energy generation often has significant uncertainty and variability. Compared to large integrated energy systems, microgrids exhibit poorer flexibility and stability, with their stable operation relying on energy storage systems [4]. In MGs, energy storage methods such as electrochemical storage, pumped storage, and hydrogen storage can be used to participate in renewable energy peak shaving. Among these, electrochemical storage is cost-effective but faces issues like lifespan degradation. To address this challenge, scholars have developed hybrid energy storage systems (HESS) that combine electrochemical storage with other forms of storage to alleviate lifespan degradation. However, in small-scale microgrids such as village-level microgrids (VMGs), research on the scheduling of hybrid storage systems and their role in mitigating battery lifespan degradation is still insufficient.

Chen et al. [5] proposed an adaptive droop control method that adjusts inertia based on the frequency disturbance process, considering active frequency support. To enhance the active support capability of microgrids using energy storage devices, Hasan et al. [6] proposed a BESS-based controller to simulate virtual inertia and improve frequency stability through active power control. However, frequent use of BESS can accelerate their lifespan degradation. To mitigate this issue, Wang et al. [7] integrated supercapacitors (SC) into the DC link of wind turbines and proposed a “dual-droop” frequency support control scheme. Building on this, Jain et al. [8] introduced a hybrid energy storage system (HESS) that combines BESS and SC for frequency support. They also developed a performance assessment model to reduce HESS investment costs and quantify the hidden contribution of BESS to inertia.

For wind–solar–storage systems in microgrids (MGs), Zhu et al. [9] introduced the addition of mobile energy storage systems (MESS) and demonstrated that MESS can enhance emergency response capabilities. MGs are small, controllable power systems that can operate independently of traditional large-scale grids within a local area or be connected to external grids. This results in two operational states: islanded and grid-connected. In both states, energy storage devices play a crucial role in maintaining stability. Further, Battery Energy Storage Systems (BESS) play a vital role in mitigating grid fluctuations and enabling peak shaving and valley filling on the user side. However, conventional control strategies often neglect the impact of charge-discharge cycle numbers, leading to accelerated battery degradation and reduced economic benefits. The flat OCV–SOC (Open Circuit Voltage–SOC) plateau characteristic of LiFePO₄ batteries further complicates consistency evaluation. A promising solution involves employing a Dynamic Reconfigurable Battery System (DRBS) to achieve fast online OCV estimation, while using the coefficient of variation in OCV as an indicator to quantitatively assess consistency. Luo et al. [10] quantified the V2G power supply capacity of EV aggregates through a reliability evaluation model based on the composite Poisson process, which provided a basis for the pre-bidding strategy, and established a microgrid optimization operation model considering V2G reliability to realize the collaborative scheduling of photovoltaic and electric vehicle aggregates. Zahraoui et al. [11] established a multi-objective optimization model with the goal of minimizing daily operating costs and carbon emission reduction, effectively coordinating the volatility of distributed renewable energy, load demand changes, and the cooperation between multiple energy storages, demonstrating the key support of optimization technology for achieving low-carbon operation of microgrid economy. Regarding HESS, Tong et al. [12] explored a complementary storage model in microgrids that combined gravity storage and super capacitors. It established corresponding control strategies and demonstrated that hybrid energy storage systems (HESS) significantly enhance efficiency compared to single storage technologies. To mitigate renewable energy grid fluctuations, Zhang et al. [13] utilized HESS along with an adaptive power optimization distribution strategy. However, Zhang et al. [13] and Yim et al. [14] focused on using HESS to address microgrid stability issues without delving into its potential to mitigate electrochemical storage lifespan degradation. In summary, HESSs that combine supercapacitors and electrochemical storage are quite common. Therefore, it is necessary to explore HESS capacity configuration in village-level microgrids, the extension of lithium battery lifespan through supercapacitors, and the impact on energy scheduling. Liu et al. [15] proposed a coordinated configuration method for electrical–hydrogen hybrid systems, leveraging the power and capacity complementarity between electrical storage and generalized hydrogen storage to balance energy imbalances. However, Tong et al. [12] and Liu et al. [15] focused excessively on the control and optimal configuration of HESS, without further exploring its scheduling role in microgrids or systems. To address supply forecast errors, Yim et al. [14] considered HESS with supercapacitors and batteries in microgrids and designed a reference power modulation strategy to balance HESS power. power.

To enhance the search capability and convergence speed of these algorithms, Xu et al. [16] introduced an energy random mutation strategy into the satin bowerbird algorithm. Liu et al. [17] improved the Slime mold-artificial bee colony algorithm to enhance the flexibility of comprehensive energy system solutions. These improvements aim to balance the local and global solving capabilities of the algorithms. Nevertheless, the generalizability of the algorithms proposed in Xu et al. [16] and Liu et al. [17] needs further improvement to enhance their ability to solve complex nonlinear scheduling problems. The snow goose algorithm proposed in this study effectively addresses the above challenges by integrating adaptive group behavior and external archiving mechanism. Different from single-agent optimization algorithms such as SPSA, smoothing function algorithm, and safety experimental dynamics algorithm, this type of algorithm has problems such as easy to fall into local optimization, slow convergence speed, and poor adaptability to high-dimensional uncertainty due to the single-point iteration characteristics. By simulating the group cooperation behavior of snow geese, SGA significantly improves the global search ability and convergence efficiency. This group-based optimization method not only reduces the dependence on local information and improves the robustness of optimization, but also provides a more efficient solution for the village-level microgrid scheduling problem with high dimension, strong uncertainty, multiple constraints and multiple objectives.

Based on the literature review, the current village-level microgrids face the following challenges:

• Degradation of life cycle due to frequent use of electrochemical storage devices: village-level microgrids operating with either single electrochemical storage or hybrid energy storage systems (HESS) based on supercapacitors have insufficiently addressed the degradation of life cycle of electrochemical storage devices and the corresponding mitigation strategies.
• Decline in active support and inertia: As renewable energy sources with weak damping and inertia continue to be integrated, there is a noticeable decline in the active support and inertia of village-level microgrids, which can adversely affect power quality.
• Development of high-performance intelligent optimization algorithms: The scheduling of village-level microgrids, which includes capacity configuration, various strategies, and optimization objectives, presents significant complexity. Developing universally applicable and quantifiable performance algorithms remains a challenge.

To address these issues, this study constructs a hybrid energy storage system for village-level microgrids, leveraging supercapacitors to mitigate lithium battery life degradation and provide active support to the microgrid. The innovations and contributions of this study are summarized as follows:

• Innovative HESS configuration for VMGs: This study proposes a novel hybrid energy storage system (HESS) that integrates supercapacitors and lithium batteries for village-level microgrids (VMGs). This HESS leverages the rapid charge/discharge capabilities of supercapacitors to mitigate the lifespan degradation of lithium batteries, enhancing VMG stability. A new supercapacitor capacity configuration model is also developed to optimize capacity allocation and maximize economic benefits.
• Supercapacitor dynamics for grid support: This research develops virtual inertia time constant expressions for supercapacitors, utilizing their rapid charge/discharge characteristics to swiftly respond to power fluctuations in VMGs. This enhances active support, improves power quality, and increases resilience against disturbances, representing a significant advancement in microgrid support.
• Enhanced optimization algorithm for scheduling: Improvements are made to the single-objective snow geese algorithm (SGA) to enhance its convergence and robustness. An external repository mechanism is introduced to construct a multi-objective SGA (MSGAR), enabling effective handling of multiple objectives like minimizing costs and losses while maximizing support capability. MSGAR demonstrates superior performance in solution quality, diversity, and convergence speed.

The remainder of this paper is organized as follows: Section 2 details the modeling process of the village-level microgrid; Section 3 introduces the SGAR and MSGAR algorithms; Section 4 validates the proposed strategies and algorithms; and Section 5 discusses the main findings, contributions, and limitations of this study.

2. Formulation of Village-Level Microgrids

2.1. Equipment Models and Operational Constraints

The microgrid system model constructed in this study mainly includes photovoltaic power generation, wind power generation, gas turbine, and hybrid energy storage system. The connections between them are as follows: photovoltaic power generation, wind power generation, and gas turbines used to provide electricity belong to the source side; The hybrid energy storage system mainly plays an energy regulation role, used to quickly respond to the regulation needs of the source side and load side. The topology of the village-level microgrid is illustrated in Figure 1.

(1)

Photovoltaic power generation equipment

Photovoltaic power generation operates without noise and pollution, but its output power is affected by light intensity and temperature:

$$P_{phvo,t}=P_{phvo}^N{\displaystyle \frac{G_t}{G_{stc}}}[1+k_{pv}(T_{env,t}-T_{stc}+30{\displaystyle \frac{G_t}{G_{stc}}})]$$

(1)

where P_phvo,t and $P_{phvo}^N$ represent the output power of photovoltaics at time t and under standard conditions, respectively; k_pv is the photovoltaic impact coefficient; G_t and G_stc represent the solar irradiance at time t and under standard test conditions, respectively; T_env,t and T_stc represent the environmental temperature at time t and under standard test conditions.

(2)

Wind power generation equipment

Currently, wind power generation is generally used in conjunction with photovoltaic generation to complement each other and reduce the output fluctuations of a single type of generation. Its mathematical model is as follows:

$$P_{WT,t}=\left\{\begin{array}{l}0\begin{array}{}\end{array}, \begin{array}{}\end{array}0\le v_{wt,t}\le s{p}_{in}\\ P_{WT}^N{\displaystyle \frac{v_{wt,t}-v_{in}}{v_N-v_{in}}}\begin{array}{}\end{array}, \begin{array}{}\end{array}{v}_{in}\le v_{wt,t}\le v_N\\ P_{WT}^N\begin{array}{}\end{array}, \begin{array}{}\end{array}{v}_N\le v_{wt,t}\le v_{out}\\ 0\begin{array}{}\end{array}, \begin{array}{}\end{array}{v}_{wt,t}\ge v_{out}\end{array}\right.$$

(2)

where P_WT,t and $P_{WT}^N$ represent the output power and rated power of the wind turbine, respectively; v_wt,t is the wind speed; v_in is the start-up wind speed; v_N is the rated wind speed, and v_out is the cut-out wind speed.

(3)

Gas turbine

The gas turbine is a core device used for regulation in microgrids, possessing rapid start-stop capabilities:

$$P_{GT,t}={\eta }_{GT}^e\cdot LH{V}_{gas}{G}_{GT}(t)$$

(3)

where P_GT,t represents the electrical energy generated by the gas turbine; G_GT(t) is the amount of natural gas consumed by the gas turbine; LHV_gas is the lower heating value of natural gas, typically taken as 9.7 (kWh)/m³; ${\eta }_{GT}^e$ is the electrical efficiency of the gas turbine.

(4)

Hybrid energy storage system comprising lithium batteries and supercapacitors

Energy storage devices mitigate some of the variability of renewable energy sources and are important peak shaving devices in microgrids:

$$\left\{\begin{array}{l}E{S}_t-(1-{\epsilon }_{Bat,e})E{S}_{t-1}=P_{chr,t}^{Bat}\cdot {\eta }_{chr}^{Bat}\Delta t\\ E{S}_t-(1-{\epsilon }_{Bat,e})E{S}_{t-1}=-{\displaystyle \frac{P_{dis,t}^{Bat}\cdot \Delta t}{{\eta }_{dis}^{Bat}}}\end{array}\right.$$

(4)

where ES_t and ES_t−1 represent the stored energy of the lithium battery at time t and t − 1, respectively; ε_Bat,e is the self-loss coefficient of the lithium battery; $P_{chr,t}^{Bat}$ and $P_{chr,t}^{Bat}$ represent the charging power and discharging power of the lithium battery at time t, respectively; ${\eta }_{chr}^{Bat}$ and ${\eta }_{dis}^{Bat}$ represent the charging and discharging efficiency of the lithium battery, respectively; Δt is the scheduling period, taken as 1 h.

The state of charge of the supercapacitor is as follows:

$$S{C}_{soc}(t)=S{C}_{soc}^0-{\displaystyle {\int }_0^t\frac{V_{SC}{i}_{SC}}{0.5S_{SC}{V}_{SC,\max }^2}dt}$$

(5)

where ${SC}_{soc}^0$, SC_soc(t) represent the initial state of charge and the state of charge at time t of the supercapacitor, respectively; S_SC is the capacity of the supercapacitor; V_SC and V_SC,max represent the voltage value at time t and the maximum allowable voltage of the supercapacitor, respectively; i_SC is the current flowing through the supercapacitor at time t.

During the system scheduling process, the model of the supercapacitor is as follows:

$$S{C}_{soc}(t)={\epsilon }_{SC}S{C}_{soc}(t-1)+\left({\eta }_{chr}^{SC}{P}_{chr,t}^{SC}-{\displaystyle \frac{P_{dis,t}^{SC}}{{\eta }_{dis}^{SC}}}\right)\Delta t$$

(6)

where $P_{chr,t}^{SC}$ and $P_{dis,t}^{SC}$ represent the charging power and discharging power of the supercapacitor at time t, respectively; ${\eta }_{chr}^{SC}$ and ${\eta }_{dis}^{SC}$ represent the charging and discharging efficiency of the supercapacitor, respectively; ε_SC is the self-loss coefficient of the supercapacitor.

During the operation of the village-level microgrid, the power balance constraint is as follows:

$$P_{phvo,t}+P_{WT,t}+P_{GT,t}+P_{dis,t}^{Bat}+P_{dis,t}^{SC}+P_{trade,t}^{MG}=P_{Load,t}+P_{chr,t}^{Bat}+P_{chr,t}^{SC}$$

(7)

where P_Load,t represents the electrical load of the village-level microgrid; $P_{trade,t}^{MG}$ is the power interaction between the microgrid and the external grid, where positive values indicate purchasing and negative values indicate selling.

The operational constraints of the gas turbine are as follows:

$$\left\{\begin{array}{l}0\le P_{GT,t}\le P_{GT}^{\max }\\ -C{P}_{GT}^{\max }\le P_{GT,t}-P_{GT,t-1}\le C{P}_{GT}^{\max }\end{array}\right.$$

(8)

where $P_{GT}^{\max }$ and $C{P}_{GT}^{\max }$ represent the maximum output power and maximum ramp-up power of the gas turbine, respectively.

The operational constraints of the hybrid energy storage system are as follows:

$$\left\{\begin{array}{l}0\le P_{chr,t}^{Bat}\le B_{chr,t}^{Bat}{P}_{chr}^{Bat,\max }\\ 0\le P_{dis,t}^{Bat}\le B_{dis,t}^{Bat}{P}_{dis}^{Bat,\max }\\ B_{chr,t}^{Bat}+B_{dis,t}^{Bat}\le 1\\ {\delta }_{Bat}^{\min }{S}_{Bat}\le E{S}_t\le {\delta }_{Bat}^{\max }{S}_{Bat}\end{array}\right.$$

(9)

where $P_{chr}^{Bat,\max }$ and $P_{dis}^{Bat,\max }$ represent the maximum charging and discharging power of the lithium battery, respectively; $B_{chr,t}^{Bat}$ and $B_{dis,t}^{Bat}$ represent the charging and discharging flags of the lithium battery, used to enforce the constraint that charging and discharging cannot occur simultaneously; ${\delta }_{Bat}^{\min }$ and ${\delta }_{Bat}^{\max }$ represent the lower and upper limits of the state of charge of the lithium battery during operation, preventing overcharging and overdischarging.

During the system scheduling process, the operational constraints of the supercapacitor are similar to Equation (9) and are described in detail in Pan et al. [18].

The power interaction constraints between the village-level microgrid and the external grid are as follows:

$$-P_{trade}^{\max }\le P_{trade,t}^{MG}\le P_{trade}^{\max }$$

(10)

where $P_{trade}^{\max }$ is the maximum transmission power of the line.

2.2. Capacity Allocation and Scheduling Strategy for Hybrid Energy Storage Systems

This paper proposes a hybrid energy storage system (HESS) combining supercapacitors and lithium batteries for village-level microgrid systems. A supercapacitor capacity allocation model is developed with the objective of minimizing the loss rate of electrochemical energy storage during the scheduling period. Additionally, optimization of supercapacitor capacity allocation and village-level microgrid scheduling is conducted to coordinate the “generation–load–storage” resources within the microgrid, addressing the variability in power supply and demand, and mitigating the degradation of lithium battery lifespan. The specific strategies are as follows:

(1) Development of the supercapacitor capacity allocation model:

$$\left\{\begin{array}{l}{F}_{HESS}^{setup}=({\lambda }_{HESS}^{bat}{N}_{HESS}^{bat}+{\lambda }_{HESS}^{SC}{N}_{HESS}^{SC})C_{HESS}^r\\ C_{HESS}^r={\displaystyle \frac{r{(1+r)}^{T_Y}}{{(1+r)}^{T_Y}-1}}\\ 0\le N_{HESS}^{SC}\le N_{HESS}^{SC,\max }\end{array}\right.$$

(11)

where $F_{HESS}^{setup}$ represents the installation (configuration) cost of the HESS, while ${\lambda }_{HESS}^{bat}$ and ${\lambda }_{HESS}^{SC}$ denote the unit costs of lithium batteries and supercapacitors, respectively; $N_{HESS}^{bat}$ and $N_{HESS}^{SC}$ represent the capacities of lithium batteries and supercapacitors, respectively; $N_{HESS}^{SC,\max }$ denotes the upper limit for the supercapacitor capacity during the capacity configuration process (Since the optimization focuses solely on the supercapacitor); $N_{HESS}^{bat}$ is set to a fixed value to simplify the optimization problem; $C_{HESS}^r$ is the capital recovery factor; r is the discount rate for the power source; and T_Y is the lifetime of the energy storage device.

(2) It is defined that the use priority of supercapacitors is higher than that of electrochemical energy storage. By buffering with supercapacitors, the energy cycling requirements of the electrochemical storage are reduced, thereby extending its lifespan.

(3) The life cycle of lithium batteries has the following relationship with DOD:

$$C_{bat}(DOD)=28270\cdot \exp (-2.401DOD)+2.214\cdot \exp (5.901DOD)$$

(12)

where DOD is the depth of discharge of the lithium battery; and C_bat denotes the available life cycle of the battery.

From the above equation, it can be observed that as the depth of discharge increases, the available life cycle of the battery decreases. Therefore, the loss rate of electrochemical energy storage in the battery over the entire scheduling period (24 h) is defined as follows:

$$F_{cap}^{loss}={\displaystyle \sum _{Do{D}_t>0.01}\frac{C_{bat}(1)}{C_{bat}(Do{D}_t)}}$$

(13)

where DoD_t > 0.01 indicates all moments when the battery experiences energy discharge; C_bat(1) represents the number of available cycles of the battery at the maximum depth of discharge; C_bat(DoD_t) denotes the number of available cycles of the battery after experiencing discharge, under the depth of discharge.

2.3. Active Support for Village-Level Microgrids

In addition to mitigating battery lifespan degradation, supercapacitors can also provide a certain level of active support (operational inertia), which helps to alleviate voltage and frequency fluctuations in village-level microgrids. A properly sized supercapacitor capacity can balance both economic considerations and active support capabilities. The calculation of the virtual inertia time constant for energy storage is as follows:

$$H_B=-{\displaystyle \frac{\Delta {\gamma }_{SOC}{W}_{ES}}{{\gamma }_{SOC}{E}_G{S}_{ES}}}{\displaystyle \frac{{\omega }_e^3{J}_G}{4\Delta {\omega }_e{p}_n^2}}$$

(14)

where Δγ_SOC and γ_SOC represent the change in state of charge (SOC) of the energy storage device at two different moments and the SOC of the energy storage device at the current moment, respectively; W_ES and S_ES denote the energy stored in the energy storage device and the total capacity of the energy storage system, respectively; E_G represents the rotational kinetic energy stored in the rotor of a synchronous machine with equivalent capacity; Δω_e and ω_e refer to the change in electrical angular velocity of the synchronous generator at two different moments and the electrical angular velocity of the synchronous generator at the current moment, respectively; p_n is the pole pair number of the synchronous generator; and J_G is the moment of inertia of the synchronous machine with equivalent capacity.

The rotational kinetic energy E_G stored in the rotor of the synchronous machine can be described by the following equation:

$$E_G={\displaystyle \frac{1}{2}}{J}_G{\omega }_e^2$$

(15)

Substituting Equation (15) into Equation (14), the virtual inertia time constant of the supercapacitor is obtained as follows:

$$H_{B,t}=-{\displaystyle \frac{\Delta {\gamma }_{SC,SOC,t}{W}_{SC}}{2\cdot {\gamma }_{SC,SOC,t}{S}_{SC}}}\cdot {\displaystyle \frac{{\omega }_e}{\Delta {\omega }_e{p}_n^2}}=-{\displaystyle \frac{\Delta {\gamma }_{SC,SOC,t}{W}_{SC}}{2\cdot {\gamma }_{SC,SOC,t}{S}_{ES}}}\cdot \delta$$

(16)

The sum of the virtual inertia time constants of the supercapacitor is:

$$H_B^T={\displaystyle \sum _{t=1}^T{H}_{B,t}}={\displaystyle \sum _{t=1}^T\left|-\frac{\Delta {\gamma }_{SC,SOC,t}{W}_{SC}}{2\cdot {\gamma }_{SC,SOC,t}{S}_{SC}}\right|}$$

(17)

where H_B,t represents the virtual inertial time constant of the supercapacitor; $H_B^T$ denotes the sum of the virtual inertial time constants of the supercapacitor over the scheduling period.

2.4. Objective Function

The objective function of VMGs comprises three components: $F_{cap}^{loss}$, $H_B^T$ and $F_{cost}^{all}$:

$$F=(\min \hspace{0.17em}{F}_{cost}^{all},\hspace{0.17em}{F}_{cap}^{loss},{\displaystyle \frac{1}{H_B^T}})$$

(18)

$F_{cost}^{all}$ is calculated as follows:

$$\begin{array}{l}{F}_{cost}^{all}={\omega }_1{F}_{trade}^{MG}+{\omega }_2{F}_{gas}^{GT}+{\omega }_3(F_{maint}+F_{poll}^{GT}+F_{HESS}^{setup})+F_{penalty}\\ \left\{\begin{array}{l}{F}_{trade}^{MG}={\displaystyle \sum _t{e}_{buy,t}^{price}\cdot P_{buy,t}}-{\displaystyle \sum _t{e}_{sell,t}^{price}\cdot P_{sell,t}}\\ F_{gas}^{GT}={\displaystyle \sum _t{e}_{gas}{G}_{GT}(t)}\\ F_{maint}={\displaystyle \sum _t{\beta }_{GT}{P}_{GT,t}+{\beta }_{Bat}(P_{chr,t}^{Bat}+\left|P_{dis,t}^{Bat}\right|)+{\beta }_{SC}(P_{chr,t}^{SC}+\left|P_{dis,t}^{SC}\right|)+{\beta }_{phvo}{\displaystyle \sum _i{P}_{phvo,t}^i}+{\beta }_{WT}}{P}_{WT,t}\\ F_{poll}^{GT}={\displaystyle \sum _t[e_{poll}{\alpha }_{poll}{G}_{GT}(t)+{\lambda }_{buy}^{{\mathrm{CO}}_2}({\sigma }_{GT}\cdot G_{GT}(t))}]\\ F_{penalty}=k_{penalty}\cdot {\displaystyle \sum _t(P_{van,t}+P_{waste,t})}\end{array}\right.\end{array}$$

(19)

where ω₁~ω₃ represent the weights obtained from the Analytic Hierarchy Process (AHP), with values of 0.5396, 0.2970, and 0.1634, respectively; P_buy,t corresponds to the positive value of $p_{trade,t}^{MG}$, while P_sell,t corresponds to the negative value of $p_{trade,t}^{MG}$; $e_{buy,t}^{price}$ and $e_{sell,t}^{price}$ denote the purchase and sale prices of electricity for the village-level microgrid from the external grid; e_gas represents the unit price of natural gas; β denotes the maintenance cost coefficient for various equipment; e_poll, α_poll, and ${\lambda }_{buy}^{{\mathrm{CO}}_2}$ represent the unit cost of pollutant treatment, the nitrogen oxide emission coefficient, and the purchase price of carbon emission rights, respectively; σ_GT is the carbon emission factor for the gas turbine; k_penalty, P_van,t, and P_waste,t refer to the power imbalance penalty coefficient, the power deficit, and the unsatisfied power, respectively.

3. Multi-Objective Snow Geese Algorithm-Based Solution

To address the limitations of the snow geese algorithm (SGA), SGA based on reinforced population adaptive behavior (SGAR) is proposed. In addition, based on SGAR, by introducing an external repository mechanism, a multi-objective SGAR is constructed to solve multi-objective optimization problems.

3.1. Snow Geese Algorithm Based on Reinforced Population Adaptive Behavior

The SGA simulates the migration behavior of snow geese to solve optimization problems [19]. The specific modeling process is as follows:

(1) The chevron formation model

During the exploration phase of the algorithm, snow geese are categorized into different health conditions:

$$Po{s}_i^{t+1}=\left\{\begin{array}{l}Po{s}_i^t+B\cdot (Po{s}_b^t-Po{s}_i^t)+V_i^{t+1}\hspace{1em},i\le {\displaystyle \frac{1}{5}}\\ Po{s}_i^t+B\cdot (Po{s}_b^t-Po{s}_i^t)-D\cdot (Po{s}_c^t-Po{s}_i^t)+V_i^{t+1}\hspace{1em},{\displaystyle \frac{1}{5}}\le i\le {\displaystyle \frac{4}{5}}\\ Po{s}_i^t+B\cdot (Po{s}_b^t-Po{s}_i^t)+D\cdot (Po{s}_c^t-Po{s}_i^t)-E\cdot (Po{s}_n^t-Po{s}_i^t)+V_i^{t+1}\hspace{1em},i\ge {\displaystyle \frac{4}{5}}\end{array}\right.$$

(20)

where ${Pos}_i^t$ and ${Pos}_b^t$ represent the positions of the ith snow goose and the best snow goose, respectively; ${Pos}_c^t$ and ${Pos}_n^t$ represent the center position of the population and the position of the lowest-ranked snow goose after sorting the population; B, D, and E are the weight coefficients for the corresponding components, and $V_i^t$ is the velocity of the ith snow goose.

(2) The linear matrix model

When the angle θ between the snow geese in the cross-shaped matrix exceeds π, they enter the second phase of flight, which is the exploitation phase:

$$Po{s}_i^{t+1}=\left\{\begin{array}{l}Po{s}_i^t+(Po{s}_{\mathrm{i}}^t-Po{s}_b^t)\cdot ran{d}_1\hspace{1em},ran{d}_1\ge {\displaystyle \frac{1}{2}}\\ Po{s}_i^t+(Po{s}_{\mathrm{i}}^t-Po{s}_b^t)\cdot ran{d}_1\oplus Brownian(dim)\hspace{1em},ran{d}_1\le {\displaystyle \frac{1}{2}}\end{array}\right.$$

(21)

where rand₁ is a random number between 0 and 1, indicating whether the snow goose is in a local optimal solution, Brownian(dim) represents standard Brownian motion (dim is the variable dimension), and ⊕ represents element-wise multiplication.

Although the SGA maintains population diversity by changing migration states, it still suffers from slow convergence and the problem of easily falling into local optimal solutions in the later iterations. To address this issue, this study proposes the SGA based on reinforced population adaptive behavior (SGAR). The specific principle of reinforced population adaptive behavior is as follows:

When the snow geese in the cross-shaped matrix deviate too much (entering the exploitation phase), they return to the normal matrix controlled by the parameter θ, which has high randomness. This study introduces an asymptotic development and exploration control factor cycle, to replace the original parameter θ:

$$\left\{\begin{array}{l}\left\{\begin{array}{l}exploration\hspace{0.33em}phase,\hspace{1em}ran{d}_2\cdot \pi \le cycle\\ exploitation\hspace{0.33em}phase,\hspace{1em}else\end{array}\right.\\ cycle=\pi \cdot \left(-1\cdot \left[{\displaystyle \frac{t\%\left(T_{\max }/C\right)}{T_{\max }/C}}\right]+1\right)\end{array}\right.$$

(22)

where T_max represents the maximum number of iterations, C is the number of cycles, and rand₂ is a random number between 0 and 1.

Under the influence of the cycle, the probability of entering the exploration phase decreases with increasing iteration count, while the probability of entering the development phase increases. This process is repeated C times, balancing the intensity of global search and local development.

(2) To better align the behaviors of the two populations during the reinforced exploration and exploitation phases with the divided population, in the exploration phase, the third part of Equation (20) is improved as follows for the last 1/5 of the population (weaker snow geese):

$$\left\{\begin{array}{l}Po{s}_i^{t+1}=Po{s}_i^t+F_{pro}\cdot (Po{s}_b^t-Po{s}_i^t)+V_i^{t+1}\cdot (Po{s}_c^t-Po{s}_i^t)\hspace{1em},i\ge {\displaystyle \frac{4}{5}}\\ F_{pro}=1+\cos (ran{d}_3(1,dim))\end{array}\right.$$

(23)

where F_pro is the protection coefficient for following the high-quality population.

As indicated by Equation (23), by simulating the migration behavior of weaker snow geese, different speeds are exhibited as they fly towards the center position of the population, enhancing the overall flight efficiency of the population.

During the exploitation phase, the concept of a radius for the high-quality population is introduced to guide the population and dynamically simulate the flight speed of the snow geese. Equation (21) is improved as follows:

$$Po{s}_i^{t+1}=\left\{\begin{array}{l}(1+\cos (ran{d}_1))\cdot Po{s}_i^t+L_R^t+N\cdot V_i^t\hspace{1em},ran{d}_1\ge {\displaystyle \frac{1}{2}}\\ Po{s}_i^t+(Po{s}_{\mathrm{i}}^t-Po{s}_b^t)\cdot ran{d}_1\oplus Brownian(dim)\hspace{1em},ran{d}_1\le {\displaystyle \frac{1}{2}}\end{array}\right.$$

(24)

$$\left\{\begin{array}{l}{L}_R^t={(-1)}^{randi}(mean(Pos(1:0.2\cdot Np,:))-Po{s}_i^t\cdot ran{d}_3(dim)\hfill \\ N={(1-{(t/T_{max})}^{(1/3)})}^{(1/3)}\hfill \end{array}\right.$$

(25)

where $L_R^t$ is the radius of the high-quality population, and N represents the coefficient of physical fitness decline caused by long-duration flight of the snow geese.

In the linear matrix, the coefficient of physical fitness decline N is introduced, which decreases as the algorithm iteration count increases. This aims to simulate the decrease in speed caused by the decline in physical fitness of the snow geese in the later stages of migration. Additionally, the radius of the high-quality population $L_R^t$ is introduced to enhance the ability of the snow geese to follow the high-quality population, significantly improving the algorithm’s local development capability.

3.2. Multi-Objective SGAR

To solve the multi-objective microgrid scheduling model developed in this study, based on SGAR, a multi-objective SGAR (MSGAR) is constructed by introducing an external repository mechanism.

The external repository mechanism involves several processes: selection of non-dominated solutions after iteration, storing non-dominated solutions in the external repository, and updating and maintaining the external repository. When solution S₁ dominates solution S₂, it is denoted as S₁ ≺ S₂, and the dominance relationship can be determined by the following equation [20]:

$$\forall i:(f_i(S_1)\le f_i(S_2)),\hspace{0.17em}\exists \hspace{0.17em}j:(f_j(S_1)<f_j(S_2))$$

(26)

where i, j = 1, 2, 3, …, N_O; N_O is the number of objective functions.

As the non-dominated solutions are continuously stored, the quantity may exceed the capacity of the external repository. In such cases, non-dominated solutions need to be removed from the crowded regions of the solution space based on crowding distance to prevent the repository from exceeding its capacity limit. The crowding distance crd_i of the ith non-dominated solution is calculated as follows [21]:

$$cr{d}_i={\displaystyle \sum _{m=1}^{No}fitnes{s}_{i,\mathrm{m}}^{\mathrm{nor}}}$$

(27)

where $fitnes{s}_{i,\mathrm{m}}^{\mathrm{nor}}$ represents the normalized fitness of the ith solution under the mth objective function.

MSGAR first generates an initial population and an empty external archive. Then, it calculates all objective function values for each individual in the population and stores the non-dominated solutions from the initial population into the archive. The main loop begins and continues until the maximum number of iterations is reached. The external archive is updated by merging the new population with the current archive. Fast non-dominated sorting is applied to the combined set to obtain the first non-dominated front. If the number of solutions in the first front exceeds the archive capacity, the crowding distance of each solution in this front is calculated, and the top N_O solutions with the largest crowding distance are retained. Finally, after the loop terminates, the solutions in the external archive serve as the obtained approximate Pareto-optimal set.

The solution process of MSGAR is presented in Figure 2.

At each iteration, each individual needs to calculate the fitness function with the time complexity of O(Np·Ti_f), where Np is the population size, Ti_f is the fitness function to calculate the time. The time complexity of population sorting, position updating and speed updating is O(Np·dim), where dim is the problem dimension. The overall time complexity is O(T_max· (Np·Ti_f + Np·dim)),where T_max is the maximum number of iterations. Non-dominated sorting is added to MSGAR with a time complexity of O(Np²·No), where No is the number of objective functions. The time complexity of external archive maintenance is O(Np·log Np), and the overall time complexity is O(T_max· (Np·Ti_f + Np²·No + Np·log Np)).

3.3. Multi-Objective Snow Geese Algorithm-Based Solution Method Process

The solution process of the VMG scheduling model is shown in Figure 3.

The solution process shown in Figure 3 can be divided into the following steps:

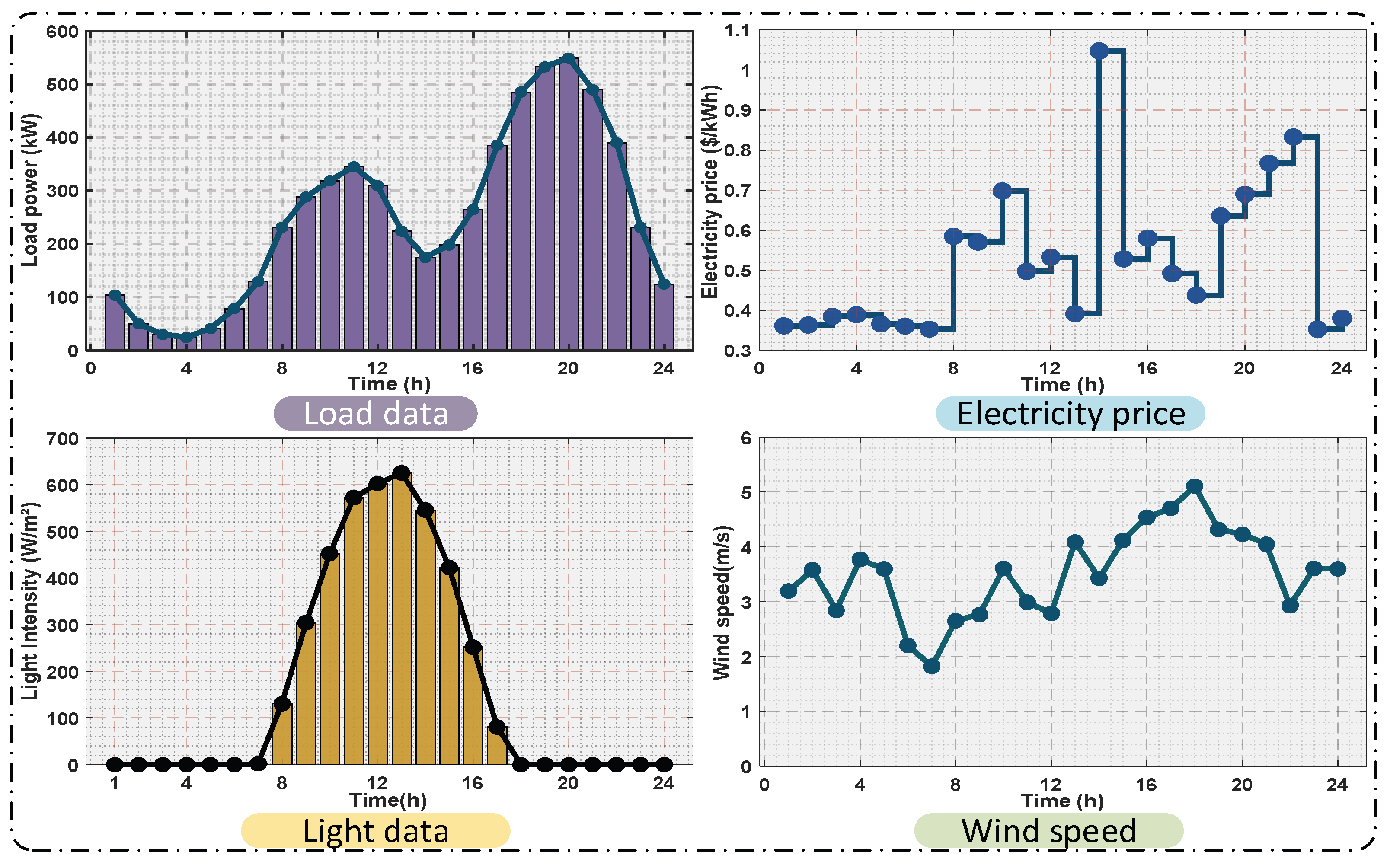
(1) Initialization: Set the device parameters, algorithm parameters, and load and weather data, ensuring they align with the operational characteristics of the village-level microgrid. Then generate a set of initial output values for the devices to prepare for evaluating the objective functions relevant to the VMG.

(2) Scheduling and objective function evaluation: Utilize the MSGAR algorithm to optimize the device outputs. The objective functions here directly correspond to the VMG’s optimization goals, such as minimizing economic costs and reducing carbon emissions. Run the VMG scheduling simulation model, calculate the power balance, and rigorously verify all operational constraints. Calculate the values of these objective functions based on the device outputs and pass them to the MSGAR algorithm to guide the optimization process.

(3) Evaluation and iteration: After evaluating the objective function values, update the population within the MSGAR framework. First, perform fast non-dominated sorting to update the external archive. Subsequently, based on this external archive, guide the population evolution to generate a new population. This new population will be used for the next iteration. If the maximum number of iterations has not been reached, the updated population is fed back into the scheduling process to refine the solutions further. This iterative process ensures that the scheduling outcomes progressively align with the VMG’s optimization objectives. If the maximum number of iterations is reached, proceed to the final step.

(4) Output of optimal results: Once the iterations are complete, output the optimal population position determined by MSGAR. Based on this position, calculate the operational status of each device within the VMG, reflecting the optimal scheduling outcomes that balance the VMG’s economic, environmental, and operational objectives. Finally, output the comprehensive scheduling results for the VMG.

4. Case Study

In the case study, Case 1 validates the effectiveness of SGAR and MSGAR through a standard test set; Case 2 analyzes the scheduling effects in scenarios with and without supercapacitors; and Case 3 further analyzes the active support effect of supercapacitors on the village microgrid under the presence of supercapacitors.

4.1. Case 1: Algorithm Testing and Performance Analysis

Representative algorithms proposed in recent years were selected for comparison, such as the Parrot Optimizer (PO) [22] and the Black-winged Kite Algorithm (BKA) [23], both proposed in 2024. The parameter settings of each algorithm during the testing process are listed in

Table 1. Parameter settings for Case 1.

Maximum Number of Iterations	Population Size	Parameter Setting	Algorithm
1000	30	C = 4	SGAR
		—	SGA
		p = 0.9	BKA
		—	PO

.

The latest CEC-2022 test set was selected to perform performance testing on the algorithms, with each test function being continuously tested 30 times. The test results of SGAR are shown in Figure 4.

As presented in Figure 4, taking function F1 as an example, the variances of SGA and PO are 477.2542 and 597.5121, respectively, indicating significant fluctuations in the results. The variances of SGAR and BKA are 6.9118 and 12.9655, respectively, indicating that the solution stability of SGAR is significantly better than that of other algorithms. For the iteration curve, the optimal solutions of F1 obtained by SGAR and BKA are 300.564 and 318.443, respectively. For F2 and F7, SGAR also obtained higher-quality optimal solutions, demonstrating its advantages in fast iteration convergence, strong iteration ability, and robustness. Overall, the test results show that the SGAR algorithm exhibits stronger competitiveness in both optimization performance and escaping local optima.

The classic multi-objective meta-universe optimization algorithm (MOMVO) [23] and non-dominated sorting genetic algorithm II (NAGA-II) [24] were selected as comparison algorithms. The parameter settings of each algorithm are shown in

Table 2. Parameter settings of multi-objective algorithms for Case 1.

Algorithm	Parameters	Population Size	Repository Size	Maximum Iteration
MSGAR	C = 4	30	100	500
MOMVO	Pemin = 0.2, Pemax = 1
NSGA-II	Pc = 0.9, Dm = 20, Dc = 20

Note: The Pemin and Pemax is experience value in MOMVO; P_c is crossover probability, D_m is distribution index for mutation and D_c is distribution index for crossover.

.

The effectiveness of the multi-objective algorithms was verified using the CEC-2009 test set, where UF1, UF2, UF6, and UF7 are bi-objective, and UF8 and UF9 are tri-objective. Each test function was continuously tested 10 times, and the IGD, SP, and HV [25] were selected as evaluation indicators. The test results of the multi-objective algorithms are presented in Figure 5.

As presented in Figure 5, MSGAR achieves the best results in terms of the average values of IGD and HV indicators. For UF1 and UF7, the average IGD values are only 0.0195 and 0.0122, respectively. For UF9, the average HV value is 0.6099. Although the IGD standard deviation for UF9 is slightly higher than the other two algorithms, MSGAR still demonstrates high stability and strong competitiveness overall. These excellent capabilities provide a solid foundation for its Scalability. The cycle control factor and population classification management mechanism introduced in the core of the algorithm do not depend on the specific structure of the problem, which makes it have the potential to deal with problems.

A box plot of the SP evaluation indicator results is presented, along with the Pareto fronts for UF1 and UF8, as shown in Figure 6.

Figure 6 reveals that the SP indicator results obtained by MSGAR are superior to those of MOMVO and NSGA-II. For UF8, the mean and standard deviation of the SP obtained by MSGAR are only 0.1025 and 0.0624, respectively. Although the CEC-2009 test functions are highly complex, the distribution and uniformity of the Pareto fronts obtained by MSGAR are the most competitive. These excellent capabilities provide a solid foundation for its Scalability. The cycle control factor and population classification management mechanism introduced in the core of the algorithm do not depend on the specific structure of the problem, which makes it have the potential to deal with problems.

4.2. Case 2: Capacitor Configuration and Scheduling Analysis of Village Microgrid with Supercapacitors

The capacity and parameter settings of each device are listed in

Table 3. Equipment capacity and maintenance parameters.

Equipment	Capacity (kW)	Maintenance Coefficient (USD/kW)	Climbing Power/ Maximum Power
Photovoltaic	350	0.009	—
Wind Turbine	180	0.015	—
Gas Turbine	300	0.05	290
Supercapacitor	[0, 100]	0.007	—
Li-on battery pack	400	0.008	200

and

Table 4. The equipment parameters of VMG.

Parameters	Value	Parameters	Value
${\eta }_{chr}^{Bat}$/${\eta }_{dis}^{Bat}$	0.95/0.95	${\delta }_{Bat}^{min}$/${\delta }_{Bat}^{max}$	0.1/0.9
${\eta }_{chr}^{SC}$/${\eta }_{dis}^{SC}$	0.95/0.95	${\delta }_{SC}^{min}$/${\delta }_{SC}^{max}$	0.1/0.9
εBat,e	0.02	kpenalty	1000
εSC	0.10	σGT	0.51 (kg/kWh)

.

The electrical load of the village microgrid, the purchasing price of electricity from the external power grid, and the weather conditions are shown in Figure 7.

In the case where the supercapacitors are not involved in capacity configuration and scheduling, the solution results of each single-objective algorithm are shown in Figure 8.

As presented in Figure 8a, the improved SGAR algorithm achieves the lowest total economic cost of USD 11,195.57 compared to other algorithms, with better optimization convergence speed and solution quality than SGA and BKA. Figure 8b illustrates the major carbon emissions (i.e., GT carbon emissions) within the scheduling period. High carbon emissions are observed between 8:00 and 9:00 and 19:00 and 22:00. As seen in Figure 8c, this is due to the lower output of renewable energy sources at these times, coupled with high load demand and electricity purchase prices, necessitating an increase in GT output to bridge the energy gap. Additionally, during the periods of 1:00–5:00 and 13:00–14:00 in Figure 8c, GT is still operational, indicating a “low-storage, high-generation” scenario after energy storage optimization. In this period, GT charges the lithium battery, enabling it to cover energy gaps during high electricity prices, thereby reducing purchase costs.

Upon enabling supercapacitors, the VMG optimization scheduling results are shown in Figure 9.

As shown in Figure 9a, MSGAR achieves a more uniform Pareto front. Although the introduction of supercapacitors increases the initial investment cost, a good cost-benefit balance is achieved through capacity optimization configuration and operation strategy adjustment. The trade-off solutions are selected based on the normalized weights of the objective values, resulting in a final $F_{cost}^{all}$ of USD 17,042 and an electrochemical energy storage loss rate $F_{cap}^{loss}$ of 0.4356. This represents a 58.09% reduction in losses compared to scheduling without supercapacitors, which means that the life of the lithium-ion battery is significantly extended, thus reducing its maintenance costs. Compared to Figure 6b, Figure 9b demonstrates a significant reduction in VMG’s carbon emissions, with almost no carbon emissions from 00:00 to 07:00. Figure 9c indicates that this outcome is due to the optimized scheduling favoring electricity purchase from the external grid rather than using GT for regulation. Overall, increasing electricity purchases and using supercapacitors for buffering can significantly reduce lithium battery losses. For a greater focus on economic efficiency, scheduling solutions can be selected from the upper left part of the Pareto front, which can mitigate lithium battery losses without significantly increasing costs.

The status of the energy storage systems when scheduling with a single lithium battery versus a hybrid energy storage system is shown in Figure 10.

Comparing with the results in Figure 8, when the supercapacitor (SC) was not utilized, during the period from 1:00 to 3:00, the “low storage, high discharge” and the consumption of new energy between 13:00 and 15:00 were both managed by the lithium battery. There were four instances of charging and discharging above 100 kW, which placed significant peak shaving pressure on the lithium battery. When the SC was enabled, the use of gas turbines (GT) was reduced. The hybrid energy storage system (HESS) experienced more “low-storage, high-discharge” situations, where external electricity was supplied to the SC, such as at 0:00 and 23:00. For new energy consumption, the SC was preferred, but at 4:00, due to the SC reaching its set energy storage limit, excess wind power was absorbed by the lithium battery. This strategy effectively shifts the load of lithium batteries, is the direct cause of its loss rate dropped significantly. Additionally, in Figure 10b, during the period from 2:00 to 7:00, the SC frequently underwent small-scale charging to ensure it had sufficient energy to address power gaps. Given that this period is characterized by lower electricity prices, “low storage, high discharge” was also achievable. Overall, the activation of the SC effectively reduced the peak shaving pressure on the lithium battery, with the instances of charging and discharging above 100 kW decreasing from 4 to 1, which proves the great value of hybrid energy storage in extending the life of main energy storage equipment, from a long-term operational point of view, the initial investment in supercapacitors can be offset by significant savings in battery replacement costs.

Table 5. Ten times of economic costs and capacity loss for Case 2.

F/Cycle	${\mathbf{F}}_{\mathbf{t}\mathbf{r}\mathbf{a}\mathbf{d}\mathbf{e}}^{\mathbf{M}\mathbf{G}}$ (USD)	${\mathbf{F}}_{\mathbf{g}\mathbf{a}\mathbf{s}}^{\mathbf{G}\mathbf{T}}$ (USD)	Fmaint (USD)	${\mathbf{F}}_{\mathbf{p}\mathbf{o}\mathbf{l}\mathbf{l}}^{\mathbf{G}\mathbf{T}}$ (USD)	Fpenalty (USD)	Fsetup (USD)	${\mathbf{F}}_{\mathbf{c}\mathbf{o}\mathbf{s}\mathbf{t}}^{\mathbf{a}\mathbf{l}\mathbf{l}}$ (USD)	${\mathbf{F}}_{\mathbf{c}\mathbf{a}\mathbf{p}}^{\mathbf{l}\mathbf{o}\mathbf{s}\mathbf{s}}$
1	1170.4	850.0	108.8	227.3	0	105,453.73	18,038.60	0.450
2	1058.4	909.2	98.4	205.8	0	102,628.84	16,037.40	0.415
3	1168.0	838.8	109.5	223.6	0	98,639.00	17,533.50	0.468
4	1050.0	928.2	97.6	202.5	0	95,000.00	15,532.30	0.402
5	1182.4	818.6	105.0	230.1	0	103,846.73	18,341.70	0.476
6	1070.0	917.6	96.5	198.4	0	93,728.84	15,941.80	0.395
7	1155.2	847.2	107.2	225.0	0	98,639.00	17,837.90	0.441
8	1045.0	936.0	95.8	200.0	0	96,200.00	16,436.70	0.420
9	1190.0	826.4	103.5	218.7	0	101,421.73	18,939.80	0.455
10	1068.8	925.8	96.7	204.4	0	102,728.84	15,638.60	0.410
AVG	1120.4	879.59	103.65	216.44	0	98,639.00	17,038.10	0.436

shows the economic costs and capacity losses of the MSGAR strategy with supercapacitors over 10 runs, as well as the average values.

Table 6. Composition of economic costs and capacity loss.

F	SGAR (Without SC)	MSGAR
${\mathrm{F}}_{\mathrm{trade}}^{\mathrm{MG}}$ (USD)	520.69	1120.4
${\mathrm{F}}_{\mathrm{gas}}^{\mathrm{GT}}$ (USD)	1401.50	879.59
Fmaint (USD)	163.22	103.65
${\mathrm{F}}_{\mathrm{poll}}^{\mathrm{GT}}$ (USD)	397.16	216.44
Fpenalty (USD)	0	0
Fsetup (USD)	63,678	98,639.00
${\mathrm{F}}_{\mathrm{cost}}^{\mathrm{all}}$ (USD)	11,195.6	17,038
${\mathrm{F}}_{\mathrm{cap}}^{\mathrm{loss}}$	1.0394	0.436

shows the average economic composition of the VMG and the electrochemical energy storage loss rate of the lithium battery under the influence of SC utilization.

As shown in Table 6, the introduction of supercapacitors (SC) led to a 54.90% rise in the installation cost of the hybrid energy storage system (HESS). Due to the significant cost of SC capacity configuration, the lithium battery’s electrochemical energy storage capacity loss rate fell by 58.09%. Despite the HESS installation cost not being a major factor in the objective function, its considerable increase still pushed up the overall economic cost by 52.18%. As a result, the scheduling strategy for energy supplementation of HESS changed from relying on gas turbines (GT) to purchasing electricity from external sources, which in turn reduced the VMG’s carbon emissions by 45.56%.

4.3. Case 3: Hybrid Energy Storage System Capacity Configuration and Active Support Optimization

For Case 3, the optimization results of the obtained VMG are presented in Figure 11.

Figure 11a indicates that compared to the results obtained by MOMVO, the Pareto front achieved by MSGAR is more balanced, with a superior compromise solution balance, showcasing a 56.23% enhancement in active support. The variation in $F_{cost}^{all}$ and $F_{cap}^{loss}$ is illustrated in Figure 11b. The loss rate of electrochemical energy storage experiences an initial decrease followed by an increase, but still exhibits a 40.49% reduction compared to the original scheduling model. In Figure 11c, the carbon emissions of VMG are consistently lower than in the two scenarios of Case 2 with and without SC involvement, with carbon emissions reduced by 59.47% and 25.55%, respectively. However, this reduction comes at the cost of sacrificing a certain level of economic benefit. The electricity balance results in Figure 11d show an increased electricity purchase compared to the results in Case 2, accompanied by a further reduction in GT usage.

Although this study clarified the carbon emission reduction effect of the hybrid energy storage system in the operation stage of village-level microgrids, reducing carbon emissions by 45.56% after the introduction of HESS and further reducing it by 59.47% after optimizing active support, it was not included in the full life cycle environmental impact assessment of supercapacitors and lithium batteries. From the perspective of life cycle, the production stage of the two types of energy storage equipment involves resource mining and high-energy manufacturing of lithium, cobalt and carbon-based materials, which will produce embodied carbon emissions and pollutants. If not properly disposed of during the disposal stage, lithium batteries may cause heavy metal leakage, and SC electrode materials can easily cause resource waste, both of which will bring additional environmental costs.

Figure 12 depicts the status of HESS in Case 3, along with the variations in $F_{cap}^{loss}$ and H_B,t at different time points under each strategy.

Comparing with the results in Figure 10, it can be observed that under the optimization of active support, the total charging amount of the lithium battery throughout the day is higher than the scenario in Case 2 where SC is used. Additionally, there is one instance of discharging at 10:00, leading to a slight increase in the loss of the lithium battery. As for the SC, the total charging amount throughout the day is approximately the same as in Case 2, but the discharging amount increases by 111.64%, resulting in stronger active support. The heat map in Figure 12b illustrates the loss rate of the lithium battery at each time point, which is positively correlated with the discharge amount. In Case 2, under the scenario of enabling SC, the maximum discharging occurs at 20:00, resulting in the highest battery loss rate of 0.31. Figure 12c demonstrates that when there is more discharging from the SC, the active support to VMG becomes more prominent.

Table 7. Ten times of economic costs and capacity loss.

F/Cycle	${\mathbf{F}}_{\mathbf{trade}}^{\mathbf{MG}}$ (USD)	${\mathbf{F}}_{\mathbf{gas}}^{\mathbf{GT}}$ (USD)	Fmaint (USD)	${\mathbf{F}}_{\mathbf{poll}}^{\mathbf{GT}}$ (USD)	Fpenalty (USD)	Fsetup (USD)	${\mathbf{F}}_{\mathbf{cost}}^{\mathbf{all}}$ (USD)	${\mathbf{F}}_{\mathbf{cap}}^{\mathbf{loss}}$
1	1357.93	563.93	83.07	153.19	0	82,073	14,653	0.5875
2	1502.86	657.71	91.81	170.06	0	100,022	17,248	0.6494
3	1296.42	562.43	82.82	147.69	0	81,873	14,633	0.5865
4	1579.35	687.71	96.18	177.37	0	100,922	17,464	0.6794
5	1328.41	596.67	86.07	156.19	0	85,273	15,153	0.6085
6	1545.23	638.92	92.36	173.06	0	98,622	16,908	0.6604
7	1301.87	575.38	83.28	149.69	0	82,573	14,753	0.5915
8	1593.92	674.62	95.68	176.37	0	100,522	17,308	0.6634
9	1284.36	585.67	84.07	151.19	0	83,573	14,853	0.5965
10	1566.38	664.32	94.81	172.06	0	99,522	17,108	0.6584
AVG	1429.4	625.19	87.44	161.25	0	91,498	15,951	0.6185

shows the economic costs and capacity losses of the MSGAR strategy after 10 runs, as well as the average values of these data.

Table 8. Composition of economic costs and capacity loss for Case 3.

F	MSGAR	NSGA-II	MOMVO
${\mathrm{F}}_{\mathrm{trade}}^{\mathrm{MG}}$ (USD)	1429.4	1249.2	491.52
${\mathrm{F}}_{\mathrm{gas}}^{\mathrm{GT}}$ (USD)	625.19	746.34	1555.3
Fmaint (USD)	87.44	142.8	170.32
${\mathrm{F}}_{\mathrm{poll}}^{\mathrm{GT}}$ (USD)	161.25	454.6	423.0463
Fpenalty (USD)	0	0	0
Fsetup (USD)	91,498	84,729	7950.7
${\mathrm{F}}_{\mathrm{cost}}^{\mathrm{all}}$ (USD)	15,951	14,035	13817
${\mathrm{F}}_{\mathrm{cap}}^{\mathrm{loss}}$	0.6185	1.1126	0.5631

presents the solution results of MSGAR, MOMVO and NSGA-II.

Table 8 shows that MOMVO achieves more economical compromise solutions compared to MSGAR. While its battery loss rate is 8.96% lower than MSGAR’s, the limited capacity allocation of SC results in weaker active support. The installation cost of the HESS is 7.99% higher than that of NSGA-II. Moreover, similar to Case 2 without SC, MOMVO’s results show higher gas turbine usage to offset electricity shortages, causing higher carbon emissions and maintenance costs. Specifically, equipment maintenance costs are 94.78% higher than MSGAR’s. Considering Table 8 and Figure 11, MSGAR’s compromise solutions better meet the optimization objective in terms of SC’s active support. Compared to NSGA-II, MSGAR reduces the loss rate of lithium battery electrochemical energy storage capacity by 44.41%.

When the output of other units is kept unchanged, the sensitivity analysis of the change of the energy storage capacity limit of HESS is carried out to observe the overall system benefit. Figure 13 depicts the effect of a change in Hess energy storage capacity on the economic cost of the system.

As can be seen in Figure 13, the total cost varies with the storage capacity and is lowest at 92%, which is 46.7% lower than 90%. After the capacity continued to increase, the cost first increased and then decreased slightly, the loss rate of lithium battery changed with the capacity, and the loss rate increased with the increase of capacity from 0.5544 to 0.6474, and the loss was the lowest at 90%, but the total cost was the highest, the loss rate is relatively stable at 95%. At 92%, the basic cost is the highest, while at 95%, it is the highest, which indicates that the state interacts more with the external power grid, the capacity limitation cost is the lowest at 95%, and it rises again at 98%, and the indicators are relatively balanced at 95%, strike the best balance between total cost, system inertia support, and battery drain.

5. Conclusions

Energy storage technologies can effectively mitigate the intermittency and volatility of renewable energy generation in microgrids, thereby enhancing the stability and reliability of the microgrid system. However, the frequent use of traditional chemical energy storage devices accelerates their lifespan degradation. To address this issue, this study proposes a hybrid energy storage system in VMG. Capacity allocation and scheduling strategies are designed for the SC to reduce the degradation of lithium batteries and fully utilize the fast charging and discharging characteristics of the SC. A virtual inertia time constant model for the SC is constructed to enhance its active support capability to the VMG. The findings of this research are as follows:

• Compared to existing evolutionary algorithms, the improved SGAR and MSGAR algorithms proposed in this paper demonstrate stronger convergence performance on both single-objective and multi-objective benchmark test functions. For the F1 function in the CEC-2022 test set, SGAR achieves a variance of 6.9118, while SGA achieves a variance of 477.2542, significantly improving the convergence effect. For the UF8 function in the CEC-2009 test set, MSGAR achieves a mean and standard deviation of SP of only 0.1025 and 0.0624, demonstrating greater competitiveness.
• With the introduction of the hybrid energy storage system (HESS), the loss rate of electrochemical energy storage decreases from the original 1.0394 to 0.4356, resulting in a 58.09% reduction in losses. Although the total cost increases due to the high installation cost of the SC, the carbon emissions of the VMG decrease by 45.56%.
• After optimizing the active support of the microgrid, the loss rate of electrochemical energy storage decreases by 40.49% compared to when HESS is not used, and the VMG carbon emissions decrease by 59.47%. The scheduling results focus on the coordination and cooperation among various components within the microgrid, ensuring the efficient operation of the entire system. Ultimately, the SC achieves a virtual inertia time constant of 0.1931 s, representing an 8.73% improvement compared to not using active support optimization.

Although the model and strategies proposed in this study have shown positive effects in reducing energy storage device losses and enhancing VMG’s active support capability, there are still limitations. First, the currently employed metaheuristic algorithms have room for optimization in terms of convergence performance. Second, the universality of the proposed strategies needs further improvement. Future research will focus on addressing these challenges. In view of the above limitations, the research can be refined from two aspects in the future: at the algorithm level, the convergence efficiency in high-dimensional problems can be improved by integrating adaptive parameter adjustment and multi-operator collaboration. At the policy level, a multi-scenario database is constructed, based on transfer learning, adaptation rules are refined, and a demand response mechanism is incorporated to enhance the versatility of the strategy in various scenarios.

Although the design, scheduling strategy and optimization algorithm of hybrid energy storage system proposed for village-level microgrids focus on small-scale rural power systems, its core technical framework has the potential to be extended to city-level microgrids or regional power systems. For urban systems, on the basis of the existing “supercapacitor lithium battery” hybrid energy storage structure, large-scale energy storage technologies such as pumped storage can be introduced to build a multi-level collaborative energy storage architecture to cope with more complex “source–load” fluctuations, and the scheduling strategy can be upgraded to a hierarchical collaborative mode, which expands the objective function to cover network loss and power supply reliability at the total scheduling layer, and coordinates the dynamic coupling relationship within the partition with the help of the improved MSGAR algorithm at the partition layer, while retaining the priority response mechanism of the supercapacitor. In terms of active support, a “virtual inertial pool” can be formed by aggregating distributed supercapacitors, and combined with virtual synchronous machine technology to realize dynamic adaptive adjustment of inertial support capacity. At the algorithm level, parallel computing and population division strategies are introduced to improve the efficiency of solving high-dimensional decision variables, so as to provide a transferable technical path for the low-carbon transformation of urban energy systems.