Modeling of Oil–Water Two-Phase Flow in Horizontal Pipes Using CFD for the Prediction of Flow Patterns
Abstract
1. Introduction
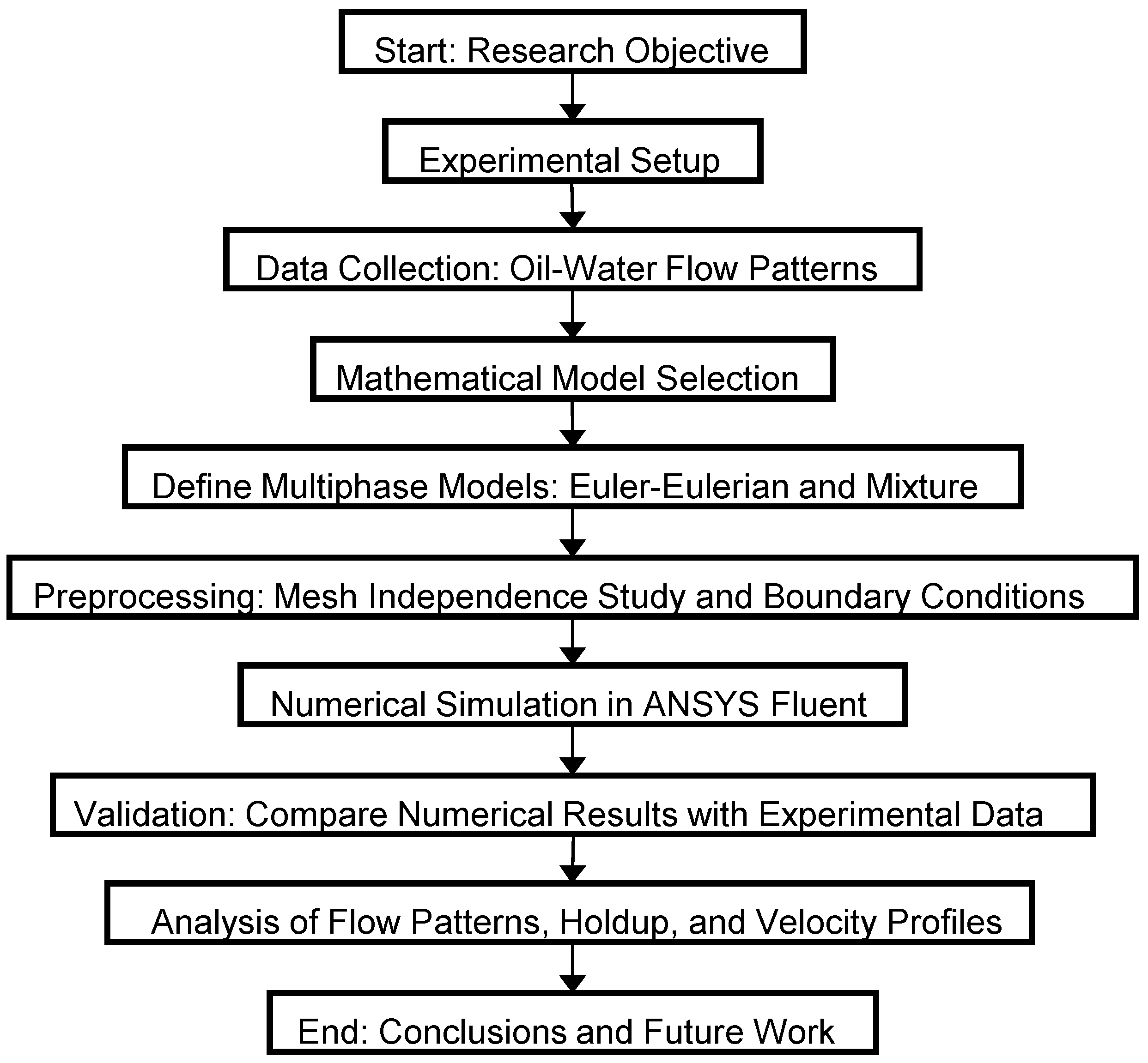
2. Methods and Materials
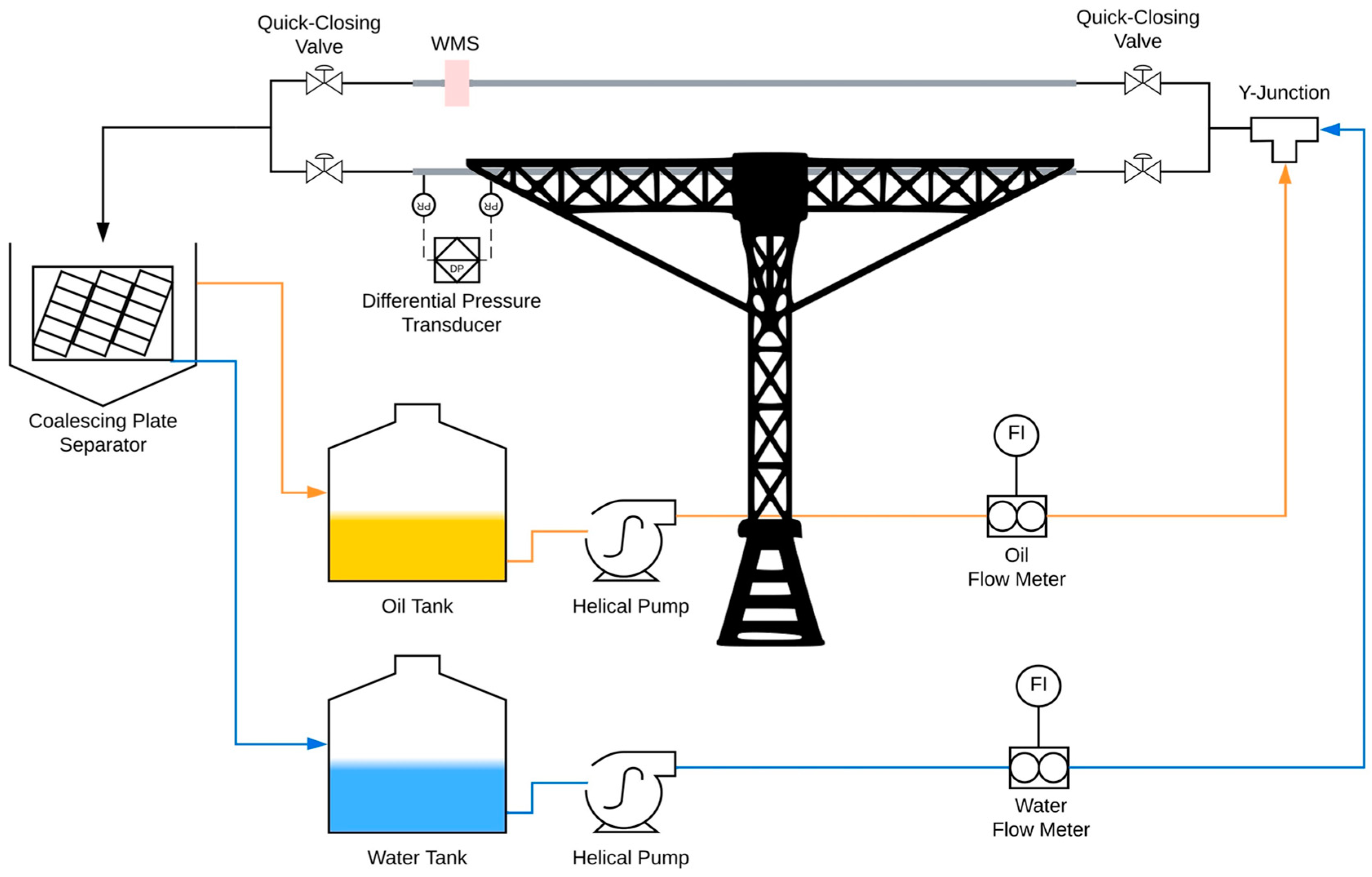
2.1. Experimental Setup
2.2. Mathematical Model
2.2.1. Eulerian Approach to Multiphase Flow
2.2.2. Interfacial Area Concentration
2.2.3. Turbulence Model
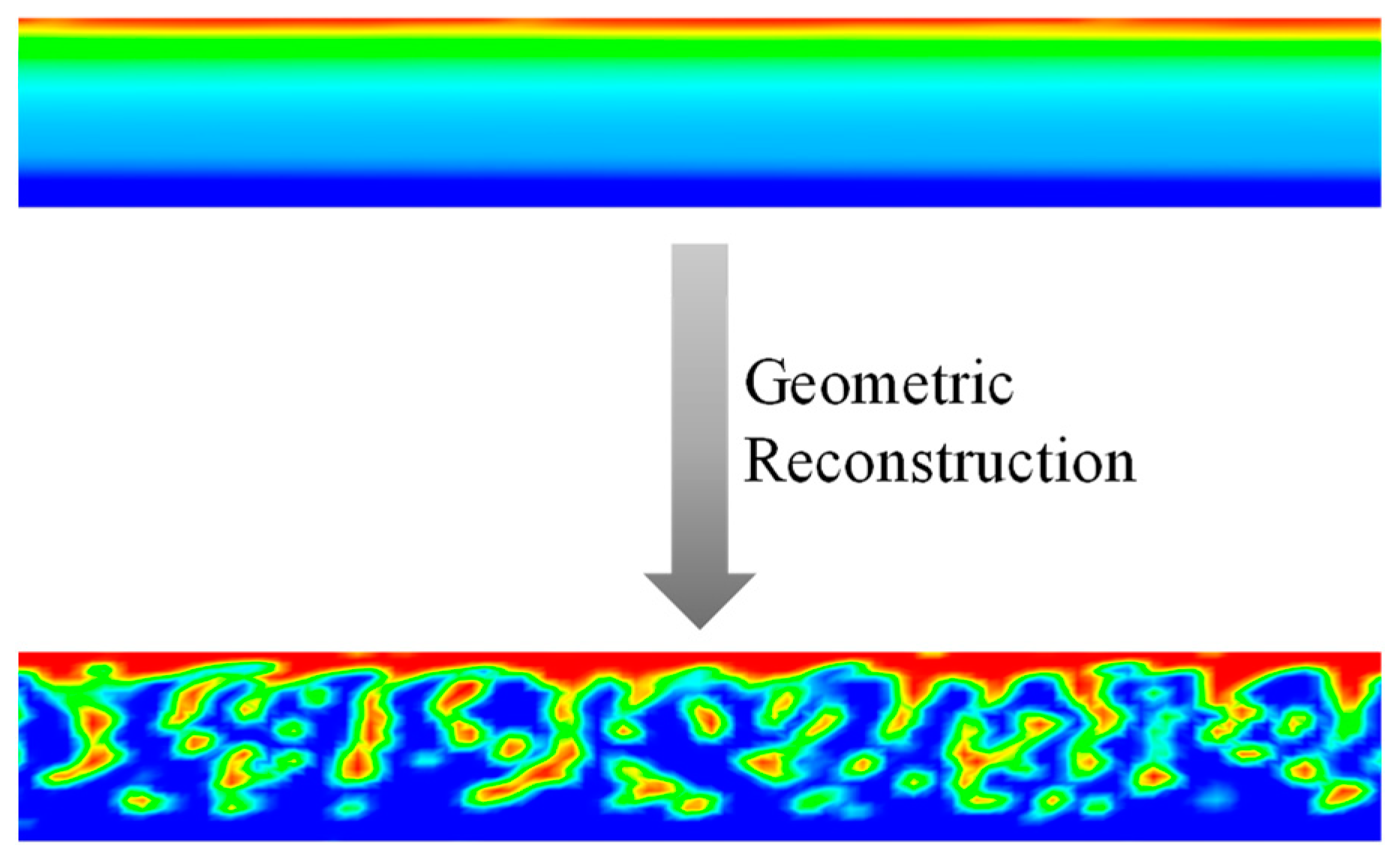
2.3. Numerical Model and Mesh Generation
Mesh Independence Test
3. Results
Model Validation
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- de Almeida Coelho, N.M.; Taqueda, M.E.S.; Souza, N.M.O.; de Paiva, J.L.; Santos, A.R.; Lia, L.R.B.; de Moraes, M.S.; de Moraes Júnior, D. Energy savings on heavy oil transportation through core annular flow pattern: An experimental approach. Int. J. Multiph. Flow 2020, 122, 103127. [Google Scholar] [CrossRef]
- AL-Dogail, A.S.; Gajbhiye, R.N. Effects of density, viscosity and surface tension on flow regimes and pressure drop of two-phase flow in horizontal pipes. J. Pet. Sci. Eng. 2021, 205, 108719. [Google Scholar] [CrossRef]
- Barnea, D. A unified model for predicting flow-pattern transitions for the whole range of pipe inclinations. Int. J. Multiph. Flow 1987, 13, 1–12. [Google Scholar] [CrossRef]
- Volino, R.J.; Devenport, W.J.; Piomelli, U. Questions on the effects of roughness and its analysis in non-equilibrium flows. J. Turbul. 2022, 23, 454–466. [Google Scholar] [CrossRef]
- Wang, S.; Di, Y.; Winterfeld, P.H.; Li, J.; Zhou, X.; Wu, Y.-S.; Yao, B. Understanding the Multiphysical Processes in Carbon Dioxide Enhanced-Oil-Recovery Operations: A Numerical Study Using a General Simulation Framework. SPE J. 2021, 26, 918–939. [Google Scholar] [CrossRef]
- Matko, T.; Chew, J.; Wenk, J.; Chang, J.; Hofman, J. Computational fluid dynamics simulation of two-phase flow and dissolved oxygen in a wastewater treatment oxidation ditch. Process Saf. Environ. Prot. 2021, 145, 340–353. [Google Scholar] [CrossRef]
- Yadigaroglu, G.; Hewitt, G.F. Introduction to Multiphase Flow, 1st ed.; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Abduvayt, P.; Manabe, R.; Watanabe, T.; Arihara, N. Analysis of oil/water-flow tests in horizontal, hilly terrain, and vertical pipes. SPE Proj. Facil. Constr. 2006, 21, 123–133. [Google Scholar] [CrossRef]
- Hamidi, M.J.; Karimi, H.; Boostani, M. Flow patterns and heat transfer of oil-water two-phase upward flow in vertical pipe. Int. J. Therm. Sci. 2018, 127, 173–180. [Google Scholar] [CrossRef]
- Boostani, M.; Karimi, H.; Azizi, S. Heat transfer to oil-water flow in horizontal and inclined pipes: Experimental investigation and ANN modeling. Int. J. Therm. Sci. 2017, 111, 340–350. [Google Scholar] [CrossRef]
- Trallero, J.L.; Sarica, C.; Brill, J.P. A study of oil/water flow patterns in horizontal pipes. SPE Prod. Facil. 1997, 12, 165–172. [Google Scholar] [CrossRef]
- Flores, J.G.; Chen, X.T.; Sarica, C.; Brill, J.P. Characterization of oil-water flow patterns in vertical and deviated wells. SPE Prod. Facil. 1999, 14, 102–109. [Google Scholar] [CrossRef]
- Brauner, N. Liquid-Liquid Two-Phase Flow Systems. In Modelling and Experimentation in Two-Phase Flow; Bertola, V., Ed.; Springer: Vienna, Austria, 2003; pp. 221–279. [Google Scholar]
- Al-Wahaibi, T.; Yusuf, N.; Al-Wahaibi, Y.; Al-Ajmi, A. Experimental study on the transition between stratified and non-stratified horizontal oil-water flow. Int. J. Multiph. Flow 2012, 38, 126–135. [Google Scholar] [CrossRef]
- Grassi, B.; Strazza, D.; Poesio, P. Experimental validation of theoretical models in two-phase high-viscosity ratio liquid–liquid flows in horizontal and slightly inclined pipes. Int. J. Multiph. Flow 2008, 34, 950–965. [Google Scholar] [CrossRef]
- Sridhar, S.; Zhang, H.Q.; Sarica, C.; Pereyra, E. Experiments and model assessment on high-viscosity oil/water inclined pipe flows. Proc.—SPE Annu. Tech. Conf. Exhib. 2011, 2, 1554–1563. [Google Scholar] [CrossRef]
- Ruiz-Diaz, C.M.; Hernández-Cely, M.M.; González-Estrada, O.A. Modelo predictivo para la identificación de la fracción volumétrica en flujo bifásico. Cienc. Desarro. 2021, 12, 49–55. [Google Scholar] [CrossRef]
- Ruiz-Diaz, C.M.; Gómez-Camperos, J.A.; Hernández-Cely, M.M. Flow pattern identification of liquid-liquid (oil and water) in vertical pipelines using machine learning techniques. J. Phys. Conf. Ser. 2022, 2163, 12001. [Google Scholar] [CrossRef]
- Amooey, A.A. Prediction of pressure drop for oil-water flow in horizontal pipes using an artificial neural network system. J. Appl. Fluid Mech. 2016, 9, 2469–2474. [Google Scholar] [CrossRef]
- Azizi, S.; Awad, M.M.; Ahmadloo, E. Prediction of water holdup in vertical and inclined oil-water two-phase flow using artificial neural network. Int. J. Multiph. Flow 2016, 80, 181–187. [Google Scholar] [CrossRef]
- Wu, Y.; Guo, H.; Song, H.; Deng, R. Fuzzy inference system application for oil-water flow patterns identification. Energy 2022, 239, 122359. [Google Scholar] [CrossRef]
- Hernández-Salazar, C.A.; Carreño-Verdugo, A.; González-Estrada, O.A. Prediction of the volume fraction of liquid- liquid two-phase flow in horizontal pipes using Long-Short Term Memory Networks. Rev. UIS Ing. 2024, 23, 19–32. [Google Scholar] [CrossRef]
- Ruiz-Díaz, C.M.; Quispe-Suarez, B.; González-Estrada, O.A. Two-phase oil and water flow pattern identification in vertical pipes applying long short-term memory networks. Emergent Mater. 2024, 7, 1983–1995. [Google Scholar] [CrossRef]
- Ruiz-Díaz, C.M.; Perilla-Plata, E.E.; González-Estrada, O.A. Two-Phase Flow Pattern Identification in Vertical Pipes Using Transformer Neural Networks. Inventions 2024, 9, 15. [Google Scholar] [CrossRef]
- Ruiz-Diaz, C.M.; Hernández-Cely, M.M.; González-Estrada, O.A. Analysis of liquid-liquid (water and oil) two-phase flow in vertical pipes, applying artificial intelligence techniques. J. Phys. Conf. Ser. 2021, 2046, 012016. [Google Scholar] [CrossRef]
- Cornejo Caceres, J.S.; Prieto, N.; Gonzalez, G.; Chaves-Guerrero, A. Numerical Simulation of a Natural Gas Cylindrical Cyclone Separator Using Computational Fluid Dynamics. Ind. Eng. Chem. Res. 2019, 58, 14323–14332. [Google Scholar] [CrossRef]
- Al-yaari, M.A.; Abu-sharkh, B.F. CFD Prediction of Stratified Oil-Water Flow in a Horizontal Pipe. Asian Trans. Eng. 2011, 1, 68–75. [Google Scholar]
- Kang, Q.; Gu, J.; Qi, X.; Wu, T.; Wang, S.; Chen, S.; Wang, W.; Gong, J. Hydrodynamic modeling of oil–water stratified smooth two-phase turbulent flow in horizontal circular pipes. Energies 2021, 14, 5201. [Google Scholar] [CrossRef]
- Bochio, G.; Cely, M.M.H.; Teixeira, A.F.A.; Rodriguez, O.M.H. Experimental and numerical study of stratified viscous oil–water flow. AIChE J. 2021, 67, e17239. [Google Scholar] [CrossRef]
- Desamala, A.B.; Dasmahapatra, A.K.; Mandal, T.K. Oil-Water Two-Phase Flow Characteristics in Horizontal Pipeline—A Comprehensive CFD Study. Int. J. Chem. Mol. Nucl. Mater. Metall. Eng. 2014, 8, 371–375. [Google Scholar]
- Shi, J.; Gourma, M.; Yeung, H. CFD simulation of horizontal oil-water flow with matched density and medium viscosity ratio in different flow regimes. J. Pet. Sci. Eng. 2017, 151, 373–383. [Google Scholar] [CrossRef]
- Shi, J.; Gourma, M.; Yeung, H. A CFD study on horizontal oil-water flow with high viscosity ratio. Chem. Eng. Sci. 2021, 229, 116097. [Google Scholar] [CrossRef]
- Walvekar, R.G.; Choong, T.S.Y.; Hussain, S.A.; Khalid, M.; Chuah, T.G. Numerical study of dispersed oil–water turbulent flow in horizontal tube. J. Pet. Sci. Eng. 2009, 65, 123–128. [Google Scholar] [CrossRef]
- Rashimi, W.; Choong, T.S.Y.; Chuah, T.G.; Hussain, S.A.; Khalid, M. Effect of Interphase Forces on Two-Phase Liquid-Liquid Flow in Horizontal Pipe. Inst. Eng. Malays. 2010, 71, 35–40. [Google Scholar]
- Parvini, M.; Dabir, B.; Mohtashami, S.A. Numerical Simulation of Oil Dispersions in Vertical Pipe Flow. J. Jpn. Pet. Inst. 2010, 53, 42–54. [Google Scholar] [CrossRef][Green Version]
- Burlutskiy, E.; Turangan, C.K. A computational fluid dynamics study on oil-in-water dispersion in vertical pipe flows. Chem. Eng. Res. Des. 2015, 93, 48–54. [Google Scholar] [CrossRef]
- Pouraria, H.; Kwan, J.; Kee, J. Numerical modelling of two-phase oil—Water flow patterns in a subsea pipeline. Ocean Eng. 2016, 115, 135–148. [Google Scholar] [CrossRef]
- Rodriguez, O.M.H.; Baldani, L.S. Journal of Petroleum Science and Engineering Prediction of pressure gradient and holdup in wavy stratified liquid—Liquid inclined pipe flow. J. Pet. Sci. Eng. 2012, 96–97, 140–151. [Google Scholar] [CrossRef]
- Hernández-Cely, M.M.; Ruiz-Díaz, C. Estudio de los fluidos aceite-agua a través del sensor basado en la permitividad eléctrica del patrón de fluido. Rev. UIS Ing. 2020, 19, 177–186. [Google Scholar] [CrossRef]
- González, G.; Prieto, N.; Mercado, I. Large Eddy Simulation (LES) Aplicado a un lecho fluidizado gas—Sólido. Parte I: Reactor a escala de laboratorio. Rev. UIS Ing. 2018, 17, 93–104. [Google Scholar] [CrossRef]
- Al-Wahaibi, T.; Smith, M.; Angeli, P. Transition between stratified and non-stratified horizontal oil–water flows. Part II: Mechanism of drop formation. Chem. Eng. Sci. 2007, 62, 2929–2940. [Google Scholar] [CrossRef]
- Rusche, H.; Issa, R.I. The effect of voidage on the drag force on particles, droplets and bubbles in dispersed two-phase flow. In Proceedings of the Japanese European Two-Phase Flow Meeting, Tshkuba, Japan, 25–29 September 2000. [Google Scholar]
- Rodriguez, O.M.H.; Rodriguez, I.H.; Ansoni, J.L. An experimental and numerical study on the wall lubrication force in dispersed liquid-liquid flow. Int. J. Multiph. Flow 2019, 120, 103094. [Google Scholar] [CrossRef]
- Brauner, N. The prediction of dispersed flows boundaries in liquid-liquid and gas-liquid systems. Int. J. Multiph. Flow 2001, 27, 885–910. [Google Scholar] [CrossRef]
- Shih, T.-H.; Liou, W.W.; Shabbir, A.; Yang, Z.; Zhu, J. A new k-ϵ eddy viscosity model for high reynolds number turbulent flows. Comput. Fluids 1995, 24, 227–238. [Google Scholar] [CrossRef]
- ANSYS Inc. ANSYS®Academic Research Mechanical, Release 21.1, Help System; ANSYS, Inc.: Canonsburg, PA, USA, 2021. [Google Scholar]
- Rudman, M. Volume-tracking methods for interfacial flow calculations. Int. J. Numer. Methods Fluids 1997, 24, 671–691. [Google Scholar] [CrossRef]






| Mesh | Number of Cells | Axial Vel. (m/s) | Error (%) |
|---|---|---|---|
| A | 24,000 | 1.509 | – |
| B | 70,200 | 1.532 | 1.53 |
| C | 153,600 | 1.504 | 1.82 |
| D | 285,000 | 1.572 | 4.51 |
| E | 475,200 | 1.589 | 1.11 |
| F | 735,000 | 1.598 | 0.56 |
| Experiment | Jw (m/s) | Jo (m/s) | Observed Pattern |
|---|---|---|---|
| 1 | 0.104 | 0.1 | ST |
| 2 | 0.304 | 0.215 | ST & MI |
| 3 | 0.724 | 0.223 | Do/w & w |
| 4 | 0.915 | 0.309 | Do/w & w |
| 5 | 1.106 | 0.115 | Do/w |
| 6 | 0.313 | 0.411 | Dw/o & o |
| 7 | 0.107 | 0.404 | Dw/o |
| Experiment | Flow Pattern | Run Time (h) | Water Holdup | ||
|---|---|---|---|---|---|
| Exp. | CFD | Error (%) | |||
| 1 | ST | ~24.5 | 0.385 | 0.256 | 33.51 |
| 2 | ST & MI | ~30.8 | 0.462 | 0.405 | 12.34 |
| 3 | Do/w & w | ~33.6 | 0.738 | 0.654 | 11.38 |
| 4 | Do/w & w | ~34.5 | 0.818 | 0.677 | 17.24 |
| 5 | Do/w | ~34.2 | 0.939 | 0.842 | 10.33 |
| 6 | Dw/o & o | ~38.2 | 0.385 | 0.377 | 2.08 |
| 7 | Dw/o | ~35.1 | 0.154 | 0.184 | 19.48 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
González-Estrada, O.A.; Hernández, S.; González-Silva, G. Modeling of Oil–Water Two-Phase Flow in Horizontal Pipes Using CFD for the Prediction of Flow Patterns. Eng 2024, 5, 3316-3334. https://doi.org/10.3390/eng5040173
González-Estrada OA, Hernández S, González-Silva G. Modeling of Oil–Water Two-Phase Flow in Horizontal Pipes Using CFD for the Prediction of Flow Patterns. Eng. 2024; 5(4):3316-3334. https://doi.org/10.3390/eng5040173
Chicago/Turabian StyleGonzález-Estrada, Octavio Andrés, Santiago Hernández, and Germán González-Silva. 2024. "Modeling of Oil–Water Two-Phase Flow in Horizontal Pipes Using CFD for the Prediction of Flow Patterns" Eng 5, no. 4: 3316-3334. https://doi.org/10.3390/eng5040173
APA StyleGonzález-Estrada, O. A., Hernández, S., & González-Silva, G. (2024). Modeling of Oil–Water Two-Phase Flow in Horizontal Pipes Using CFD for the Prediction of Flow Patterns. Eng, 5(4), 3316-3334. https://doi.org/10.3390/eng5040173








