On the Game-Based Approach to Optimal Design

Abstract

A game problem of structural design is defined as a problem of playing against external circumstances. There are two classes of players, namely the “ordinal” and “cardinal” players. The ordinal players, designated as the “operator” and “nature”, endeavor to, respectively, minimize or maximize the payoff function, operating within the constraints of limited resources. The fundamental premise of this study is that the action of player “nature” is a priori unknown. Statistical decision theory addresses decision-making scenarios where these probabilities, whether or not they are known, must be considered. The solution to the substratum game is expressed as a value of the game “against nature”. The structural optimization extension of the game considers the value of the game “against nature” as the function of certain parameters. Thus, the value of the game is contingent upon the design parameters. The cardinal players, “designers”, choose the design parameters. There are two formulations of optimization. For the single cardinal player, the pursuit of the maximum and minimum values of the game reduces the problem of optimal design. In the second formulation, there are multiple cardinal players with conflicting objectives. Accordingly, the superstratum game emerges, which addresses the interests of the superstratum players. Finally, the optimal design problems for games with closed forms are presented. The game formulations could be applied for optimal design with uncertain loading, considering “nature” as the source of uncertainty.

1. Introduction

1.1. The overarching objective of optimal structural design theory is to identify a structure that optimizes a specific mechanical characteristic while adhering to the prescribed constraints. In the classical optimal design problem, there is a single decision-maker, or “designer”, who must consider the shapes, sizes, material properties, and mutual positions of the structural members. These parameters are referred to as design parameters. Additionally, the conditions of exploitation and external actions on the structure must be defined.

The scalar and vector problems are commonly studied in structural optimization. The goal of scalar design optimization is to select the values of the design variables, given various constraints, so that a single objective function reaches an extreme value. A characteristic feature of such multi-criteria optimization problems is the occurrence of objective conflict, i.e., none of the feasible solutions allows for the simultaneous minimization of all objectives or the individual solutions of each individual objective function differ. Consequently, multiobjective optimization deals with all kinds of conflicting problems, (Section 1.2 in [1]). In the current context, the scalar optimization formulation is represented by an antagonistic game formulation. Analogously, the vector optimization formulation corresponds to the bi-matrix game. Each of the two players has its own payoff matrix. These concepts will be discussed in detail later.

1.2. Game theory is a framework for understanding situations of conflict and cooperation between rational decision-makers. It builds on the ideas of mainstream decision theory and economics, which say that people act rationally when they choose actions that maximize their payoff, given the constraints they face. The field of game theory is primarily concerned with the logical foundations of decision-making processes in situations where the outcome is contingent upon the actions of two or more autonomous agents. A crucial aspect of such scenarios is that each decision-maker possesses only partial control over the resulting outcomes. The phrase “the theory of interdependent decision-making” more accurately encapsulates the core tenets of the theory. Game theory pertains to situations wherein the options at the disposal of each decision-maker and their potential consequences are clearly delineated, and each decision-maker exhibits consistent preferences regarding the prospective outcomes. The primary objective of game theory is to identify solutions to games. Matrix games are two-person games with finite strategy sets. A matrix game with the matrix $\mathit{A}=\{a_{ij}$} of size $m\times n$ is a zero-sum game with two players. In classical game theory, the coefficients of the payoff matrix are the given fixed values. The first player has $m$ strategies. This player is referred to as “nature” in the current context. The opposite player has $n$ strategies. In this context, the second player is called “operator”. The payoff function of the first player is defined by $a_{i,j}$. The payoff function of the second player is defined by $-a_{i,j}$. The first player selects a row$i$ of the matrix and wants to maximize $a_{i,j}$, while the opponent second player selects a column $j$ of the matrix and wants to minimize $a_{i,j}$. A matrix game is a zero-sum game, which means that, when the strategies of row and column players are fixed, the sum of the payoffs for the two players is zero.

The most important theorem in matrix games is Neumann’s minimax theorem [2]. Neumann’s theorem was proved using Brouwer’s fixed point theorem. Another proof from 1944 was based on dual linear programming [3]. A solution is defined as a set of criteria that delineates the decision to be made and the subsequent outcome that will be reached if the decision-makers adhere to the established rationality criteria. One potential approach to structural optimal design can be formulated as follows. External actions are suboptimal in that they result in the greatest stress intensity, maximal deflection, or highest level of fracture. In game theory, the term “payoff function” is typically used in place of the “aim function”, which is the goal of the optimal design problem. Game theory is concerned with analyzing the conflict situations in which the participants are conscious and rational beings trying to achieve a certain goal. However, in many cases, one of the participants cannot be considered a conscious individual with preferences and goals. Consequently, the other players cannot assume that this participant will behave rationally.

1.3. The application of game theory to optimal design is a long-standing field of study. It has been demonstrated [4] that the role of the payoff function in ensuring integral compliance can be expressed in terms of the minimal eigenvalue of the inverse operator of the system (continual case) or the response matrix (discrete case). This is a fundamental characteristic of the game, and it is, therefore, referred to as the upper game value. A game-theoretic approach to robust topological optimization with uncertain loading is illustrated using three different games for the design of both two-dimensional and three-dimensional structures.

1.4. For optimization purposes, the payoff matrix is modified by the player “designer” acting according to the “cardinal” strategy. The alteration is made in favor of the player who receives the winnings. Once the “substratum” game has commenced, it is no longer possible to modify the payout matrix. The degrees of freedom of the “cardinal” players are known under the same names as those used in classical structural optimization. The degrees of freedom of the “cardinal” players are identified as “control functions” or “design parameters”. In the event that there is only one “cardinal” player, no conflict of interest arises. In the event that there are multiple “cardinal” players with disparate interests, a situation of conflict may arise. The aforementioned conflict gives rise to the “superstratum” game on the upper level. This scenario is typical in the field of engineering. For example, the objective of the system designer is to achieve the optimal performance of the system. The production designer seeks to implement the system in the most effective and cost-efficient manner. The operating ecology manager aims to ensure the lowest emission level during the system’s operational phase. The production ecology manager recognizes the necessity of reducing emissions during the manufacturing stage. Ultimately, the customer strives to minimize the system’s overall cost and operational expenses. However, these objectives are not always aligned, leading to potential conflicts among the “cardinal players”.

1.5. The term “stratified game” can be more easily defined by reference to the concept of matrix games. The typical game formulations utilize a fixed game matrix. The objective of the game is to identify the optimal strategies for the players, given the predefined and unchanging game matrix. In light of the aforementioned statements, the term “stratified game” is defined as a game formulation with a controllable value. In a stratified game, the elements of the matrix are predefined functions of the design parameters. Accordingly, the value of the game is a function of the design parameters. The value of the game is the result of the lower-level (substratum) game task for each fixed set of design parameters. The determination of the maximum value of the game value as a function of the design parameters is the upper-level (superstratum) task. For an upper-level task, the methods of optimization or control theories are applied. The occurrence of these two levels leads to the term “stratified game”.

The mentioned line of reasoning can be applied to diverse optimization problems that involve multiple levels of decision-making. To illustrate, lawmakers can be considered the “superstratum” of a social game. The actions of the superstratum players shape the governing equations of the game, such as those related to taxation or ecological laws. Meanwhile, the players in the “substratum” adhere to the legislation that defines their objectives and the associated modus vivendi.

1.6. There is a fundamental difference between the concepts of game theory in social sciences and operations theory on the one hand, and in engineering and natural sciences on the other. The difference lies in the understanding of the resource limits of the game players. It is possible to examine the issue of resource constraints from the perspective of functional analysis. In functional analysis and related areas of mathematics, a sequence space is a vector space whose elements are infinite sequences of real or complex numbers. $L_p$-norm is a norm on the space of $p$-integrable functions [5]. These are special cases of $L_p$ spaces for the counting measure on the set of natural numbers. The most important sequence spaces in the analysis are the $l_p$ spaces, which consist of sequences summable to the $p$-th power with the p-norm. $l_p$-norm denotes the norm in the space of $p$-summable sequences.

The total resources in social sciences and operations theory are the linear sum of the partial resources of each player. For example, the bank account represents the total amount of money of the player. Each element of the sequence is the transaction to or from the account. That is, the actual state of the account is the linear sum of sequences. Each operation is the linear addition of some amount of money. The power $p$ in the sequences that arise in the usual game theory of social sciences is one. The summation of probabilities in the decision-making theory is linear per definition as well. The corresponding game theory with linearly summed resources (i.e., $p=1$) is fully established in well-known works [2,3] and does not require revision or extension.

The application of game-theoretic methods to problems of a physical nature presents a different situation. The total resources in engineering and science are the quadratic sum of the partial resources of each player (i.e., $p=2$). The Euclidean norm, standard norm, or 2-norm is a vector norm commonly used in science and engineering. In two- and three-dimensional Euclidean space, the Euclidean norm corresponds to the visual length or magnitude of a vector and can be calculated using the Pythagorean theorem. More generally, the Euclidean norm is also defined for real and complex vector spaces of arbitrary finite dimension and is then the norm derived from the standard scalar product. For example, the total energy of vibration is composed of a sequence of vibrational modes. From the viewpoint of the sequence space concept, each element of the sequence is the energy of a vibrational mode. The total energy is the quadratic sum of the partial energies of each mode. That is, the total energetic resource is the quadratic sum of sequences. The power $p$ in the sequences arising in the common game theory for engineering and science is two. The possible applications of quadratic sequences to the quadratic estimation of energy are numerous. The Poynting vector represents the directional energy flux (the energy transfer per unit area, per unit time) or power flux of an electromagnetic field. The intensity of an electromagnetic wave is the average of the squares of the sinusoidal functions for each mode. The quadratic summation of sequences is widely used in the natural sciences and is used to evaluate the energy of seismic waves and the energy of wind and ocean currents and to calculate the elastic deformation energy of external excitations. In light of the application of game theory in engineering, it is necessary to revisit the concept of resource limitation, which should be revised from a linear summation to a quadratic one.

1.7. In summary, the tasks of the study and the central ideas for their solution are the following.

• The fundamental premise of this study is that the probability distribution governing nature’s “choice” of states remains unknown. Statistical decision theory addresses decision-making scenarios where these probabilities, whether objective or subjective, are pertinent factors;
• In classical structural optimization, the “cardinal” players are responsible for assuming the role of “design parameters” or “control functions”. If the number of design freedoms is finite, one speaks about “design parameters”. For the continuous design freedom, the “control functions” are involved according to Pontryagin’s maximum principle [6]. In an actual context, the “cardinal” players modify the governing equations and payoff functions in the game formulations [1]. In structural optimization, the “cardinal” players are responsible for determining the coefficients of the governing equations. In essence, their function is to establish the rules of engagement, which may result in conflict between certain players. In the context of the stratified game approach, the “cardinal” players form the “superstratum”, or the upper level of the game. The “cardinal payers” are designated as “designers” due to their capacity to alter, for instance, the coefficients of matrices in matrix games with the objective of attaining a superior value for the game;
• Furthermore, other participants act in accordance with the governing equations, which are determined by the “cardinal” players. In the context of the stratified game approach, the “ordinal” players represent the “substratum”. “Ordinal” players are permitted to make decisions within their respective stratum, but they are unable to impact the governing equations. The “ordinal” payers could be referred to as “nature” or “operators”. Certain “ordinal” participants represent the external forces. These external factors are typically referred to as “nature”. For the sake of clarity, it may be more appropriate to refer to nature’s strategies as “states” rather than strategies. Such games are, therefore, classified as “games against nature”. The remaining “ordinal” participants aim to offset the impact of “nature” in order to mitigate potential risks or to achieve the most favorable outcome [4]. For the sake of clarity, these participants will henceforth be referred to as “operators” and “nature”. In the case of an antagonistic matrix game, the payout matrix is only relevant for “operators”. The role of “cardinal players” is inherited from the common optimization formulations;
• The conflict between the two “ordinal” players, namely “nature” and “operators”, is studied for the linearly summed resources using the common principles of game theory. This case is typical for interdependent decision-making in operational research and social games;
• The application of game formulations for problems of engineering and natural sciences assumes the quadratically summed resources of the ordinal players. The solutions of matrix and bi-matrix games with quadratically summed resources are essential for the application of a game-theoretical approach to engineering and physical tasks.

1.8. The following summarizes the results of the current study.

• In the matrix game, there is a single payoff matrix. From the perspective of optimization theory, there is a single objective function. In consequence, the optimization problem is of a scalar nature. This value represents the goal function of the matrix game. At the low-level (substratum level), the win of “nature” is the loss of the “operator” This game is antagonistic, with a single goal function. The theory of quadratically constrained matrix and bi-matrix games is presented in Section 2 and Section 3;
• The solution of the stratified matrix game is presented in Section 2. In a bi-matrix game, payoff matrices are employed. From the perspective of optimization theory, there are two distinct goal functions. The optimization problem is of a vector type. These goal functions are derived from the solution of a bi-matrix game. The equilibrium between the interests of “nature” and “operator” results in a solution to the game at the lower level. The designer determines the optimal value for the goal function in accordance with the methods of vector optimization. The solution of the stratified bi-matrix game is presented in Section 3;
• In Section 4, the results of the aforementioned sections are generalized for self-adjoint positive definite differential operators. The optimization of elastic energy was selected as an example of an optimization task with a closed form of solution. The action of “Nature” is the external load. The load that results in the greatest structural response among all permissible loads and represents the strategy of “nature” in low-level tasks. The upper value of the game could be determined in all cases. The third player, the “designer”, acts on the upper level. The “Designer” determines the optimal value for the aforementioned goal function, manipulating the “design variables”. The designer optimizes the upper value, creating a stiffer structural element for the most dangerous action of “nature”. The corresponding examples are given in Section 4, Section 5, Section 6 and Section 7;
• For a special type of game with stored energy, the value of the game is shown to be equal to the eigenvalue of the structural matrix. The optimal strategies of the “operator” and “nature” are uniquely determined. In the simplest formulation, the resources of the “operator” are limited to zero. In this case, there is no opposite reaction to all possible actions of “nature” on the lower level. In this case, the role of the opposite player takes the cardinal player, the “designer”. The “designer” modifies the coefficients of the payoff matrix, while “nature” alters both the left and right vectors of the payoff function;
• The application of the aforementioned considerations to structural optimization problems will be discussed in the following sections. Section 5 and Section 6 demonstrate the applications of the developed technique for structural optimization problems with continuous control functions. In Section 5, the beam is subjected to arbitrary bending efforts, and the designer determines the optimal beam shape for resisting these forces. In Section 6, the rod is subjected to arbitrary twist moments, and the designer determines the optimal design of the twisted bar, ensuring the greatest stiffness;
• Section 7 presents a mathematical analysis of the solutions presented in Section 5 and Section 6, employing the tools of inequalities theory to elucidate the underlying mathematical principles of the PARETO and NASH fronts.

2. Antagonistic Matrix Stratified Games

2.1. This section contains basic information from the theory of finite antagonistic (matrix) games. The existence theorem of the equilibrium situation in the class of mixed strategies, the properties of optimal mixed strategies, and methods for solving matrix games are well-established areas of research.

The study of game theory commences with the most basic static model, namely a matrix game in which two players engage, the set of strategies available to each player is finite, and the gain of one player is equal to the loss of the other:

$${\Gamma }_{K\left[\mathit{a}\right]}=(X,Y,K[\mathit{a}\left]\right),$$

(1)

where $X$ and $Y$ are nonempty sets, and the function $K\left[\mathit{a}\right] : X\times Y \to R^1$ is called an antagonistic stratified game in normal form. The elements $x \in X$ and $y \in Y$ are called the strategies of ordinal players 1 and 2, respectively, in the game ${\Gamma }_{K\left[\mathit{a}\right]}$. The elements of the Cartesian product $X\times Y$ (i.e., the pair of strategies $(x, y)$ where $x \in X$ and $y \in Y$) are situations, and the function $K\left[\mathit{a}\right]$ is the win function of player 1. The payoff of player 2 in situation $(x, y)$ is assumed to be equal to $[-K[\mathit{a}\left]\right(x, y\left)\right]$. Therefore, the function $K\left[\mathit{a}\right]$ is also called the win function of game ${\Gamma }_{K\left[\mathit{a}\right]}$ itself, and game ${\Gamma }_{K\left[\mathit{a}\right]}$ is called a zero-sum game.

Thus, using the accepted terminology to define game ${\Gamma }_{K\left[\mathit{a}\right]}$, it is necessary to define the sets of strategies $X, Y$ of ordinal players 1 and 2 and also the winning function $K\left[\mathit{a}\right]$, defined on the set of all situations $X\times Y$.

The stratified game ${\Gamma }_{K\left[\mathit{a}\right]}$ is interpreted as follows. Ordinal players simultaneously and independently choose strategies $x \in X, y \in Y$. In the substratum game, ordinal player 1 then receives a payoff equal to $K\left[\mathit{a}\right](x, y)$, and ordinal player 2 receives $(-K[\mathit{a}\left]\right(x, y\left)\right).$ The elements $\mathit{a} \in \mathsf{A}$ are called the strategies of cardinal players in the stratified game ${\Gamma }_{K\left[\mathit{a}\right]}$.

In a stratified game, the elements $\mathit{a} \in \mathsf{A}$ are referred to as the strategies of cardinal players. The superstratum game pertains to the strategies for cardinal players $\mathit{a}$ that ensure the maximal and minimal values of the substratum payoff function. When there is only one cardinal player, the superstratum game reduces to the optimization problem. In contrast, when there are two or more cardinal players, their interests may be in opposition, resulting in what is known as an antagonistic game. The total payoff for both ordinal players on the lower level is zero. The goal function on the upper level is the payoff of the oppositely acting ordinal players, e.g., the “nature” and “operator”. This objective function is modified by the “designer” at the upper level.

2.2. The following definition is proposed: antagonistic games in which both ordinal players possess finite strategy sets are designated as substratum matrix games.

In the matrix game, ordinal player 1 is assumed to have only $m$ strategies. The set of strategies available to the first ordinal player, $X$, must be ordered [7,8]. That is, a one-to-one correspondence must be established between $X$ and $M=\{1, 2, \dots , m\}$. The same process must be repeated for the second ordinal player, with $N=\{1, 2, \dots , n\}$ and $Y$. The sets $M$ and $N$ are then ordered in a one-to-one correspondence with $X$ and $Y$, respectively, where $M$ and $N$ are finite sets of the cardinalities $m$ and $n$, respectively.

The substratum matrix game $\Gamma$ is thus completely defined by the matrix $\mathit{A}=\mathit{A}\left[\mathit{a}\right]$, where $\mathit{A}$ is defined as follows:

$$\mathit{A}=\left\{a_{ij}\right\},$$

(2)

where:

$$\begin{array}{c}{a}_{ij}=K\left(x_i,y_j\right)\\ \begin{array}{cc}\left(x_i,y_j\right)\in X\times Y,& \left(i,j\right)\in M\times N,\end{array}\\ \begin{array}{cc}i\in M,& j\in N\end{array}. \end{array}$$

This is the rationale behind the name of the game, which is derived from the aforementioned matrix. In this instance, the game $\Gamma$ is realized as follows. Player 1 selects a row, $i \in M$, and player 2 (simultaneously with player 1 and independently of him) chooses a column,$j \in N$. Ordinal player 1 then receives a payoff, $a_{ij}$, and ordinal player 2 receives $-a_{ij}$. In the event that the payoff is a negative number, it constitutes an actual loss for the ordinal player.

We denote the substratum game $\Gamma$ with win matrix $\mathit{A}\left[\mathit{a}\right]$ by ${\Gamma }_{A\left[\mathit{a}\right]}$ and refer to it as an $(m\times n)-$ game, in accordance with the dimensions of matrix $\mathit{A}\left[\mathit{a}\right]$ with the fixed values of strategies for cardinal players $\mathit{a}$.

2.3. The question of the optimal behavior of players in an antagonistic game is worthy of consideration. It is reasonable to conclude that a situation $(x^{*},y^{*})$ in the game ${\Gamma }_{K\left[\mathit{a}\right]}=(X, Y, K[\mathit{a}\left]\right)$ is optimal if deviating from it is not favorable for any of the players. Such a situation $(x^{*},y^{*})$ is referred to as an equilibrium, and the optimality principle based on the construction of an equilibrium situation is known as the equilibrium principle.

For an equilibrium situation to exist in substratum game ${\Gamma }_{K\left[\mathit{a}\right]}=(X, Y,K[\mathit{a}\left]\right)$, it is necessary and sufficient that there exist a minimax and a maximin:

$$\underset{y}{\min } \underset{x}{\sup } K\left[\mathit{a}\right](x,y), \underset{x}{\max } \underset{y}{\inf } K\left[\mathit{a}\right](x,y),$$

and the equality is satisfied:

$$v^{*}\left[\mathit{a}\right]=\underset{y}{\min } \underset{x}{\sup } K\left[\mathit{a}\right](x,y)=\underset{x}{\max } \underset{y}{\inf } K\left[\mathit{a}\right](x,y)=v^{**}\left[\mathit{a}\right].$$

(3)

Equation (3) establishes a connection between the equilibrium principle and the minimax and maximin principles in an antagonistic game. Games in which equilibrium situations exist are called well-defined games. Therefore, this theorem establishes a criterion for a well-defined game and can be reformulated as follows. For a game to be well-defined, it is necessary and sufficient that there exist $\mathrm{m}\mathrm{i}\mathrm{n} \mathrm{s}\mathrm{u}\mathrm{p}$ and $\mathrm{m}\mathrm{a}\mathrm{x} \mathrm{i}\mathrm{n}\mathrm{f}$ in Equation (3), and the equality in minimax is satisfied.

If there exists an equilibrium situation, then the minimax is equal to the maximin. According to the definition of the equilibrium situation, each player can communicate his optimal (maximin) strategy to the opponent, and neither player can obtain an additional benefit from it.

2.4. Now, suppose that there is no equilibrium situation in the substratum game ${\Gamma }_{A\left[\mathit{a}\right]}$. Since a random variable is characterized by its distribution, we will further identify a mixed strategy with a probability distribution on the set of pure strategies of ordinal players. Thus, the mixed strategy $x$ of ordinal player 1 in the substratum game is an $m$-dimensional vector, which is constrained by the following equation:

$$\mathit{x}=\left({\xi }_1,\dots ,{\xi }_m\right),{ ‖\mathit{x}‖}_{p,m}=1.$$

(4)

where the $L^p$ norm in the real vector space ${\mathbb{R}}^q$ is defined as [5]:

$${ ‖\mathit{x}‖}_{p,q}\stackrel{\scriptscriptstyle\mathrm{def}}{=}{\left({\sum }_{i=1}^q{{\xi }_i}^p\right)}^{1/p}.$$

(5)

Similarly, the mixed strategy y of player 2 is an $n$-dimensional vector:

$$\mathit{y}=\left({\eta }_1,\dots ,{\eta }_n\right),{ ‖\mathit{y}‖}_{p,n}=1.$$

(6)

The positive natural number $p$ determines the class of the game. Note that the numbers n and m must not equal.

2.5. If $p=1$, the values ${\xi }_i\ge 0$ and ${\eta }_i\ge 0$ are the probabilities of choosing pure strategies $i \in M$ and$j \in N$, respectively, when ordinal players use mixed strategies $x$ and $y$. Let us denote by $X$ and $Y$ the sets of mixed strategies of the first and second players, respectively. It is easy to see that the set of mixed strategies of each player is a compact in the corresponding finite-dimensional Euclidean space (a closed, bounded set). A mixed set represents an extension of the pure strategy space available to the player. An arbitrary matrix game is well-defined within the class of mixed random strategies. The von Neumann theorem of matrix games states that in the case $p=1,$every matrix game has an equilibrium situation within the context of mixed strategies [7]. The cited literature provides an overview of the methods used to evaluate game values. The setting $p=1$ is typical for the application of game theory fields of economics, political science, and the social sciences. This setting reflects the fact that the mixed strategy for ordinal players is simply a probability distribution over their pure strategies. The probability of any event must be positive, and the total probability of all events must be one. Consequently, any mixed strategy must adhere to the following conditions:

$$\begin{array}{cc}{‖\mathit{x}‖}_{1,m}=1,& {‖\mathit{y}‖}_{1,m}=1.\end{array}$$

2.6. If $p=2$, the values ${\xi }_i$ and ${\eta }_i$ are the Euclidian coordinates of vector strategies $\mathit{x}$, $\mathit{y}$ of the ordinal players. The Euclidean length of a vector $\mathit{x},\mathit{y}$ in the real vector spaces ${\mathbb{R}}^n$ and ${\mathbb{R}}^m$ are given by their Euclidean norms:

$${ ‖\mathit{x}‖}_{2,m}\equiv {\left({\sum }_{i=1}^m{{\xi }_i}^2\right)}^{{\displaystyle \frac{1}{2}}}, { ‖\mathit{y}‖}_{2,n}\equiv {\left({\sum }_{i=1}^n{{\eta }_i}^2\right)}^{1/2}.$$

(7)

As illustrated in the aforementioned examples, this scenario is typical in the game formulations of engineering and physical applications. In such applications, the module of actions for the ordinal players is restricted. The modules of strategy vectors are less than or equal to one:

$$\begin{array}{cc}{‖\mathit{x}‖}_{2,m}\le 1,& {‖\mathit{y}‖}_{2,n}\le 1.\end{array}$$

(8)

With definitions (4) and (5), the payoff function of the matrix game on the lower substratum level reads:

$$\mathcal{I}\left[\mathit{x},\mathit{y},\mathit{a}\right]={\displaystyle \frac{1}{2}}〈\mathit{A}\left[\mathit{a}\right]\mathit{x},\mathit{y}〉.$$

(9)

The Lagrangian combines the payoff function (9) with the constraints (8), taken with the non-negative multipliers $\lambda ,\mathsf{\mu }$:

$$\mathcal{L}\left[\mathit{x},\mathit{y},\mathit{a}\right]\stackrel{\scriptscriptstyle\mathrm{def}}{=}\mathcal{I}\left[\mathit{x},\mathit{y},\mathit{a}\right]+\lambda \left({‖\mathit{x}‖}_{2,m}-1\right)+\mathsf{\mu }\left({‖\mathit{y}‖}_{2,n}-1\right).$$

(10)

For the payoff function (9) with the conditions (8), the equilibrium state $\left({\mathit{x}}^{\mathbf{*}},{\mathit{y}}^{\mathbf{*}}\right)$ satisfies the equations:

$$\begin{array}{cc}{\displaystyle \frac{\partial \mathcal{L}}{\partial \mathit{x}}}\equiv {\mathit{A}}^{\mathit{T}}\left[\mathit{a}\right]\mathit{y}+\lambda \mathit{x}=0,& {\displaystyle \frac{\partial \mathcal{L}}{\partial \mathit{y}}}\equiv \mathit{A}\left[\mathit{a}\right]\mathit{x}+\mathsf{\mu }\mathit{y}=0.\end{array}$$

(11)

The resolution of Equation (11) reads:

$$\begin{array}{cc}\mathit{A}\left[\mathit{a}\right]{\mathit{A}}^T\left[\mathit{a}\right]\mathit{y}=\lambda \mathsf{\mu }\mathit{y},& {\mathit{A}}^T\left[\mathit{a}\right]\mathit{A}\left[\mathit{a}\right]\mathit{x}=\lambda \mathsf{\mu }\mathit{x}.\end{array}$$

(12)

The left sides of Equation (12) contain two auxiliary matrices:

$$\begin{array}{cc}{\mathcal{K}}_A\stackrel{\scriptscriptstyle\mathrm{def}}{=}{\mathit{A}}^T\left[\mathit{a}\right]\mathit{A}\left[\mathit{a}\right],& {\mathcal{K}}_B\stackrel{\scriptscriptstyle\mathrm{def}}{=}\mathit{A}\left[\mathit{a}\right]{\mathit{A}}^T\left[\mathit{a}\right]\end{array}.$$

The matrix ${\mathcal{K}}_A$ is an $m$ square Hermitian matrix. The matrix ${\mathcal{K}}_B$ is an $n$ square Hermitian matrix. A real symmetric matrix is Hermitian. A Hermitian matrix is always self-adjoint. It follows from (Theorem 2.8, Section 2.4 in [9]), that both matrices ${\mathcal{K}}_A$ and ${\mathcal{K}}_B$ have the same nonzero eigenvalues, counting multiplicity. The matrices ${\mathcal{K}}_A$ and ${\mathcal{K}}_B$ are positive-semidefinite (Theorem 7.3, Section 7.1 in [9]). The number of zero eigenvalues of ${\mathcal{K}}_A$ and ${\mathcal{K}}_B$ is at least $\left|\mathrm{m}-\mathrm{n}\right|$. Let ${\mathcal{K}}_1$ be the matrix with the smallest dimensions of ${\mathcal{K}}_A$ and ${\mathcal{K}}_B$. In other words,

$${\mathcal{K}}_1\stackrel{\scriptscriptstyle\mathrm{def}}{=}\left\{\begin{array}{cc}{\mathcal{K}}_A& \mathrm{if} m\le n,\\ {\mathcal{K}}_B& \mathrm{if} m>n.\end{array}\right.$$

Generally saying, the matrix ${\mathcal{K}}_1$ is positive-semidefinite. The eigenvalues of matrix ${\mathcal{K}}_1$ are:

$$\begin{array}{c}{\mathbb{L}}_i=\mathrm{e}\mathrm{i}\mathrm{g}\mathrm{e}\mathrm{n}\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e}\mathrm{s}\left({\mathcal{K}}_2\right)\ge 0,\\ i=1,\dots ,j,\\ j\stackrel{\scriptscriptstyle\mathrm{def}}{=}\mathrm{m}\mathrm{i}\mathrm{n}\left(m,n\right).\end{array}$$

(13)

If $m=n$, then the matrices are equal ${\mathcal{K}}_A$ = ${\mathcal{K}}_B$ and have the same set of eigenvalues.

If ${\mathcal{K}}_1$ is positive definite, the number of its zero eigenvalues is exactly $\left|\mathrm{m}-\mathrm{n}\right|$. The eigenvalues of the positive definite matrix ${\mathcal{K}}_S$ are:

$$\begin{array}{c}{\mathbb{L}}_i=\mathrm{e}\mathrm{i}\mathrm{g}\mathrm{e}\mathrm{n}\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e}\mathrm{s}\left({\mathcal{K}}_1\right)>0,\\ i=1,\dots ,j,\\ j\stackrel{\scriptscriptstyle\mathrm{def}}{=}\mathrm{m}\mathrm{i}\mathrm{n}\left(m,n\right).\end{array}$$

From Equation (12), it follows that ${\lambda }_i{\mathsf{\mu }}_i={\mathbb{L}}_i$. Finally,

$${\lambda }_i{=\mathsf{\mu }}_i=\sqrt{{\mathbb{L}}_i}, i=1,\dots ,j.$$

(14)

Consequently, every matrix quadratic game possesses the equilibrium situation within the context of mixed strategies.

2.7. In this section, the solution (14) to the substratum matrix game with constrained actions (Equations (4), (6) and (8)) is identified. The objective of the superstratum task is to determine the optimal solution for the “designer” by searching for the extremal value of (14) through a manipulation of the design variables [10].

If the resources available to both players are identical, as illustrated in Equation (8), the resulting total payoff is zero. In the event that player $\mathit{x}$ possesses a greater quantity of resources than player $\mathit{y}$, the possibilities available to them are subject to different constraints: ${‖\mathit{x}‖}_{2,m}>{‖\mathit{y}‖}_{2,n}$. In this case, the “designer”, who shares similar interests with the “operator”, attempts to minimize the maximum potential damage. The maximal potential damage is represented by the maximal eigenvalue ${\mathbb{L}}_j$ with a negative sign. Consequently, the objective is to minimize the maximal eigenvalue, ${\mathbb{L}}_j\left[\mathit{a}\right]$.

In the case that player $\mathit{x}$ holds fewer resources, than player $\mathit{y}$, we get the following inequality: ${‖\mathit{x}‖}_{2,m}<{‖\mathit{y}‖}_{2,n}$. The designer will ensure that the payoff is guaranteed to be certain outcome, regardless of the potential actions of the first player $\mathit{x}$, designated as “nature”. The equilibrium point is identified as the minimal positive eigenvalue ${\mathbb{L}}_1$. In this case the objective of “designer” is to maximize the minimal eigenvalue, ${\mathbb{L}}_1\left[\mathit{a}\right]$. This latter scenario will be the focus of subsequent analysis.

3. Bi-Matrix Stratified Games

3.1. In game theory, a bi-matrix game is defined as a simultaneous game for two players, each of whom has a finite set of possible actions. Such a game can be represented by two matrices: matrix $\mathit{A}$, which outlines the payoffs for ordinal player 1, and matrix $\mathit{B}$, which outlines the payoffs for ordinal player 2. The substratum bi-matrix game deals with two $m\times n$ matrices, $\mathit{A}\left[\mathit{a}\right]$ and $\mathit{B}\left[\mathit{a}\right]$, whose elements depend parametrically upon the design vector $\mathit{a}$ of the cardinal players. For the fixed values of strategies for cardinal players $\mathit{a}$, the wins of the first and second ordinal players are, correspondingly:

$$\begin{array}{cc}{\mathcal{I}}_1\left[\mathit{x},\mathit{y},\mathit{a}\right]={\displaystyle \frac{1}{2}}〈\mathit{A}\left[\mathit{a}\right] \mathit{x},\mathit{y}〉,& {\mathcal{I}}_2\left[\mathit{x},\mathit{y},\mathit{a}\right]={\displaystyle \frac{1}{2}}〈\mathit{B}\left[\mathit{a}\right] \mathit{x},\mathit{y}〉\end{array}.$$

(15)

The mixed strategies of both ordinal players at the substratum level of the game are vectors, which are constrained by the following equations:

$$\begin{array}{cc}\mathit{x}=\left({\xi }_1,\dots ,{\xi }_m\right),& {‖\mathit{x}‖}_{p,m}=1,\\ \mathit{y}=\left({\eta }_1,\dots ,{\eta }_n\right),& {‖\mathit{y}‖}_{p,n}=1.\end{array}$$

(16)

3.2. It is well known that, for $p=1$, the bi-matrix game has an equilibrium in randomized strategy [7,8,11]. Thus, the linear case does not require further investigation.

3.3. In the vector case $p=2$, the substratum bi-matrix game has an equilibrium solution, which reduces to the generalized eigenvalue problem [12,13]. We study the following bi-matrix game:

$$\underset{x}{\max } {\mathcal{I}}_1\left[\mathit{x},\mathit{y},\mathit{a}\right] \mathrm{subject} \mathrm{to} {\mathcal{I}}_2\left[\mathit{x},\mathit{y},\mathit{a}\right]\ge 1 \mathrm{for} \mathrm{all} \mathit{y}.$$

(17)

According to the generalized Rayleigh–Ritz quotient method [14], this optimization problem can be restated as:

$$\underset{x}{\min } \underset{y}{\max } {\displaystyle \frac{{\mathcal{I}}_1\left[\mathit{x},\mathit{y},\mathit{a}\right]}{{\mathcal{I}}_2\left[\mathit{x},\mathit{y},\mathit{a}\right]}}.$$

(18)

The Lagrangian for (17) reads:

$$\mathcal{L}\left[\mathit{x},\mathit{y},\mathit{a}\right]\stackrel{\scriptscriptstyle\mathrm{def}}{=}{\mathcal{I}}_1\left[\mathit{x},\mathit{y},\mathit{a}\right]+\lambda \left({ ‖\mathit{x}‖}_{2,m}-1\right)+\mathsf{\mu }\left({ ‖\mathit{y}‖}_{2,n}-1\right)+\Lambda \left({\mathcal{I}}_2\left[\mathit{x},\mathit{y},\mathit{a}\right]-1\right),$$

(19)

where $\lambda$, $\mathsf{\mu },\Lambda$ are the Lagrange multipliers. Equating the derivatives of $\mathcal{L}$ to zero gives:

$$\left\{\begin{array}{c}{\displaystyle \frac{\partial \mathcal{L}}{\partial \mathit{x}}}\equiv {\mathit{C}}^{\mathit{T}}\left[\mathit{a}\right]\mathit{y}+\lambda \mathit{x}=\mathbf{0},\\ {\displaystyle \frac{\partial \mathcal{L}}{\partial \mathit{y}}}\equiv \mathit{C}\left[\mathit{a}\right]\mathit{x}+\mathsf{\mu }\mathit{y}=\mathbf{0},\\ \mathit{C}\left[\mathit{a},\mathsf{\rho }\right]=\left(1-\Lambda \right)\mathit{A}\left[\mathit{a}\right]+\Lambda \mathit{B}\left[\mathit{a}\right].\end{array}\right.$$

(20)

The resolution of Equation (20) reads:

$$\left\{\begin{array}{c}{\mathcal{K}}_C\mathit{y}-\lambda \mathsf{\mu }\mathit{y}=\mathbf{0},\\ {\mathcal{K}}_D\mathit{x}-\lambda \mathsf{\mu }\mathit{x}=\mathbf{0}.\end{array}\right.$$

(21)

The symmetric semi-positive matrices in (21) are the following:

$$\left\{\begin{array}{c}{\mathcal{K}}_C\left[\mathit{a},\Lambda \right]\stackrel{\scriptscriptstyle\mathrm{def}}{=}\mathit{C} {\mathit{C}}^T\equiv {\left(1-\Lambda \right)}^2\mathit{A}{\mathit{A}}^{\mathit{T}}+\Lambda ·\left(1-\Lambda \right)\left(\mathit{A}{\mathit{B}}^{\mathit{T}}+\mathit{B}{\mathit{A}}^{\mathit{T}}\right)+{\Lambda }^2\mathit{B}{\mathit{B}}^{\mathit{T}},\\ {\mathcal{K}}_D\left[\mathit{a},\Lambda \right]\stackrel{\scriptscriptstyle\mathrm{def}}{=}{\mathit{C}}^T\mathit{C}\equiv {\left(1-\Lambda \right)}^2{\mathit{A}}^{\mathit{T}}\mathit{A}+\Lambda ·\left(1-\Lambda \right)\left({\mathit{B}}^{\mathit{T}}\mathit{A}+{\mathit{A}}^{\mathit{T}}\mathit{B}\right)+{\Lambda }^2{\mathit{B}}^{\mathit{T}}\mathit{B}.\end{array}\right.$$

For briefness, the auxiliary matrix ${\mathcal{K}}_2$ will be defined. This matrix represents the matrix with the smallest dimensions of ${\mathcal{K}}_C$ and ${\mathcal{K}}_D$. In other words,

$${\mathcal{K}}_2\left[\mathit{a},\rho \right]\stackrel{\scriptscriptstyle\mathrm{def}}{=}\left\{\begin{array}{cc}{\mathcal{K}}_C& \mathrm{if} m\le n,\\ {\mathcal{K}}_D& \mathrm{if} m>n.\end{array}\right.$$

The $\mathit{x},\mathit{y}$ are the eigenvectors, and the $\lambda =\mu$ are the non-zero eigenvalues of the symmetric semi-positive matrix ${\mathcal{K}}_2$:

$$\begin{array}{c}{\tilde{\mathbb{L}}}_i\stackrel{\scriptscriptstyle\mathrm{def}}{=}\mathrm{e}\mathrm{i}\mathrm{g}\mathrm{e}\mathrm{n}\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e}\mathrm{s}\left({\mathcal{K}}_2\right)\ge 0,\\ \begin{array}{ccc}{0\le \tilde{\mathbb{L}}}_1\le {\tilde{\mathbb{L}}}_2\le \dots \le {\tilde{\mathbb{L}}}_j,& {\tilde{\mathbb{L}}}_{\mathrm{m}\mathrm{i}\mathrm{n}}\stackrel{\scriptscriptstyle\mathrm{def}}{=}{\tilde{\mathbb{L}}}_1,& {\tilde{\mathbb{L}}}_{\mathrm{m}\mathrm{a}\mathrm{x}}\stackrel{\scriptscriptstyle\mathrm{def}}{=}{\tilde{\mathbb{L}}}_j,\end{array}\\ \begin{array}{cc}i=1,\dots ,j,& j\stackrel{\scriptscriptstyle\mathrm{def}}{=}\mathrm{m}\mathrm{i}\mathrm{n}\left(m,n\right).\end{array}\end{array}$$

(22)

The eigenvalues depend parametrically upon the strategies for cardinal players $\mathit{a}$ and the parameter $\Lambda$ of Equation (20):

$${\tilde{\mathbb{L}}}_i={\tilde{\mathbb{L}}}_i\left(\mathit{a},\Lambda \right).$$

(23)

The eigenvectors $\mathit{x},\mathit{y}$ are the functions of these parameters as well. The parameter $\Lambda$ plays the role of Lagrange multiplier. It parametrizes the front of the bi-matrix game. If the second player fixes its payoff in Equation (17) to ${\mathcal{I}}_2\left[\mathit{x},\mathit{y},\mathit{a}\right]=1$, the value of the Lagrange multiplier ${\Lambda }^{*}$ follows from this constraint. If Equation (17) displays a maximization problem, the eigenvector is the one with the largest eigenvalue of matrix ${\mathcal{K}}_2$:

$${\tilde{\mathbb{L}}}_{\mathrm{m}\mathrm{a}\mathrm{x}}\left[\mathit{a},{\Lambda }^{*}\right]=\underset{\mathit{u}}{\max } {\displaystyle \frac{〈{\mathcal{K}}_2\left[\mathit{a},{\Lambda }^{*}\right]\mathit{u},\mathit{u}〉}{〈\mathit{u},\mathit{u}〉}}.$$

Alternatively, if Equation (17) is a minimization problem, the eigenvector is the one with the smallest eigenvalue:

$${\tilde{\mathbb{L}}}_{min}\left[\mathit{a},{\Lambda }^{*}\right]=\underset{\mathit{u}}{\min } {\displaystyle \frac{〈{\mathcal{K}}_2\left[\mathit{a},{\Lambda }^{*}\right]\mathit{u},\mathit{u}〉}{〈\mathit{u},\mathit{u}〉}}.$$

The payoff of the first player satisfies the inequalities:

$$\left\{\begin{array}{c}{{\lambda }_{min}\le \mathcal{I}}_2\le {\lambda }_{max}.\\ {\lambda }_{min}\left[\mathit{a},{\Lambda }^{*}\right]\stackrel{\scriptscriptstyle\mathrm{def}}{=}\sqrt{{\tilde{\mathbb{L}}}_{min}\left[\mathit{a},{\Lambda }^{*}\right]},\\ {\lambda }_{max}\left[\mathit{a},{\Lambda }^{*}\right]\stackrel{\scriptscriptstyle\mathrm{def}}{=}\sqrt{{\tilde{\mathbb{L}}}_{max}\left[\mathit{a},{\Lambda }^{*}\right]}.\end{array}\right.$$

(24)

This solves the substratum bi-matrix game problem for the ordinal players on the lower, substratum level in the vector case $p=2$.

Based on the substratum game value, the superstratum problem optimizes the eigenvalue in accordance with the goals of the cardinal players:

$$\lambda \left[\mathit{a}\right]\underset{\mathit{a}}{\to }\mathrm{e}\mathrm{x}\mathrm{t}\mathrm{r}\mathrm{e}\mathrm{m}\mathrm{u}\mathrm{m}.$$

If there is only one cardinal player, namely a “designer”, finding the extremum in the above equation is a common optimization task. In the actual context, there is only one cardinal player involved, which reduces the extremum search to a common task of mathematical programming.

In general, finding the extremum in the above equation can be a game optimization task, depending on the number of cardinal players involved. If there is no conflict between these players, finding the extremum is a standard optimization. Studying this is beyond the scope of the current manuscript.

3.4. This section presents the solution (24) to the substratum bi-matrix game with constrained actions (Equation (16)). The objective of the superstratum task is to identify the optimal solution for the “designer” by searching for the extremal value of (24) through variation of the design variables.

4. Optimization Games with One “Cardinal Player”

4.1. The results of Section 3 can be generalized for self-adjoint positive definite differential operators using the technique of control theory [15]. A comparable interpretation will be made from the perspective of game theory, with regard to the optimization tasks involving an infinite number of design parameters for each player. In lieu of the payoff function, the payoff functional emerge. The system described by the equilibrium equations is to be considered in the following form:

$$\mathcal{K}u=m.$$

(25)

The self-adjoint positive definite operator $\mathcal{K}$ describes the state of the system. In structural optimization, there are definite “ordinal players”. In the most basic formulation of the self-adjoint operator of the continuous system, the actions of both ordinal “nature” and “operator” match. In the matrix formulation, it was shown in Section 2, Equation (12). The “designer” modifies the coefficients of the payoff matrix, while both ordinal players simultaneously alter symmetrically both the left and right vectors of the payoff function. In the self-adjoint formulation, the solution of the game problem for the continuous system is essentially simplified. In Equation (25), $u$ is the function of the state variables and $m$ is the function of the external loads of an ordinal player, “nature” or “operator”. All values are determined in some domain $\mathsf{\Omega }$. In the one-dimensional case, the domain $\mathsf{\Omega }$ could be thought of as an open interval.

The vector of “nature” and “operator” actions should belong to the set of admissible external loads $m\in \mathit{P}$, $\tilde{m}\in \mathit{P}$, which $L_p$-norm on the space of $p$-integrable functions [5] is constrained. We consider the set of real measurable functions whose absolute value raised to the $p$-th power has a constraint integral:

$${‖m‖}_p\le 1, {‖\tilde{m}‖}_p\le 1.$$

(26)

As discussed in Section 2, in addition to the “ordinal players” there is the “cardinal player”. The “cardinal player” owns the “design variables” $\mathit{a}$. For example, the function $\mathit{a}$ describes the mechanical properties along the length of the element. In essence, this function can be conceived of as a vector function. The coefficients of the operator depend upon $\mathit{a}$:

$$\mathcal{K}=\mathcal{K}\left[\mathit{a}\right].$$

(27)

As usual, certain isoperimetric conditions restrict the possible designs. For example, the total volume of the element could be restricted:

$$\mathcal{V}\left[\mathit{a}\right]\le {\mathcal{V}}_0.$$

(28)

The payoff functional is the functional of the design and loads of both players:

$$\mathcal{I}=\mathcal{I}\left[m,\tilde{m},\mathit{a}\right].$$

(29)

This functional characterizes the essential mechanical characteristic of the structure, for example, compliance, period of vibration, maximal stress, etc. Putting it roughly, the natural aim of the “operator” $\tilde{m}$ is to minimize the functional $\mathcal{I}$ for all possible actions of “nature”.

The upper and lower game values are defined as follows:

$$\left\{\begin{array}{c}{\mathcal{P}}^{*}\left[\mathit{a}\right]=\underset{\tilde{m}\in \mathit{P}}{\min } \underset{\mathit{f}\in \mathit{P}}{\max } \mathcal{I}\left[m,\tilde{m},\mathit{a}\right],\\ {\mathcal{P}}^{**}\left[\mathit{a}\right]=\underset{m\in \mathit{P}}{\max } \underset{\tilde{m}\in \mathit{P}}{\min } \mathcal{I}\left[m,\tilde{m},\mathit{a}\right].\end{array}\right.$$

(30)

The minimax theorem states that, in general,

$${\mathcal{P}}^{**}\left[\mathit{a}\right]\le {\mathcal{P}}^{*}\left[\mathit{a}\right]$$

(31)

If the upper value of the game is equal to the lower value, the common value of minimaxes ${\mathcal{P}}^{*}$ and ${\mathcal{P}}^{**}$ is called the value of the game:

$$\mathcal{G}\left[\mathit{a}\right]={\mathcal{P}}^{**}\left[\mathit{a}\right]={\mathcal{P}}^{*}\left[\mathit{a}\right]$$

(32)

4.2. The case $p=1$ was considered in (Ch. 16, [8]). In classical game theory, the games played over the unit square are considered as a generalization of the matrix games. The payoff function in “game played over the unit square” is thus defined for the non-negative functions. In this case, a single continuous variable was retained for each individual due to the limitations imposed upon the strategies of each player:

$$0\le a\le 1,{‖m‖}_1\le 1,{‖\tilde{m}‖}_1\le 1,m\ge 0,\tilde{m}\ge 0.$$

4.3. In the current contest of application of game theory to structural optimization the value $p=2$. The payoff functional will be the stored elastic energy of the structural element [16]. This functional has the physical meaning of integral compliance. Thus, this is the game with the payoff functional (29) with the scalar product:

$$〈m,u〉\stackrel{\scriptscriptstyle\mathrm{def}}{=}{\int }_{\mathsf{\Omega }}m\left(x\right)u\left(x\right)\mathrm{d}x$$

(33)

In Equation (33), the symbol $〈m,u〉$ stays for the bilinear form, or scalar product, satisfying:

$$〈u,m〉=〈m,u〉,〈m,m〉>0\mathrm{for}m\ne 0.$$

(34)

The solution to Equation (25) may be expressed in the following form:

$$u=\mathcal{L}\left[\mathit{a}\right]m.$$

(35)

In Equation (35), the operator

$$\mathcal{L}\left[\mathit{a}\right]={\mathcal{K}}^{-1}\left[\mathit{a}\right]$$

(36)

is the symbolic inverse of the $\mathcal{K}\left[\mathit{a}\right]$ operator.

As shown above, the restriction is assumed in quadratic form:

$${‖m‖}_2\equiv {\int }_{\mathsf{\Omega }}m\left(x\right)·m\left(x\right)\mathrm{d}x\le 1.$$

(37)

4.4. Following the substitution of (35) into Equation (33), the bi-linear payoff functional is expressed as follows:

$$\mathcal{I}=〈\mathcal{L}\left[\mathit{a}\right]m,\tilde{m}〉.$$

(38)

The objective is to reduce the stored energy (38), given the restricted resources (37).

The expression

$$\mathcal{G}\left[\mathit{a}\right]\stackrel{\scriptscriptstyle\mathrm{def}}{=}〈\mathcal{L}\left[\mathit{a}\right]\mathfrak{m},\tilde{\mathfrak{m}}〉=\underset{\tilde{m}\in \mathit{P}}{\min } \underset{m\in \mathit{P}}{\max } 〈\mathcal{L}\left[\mathit{a}\right]m,\tilde{m}〉$$

(39)

stays for the average elastic energy, which cause the stochastic actions of “nature” under the stochastic compensating action of the “operator”, $m=-\tilde{m}$. The determination of the minimal value of the game $\mathcal{G}\left[\mathit{a}\right]$ is reduced to an ordinary optimization problem with the unknown design function $\mathit{a}$. The optimization game with the stored elastic energy as the payoff function could be referred to as a “compliance game”.

Using the variational property of eigenvalues [17], one can obtain the equivalent expression:

$$\mathcal{G}\left[\mathit{a}\right]={\displaystyle \frac{\mathbb{P}}{\mathbb{L}\left[\mathit{a}\right]}}.$$

In the above Equation, $\mathbb{L}\left[\mathit{a}\right]$ is the minimal eigenvalue of the operator $\mathcal{K}\left[\mathit{a}\right]$. $\mathrm{C}\mathrm{o}\mathrm{r}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{p}\mathrm{o}\mathrm{n}\mathrm{d}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{l}\mathrm{y},{\mathbb{L}}^{-1}\left[\mathit{a}\right]$ is the maximal eigenvalue of the operator $\mathcal{L}\left[\mathit{a}\right]$:

$$\left\{\begin{array}{c}\mathbb{L}\left[\mathit{a}\right]=\underset{\mathit{u}}{\min } {\displaystyle \frac{〈\mathcal{K}\left[a\right]u,u〉}{〈u,u〉}}\equiv {\displaystyle \frac{〈\mathcal{K}\left[\mathit{a}\right]\mathfrak{u},\mathfrak{u}〉}{〈\mathfrak{u},\mathfrak{u}〉}},\\ {\mathbb{L}}^{-1}\left[\mathit{a}\right]=\underset{m\in \mathit{P}}{\min } {\displaystyle \frac{〈m,m〉}{〈\mathcal{L}\left[\mathit{a}\right]m,m〉}}\equiv {\displaystyle \frac{〈\mathfrak{m},\tilde{\mathfrak{m}}〉}{〈\mathcal{L}\left[\mathit{a}\right]\tilde{\mathfrak{m}},\tilde{\mathfrak{m}}〉}}.\end{array}\right.$$

(40)

Formulas (40) manifest in the sense of equilibrium strategies $\mathfrak{m}$ of “nature”. The strategy of both concurrent players is given by the eigenvector of operator $\mathcal{L}\left[\mathit{a}\right]$, which corresponds to its eigenvalue ${\mathbb{L}}^{-1}\left[\mathit{a}\right]$:

$$\mathcal{L}\left[\mathit{a}\right]\mathfrak{m}={\displaystyle \frac{1}{\mathbb{L}\left[\mathit{a}\right]}}·\mathfrak{m}.$$

In the case, a single continuous variable was selected for each individual, given the limitations imposed by the strategies of each player:

$$0\le a\le 1,{‖m‖}_2\le 1,{‖\tilde{m}‖}_2\le 1.$$

The equilibrium loads represent in the saddle point of structural response among all permissible loads. At least the upper value of the game could be determined in all cases. The application of the aforementioned considerations to structural optimization problems will be discussed in the following sections.

5. Game Formulation for the Beam Subjected to Arbitrary Bending Moments

5.1. Consider the beam of a certain cross-section. The beam, or rod, is placed horizontally along the $x$ axis. The beam is subjected to an external moment $m\left(x\right)$ distributed perpendicularly to a longitudinal axis of the element. The applied compensating moment $\tilde{m}\left(x\right)$ is a priori unknown. When a transverse load is applied on it, the beam deforms, and stresses develop inside it. According to the Euler–Bernoulli theory of slender beams, the equation-describing beam deflection can be presented as:

$$E J u^{″}=m.$$

$E$ is the Young’s modulus, $J$ is the area moment of inertia of the cross-section, and $m$ is the internal bending moment in the beam. The quantity $E J$ in the above equation stays for the bending stiffness of the beam. The bending moment $m$ is a two-times continuously differentiable function on $0\le x\le l.$ The area moment of inertia of the cross-section is given by the relation:

$$J=\mathcal{C} a^k,$$

where $k$ is the shape exponent and $\mathcal{C}=$ $\mathcal{C}\left(k\right)$ is the shape factor. The shape factor depends on the cross-sectional shape. The admissible cross-sectional area of the rod is the scalar function $a=a\left(x\right)$. The function is two times continuously differentiable. The cross-sectional area $a$ plays the role of the strategy of “designer”. The shape exponent $k$ takes the values of one, two, and three [12]. In all of these cases, the game will be convex, and both players have pure strategies. The case $k=2$ corresponds to a similar variation of the form of the cross-section. The areas, area moment of inertia, and shape factors for the similar variation of the form of the cross-section $k$ = 2 are shown in

Table 1. Areas, area moment of inertia, and shape factors for the similar variation of the cross-section $k=2$.

Solid or (Filled) Cross Section	Equilateral Triangle	Regular Hexagon	Square	Circular Area
	side length of s			$\mathrm{radius}s$
$\mathrm{area}a$	${\displaystyle \frac{\sqrt{3}{s}^2}{4}}$	${\displaystyle \frac{3\sqrt{3}{s}^2}{2}}$	$s^2$	$\pi s^2$
$\mathrm{area}\mathrm{moment}\mathrm{of}\mathrm{inertia}J$	${\displaystyle \frac{s^4}{32\sqrt{3}}}$	${\displaystyle \frac{{5\sqrt{3}s}^4}{16}}$	${\displaystyle \frac{s^4}{12}}$	${\displaystyle \frac{\pi s^4}{4}}$
$\mathrm{shape}\mathrm{factor}\mathcal{C}$	${\displaystyle \frac{\sqrt{3}}{18}}$	${\displaystyle \frac{5\sqrt{3}}{108}}$	${\displaystyle \frac{1}{12}}$	${\displaystyle \frac{1}{4\pi }}$

. These formulas are valid for both a horizontal and a vertical axis through the centroid and, therefore, are also valid for an axis with an arbitrary direction that passes through the origin of the regular cross-sections. The a priori unknown cross-sectional area $a$ is the variable function along the span of the beam.

For brevity, the authors use the integral of an arbitrary function $\phi \left(x\right), 0\le x\le l$ for the symbolization:

$$⟨\phi ⟩\stackrel{\scriptscriptstyle\mathrm{def}}{=}{\int }_0^l\phi \left(\xi \right)\mathrm{d}\xi$$

The boundary conditions must be prescribed as well. For easiness, the rod is hinged at the end $x=-l$ and clamped at the end $x=0$. The boundary conditions are [4]:

$${\left.m^{\prime }\right|}_{x=0}=0,{\left.u^{\prime }\right|}_{x=0}=0, {\left.m\right|}_{x=l}=0,{\left.u\right|}_{x=l}=0.$$

(41)

5.2. The payoff functional $\mathcal{P}$ is the integral distortion of the structural element. It is reasonable to express the integral distortion as the stored elastic energy $\mathcal{W}$:

$$\mathcal{I}\left[m,\tilde{m},a\right]\stackrel{\scriptscriptstyle\mathrm{def}}{=}\mathcal{W}=〈{\displaystyle \frac{m\widetilde{ m}}{EJ}}〉.$$

(42)

The game problem is defined exactly as already presented for the general status quo. There are two active ordinal players, “nature” and “operator” who behave recurrently and stochastically. The player (“nature”) can apply an arbitrary admissible external load $m=m\left(x\right)$ in order to affect the maximal elastic energy $\mathcal{W}$. Due to the symmetry of the game, the “operator” applies the opposite moments $\tilde{m}=\tilde{m}\left(x\right)$. These moments compensate for the deformation caused by “nature” $m$. The total efforts of the “nature” and “operator” are restricted:

$$〈{m^{\prime }}^2〉=〈{{\tilde{m}}^{\prime }}^2〉=1.$$

(43)

Admissible is any effort of “nature” and “operator”, which is a continuously differentiable function, that satisfies (43) and certain boundary conditions. Because the quadratic norm (43) is restricted, the sign of the moment statistically plays no role. The game will be symmetric in the sense of Nash [18].

The third player, “designer”, attempts to select the most appropriate shape $J=\mathcal{C} a^k\left(x\right)$, which will guarantee the smallest deformation energy during the exploitation of the structural element. The most appropriate shape is generally referred to as $\mathit{a}$. Once completed, the design remains unaltered over the period of exploitation. That is why the “designer” is considered as the “passive” player, contrary to both of the other opponent players, “nature” and “operator”.

The stiffest design corresponds to the minimal integral measure of deformation, which is presented by the stored energy $\mathcal{I}=\mathcal{W}$. The attempts of the “designer” to withstand the deformation are also limited. Namely, the material volumes of all of the competing designs of the rods are less than the certain, fixed volume of material $\mathcal{V}$:

$$〈a〉\le \mathcal{V}.$$

(44)

The conflict leads to the antagonistic game formulation of the optimization task. This game is referred to as the functional game because the values of the game depend on function $a$. According to Equation (40), the optimal value of the game in mixed strategies is equal to:

$$\begin{array}{cc}{\mathcal{G}}_{opt}=\underset{⟨a⟩\le \mathcal{V}}{\min } \mathcal{G}\left[a\right],& \mathcal{G}\left[a\right]={\displaystyle \frac{\mathbb{P}}{E\mathcal{C}\mathbb{L}\left[a\right]}}\end{array}.$$

(45)

The symbol $\mathbb{L}$ in (45) signifies the minimal eigenvalue of the game of the ordinary differential equation with the boundary conditions:

$$\left\{\begin{array}{c}{m}^{″}+\mathbb{L}\left[a\right]·a^{-k}m=0\\ {\left.m^{\prime }\right|}_{x=0}=0, {\left.m\right|}_{x=l}=0.\end{array}\right.$$

(46)

The optimization game with the minimal eigenvalue as the payoff function could be referred to as the “eigenvalue game”. From (45) and (46), it follows that the maximization of the upper value of the game reduces to the maximization of the minimal eigenvalue:

$${\displaystyle \frac{1}{{\mathcal{G}}_{opt}}}={\displaystyle \frac{1}{\underset{ ⟨a⟩\le \mathcal{V}}{\min } \mathcal{G}\left[a\right]}}=\underset{ ⟨a⟩\le \mathcal{V}}{\max } {\displaystyle \frac{1}{\mathcal{G}\left[a\right]}}={\displaystyle \frac{E\mathcal{C}}{\mathbb{P}}}\underset{⟨a⟩\le \mathcal{V}}{\max } \mathbb{L}\left[a\right].$$

(47)

The cross-section for the Nash equilibrium state will be designated with the capital letter $\mathcal{A}$, leaving the small letter $a$ for any admissible cross-section function. The optimal cross-section presents the strategy for the active players. In other words, the beam with the thickness distribution $\mathcal{A}$ possesses the guaranteed stiffness:

$${\displaystyle \frac{1}{{\mathcal{G}}_{opt}}}={\displaystyle \frac{E\mathcal{C}}{\mathbb{P}}}·\underset{⟨a⟩\le \mathcal{V}}{\max } \mathbb{L}\left[a\right]\stackrel{\scriptscriptstyle\mathrm{def}}{=}{\displaystyle \frac{E\mathcal{C}}{\mathbb{P}}} \mathbb{L}\left[\mathcal{A}\right].$$

(48)

The eigenvalue problem (46) is self-adjoint. The boundary conditions (46) are of the Sturm type, see [19]. There exists an infinite set of eigenvalues. All eigenvalues are real and positive and can be arranged as a monotonic sequence, and each eigenvalue is simple:

$$\mathbb{L}\left[a\right]\equiv {\lambda }_1\left[a\right]<\dots <{\lambda }_{2k-1}\left[a\right]<{\lambda }_{2k}\left[a\right]<\dots .$$

(49)

Rayleigh’s quotient for the eigenvalue problem (46) reads as:

$$\mathcal{R}\left[\mathfrak{m},a\right]={\displaystyle \frac{⟨{\mathfrak{m}}^{\prime 2}⟩}{⟨a^{-k}{\mathfrak{m}}^2⟩}}.$$

In the Rayleigh’s quotient, the admissible functions $\mathfrak{m}\left(x\right)$ are all functions, having piecewise continuous first derivatives, satisfying the boundary conditions (46). The admissible moment of both active players: $\mathfrak{m}=\mathfrak{m}\left(x\right)$ stays as the argument in the Rayleigh’s quotient. The Rayleigh’s quotient plays the role of the payoff functional of “nature”. The player “nature” wants to maximize $-\mathcal{R}\left[\mathfrak{m},a\right]$, while the opposite player “operator” wants to minimize $\mathcal{R}\left[\mathfrak{m},a\right]$. The game is a zero-sum game, which means that, when the strategies of both players are fixed, the sum of the payoffs for the two players is zero. The self-adjointness of the eigenvalue problem implies that the action of the “operator” is opposite, but proportional to the action of the physical process, which we may refer to as “nature”.

Among all of the admissible strategies of “nature”, the most favorable strategy set for “nature” is $m=m\left(x\right)$. This choice delivers the minimal value for the Rayleigh’s quotient:

$$\mathbb{L}\left[a\right]=\underset{\mathfrak{m}}{\min } \mathcal{R}\left[\mathfrak{m},a\right], \mathbb{L}\left[a\right]\equiv {\lambda }_1\left[a\right].$$

(50)

The favorable strategy set that minimizes the Rayleigh’s quotient increases, according to (45), the energy of deformation $\mathcal{W}$ from (42) under its condition (43).

5.3. The “designer” has the opposite task. The necessity of the “designer” is to minimize the energy of deformation for all admissible $a$ under his condition (44). This task is equivalent to the maximization of the Rayleigh’s quotient with the restriction (43), see [20]. The Lagrangian functional is the sum of (50) and (44):

$$\mathcal{I}=⟨l⟩, l=a^{-k}{m}^2+\Lambda a.$$

Here, $\Lambda$ represents the Lagrange multiplier of the variational calculus problem. The variation of the Hamiltonian functional reads:

$$\mathsf{\delta }\mathcal{I}=⟨{\displaystyle \frac{\partial l}{\partial a}}⟩\mathsf{\delta }a, {\displaystyle \frac{\partial l}{\partial a}}=-k{a}^{-k-1}{m}^2+\Lambda .$$

The nullification of the derivative $\partial l/\partial a=0$ leads to the necessary optimality condition. The strategies in the state of Hash equilibrium are $m\to \mathcal{M}$, $a\to \mathcal{A}$, and consequently:

$${\mathcal{M}}^2={\displaystyle \frac{\Lambda }{k}}{\mathcal{A}}^{k+1}$$

(51)

From the viewpoint of the “designer”, the thickness distribution $\mathcal{A}$ must satisfy the necessary optimality condition (51).

From the viewpoint of the “designer”, the beam with the thickness distribution $\mathcal{A}$ guarantees the highest effectiveness for the most unfavorable effort of the player (“nature”). Again, due to the self-adjoint nature of differential equations, the answer of the “operator” in equilibrium is exactly the opposite of the action of “nature”.

5.4. The next task is to determine the Nash equilibrium strategies for the “designer” $\mathcal{A}$ and for the “nature” $\mathcal{M}$. The governing equation is the nonlinear ordinary differential equations of the second order:

$${\mathcal{M}}^{″}+\mathbb{L}·{\mathcal{A}}^{-k}\mathcal{M}=0 \mathcal{A}={\mathcal{M}}^{{\displaystyle \frac{2}{k+1}}}.$$

(52)

In the Equations of this Section, $\mathbb{L}$ signifies the minimal eigenvalue (49) in the Nash equilibrium point:

$$\mathbb{L}=\mathbb{L}\left[\mathcal{A}\right]\equiv {\lambda }_1\left[\mathcal{A}\right].$$

The boundary conditions (41) could be proven to be optimal for the boundary conditions of the Sturm type. The equilibrium conditions of the game task are equivalent to the necessary optimality condition for a column’s Euler buckling load. The substitution of Equation (51) into (52) gives:

$${\mathcal{M}}^{″}+\mathbb{L}·{\mathcal{M}}^{{\displaystyle \frac{1-k}{1+k}}}=0.$$

(53)

The solution of the boundary value problem (41), and (53) determines the strategy of “nature” $\mathcal{M}$. With this solution, the highest possible eigenvalue (52) and, consequently, the upper value of the game have to be evaluated:

$$\begin{array}{cc}{\mathcal{P}}^{*}={\displaystyle \frac{\mathbb{P}}{E\mathcal{C}\mathbb{L}}},& \mathbb{L}=\mathbb{L}\left[\mathcal{A}\right]\end{array}.$$

The dependent variable $\mathcal{M}$ and independent variable $x$ of Equation (53) are to be exchanged. In the new variables $x\left(\mathcal{M}\right)$, Equation (53) turns into the ordinary differential equation of the second order of Emden–Fowler type (Section 14.3 of [21]):

$${\displaystyle \frac{d^{2}x}{d{\mathcal{M}}^2}}=\mathbb{L}{·\left({\displaystyle \frac{dx}{d\mathcal{M}}}\right)}^3{\mathcal{M}}^R, R\stackrel{\scriptscriptstyle\mathrm{def}}{=}{\displaystyle \frac{1-k}{1+k}}.,$$

(54)

The Emden–Fowler Equation (54) has the following parameters:

$${\displaystyle \frac{d^{2}x}{d{\mathcal{M}}^2}}=\mathbb{L}{·\left({\displaystyle \frac{dx}{d\mathcal{M}}}\right)}^{1-S}{\mathcal{M}}^{P-1}, \begin{array}{ccc}S=-2,& R=P-1,& P={\displaystyle \frac{2}{k+1}}\end{array}.$$

(55)

The closed-form solution results in an arbitrary acceptable value of the shape exponent $k$. The general solution of Equation (54) for $k>1$ is:

$$x=i\sqrt{P}·{\int }_n^{\mathcal{M}}{\displaystyle \frac{\mathrm{d}t}{\sqrt{2\mathbb{L}{t}^P-\mathcal{N}}}}$$

(56)

The symbols $n$ and $\mathcal{N}$ stay for the integration constants. The integration constants are to evaluated from the solution of the nonlinear transcendental equations. To avoid the solutions of the nonlinear equations, the authors prefer the symmetrical sights. Specifically, the sense of the constant $n$ is the moment on the end $x=0$:

$$n\stackrel{\scriptscriptstyle\mathrm{def}}{=}\mathcal{M}(x=0).$$

Due to the symmetry of the equations, with respect to the point $x=0$, the function $\mathcal{M}\left(x\right)$ must be an even function of the variable $x$. This condition fixes the relation between the integration constants: $\mathcal{N}=2\mathbb{L}{n}^P.$

With this value, integral (56) evaluates in the closed form. For the shape exponent $k\ge 1$ and $K=0$, the solution reads as:

$$\left\{\begin{array}{c}x\left(\mathcal{M}\right)=c_L·{\int }_0^{\mathcal{M}}{\displaystyle \frac{\mathrm{d}s}{\sqrt{n^P-s^P}}},\\ x\left(\mathcal{M}\right)=n^{-{\displaystyle \frac{1}{k+1}}}·\mathcal{M}·{}_2\mathbf{F}_2\left(\left[{\displaystyle \frac{1}{2}},{\displaystyle \frac{k+1}{2}}\right],\left[{\displaystyle \frac{k+3}{2}}\right],{\left({\displaystyle \frac{\mathcal{M}}{n}}\right)}^{{\displaystyle \frac{2}{k+1}}}\right)\\ x\left(n\right)=\sqrt{\pi }{n}^{-{\displaystyle \frac{k}{k+1}}}·{\displaystyle \frac{\Gamma \left(\frac{k+3}{2}\right)}{\Gamma \left(\frac{k+1}{2}\right)}}.\end{array}\right.,$$

(57)

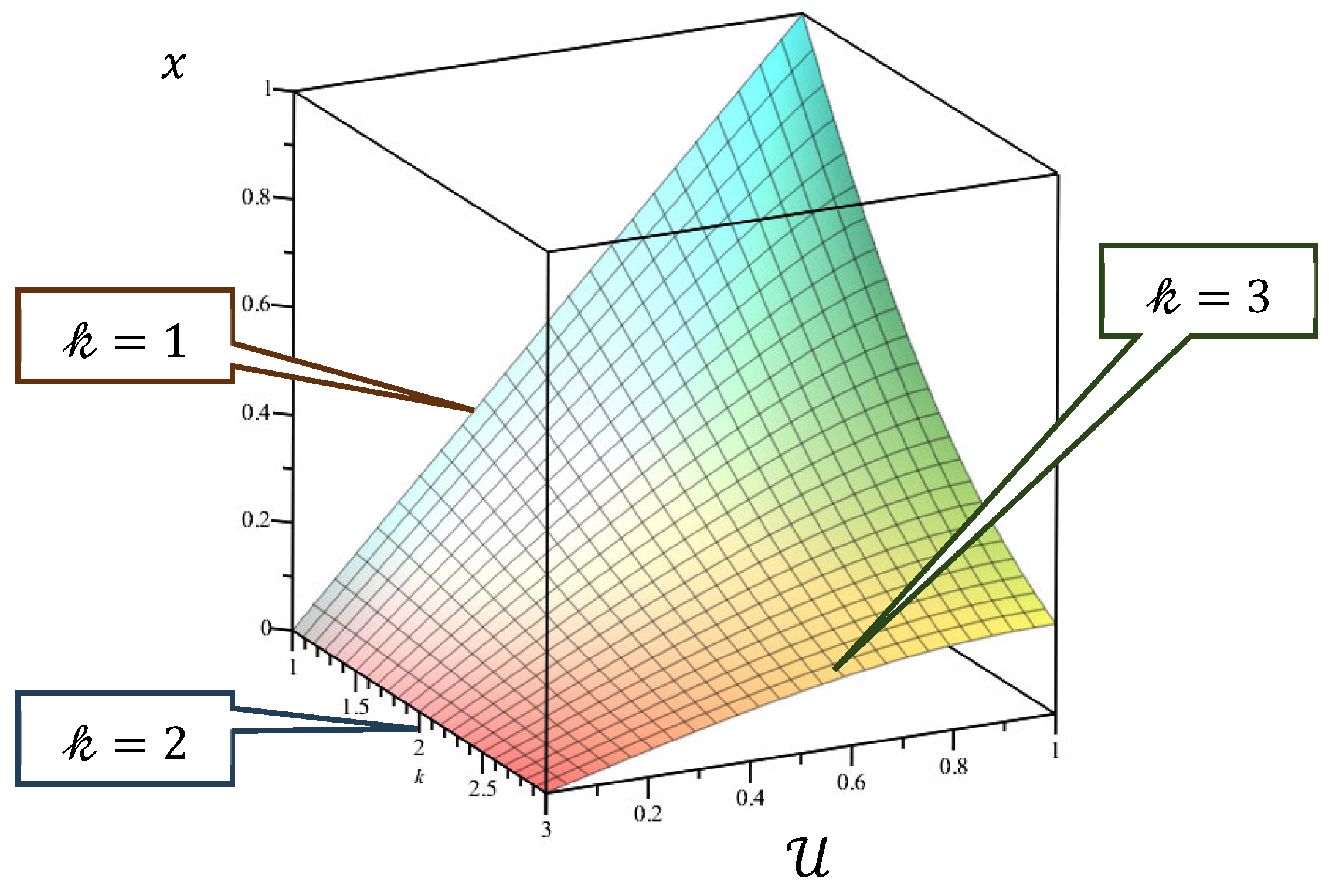
Equation (57) presents the axial coordinate $x$ as the function of the new independent parameter $\mathcal{M}$. For $k=\mathrm{1,2},3$, the hypergeometric function from Equation (57) expresses in terms of elementary functions (

Table 2. Expressions for axial coordinate $\mathit{x}$ as the function of $\mathcal{M}$ for $k=1$ and $k=2$.

$k$	$x\left(\mathcal{M}\right)$
1	$x={\displaystyle \frac{\mathcal{M}}{1+\sqrt{1-4\mathcal{M}}}}$
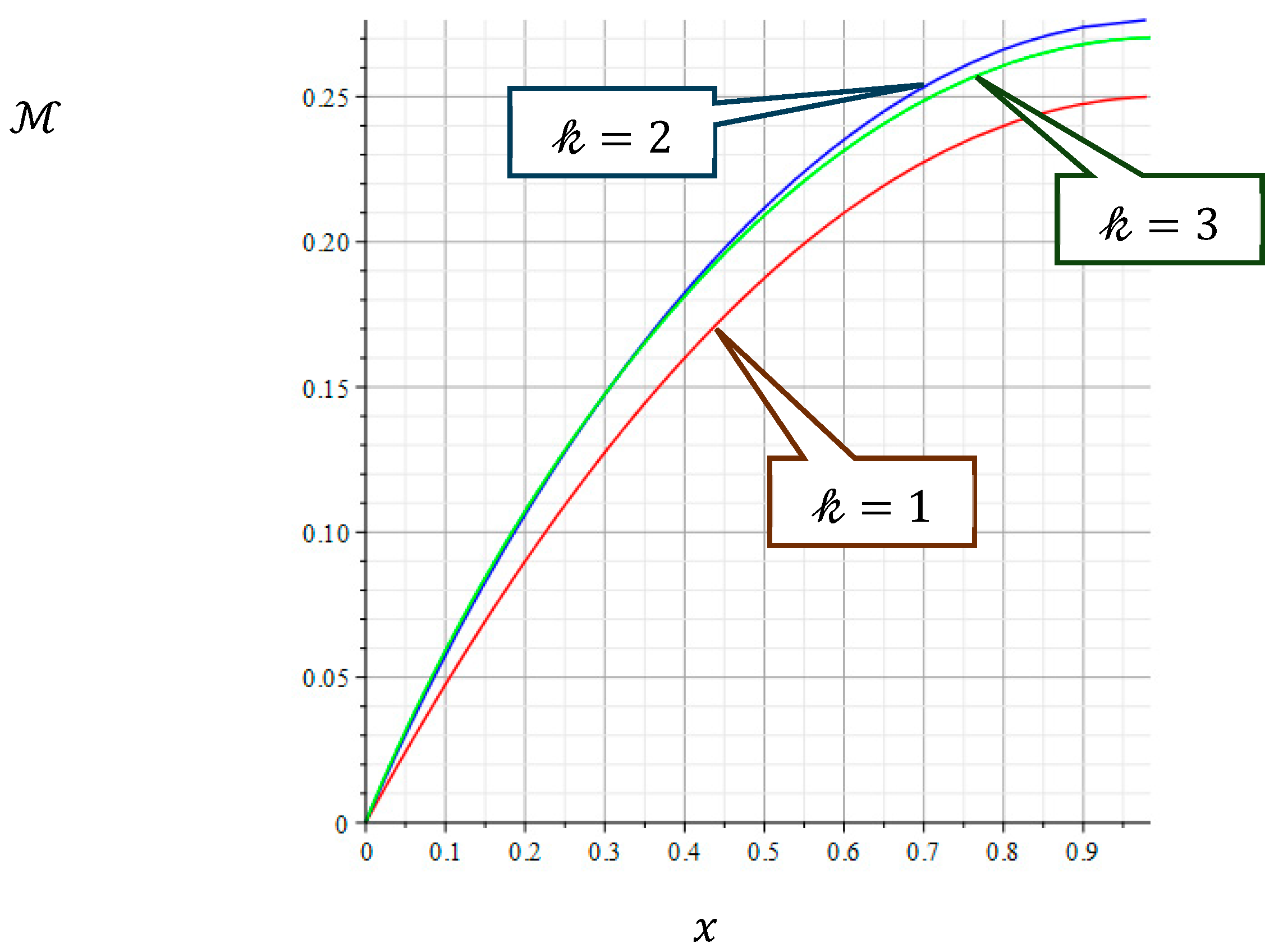
2	$x={\displaystyle \frac{2}{\pi }}·\arcsin \left({\displaystyle \frac{\sqrt{3\pi }}{2}}\sqrt[3]{\mathcal{M}}\right)-{\displaystyle \frac{\sqrt{3}}{2\sqrt{\pi }}}·\sqrt[3]{\mathcal{M}}·\sqrt{4-3\pi \sqrt[3]{{\mathcal{M}}^2}}$

). The graphs of the solutions are displayed for different values of parameters $k$ on Figure 1.

According to the boundary conditions (41), the dimensionless moment $m$ vanishes on the hinged end: ${\left.\mathcal{M}\right|}_{x=l}=0$. From this condition, the length of the rod could be determined as the function of an unknown integration constant $n$. Because the length $l$ of the rod is known, the unknown constant $n$ evaluates from the solution of the equation:

$$x\left(n\right)=l.$$

From its solution, the integration constant $n$ follows as:

$$n={\left( {\displaystyle \frac{\Gamma \left(\frac{k}{2}+1\right)}{\Gamma \left(\frac{k+3}{2}\right)}}{\displaystyle \frac{l}{\sqrt[]{\pi }}}\right)}^{{\displaystyle \frac{k+1}{k}}}.$$

(58)

To find the volume of the element, the authors evaluate the proper integral of the cross-section area $\mathcal{A}\left(\mathcal{M}\right).$ For all values of $k$ that are higher that one, the volume of the optimal structural element will be:

$$\mathcal{V}={\displaystyle \frac{1+k}{2+k}}·\sqrt[k]{{\displaystyle \frac{k^2}{\pi }}{\displaystyle \frac{l^{2+k}}{{\left(1+k\right)}^2}}{\displaystyle \frac{{\Gamma }^2\left(\frac{k}{2}\right)}{{\Gamma }^2\left(\frac{k+1}{2}\right)}}}.$$

(59)

The authors define one other constant that was referred to above as the total stiffness $\mathcal{E}$ of the structural element. The total stiffness $\mathcal{E}$ of the beam expresses as an integral of the moment of inertia of the cross-sections along the length $l$ of the beam. To find the total stiffness of element in the Nash equilibrium state, the authors evaluate another proper integral. The integral follows of the energy density ${\mathcal{M}}^2/{E\mathcal{C}\mathcal{A}}^k$ as:

$${\displaystyle \frac{\mathcal{W}}{E\mathcal{C}}}={\displaystyle \frac{1+k}{2+k}}·\sqrt[k]{{\displaystyle \frac{4}{\pi }}{\displaystyle \frac{l^{2+k}}{{\left(2+k\right)}^2}}{\displaystyle \frac{{\Gamma }^2\left(2+\frac{k}{2}\right)}{{\Gamma }^2\left(\frac{k+3}{2}\right)}}}.$$

(60)

According to Equation (60), the elastic energy density is constant over the length of the structural element.

Finally, the eigenvalue $\mathbb{L}\left[\mathcal{A}\right]\equiv {\lambda }_1\left[\mathcal{A}\right]$ equals the Nash equilibrium point to:

$$\mathbb{L}\equiv {\displaystyle \frac{2{k^{2}l}^2}{9\pi }}·{\displaystyle \frac{k+2}{{\left(k+\frac{2}{3}\right)\left(k+1\right)}^3}}·{\displaystyle \frac{\Gamma \left(\frac{3k+3}{2}\right)}{\Gamma \left(\frac{3k}{2}\right)}}·{\displaystyle \frac{{\Gamma }^3\left(\frac{k}{2}\right)}{{\Gamma }^3\left(\frac{k+1}{2}\right)}}$$

(61)

Equations (59)–(61) characterize the principal mechanical properties in the Nash equilibrium state. The stored elastic energy and volume for Nash equilibrium $\mathbb{L}=\mathbb{L}\left[\mathcal{A}\right]$is presented for different values of the constant $k$ in

Table 3. Stored elastic energy and volume for Nash equilibrium $\mathbb{L}=\mathbb{L}\left[\mathcal{A}\right]$.

$\mathcal{k}$	$\mathbb{P}$	$\frac{\mathcal{W}}{\mathit{E}\mathcal{C}}~\mathcal{V}$	$\mathsf{\Psi }\left(\mathcal{k}\right)$
1	${\displaystyle \frac{l^5}{30}}$	${\displaystyle \frac{l^3}{6}}$	${\displaystyle \frac{1}{5}}$
2	${\displaystyle \frac{{35l}^4}{27{\pi }^3}}$	${\displaystyle \frac{l^2}{\pi }}$	${\displaystyle \frac{35}{27{\pi }^2}}$
3	${\displaystyle \frac{1}{154}}\sqrt[3]{{\displaystyle \frac{3^5}{l^{11}}}}$	${\displaystyle \frac{1}{5}}\sqrt[3]{{\displaystyle \frac{3^2}{l^5}}}$	${\displaystyle \frac{15}{154}}$

.

For the state of Nash equilibrium, the eigenvalue depends on the known constants:

$$\begin{array}{c}\Psi \left(k\right)\stackrel{\scriptscriptstyle\mathrm{def}}{=}E\mathcal{C}{\displaystyle \frac{\mathbb{P}}{\mathcal{E}}}={\displaystyle \frac{\mathbb{L}}{l^2}},\\ \Psi \left(k\right)=k^3·{\displaystyle \frac{\Gamma \left(\frac{3k+3}{2}\right)}{\Gamma \left(\frac{3k+4}{2}\right)}}·{\displaystyle \frac{{\Gamma }^3\left(\frac{k}{2}\right)}{{\Gamma }^3\left(\frac{3+k}{2}\right)}}·{\displaystyle \frac{2+k}{16\pi }}.\end{array}$$

(62)

The dimensionless $\Psi \left(k\right)$ function is displayed on Figure 2.

5.5. Our next task is to establish the relation between the eigenvalues $\mathbb{L}\left[\mathcal{A}\right]$ and $\mathbb{L}\left[a\right]$. In the convex case $k\ge 1$, the relation could be rigorously proven as the certain isoperimetric inequality. For this purpose, the lowest eigenvalues for two different thickness functions $a$ and $\mathcal{A}$ are the minimal values of the two corresponding Rayleigh’s quotients [17]:

$$\mathcal{R}\left[\mathfrak{m},a\right]={\displaystyle \frac{⟨{\mathfrak{m}}^{\prime 2}⟩}{⟨a^{-k}{\mathfrak{m}}^2⟩}}, \mathcal{R}\left[\mathfrak{m},\mathcal{A}\right]={\displaystyle \frac{⟨{\mathfrak{m}}^{\prime 2}⟩}{⟨{\mathcal{A}}^{-k}{\mathfrak{m}}^2⟩}}.$$

The Rayleigh’s quotients are the functionals of functions $\mathfrak{m}$ and $a$ or $\mathcal{A}$, correspondingly. The functions $a$ or $\mathcal{A}$ are assumed in this section to be fixed. The function $\tilde{\mathfrak{m}}$ is an arbitrary admissible function, which is differentiable and satisfies the boundary conditions (41). The critical point of a functional is that point where the functional attains a minimum (or maximum) in the presence of constraints [17]. We, therefore, examine the conditions when a functional attains a minimum. For the thickness function $a,$ the critical point of the Rayleigh’s quotient $\mathcal{R}\left[\mathfrak{m},a\right]$ is the eigenfunction $m$. To the eigenfunction $m$ corresponds the lowest eigenvalue $\mathbb{L}\left[a\right]$. This guarantees that:

$$\mathbb{L}\left[a\right]={\displaystyle \frac{⟨m^{\prime 2}⟩}{⟨a^{-k}{m}^2⟩}}=\underset{\mathfrak{m}}{\min } \mathcal{R}\left[\mathfrak{m},a\right],$$

Analogously, for the thickness function $\mathcal{A},$ the critical point of the Rayleigh’s quotient $\mathcal{R}\left[\mathfrak{m},\mathcal{A}\right]$ is the eigenfunction $\mathcal{M}$. To this function corresponds the lowest eigenvalue $\mathbb{L}\left[\mathcal{A}\right]$:

$$\mathbb{L}\left[\mathcal{A}\right]={\displaystyle \frac{⟨{\mathcal{M}}^{\prime 2}⟩}{⟨{\mathcal{A}}^{-k}{\mathcal{M}}^2⟩}}=\underset{\mathfrak{m}}{\min } \mathcal{R}\left[\mathfrak{m},\mathcal{A}\right] .$$

The right sides of the two above Equations must be compared. In order to state the desired isoperimetric inequality, the following auxiliary inequalities have to be approved:

$$\left\{\begin{array}{c}{\displaystyle \frac{⟨m^{\prime 2}⟩}{⟨a^{-k}{m}^2⟩}}\le {\displaystyle \frac{⟨{\mathcal{M}}^{\prime 2}⟩}{⟨{\mathcal{A}}^{-k}{\mathcal{M}}^2⟩}},\\ {\mathcal{M}}^{″}+\mathbb{L}\left[\mathcal{A}\right] {\mathcal{A}}^{-k}\mathcal{M}=0,\\ m^{″}+\mathbb{L}\left[a\right] a^{-k}m=0.\end{array}\right.$$

(63)

The numerators of the fractions to the left and right of the auxiliary inequality (63) are identical. The denominators in the first Equation (63) are, however, different. Thus, the denominators should be compared. The inequality for the denominators that has to be proven reads:

$$⟨{\mathcal{A}}^{-k}{\mathcal{M}}^2⟩\le ⟨a^{-k}{\mathcal{M}}^2⟩\le ⟨a^{-k}{m}^2⟩.$$

(64)

At this point, the optimality condition (51) with $\lambda =k$ will be used:

$${\mathcal{M}}^2={\mathcal{A}}^{k+1}.$$

Namely, the substitution of the optimality condition (51) into (64) delivers the inequality for $k\ge 1$:

$$⟨{\displaystyle \frac{{\mathcal{A}}^{k+1}}{{\mathcal{A}}^k}}⟩\le ⟨{\displaystyle \frac{{\mathcal{A}}^{k+1}}{a^k}}⟩.$$

(65)

The equality in (65) takes place only for $\mathcal{A}=a$. The validity of the as yet suspected inequality (65) follows directly from the Hölder’s inequality (Ch. III of [22]). Consequently, from Hölder’s inequality follows the inequality for denominators (65) and, finally, the desired inequality (63).

Combining (63) and (65) delivers:

$$\mathbb{L}\left[a\right]={\displaystyle \frac{⟨m^{\prime 2}⟩}{⟨a^{-k}{m}^2⟩}}\le {\displaystyle \frac{⟨{\mathcal{M}}^{\prime 2}⟩}{⟨a^{-k}{\mathcal{M}}^2⟩}}\equiv {\displaystyle \frac{⟨{\mathcal{M}}^{\prime 2}⟩}{⟨\frac{{\mathcal{A}}^{k+1}}{a^k}⟩}}\le {\displaystyle \frac{⟨{\mathcal{M}}^{\prime 2}⟩}{⟨\frac{{\mathcal{A}}^{k+1}}{{\mathcal{A}}^k}⟩}}={\displaystyle \frac{⟨{\mathcal{M}}^{\prime 2}⟩}{⟨{\mathcal{A}}^{-k}{\mathcal{M}}^2⟩}}\equiv \mathbb{L}\left[\mathcal{A}\right].$$

Consequently, it was proven that, for all arbitrary $a$, the eigenvalue is less than $\mathbb{L}\left[\mathcal{A}\right]$:

$$\mathbb{L}\left[a\right]\le \mathbb{L}\left[\mathcal{A}\right].$$

(66)

The equality in Equation (66) was attained only for the optimal beam, which has the optimal shape $\mathcal{A}$ and the maximal possible volume of material $\mathcal{V}$. For the shape exponent $k\ge 1$, the game is convex. Generally, the game will be convex for any convex function $J=J \left(a\right)$.

Finally, the beam, which obeys the necessary optimality conditions (51), delivers the lowest possible upper value of the game:

$$\mathcal{G}\left[a\right]={\displaystyle \frac{\mathbb{P}}{E\mathcal{C} \mathbb{L}\left[a\right]}}\ge {\displaystyle \frac{\mathbb{P}}{E\mathcal{C} \mathbb{L}\left[\mathcal{A}\right]}}\stackrel{\scriptscriptstyle\mathrm{def}}{=}{\mathcal{G}}_{opt}.$$

(67)

Consequently, the value of functional game ${\mathcal{G}}_{opt}=\mathcal{W}\left[\mathcal{A}\right]$ for the optimal distribution of thickness $\mathcal{A}\left(\xi \right)$ is lower than the payoff functional (distortion energy) for an arbitrary distribution of thickness $a\left(\xi \right)$ of the same volume:

$$⟨a⟩=⟨\mathcal{A}⟩=\mathcal{V}.$$

(68)

If the volume of an arbitrary thickness distribution is lower, the stronger inequality follows:

$$⟨a⟩<⟨\mathcal{A}⟩⟹\mathbb{L}\left[a\right]<\mathbb{L}\left[\mathcal{A}\right].$$

(69)

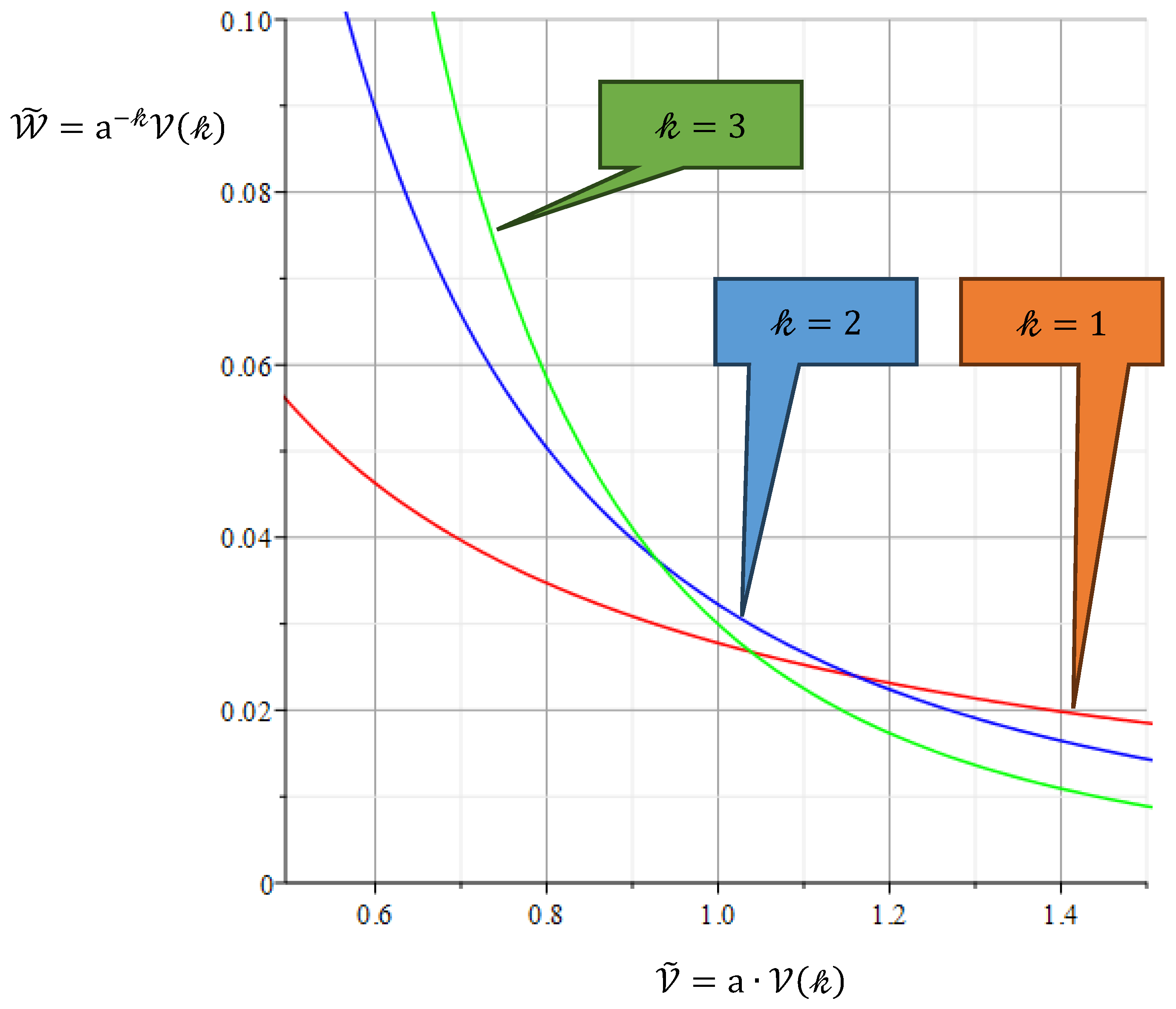
The relations (67)–(69) solve the “superstratum” game with the undefined, but constrained, bending moment function. From the viewpoint of the “designer”, the optimal distribution of thickness $\mathcal{A}\left(\xi \right)$ guarantees the best compromise for the most unfavorable option for the “designer” action of “nature”. Because of the self-adjoint nature of the eigenvalue problem, the action of the “operator” is proportional to the action of “nature”. This compromise is the equilibrium in the functional game. The eigenvalue $\mathbb{L}\left[\mathcal{A}\right]$ in the equilibrium point is shown on Figure 3 as the function of the length $l$ and the shape factor $k$.

5.6. In Section 5, the beam is subjected to arbitrary bending efforts, and the designer determines the optimal beam shape for resisting these forces.

6. Game Formulation for the Rod Subjected to Arbitrary Torque

6.1. Consider the rod with the circular cross section, subjected to the positive distributed torque along its axis. The torque distribution is arbitrary, but the quadratic integral of the torque is fixed:

$$〈u^2〉=〈u^2〉=1.$$

The governing equation for this problem is similar to Equation (46), but the order is twice lower [2]. In this case, the symbol $\mathbb{L}$ signifies the minimal eigenvalue of the game of the ordinary differential equation:

$${\left({E\mathcal{C}a}^{-k}{u}^{\prime }\right)}^{\prime }+\mathbb{L}\left[a\right]u=0,$$

(70)

with the boundary conditions:

$${\left.u\right|}_{x=0}=0, {\left.u^{\prime }\right|}_{x=l}=0.$$

(71)

The optimal cross-section will be designated with the capital letter $\mathcal{A}$, leaving the small letter $a$ for any admissible cross-section function. The optimal cross-section presents the strategy for the “nature”. In other words, the rod with the thickness distribution $\mathcal{A}$ possesses a guaranteed stiffness:

$${\displaystyle \frac{1}{{\mathcal{P}}^{*}}}={\displaystyle \frac{E\mathcal{C}}{\mathbb{P}}}\underset{⟨a⟩\le \mathcal{V}}{\max } \mathbb{L}\left[a\right]\stackrel{\scriptscriptstyle\mathrm{def}}{=}{\displaystyle \frac{E\mathcal{C}}{\mathbb{P}}} \mathbb{L}\left[\mathcal{A}\right].$$

(72)

The eigenvalue problem (70) and (71) is self-adjoint. The conditions (71) are again of the Sturm type. Once again, there is an infinite set of simple eigenvalues, and all eigenvalues are real and positive and can be arranged as a monotonic sequence:

$$\mathbb{L}\left[a\right]\equiv {\lambda }_1<{\lambda }_2<\dots <{\lambda }_{2k-1}<{\lambda }_{2k}<\dots .$$

(73)

The Rayleigh’s quotient is:

$$\tilde{\mathcal{R}}\left[\mathfrak{u},a\right]={\displaystyle \frac{⟨a^k{\mathfrak{u}}^{\prime 2}⟩}{⟨{\mathfrak{u}}^2⟩}}.$$

(74)

In Equation (74), the admissible functions $\mathfrak{u}\left(x\right)$ are all functions, having piecewise continuous first derivatives and satisfying the boundary conditions (71). In the Rayleigh’s quotient stays the admissible twist of “nature”: $\mathfrak{u}=\mathfrak{u}\left(x\right)$.

6.2. Among all admissible strategies of “nature”, the most favorable strategy set for “nature” is $u=u\left(x\right)$. This choice delivers the minimal value for the Rayleigh’s quotient:

$$\mathbb{L}\left[a\right]=\underset{\mathfrak{u}}{\min } \tilde{\mathcal{R}}\left[\mathfrak{u},a\right], \mathbb{L}\left[a\right]\equiv {\Lambda }_1\left[a\right].$$

(75)

The favorable strategy set minimizes the Rayleigh’s quotient and increases the energy of deformation $⟨a^k{\mathfrak{u}}^{\prime 2}⟩$ under the condition $⟨{\mathfrak{u}}^2⟩=1$ and (71).

The “designer” has the opposite task. The necessity of “designer” is to minimize the energy of deformation for all admissible $a$ under the condition. This task is equivalent to the maximization of the Rayleigh’s quotient with the restriction (44). The Lagrangian functional is the sum of (74) and (44):

$$\mathcal{I}=⟨l⟩, l=a^k{u^{\prime }}^2+\Lambda a.$$

Here, $\Lambda$ represents the Lagrange multiplier of the variational calculus problem. The variation of the Lagrangian functional reads:

$$\mathsf{\delta }\mathcal{I}=⟨{\displaystyle \frac{\partial l}{\partial a}}⟩\mathsf{\delta }a, {\displaystyle \frac{\partial l}{\partial a}}=k{a}^{k-1}{u^{\prime }}^2-\Lambda .$$

The nullification of the derivative $\partial l/\partial a=0$ leads to the necessary optimality condition. The strategies in the state of Hash equilibrium are $u\to \mathcal{U}$, $a\to \mathcal{A}$, and consequently:

$$\mathcal{A}=\sqrt[k-1]{{\displaystyle \frac{\Lambda }{k{{\mathcal{U}}^{\prime }}^2}}}.$$

(76)

From the viewpoint of the “designer”, the thickness distribution $\mathcal{A}$ must satisfy the necessary optimality condition (76). Remarkably, that the equilibrium conditions of the game task are equivalent to the necessary optimality condition for the twist divergence of a wing [23,24].

6.3. The next task is to determine the Nash equilibrium strategies for the “designer” $\mathcal{A}$ and for the “nature” $\mathcal{M}$. For the briefness of formulas, we temporarily put $\lambda =k$. The governing equation is the nonlinear ordinary differential equations of the second order:

$${\left({\mathcal{A}}^k{\mathcal{U}}^{\prime }\right)}^{\prime }+\mathbb{L} \mathcal{U}=0 \mathcal{A}={{\mathcal{U}}^{\prime }}^{{\displaystyle \frac{2}{1-k}}}.$$

(77)

In the above Equations, $\mathbb{L}$ signifies the minimal eigenvalue in the Nash equilibrium point:

$$\mathbb{L}=\mathbb{L}\left[\mathcal{A}\right]\equiv {\lambda }_1\left[\mathcal{A}\right].$$

The substitution of Equation (77) into (70) gives:

$${\left({\left({\mathcal{U}}^{\prime }\right)}^{1/R}\right)}^{\prime }+\mathbb{L}\mathcal{U}=0, R\stackrel{\scriptscriptstyle\mathrm{def}}{=}{\displaystyle \frac{1-k}{1+k}}.$$

(78)

For the solution of the boundary value problem (77), (78) determines the strategy of “nature” $\mathcal{U}$. The dependent and independent variables of Equation (78) are to be exchanged. In the new variables, Equation (78) turns into the Emden–Fowler equation [21]:

$${\displaystyle \frac{d^{2}x}{d{\mathcal{U}}^2}}=\mathbb{L}·R{·\mathcal{U}·\left({\displaystyle \frac{dx}{d\mathcal{U}}}\right)}^{{\displaystyle \frac{k-3}{k-1}}} , x\left(\mathcal{U}=0\right)=0.$$

(79)

The Emden–Fowler Equation (79) has the following parameters:

$$S={\displaystyle \frac{2}{k-1}}, P=2.$$

The closed-form solution results for an arbitrary value of the shape exponent are $k\ge 0$. The solution of (79) reads as:

$$\left\{\begin{array}{c}x\left(\mathcal{U}\right)={\left({\displaystyle \frac{\mathbb{L}}{1+k}}\right)}^{{\displaystyle \frac{k-1}{2}}}\mathcal{U} {}_2\mathbf{F}_{2}2\left(\left[{\displaystyle \frac{1}{2}},{\displaystyle \frac{1-k}{2}}\right],\left[{\displaystyle \frac{3}{2}}\right],{\mathcal{U}}^2\right),\\ x\left(\mathcal{U}=1\right)={\displaystyle \frac{\sqrt{\pi }}{2}}{\left({\displaystyle \frac{\mathbb{L}}{1+k}}\right)}^{{\displaystyle \frac{k-1}{2}}}{\displaystyle \frac{\Gamma \left(\frac{k+1}{2}\right)}{\Gamma \left(\frac{k+2}{2}\right)}}.\end{array}\right. ,$$

(80)

Equation (80) presents the axial coordinate $x$ as the function of the independent parameter $\mathcal{U}$. For $k=\mathrm{1,2},3$, the hypergeometric function from Equation (80) expresses in terms of elementary functions (

Table 4. Expressions for axial coordinate $x$ as the function of $\mathcal{U}$ for $k=1$, 2, 3.

$\mathcal{k}$	$\mathit{x}\left(\mathcal{U}\right)$	$\mathit{x}\left(1\right)$
1	$\mathcal{U}$	1
2	${\displaystyle \frac{1}{2}}\sqrt{{\displaystyle \frac{\mathbb{L}}{3}}}\left(\mathcal{U}\sqrt{1-{\mathcal{U}}^2}+\arcsin \left(\mathcal{U}\right)\right)$	$\sqrt{{\displaystyle \frac{\mathbb{L}}{12}}}$
3	${\displaystyle \frac{\mathbb{L}\mathcal{U}}{4}}\left(1-{\displaystyle \frac{{\mathcal{U}}^2}{3}}\right)$	${\displaystyle \frac{\mathbb{L}}{6}}$

). Optimal shapes of twisted rods for the Nash equilibrium states are shown on Figure 4.

6.4. The next task is to establish the relation between the eigenvalues $\mathbb{L}\left[\mathcal{A}\right]$ and $\mathbb{L}\left[a\right]$. In the convex case, where $k\ge 1$, the relation could be rigorously proven as the certain isoperimetric inequality. For this purpose, the lowest eigenvalues for two different thickness functions $a$ and $\mathcal{A}$ are the minimal values of the two corresponding Rayleigh’s quotients:

$$\tilde{\mathcal{R}}\left[\mathfrak{u},a\right]={\displaystyle \frac{⟨a^k{\mathfrak{u}}^{\prime 2}⟩}{⟨{\mathfrak{u}}^2⟩}}, \tilde{\mathcal{R}}\left[\mathfrak{u},\mathcal{A}\right]={\displaystyle \frac{⟨{\mathcal{A}}^k{\mathfrak{u}}^{\prime 2}⟩}{⟨{\mathfrak{u}}^2⟩}}.$$

The Rayleigh’s quotients are the functionals of functions $\tilde{\mathfrak{m}}$ and $a$ or $\mathcal{A}$, correspondingly. The functions $a$ or $\mathcal{A}$ are assumed in this section to be fixed. The function $\tilde{\mathfrak{m}}$ is an arbitrary admissible function, which is differentiable and satisfies boundary conditions. The critical point of a functional is that point where the functional attains a minimum (or maximum) in the presence of constraints. We, therefore, examine the conditions when a functional attains a minimum. For the thickness function $a,$ the critical point of the Rayleigh’s quotient $\tilde{\mathcal{R}}\left[\mathfrak{u},a\right]$ is the eigenfunction $u$. To the eigenfunction $u$ corresponds the lowest eigenvalue $\mathbb{L}\left[a\right]$. The guarantees that:

$$\mathbb{L}\left[a\right]={\displaystyle \frac{⟨a^k{u}^{\prime 2}⟩}{⟨u^2⟩}}=\underset{\mathfrak{u}}{\min } \tilde{\mathcal{R}}\left[\mathfrak{u},a\right].$$

(81)

Analogously, for the thickness function $\mathcal{A},$ the critical point of the Rayleigh’s quotient $\tilde{\mathcal{R}}\left[\mathfrak{u},\mathcal{A}\right]$is the eigenfunction $\mathcal{U}$. To this function corresponds the lowest eigenvalue $\mathbb{L}\left[\mathcal{A}\right]$:

$$\mathbb{L}\left[\mathcal{A}\right]={\displaystyle \frac{⟨{\mathcal{A}}^k{\mathcal{U}}^{\prime 2}⟩}{⟨{\mathcal{U}}^2⟩}}=\underset{\mathfrak{u}}{\min } \tilde{\mathcal{R}}\left[\mathfrak{u},\mathcal{A}\right].$$

(82)

The right sides of Equations (81) and (82) must be compared. In order to state the desired isoperimetric inequality, the following auxiliary inequality has to be approved:

$$\begin{array}{c}{\displaystyle \frac{⟨a^k{u}^{\prime 2}⟩}{⟨u^2⟩}}\le {\displaystyle \frac{⟨{\mathcal{A}}^k{\mathcal{U}}^{\prime 2}⟩}{⟨{\mathcal{U}}^2⟩}} \mathrm{for} ⟨{\mathcal{U}}^2⟩=⟨u^2⟩,\\ {\left({\mathcal{A}}^k{\mathcal{U}}^{\prime }\right)}^{\prime }+\mathbb{L}\left[\mathcal{A}\right]\mathcal{U}=0, {\left(a^k{u}^{\prime }\right)}^{\prime }+\mathbb{L}\left[a\right]u=0.\end{array}$$

(83)

The denominators of the fractions to the left and right of the auxiliary inequality (83) are identical. The nominators in the inequality (83) are, however, different. Thus, the nominators should be compared. The inequality for the nominators, which has to be proven, reads:

$$⟨a^k{u}^{\prime 2}⟩\le ⟨a^k{\mathcal{U}}^{\prime 2}⟩\le ⟨{\mathcal{A}}^k{\mathcal{U}}^{\prime 2}⟩.$$

(84)

At this point, the optimality condition (71) with $\lambda =k$ will be used:

$$\mathcal{A}={{\mathcal{U}}^{\prime }}^{{\displaystyle \frac{2}{1-k}}}.$$

Namely, the substitution of the optimality condition (71) into (84) delivers the inequality for $k\ge 1$:

$$⟨{a^k\mathcal{A}}^{1-k}⟩\le ⟨{{\mathcal{A}}^k\mathcal{A}}^{1-k}⟩, ⟨\mathcal{A}⟩=⟨a⟩.$$

(85)

The equality in (85) takes place only for $\mathcal{A}=a$. The validity of the yet suspected inequality (85) follows directly from the Hölder’s inequality [22]. Consequently, it follows the inequality for nominators (85) and, finally, the desired inequality (83).

Combining (83) and (85) delivers:

$$\mathbb{L}\left[a\right]=⟨a^k{u}^{\prime 2}⟩\le ⟨a^k{\mathcal{U}}^{\prime 2}⟩\equiv ⟨{a^k\mathcal{A}}^{1-k}⟩\le ⟨{{\mathcal{A}}^k\mathcal{A}}^{1-k}⟩=⟨{\mathcal{A}}^k{\mathcal{U}}^{\prime 2}⟩\equiv \mathbb{L}\left[\mathcal{A}\right]$$

It was thus demonstrated that, for any arbitrary value of $a$, the associated eigenvalue is less than

$$\mathbb{L}\left[a\right]\le \mathbb{L}\left[\mathcal{A}\right].$$

(86)

The equality in Equation (86) is only achieved for the optimal configuration of twisted rod, characterized by its optimal shape, $\mathcal{A}$, and the limited volume of material, $\mathcal{V}$. When the shape exponent, $k\ge 1$, is employed, the game is convex. In general, the game will be convex if the function $J=J \left(a\right)$ is convex with respect to its argument.

In accordance with the necessary optimality conditions (71), the rod is capable of delivering the lowest possible upper value of the game:

$$\mathcal{G}\left[a\right]={\displaystyle \frac{\mathbb{P}}{E\mathcal{C} \mathbb{L}\left[a\right]}}\ge {\displaystyle \frac{\mathbb{P}}{E\mathcal{C} \mathbb{L}\left[\mathcal{A}\right]}}\stackrel{\scriptscriptstyle\mathrm{def}}{=}{\mathcal{G}}_{opt}.$$

(87)

It follows from (87), that the value of functional game ${\mathcal{G}}_{opt}=\mathcal{W}\left[\mathcal{A}\right]$ for the optimal distribution of thickness $\mathcal{A}\left(\xi \right)$ is less than the payoff functional (distortion energy $\mathcal{G}\left[a\right]$) for an arbitrary distribution of thickness $a\left(\xi \right)$ of the same volume:

$$⟨a⟩=⟨\mathcal{A}⟩=\mathcal{V}.$$

(88)

If the volume of an arbitrary thickness distribution is inferior to the volume of the optimal thickness distribution, the stronger inequality follows.

$$⟨a⟩<⟨\mathcal{A}⟩\Rightarrow \mathbb{L}\left[a\right]<\mathbb{L}\left[\mathcal{A}\right].$$

(89)

The relations (87)–(89) solve the “superstratum” game for the twisted rod with a torque distribution that is not uniquely defined.

6.5. In Section 6, the rod is subjected to arbitrary twist moments, and the designer determines the optimal design of the twisted bar, ensuring the greatest stiffness.

7. Nash and Pareto Fronts

7.1. Pareto efficiency is a specific characteristic of multifunctional equilibrium. A situation is defined as efficient, or Pareto-optimal, if no entity can improve its satisfaction of needs through further activities without threatening any other entities. The central prerequisite for this state is perfect competition, without which the optimum cannot be realized in principle, as only this leads to the necessary equilibrium efforts [25]. Simply put, Pareto efficiency improvement makes at least one player better off but no one worse off. Consequently, a strategy combination is called Pareto-efficient if no Pareto efficiency improvement is possible.

We examine the above solution from the viewpoint of inequalities theory and reveal the mathematical sense of the PARETO and NASH fronts [26,27]. There exists the relation between objective functionals, which expresses as the isoperimetric inequality:

$$E\mathcal{C}{l}^2{\displaystyle \frac{\mathbb{P}}{\mathcal{W}}}=\mathbb{L}\left[a\right]\le \mathbb{L}\left[\mathcal{A}\right]=E\mathcal{C}{l}^2{\displaystyle \frac{\mathbb{P}}{\mathcal{G}}}.$$

(90)

7.2. The Pareto and Nash fronts were coincided in this case [28]. The fronts emerge as the equality case $\mathcal{G}=\mathcal{W}\left[\mathcal{A}\right]$. Pareto fronts for the states of Nash equilibrium for different shape factors are displayed on Figure 5.

Section 7 examines the solution of Section 5 and Section 6 from the perspective of inequalities theory, elucidating the mathematical significance of the Pareto and Nash fronts [29].

8. Conclusions

The premise of this study is that there is currently no definitive understanding of the factors that influence the states of nature. The game method for structural optimization problems can be applied in situations when the external loads are not definitively prescribed [30,31,32]. Statistical decision theory is concerned with making decisions in the absence of precise probability information. The conflict between nature and operators (“ordinal players”) is examined through the lens of game theory (“substratum” game). The payout matrix is relevant for one ordinal player (“operator”) and the profit he makes if he employs his strategy while the second natural player (“nature”) is in a specific state. For greater accuracy, we propose referring to nature’s strategies as states. The content of the consequent theory could be summarized as follows. In the matrix game, there is a single payoff matrix. From the viewpoint of the optimization theory, there is one goal function. Thus, the optimization problem is of a scalar type. This goal function is the value of the matrix game. The win of “nature” is the loss of the “operator” as both players on the low-level. This game is antagonistic with only one goal function. The designer achieves the most appropriate value for this goal function.

In the bi-matrix game, there are two payoff matrices. From the viewpoint of optimization theory, there are two goal functions. The optimization problem is of a vector type. These goal functions come from the solution of bi-matrix game. The equilibrium state between the interests of “nature” and “operator” results in the solution of the game on the low-level. The designer achieves the most appropriate value for this goal function in accordance with the methods of vector optimization

The essence of the method is to identify the structure that optimally resists the worst external load. In the context of classical structural optimization, the “cardinal” players are tasked with assuming the role of “control functions”. Similarly, the “cardinal” players are responsible for modifying the governing equations and payoff functions in the game formulations (“superstratum” game). If a relation between objective functionals, which could be expressed in terms of an isoperimetric inequality, exists, then the Pareto and Nash fronts coincide and emerge as the equality case of the isoperimetric inequality.