Empowering Remote Living: Optimizing Hybrid Renewable Energy Systems in Mexico

Abstract

The developing environmental consequences of excessive dependence on fossil fuels have pushed many countries to invest in clean and renewable energy sources. Mexico is a country that, due to its geographic and climatic diversity, can take advantage of this potential in renewable energy generation and reduce its dependence on fossil fuels while developing strategies to improve its energy system. This study investigated the feasibility of the autonomous use of two hybrid renewable energy systems and a photovoltaic system to power homes in a remote location. With the help of HOMER Pro Version 3.14.5 software, a model was made to evaluate the operation of three systems for one year, and the demand was predicted according to a given scenario. In addition, the optimal configuration of the components of each system was determined. The results showed that the simultaneous use of solar systems with a converter and a backup system consisting of a diesel generator and batteries would be the most viable and reliable option for generating renewable energy at the selected location, offering electricity with a renewable fraction of more than 80%.

1. Introduction

Currently, access to electricity is seen as a key indicator of a country’s sustainable economic development and the well-being of its inhabitants. It is essential for any nation aspiring to progress and prosper to ensure its citizens have access to electricity. In recent years, the rapid growth of the population, combined with technological advancements, has created a significant energy demand, particularly electricity [1]. Conversely, many rural and remote areas, especially in developing countries, still lack access to electricity. To address this challenge, solutions such as extending existing electrical grids or deploying standalone or off-grid energy generation systems can be considered [2]. However, a significant portion of the world’s electricity, approximately 75%, is still generated using fossil fuels [3]. The problems associated with heavy reliance on these fuels, such as environmental degradation and climate change due to CO₂ emissions, have driven the growth of renewable energies. Energy sources like wind, solar, and geothermal are becoming increasingly popular and are seen as viable alternatives to mitigate these negative effects [4]. Nevertheless, using renewable energy systems that operate independently of the grid to meet local energy demands presents various challenges, primarily due to the high initial investment costs and the low reliability resulting from the inherent unpredictability of renewable sources [5].

The hybrid renewable energy system (HRES) concept has been developed to tackle these challenges. The HRES combines conventional and renewable energy sources and is designed to generate and store electricity autonomously or off the grid, catering to specific demand points. These systems are particularly effective in bringing electricity to remote and hard-to-reach rural areas [6,7].

These systems are designed to maximize efficiency, reliability, and sustainability in energy generation. HRESs offer certain advantages over single-source generation methods, including reducing dependency on a single energy source, thereby achieving greater reliability and stability in supply. They also optimize space usage by combining different technologies to better utilize the available land. Additionally, they allow for diversification and complementarity by leveraging the strengths of each generation source and providing greater resilience to climatic and resource variations. However, challenges include implementation costs, operational complexity, and integrating different energy sources. Therefore, the system choice depends on local resource availability, energy needs, budget, and environmental objectives [7].

Several studies have explored hybrid renewable energy systems (HRESs). A statistical analysis was conducted to determine the key criteria for optimizing hybrid systems and the tools employed in their development [8]. An updated review on the optimal multi-objective design of hybrid energy systems offers pertinent and current information on this subject [9]. This review emphasizes four fundamental categories of HRES: sizing, optimization, control, and energy management [10]. Various modeling techniques and computer simulation tools have been developed and advanced over time [11]. One study focused on detailed modeling of hybrid energy resources, standby power systems, power conditioning units, and techniques for managing energy flow [12]. A comprehensive review was conducted on different types of energy storage systems (ESSs), including their structures, classifications, advantages, and disadvantages in microgrid applications [13]. Another detailed analysis provided fundamental reasons and advantages driving the adoption of HRES [14]. A review examined the tools and limitations for optimizing HRES systems, along with an analysis of available types of storage and backup systems [15]. Additionally, recent classifications, evaluation indicators, and sizing methodologies for hybrid renewable energy systems were reviewed [16].

Additionally, several articles analyze case studies on the implementation of hybrid renewable energy systems (HRESs) in rural residential communities. For example, one study [17] explores an HRES designed for a rural residential community, integrating photovoltaic panels (PVs), a wind energy conversion system (WECS), a battery energy storage system (BESS), and a diesel generator (DG) with a total capacity of 32 kW to meet the energy demands of 20 households. Another case study [18] highlights a similar system with a total installed capacity of 56 kW, designed to cater to the energy needs of over 50 homes and six stores. A third case study [19] focuses on an HRES deployed in a rural residential area, integrating PVs, WECS, BESS, and DG, with an installed capacity of 44.1 kW to meet the energy needs of 10 homes. Further research [20] evaluates various energy sources deployed in a rural residential area with an installed capacity ranging between 50 and 60 kW and servicing 41 homes, and includes an assessment of different energy generation technologies such as solar PVs, WECSs, diesel generators, and BESSs. Another study [21] summarizes the installation of a PV-PEMFC hybrid system in a rural residential area, focusing on its capacity and the benefits of combining solar and fuel cell technologies to meet energy demands sustainably. These systems are designed to integrate multiple renewable energy sources and storage technologies to optimize energy production, storage, and management in a rural residential setting [22]. Each configuration varies slightly in installed capacity and the combination of renewable energy and storage components, aiming to provide sustainable and reliable electricity while reducing dependence on traditional fossil fuels.

To achieve Net Zero-Energy Buildings (NZEBs), it is essential to minimize energy consumption through efficient design and fulfill the remaining energy needs with renewable energy sources. Hybrid renewable energy systems (HRESs) integrate multiple renewable sources, such as solar, wind, and biomass, and are often paired with storage solutions to ensure a dependable energy supply. Reaching NZEBs through the optimization of HRESs involves a comprehensive approach that combines advanced energy efficiency strategies, the strategic integration of various renewable energy sources, and intelligent control and management systems. Focusing on these areas allows buildings to reduce their energy demand and rely on clean, renewable energy, moving closer to the goal of zero-energy consumption [23].

2. Materials and Methods

2.1. Study Area

In this case study, the Yucatan Peninsula region in Mexico, which has excellent natural resources for electricity generation, was analyzed. In addition, government databases were searched for localities without access to electricity. The selected locality was in the state of Campeche, municipality of Carmen, El Arca.

El Arca is located 101.8 km from Ciudad del Carmen, Campeche, the most populated locality of the municipality, in a westerly direction. As of 2020, it is known that there are 48 inhabited dwellings in the village, of which more than 50% do not have electricity services, with an equivalent of twenty-five dwellings without electricity. Figure 1 shows the maps of Mexico and the state of Campeche, where the study locality is located.

2.2. Estimation of Electricity Consumption

The off-grid hybrid system has been meticulously designed to provide a reliable source of electricity for the town of Arca, located in Ciudad del Carmen, Campeche. The village has both solar and wind potential. This community consists of several houses and is mainly focused on agricultural activities. The energy demand consists of 25 households that require a supply of lights and appliances.

Specific details of the energy consumption reveal that the total demand for one dwelling is 4.88 kW with an energy consumption of 177.14 kWh/day and a load factor of 0.123. By incorporating a random variable of 52.184% from hour to hour and 11.082% from day to day, variability is introduced into the load data throughout the year.

Table 1. Daily and monthly load profile of El Arca.

Equipment per House	Power (W)	Units (u)	Total Load (kW)	Operating Time (h/Day)	Power Consumption (kW*h/Day)
Refrigerator	60	1	0.06	5	0.3
Fan	85	2	0.17	5	0.85
Electric Cooker	1000	1	1	2	2
LED lamps	9	8	0.072	16	0.238
Television	60	1	0.06	6	0.36
Washing machine	450	1	0.45	1	0.450
Iron	1200	1	1.2	0.5	0.6

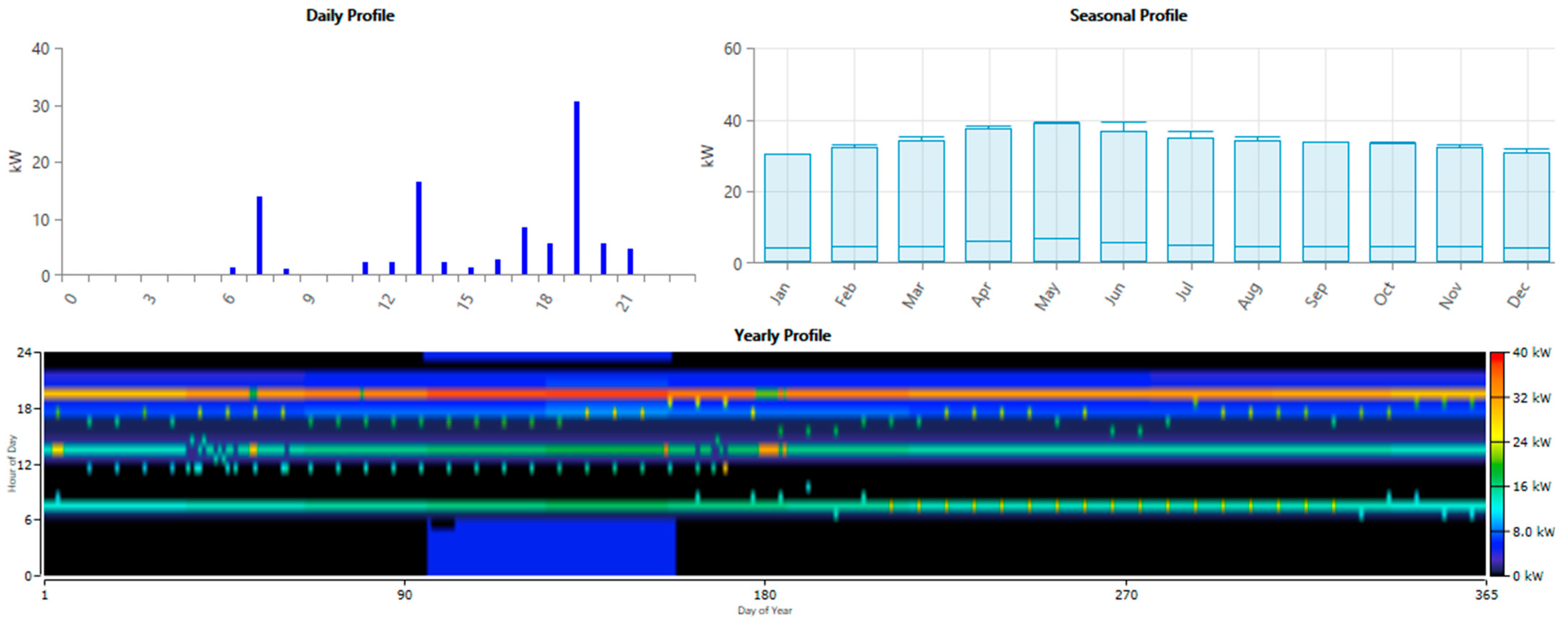
shows the equipment to be considered for the profile estimation [24]. These load data are entered into the HOMER Pro Version 3.14.5 software, which allows graphical representations of hourly and monthly load profiles, as shown in Figure 2.

Figure 2 shows the estimated load behavior in hours, days, months, and within a year. In the day behavior, there are three hours when the demand is high, mainly due to the use of food-cooking equipment.

Specific energy consumption details reveal that the total demand for a home is 4.8 kW, with an energy consumption of 177.14 kWh/day and a load factor of 0.123. By incorporating a random variable of 52.184% from hour to hour and 11.082% from day to day, variability is introduced into the load data throughout the year.

2.3. Solar Panel

The power output of a solar panel is a crucial measure that determines its ability to generate electricity from solar energy. HOMER calculates the power output using the equation below [17,25,26].

$$P_{PV}=Y_{PV}\ast F_{PV}\ast \left(\frac{G_T}{G_{T,STC}}\right)\ast [1+{\alpha }_P\ast (T_c-T_{c,STC}\left)\right]$$

(1)

where:

$Y_{PV}$: The nominal capacity of the PV generator, i.e., its power output under standard test conditions [kW].

$F_{PV}$: The photovoltaic derating factor [%].

$G_T$: Incident solar radiation on the photovoltaic field at the current time step [kW/m²].

$G_{T,STC}$: Incident radiation under standard test conditions [1 kW/m²].

${\alpha }_P$: The power temperature coefficient [%/°C].

$T_c$: The temperature of the photovoltaic cell at the current time step [°C].

$T_{c,STC}$: The temperature of the photovoltaic cell under standard test conditions [25 °C].

2.4. Wind Turbine

First, HOMER estimates the wind speed at the hub height of the wind turbine. This calculation involves adjusting the measured wind speed at a specific height (typically ground level) to the hub height, considering how wind speed changes with elevation. Then, HOMER uses the previously calculated wind speed to estimate the amount of energy generated by the turbine at that speed, assuming standard air density. This estimation is derived from the turbine’s power curve, which illustrates how wind speed correlates with electrical power production. Lastly, HOMER adjusts the generated energy value to account for the actual air density at the turbine’s location. Air density varies with altitude, temperature, and atmospheric pressure, influencing the turbine’s efficiency and power generation. This adjustment ensures the energy estimation accurately reflects the specific environmental conditions surrounding the turbine [2,26].

2.4.1. Calculation of Hub Height Wind Speed

At each time interval, HOMER determines the wind speed at the turbine’s hub height by utilizing the inputs provided on the Wind Resource page along with the Wind Shear setting you specify. If the logarithmic law is applied, HOMER calculates the wind speed at hub height using the following equation:

$$U_{hub}=U_{anem}*\frac{\ln (Z_{hub}/Z_0)}{\ln (Z_{anem}/Z_0)}$$

(2)

where:

$U_{hub}$: Wind speed at the wind turbine hub height [m/s].

$U_{anem}$: Wind speed at the height of the anemometer [m/s].

$Z_{hub}$: Wind turbine hub height [m].

$Z_{anem}$: The height of the anemometer [m].

$Z_0$: The length of the surface roughness [m].

2.4.2. Calculation of Turbine Power Output with Standard Air Density

Once HOMER calculates the wind speed at the hub height, it refers to the wind turbine’s power curve to estimate the power output at that specific wind speed under standard temperature and pressure conditions. In Figure 3, the red dotted line shows the wind speed at the hub height, while the blue dotted line represents the power output predicted by the power curve for that wind speed. If the wind speed at the hub height falls outside the range specified by the power curve, the turbine does not generate power, based on the assumption that wind turbines do not operate at speeds below the minimum or above the maximum cut-off thresholds [26].

2.4.3. Applying Density Correction

Once HOMER determines the wind speed at hub height, it queries the wind turbine power curve to calculate the expected power output of the wind turbine at that wind speed under standard temperature and pressure conditions.

Power curves typically outline the performance of wind turbines under standard temperature and pressure conditions. To align these predictions with real-world conditions, HOMER adjusts the power value indicated by the power curve by multiplying it by the air density ratio. This adjustment is made according to the following equation [1,2,26]:

$$P_{WTG}=P_{WTG,STP}\ast \left(\frac{\rho }{{\rho }_0}\right)$$

(3)

where:

$P_{WTG}$: The power of the wind turbine [kW].

$P_{WTG,STP}$: The wind turbine power at standard temperature and pressure [kW].

$\rho$: The actual density of the air [kg/m³].

${\rho }_0$: The density of air at standard temperature and pressure (1225 kg/m³).

2.5. Inverter

AC and DC power supplies require conversion between the two since the load demand is AC. A power inverter is needed to convert the DC generated by the PV module and batteries to AC for the load to consume. The inverter selected is the MEAN WELL TS 3000-148 (MEAN WELL USA Inc., Fremont, CA, USA), with a power rating of 3 kW and a capital cost of $1600. The lifetime of the inverter is estimated at ten years, and its efficiency is 91% [1,27].

2.6. Diesel Generator

In this study, it is assumed that a diesel generator serves as a backup power source to provide extra electricity when the supply from renewable sources is not enough to meet the demand. Most calculations in this section are based on the fuel curve, which shows how much fuel the generator consumes to produce electricity. For simplicity, it is assumed that the fuel curve is linear. Consequently, the fuel consumption of the generator is expressed with the following equation [17]:

$$m_{fuel}=\mathrm{F}=F_0\ast Y_{gen}+F_1\ast P_{gen}$$

(4)

In this context, $F_0$ represents the interpolated coefficient of the fuel curve, while $F_1$ is the slope of the fuel curve. $Y_{gen}$ denotes the rated power capacity of the generator, and $P_{gen}$ is the actual power output of the generator. The efficiency of the generator is defined as the ratio of the electrical power output it produces to the total power consumed during the combustion process.

$$n_{gem}=\frac{3.6\ast P_{gen}}{m_{fuel}\ast {LHV}_{fuel}}$$

(5)

In this equation, LHV_fuel refers to the lower heating value of the fuel. To find the optimal capacity for the diesel generator, this parameter was varied incrementally from 0 to 100 kW in steps of 10 kW [17,26].

2.7. Battery

HOMER determines the maximum power that the storage bank can absorb at each time step. This maximum absorbable power is crucial for HOMER to decide whether the storage bank can take in all the excess renewable energy or how much extra power a cyclic load generator should produce. The maximum load power that the storage bank can handle changes at each time step based on its current state of charge and its recent charging and discharging patterns.

HOMER applies three distinct constraints on the maximum load power that the storage bank can accept. The first of these limitations is derived from the kinetic storage model and it is represented by the following equation:

$$P_{batt,cmax,kbm}=\frac{k\ast Q_1\ast e^{-k∆t}+Q\ast k\ast c(1-e^{-k∆t})}{1-e^{-k∆t}+c(k\ast ∆t{-1+e}^{-k∆t})}$$

(6)

where:

$Q_1$: The available energy [kWh] in the accumulator at the beginning of the time step.

$Q$: The total energy [kWh] stored at the beginning of the time step.

$c$: The storage capacity coefficient.

$k$: The storage rate constant.

$∆t$: The time step length [h].

The second limitation refers to the maximum loading rate of the Al-storage Component. The storage charge power corresponding to this maximum charge rate is given by the following equation:

$$P_{batt,cmax,mcr}=\frac{(1-e^{-{\alpha }_c∆t})(Q_{max}-Q)}{∆t}$$

(7)

where:

${\alpha }_c$: The maximum charge rate of the accumulator [A/Ah].

$Q_{max}$: The total capacity of the storage bank [kWh].

The third limitation refers to the maximum load current of the storage component. The maximum load power of the storage bank corresponding to this maximum load current is given by the following equation:

$$P_{batt,cmax,mcc}=\frac{(N_{batt}*I_{max}*V_{nom})}{1000}$$

(8)

where:

$N_{batt}$ = number of storage bank batteries.

$I_{max}$ = maximum battery charging current [A].

$V_{nom}$ = nominal voltage of the accumulator [V].

HOMER sets the maximum storage load power equal to the lowest of these three values, assuming that each is applied after load losses, therefore:

$$P_{batt,cmax}=\frac{MIN(P_{batt,cmax,kbm},P_{batt,cmax,mcr},P_{batt,cmax,mcc})}{n_{batt,c}}$$

(9)

where $n_{batt,c}$ is the storage load efficiency.

The maximum discharge power ${(P}_{batt,cmax}$) of the battery banks is calculated according to Equations (6)–(8).

$$P_{batt,dmax}=n_{batt,d}\ast P_{batt,dmax,kbm}$$

(10)

where:

$$P_{batt,dmax,kbm}=\frac{-k\ast Q_1\ast e^{-k∆t}+Q\ast k\ast c(1-e^{-k∆t})}{1-e^{-k∆t}+c(k\ast ∆t{-1+e}^{-k∆t})}$$

(11)

$n_{batt,d}$: The storage discharge efficiency.

2.8. Economic Assessment

HOMER defines the levelized cost of energy (COE) as the average expense incurred for each kWh of useful electrical energy generated by the system. To determine the COE, HOMER calculates it by dividing the annualized cost of electricity production (which is the total annualized cost minus the expenses associated with serving the thermal load) by the total electrical load that has been met. This calculation is performed using the following equation:

$$COE=\frac{C_{ann,tot}-C_{boliler}{\ast H}_{served}}{E_{served}}$$

(12)

where:

C_ann,tot = total annualized system cost [$/year].

C_boiler = marginal boiler cost [$/kWh].

H_served = total thermal load served [kWh/year].

E_served = total electrical load served [kWh/year].

The second term in the numerator represents the part of the annualized cost attributed to serving the thermal load. In systems like wind or photovoltaic systems, which do not provide a thermal load, this second term is zero (H_thermal = 0). Thus, it does not contribute to the annualized cost.

$$COE=\frac{C_{ann,tot}}{E_{served}}$$

(13)

The levelized cost of energy (COE) is a useful metric for comparing different energy systems, but HOMER does not use it to rank these systems. Instead, HOMER ranks systems based on their total Net Present Cost (NPC). The NPC represents the present value of all costs incurred over the system’s lifetime, subtracted by the present value of all the revenues it generates.

Costs in the NPC calculation include capital expenditures, replacement costs, operational and maintenance expenses, fuel costs, emission penalties, and the cost of purchasing power from the grid. Revenues include the residual value at the end of the project and income from selling electricity back to the grid.

To calculate the total NPC, HOMER sums the discounted cash flows for each year over the project’s lifetime. This total NPC is HOMER’s primary economic output and the criterion by which it ranks all system configurations in the optimization results. It also serves as the foundation for calculating the total annualized cost and the levelized cost of energy. The NPC is calculated using the following equations:

$$\mathrm{N}\mathrm{P}\mathrm{C}=\frac{C_{ann,tot}}{{CRF}_{(i,N)}}$$

(14)

where:

CRF: This capital recovery factor is calculated using the following equation.

$$\mathrm{C}\mathrm{R}\mathrm{F}=\frac{{i(1+i)}^N}{{(1+i)}^N-1}$$

(15)

where i is the real interest rate, N is the estimated lifetime for the system, and i is calculated as shown in the following equation, where $i\mathbf{’}$ is the nominal interest rate 0.

$$i=\frac{i’-f}{i+f}$$

(16)

2.9. Renewable Fraction (RF)

The renewable portion refers to the share of overall electric power generated from renewable sources. It is calculated as the ratio between the total power generated by renewable energy sources and the total power produced by the system as a whole. This calculation is performed as follows:

$$\mathrm{R}\mathrm{F}\left(\mathrm{\%}\right)=1-\left(\frac{{\mathsf{\Sigma }P}_{diesel}}{{\mathsf{\Sigma }P}_{renewable}}\right)\ast 100$$

(17)

where $P_{diesel}$ is the power output of the diesel generator and $P_{renewable}$ is the power output of renewable sources (wind and solar) of the considered system [17].

2.10. Emission

HOMER calculates the emissions of the following six pollutants.

•

Carbon dioxide (CO₂)

•

Carbon monoxide (CO)

•

Unburned hydrocarbons (UHC)

•

Particulate matter (PM)

•

Sulfur dioxide (SO₂)

•

Nitrogen oxides (NO_X)

HOMER calculates emissions of various pollutants from electricity generation, thermal energy production, and grid electricity consumption. Before simulating the power system, HOMER determines the emissions factor for each pollutant (expressed in kilograms emitted per unit of fuel consumed). Following the simulation, annual pollutant emissions are computed by multiplying these factors by the total annual fuel consumption.

Emission factors are directly provided for carbon monoxide, unburned hydrocarbons, particulate matter, and nitrogen oxides. For carbon dioxide and sulfur dioxide, HOMER calculates emissions factors based on the carbon and sulfur content of the fuel. This process relies on three primary assumptions [26]:

•

All carbon present in the fuel that is not emitted as carbon monoxide or unburned hydrocarbons is emitted as carbon dioxide.

•

The fraction of carbon in the emissions from unburned hydrocarbons is identical to the fraction of carbon present in the fuel itself.

•

All sulfur in the burned fuel that is not emitted as particulate matter is emitted as sulfur dioxide.

2.11. Dispatch Strategy

A dispatch strategy refers to a defined set of rules governing how generators and battery banks operate within a system. HOMER offers modeling for two primary dispatch strategies: cyclic load and load following. The optimal strategy depends on various factors such as generator and battery bank sizes, fuel prices, operational and maintenance costs, the proportion of renewable energy in the system, and the characteristics of renewable resources. When both strategies are modeled, HOMER simulates each system using both approaches, allowing users to determine which strategy is most optimal based on the simulation results.

The Cyclic Charging (CC) strategy operates such that whenever the diesel generator is running, it operates at its maximum capacity. Any surplus energy generated beyond immediate demand is directed towards charging the battery bank. This strategy is typically advantageous in systems where there is limited or no renewable energy available [2,17].

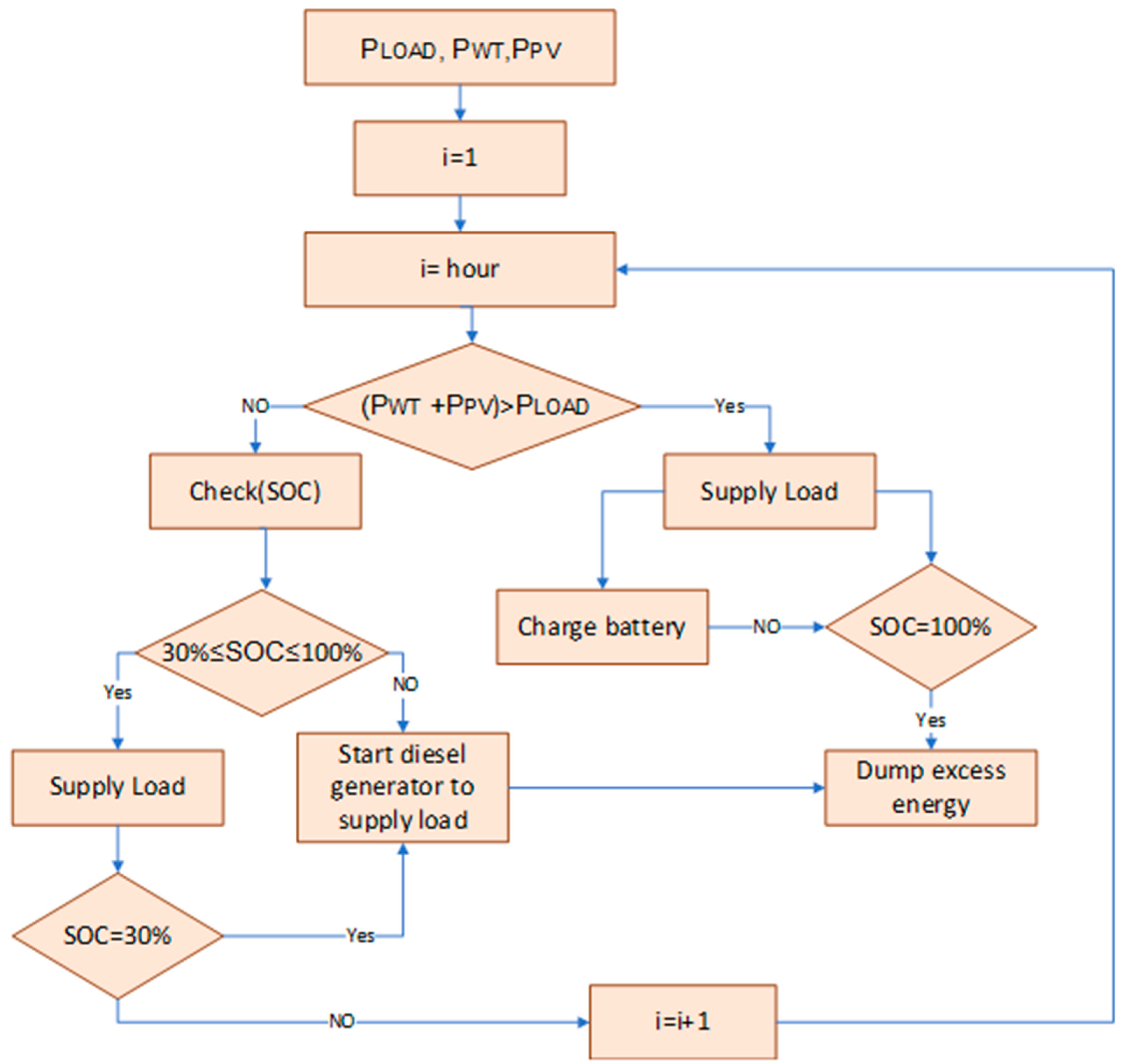
The Load-Following (LF) strategy involves the diesel generator producing enough power to meet current demand whenever it is required without running at full capacity unnecessarily. Figure 4 shows the Load-Following strategy diagram. LF is usually preferred in systems with various renewable energy sources, where fluctuations in renewable energy production can sometimes exceed the immediate load requirements. For this study, the LF strategy will be employed [26,28].

3. Design and Specification Description of Hybrid System

3.1. Potential of Renewable Energy Sources

To design a solar photovoltaic system, it is essential to have information about the solar radiation and brightness index specific to the site. The feasibility of harnessing solar energy largely depends on the availability of sufficient daylight hours in the area [2]. For this assessment, data used for analysis were sourced from the National Aeronautics and Space Administration (NASA) via HOMER Pro Version 3.14.5 software based on the latitude and longitude coordinates of the site located in the state of Campeche, Mexico (latitude 18°54.0′ N, longitude 90°54.6′ W). The daily average solar radiation forecast for the site is 5.31 kW/m²/day. Over a span of twenty-two years, solar data, including clearness index and solar radiation, were obtained from NASA, varying from 0.533 to 0.605 for clearness index and from 4.040 kW/m²/day to 6.350 kW/m²/day for solar radiation, as detailed in

Table 2. Monthly average values of solar radiation and brightness at El Arca, Campeche.

Months	Clearness	Daily Radiation (kWh/m2/Day)
January	0.559	4.280
February	0.588	5.060
March	0.605	5.880
April	0.603	6.350
May	0.575	6.250
June	0.538	5.870
July	0.533	5.780
August	0.533	5.650
September	0.535	5.330
October	0.537	4.780
November	0.569	4.460
December	0.552	4.040
Annual Average	0.56	5.31

. The month of November recorded the lowest solar radiation value at 4.040 kW/m²/day, while March saw the highest at 6.350 kW/m²/day. Despite the lowest solar radiation value occurring in November, the solar system remains capable of generating electricity.

Wind energy represents another viable renewable source for generating electricity. Wind turbines are equipped with generators designed to convert the kinetic energy from wind into electrical energy. This process allows wind power to contribute to the overall renewable energy mix by generating electricity efficiently and sustainably [27]. The site under evaluation must have adequate wind speeds to effectively drive wind turbines for efficient electrical energy generation. Wind turbines designed for electric power generation can operate within specific wind speed ranges as specified by manufacturers, typically starting from 2.5 m/s and reaching up to 25 m/s.

At the case study location for this evaluation, the average wind speed over the year is 3.05 m/s at a height of 50 m. Throughout the year, wind speeds vary between 2.05 m/s and 25 m/s, indicating a range suitable for harnessing wind energy effectively [28]. The wind speed at the research site varies between 2.660 m/s and 3.340 m/s throughout the year, as determined from data obtained via NASA using HOMER Pro Version 3.14.5 software and detailed in

Table 3. Monthly average wind speed values for El Arca, Campeche.

Months	Average Speed (m/s)
January	3.100
February	3.160
March	3.340
April	3.320
May	3.150
June	3.060
July	3.080
August	2.840
September	2.660
October	2.870
November	3.000
December	3.040
Annual Average	3.05

. The lowest wind speed occurs in September, while March experiences the highest wind speed at 3.34 m/s. Despite these fluctuations, the average wind speed at the research site remains within the range necessary for harnessing energy and efficiently generating electricity from wind power.

Environmental temperature significantly impacts the efficiency and performance of various technologies, such as solar panels and energy storage systems. Temperature variations can influence photovoltaic energy production, directly affecting the efficiency of solar cells. Likewise, ambient temperature influences the storage capacity and lifetime of the batteries used in these systems. Understanding and accounting for these thermal effects is crucial to optimize the operation and overall efficiency of the hybrid system, thus ensuring sustainable and reliable performance over time. Temperature values ranging from 23.520 degrees Celsius to 29.970 degrees Celsius are measured at the location being studied. The lowest temperature is found in December and the highest in May.

Table 4. Average monthly temperatures in El Arca, Campeche.

Months	Temperature (℃)
January	23.540
February	25.150
March	27.170
April	29.570
May	29.970
June	27.890
July	26.970
August	26.920
September	26.410
October	25.430
November	24.100
December	23.520
Annual Average	26.39

shows the average monthly values.

3.2. Hybrid Renewable Energy Network Design

The design and simulation process involves integrating advanced technologies, energy management algorithms, and accurate mathematical models to evaluate grid performance under different conditions.

This methodology makes it possible to anticipate and address challenges, such as the inherent variability of some renewable sources, thus optimizing energy generation, storage, and distribution. The successful implementation of these hybrid grids contributes to reducing greenhouse gas emissions and promotes energy independence and adaptation to a changing energy landscape. Figure 5 shows the architecture used by HOMER to perform the techno-economic analysis.

Some criteria were defined for analyzing the different scenarios, and all will be implemented in the same way.

Table 5. Voltage levels by stages [29].

Sources	Output Voltage (V)	Converters (V)	BUS Voltage (V)	Inverter (V)
Solar Panels	348	348/48	48	48/127
Wind Turbine	48/110	110/48	48
Diesel Generator	110	110/48	48
Battery Systems	24	24/48 (Bidirectional)	48

and

Table 6. Technical and economic data [30].

Parameters	Wind Turbine	Panels	Batteries	Generator	Inverter
Model	Aeolos-V1kW	CS6K-285M	Generic	Generic	TS 3000-148
Manufacturer	Lotus Energy (Qingdao, China)	Canadian Solar (Guelph, ON, Canada)	Generic (Berthierville, QC, Canada)	Generic (Berthierville, QC, Canada)	MEAN WELL (Fremont, CA, USA)
Capacity (kW)	1	0.285	1.02	50	3000
Capital cost ($)	5320	240	3500	500	1600
Replacements ($)	5320	240	3500	500	1600
Maintenance ($/year)	200	10	50	0.03$/op hr
Lifetime (year)	20	25	15	15	10
Nominal voltage (V)	48/110	38.6	3.7	110	48/120
Current (A)	20.8/9	9.5	276	-	75

show the criteria established for the design of the hybrid systems.

Table 5 shows the output voltage values of each generation source (in the case of the panels, there would be a string of nine panels with an output voltage of 348 V). They will then be regulated by DC-DC converters to a value of 48 V and brought to a voltage of 127 AC by an inverter.

4. Simulation Results and Discussion

4.1. Optimization Analysis of the Hybrid Electric System

The following tables provide a detailed breakdown of different power generation and storage scenarios, focusing on the combination of solar panels (PV), wind turbines (WT), battery systems (BS), and diesel generators (DG). Each scenario represents a unique configuration that addresses the need to balance sustainable solar power generation with storage capacity and the availability of diesel generator backup. These scenarios are analyzed below (

Table 7. Sizing of each system.

Scenarios	PV (kW)	WT (kW)	BESS (kW)	DG (kW)	Inverter
I. PV-WT-BS-DG	45.5	1	150	50	42.5
II. PV-BS-DG	45.8	-	150	50	42.2
III. PV-BS	94.5	-	267	-	44.3

), highlighting key capabilities and strategies to ensure a robust and reliable electricity supply. This analysis provides a comprehensive view of the options available regarding power generation and storage, considering different combinations to meet energy demands in various contexts.

Table 7 shows the installed capacity of each generation element for the different scenarios. In the first two scenarios, the values of each component are almost the same despite not having the same number of elements. In the first scenario, wind generation contributes almost no generation to the system (Figure 6). The third scenario presents higher values, which means that to satisfy the demand, it is necessary to increase the capacity of the panels since there are no other generation sources to supply the market at times of low solar irradiance.

4.2. Economic Analysis of the Hybrid Electric System

One of the most important parts of evaluating any energy project is the economic analysis of its cost flows. The following table shows each system or scenario’s NPC and COE values.

Table 8. Overall costs of each scenario.

Scenarios	Operating Cost ($)	COE ($)	NPC ($)	NPC (%)
I. PV-WT-BS-DG	10,928	0.527	338,580	2.7
II. PV-BS-DG	10,687	0.513	329,687	-
III. PV-BS	10,990	0.632	406,093	18.8

defines the scenarios based on their profitability. We can conclude that scenario III has the highest NPC and COE, with a difference of 18.8% for scenario II and 16.1% for scenario I.

Table 9. Costs for each system.

Scenarios	Replacements ($)	Initial Cost ($)	Maintenance ($)	Return ($)	Fuel ($)
I. PV-WT-BS-DG	70,408.71	174,211	60,858.03	−16,565.18	49,667.63
II. PV-BS-DG	67,966.88	168,944	57,131.05	−15,035.38	50,680.23
III. PV-BS	97,980.04	240,804	87,140.08	−19,830.59	0

shows the cost flows of the three scenarios by type of cost for a more precise evaluation.

In Table 9, it can be seen that Scenario III has the highest initial cost (since it requires more equipment in panels and batteries) and has a higher cost in replacements and maintenance, indicating that it could not be economically profitable in the long term. Not having a diesel generator is an advantage in fuel costs, and being a system composed of panels and batteries and having a useful life longer than 20 years, it can be understood that scenario III will have a higher return. On the other hand, scenario II, despite having fuel costs and a lower return than the other scenarios, presents a lower NPC (Table 7) since most of the costs presented in the previous table are lower than those of the other proposed systems.

4.3. Output Energy Analysis of the Hybrid Electric System

Table 10. Energy production rates.

Scenarios	Energy Production (kWh/Year)	Energy Consumption (kWh/Year)	Excess Energy (kWh/Year)	Renewable Fraction (%)	Total Fuel (L/Year)
PV-WT-BS-DG	81,586	42,756	32,100	84.9	2575
PV-BS-DG	77,825	42,756	24,332	83.9	2724
PV-BS	155,032	42,728	105,612	100	0

shows the generation and energy consumption values for each system. In addition, the percentage of renewable energy for each scenario is shown.

Table 10 shows that, for the same demand, scenario III needs to produce the most energy. Therefore, it wastes the most energy per year (since no system is contemplated to drain this excess energy) and consequently has a higher energy cost, as shown in Table 9.

4.4. Environmental Analysis of the Hybrid System

The following table shows the environmental impact of these systems, including the number of substances released into the environment.

Table 11. Environmental parameters.

Contaminants	PV-WT-DG-B (kg/Year)	PV-DG-BS (kg/Year)	PV-BS (kg/Year)
Carbon Dioxide	6741	7130	0
Carbon Monoxide	42.1	44.5	0
Unburned Hydrocarbons	1.85	1.96	0
Sulfide Dioxide	16.5	17.5	0
Nitrogen Oxides	39.5	41.8	0
Suspended Particles	0.252	0.267	0
Total	6841	7237	0

shows that the second scenario is the most polluting since it is the one in which the diesel generator uses the most working hours, which is the most polluting element. The third scenario, composed only of solar panels, is not considered polluting.

5. Conclusions

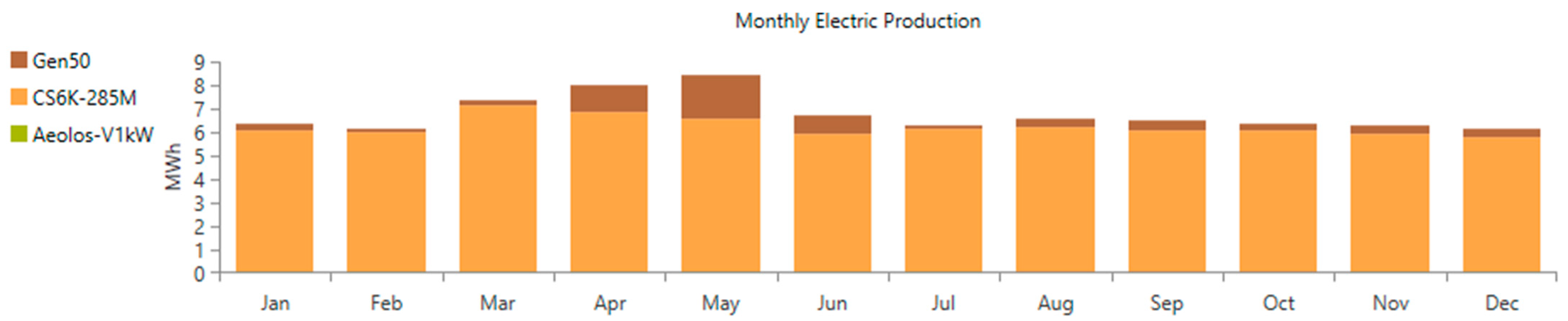
Management strategies employed in hybrid renewable energy systems are chosen based on specific study objectives. Many researchers prioritize techno-economic goals, examining both technical factors like duration, demand fulfillment, and system performance, as well as economic factors such as minimizing costs, maximizing savings, and reducing energy expenses.

To achieve these objectives, researchers utilize various algorithms, including fuzzy logic, particle swarm optimization, neural networks, and specialized software such as HOMER. These tools facilitate monitoring and optimization of components within hybrid renewable energy systems, enabling efficient evaluation of system performance and economic viability. From the scenarios analyzed above, it is concluded that the most appropriate scenario for this location is composed of photovoltaic panel systems, battery systems, and a diesel generator (PV-BESS-DG). Focusing on the PV-BESS-DG scenario shows a combination that stands out for its economic feasibility and operational balance. The PV-BESS-DG scenario demonstrates solid economic feasibility with the lowest NPC of $308,911 and a levelized COE of $0.480/kWh, efficiently integrating PV with BESS and DG. The absence of WT suggests a storage strategy prioritizing efficiency and cost control. Combining PV and BESS allows continuous generation and greater operational autonomy, optimizing available solar resources. Including the DG as strategic support guarantees the reliability of the supply, especially in situations of low solar generation or adverse weather conditions. On the other hand, scenario III, composed of photovoltaic energy and battery storage, is the least profitable of those analyzed despite having the best return on investment. Their high initial capital and replacement costs make the proposed hybrid systems more attractive when making an investment estimated in 25 years.