Risk Management and Assessment Hybrid Framework for Business Process Reengineering Projects: Application in Automotive Sector
Abstract
1. Introduction
2. Literature Review
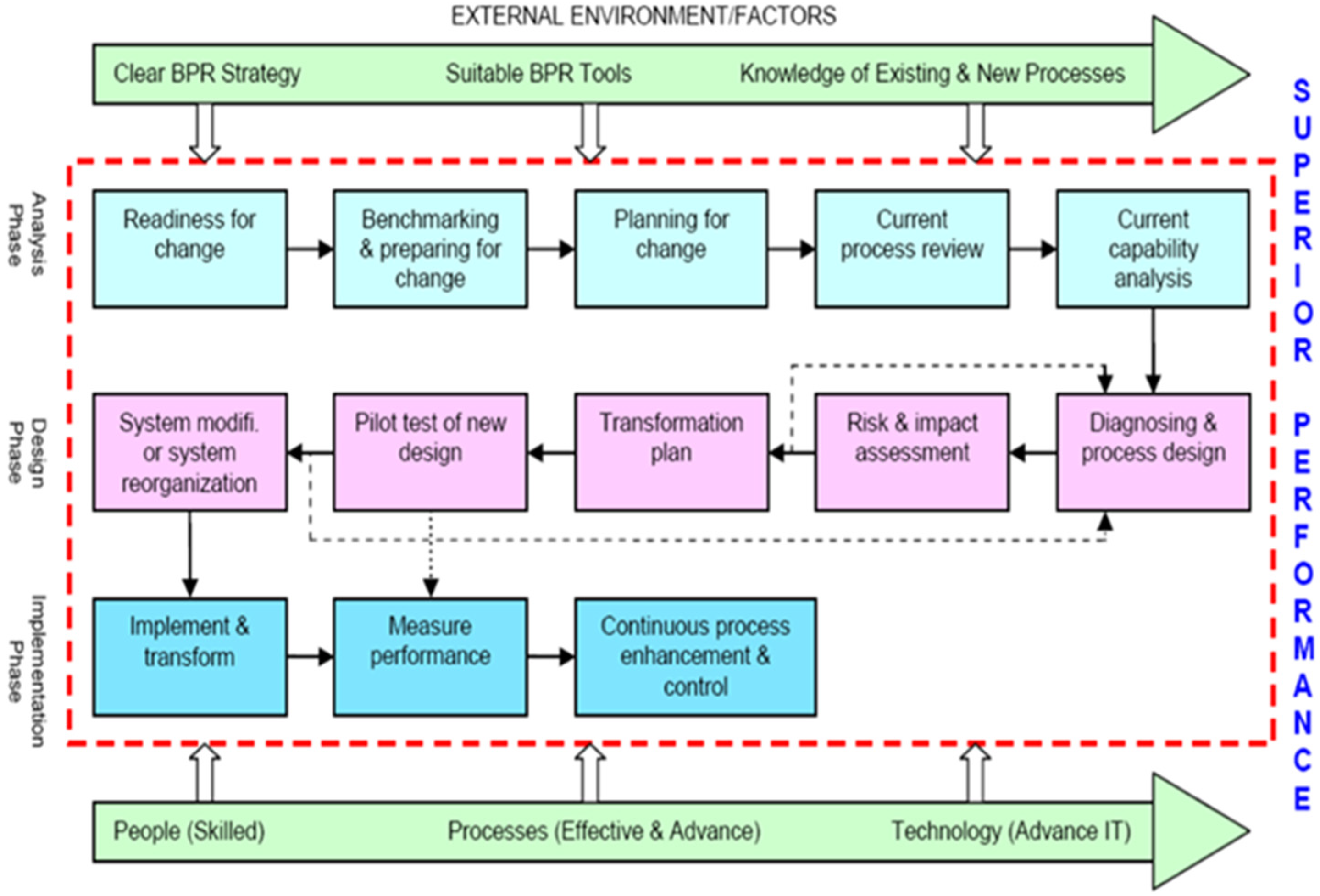
2.1. BPR
2.2. Risk Management and Methodologies
2.3. FMEA
2.4. PFMEA
2.5. DEA
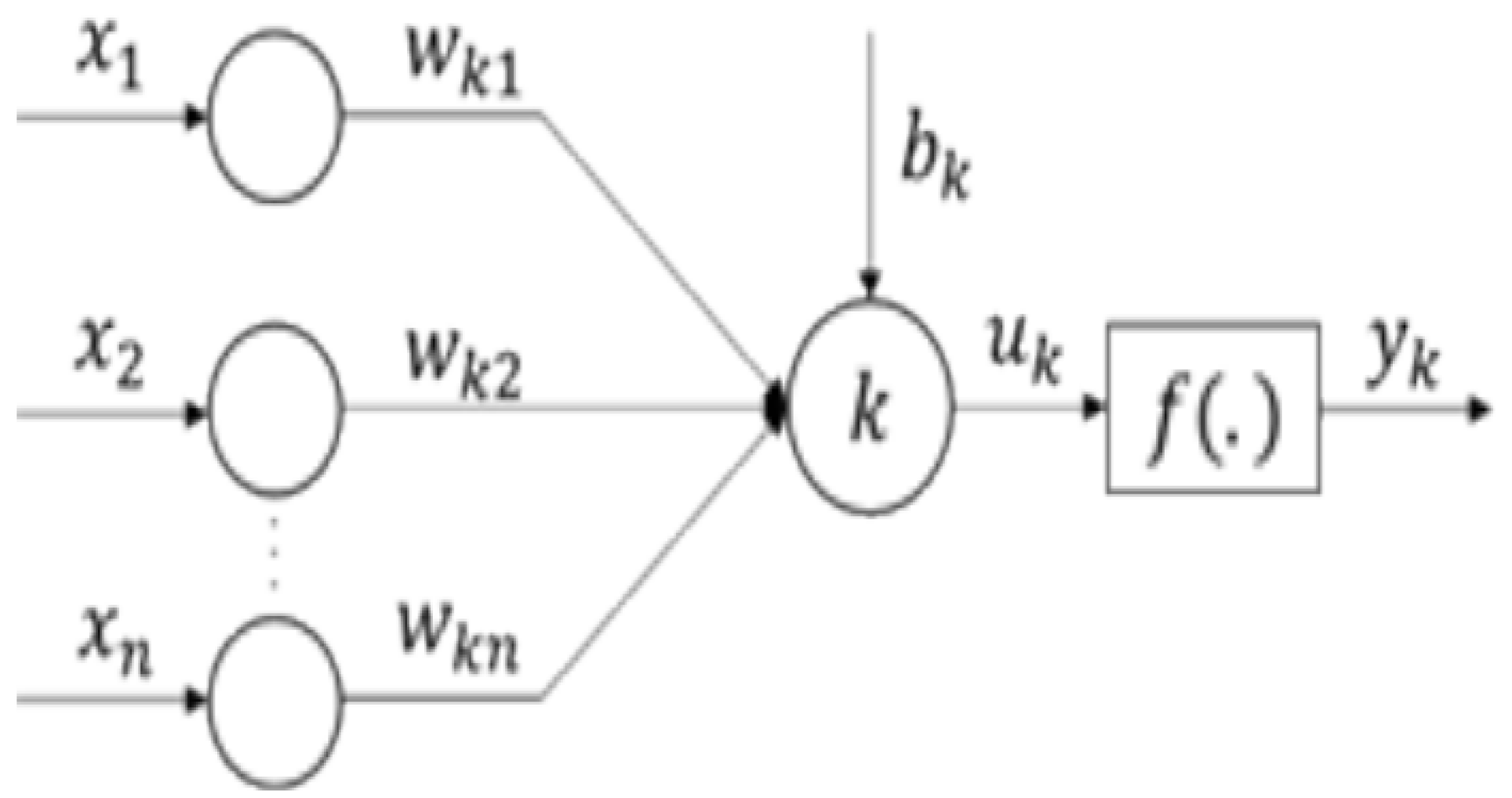
2.6. Machine Learning in Risk Management
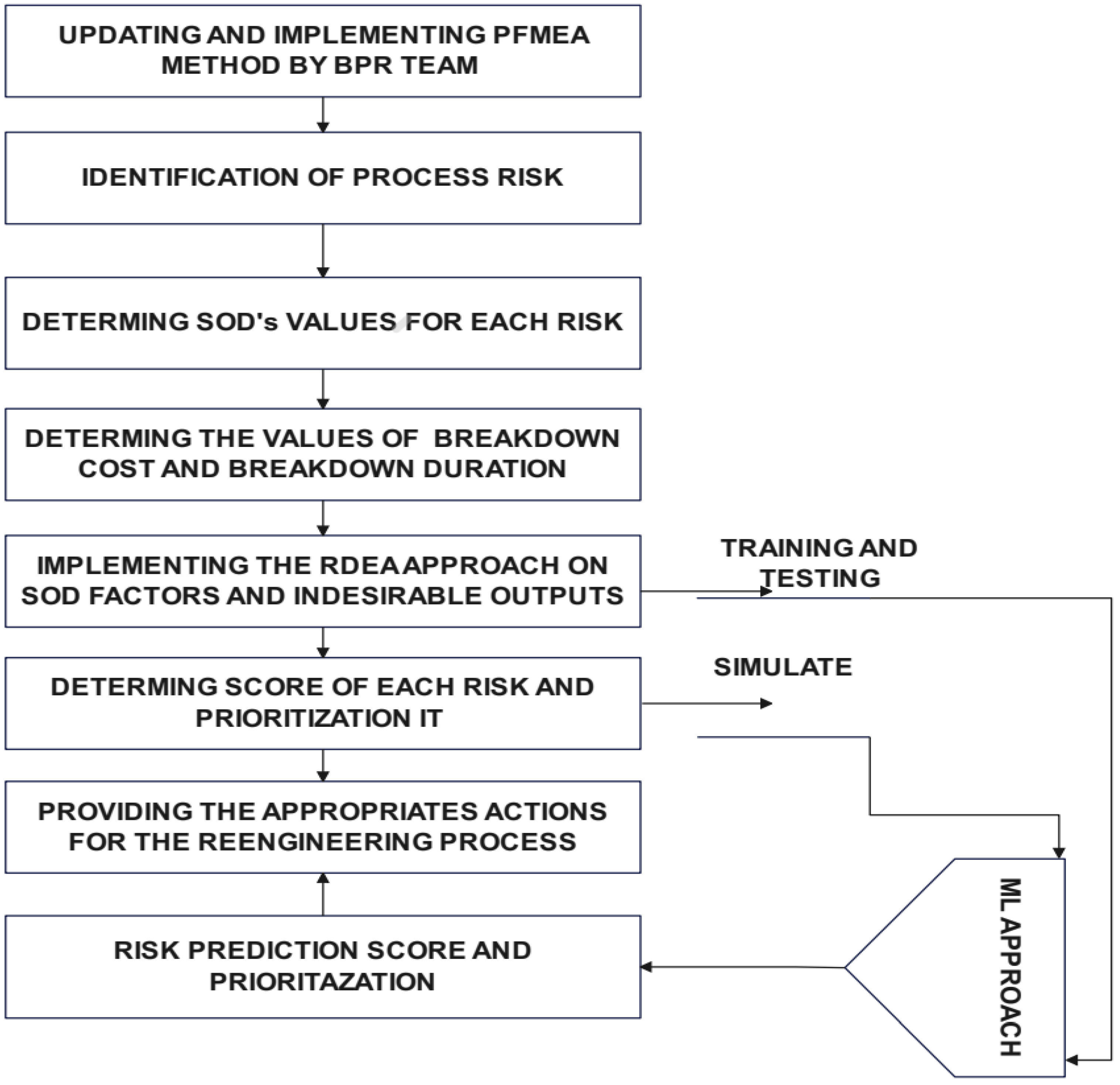
3. Proposed Approach
3.1. RDEA
3.2. ML Application
4. Case Study
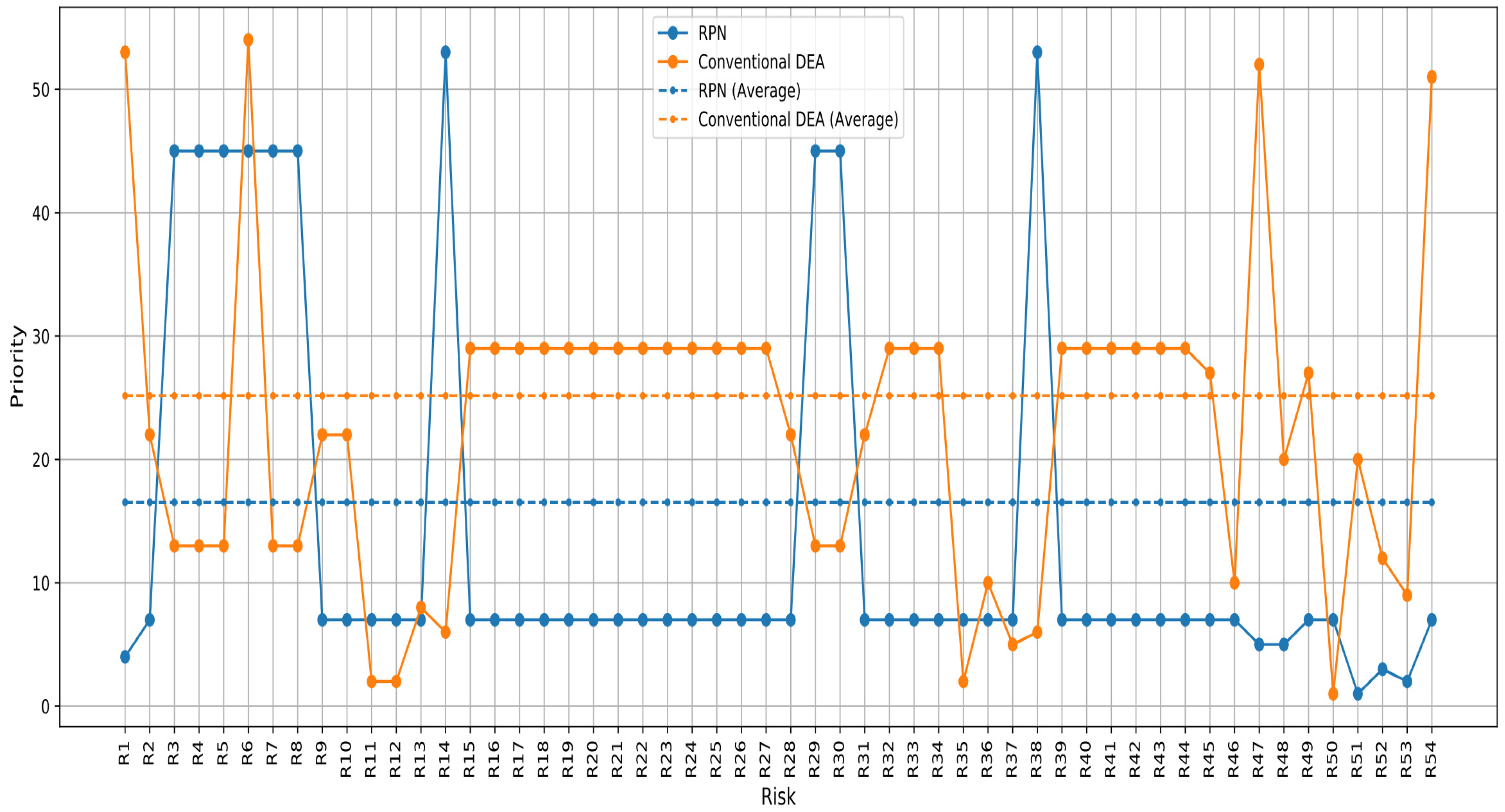
5. Results
6. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Harmon, P. Business Process Change: A Business Process Management Guide for Managers and Process Professionals; Morgan Kaufmann Publishers: Burlington, MA, USA, 2019. [Google Scholar]
- Nisar, Q.A.; Ahmad, S.; Ahmad, U. Exploring factors that contribute to success of business process reengineering and impact of business process reengineering on organizational performance: A qualitative descriptive study on banking sector at Pakistan. Asian J. Multidiscip. Stud. 2014, 2, 219–224. [Google Scholar]
- Tsakalidis, G.; Vergidis, K. Towards a Comprehensive Business Process Optimization Framework. In Proceedings of the 2017 IEEE 19th Conference on Business Informatics (CBI), Thessaloniki, Greece, 24–27 July 2017; IEEE: Piscataway, NJ, USA, 2017; Volume 1, pp. 129–134. [Google Scholar] [CrossRef]
- Ghanadbashi, S.; Ramsin, R. Towards a method engineering approach for business process reengineering. IET Softw. 2016, 10, 27–44. [Google Scholar] [CrossRef]
- Weerakkody, V.; Janssen, M.; Dwivedi, Y.K. Transformational change and business process reengineering (BPR): Lessons from the British and Dutch public sector. Gov. Inf. Q. 2011, 28, 320–328. [Google Scholar] [CrossRef]
- Erim, A.; Vayvay, O. Is the business process reengineering (BPR) proved itself to be a trustable change management approach for multinational corporations’ case studies from the literature. J. Aeronaut. Space Technol. 2010, 4, 23–30. [Google Scholar]
- Goksoy, A.; Ozsoy, B.; Vayvay, O. Business process reengineering: Strategic tool for managing organizational change an application in a multinational company. Int. J. Bus. Manag. 2012, 7, 89–112. [Google Scholar] [CrossRef][Green Version]
- Razalli, M.R.; Ringim, K.J.; Hasnan, N.; Hassan, M.G. A framework of best practices in managing business reengineering for Islamic. J. Adv. Manag. Sci. 2015, 3, 22–25. [Google Scholar] [CrossRef][Green Version]
- Bhaskar, H.L. A critical analysis of information technology and business process reengineering. Int. J. Product. Qual. Manag. 2016, 19, 98–115. [Google Scholar] [CrossRef]
- Chiplunkar, C.; Deshmukh, S.G.; Chattopadhyay, R. Application of principles of event related open systems to business process reengineering. Comput. Ind. Eng. 2003, 45, 347–374. [Google Scholar] [CrossRef]
- Hussain, M.; Saleh, M.; Akbar, S.; Jan, Z. Factors affecting readiness for business process reengineering-developing and proposing a conceptual model. Eur. J. Bus. Manag. 2014, 6, 55–60. [Google Scholar]
- Habib, M.N.; Shah, A. Business process reengineering: Literature review of approaches and applications. In Proceedings of the 3rd Asia-Pacific Business Research Conference, Kuala Lumpur, Malaysia, 25–26 February 2013; pp. 1–25, ISBN 978-1-922069-19-1. [Google Scholar]
- Alghamdi, H.A.; Alfarhan, M.A.; Abdullah, A.L. BPR: Evaluation of existing methodologies and limitations. Int. J. Comput. Trends Technol. 2014, 7, 224–227. [Google Scholar] [CrossRef]
- Bhaskar, H.L. Business process reengineering framework and methodology: A critical study. Int. J. Serv. Oper. Manag. 2018, 29, 527–556. [Google Scholar] [CrossRef]
- Covello, V.T.; Merkhoher, M.W. Risk Assessment Methods: Approaches for Assessing Health and Environmental Risks; Springer Science & Business Media: New York, NY, USA, 2013. [Google Scholar]
- Arabian-Hoseynabadi, H.; Oraee, H.; Tavner, P.J. Failure modes and effects analysis (FMEA) for wind turbines. Int. J. Electr. Power Energy Syst. 2010, 32, 817–824. [Google Scholar] [CrossRef]
- Feili, H.R.; Akar, N.; Lotfizadeh, H.; Bairampour, M.; Nasiri, S. Risk analysis of geothermal power plants using Failure Modes and Effects Analysis (FMEA) technique. Energy Convers. Manag. 2013, 72, 69–76. [Google Scholar] [CrossRef]
- Trafialek, J.; Kolanowski, W. Application of Failure Mode and Effect Analysis (FMEA) for audit of HACCP system. Food Control 2014, 44, 35–44. [Google Scholar] [CrossRef]
- Rezaee, M.J.; Yousefi, S.; Babaei, M. Multi-stage cognitive map for failures assessment of production processes: An extension in structure and algorithm. Neurocomputing 2017, 232, 69–82. [Google Scholar] [CrossRef]
- An, Q.; Meng, F.; Ang, S.; Chen, X. A new approach for fair efficiency decomposition in two-stage structure system. Oper. Res. 2018, 18, 257–272. [Google Scholar] [CrossRef]
- Yan, L.; Tong, W.; Hui, D.; Zongzhi, W. Research and application on risk assessment DEA model of crowd crushing and trampling accidents in subway stations. Procedia Eng. 2012, 43, 494–498. [Google Scholar] [CrossRef]
- Rezaee, M.J.; Salimi, A.; Yousefi, S. Identifying and managing failures in stone processing industry using cost-based FMEA. Int. J. Adv. Manufact. Technol. 2017, 88, 3329–3342. [Google Scholar] [CrossRef]
- Sadjadi, S.J.; Omrani, H. Data envelopment analysis with uncertain data: An application for Iranian electricity distribution companies. Energy Policy 2008, 36, 4247–4254. [Google Scholar] [CrossRef]
- Bertsimas, D.; Sim, M. The price of robustness. Operat. Res. 2004, 52, 35–53. [Google Scholar] [CrossRef]
- Zhu, N.; Zhu, C.; Emrouznejad, A. A combined machine learning algorithms and DEA method for measuring and predicting the efficiency of Chinese manufacturing listed companies. J. Manag. Sci. Eng. 2020, 6, 435–448. [Google Scholar] [CrossRef]
- Fan, Y.; Stevenson, M. A review of supply chain risk management: Definition, theory, and research agenda. Int. J. Phys. Distrib. Logist. Manag. 2018, 48, 205–230. [Google Scholar] [CrossRef]
- Abidoye, R.B.; Chan, A.P.C.; Abidoye, F.A.; Oshodi, O.S. Predicting property price index using artificial intelligence techniques. Int. J. Hous. Mark. Anal. 2019, 12, 1072–1092. [Google Scholar] [CrossRef]
- Sun, T.; Sales, L.J. Predicting public procurement irregularity: An application of neural networks. J. Emerg. Technol. Account. 2018, 15, 141–154. [Google Scholar] [CrossRef]
- Zhang, W.; Feng, X.; Goerlandt, F.; Liu, Q. Towards a convolutional neural network model for classifying regional ship collision risk levels for waterway risk analysis. Rel. Eng. Syst. Saf. 2020, 204, 107127. [Google Scholar] [CrossRef]
- Salehi, V.; Veitch, B.; Musharraf, M. Measuring and improving adaptive capacity in resilient systems by means of an integrated DEA-machine learning approach. Appl. Ergonom. 2020, 82, 102975. [Google Scholar] [CrossRef]
- Yin, G. BPR application. Mod. Appl. Sci. 2010, 4, 96–101. [Google Scholar] [CrossRef][Green Version]
- Hammer, M.; Champy, J. Reengineering the corporation: A manifesto for business revolution. Bus. Horiz. 1993, 36, 90–91. [Google Scholar] [CrossRef]
- Hammer, M. Reengineering work: Don’t automate, obliterate. Harv. Bus. Rev. 1990, 68, 104–112. [Google Scholar]
- Kontio, J. Business process re-engineering: A case study at Turku University of Applied Sciences. In Proceedings of the European and Mediterranean Conference on Information Systems, Valencia, Spain, 24–26 June 2007; pp. 24–26. [Google Scholar]
- Setegn, D.; Ensermu, M.; Moorthy, P.K. Assessing the effect of business process reengineering on organizational performance: A case study of Bureau of Finance and Economic Development (BOFED), Oromia Regional State, Ethiopia. Res. World 2013, 4, 115–123. [Google Scholar]
- Bhaskar, H.L.; Singh, R.P. Business process reengineering: A recent review. Glob. J. Bus. Manag. 2014, 8, 24–51. [Google Scholar]
- Eke, G.J.; Achilike, A.N. Business process reengineering in organizational performance in Nigerian banking sector. Acad. J. Interdiscip. Stud. 2014, 3, 113–124. [Google Scholar] [CrossRef]
- Mlay, S.V.; Zlotnikova, I.; Watundu, S. A quantitative analysis of business process reengineering and organizational resistance: The case of Uganda. Afr. J. Inf. Syst. 2013, 5, 1–26. [Google Scholar]
- Jamali, G.; Abbaszadeh, M.A.; Ebrahimi, M.; Maleki, T. Business process reengineering implementation: Developing a causal model of critical success factors. Int. J. E-Educ. E-Bus. E-Manag. E Learn. 2011, 1, 354–358. [Google Scholar] [CrossRef]
- Al-Anqoudi, Y.; Al-Hamdani, A.; Al-Badawi, M.; Hedjam, R. Using Machine Learning in Business Process Re-Engineering. Big Data Cogn. Comput. 2021, 5, 61. [Google Scholar] [CrossRef]
- Omidi, A.; Khoshtinat, B. Factors Affecting the Implementation of Business Process Reengineering: Taking into Account the Moderating Role of Organizational Culture (Case Study: Iran Air). Procedia Econ. Financ. 2016, 36, 425–432. [Google Scholar] [CrossRef]
- Hussein, B.; Hammoud, M.; Bazzi, H.; Haj-Ali, A. PRISM—Process reengineering integrated spiral model: An agile approach to business process reengineering (BPR). Int. J. Bus. Manag. 2014, 9, 134–142. [Google Scholar] [CrossRef]
- Motwani, J.; Kumar, A.; Jiang, J.; Youssef, M. Business process reengineering: A theoretical framework and an integrated model. Int. J. Oper. Prod. Manag. 1998, 18, 964–977. [Google Scholar] [CrossRef]
- Luo, W.; Tung, Y.A. A framework for selecting business process modeling methods. Ind. Manag. Data Syst. 1999, 99, 312–319. [Google Scholar] [CrossRef]
- Project Management Institute. A Guide to the Project Management Body of Knowledge: PMBOK Guide, 4th ed.; Project Management Institute: Newtown Square, PA, USA, 2009. [Google Scholar]
- ISO 31000:2009; Risk Management. ISO: Geneva, Switzerland, 2009.
- Duhamel, F.; Carbone, V.; Moatti, V. The impact of internal and external collaboration on the performance of supply chain risk management. Int. J. Logist. Syst. Manag. 2016, 23, 534–557. [Google Scholar] [CrossRef]
- Purdy, G. ISO 31000: 2009—Setting a new standard for risk management. Risk Anal. Int. J. 2010, 30, 881–886. [Google Scholar] [CrossRef] [PubMed]
- Lyon, B.K.; Popov, G. Risk treatment strategies: Harmonizing the hierarchy of controls and inherently safer design concepts. Prof. Saf. 2019, 64, 34–43. [Google Scholar]
- Cox, L.A., Jr.; Babayev, D.; Huber, W. Some limitations of qualitative risk rating systems. Risk Anal. 2005, 25, 651–662. [Google Scholar] [CrossRef] [PubMed]
- de Almeida, A.T.; Alencar, M.H.; Garcez, T.V.; Ferreira, R.J.P. A systematic literature review of multicriteria and multi-objective models applied in risk management. IMA J. Manage. Math. 2017, 28, 153–184. [Google Scholar] [CrossRef]
- Kaewfak, K.; Huynh, V.-N.; Ammarapala, V.; Ratisoontorn, N. A risk analysis based on a two-stage model of fuzzy AHP-DEA for multimodal freight transportation systems. IEEE Access 2020, 8, 153756–153773. [Google Scholar] [CrossRef]
- Bowles, J.B.; Peláez, C.E. Fuzzy logic prioritization of failures in a system failure mode, effects and criticality analysis. Reliab. Eng. Syst. Saf. 1995, 50, 203–213. [Google Scholar] [CrossRef]
- Wang, Y.M.; Chin, K.S.; Poon, G.K.K.; Yang, J.B. Risk evaluation in failure mode and effects analysis using fuzzy weighted geometric mean. Expert Syst. Appl. 2009, 36, 1195–1207. [Google Scholar] [CrossRef]
- Chang, K.H.; Cheng, C.H. Evaluating the risk of failure using the fuzzy OWA and DEMATEL method. J. Intell. Manuf. 2011, 22, 113–129. [Google Scholar] [CrossRef]
- Rakesh, R.; Jos, B.C.; Mathew, G. FMEA analysis for reducing breakdowns of a sub system in the life care product manufacturing industry. Int. J. Eng. Sci. Innov. Technol. 2013, 2, 218–225. [Google Scholar]
- Liu, H.-C.; Liu, L.; Liu, N.; Mao, L.-X. Risk evaluation in failure mode and effects analysis with extended VIKOR method under fuzzy environment. Expert Syst. Appl. 2012, 39, 12926–12934. [Google Scholar] [CrossRef]
- Chin, K.-S.; Wang, Y.-M.; Poon, G.K.K.; Yang, J.-B. Failure mode and effects analysis by data envelopment analysis. Decis. Support Syst. 2009, 48, 246–256. [Google Scholar] [CrossRef]
- Chang, D.S.; Chung, J.H.; Sun, K.L.; Yang, F.C. A novel approach for evaluating the risk of health care failure modes. J. Med. Syst. 2012, 36, 3967–3974. [Google Scholar] [CrossRef] [PubMed]
- Chang, D.; Sun, K.P. Applying DEA to enhance assessment capability of FMEA. Int. J. Qual. Rel. Manag. 2009, 26, 629–643. [Google Scholar] [CrossRef]
- Garcia, P.A.D.A.; Junior, L.; Curty, I.; Oliveira, M.A. A weight restricted DEA model for FMEA risk prioritization. Production 2013, 23, 500–507. [Google Scholar] [CrossRef]
- Vahdani, B.; Salimi, M.; Charkhchian, M. A new FMEA method by integrating fuzzy belief structure and TOPSIS to improve risk evaluation process. Int. J. Adv. Manuf. Technol. 2015, 77, 357–368. [Google Scholar] [CrossRef]
- Baghery, M.; Yousefi, S.; Rezaee, M.J. Risk measurement and prioritization of auto parts manufacturing processes based on process failure analysis, interval data envelopment analysis and grey relational analysis. J. Intell. Manuf. 2016, 29, 1803–1825. [Google Scholar] [CrossRef]
- Sakthivel, G.; Ikua, B.W. Failure mode and effect analysis using fuzzy analytic hierarchy process and GRA TOPSIS in manufacturing industry. Int. J. Product. Qual. Manag. 2017, 22, 466–484. [Google Scholar] [CrossRef]
- Razi, F.F.; Hoseini, E. Proposing a new model of failure mode and effect analysis for clustering and ranking of manufacturing process. Int. J. Product. Qual. Manag. 2017, 21, 45–71. [Google Scholar] [CrossRef]
- Ahmadi, M.; Molana, S.M.H.; Sajadi, S.M. A hybrid FMEA-TOPSIS method for risk management, case study: Esfahan Mobarakeh Steel Company. Int. J. Process Manag. Benchmarking 2017, 7, 397–408. [Google Scholar] [CrossRef]
- Certa, A.; Enea, M.; Galante, G.M.; La Fata, C.M. ELECTRE TRI-based approach to the failure modes classification on the basis of risk parameters: An alternative to the risk priority number. Comput. Ind. Eng. 2017, 108, 100–110. [Google Scholar] [CrossRef]
- Fattahi, R.; Khalilzadeh, M. Risk evaluation using a novel hybrid method based on FMEA, extended MULTIMOORA, and AHP methods under fuzzy environment. Saf. Sci. 2018, 102, 290–300. [Google Scholar] [CrossRef]
- Peeters, J.F.W.; Basten, R.J.I.; Tinga, T. Improving failure analysis efficiency by combining FTA and FMEA in a recursive manner. Reliab. Eng. Syst. Saf. 2018, 172, 36–44. [Google Scholar] [CrossRef]
- Yousefi, S.; Alizadeh, A.; Hayati, J.; Baghery, M. HSE risk prioritization using robust DEA-FMEA approach with undesirable outputs: A study of automotive parts industry in Iran. Saf. Sci. 2018, 102, 144–158. [Google Scholar] [CrossRef]
- Baynal, K.; Sarı, T.; Akpınar, B. Risk management in automotive manufacturing process based on FMEA and grey relational analysis: A case study. Adv. Prod. Eng. Manag. 2018, 13, 69–80. [Google Scholar] [CrossRef]
- Bhuvanesh Kumar, M.; Parameshwaran, R. Fuzzy integrated QFD, FMEA framework for the selection of lean tools in a manufacturing organization. Prod. Plan. Control. 2018, 29, 403–417. [Google Scholar] [CrossRef]
- Liu, H.C.; Liu, L.; Liu, N. Risk evaluation approaches in failure mode and effects analysis: A literature review. Expert Syst. Appl. 2013, 40, 828–838. [Google Scholar] [CrossRef]
- Liu, H.-C.; You, J.-X.; Lin, Q.-L.; Li, H. Risk assessment in system FMEA combining fuzzy weighted average with fuzzy decision-making trial and evaluation laboratory. Int. J. Comput. Integr. Manuf. 2015, 28, 701–714. [Google Scholar] [CrossRef]
- Rezaee, M.J.; Yousefi, S.; Eshkevari, M.; Valipour, M.; Saberi, M. Risk analysis of health, safety and environment in chemical industry integrating linguistic FMEA, fuzzy inference system and fuzzy DEA. Stochastic Environ. Res. Risk Assess. 2020, 34, 201–218. [Google Scholar] [CrossRef]
- Liu, H.-C.; Chen, X.-Q.; Duan, C.-Y.; Wang, Y.-M. Failure mode and effect analysis using multi-criteria decision makin methods: A systematic literature review. Comput. Ind. Eng. 2019, 135, 881–897. [Google Scholar] [CrossRef]
- Norman, M.; Stoker, B. Data Envelopment Analysis: The Assessment of Performance; Wiley: Hoboken, NJ, USA, 1991. [Google Scholar]
- Wu, J.; Chu, J.; Sun, J.; Zhu, Q. DEA cross-efficiency evaluation based on Pareto improvement. Eur. J. Oper. Res. 2016, 248, 571–579. [Google Scholar] [CrossRef]
- Ray, A.; Chaudhuri, A.K. Smart healthcare disease diagnosis and patient management: Innovation, improvement and skill development. Mach. Learn. Appl. 2021, 3, 100011. [Google Scholar] [CrossRef]
- Leo, M.; Sharma, S.; Maddulety, K. Machine learning in banking risk management: A literature review. Risks 2019, 7, 29. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Z.; Pu, Z.; Xu, C. Comparing prediction performance for crash injury severity among various machine learning and statistical methods. IEEE Access 2018, 6, 60079–60087. [Google Scholar] [CrossRef]
- Chandrinos, S.K.; Sakkas, G.; Lagaros, N.D. AIRMS: A risk management tool using machine learning. Expert Syst. Appl. 2018, 105, 34–48. [Google Scholar] [CrossRef]
- Paltrinieri, N.; Comfort, L.; Reniers, G. Learning about risk: Machine learning for risk assessment. Saf. Sci. 2019, 118, 475–486. [Google Scholar] [CrossRef]
- Gondia, A.; Siam, A.; El-Dakhakhni, W.; Nassar, A.H. Machine learning algorithms for construction projects delay risk prediction. J. Construct. Eng. Manag. 2020, 146, 04019085. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Ben-Tal, A.; Nemirovski, A. Robust solutions to uncertain programs. Oper. Res. Lett. 1999, 25, 1–13. [Google Scholar] [CrossRef]
- Soyster, A.L. Technical note—Convex programming with set-inclusive constraints and applications to inexact linear programming. Operat. Res. 1973, 21, 1154–1157. [Google Scholar] [CrossRef]
- Ben-Tal, A.; Nemirovski, A. Robust solutions of linear programming problems contaminated with uncertain data. Math. Program 2000, 88, 411–424. [Google Scholar] [CrossRef]
- Lima-Junior, F.R.; Carpinetti, L.C.R. Predicting supply chain performance based on SCOR metrics and multilayer perceptron neural networks. Int. J. Prod. Econ. 2019, 212, 19–38. [Google Scholar] [CrossRef]
- Fath, A.H.; Madanifar, F.; Abbasi, M. Implementation of multilayer perceptron (MLP) and radial basis function (RBF) neural networks to predict solution gas-oil ratio of crude oil systems. Petroleum 2020, 6, 80–91. [Google Scholar] [CrossRef]
- Seiford, L.M.; Zhu, J. Modeling undesirable factors in efficiency evaluation. Eur. J. Oper. Res. 2002, 142, 16–20. [Google Scholar] [CrossRef]

| Category | Factor | Success | Failure |
|---|---|---|---|
| Strategic | Focus on change | Readiness for change, courage and willpower | Lack of readiness and resistance to change |
| Driver | Methodology and framework | Selecting the best methodology and framework for the project | Lack of suitable and effective BPR framework and methodology |
| Enabler | Working environment | Collaborative and working toward shared objectives and targets | Lack of collaborative working |
| Strategic | Top management | Highly engaged, supportive and committed | Lack of top management commitment |
| Driver | BPR strategies, IT capabilities (IT integration, IT infrastructure and redesign, etc.) | Aligned strategies | Lack of reliable advanced technology (IT) |
| Enabler | Data | Data-driven change based on facts and figures | Not having sufficient data |
| Enabler | Culture | Flat and less bureaucratic structure | Poor leadership style |
| Enabler | Communication | Effective communication, motivation | Lack of communication with all stakeholders |
| Strategic | Financial support | Adequate financial support | Inadequate financial support |
| Driver | Business needs analysis | Customer focus | Inadequate business case: unclear, unreasonable, unrealistic scope and unjustifiable expectations from the BPR project |
| Enabler | BPR team | Effective and skilled BPR team training, education, fair reward system provided at all levels | Lack of training and education and fair reward |
| Score | BD-Cost (EUR) | BD-Duration (Day) |
|---|---|---|
| 1 | ≤100 | ≤1 |
| 2 | ]100, 500] | ]1, 3] |
| 3 | ]500, 3000] | ]3, 5] |
| 4 | ]3000, 6000] | ]5, 6] |
| 5 | >6000 | >6 |
| S | O | D | BD-Cost | BD-Duration | Undesirable BD-Cost | Undesirable BD-Duration |
|---|---|---|---|---|---|---|
| 6 | 6 | 3 | 1 | 1 | 428 | 155 |
| 9 | 2 | 2 | 1 | 1 | 440 | 182 |
| 8 | 2 | 2 | 1 | 2 | 440 | 182 |
| 8 | 2 | 2 | 1 | 1 | 443 | 179 |
| 8 | 2 | 2 | 1 | 1 | 443 | 179 |
| 8 | 2 | 2 | 3 | 2 | 433 | 180 |
| 8 | 2 | 2 | 1 | 1 | 443 | 179 |
| 8 | 2 | 2 | 1 | 1 | 443 | 179 |
| 9 | 2 | 2 | 1 | 1 | 440 | 182 |
| 9 | 2 | 2 | 1 | 1 | 440 | 182 |
| 6 | 2 | 3 | 3 | 4 | 302 | 107 |
| 6 | 2 | 3 | 3 | 4 | 302 | 107 |
| 6 | 2 | 3 | 4 | 4 | 433 | 182 |
| 6 | 2 | 2 | 1 | 1 | 424 | 180 |
| 6 | 2 | 3 | 1 | 1 | 427 | 173 |
| 6 | 2 | 3 | 1 | 1 | 427 | 173 |
| 6 | 2 | 3 | 1 | 1 | 427 | 173 |
| 6 | 2 | 3 | 1 | 1 | 427 | 173 |
| 6 | 2 | 3 | 1 | 1 | 427 | 173 |
| 6 | 2 | 3 | 1 | 1 | 427 | 173 |
| 6 | 2 | 3 | 1 | 1 | 427 | 173 |
| 6 | 2 | 3 | 1 | 1 | 427 | 173 |
| 6 | 2 | 3 | 1 | 1 | 427 | 173 |
| 6 | 2 | 3 | 1 | 1 | 427 | 173 |
| 6 | 2 | 3 | 1 | 1 | 427 | 173 |
| 6 | 2 | 3 | 1 | 1 | 427 | 173 |
| 6 | 2 | 3 | 1 | 1 | 427 | 173 |
| 9 | 2 | 2 | 1 | 1 | 440 | 182 |
| 8 | 2 | 2 | 1 | 1 | 443 | 179 |
| 8 | 2 | 2 | 1 | 1 | 443 | 179 |
| 9 | 2 | 2 | 1 | 1 | 440 | 182 |
| 6 | 2 | 3 | 1 | 1 | 427 | 173 |
| 6 | 2 | 3 | 1 | 1 | 427 | 173 |
| 6 | 2 | 3 | 1 | 1 | 427 | 173 |
| 6 | 2 | 3 | 3 | 1 | 302 | 107 |
| 6 | 2 | 3 | 4 | 2 | 255 | 125 |
| 6 | 2 | 3 | 3 | 1 | 349 | 131 |
| 6 | 2 | 2 | 1 | 1 | 424 | 180 |
| 6 | 2 | 3 | 1 | 1 | 427 | 173 |
| 6 | 2 | 3 | 1 | 1 | 427 | 173 |
| 6 | 2 | 3 | 1 | 1 | 427 | 173 |
| 6 | 2 | 3 | 1 | 1 | 427 | 173 |
| 6 | 2 | 3 | 1 | 1 | 427 | 173 |
| 6 | 2 | 3 | 1 | 1 | 427 | 173 |
| 6 | 2 | 3 | 5 | 3 | 427 | 173 |
| 6 | 2 | 3 | 4 | 2 | 255 | 125 |
| 6 | 3 | 3 | 1 | 1 | 417 | 173 |
| 9 | 2 | 3 | 3 | 2 | 437 | 173 |
| 6 | 2 | 3 | 5 | 3 | 423 | 173 |
| 6 | 2 | 3 | 4 | 2 | 417 | 169 |
| 6 | 7 | 5 | 4 | 2 | 418 | 170 |
| 9 | 3 | 5 | 5 | 2 | 412 | 171 |
| 9 | 2 | 10 | 5 | 3 | 477 | 123 |
| 9 | 2 | 2 | 5 | 3 | 447 | 73 |
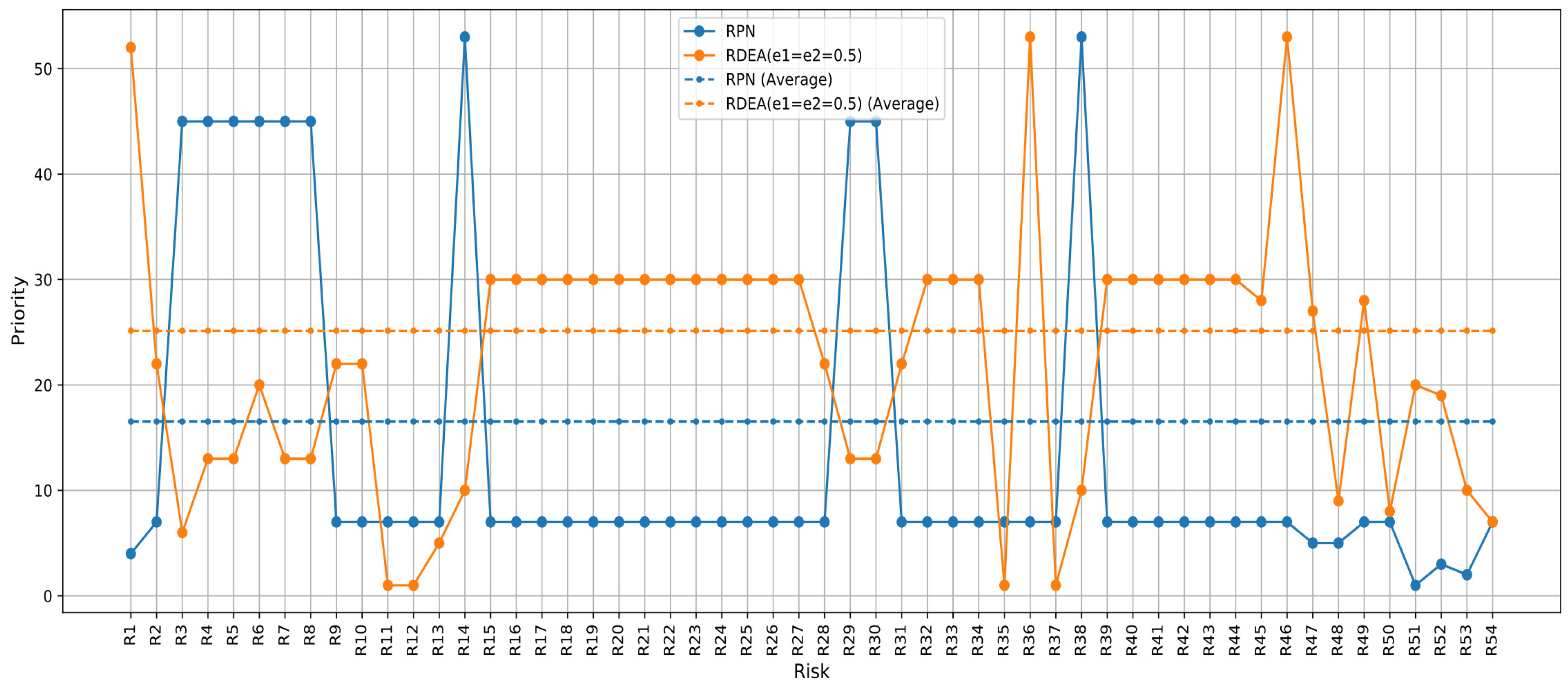
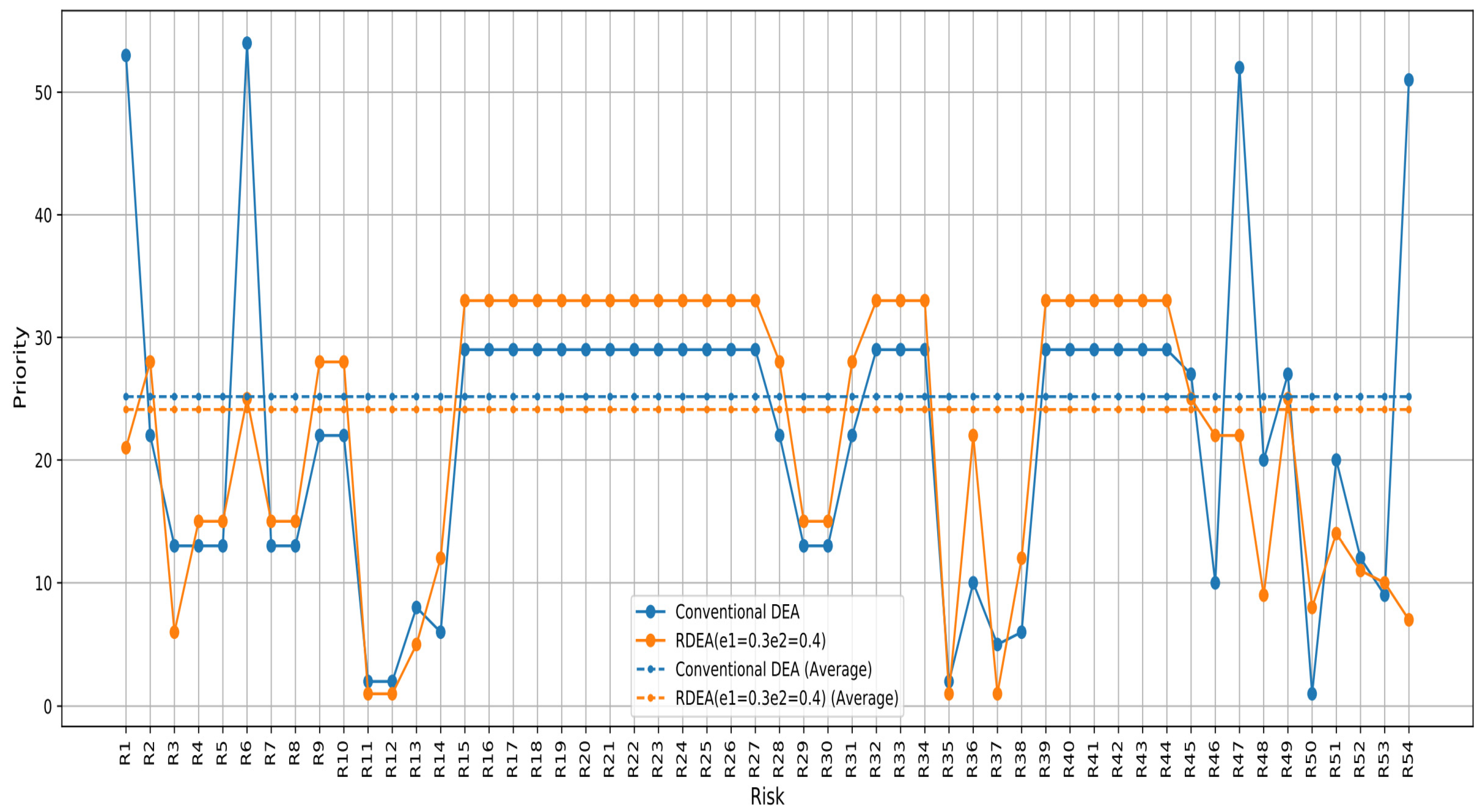
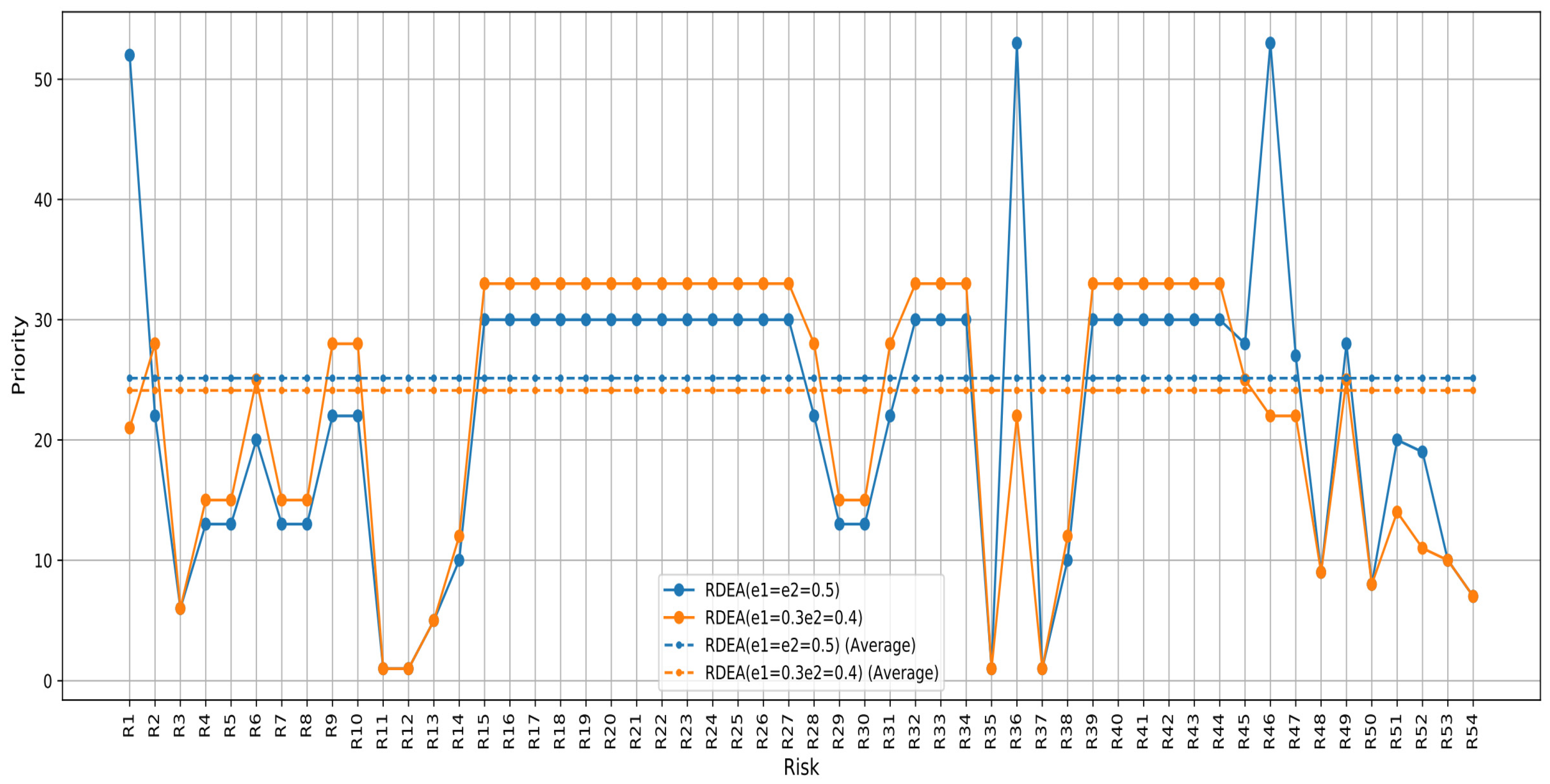
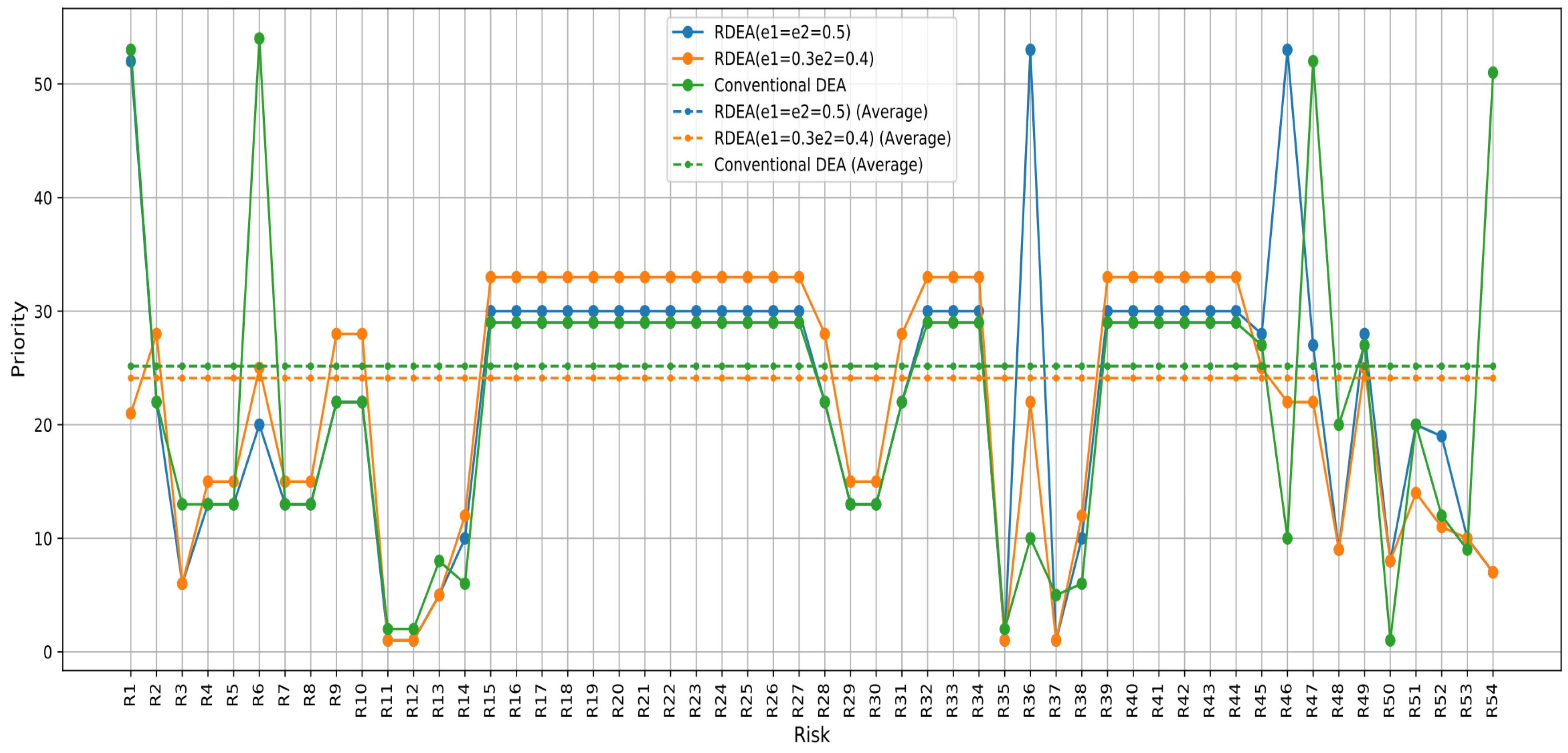
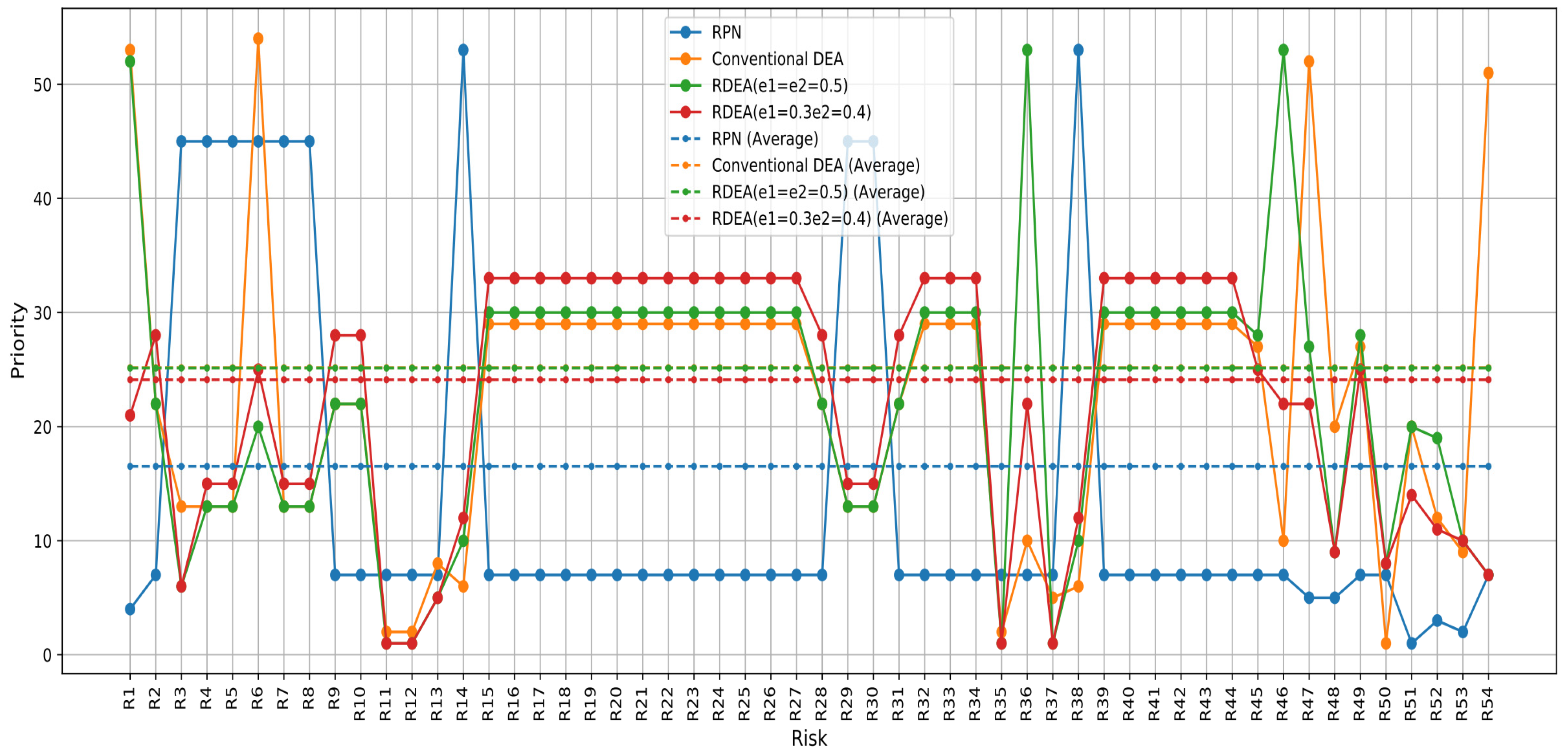
| Risks | RPN | Conventional DEA | RDEA (e1 = e2 = 0.5) | RDEA (e1 = 0.3 e2 = 0.4) | ||||
|---|---|---|---|---|---|---|---|---|
| Score | Priority | Score | Priority | Score | Priority | Score | Priority | |
| R1 | 108 | 4 | 0.87 | 53 | 0.9000000000000004 | 52 | 0.8500000000000003 | 21 |
| R2 | 36 | 7 | 0.77 | 22 | 0.8300000000000001 | 22 | 0.8800000000000001 | 28 |
| R3 | 32 | 45 | 0.65 | 13 | 0.5 | 6 | 0.44999999999999996 | 6 |
| R4 | 32 | 45 | 0.65 | 13 | 0.7999999999999998 | 13 | 0.8499999999999999 | 15 |
| R5 | 32 | 45 | 0.65 | 13 | 0.7999999999999998 | 13 | 0.8499999999999999 | 15 |
| R6 | 32 | 45 | 0.89 | 54 | 0.8200000000000003 | 20 | 0.8700000000000003 | 25 |
| R7 | 32 | 45 | 0.65 | 13 | 0.7999999999999998 | 13 | 0.8499999999999999 | 15 |
| R8 | 32 | 45 | 0.65 | 13 | 0.7999999999999998 | 13 | 0.8499999999999999 | 15 |
| R9 | 36 | 7 | 0.77 | 22 | 0.8300000000000001 | 22 | 0.8800000000000001 | 28 |
| R10 | 36 | 7 | 0.77 | 22 | 0.8300000000000001 | 22 | 0.8800000000000001 | 28 |
| R11 | 36 | 7 | 0.18 | 2 | 0.05252000000000123 | 1 | 0.0025200000000012157 | 1 |
| R12 | 36 | 7 | 0.18 | 2 | 0.0525200000000123 | 1 | 0.0025200000000012157 | 1 |
| R13 | 36 | 7 | 0.45 | 8 | 0.1999999999999993 | 5 | 0.2499999999999993 | 5 |
| R14 | 24 | 53 | 0.38 | 6 | 0.7699999999999996 | 10 | 0.8199999999999996 | 12 |
| R15 | 36 | 7 | 0.81 | 29 | 0.8999999999999986 | 30 | 0.8999999999999986 | 33 |
| R16 | 36 | 7 | 0.81 | 29 | 0.8999999999999986 | 30 | 0.8999999999999986 | 33 |
| R17 | 36 | 7 | 0.81 | 29 | 0.8999999999999986 | 30 | 0.8999999999999986 | 33 |
| R18 | 36 | 7 | 0.81 | 29 | 0.8999999999999986 | 30 | 0.8999999999999986 | 33 |
| R19 | 36 | 7 | 0.81 | 29 | 0.8999999999999986 | 30 | 0.8999999999999986 | 33 |
| R20 | 36 | 7 | 0.81 | 29 | 0.8999999999999986 | 30 | 0.8999999999999986 | 33 |
| R21 | 36 | 7 | 0.81 | 29 | 0.8999999999999986 | 30 | 0.8999999999999986 | 33 |
| R22 | 36 | 7 | 0.81 | 29 | 0.8999999999999986 | 30 | 0.8999999999999986 | 33 |
| R23 | 36 | 7 | 0.81 | 29 | 0.8999999999999986 | 30 | 0.8999999999999986 | 33 |
| R24 | 36 | 7 | 0.81 | 29 | 0.8999999999999986 | 30 | 0.8999999999999986 | 33 |
| R25 | 36 | 7 | 0.81 | 29 | 0.8999999999999986 | 30 | 0.8999999999999986 | 33 |
| R26 | 36 | 7 | 0.81 | 29 | 0.8999999999999986 | 30 | 0.8999999999999986 | 33 |
| R27 | 36 | 7 | 0.81 | 29 | 0.8999999999999986 | 30 | 0.8999999999999986 | 33 |
| R28 | 36 | 7 | 0.77 | 22 | 0.8300000000000001 | 22 | 0.8800000000000001 | 28 |
| R29 | 32 | 45 | 0.65 | 13 | 0.7999999999999998 | 13 | 0.8499999999999999 | 15 |
| R30 | 32 | 45 | 0.65 | 13 | 0.7999999999999998 | 13 | 0.8499999999999999 | 15 |
| R31 | 36 | 7 | 0.77 | 22 | 0.8300000000000001 | 22 | 0.8800000000000001 | 28 |
| R32 | 36 | 7 | 0.81 | 29 | 0.8999999999999986 | 30 | 0.8999999999999986 | 33 |
| R33 | 36 | 7 | 0.81 | 29 | 0.8999999999999986 | 30 | 0.8999999999999986 | 33 |
| R34 | 36 | 7 | 0.81 | 29 | 0.8999999999999986 | 30 | 0.8999999999999986 | 33 |
| R35 | 36 | 7 | 0.18 | 2 | 0.05252000000000123 | 1 | 0.0025200000000012157 | 1 |
| R36 | 36 | 7 | 0.57 | 10 | 0.9199999999999999 | 53 | 0.8699999999999999 | 22 |
| R37 | 36 | 7 | 0.23 | 5 | 0.05252000000000123 | 1 | 0.0025200000000012157 | 1 |
| R38 | 24 | 53 | 0.38 | 6 | 0.7699999999999996 | 10 | 0.8199999999999996 | 12 |
| R39 | 36 | 7 | 0.81 | 29 | 0.8999999999999986 | 30 | 0.8999999999999986 | 33 |
| R40 | 36 | 7 | 0.81 | 29 | 0.8999999999999986 | 30 | 0.8999999999999986 | 33 |
| R41 | 36 | 7 | 0.81 | 29 | 0.8999999999999986 | 30 | 0.8999999999999986 | 33 |
| R42 | 36 | 7 | 0.81 | 29 | 0.8999999999999986 | 30 | 0.8999999999999986 | 33 |
| R43 | 36 | 7 | 0.81 | 29 | 0.8999999999999986 | 30 | 0.8999999999999986 | 33 |
| R44 | 36 | 7 | 0.81 | 29 | 0.8999999999999986 | 30 | 0.8999999999999986 | 33 |
| R45 | 36 | 7 | 0.8077 | 27 | 0.8769999999999989 | 28 | 0.8769999999999989 | 25 |
| R46 | 36 | 7 | 0.5700 | 10 | 0.9199999999999999 | 53 | 0.8699999999999999 | 22 |
| R47 | 54 | 5 | 0.8541 | 52 | 0.8655000000000008 | 27 | 0.8655000000000008 | 22 |
| R48 | 54 | 5 | 0.71 | 20 | 0.7403200000000005 | 9 | 0.7403200000000005 | 9 |
| R49 | 36 | 7 | 0.8077 | 27 | 0.8769999999999989 | 28 | 0.8769999999999989 | 25 |
| R50 | 36 | 7 | 0.09998 | 1 | 0.6589999999999989 | 8 | 0.6589999999999989 | 8 |
| R51 | 210 | 1 | 0.71 | 20 | 0.8240000000000016 | 20 | 0.8240000000000016 | 14 |
| R52 | 135 | 3 | 0.6 | 12 | 0.8000000000000007 | 19 | 0.8000000000000007 | 11 |
| R53 | 180 | 2 | 0.54381 | 9 | 0.7654899999999998 | 10 | 0.7654899999999998 | 10 |
| R54 | 36 | 7 | 0.843221 | 51 | 0.5413899999999998 | 7 | 0.5413899999999998 | 7 |
| RDEA Score | ML Score | Error |
|---|---|---|
| 0.8500000000000003 | 0.8514999999999994 | 0.001 |
| 0.8800000000000001 | 0.8804196522776031 | 0.0004 |
| 0.44999999999999996 | 0.4746742857142863 | 0.02 |
| 0.8499999999999999 | 0.8628437016205744 | 0.01 |
| 0.8700000000000003 | 0.8658000000000005 | 0.005 |
| 0.8800000000000001 | 0.8804196522776031 | 0.0005 |
| 0.8800000000000001 | 0.8804196522776031 | 0.0005 |
| 0.0025200000000012157 | 0.0049948000000000015 | 0.002 |
| 0.2499999999999993 | 0.2475252 | 0.002 |
| 0.8199999999999996 | 0.8423190166500167 | 0.01 |
| 0.8999999999999986 | 0.8398135963221486 | 0.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hicham, R.; Abdallah, L.; Mohamed, M. Risk Management and Assessment Hybrid Framework for Business Process Reengineering Projects: Application in Automotive Sector. Eng 2024, 5, 1360-1381. https://doi.org/10.3390/eng5030071
Hicham R, Abdallah L, Mohamed M. Risk Management and Assessment Hybrid Framework for Business Process Reengineering Projects: Application in Automotive Sector. Eng. 2024; 5(3):1360-1381. https://doi.org/10.3390/eng5030071
Chicago/Turabian StyleHicham, Raffak, Lakhouili Abdallah, and Mansouri Mohamed. 2024. "Risk Management and Assessment Hybrid Framework for Business Process Reengineering Projects: Application in Automotive Sector" Eng 5, no. 3: 1360-1381. https://doi.org/10.3390/eng5030071
APA StyleHicham, R., Abdallah, L., & Mohamed, M. (2024). Risk Management and Assessment Hybrid Framework for Business Process Reengineering Projects: Application in Automotive Sector. Eng, 5(3), 1360-1381. https://doi.org/10.3390/eng5030071






