Recalibrated Correlations between Dynamic Cone Penetrometer (DCP) Data and California Bearing Ratio (CBR) in Subgrade Soil
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussions
3.1. Test Results for Strength Parameters of Subgrade Soils
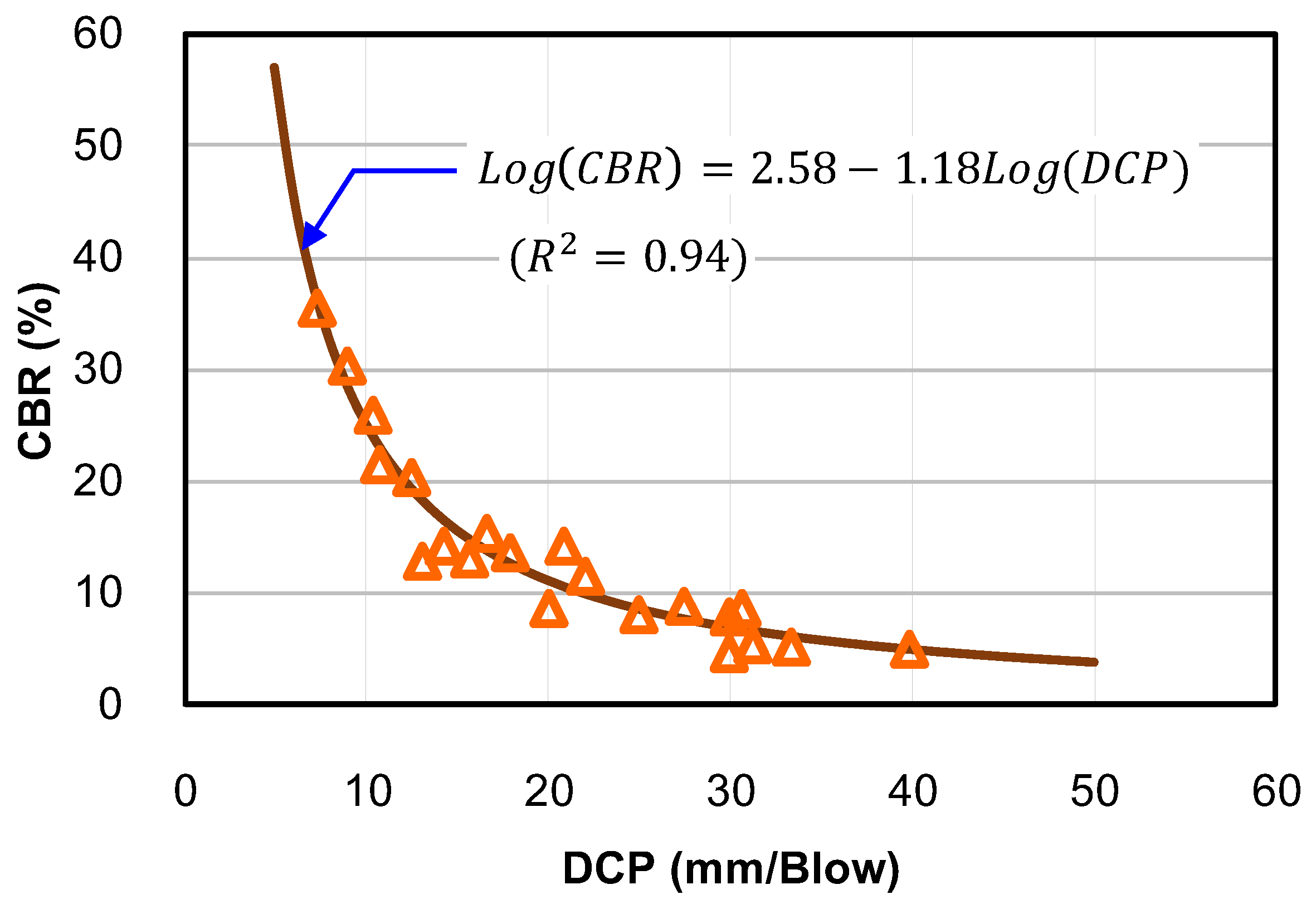
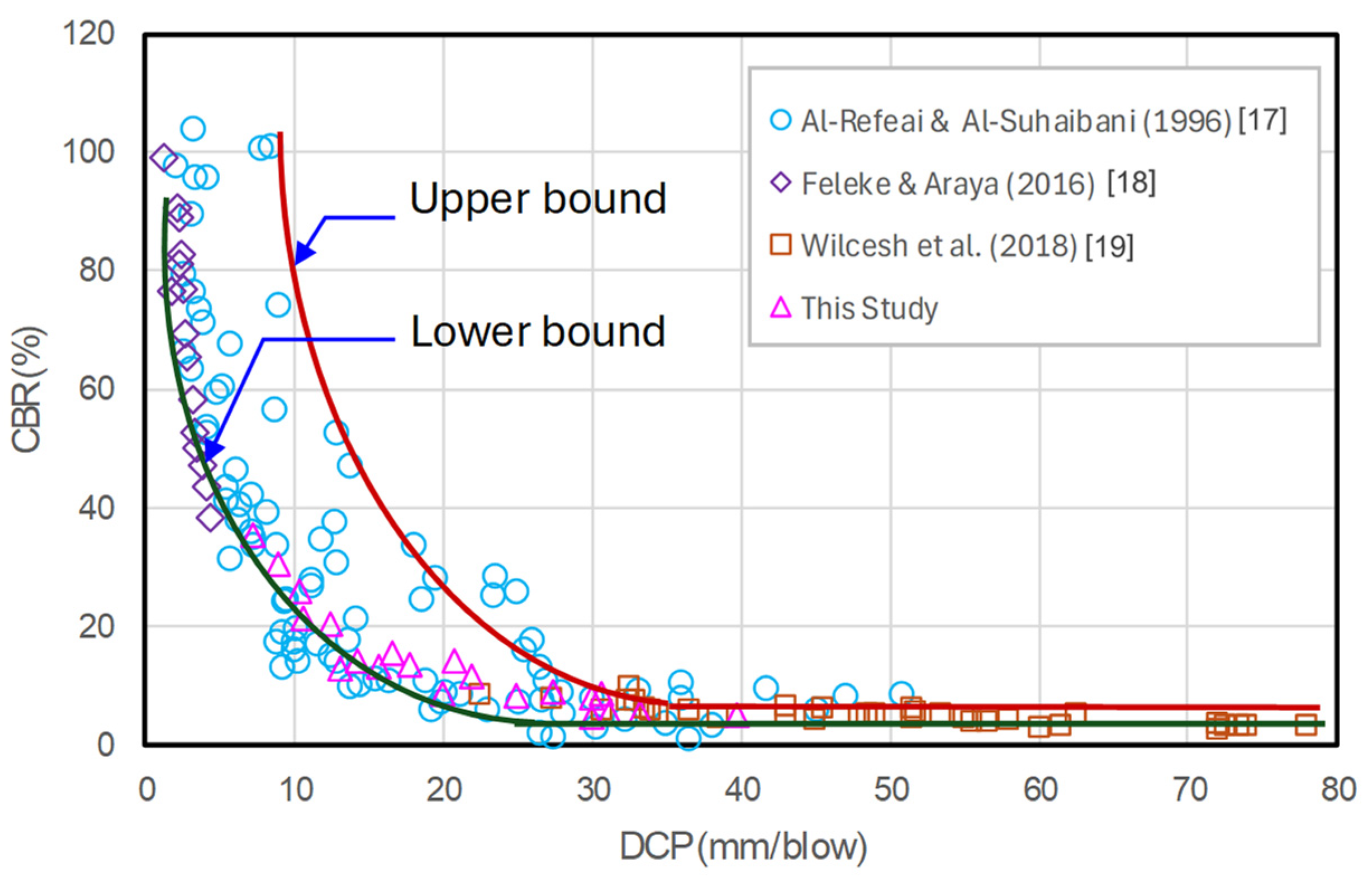
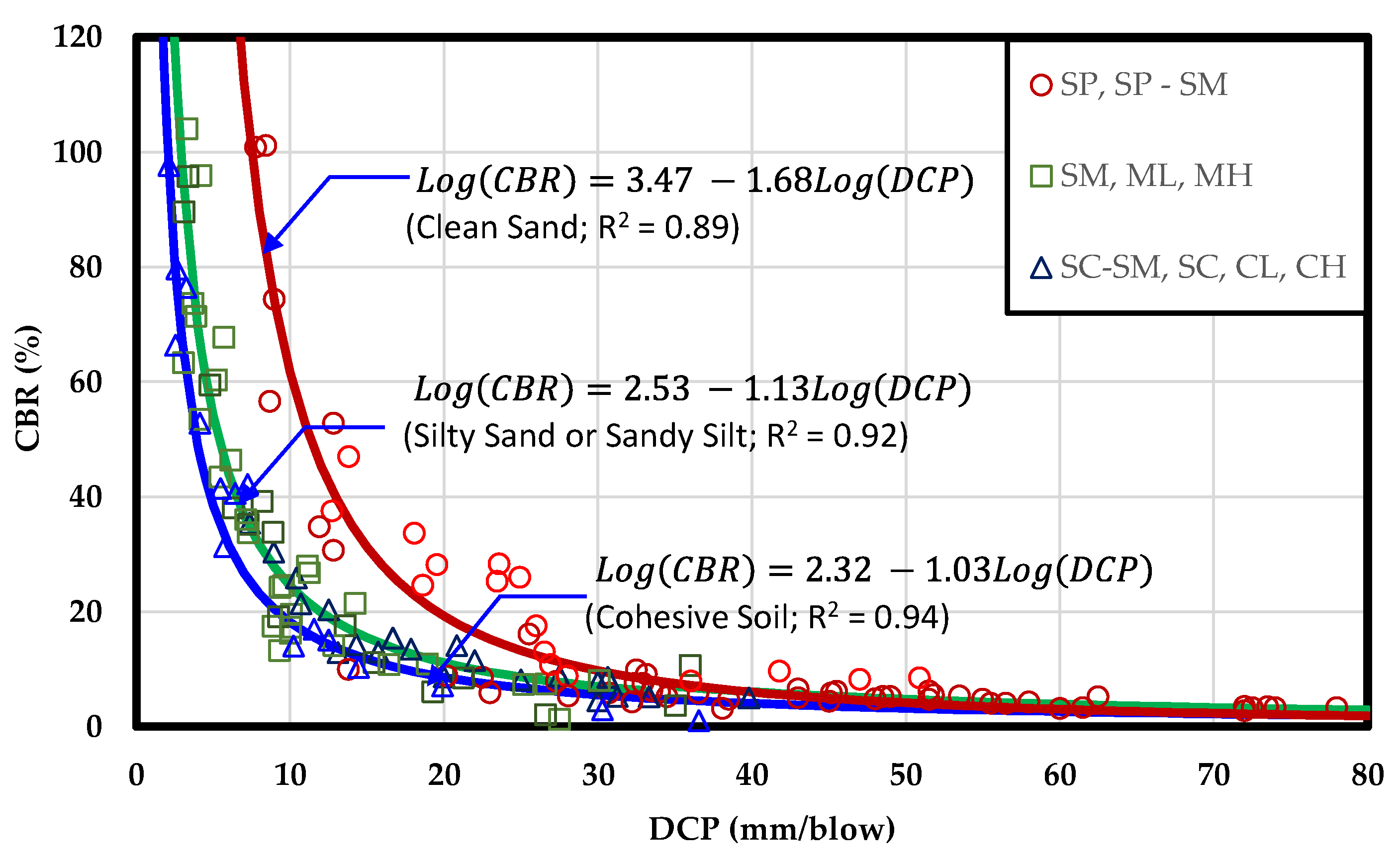
3.2. Recalibration of the Correlations
- (1)
- The proposed correlations should be in the form of Equation (1) and provide fewer changes or a constant value of CBR when DCP is greater than 30 mm/blow;
- (2)
- The correlation should be separated for the cohesionless and cohesive soil;
- (3)
- For cohesionless soil in which the data points were more scattered, the subgroup, such as clean sand or sand mixed with non-plastic silt (both silty sand and sandy silt), could be an important condition.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lines, S.; Williams, D.J.; Galindo-Torres, S.A.; Danyaya, H.A. Determination of Thermal Conductivity of Soil Using Standard Cone Penetration Test. In Proceedings of the 2nd International Conference on Advances on Clean Energy Research, Berlin, Germany, 7–9 April 2017. [Google Scholar]
- Mukesh, A.P.; Patel, H.S.; Gautam Dadhich, E.F. Prediction of Subgrade Strength Parameters from Dynamic Cone Penetrometer Index, Modified Liquid Limit and Moisture Content. In Proceedings of the 2nd Conference of Transportation Research Group of India, Agra, India, 12–15 December 2013. [Google Scholar]
- Mukesh, A.P.; Patel, H.S. Experimental Study to Correlate the Test Results of PBT, UCS, and CBR with DCP on Various soils in soaked condition. IJE 2012, 6, 244–261. [Google Scholar]
- Mukesh, A.P.; Patel, H.S. Laboratory Assessment to Correlate Strength Parameter from Physical properties of Subgrade. In Proceedings of the Non-Circuit Branches of the 3rd Nirma University International Conference on Engineering, Ahmedabad, India, 6–8 December 2012. [Google Scholar]
- Bayamack, J.F.N.; Onana, V.L.; Ndzié Mvindi, A.T.; Ze, A.N.; Ohandja, H.N.; Eko, R.M. Assessment of the determination of Californian Bearing Ratio of laterites with contrasted geotechnical properties from simple physical parameters. Transp. Geotech. 2012, 19, 84–95. [Google Scholar] [CrossRef]
- Kumar, S.; Singh, D. Prediction of UCS and CBR behavior of fiber-reinforced municipal solid waste incinerator bottom ash composites using experimental and machine learning methods. Constr. Build. Mater. 2023, 367, 130230. [Google Scholar] [CrossRef]
- Othman, K.; Abdelwahab, H. The application of deep neural networks for the prediction of California Bearing Ratio of road subgrade soil. Ain Shams Eng. J. 2023, 14, 101988. [Google Scholar] [CrossRef]
- Nagaraj, H.B.; Suresh, M.R. Influence of clay mineralogy on the relationship of CBR of fine-grained soils with their index and engineering properties. Transp. Geotech. 2018, 15, 29–38. [Google Scholar] [CrossRef]
- Rehman, Z.U.; Khalid, U.; Farooq, K.; Mujtaba, H. Prediction of CBR Value from Index Properties of different Soils. IRJET 2017, 22, 17–26. [Google Scholar]
- Yildirim, B.; Gunaydin, O. Estimation of California bearing ratio by using soft computing systems. Expert Syst. Appl. 2011, 30, 6381–6391. [Google Scholar] [CrossRef]
- Shirur, N.B.; Hiremath, S.G. Establishing Relationship between CBR Value and Physical Properties of Soil. IOSR-JMCE 2014, 11, 26–30. [Google Scholar] [CrossRef]
- Priya, G.; Arya, K.S.; Manjummekudiyil, E.M.; Unni, A.; Menon, V.S. Prediction of CBR Value from Index Properties of Soil. IRJET 2019, 6, 4029–4033. [Google Scholar]
- Perić, D.; Goh, G.; Saeidaskari, J.; Rashk Olia, A.S.; Ayar, P. Development of Prediction Models for Performance of Flexible Pavements in Kansas with Emphasis on the Effects of Subgrade and Unbound Layers. Sustainability 2022, 14, 9020. [Google Scholar] [CrossRef]
- Baghbani, A.; Nguyen, M.D.; Alnedawi, A.; Milne, N.; Baumgartl, T.; Abuel-Naga, H. Improving Soil Stability with Alum Sludge: An AI-Enabled Approach for Accurate Prediction of California Bearing Ratio. Appl. Sci. 2023, 13, 4934. [Google Scholar] [CrossRef]
- Bandara, N.; Hettiarachchi, H.; Jensen, E.; Binoy, T.H.; Perera, R. Using Kiln Dust to Improve Weak Subgrades for Pavement Construction: A Field Verification in Michigan, USA. Geotechnics 2023, 3, 179–192. [Google Scholar] [CrossRef]
- Dafalla, M.; Shaker, A.; Al-Shamrani, M. Use of the Dynamic Cone Penetrometer in Compacted Clay–Sand Layers. Appl. Sci. 2022, 12, 11547. [Google Scholar] [CrossRef]
- AI-Refeai, T.; Al-Suhaibani, A. Prediction of CBR Using Dynamic Cone Penetrometer. J. King Saud Univ.-Eng. Sci. 1997, 9, 191–203. [Google Scholar]
- Feleke, G.G.; Araya, A.A. Prediction of CBR using DCP for Local Subgrade Materials. In Proceedings of the 1st International Conference on Transportation and Road Research, Mombasa, Kenya, 15–17 March 2016. [Google Scholar]
- Wilches, F.J.; Feria-Díaz, J.J.; Hernandez Ávila, J.R. Correlation between California Bearing Ratio (CBR) and Dynamic Cone Penetrometer (DCP) for soil from Sincelejo city in Colombia. Int. J. Appl. Eng. Res. 2018, 13, 2068–2071. [Google Scholar]
- Harison, J.A. Correlation Between California Bearing Ratio and Dynamic Cone Penetrometer Strength Measurement of Soils. Proc. Inst. Civ. Eng. 1987, 83, 833–844. [Google Scholar] [CrossRef]
- Livneh, M. Validation of Correlations Between a Number of Penetration Test and in Situ California Bearing Ratio Tests. Transp. Res. Rec. 1989, 1219, 56–67. [Google Scholar]
- US Army Corps of Engineers. Available online: https://www.kesslerdcp.com/images/phocadownload/PDF-Documents/USACE%20Report%20GL-92-3%20on%20DCP.pdf (accessed on 12 February 2024).
- Soil Property Testing Limited. Available online: https://www.soilpropertytesting.com/Downloads_files/The%20TRL%20Dynamic%20Cone%20Penetrometer%20Test.pdf (accessed on 13 February 2024).
- Desalegn, Y. Developing Correlation between DCP and CBR for Locally Used Subgrade Materials. Master’s Thesis, Addis Ababa University (AAU), Addis Ababa, Ethiopia, 16 July 2018. [Google Scholar]
- IDOT (.gov). Available online: https://idot.illinois.gov/content/dam/soi/en/web/idot/documents/transportation-system/research/pavement-technology-advisories/testing-and-data-collection-series/ptat4.pdf (accessed on 12 February 2024).
- Lee, J.S.; Kim, S.Y.; Hong, W.T.; Byun, Y.H. Assessing Subgrade Strength Using an Instrumented Dynamic Cone Penetrometer. Soils Found. 2019, 59, 930–941. [Google Scholar] [CrossRef]
- Amadi, A.A.; Sadiku, S.; Abdullahi, M.; Danyaya, H.A. Case study of construction quality control monitoring and strength evaluation of a lateritic pavement using the dynamic cone penetrometer. Int. J. Pavement Res. Technol. 2018, 11, 530–539. [Google Scholar] [CrossRef]
- Salgado, R.; Yoon, S.; Hernandez Ávila, J.R. Dynamic Cone Penetration Test (DCPT) for Subgrade Assessment. Publication FHWA/IN/JTRP-2002/30. Joint Transportation Research Program, Indiana Department of Transportation and Purdue University, West Lafayette, Indiana, 2003. [CrossRef]
- Kaewhanam, N.; Juntasan, P.; Narong, S. Evaluation of Highway Subgrade Compaction by Dynamic Cone Penetrometer. In Proceedings of the Fifth International Conference on Science, Technology and Innovation for Sustainable Well-Being, Luang Prabang, Lao PDR, 4–6 September 2013. [Google Scholar]
- Lakshmi, S.M.; Gani, M.A.; Kamalesh, V.; Mahalakshmi, V.; Padmesh, P.M. Correlating unsoaked CBR with UCC strength for SC and SP soil. Mater. Today Proc. 2021, 43, 1293–1303. [Google Scholar] [CrossRef]
- Livneh, M. In-situ CBR testing by indirect methods. In Proceedings of the 12th International Conference on Soil Mechanics and Foundation Engineering, Rio De Janeiro, Brazil, 13–18 August 1989. [Google Scholar]
- Livneh, M.; Ishai, I. Prediction of CBR Values Under Covered Areas. In Proceedings of the 2nd Australia—New Zealand Conference on Geomechanics, Brisbane, Australia, 21–25 July 1975. [Google Scholar]
- Shahien, M.M.; Farouk, A. Estimation of deformation modulus of gravelly soils using dynamic cone penetration tests. Ain Shams Eng. J. 2013, 4, 633–640. [Google Scholar] [CrossRef]
- Benz-Navarrete, M.A.; Breul, P.; Gourvès, R. Application of wave equation theory to improve dynamic cone penetration test for shallow soil characterisation. J. Rock Mech. Geotech. Eng. 2022, 14, 289–302. [Google Scholar] [CrossRef]
- George, V.; Rao, N.C.; Shivashankar, R. PFWD, DCP and CBR correlations for evaluation of lateritic subgrades. Int. J. Pavement Eng. 2009, 10, 189–199. [Google Scholar] [CrossRef]
- Taskiran, T. Prediction of California bearing ratio (CBR) of fine grained soils by AI methods. Adv. Eng. Softw. 2010, 41, 886–892. [Google Scholar] [CrossRef]
- Sabat, A.K. Prediction of california bearing ratio of a soil stabilized with lime and quarry dust using artificial neural network. Electron. J. Geotech. Eng. 2013, 18, 3261–3272. [Google Scholar]
- Roy, T.K.; Kuity, A.; Roy, S.K. Prediction of soaked CBR for subgrade layer by using artificial neutral network model. In Proceedings of the International Symposium on Engineering under Uncertainty: Safety Assessment and Management, Kolkata, India, 4 January 2013. [Google Scholar]
- Bhatt, S.; Jain, P.K.; Pradesh, M. Prediction of California bearing ratio of soils using artificial neural network. Am. Int. J. Res. Sci. Technol. Eng. Math. 2014, 8, 156–161. [Google Scholar]
- Erzin, Y.; Turkoz, D. Use of neural networks for the prediction of the CBR value of some Aegean sands. Neural Comput. Appl. 2016, 27, 1415–1426. [Google Scholar] [CrossRef]
- Taha, S.; Gabr, A.; El-Badawy, S. Regression and neural network models for California bearing ratio prediction of typical granular materials in Egypt. Arab. J. Sci. Eng. 2019, 44, 8691–8705. [Google Scholar] [CrossRef]
- Bardhan, A.; Samui, P.; Ghosh, K.; Gandomi, A.H.; Bhattacharyya, S. ELM-based adaptive neuro swarm intelligence techniques for predicting the California bearing ratio of soils in soaked conditions. Appl. Soft Comput. 2010, 110, 107595. [Google Scholar] [CrossRef]
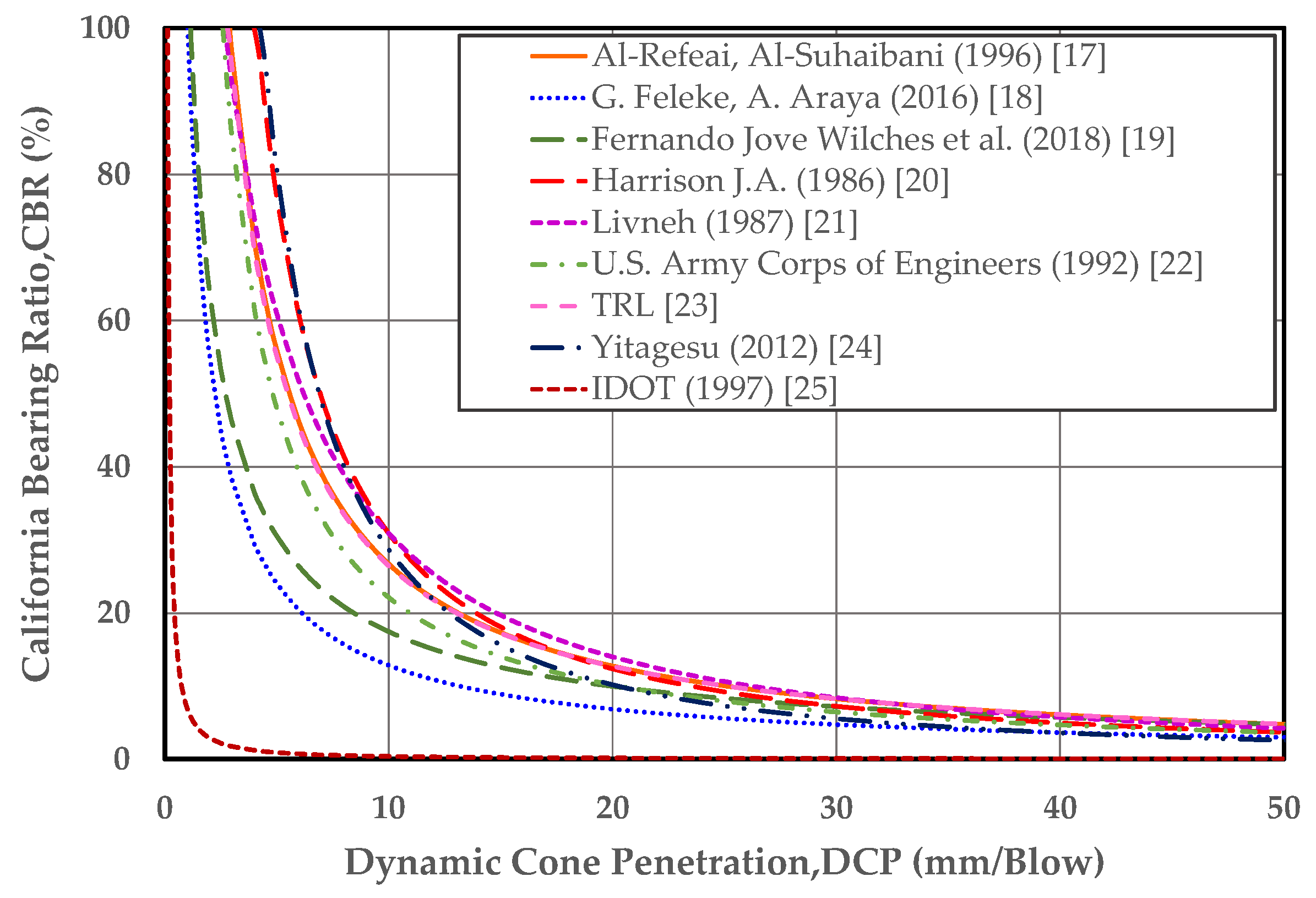


| Equation No. | Correlation CBR (%), DCP (mm/Blow) | Researchers |
|---|---|---|
| 1 | Al-Refeai, Al-Suhaibani (1996) [17] | |
| 2 | Feleke & Araya (2016) [18] | |
| 3 | Wilcesh et al. (2018) [19] | |
| 4 | Harrison (1986) [20] | |
| 5 | Livneh (1989) [21] | |
| 6 | U.S. Army Corps of Engineers (1992) [22] | |
| 7 | TRL [23] | |
| 8 | Yitagesu (2012) [24] | |
| 9 | IDOT (1997) [25] |
| Sample No. | LL (%) | PI (%) | Gs | Soil Classification | |
|---|---|---|---|---|---|
| AASHTO | USCS | ||||
| 1 | 18.27 | 5.54 | 2.69 | A-2-4 | SC–SM |
| 2 | 24.50 | 13.21 | 2.67 | A-2-6 | SC |
| 3 | 15.99 | 4.51 | 2.65 | A-2-4 | SC–SM |
| 4 | 17.43 | 9.04 | 2.65 | A-2-4 | SC |
| 5 | 19.27 | 9.75 | 2.67 | A-2-4 | SC |
| 6 | 20.12 | 11.15 | 2.65 | A-2-6 | SC |
| 7 | 19.50 | 15.48 | 2.66 | A-2-6 | SC |
| 8 | 18.02 | 9.57 | 2.68 | A-2-4 | SC |
| 9 | 21.89 | 16.44 | 2.63 | A-2-6 | SC |
| 10 | 15.78 | 10.84 | 2.67 | A-2-6 | SC |
| 11 | 20.56 | 8.86 | 2.67 | A-2-4 | SC |
| 12 | 27.56 | 20.04 | 2.66 | A-2-6 | SC |
| 13 | 19.95 | 8.22 | 2.64 | A-2-4 | SC |
| 14 | 23.21 | 14.61 | 2.63 | A-2-6 | SC |
| 15 | 18.27 | 6.08 | 2.62 | A-2-4 | SC–SM |
| 16 | 20.32 | 14.69 | 2.65 | A-2-4 | SC |
| 17 | 19.81 | 14.92 | 2.66 | A-2-4 | SC |
| 18 | 17.23 | 10.98 | 2.68 | A-2-6 | SC |
| 19 | 16.72 | 5.56 | 2.63 | A-2-4 | SC–SM |
| 20 | 17.25 | 6.12 | 2.62 | A-2-4 | SC–SM |
| 21 | 18.33 | 11.23 | 2.64 | A-2-4 | SC |
| Sample No. | Soil Classification | MDD (g/cm3) | DCP (mm/Blow) | CBR (%) |
|---|---|---|---|---|
| 1 | SC–SM | 1.84 | 20.83 | 14.18 |
| 2 | SC | 1.79 | 13.10 | 12.92 |
| 3 | SC–SM | 1.71 | 31.25 | 5.32 |
| 4 | SC | 1.75 | 20.00 | 8.66 |
| 5 | SC | 1.74 | 25.00 | 8.13 |
| 6 | SC | 1.79 | 30.00 | 7.88 |
| 7 | SC | 1.89 | 16.67 | 15.44 |
| 8 | SC | 1.64 | 30.00 | 4.54 |
| 9 | SC | 1.76 | 10.70 | 21.42 |
| 10 | SC | 1.73 | 27.50 | 8.82 |
| 11 | SC | 1.78 | 22.00 | 11.50 |
| 12 | SC | 1.86 | 15.71 | 13.02 |
| 13 | SC | 1.94 | 12.50 | 20.37 |
| 14 | SC | 1.86 | 17.86 | 13.55 |
| 15 | SC–SM | 1.85 | 11.09 | 14.28 |
| 16 | SC | 1.76 | 30.64 | 8.65 |
| 17 | SC | 1.93 | 10.42 | 25.87 |
| 18 | SC | 1.70 | 33.33 | 5.25 |
| 19 | SC–SM | 1.95 | 8.93 | 30.36 |
| 20 | SC–SM | 1.94 | 7.35 | 35.46 |
| 21 | SC | 1.69 | 39.82 | 5.04 |
| Equation Number | Al-Refeai & Al-Suhaibani (1996) [17] | Feleke & Araya (2016) [18] | Wilches et al. (2018) [19] | This Study |
|---|---|---|---|---|
| 1 | 0.82 | 0.45 | 0.96 | 0.97 |
| 2 | 0.59 | 0.85 | 0.83 | 0.77 |
| 3 | 0.78 | 0.92 | 0.97 | 0.91 |
| 4 | 0.43 | 0.00 | 0.92 | 0.93 |
| 5 | 0.85 | 0.74 | 0.93 | 0.92 |
| 6 | 0.82 | 0.67 | 0.92 | 0.97 |
| 7 | 0.83 | 0.51 | 0.96 | 0.97 |
| 8 | 0.09 | 0.00 | 0.81 | 0.95 |
| 9 | 0.03 | 0.06 | 0.02 | 0.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chokkerd, J.; Udomchai, A.; Sultornsanee, S.; Angkawisittpan, N.; Jantosut, P.; Sangiamsak, N.; Kaewhanam, N. Recalibrated Correlations between Dynamic Cone Penetrometer (DCP) Data and California Bearing Ratio (CBR) in Subgrade Soil. Eng 2024, 5, 1173-1182. https://doi.org/10.3390/eng5030064
Chokkerd J, Udomchai A, Sultornsanee S, Angkawisittpan N, Jantosut P, Sangiamsak N, Kaewhanam N. Recalibrated Correlations between Dynamic Cone Penetrometer (DCP) Data and California Bearing Ratio (CBR) in Subgrade Soil. Eng. 2024; 5(3):1173-1182. https://doi.org/10.3390/eng5030064
Chicago/Turabian StyleChokkerd, Jirawat, Artit Udomchai, Sivarit Sultornsanee, Niwat Angkawisittpan, Piyanat Jantosut, Noppadol Sangiamsak, and Nopanom Kaewhanam. 2024. "Recalibrated Correlations between Dynamic Cone Penetrometer (DCP) Data and California Bearing Ratio (CBR) in Subgrade Soil" Eng 5, no. 3: 1173-1182. https://doi.org/10.3390/eng5030064
APA StyleChokkerd, J., Udomchai, A., Sultornsanee, S., Angkawisittpan, N., Jantosut, P., Sangiamsak, N., & Kaewhanam, N. (2024). Recalibrated Correlations between Dynamic Cone Penetrometer (DCP) Data and California Bearing Ratio (CBR) in Subgrade Soil. Eng, 5(3), 1173-1182. https://doi.org/10.3390/eng5030064







