Investigation and Sensitivity Analysis of Economic Parameters on the Operation of Cogeneration Systems to Supply Required Energies for Residential Buildings

Abstract

The Combined Cooling, Heat, and Power (CCHP) System is an efficient technology that reduces primary energy consumption and carbon dioxide emissions by generating heat, cold, and electricity simultaneously from the same fuel source. This study developed an economic optimization model using linear mathematical program theory to determine the optimal sizes of different components in a CCHP system. The study found that CCHP systems with internal combustion engines have the largest optimal size due to lower capital expenditure and improved hourly changes in combined energy production by considering electrical and absorption chillers simultaneously. The analysis compared the size determination of CCHP systems with internal combustion engine (ICE), sterling engine (SE), and proton exchange membrane fuel cell (PEMFC) technologies. PEMFC had the highest annual overall cost among the technologies studied. The results of determining the size of the CCHP system are compared with ICE, SE, and PEMFC technologies. It has been noted that PEMFC has the highest annual overall cost among the studied technologies. The usefulness index of the CCHP system increased from 23% to almost 40% when electricity was sold to the grid using internal combustion engine technology.

1. Introduction

Energy is one of the most influential factors in the economic and social sectors of a country. The rapid reduction in the ratio of fossil energy resources reserves to its production, increased energy consumption (energy security), and environmental pollution (climate change) are serious global concerns [1,2,3]. In this regard, the global demand for optimizing energy consumption and systems and energy failure has grown without contamination or less pollution. This need has led the world to decentralized energy systems including renewable energy systems (RE) and low-carbon technology (LCT) such as Combined Cold, Heat, and Power (CCHP) [4,5,6].

According to the International Energy Agency, the construction sector in the world accounted for about 34.7 percent of total energy consumption in 2011, the largest share in energy consumption in the world compared to other major sectors (industry and transportation). Also, according to Iran’s energy balance sheet, in 2011, the construction sector accounted for 37.08% of total energy consumption in Iran, so for two decades, the share of buildings in final energy consumption in Iran has grown by 21.59% (

Table 1. The percent of ultimate energy consumption by different sections in Iran [9].

The Ultimate Energy Consumption by Sections (%)	1990	2010	Rate (%)
Building	30/50	37/08	21/59
Industry	28/11	24/61	−12/43
Transportation	23/95	25/55	6/67
Agriculture	7/39	3/98	−46/20
Other consumptions	17/45	12/76	−26/85

) [7,8,9]. One of the problems of Iran’s energy sector is the high loss of energy in distribution and electricity transmission networks, so from a total of 56,181 MW of electricity generation in 2009, 17.04%, i.e., 9573 MW, was wasted in power distribution and transmission networks [10,11,12]. Therefore, one of the solutions for eliminating or minimizing the severe inefficiencies of electricity distribution and transmission in Iran is the use of decentralized systems of cogeneration of electricity and heat.

The aim of determining the size is to design a system in such a way that the main parameters including the size of different components of the cogeneration system are defined optimally. Many studies have been conducted in this field. In this study, the cogeneration system has been evaluated for a set of stores, a mathematical model was developed to calculate the optimum size of the CHP system, and evaluations were carried out based on energy efficiency considerations and economic considerations.

In [13,14], two common CHP options, gas engines and fuel cells, for residential buildings were analyzed. For each system, two operational modes including cost-minimization operations and minimum pollution operations were considered using an evaluation and planning model for CHP systems of residential buildings. The results showed that the fuel cell system for residential buildings is a better option both economically and environmentally. Optimal forming of facilities of a specified commercial building, by selecting the sizes and number of cogeneration systems and auxiliary equipment based on annual demands of electricity, heating, and cooling can be calculated. The purpose of this paper is to evaluate the profit-making of CHP systems for residential building applications. An integrated CHP system includes a primary axle, an electrical energy storage system, a thermal storage system, and an additional boiler. In this research, a thermo-economic analysis is performed. To define the optimal size of CHP-integrated system components, the code developed is profitable and saves primary energy compared to the separate generation of electricity and heat.

Various techniques can be used to determine the size of energy systems such as the maximum rectangular (MR) design method, linear programming (LP), nonlinear programming (NLP), mixed-integer nonlinear programming (MINLP), fuzzy logic (FL), and genetic algorithms (GA) [15]. In this study [16], mixed-integer linear programming was used to find the optimal solution. The optimal forming of system equipment and the optimal operational model were calculated based on the annual cost method for installing the cogeneration system of a hospital and an apartment group in Seoul, Republic of Korea. The authors of [17,18] developed a definitive linear programming model 1 that minimizes the annual costs of the system, taking into account the size of the system. Considering the most widely used technologies such as internal combustion engines, sterling engines, and fuel cells for this type of application, the research was conducted. The result of this study was that electrical and thermal demands are essential entrances for each model of size selection and different technologies create different sizes in the model.

Also, NLP and MINLP techniques have been used to optimize energy systems. An optimal programming method for cogeneration facilities based on the nonlinear mathematical programming theory of mixed integers in the study [19] has been suggested. The optimum values of equipment capacities have been calculated considering operational strategy. It has been proven that optimal size and logical operations are very important for achieving the most economic advantages of the cogeneration system.

Using a nonlinear mixed-number programming model, the paper analyzed the effect of long-term thermal storage on the long-term operation of the CHP system in a thermal network. In this study, an optimization model based on a nonlinear programming method is used to research the optimal operational strategy and economical study of CHP systems in residential, commercial, and health centers. In this study, to use the maximum potential of CHP systems in buildings, a nonlinear programming optimization model has been developed to select the optimum capacity to determine the optimal performance pattern of microturbine systems [20,21].

Previous studies separated electrical and absorption chillers to evaluate the CCHP system. In this study, a CCHP system that considers electrical and absorption chiller simultaneously is introduced and the optimum size of CCHP system equipment (including CHP unit, boiler, electric chiller, and absorption chiller) is calculated. In this paper, an economic analysis of the CCHP system is carried out in detail in a residential building in Ardabil. The demand for cooling, heating, and electricity has been made for a building. The optimization model has been developed by the linear programming method. Finally, sensitivity analysis is performed.

2. Materials and Method

2.1. Expressing the Problem

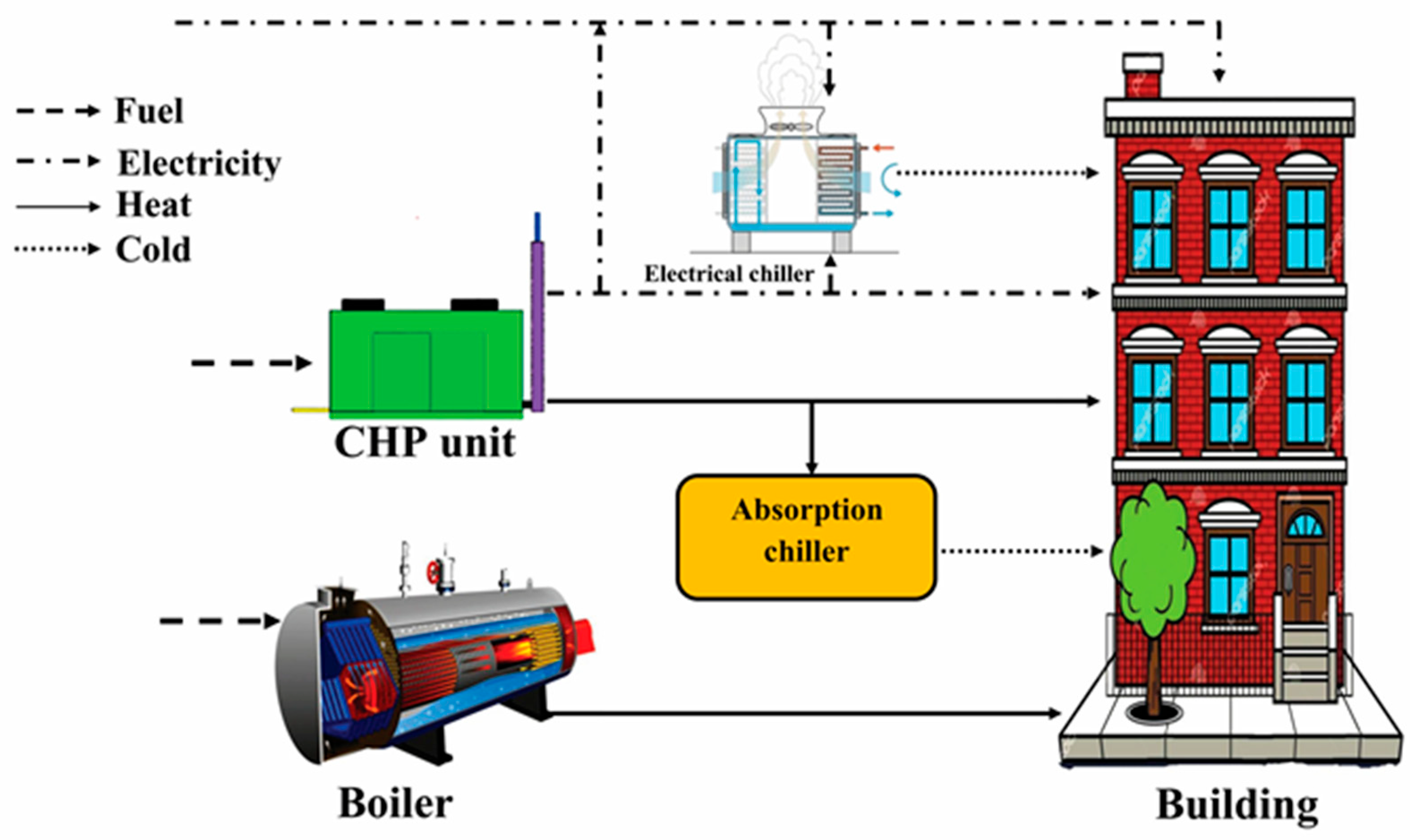
In modeling, it is necessary to create an energy flow diagram that represents the conceptual model of energy flow. The energy flow diagram of the building CCHP system, which has different, possible, and comprehensive equipment and has been investigated in this study, is shown in Figure 1.

The CCHP system in question includes a CHP unit, an auxiliary boiler, an absorbent chiller, and an electric chiller. The CHP unit works with natural gas to match the building’s heat and electricity demands. Lighting power and equipment are supplied to the consumer of the building by combining the direct activity of the CHP unit, and the electricity purchased from the external network. In case of insufficient electricity generated by CHP, electricity is purchased from the network. The building heat demand is supplied by the recycled heat generated by the CHP unit activity and the heat generated by the auxiliary boiler. Additional heat recycled by the CHP unit can be used in the summer in the absorption chiller to produce cooling. In case of insufficient heat generated by the CHP unit, the residual heat boiler supplies the demand. The cooling demand is matched by the electric chiller and absorption chiller. Electric chiller in-energy power is provided from the CHP unit or purchased from the grid, and the heat entering the absorption chiller is also supplied from the CHP unit heat recovery system.

The evaluation is based on hourly loads. Therefore, all parameters except performances refer to the sum over an hour. Some of the assumptions in this study are as follows:

•

CCHP system equipment performances are constant values at different partial loads.

•

All CCHP system equipment can work steadily from 0 to 100 percent.

•

Because Iran’s electricity policies and prices are unclear, it is assumed that the additional electricity generated will not be sold to the grid. But in another scenario, we assume that the extra electricity generated could be sold to the grid.

Aims of the Research

Among the objectives of this research, the following can be mentioned:

• Cogeneration system modeling for electricity supply, heating, and cooling.
• Energy analysis combined with economic parameters.
• Optimizing the desired system with the approach of the lowest cost and the highest amount of energy produced.
• Sensitivity analysis on the cost of electricity produced for sale.

2.2. Mathematical Model

The mathematical model of the problem of determining the optimal size and optimal operational strategy is formulated as an LP minimization model. The annual cost of energy, along with the annual investment cost of the initial amounts of equipment, earns the total annual cost. In the following relationships, abschiller, elechiller, CHP, and Boiler symptoms indicate CHP unit or co-production, electric chiller, absorption chiller, and auxiliary boiler, respectively.

2.2.1. Target Function

The objective function of the optimal size determination problem is minimizing the total annual cost, which includes annual investment cost and annual operating cost of energy:

$$\mathrm{Min}\left({\mathrm{C}}_{\mathrm{invest}}+{\mathrm{C}}_{\mathrm{run}}\right)$$

(1)

Or in other words,

$$\mathrm{Min}\left({\mathrm{C}}_{\mathrm{invest}}^{\mathrm{CHP}}+{\mathrm{C}}_{\mathrm{invest}}^{\mathrm{elechiller}}+{\mathrm{C}}_{\mathrm{invest}}^{\mathrm{abschiller}}+{\mathrm{C}}_{\mathrm{invest}}^{\mathrm{Boiler}}+{\mathrm{C}}_{\mathrm{run}}^{\mathrm{CHP}}+{\mathrm{C}}_{\mathrm{run}}^{\mathrm{Boiler}}+{\mathrm{C}}_{\mathrm{run}}^{\mathrm{abschiller}}+{\mathrm{C}}_{\mathrm{build}}^{\mathrm{grid}}+{\mathrm{C}}_{\mathrm{sale}}^{\mathrm{grid}}\right)$$

(2)

In the above relationship, C_invest and C_run represent the annual investment cost and annual operating cost related to various cogeneration system equipment, C^grid_build, the cost of electricity purchased from the grid for non-air conditioning equipment of the building, and I^grid_sale, the proceeds of electricity sold to the power grid. To expand the investment costs of system components per year, uniform serenities capital recycling (USCR) is used to convert the current value into an egalitarian annual payment flow over time and at specified interest rates.

$$\mathrm{USCR}={\displaystyle \frac{\mathrm{i}{\left(1+\mathrm{i}\right)}^{\mathrm{N}}}{{\left(1+\mathrm{i}\right)}^{\mathrm{N}}-1}}$$

(3)

i is the interest rate considered equal to 9% and N is the lifetime of the equipment. In the following equations, the annual investment costs of the CHP unit, auxiliary boiler, electric chiller, and absorption chiller are described. These equations are the process of extending the initial cost (based on taking into account the time value of money) over the lifetime of the system. Therefore,

$${\mathrm{C}}_{\mathrm{invest}}^{\mathrm{CHP}}={\mathrm{C}}_{\mathrm{c}}^{\mathrm{CHP}}\times {\mathrm{C}}_{\mathrm{p}}^{\mathrm{CHP}}\times \mathrm{USCR}$$

(4)

$${\mathrm{C}}_{\mathrm{invest}}^{\mathrm{Boiler}}={\mathrm{C}}_{\mathrm{c}}^{\mathrm{Boiler}}\times {\mathrm{C}}_{\mathrm{p}}^{\mathrm{Boiler}}\times \mathrm{USCR}$$

(5)

$${\mathrm{C}}_{\mathrm{invest}}^{\mathrm{elechiller}}={\mathrm{C}}_{\mathrm{c}}^{\mathrm{elechiller}}\times {\mathrm{C}}_{\mathrm{p}}^{\mathrm{elechiller}}\times \mathrm{USCR}$$

(6)

$${\mathrm{C}}_{\mathrm{invest}}^{\mathrm{abschiller}}={\mathrm{C}}_{\mathrm{c}}^{\mathrm{abschiller}}\times {\mathrm{C}}_{\mathrm{p}}^{\mathrm{abschiller}}\times \mathrm{USCR}$$

(7)

C_c represents the cost of different equipment of the cogeneration system in the size of one unit and C_p indicates the capacity of different equipment of the system. Commissioning costs include operating and maintenance costs, and for the absorption chiller, the cost of commissioning only includes maintenance costs. These equations are as follows:

$${\mathrm{C}}_{\mathrm{run}}^{\mathrm{CHP}}={{\displaystyle \sum }}_{\mathrm{m}=1}^{12}{{\displaystyle \sum }}_{\mathrm{d}=1}^1{{\displaystyle \sum }}_{\mathrm{h}=1}^{24}{\displaystyle \frac{{\mathrm{E}}_{\mathrm{sale}}^{\mathrm{CHP}}+{\mathrm{E}}_{\mathrm{build}}^{\mathrm{CHP}}+{\mathrm{E}}_{\mathrm{elechiller}}^{\mathrm{CHP}}}{{\mathrm{n}}_{\mathrm{e}}^{\mathrm{CHP}}}}\times {\mathrm{P}}_{\mathrm{NG}}+{{\displaystyle \sum }}_{\mathrm{m}=1}^{12}{{\displaystyle \sum }}_{\mathrm{d}=1}^1{{\displaystyle \sum }}_{\mathrm{h}=1}^{24}\left({\mathrm{E}}_{\mathrm{sale}}^{\mathrm{CHP}}+{\mathrm{E}}_{\mathrm{build}}^{\mathrm{CHP}}+{\mathrm{E}}_{\mathrm{elechiller}}^{\mathrm{CHP}}\right)\times {\mathrm{C}}_{\mathrm{m}}^{\mathrm{CHP}}$$

(8)

$${\mathrm{C}}_{\mathrm{run}}^{\mathrm{Boiler}}={{\displaystyle \sum }}_{\mathrm{m}=1}^{12}{{\displaystyle \sum }}_{\mathrm{d}=1}^1{{\displaystyle \sum }}_{\mathrm{h}=1}^{24}{\displaystyle \frac{{\mathrm{H}}_{\mathrm{build}}^{\mathrm{Boiler}}}{{\mathrm{n}}_{\mathrm{th}}^{\mathrm{CHP}}}}\times {\mathrm{P}}_{\mathrm{NG}}+{{\displaystyle \sum }}_{\mathrm{m}=1}^{12}{{\displaystyle \sum }}_{\mathrm{d}=1}^1{{\displaystyle \sum }}_{\mathrm{h}=1}^{24}\left({\mathrm{H}}_{\mathrm{build}}^{\mathrm{Boiler}}\right)\times {\mathrm{C}}_{\mathrm{m}}^{\mathrm{Boiler}}$$

(9)

$${\mathrm{C}}_{\mathrm{run}}^{\mathrm{elechiller}}={{\displaystyle \sum }}_{\mathrm{m}=1}^{12}{{\displaystyle \sum }}_{\mathrm{d}=1}^1{{\displaystyle \sum }}_{\mathrm{h}=1}^{24}\left({\mathrm{E}}_{\mathrm{elechiller}}^{\mathrm{grid}}\right)\times {\mathrm{P}}_{\mathrm{purch},\mathrm{ele}}+{{\displaystyle \sum }}_{\mathrm{m}=1}^{12}{{\displaystyle \sum }}_{\mathrm{d}=1}^1{{\displaystyle \sum }}_{\mathrm{h}=1}^{24}\left({\mathrm{R}}_{\mathrm{build}}^{\mathrm{elechiller}}\right)\times {\mathrm{C}}_{\mathrm{m}}^{\mathrm{elechiller}}$$

(10)

$${\mathrm{C}}_{\mathrm{run}}^{\mathrm{abschiller}}={{\displaystyle \sum }}_{\mathrm{m}=1}^{12}{{\displaystyle \sum }}_{\mathrm{d}=1}^1{{\displaystyle \sum }}_{\mathrm{h}=1}^{24}\left({\mathrm{R}}_{\mathrm{build}}^{\mathrm{abschiller}}\right)\times {\mathrm{C}}_{\mathrm{m}}^{\mathrm{abschiller}}$$

(11)

E^CHP_sale is the amount of electricity sold by the CHP system to the grid, E^CHP_build is the amount of electricity given from the simultaneous production system to the non-ventilation equipment of the building, E^CHP_elechiller is the amount of electricity given from the cogeneration system to the electric chiller, the η^CHP_e is the electrical efficiency of the PNG unit, the CHP natural gas price, the H^Boiler_build is heated from the auxiliary boiler to the building, η^Boiler_th is the thermal efficiency of the boiler, α the conversion coefficient of kWh m3 natural gas, E^grid_elechiller is the electricity purchased from the network for electric chiller, P_purch,ele is the price of electricity purchased from the network, R^elechiller_build is cooling supplied from the built-in electric chiller, and R^abschiller_build is cooling supplied from the heater absorbed into the building. Also, c_m represents the cost of maintaining a production unit related to various equipment of the cogeneration system. The cost of electricity purchased from the network for non-air conditioning equipment of the building is as follows:

$${\mathrm{C}}_{\mathrm{build}}^{\mathrm{grid}}={{\displaystyle \sum }}_{\mathrm{m}=1}^{12}{{\displaystyle \sum }}_{\mathrm{d}=1}^1{{\displaystyle \sum }}_{\mathrm{h}=1}^{24}\left({\mathrm{E}}_{\mathrm{build}}^{\mathrm{grid}}\right)\times {\mathrm{P}}_{\mathrm{purch},\mathrm{ele}}$$

(12)

E^grid_build is the network-purchased electricity for the building’s non-air-conditioned equipment. The proceeds from the sale of additional electricity to the grid are described as follows:

$${\mathrm{I}}_{\mathrm{sale},\mathrm{ele}}={{\displaystyle \sum }}_{\mathrm{m}=1}^{12}{{\displaystyle \sum }}_{\mathrm{d}=1}^1{{\displaystyle \sum }}_{\mathrm{h}=1}^{24}\left({\mathrm{E}}_{\mathrm{sale}}^{\mathrm{CHP}}\right)\times {\mathrm{P}}_{\mathrm{sale},\mathrm{ele}}$$

(13)

The p_sale,ele is the price of electricity to the grid.

2.2.2. Restrictions

Problem constraints consist of two parts called functional specifications of each piece of equipment and the relationships of the energy flow of the system. Performance specifications for each piece of equipment are formulated as follows:

2.2.3. The CHP Unit

Power generation and the heat recovery from the CHP unit should not exceed its maximum capacity at any time, or in other words,

$${\mathrm{E}}_{\mathrm{sale}}^{\mathrm{CHP}}+{\mathrm{E}}_{\mathrm{build}}^{\mathrm{CHP}}+{\mathrm{E}}_{\mathrm{elechiller}}^{\mathrm{CHP}}\le {\mathrm{C}}_{\mathrm{p}}^{\mathrm{CHP}}$$

(14)

$${\mathrm{H}}_{\mathrm{build}}^{\mathrm{CHP}}+{\mathrm{H}}_{\mathrm{abschiller}}^{\mathrm{CHP}}\le \left({\mathrm{E}}_{\mathrm{sale}}^{\mathrm{CHP}}+{\mathrm{E}}_{\mathrm{build}}^{\mathrm{CHP}}+{\mathrm{E}}_{\mathrm{elchiller}}^{\mathrm{CHP}}\right)\times \mathrm{HP}\times {\mathfrak{y}}_{\mathrm{heat},\mathrm{rec}}^{\mathrm{CHP}}$$

(15)

H_build^CHP is heat from the CHP unit to the building, H_abschiller^CHP is heat from the CHP unit to absorption chiller, HP is the heat-to-power ratio CHP system, and η_heat^CHP is the rec efficiency heat recovery CHP system.

2.2.4. Auxiliary Boiler

The heat production of the auxiliary boiler should not exceed its maximum capacity.

$${\mathrm{H}}_{\mathrm{build}}^{\mathrm{Boiler}}\le {\mathrm{C}}_{\mathrm{p}}^{\mathrm{boiler}}$$

(16)

2.2.5. Electric Chiller

The production of electric chiller cooling should not exceed its capacity.

$${\mathrm{R}}_{\mathrm{build}}^{\mathrm{elchiller}}\le {\mathrm{C}}_{\mathrm{p}}^{\mathrm{elechiller}}$$

(17)

$${\displaystyle \frac{{\mathrm{R}}_{\mathrm{build}}^{\mathrm{elechiller}}}{{\mathrm{E}}_{\mathrm{elechiller}}^{\mathrm{chp}}+{\mathrm{E}}_{\mathrm{elechiller}}^{\mathrm{grid}}}}={\mathrm{COP}}_{\mathrm{elechiller}}$$

(18)

COP_abschiller is the yield coefficient of the absorption chiller.

2.2.6. Absorption Chiller

The production of electric chiller cooling should not exceed its capacity.

$${\mathrm{R}}_{\mathrm{build}}^{\mathrm{abschiller}}\le {\mathrm{C}}_{\mathrm{p}}^{\mathrm{abschiller}}$$

(19)

$${\displaystyle \frac{{\mathrm{R}}_{\mathrm{build}}^{\mathrm{abschiller}}}{{\mathrm{H}}_{\mathrm{abschiller}}^{\mathrm{chp}}}}={\mathrm{COP}}_{\mathrm{abschiller}}$$

(20)

COP_abschiller is the yield coefficient of the absorption chiller. Another group of constraints is the energy balance of the whole system for each energy flow. The supply of cooling, heat, and electricity from the cogeneration system and the network must comply with the demands of cooling, heating, and electricity of the building every hour of every day of the different months of the year.

$${\mathrm{E}}_{\mathrm{build}}^{\mathrm{CHP}}+{\mathrm{E}}_{\mathrm{build}}^{\mathrm{grid}}\ge {\mathrm{D}}_{\mathrm{ele}}$$

(21)

$${\mathrm{H}}_{\mathrm{build}}^{\mathrm{CHP}}+{\mathrm{H}}_{\mathrm{build}}^{\mathrm{Boiler}}\ge {\displaystyle \frac{{\mathrm{D}}_{\mathrm{heating}}}{{\mathsf{\eta }}_{\mathrm{th}}^{\mathrm{heatingsystem}}}}+{\mathrm{D}}_{\mathrm{hotwater}}$$

(22)

$${\mathrm{R}}_{\mathrm{build}}^{\mathrm{abschiller}}+{\mathrm{R}}_{\mathrm{build}}^{\mathrm{elechiller}}\ge {\mathrm{D}}_{\mathrm{cooling}}$$

(23)

In the above equations, D_ele is the demand for the building’s non-air conditioning electricity, D_heating is the building’s heating, η_th^{heatingsystem} is thermal efficiency of the building heating system, D_hotwater demands hot water consumed by the building, and D_cooling demands the cooling of the building.

2.2.7. Evaluation Criteria

In this study, the cost savings ratio (CSR) is used as one of the indicators of economic evaluation that expresses the profitableness of the CCHP system and is defined as the rate of total annual energy difference between CCHP and the traditional system at the cost of the annual energy of the traditional system and is shown as the following equation:

$$\mathrm{CSR}={\displaystyle \frac{{\mathrm{C}}^{\mathrm{conv}}-{\mathrm{C}}^{\mathrm{CCHP}}}{{\mathrm{C}}^{\mathrm{conv}}}}$$

(24)

In this equation, C^conv and C^CCHP are the annual energy costs of the traditional system and CCHP system, respectively. Both energy costs are mainly composed of a combination of investment costs (initial cost) and startup costs, which are defined as follows:

$${\mathrm{C}}^{\mathrm{conv}}={\mathrm{C}}_{\mathrm{invest}}^{\mathrm{Boiler}}+{\mathrm{C}}_{\mathrm{run}}^{\mathrm{Boiler}}+{\mathrm{C}}_{\mathrm{build}}^{\mathrm{geid}}$$

(25)

$${\mathrm{C}}^{\mathrm{CCHP}}={\mathrm{C}}_{\mathrm{invest}}^{\mathrm{CHP}}+{\mathrm{C}}_{\mathrm{invest}}^{\mathrm{elechiller}}+{\mathrm{C}}_{\mathrm{invest}}^{\mathrm{abschiller}}+{\mathrm{C}}_{\mathrm{invest}}^{\mathrm{Boiler}}+{\mathrm{C}}_{\mathrm{run}}^{\mathrm{CHP}}+{\mathrm{C}}_{\mathrm{run}}^{\mathrm{Boiler}}+{\mathrm{C}}_{\mathrm{build}}^{\mathrm{grid}}+{\mathrm{C}}_{\mathrm{elechiller}}^{\mathrm{grid}}-{\mathrm{I}}_{\mathrm{sale}}^{\mathrm{grid}}$$

(26)

The above investment parameters are annually invested expenses, which are calculated by extending the initial cost of an option during the lifetime of that system while taking into account the time value of the money. These parameters are defined in previous sections.

3. Results

To apply the proposed optimization model, hourly information on building energy consumption is needed. In this section, Carrier software versions 3 and 4 have been selected to analyze the heating and cooling energy consumption of a residential building in Ardabil. Also, non-air conditioning electrical loads and indoor hot water demand of the building should be calculated.

The study building consists of five floors and its user is residents. The infrastructure of each floor of the building is 212 square meters and the number of people located in the building is about 25 people according to the investigations, and the use of the building is considered 24 h (this building is a standard example of buildings that are used by the general public in Ardabil).

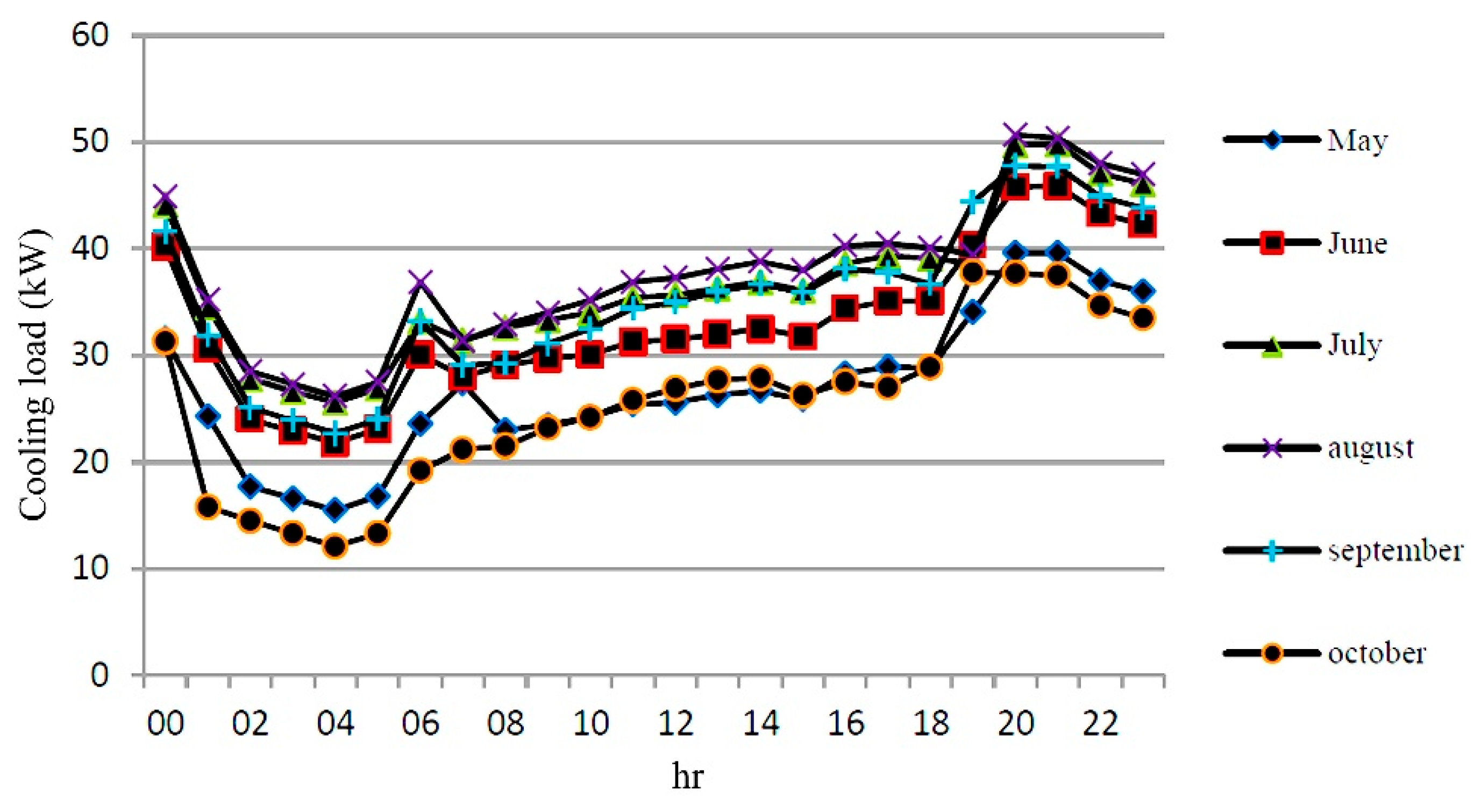
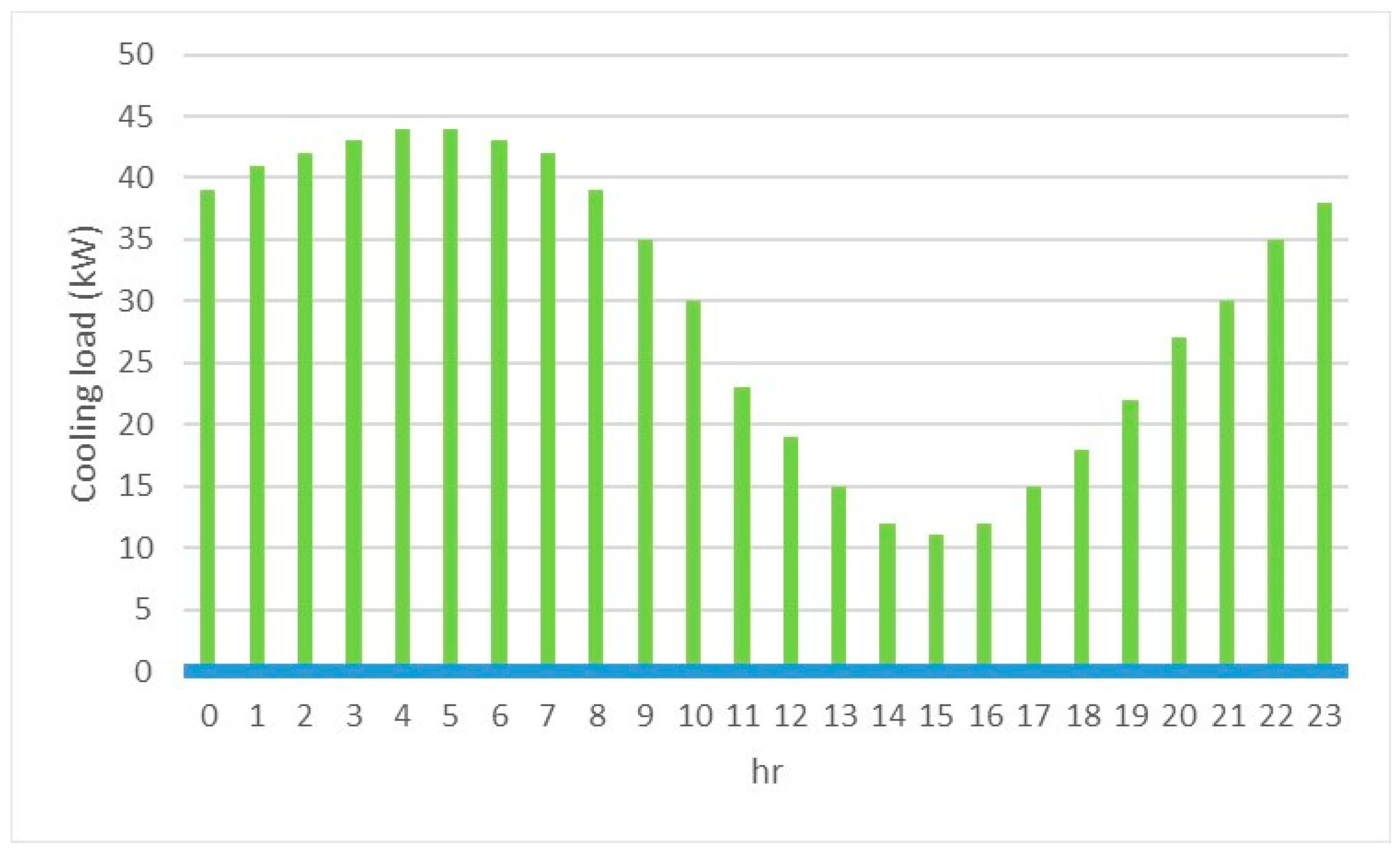
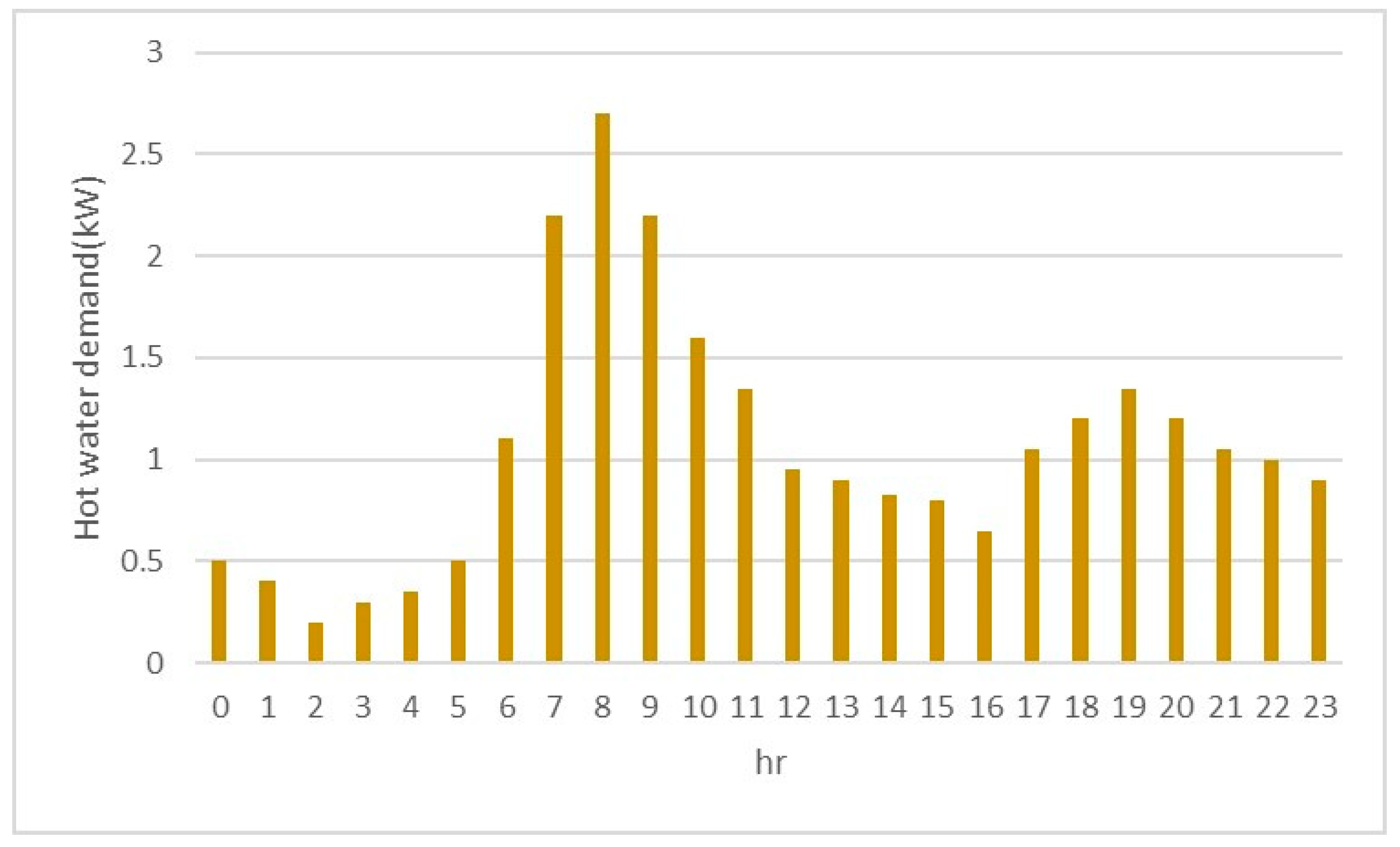
By applying the audited building information in the software, the cooling loads in different cooling months at different hours are shown in Figure 2. Also, the heating load on one day of January is shown in Figure 3. There are different methodologies for calculating hot water energy demand, which are described in various articles and reports. In this study, today’s algorithm described in [8] has been used. 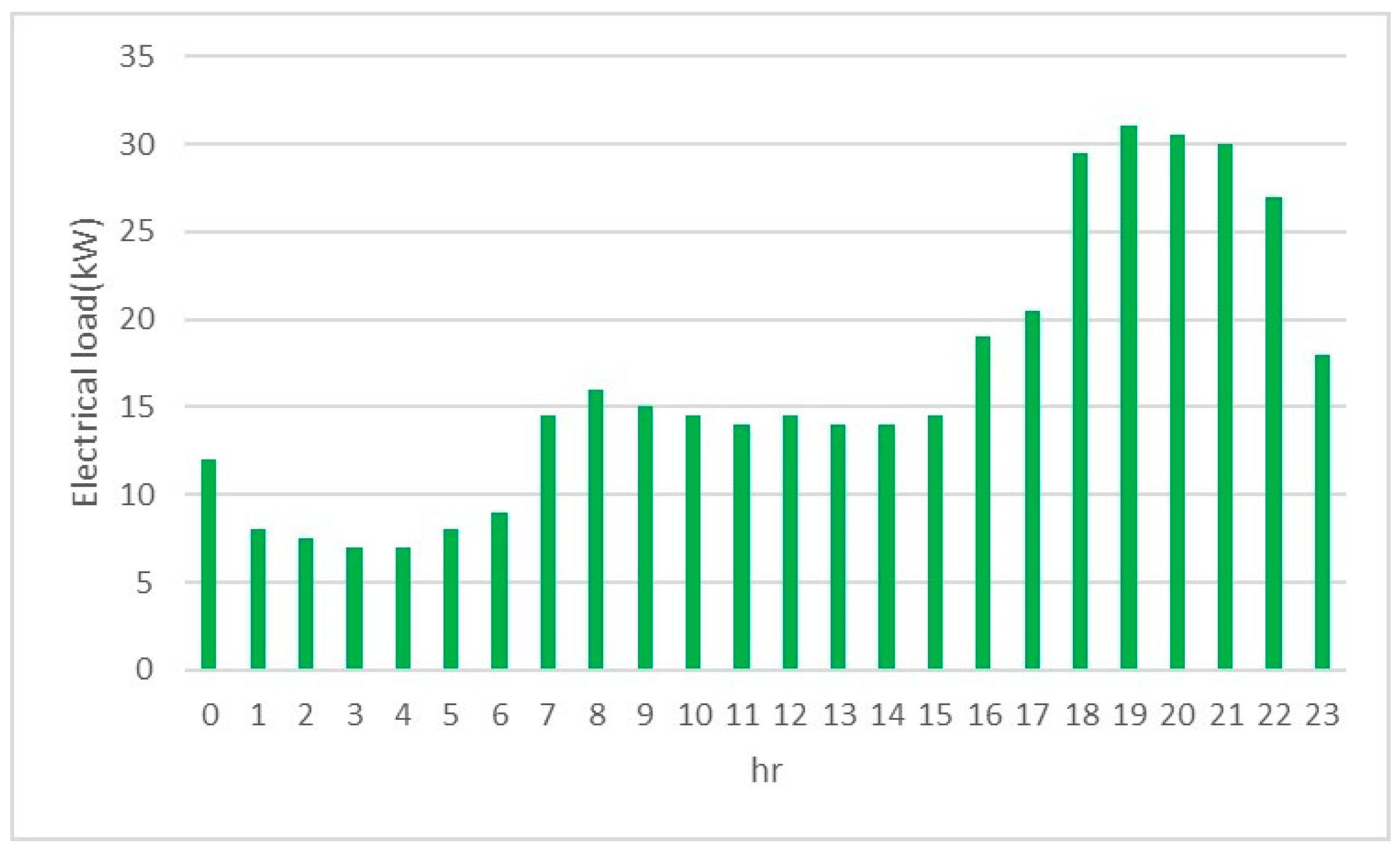Using this methodology in the studied building, the energy demand for hot water consumed is shown in Figure 4. Electrical demand for lighting and equipment is defined as the sum of electricity requirements of each vehicle according to the occupant profiles of the residents. Electrical demand for lighting and equipment is defined as the sum of electricity requirements of each vehicle according to the occupant profiles of the residents. The electricity demand profile diagram is obtained in the form of Figure 5.

Four different technologies are intended for the CHP unit because these four types of systems are common for residential building applications. These technologies include sterling engine (SE), internal combustion engine (ICE), SOFC fuel cell, and PEMFC fuel cells. Two engines and two fuel cells with fuel consumption (natural gas) in this order produces mechanical and electrical energy. The mechanical energy in two engines with generators turned into electric energy information on investment costs and maintenance costs of cogeneration systems and technical characteristics of systems are shown in

Table 2. The features of used equipment in the model.

Equipment	Output	Heat to Power Ration	Maintenance Cost (USD/KWh)	Investment Cost (USD/kW)	The Life of Equipment (Year)
Sterling engine(Mapna, Tehran, Iran)	0.25	2.8	0.00252	1040	20
Fuel cell EMFC (Mapna, Tehran, Iran)	0.45	1.11	0.00945	1565	30
Fuel cell SOFC (Mapna, Tehran, Iran)	0.5	0.9	0.00945	2898	30
Internal combustion engine (Mapna, Tehran, Iran)	0.4	1.25	0.00466	454	20
Auxiliary boiler (Mapna, Tehran, Iran)	0.8	-	0.00252	66	20
Electrical chiller (Mapna, Tehran, Iran)	3	-	0.00252	149	20
Absorption chiller (Mapna, Tehran, Iran)	0.7	-	0.00252	185	20

. Gas and electricity tariffs are key factors in the economic study of cogeneration systems. Gas and electricity prices used in the model have been extracted based on the average energy prices in Iran in 2019 and 2020 [22,23,24]. Purchased electricity prices, natural gas, and electricity sold are considered at a fixed rate of USD 0.19/kWh, USD 32.07/m, and USD 0.085/kWh. To simplify as well as provide a non-supplier picture of the economy of distributed generation systems, a fixed average rate tariff is considered acceptable.

To evaluate the proposed optimization model, two simulation scenarios are investigated to determine how the CCHP system works and the amount of annual total costs related to it.

Table 3. The size of various CCHP system equipment considering four simultaneous production technologies in the scenario of the impossibility of selling electricity to the grid.

	Internal Combustion Engine (kW)	Sterling Engine (kW)	SOFC (kW)
CHP unit	20.1	9.4	6.9
Auxiliary boiler	20.2	18	37.6
Electrical chiller	30.6	28.9	44.5
Absorption chiller	20.1	21.8	6.2
Annually total cost	1270.4	1546.2	16.46
Cost-effectiveness index	23.2	5.9	0.5

shows the results of determining the size of different equipment of the CCHP system for demand, taking into account four cogeneration technologies in the scenario of the impossibility of selling electricity to the grid. From Table 3 it can be seen that the technical side of the internal combustion engine is the largest compared to other technologies, because its investment cost is the lowest, while due to the highest investment cost for fuel cell technology, its size is smallest. This table also shows the annual cost and usefulness index. If it is possible to sell electricity for USD 1.0 per kilowatt-hour of electricity sold, the size of the equipment is shown in

Table 4. The size of various CCHP system equipment considering four simultaneous production technologies in the scenario of the selling electricity to the grid.

	Internal Combustion Engine (kW)	Sterling Engine (kW)	SOFC (kW)
CHP unit	36.3	12.2	7.2
Auxiliary boiler	-	11.2	37.3
Electrical chiller	15.5	23.4	34.3
Absorption chiller	35.2	27.3	6.4
Annually total cost	1008	15.28	16.46
Cost-effectiveness index	39	7,6	0.5

.

The results of Table 3 and Table 4 show that considering the scenario of electricity sales, the usefulness index increases. This is because electricity sales allow more on-site production, and therefore, systems with different technologies with higher electrical efficiency can sell more additional electricity to the public industry network.

This study shows that the economic evaluation of the cogeneration system depends heavily on the feasibility of electricity sales to the grid, especially in residential buildings that have less electrical demand compared to other sectors. Another point is that if it is possible to sell electricity to the grid compared to not selling electricity, the size of the system does not increase the usefulness index. If it is possible to sell electricity, the size larger than the optimal size decreases due to the increase in unused heat loss. Although electricity is not yet possible in Iran, one of the incentives for the development of distributed energy systems and increasing their efficiency is creating such conditions.

3.1. Sensitivity Analysis

A sensitivity analysis is performed to evaluate the effects of key parameters on the selection of cogeneration systems. In the following, an analysis is performed on internal combustion engine technology.

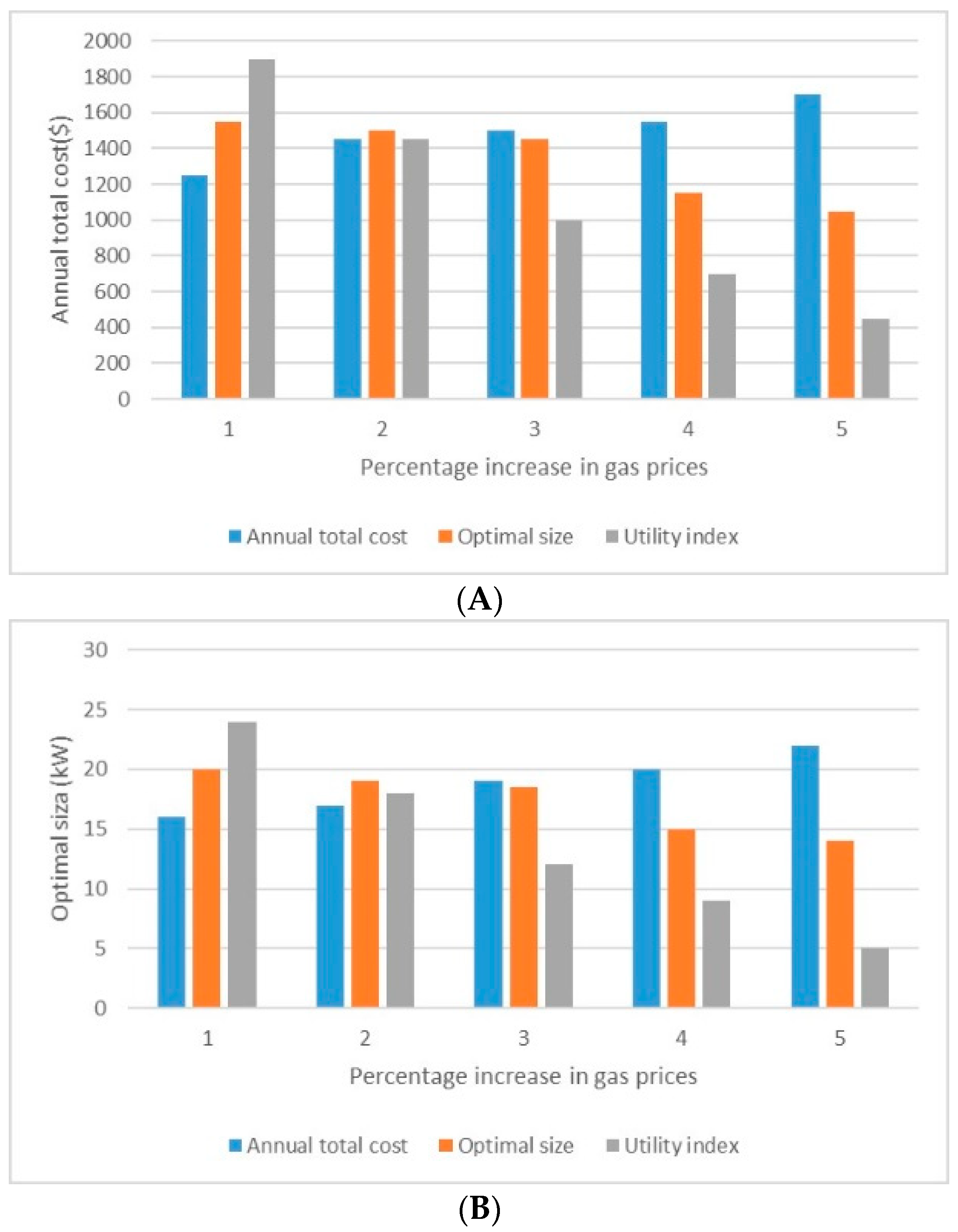
3.2. Sensitivity Analysis of Natural Gas Price

Natural gas prices greatly affect the cost of heating and cooling loads of buildings, and since global energy demand is increasing and energy resources are limited, this can lead to changes in natural gas prices. Also, considering that in Iran, subsidies are paid several times the actual price of natural gas and electricity, a suitable sensitivity analysis of the price of these energy carriers on optimal size, annual total cost, and usefulness index of cogeneration systems can be very useful for the application of these systems in Iran. Figure 6 shows the sensitivity of the annual cost, optimal capacity, and usefulness index of CCHP systems in terms of different natural gas prices relative to the current price. In any case, the effect of changes in gas prices on the size of the cogeneration unit is very low.

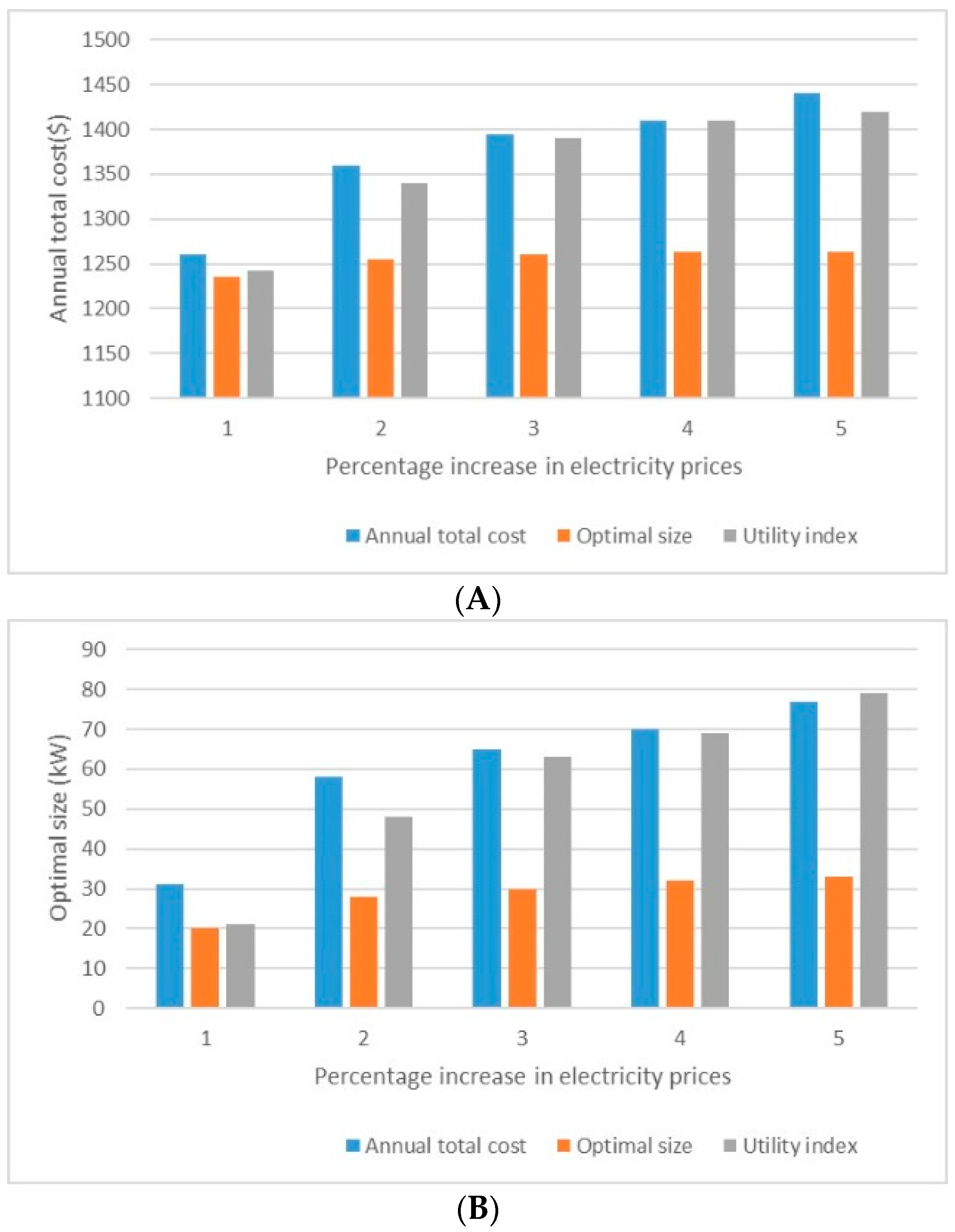
3.3. Sensitivity Analysis of Electricity Price

Electricity prices are another important factor that affects the total cost of energy systems and show the economic advantages of installing cogeneration systems in buildings. Also, due to the increase in electricity demand, electricity prices can increase, and as mentioned earlier, electricity prices in Iran are lower than the actual price up to several times the actual price due to subsidies. Figure 7 shows the sensitivity analysis of electricity purchase price for the studied demand. This form states that as electricity prices increase, the annual cost increases. It can also be realized that with the increase in electricity prices, the optimal size of the system also increases. Increasing the cost and optimal size is such that it can be seen that the usefulness index also increases greatly.

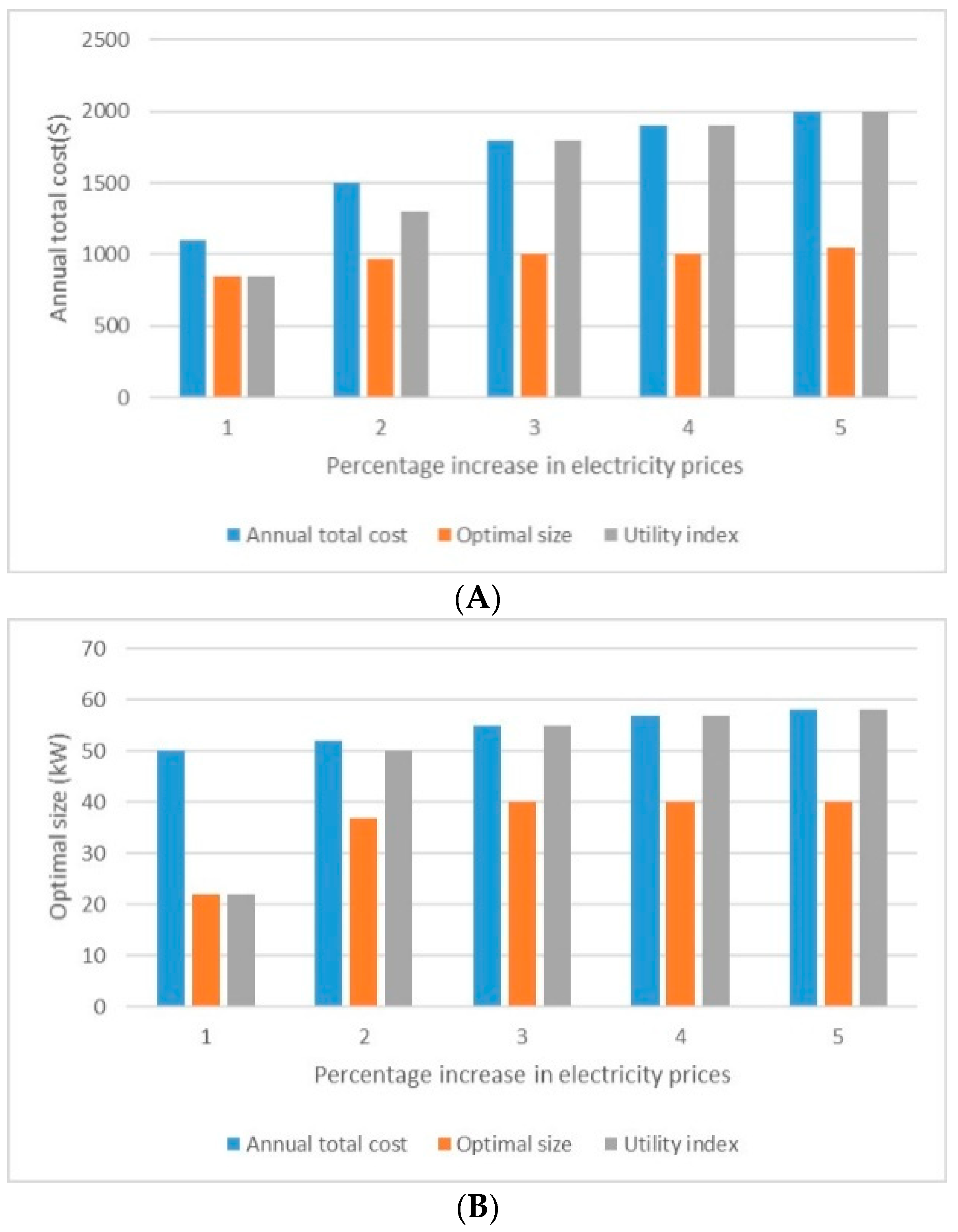
3.4. Sensitivity Analysis of Gas and Electricity Prices Simultaneously

Considering that with the increase in gas and electricity prices, the usefulness index changes against each other, it is appropriate to perform a sensitivity analysis on gas and electricity prices simultaneously. Figure 8 shows the sensitivity of annual cost, optimal capacity, and usefulness index in terms of energy carrier prices compared to the current price. This form states that by increasing the price of gas and electricity simultaneously and with equal ratios compared to the current price, the benefit index also increases.

3.5. Sensitivity Analysis of Electricity Prices

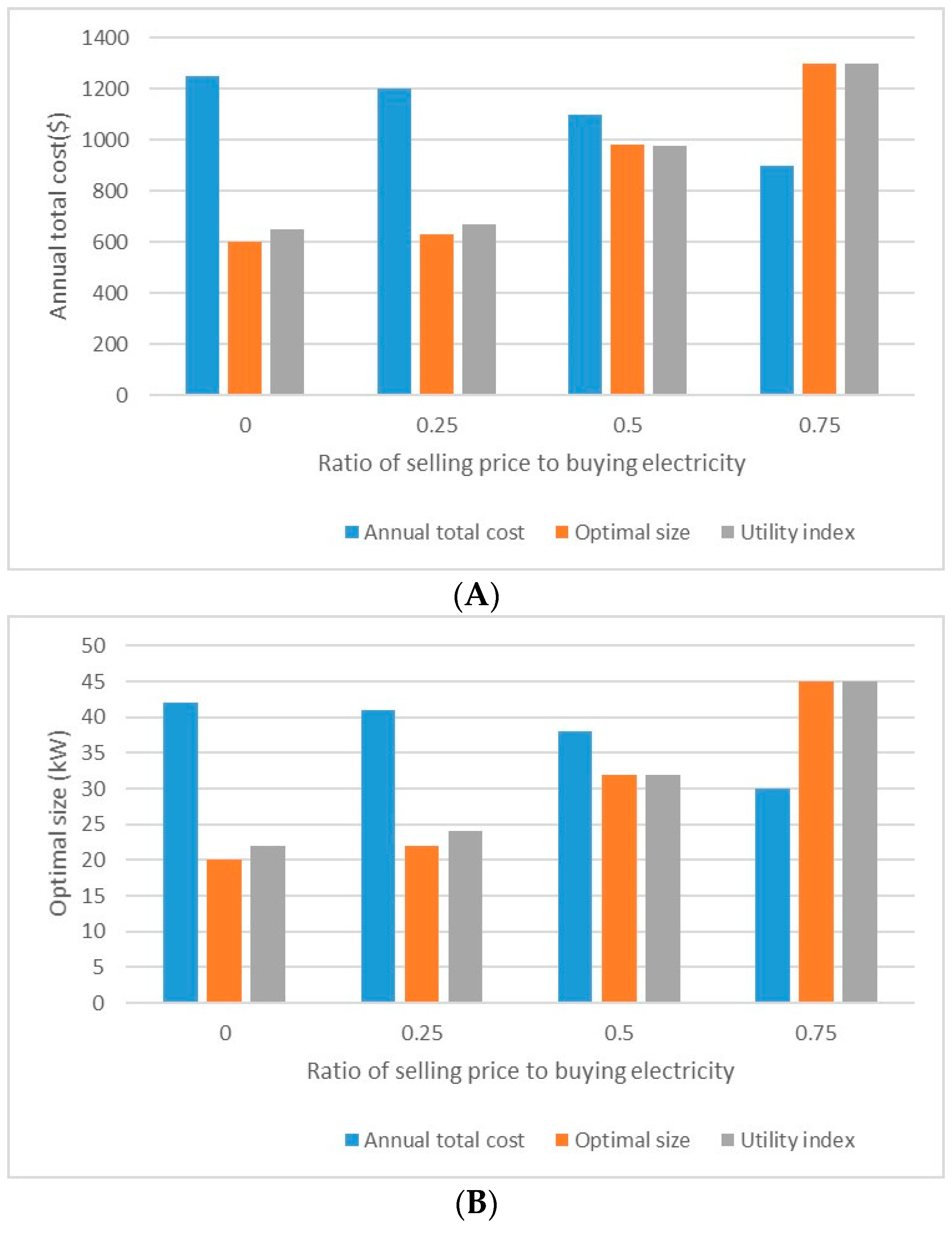
Since some governments have recently purchased additional electricity for these systems to encourage the use of renewable energy technologies such as wind turbines and efficient technologies such as cogeneration systems, the value of these systems is increasing. In Figure 9, sensitivity analysis of the price of electricity for sale is shown. From the figure, it can be realized that by using the higher price of electricity for sale, annual costs are significantly reduced and the size of the system increases. This is because the increase in the price of electricity for sale makes heat production much more valuable and suitable and the usefulness index increases.

4. Conclusions

In this study, an optimization model was used to determine the optimum size of CCHP systems and was analyzed economically. The optimization model was developed using linear programming. The model can measure the optimum capacity of CCHP system equipment (CHP unit, boiler, electric chiller, and absorption chiller). A sensitivity analysis was conducted to investigate the effects of different parameters on the acceptance of CCHP systems in the building. This study has been innovated by improving hourly changes in combined energy production by considering electrical and absorption chillers simultaneously.

The results of determining the size of the CCHP system are compared with ICE, SE, and PEMFC technologies. It has been noted that PEMFC has the highest annual overall cost among the studied technologies. It is also seen that the usefulness index of the CCHP system goes from 23% in the case of the impossibility of selling electricity, to almost 40% if electricity is sold to the grid, for internal combustion engine technology. In the case of selling electricity to the grid, despite the increase in the size of the CHP unit, the size of the electric chiller is smaller and the size of the absorption chiller becomes larger.

Future research is recommended in the following areas:

•

Investigation of exergy flow in different equipment.

•

Considering pollution factors to determine the optimal size.

•

Multi-objective optimization considering the reliability indicators of the required energy supply with intelligent algorithms.