Abstract
Google Scholar produces about 278 hits for the term “inertial propulsion”. If patents are also included, the number of hits increases to 536. This paper discusses, in a critical way, some characteristic aspects of this controversial topic. The review starts with the halteres of athletes in the Olympic games of ancient times and then continues with some typical devices which have been developed and/or patented from the second quarter of the twentieth century to the present day.
1. Introduction
The origin of the term “inertial propulsion” is not clear. Some of the early scientific papers mentioning this term around the mid-1960s are [1,2]. In 1977, this term was included as an entry in a technical encyclopedia [3] but was restricted to experimental works by Professor Eric Laithwaite [4]. We could say that inertial propulsion typically refers to a hypothetical concept in which a propulsion system generates thrust without expelling mass or propellant. It is widely accepted that such concepts often fall into the realm of speculative or fringe ideas and may lack scientific validation or consensus. A paper that demonstrates that an inertia-propelled device under dry friction moves in the opposite direction to the same device under viscous friction is [5]. In other words, the effect of external friction is crucial. According to [5], it is Newton’s first law of motion that precludes inertial propulsion in a vacuum. In contrast, the author of the present paper believes that the preclusion is mainly due to Newton’s third law (action equal and opposite to reaction).
Despite this unfavorable point of view of this controversial term, there are also many useful applications of inertial propulsion which will be discussed to a certain degree in this review paper. Interestingly, this idea has attracted the interest of many practitioners, as well as many serious researchers of high academic background, including persons coming from the aerospace industry or academia who have been granted a considerable number of patents (e.g., [6] among many others).
The motivation of researchers on inertial propulsion is varied. Some of them found a supposed way to break physical laws, and thus to achieve action-without-reaction (violating Newton’s third law) and thus to increase the efficiency of machines; this has not been possible to date. Others have found an alternative way to move heavy objects by vibrations without actual lifting, thus saving energy costs (e.g., [7,8,9,10,11]). Also, gyroscopes have been used for harvesting energy from waves [12,13].
Concerning space applications, the tendency of researchers to replace fuel-consuming rockets for interstellar space travels is also a particular topic of high importance for the future of mankind. Some alternatives have been reported in [14,15]. And because the supply of new inventive ideas is plentiful and pressing (more than three applications per day), in the year 2006 NASA decided to release a report to discourage new inventors [16].
Nevertheless, although the topic of inertial propulsion does not seem to provide a practical means for space propulsion by itself (it is useful for navigation [17,18] and attitude control [19], though), it is interesting to record the course the human mind has followed so far while dreaming of a better future without propellants. This review also offers a global approach to future researchers of this kind.
From the above short discussion, it has become apparent that there are two classes of inertial propulsion devices:
- Class 1: those that have been designed to generate external ratcheting reaction forces, usually (but not restrictively) opposed to the frictional environment.
- Class 2: those that have been designed to operate in a vacuum, in which reaction forces cannot be generated, but motion control is possible.
The structure of the paper is as follows. Section 2 refers to ancient times. Section 3 discusses progress in the 20th century, while Section 4 continues with the 21st century. Section 5 refers to the mechanics involved in inertial drives, which show that the relevant devices cannot produce net thrust, and Section 6 is a thorough discussion in which additional breakthrough methods are also mentioned.
2. Ancient Times and Fictional References
As previously mentioned, there are several reasons for this kind of research. If we begin from ancient times, Greek athletes used hand-held weights (called “halteres”, see Figure 1), aiming to extend the distance travelled in the Olympic long jump [20]. It is hypothesized that when the athlete was in the air, conservation of momentum allowed them to control their horizontal motion by lowering the inertial mass (see [21,22] and papers therein). Clearly, halteres are devices from Class 2.

Figure 1.
Halteres used in athletic games in ancient Greece, National Archaeological Museum, Athens (from https://en.wikipedia.org/wiki/Halteres_(ancient_Greece), accessed on 20 January 2024).
In a chronological sequence, the second written record exists in one of the stories regarding Baron Munchausen, a fictional German nobleman created by the writer Rudolf Erich Raspe in his 1785 book. Munchausen is trapped on his horse into a lake of mud, and he tries to pull his hair to give his body a boost to escape (Figure 2) [23]. Of course, in the real world this is not possible because the pulling force is internal, and thus the center of mass cannot move (Newton’s Second Law). Nevertheless, it is a case for reflection as to whether release is possible, for example using concepts from accepted vibrational mechanics ([7,8,9,10,11]), of course considering the action of friction between the mud and the horse.

Figure 2.
Baron Munchausen uses support-less propulsion to escape from the swamp by pulling himself up by his hair (source: [23]).
3. Inventions in the Twentieth Century
3.1. Rotating Masses
Since the second quarter of twentieth century, many “inertial drives” have been developed and some of them were patented. The main idea is that unidirectional thrust may be caused by contra-rotating eccentric masses (the assembly is called inertial drive) which are attached to a vehicle or a cart. The need for two masses (of even number in general) is related to the cancellation of the forces in the vertical (undesirable) direction of the vehicle’s motion.
The first official record is probably the patent by the Italian Professor Marco Todeschini (1933) [24], in which the drive consists of two contra-rotating masses (shown in Figure 3 by ‘H’ and connected through rigid rods to the ‘satellites’ C and D, respectively) moving on a three-dimensional curve, thus offering a net thrust and motion of the vehicle (i.e., toward the vertical axis ‘F’ on the Earth’s surface).
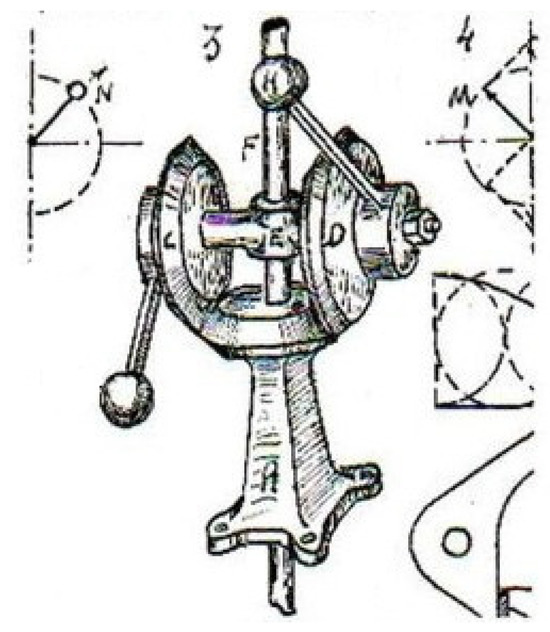
Figure 3.
Extract from Todeschini’s patent [24] (source: https://www.circolotodeschini.com/brevetto-provatidis/, accessed on 20 January 2024).
Obviously, the abovementioned inertial device can work on the ground (of Earth or of another planet) or in the water, where friction exists (Class 1 device). In contrast, it cannot produce a continuous net thrust per revolution when moving into the air because there is not support for the development of a reaction, and thus the weight of the system in space cannot be permanently cancelled out.
Interestingly, twenty-five years after Todeschini’s invention, the American citizen Norman Dean proposed a different setup (using two contra-rotating masses on circular paths) and claimed that it could assist in space travel (Figure 4) [25,26]. This topic has kept researchers from the civilian and military sectors busy, and therefore a lot of favorable publications are available [27,28,29,30,31,32]. Despite the advanced electronic equipment, the mechanical principle of the Dean drive is simpler but very similar to that of the abovementioned Todeschini’s drive, and thus the same criticism applies. A deeper mechanical analysis of the Dean drive is provided in Appendix A and Appendix B, the discussion of which generally covers all the relevant inertial propulsion devices.

Figure 4.
The Dean drive (source: https://en.wikipedia.org/wiki/Dean_drive, accessed on 20 January 2024).
It is worth mentioning that, a few years later (in 1963), the “Dean drive” was rejected for the first time in a scientific paper by Professor Stepanov [33], while later negative references on the same issue from Russian academics (already mentioned) are provided in [7,8].
The abovementioned negative comments of the Russian scientists did not influence the Italian Professor Alfio Di Bella, who extended the ideas of his compatriot Marco Todeschini [24], first by filing a patent in May 1967 [34] and then fifteen months later (August 1968) presenting an experimental prototype accompanied with theoretical results [35]. Briefly, with respect to Figure 5, motor 1 turns frame 4, carrying axle 9, counterweight 11 and bevel gear 10, which meshes with fixed bevel gear 14. This causes the out-of-balance mass shown (item 13) to follow the eight-shaped locus known to mathematicians as Viviani’s curve, or Viviani’s window (see [36]). Similar differential mechanisms for ornithopters were later reported by [37]. Since the prototype worked on the water, it is classified as a Class 1 device.
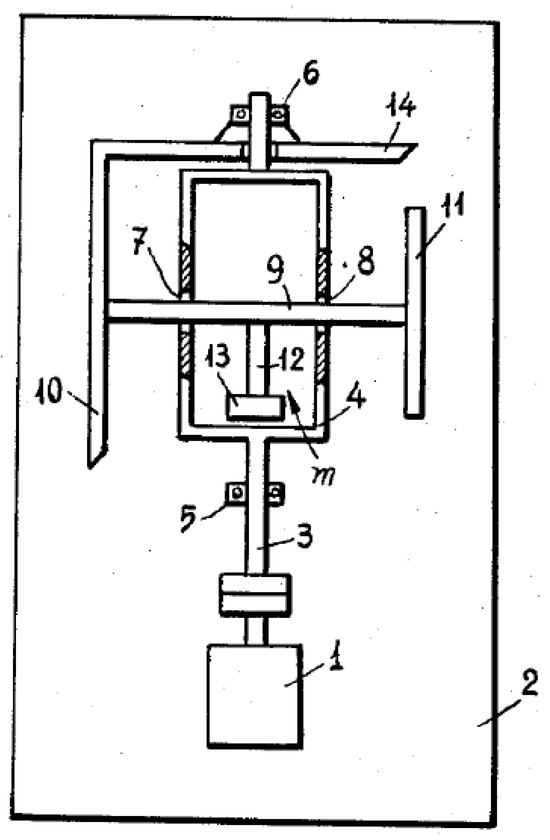
Figure 5.
The Di Bella mechanism (source: [34]).
According to [38], as well as additional Internet sources, in the year 1936, the Russian engineer Vladimir Tolchin (an engineer and head of the design office at Perm’s Dzerzhinsky Machine Plant) invented, described, and engineered a mechanism which he called the “inertioid”. It was a cart on which one or two loads were moved about—one slower, the other faster—by means of a spring motor. The cart itself then moved in an uneven fashion, even though no power was transmitted to the wheels. What is most interesting in the story of the inertioid (and its numerous variations) is the ontological interpretation of its principle of motion. Tolchin believed his cart moved without propulsion (there was no transmission mechanism from the motor to the wheels), arguing at the same time that it functioned “in accordance with the laws of a full mechanical process”, some aspects of which he interpreted in a new way [39]. However, the Perm designer’s intemperate followers, responding to critics who pointed out that the movement of Tolchin’s cart violated the law of conservation of momentum, made the dizzying conclusion that the inertioid challenged existing physical laws. New physics was needed to explain its motion. By the time Tolchin published his book in the late 1960s (first edition), the “natural” objects of this other physics had, in fact, been in evidence for some time. For the demonstration of an experimental prototype the reader is directed to [40]. After this discussion, it may be concluded that Tolchin’s device belongs to Class 1, because it uses the friction between the vehicle and the ground to develop adequate centrifugal force.
The fact that the use of vibrational methods was a favorite subject of Eastern scientists is confirmed by [7,8,9,10], as well as the numerous bibliographic references cited in the works of the Bulgarian Professor Ivan Lukanov, whose second language is Russian (see Section 4.2).
From the above discussion it becomes evident that the “Dean drive” which appeared in the USA in late 1950s and caused much ‘noise’ was not a local event, but an issue that had kept inventors busy some years earlier, at least in Italy and Russia. It is worth mentioning that in the mid-1960s, the concept of propulsion without wheels was also an attractive topic in the United Kingdom to Professor Eric Laithwaite, but was based mostly on electromagnetic considerations [41] (first printed in 1966).
In addition to Appendix A and the associated Appendix B, which refer to all the devices from Section 3.1, a still deeper discussion regarding the incapability of all the inertial propulsion devices to provide net thrust is provided in Section 5.
3.2. Gyroscopes and Spinning Wheels
Apart from the unidirectional thrust caused by contra-rotating eccentric masses, there have been several relevant experiments performed on gyroscopes. It was written in [42] that Professor Eric Laithwaite (1921–1997) was an able communicator and made many television appearances, including his Royal Institution Christmas Lectures to young people in 1966 and 1974. The latter of these made much of the surprising properties of the gyroscope. In his 1974 lectures, Laithwaite suggested that Newton’s laws of motion could not account for the behavior of gyroscopes and that they could be used as a means for reactionless propulsion. The members of the Royal Institution rejected his ideas, and his lectures were not published at the time, a first for the Royal Institution. His lectures were subsequently published independently as Engineer Through the Looking-Glass and on the Royal Institution website [43].
At almost the same time, another scientific attempt to study rotating gyroscopes was due to Bruce De Palma (1935–1997), who was working at MIT as a lecturer in Photographic Science in the Laboratory of Dr. Harold Edgerton and directed 3D color photographic research for Dr. Edwin Land of the Polaroid Corporation [44]. Based on photographic experiments from 1974 until his untimely death in October 1997, he claimed to have measured a delay in a falling gyro or an increase in its upper level in an oblique shot [45,46,47].
Thirteen years after De Palma’s experiments, Hayasaka and Takeuchi measured a weight reduction of gyros when rotating in the right direction (spin vector pointing downward) [48]; they showed that the higher the gyro revolutions per minute, the higher the weight loss. This finding was disputed by many others [49,50,51,52,53,54,55]. However, it is not perhaps widely known that Hayasaka insisted on his findings, and eight years later he cooperated with three other coworkers and presented similar measurements when the rotating gyro falls from a height [56] (unfortunately, the volume in which this paper belongs has been withdrawn from the electronic version of the Journal, so the interested reader has to ask for a hard copy in a library). In contrast, in a later paper Luo et al. [57] reported that:
“… the differential acceleration between a rotating mechanical gyroscope and a nonrotating one was directly measured by using a double free-fall interferometer, and no apparent differential acceleration has been observed at the relative level of 2 × 10−6. It means that the equivalence principle is still valid for rotating extended bodies, i.e., the spin-gravity interaction between the extended bodies has not been observed at this level. Also, to the limit of our experimental sensitivity, there is no observed asymmetrical effect or antigravity of the rotating gyroscopes as reported by Hayasaka et al. [48]”.
Moreover, the last paper in favor of Hayasaka’s theory is [58] (influenced by the work of professor N.A. Kozyrev), and probably those by professor Dmitriev [59,60] (closely related papers by the same author are [59,61,62]). Recently, it has been shown that within the context of Newtonian mechanics, a possible explanation for the decrease in the observed gravitational acceleration may be the change in the inclination of the falling gyroscope [63].
One of the latest papers concerning gyroscopes, and particularly Laithwaite’s experiments, is probably due to the British physicist Wayte [64], who reported a weight loss of 8 percent (it is noted that this loss has been calculated as a time integral of measured impulse of the reaction force). This finding was later disputed by Lőrincz and Tajmar [65]. In addition, the mechanics of Laithwaite’s engine have been studied until recently by Provatidis [66,67] and this issue will be discussed later in the present paper (see Section 4.3).
4. Progress in the Twenty-First Century
4.1. Theoretical Contributions
By the turn of the twenty-first century, a lot of questions regarding ‘gravity control’ had not been answered, and thus at least three projects were running simultaneously.
The first was Project Greenglow (The Quest for Gravity Control), which started in the mid-1990s, and was run officially under the management of the mathematician Ron Evans at BAE (British Aerospace) [68,69,70,71,72].
For the second project, called GRASP (Gravity Research for Advanced Space Propulsion), it has been written that it took place at The Boeing Co. although the company said that it did not spend money on that [72,73,74]. The latter is certainly related to Eugene Podkletov, but not much information is available in the public domain [75].
Regarding the third project, in 1996, a team of (USA) government, university and industry researchers proposed a program to seek the ultimate breakthroughs in space transportation: propulsion that requires no propellant mass, propulsion that can approach and, if possible, circumvent light speed, and breakthrough methods of energy production to power such devices [76]. In the period 1996–2004, NASA funded the Breakthrough Physics Program, managed by Marc Millis (open access reports are [76,77,78]), and the very final report was documented in a book of 740 pages [79].
Within the context of the abovementioned NASA project, it was concluded that ‘mechanical antigravity’ is impossible, and thus a particular report was released in December 2006 to prevent future inventors from disturbing them [16].
Despite the suggestions by NASA, the USA Patent Office continued to grant patents related to the term “antigravity” or other closely related ones. An internet search in Google Patents in January 2024 showed about 10,000 entries for the word “antigravity”, 7777 entries for the word “gravity control”, 17 entries for the word “antigravity propulsion”, and another 18 entries for the word “reactionless propulsion”. Considering that more than 20 alternative principles of physics can be used to achieve propulsion (as has been documented in [79,80]), of which one such methodology is inertial propulsion, it becomes evident that this review paper cannot cover the whole topic. Instead of this, the present paper is restricted to the use of masses and gyroscopes and occasionally refers to other noteworthy methods only when it makes sense to do so.
As already mentioned, the conventional Dean drive consists of two contra-rotating out-of-balance masses (eccentrics), and thus each mass traces out a complete closed circular path when the cart is still immobile. As a result, as the mass rotates, the impulse of the inertial (centripetal) force given in the upper half of this circle is cancelled by the impulse of the lower half of the same circle. To restore this shortcoming and break the symmetry (i.e., upper equals lower impulse), some inventors have tried to modify the lower part (see, e.g., Robertson [81] in Figure 6, in which the upper part of the rigid rod carrying the rotating mass No. 182 is longer than the lower part) or to introduce a secondary motion on the articulation of the rotating masses on the vehicle or to modify the ideally symmetric shape of the curve [82,83], thus causing a sort of time delay (as they claim).
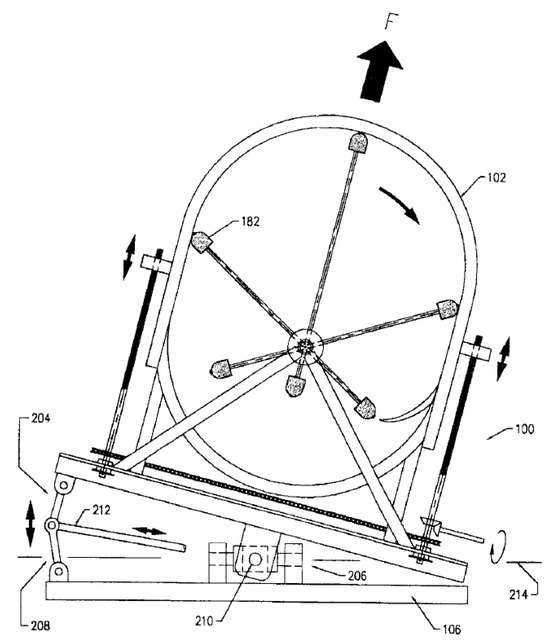
Figure 6.
One way to modify the lower radius in the path of the eccentric masses (from Robertson [81]).
Another way to modify the symmetrical shape of the circle traced by the two contra-rotating masses is as follows. A patent filed in October 2008 [84] smoothly modifies the lower part of the circular path of the rotating masses, using a special differential mechanism as explained in [85,86]. In more detail, the rotating masses trace a figure-eight-shaped path (the symbol of infinity, ∞) which is also inscribed into a half-spherical surface. This configuration (i) preserves the motion of the rotating masses in the upper part (either above or below the center of the sphere) and (ii) allows for the orientation of the axis of symmetry (of the said half-spherical surface) towards the desired direction of motion. But although this setup introduces a sort of asymmetry, it is obvious that after every 360 degrees of rotation (at angular velocity ) the masses always take the same initial position, and thus the time integral of the inertial force over a period vanishes. To overcome this shortcoming, the axis of symmetry of the said half-spherical surface is subject to a second rotation (at angular velocity ), thus fully breaking the symmetry, except for in the case that its angular velocity is a multiple of the angular velocity of the contra-rotating masses (i.e., , where is an integer number) (for details, see [86]). Nevertheless, despite the title of that paper, and even though it is unlikely that two upper points of the traced curve will be at the same altitude (height) on the vertical -axis, during the almost chaotic motion of each rotating mass there will always be two successive points along the curve (if the first point is the local lowest, the next will be the local highest) at which the horizontal velocity components will both vanish (see, Figure 7). In conclusion, despite the title of [86], within the context of Newtonian mechanics, it is not possible to continuously obtain net thrust.
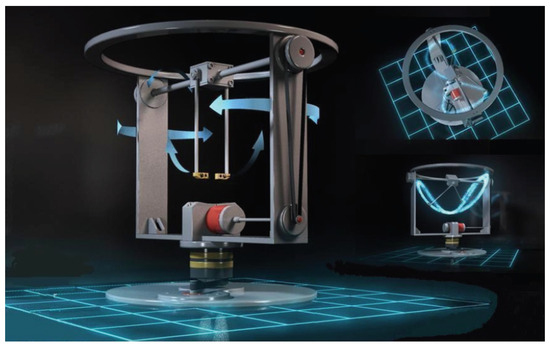
Figure 7.
The concept of the figure-eight-shaped drive [84,85,86] (artwork by S. Frigas).
It has been widely written that the most simplistic way to break the symmetry is to force the rods of the rotating masses to trace a circular arc of only 180 degrees, like car wiper blades. However, a mechanical study reveals a vanishing impulse per period, and thus null net thrust (see, Appendix C).
Another idea has come from the axial impact of an elastic beam (Figure 8). It is well-known from the theory of elasticity that when a Heaviside axial force is exerted on an elastic bar it takes some time until the elastic wave reaches the fixation, and then the reaction force becomes double (i.e., equal to ) and remains constant during the half period [87]. This fact is not against Newton’s third law (action equals to reaction) because the total impulse is preserved (see, Figure 8b). Based on this observation, it was thought that the rectification of the axial force would be possible if the beam was rotating with a period equal to the period of the elastic wave. The initial thought was that the dead time-interval in which the reaction force vanishes could correspond to positions of the beam below the horizontal line passing through the articulation point , and thus when the reaction force becomes non-zero then the beam would be found in the upper half space and would be pushed upwards. Unfortunately, this supposedly “brilliant” idea did not work for the following two reasons: (i) because the reaction force was internal to the system, and (ii) because a Coriolis force cancels its action. And since the Coriolis force does not exist in electromagnetics, a mechanical model of the Dean drive was compared with a Tesla-like electromagnetically based model [88] (a paper approved by The Boeing Co.). In other words, both models, i.e., the mechanical Dean drive (based on circular track) and the electromagnetic model, showed null thrust. A report describing the atmosphere of a relevant conference meeting, with the eyes of a specialized journalist, is [89].
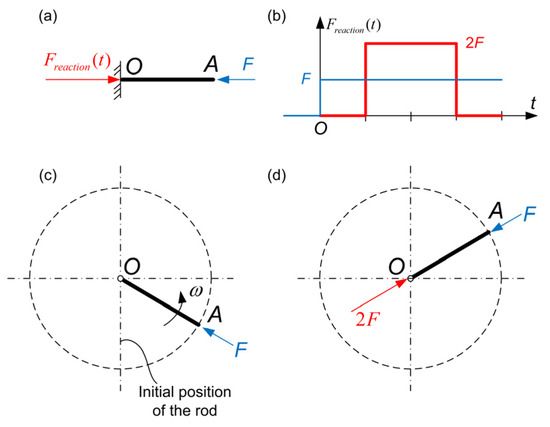
Figure 8.
The concept of the rotating elastic rod under an impact force: (a) immobile rod, (b) reaction force, (c) first half, (d), second half of period.
The reader may easily find many Internet (e.g., YouTube) videos in which a black box swims or jumps up by itself or a cart moves aided by a sort of inertial drive. In other words, inertial propulsion is an experimental fact, but its limits had not been explored, or at least had not been published until the end of the first decade of 2000. The only “scientific” work is that of Davis [30], in which a ‘fourth law of motion’ is proposed (in addition to the three by Isaac Newton). On the other hand, one may still find a lot of (pseudo-scientific) explanations that have been posted to the Internet.
To the best of our understanding, until the end of the twentieth century, the literature was reduced to the description of existing patents and/or qualitative characteristics of them [90,91,92,93]. At the beginning of the 21st century (2006), a Ph.D. thesis focusing on some existing inertial propulsion patents, without encouraging results on the possibility of net thrust, was defended [94]. Another relevant paper is [95].
To show the capabilities of the conventional Dean drive (let us call it so) operating in the air, Provatidis [96,97,98,99] published his first four papers considering that the rotating masses track circular curves (the simplest case). To make robust conclusions, several formulations were applied such as (i) the decomposition of the mechanical system into free body-diagrams and the further application of Newton’s laws, (ii) the study of the center of mass, (iii) the application of Lagrange equations, and (iv) the conservation of linear momentum. Obviously, all these four approaches have led to the same result, which for ‘motion in the air’ is as follows (see, [96,97,98,99] as well as Appendix A and Appendix B):
- An inertial drive attached to a vehicle or cart, which initially lies on the ground, causes alternating (sinusoidal) support forces on it. For an immobilized vehicle, the total linear momentum of the contra-rotating masses varies in time and its derivative with respect to time equals the vertical support force (ground reaction exerted on the vehicle or cart). For the continuous motion of the contra-rotating masses at a constant angular velocity , external energy is generally required to withstand the friction losses [96].
- When the magnitude of the constant angular velocity, , is adequately high, the vehicle (cart) can perform a vertical jump. This happens because in the upward motion of the rotating masses (i) the reaction force is higher than the weight, and (ii) the center of mass of the system (cart + rotating masses) has an adequately large initial velocity which allows for a vertical shot.
- An alternative explanation for the motion of the vehicle due to the attached inertial drive is as follows. In the beginning, the rotating masses of the inertial drive possess a certain linear momentum towards the vertical -axis. When the orientation of the connecting rods (radii of out-of-balance masses) becomes vertical, the velocity vectors of these masses become horizontal, and thus the linear momentum of the rotating masses vanishes. If, for example, the angular velocity is high, the change in linear momentum per revolution () will be a small percentage of the total initial value, and thus practically, the linear momentum of the system is preserved. Due to the said conservation of linear momentum in the vertical -axis, the lost momentum is undertaken by the vehicle. But after 90 degrees, the connecting rods will become horizontal with peak velocities, and thus the instantaneous velocity of the vehicle vanishes, and so on [97].
- Obviously, if no extra energy is transmitted to the inertial drive, the initial angular velocity of the rotating masses cannot be preserved at a constant value ; however, again, the vehicle can jump [97].
- The maximum height that the mechanical system “vehicle + drive” can reach depends on the initial velocity of the center of mass of this system.
- The initial velocity of the center of mass occurs when the two connecting rods to which the masses are attached are found on a horizontal position and at the same time the ground suddenly opens like the cover of a well. Then, the conservation of the linear momentum toward the vertical axis is practically ensured (almost closed system by ignoring the gravitational effect) [97]. Again, we recall that while the vehicle stands on the ground the linear momentum is not preserved, because the system is open.
- Depending on the level of the initial velocity at the zero level, the vehicle may elevate following an oscillating mode, with the rods usually having performed many revolutions, until the center of mass takes a zero value (due to the gravitation). Then, the vehicle starts falling, following an oscillating mode, until it returns to the zero level, having its initial velocity but in the opposite direction.
- During an extremely short time interval, it is possible to keep the vehicle immobile in the air by varying the angular velocity according to Equation (A8), shown in Appendix A. Unfortunately, this phase ends when the rods which carry the rotating masses become vertical, and thus the denominator of the closed-form expression (A8) vanishes and the fraction becomes infinite [96].
- In some sense, the sinusoidal support forces are very similar to those exerted on the ground by a spring-mass system [99]. To better understand this issue, note that when the topic of oscillations is presented in high-schools or colleges, teachers say that oscillation is the projection of a moving material point on a circle determined by the extreme positions of that oscillation.
- Overall, the center of mass of the system performs a vertical shot, but an oblique shot is also possible [98].
From the above conclusions, one may understand that an inertial drive essentially offers the initial velocity to the center of mass (as far as the vehicle presses the ground), and this velocity could alternatively be given through a catapult. In conclusion, within the context of inertial propulsion the inertial drive practically replaces the catapult.
Now, the above observation can justify the ‘peculiar’ behavior of an untransparent box within which an inertial drive exists, i.e., that the said ‘magic’ box may perform an unexpected upward jump, vertical or oblique, or even to climb an inclined plane. The only condition is that when the box is left to move or fall, the connecting bars (carrying the rotating masses) must be close to the horizontal direction to ensure linear momentum in the upward vertical -direction.
Similar conclusions may be derived for an object floating on water. Since the influence of gravity is indirect (it affects only the weight), the difference from the previous case is that now water resistance appears, depending on the Reynolds number. The boat travels a certain distance on the water, and when it reaches a maximum distance from the starting point it basically stops (it performs a slight oscillation). A publication dedicated to this issue is [100], accompanied by some videos.
Of major practical importance is motion on the ground. Typical cases are the possible motion of a washing machine or the motion from the bumper of a mobile cellphone. In general, the inertial drive induces centripetal forces which may overcome the static friction, thus causing motion. This is a rather old story, which has been applied to vibrational transportation [7,8,9,10,11] and to micro- and nano-robots [101,102,103,104,105,106]. Later, the concept of Dean drive (although not clearly mentioned therein) was applied to the modeling and control of micro-robotic systems by Vartholomeos and Papadopoulos [107,108]. Quite independently, the theoretical capability of the Dean drive to perform the motion of a vehicle was further elucidated by Provatidis [109,110] and a particular study for an alternative figure-eight shaped drive, controlling the orientation of the unidirectional motion, was reported in [111]. Also, a state-of-the-art report up to 2011, including more propulsive methods than those by inertial drives, is [112,113].
In August 2015, Mike Gamble, a senior electrical engineer at The Boeing Co., presented a released paper regarding the history of Boeing (CMG) Control Moment Gyros [114]. His presentation was mainly a non-technical pictorial history of Boeing’s CMG work, which started back in the 1960s and continued into the 1990s. He became involved with it in 1995, when he took over operations of the (GN&C) Guidance, Navigation and Controls lab at the Boeing Kent (WA) Space Center. This lab and the building that housed it were badly damaged in the 2001 Seattle earthquake and later demolished. The pictures in his presentation show many of the different types of test articles built and used, along with some of the lab facilities.
At the same conference, Mike Gamble presented a second paper [115], from which the extracted chart of Figure 9 shows the sawtooth input torquing rate waveshape (scissoring) for generating the pulsed output force. He has claimed that torquing fast in one direction and slow in the other generates a pulsed (average) output force which is similar in waveshape to that of the examples based on rotating masses.

Figure 9.
The average thrust produced by the gyro scissor operation (from [115] with permission).
Remaining within the field of gyroscopes, a remarkable work is that by Alexander Dmitriev, a former professor at the University of Saint Petersburg in the laboratory of Optics, who has shown that a horizontally spinning rotor loses more weight the faster it spins [59,60,61,62]. The American mathematician Dennis Allen Jr. was highly influenced by these experiments, as well as those by V.N. Samokhvalov [116,117], and thus he developed a new theory according to which Newton’s Second Law has to be revised by modifying the inertial mass to its updated form:
where are experimentally determined constants, is an angle in degrees, is the magnitude of the acceleration vector, and is the magnitude of the surge vector (i.e., ). Details may be found in a chapter of his revised book, written jointly with the senior lecturer Jeremy Dunning-Davies [118].
Until now, reviews have been reduced to rotating masses and gyroscopes. Since friction causes fast decay in both, some patents have introduced the concept of the pendulum, in which decay is much smaller [119]. A particular patent by the talented inventor Mr. Veljko Milkovic in which an inclined pendulum could offer inertial propulsion to a cart was studied by Allen and Provatidis [120]. The latter study was based on mechanics and computer methods that had been previously developed and documented in [121,122].
4.2. Practical Applications
Ivan Loukanov’s devices: Before his retirement, he was a professor of mechanical engineering at the universities of Botswana (South Africa) and Sofia (Bulgaria). Although he worked independently, the knowledge of the Russian language assisted him in critically evaluating and improving the design solutions he dealt with, as reflected by the references cited in his papers. In brief, he designed and manufactured many inertial propulsion devices, initially for agricultural applications. Later, he studied mobile wheeled robots intended for inspections and observations of air ducts or for any other restricted environments to which humans do not have direct access (e.g., dangerous military, chemical or radiation sites, such as nuclear power stations, chemical reactors, etc.). In the last works, the vibration-driven robot consisted of a shaker and a chassis. The latter was mounted on wheels furnished with one-way clutch bearings built into the wheel hubs, and thus only forward motion of the chassis was allowed. Through a DC motor the robot is propelled by the resonance vibrations created by the shaker’s rotating masses, which generate propulsive impulses transmitted to the chassis. Typical devices are shown in Figure 10. The interested reader may also consult [123,124,125,126] and papers therein.

Figure 10.
Devices based on professor Loukanov’s activity (inertial pumps and inertial driven vehicles) (from [123,124,125,126]).
4.3. Other Patents and Broadcasts
Since the period of “Dean drive”, a lot of somehow relevant patents have appeared (see Robertson [81], Cook [127], Thornson [128], Foster [129], Hoshino [130], Chung [131], Tanner [132], and Farral [133], among others) and have attracted the interest of technicians and scientists, mostly in the United States of America (USA), perhaps because this attempt is also encouraged by established scholars such as [134,135].
Furthermore, it has also occupied educational television programs such as the German Channel 2 (Zweites Deutsches Fernsehen: ZDF), where the Austrian engineer Johann Klimpfinger participated, on 26 February 2012, in a 30 min documentary on flywheel energy storage systems for mobile applications [136] which at the end showed a remote-controlled model of the granted UK patent “Propulsion system” by Eric Laithwaite [137] as a possibly functional Inertial Propulsion Device. There are relevant publications (e.g., Hilscher [138]) and YouTube videos such as Gyro Precession Drive [139] concerning this remote-controlled model.
In the United Kingdom, the influence of Eric Laithwaite is still alive. The author has been recently informed that William Stoney, owner of the “Thermo Inertial Research” company, involving background aircraft prototyping and business jet flying, met Eric Laithwaite and Bill Dawson in the late 1990s and has kept up an ongoing discussion with Bill Dawson, who kindly gave him most of their experimental gyroscopes, including the 14 kg gyro that featured in the BBC documentary. Since then, he has spent many thousands of hours testing different configurations and measuring them. In 2022, he filed a relevant patent [140] in which an existing prototype was described. Know-how was derived from the setup shown in Figure 11. The unit consisted of two air-driven gyroscopes, spinning at 5000 RPM (rounds per minute) and weighing 2 kg, each mounted on the end of short arms, both fully articulated at hinge points at the half radius point. The two hinges were mounted on a central rotor arm attached to the main central (horizontally orientated) precession shaft. The rotor arms had an accelerated stop rotation pattern averaging 2 RPS (rounds per second) and oscillating between 4 RPS max and 0 RPS minimum four times for every one complete orbit of the gyros. This caused the gyros to be subject to an alternating high precession rate when the hinge point slowed down, and then a subsequent low precession rate as the hinge point accelerated again. The resulting eight-cycles-per-second precession rate oscillation caused the gyro arms to deflect up and down against the uniform input torque supplied by the two air-pressurized actuators. The gyro orbits formed an eight-cycle-per-second wave path as they orbited at near-constant translational velocity. It is the study of the force–acceleration relationship of this wave path, parallel to the central precession axis shaft, that is the object of the experiment.

Figure 11.
Gyroscope test unit built in 2003 by Thermo Inertial Research, U.K. (with permission).
But the most difficult-to-review information comes from Russia, where (because of the language) it is not at all easy to distinguish science from pseudo-science. On this issue, the author tries to remain neutral. For the sake of completeness, we will not avoid the temptation to expand the review a little beyond the narrow margins of inertial propulsion, but in no case can we fully cover the subject. As was mentioned at the beginning, the Russian academicians used inertial propulsion for practical reasons, such as the motion of heavy objects by vibrational techniques [7,8,9,10]. Nevertheless, they denied the capability of the Dean drive to be useful for space applications [33]. They did the same with their compatriot Vladimir Tolchin, who introduced the term “inertiod” [39].
As previously said, due to the Russian language, it is not an easy task to overview the topic in a complete way, but it seems that tens of unexplainable microscopic and macroscopic effects in natural sciences and especially in physics and biology have been revealed and investigated. It should be emphasized that a large part of these phenomena was demonstrated by objects having spin or angular momentum. Probably the first researcher who experimentally detected the unusual effects associated with torsion was Professor Myshkin of the Russian physical–chemical society [141], who, at the end of the nineteenth century, conducted a series of experiments using scales. These experiments were successfully repeated in the 1960s by Professor N.A. Kozyrev [142,143] and V.V. Nasonov, and later by V.S. Belyaev, S.P. Mikhailov, A.G. Parkhomov, and others. For more details, the interested reader can consult an Internet website [144], while an opposing reference for the more recent activities of this “school” is [145]. Recent out-of-stream works are Linevich and Ezshov [146] and Kouznetsov [147], as well as Shipov [148], among others.
According to the Russian NTV correspondent Vladislav Sorokin [149], on 2 April 2006, members of the ‘Suburban Institute of Space Systems’ invented an engine called ‘gravitsapu («гpaвицaпy»)’ which, according to the creators, can accelerate to infinity; their final wish is to send it into space. However, the Russian Academy of Sciences did not recognize the theory underlying the creation of this invention. Later, in 2009, details were reported by the newspaper “Pravda” [150]. For more relevant information, the interested reader can consult Internet resources such as [151,152].
In China, the use of shaking masses has definitely been explored in terrestrial applications (Zhao et al. [153,154,155]), while publications refer to novel electromagnetic drives as well [156].
5. A Critical Note on the Mechanics Involved in Inertial Drives
According to Newton’s Second Law of mechanics, the sum of the external forces to a system of masses equals the total mass times the acceleration of the center of mass. The proof of this law is based on (i) the individual use of Newton’s Second Law on the mass of each system and (ii) on the assumption of Newton’s Third Law (action = reaction). The reader may refer, for example, to Halliday and Resnick [157] (pp. 59–61) as well as to Casey [158,159].
Despite the above established laws, there are many people who believe that these laws are not always applicable, especially when the bodies are rotating. This is mostly supported by experiences drawn from the mechanical behavior of the gyroscopes [4,41,42,43,48,56,137,160], and have been the subject of research in physics journals such as [161].
In the present paper, we limited ourselves to the simplest case of the Dean drive shown in Figure 12. At the initial time , the masses are attached to the endpoints A1 and A2 of contra-rotating rigid rods, the latter articulated to the vehicle at the joints J1 and J2, respectively. Obviously, after a full rotation of the rods by 360 degrees, the two masses will again be at the same position (shown in Figure 12).
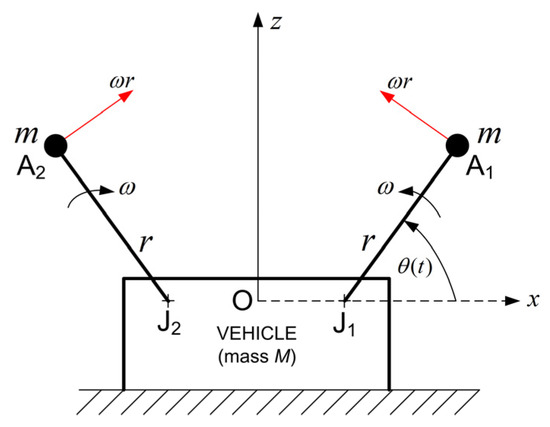
Figure 12.
Contra-rotating masses.
If the angular velocity is constant, each mass will have the same velocity as it had at time . Therefore, the change in linear momentum will be zero, and thus the integral of the external forces with respect to time (i.e., the impulse) will become zero. In other words, the attached Dean drive will produce no net thrust to the vehicle.
Nevertheless, some inventors have modified the above principle. They either changed the circular shape of the orbit of the rotating masses or varied their angular velocity. For example, based on a record from the book of Gutsche [162] (p. 109), regarding measurements on a three-bar mechanism (a similar analogue is also described in [163]), an investigator (with a background in mathematics) calculated a nonvanishing impulse, and thus he concluded that net thrust is produced [164].
Below, we show the reason why it is not possible to obtain net thrust.
Continuing with the circular orbits in the setup shown in Figure 12, if the angular velocity is not constant, after a full rotation of 360 degrees each mass will be at the same position but will not have the same velocity as it had at time , and hence a change in the linear momentum may be produced. Having said this, we will show that, again, no net thrust is produced for the following reason. If we start counting time from the moment the rigid bars J1A1 and J2A2 are vertical (say downward at polar angle ), the normal projection of each particle velocity onto the vertical -axis will obviously vanish. Also, the same will occur after a half-rotation of 180 degrees, at the upward polar angle . Therefore, for every half revolution of the rigid bars, the change in linear momentum will be zero, and hence the integral of the external forces with respect to time will vanish. The latter is a rigorous proof that no net thrust may be produced by the inertial forces induced on rotating masses moving along a circular path.
Moreover, the same will occur when the path followed by the masses is non-circular. Actually, whatever the shape of the curvilinear path (circular or not) and whatever the function of the angular velocity is, the passage of each mass through the upper and the lowest points, where the velocity vector is horizontal (and thus its vertical component vanishes), dictates the zeroing of the change in the linear momentum, and thus the zeroing of the impulse between any two halves per 180 degrees. Overall, the (internal) inertial force cannot produce any net thrust.
6. Discussion
In his paper opposing the claim of the Dean drive, Professor Stepanov [33] begins his introduction as follows: “In 1907, the famous Russian scientist V.L. Rirpichev, speaking about people who spent their energy on creating perpetual motion machines, indicated that “… and now every professor of mechanics constantly has to deal with the inventors of such chimeras. From my personal experience, I must say that these are almost always respectable persons, conscientiously devoted to the idea, but carried away by it so much that they are absolutely deaf to the arguments of reason. They are not affected, not only by verbal, logical proofs, but even by such strong proofs, which the products of their ingenuity present to them with their complete inertia”… Here, we are already dealing with material that is interesting not for mechanics, but for psychology”.
The counterargument to the above concept is that we should perhaps “let all the birds sing” (metaphorically), because in such a difficult technical issue the final solution (if indeed there is one) will perhaps be given by unconventional researchers, as for example the Wright brothers were (17 December 1903), while everyone in the USA expected that it would be given by the renowned late Professor Langley. At some point in their lives, when insurmountable obstacles are met, many people go through states of inner searching and transcendence [165,166] with the final purpose of drawing strength from within themselves.
Since the third decade of the twentieth century, many scientists and practitioners all over the world have conceived of the concept of inertial propulsion, and most of them believed that they had discovered a propulsive means without reaction. Since most experimental prototypes concerned terrestrial devices, the apparent explanation for their propulsive capability was attributed to the friction of the ground, similar to the friction induced when a person walks.
It has been made clear that, in the context of Newtonian mechanics, it is not possible for a vehicle to perform unlimited motion by virtue of an inertial drive. In brief, the inertial drive offers an initial velocity at the center of mass of the mechanical system “vehicle + drive”, and thus it acts as the result of a catapult. This initial velocity is strongly related to the fixed support of the vehicle, which assists in the development of a large reaction force, as happens when a spring-mass system is highly compressed on the ground. In either case, when the center of mass jumps and reaches its upper position, we again need to support the system to develop an external reaction for a second time, and so on. This event is like the motion of a monkey on a tree, which jumps higher and higher, successively caught by the branches at increasing heights on the tree.
To make a breakthrough in alternative propulsion, it is necessary to find a case in which the physical laws break. For example, Newton’s third law states that action equals reaction, but this is not always exact. For example, when two electrically charged particles move along two skewed straight lines (not intersecting and non-parallel), the mutual electromagnetic (Lorentz) forces are equal in magnitude but vertical in orientation, and thus we talk about a “weak formulation” of Newton’s third law [167]. Although this mismatch gives advantage to electromagnetics, the comparative study [88] revealed null net thrust.
The imaginations of many researchers and inventors have been fired by strange phenomena such as the ‘magical’ support of an aluminum triangle in the air; such a case has been fully attributed to the existence of ionized air [168,169]. Other peculiar phenomena such as the Indian rope trick (where a rope rise is caused by sounds) have been analyzed by eminent scientists [170,171,172]. Also, the unexpected behavior of Laithwaite’s experiment has been analyzed experimentally [173,174] and theoretically [66,67] as well. Closely related is the generally applicable work by Sheheitli [175,176].
For a thorough description of gravity-controlled (‘antigravity’) systems, the reader is directed to [177,178], among others.
As also happened with the Michelson–Morley experiment, which positively supported the General Theory of Relativity (GTR), the analogous testbed to justify whether the eternal laws of Nature can be (or have been) bypassed (or broken) is the “gyroscope” [179]. There are many scientists who claim that they have discovered an issue on the gyroscope which contrasts with Newton’s laws [180,181].
Based on Newtonian mechanics, it has been shown that the easiness with which Eric Laithwaite could raise a heavy gyroscope was due to the axle of the spinning wheel performing precisely, and thus the hand is able to operate as an articulation (pin) and not as a fixed point (clamp) [66]. The latter allows for a normal force distribution of the forces in the bicep and tricep muscles, otherwise the torque at a supposed stiff articulation would lead to insufferable loads [66]. This topic has been also discussed in [182,183], but the utilization of physical units therein causes confusion. Note that while the gyroscope may be easily risen, it is very difficult to stop it when falling at the second half of a period, and thus a null resultant over a whole period occurs [67].
Regarding the supposed inertial propulsion in satellites mentioned in [114], it is true that scissoring (twin) gyroscopes may perform attitude control (i.e., changes in the orientation) simply by applying internal torques, without using small rockets (for the mechanics involved, see Appendix D). Nevertheless, this is quite different from saying that a net thrust may be produced by the gyroscopes.
Continuing the fourth paragraph of this section regarding motion in vacuum, by consuming energy and with the vehicle on the ground, it is possible to accelerate the connecting rods of the inertial device (shown in Figure 12) and thus produce linear momentum in the vertical direction. This change in linear momentum over time equals the reaction force from the ground to the vehicle. Obviously, if the amplitude of the alternating reaction force happens to be sufficiently large, the vehicle may perform a jump within the air of which the maximum distance travelled depends on the initial velocity of the center of mass. Again, note that at the end of this cycle (from the ground to the upper position) there is no ground (support) to resist, and thus the reaction force cannot be exerted for a second time. Of course, if someone ever invents a viable way to offer physical support to allow the development of substantial reaction forces (only small forces based on the gradient of the magnetic or gravitational fields have been reported so far), then inertial propulsion will become possible. While the development of external forces seems to be impossible, it is easier to harvest the required energy from the cosmic environment (cosmic radiation, ionized air, magnetic energy, etc.). Overall, the development of (non-aerodynamic) external forces in vacuum remains an unsolved problem.
In contrast to the motion in vacuum, it is easier to apply inertial propulsion in the water and particularly on the ground. In the first case, when a floating object reaches the longest position where the center of mass obtains a zero velocity, the surrounding water can probably somehow work to offer instantaneous artificial fixation (support), making it possible for the rotating bars to be almost vertical compared to the desired direction of motion at the time of the second departure. In the second case, regarding motion on frictional ground, using a Dean drive, limited [110] or unlimited [109] motion is possible. Moreover, a MSc thesis in Sweden [184] and a Ph.D. thesis at Cornell University [185] have independently proposed gyroscopic drives of cubic shape to be used as Mars rovers [186,187,188]. A similar inertial cube consisting of gyroscopes has also been developed in Switzerland [189].
The interested reader may watch a 16 min video which covers a broad spectrum of inertial propulsion [190], a gyroscopic precession powered car [191], and a cart powered by two contra-rotating oscillating gyroscopes [192].
Outside the field of space propulsion, some inventors present inertial propulsion devices as educational toys [163] to point out the peculiar properties of gyroscopes. Personally, I still remember the experimental setup of my professor in physics, Evangelos Anastassakis [193], who demonstrated, in his (auditorium) lectures, a miniature gyroscope lifting itself into an inclined plane.
During the last few years, the focus of research in inertial propulsion has returned to gyroscopes [194,195,196,197] or to asymmetric fields [198], while an out-of-stream relevant book is [199].
Since Newtonian mechanics do not allow for the development of repeated inertial propulsion, some researchers have turned to non-Newtonian or Modified Newtonian Dynamics (MoND) considerations. Mike McCulloch developed a theory of Quantized Inertia (QI) [200], formerly known by the acronym MiHsC [201] in 2007, aiming at human space travel [201]. This theory has also been used to explain the weight loss which has been reported in Podkletnov’s experiments of rotating superconductive materials [202]. After a grant from the United States Defense Advanced Research Projects Agency (DARPA) in 2018, aimed to make the concept a reality [203], one of those collaborations led him to work with IVO Ltd., based in Virginia, and they unveiled the first pure electric thruster for satellites that claimed to use zero fuel [204,205]. Nevertheless, Barry-1 experienced ongoing power-system issues on the satellite’s bus immediately after its launch (11 November 2023) and all throughout the LEOP (Launch and Early Orbit Phase). Then, after two months of operations, the company said, on 9 February 2024, that they had lost all communication with the satellite [206,207].
Quite recently, Charles Buhler, from NASA Electrostatics and Surface Physics Laboratory, has independently developed and patented a similar device [208,209].
As previously mentioned in Section 4.1, there are more than twenty physical principles in which breakthrough propulsion (such as electric propulsion [210], inertia modification, space drive (sails and fields), negative matter propulsion, electromagnetic techniques, mechanical techniques, spacetime modification/gravity control, quantum approaches to gravity control, brute fast methods, spacetime modification for faster-than-light, quantum nonlocality for faster-than-light information, quantum vacuum energy conversion, novel nuclear processes, etc.) might be possible [79,80]. One of them is based on General Relativity, according to which when a mass is near a rapidly rotating ring, not only a centripetal but also an axial force will be induced [211,212]; this effect is a consequence of Mach’s principle [213]. In the same direction, there are some newer thoughts on the frame-dragging effect by Tajmar [214], which were later extended by Millis [215].
But the most striking publication is probably that describing the theory by Wisdom [216], according to which “…translation in space can be accomplished merely by cyclic changes in shape, without thrust or external forces”. This claim gives much hope to inventors who can still dream. For example, one could claim that if the figure-eight-shaped motion of the contra-rotating masses (or circulating fluid such as mercury) such as those in the setup described in [86,111] is combined with a revolution of the whole system under the prism of GRT [212], small axial forces could be developed, as has been explained by Forward [211]. Who could a priori deny that the frame-dragging effect in conjunction with a resonance between these two rotations should be abandoned to offer promising results to interstellar space propulsion?
7. Conclusions
This paper is a critical review of many human attempts to create thrust by consuming energy, but without expelling material from a vehicle, merely using rotating masses. While the shot of an apparently stationary object into a vacuum is possible using an inertial drive, the repetition of the same cycle is impossible unless an external force is exerted upon it. The combination of Newton’s second and third laws justify that, in the absence of external forces, the center of mass moves at a constant velocity, a fact also sustained by the conservation of linear momentum. The maximum distance travelled by the vehicle (on water or ground) is proportional to the square root of motor speed and the cosine of the initial polar angle and is a few times longer than the value predicted by classical mechanics regarding a sliding object. In the case of gyroscopes, the lifting force in the first half of the period is cancelled by the downward one in the second half, and thus no net thrust is produced. For a satellite, the motion of the rotating masses causes rotations but no displacement for the center of mass. Overall, it is possible to use inertial masses and gyroscopes to change the orientation of the satellite (attitude control), thus avoiding the use of small-scale liquid rockets.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A. The Mechanics of Contra-Rotating Masses on the Vertical Plane
This appendix aims to present the basics of the mechanics involved in those inertial drives which consist of two contra-rotating masses. In this context, let us consider a cart (vehicle) of mass to which an inertial drive of total mass is attached through articulated beams. For the sake of brevity and easiness, let us consider that the cart lies on the horizontal ground (of the Earth or another planet), and that two lumped masses (each of them is ) contra-rotate on the vertical plane, as shown in Figure 12.
When each mass rotates at a constant angular velocity and the connecting rods, each of radius , form the polar angle with the horizontal ground, the vertical resultant of the two centrifugal forces will be
If the half-amplitude is smaller than the total weight and also the connecting rods lie in the upper half of the vertical plane, the reaction force from the ground to the cart will be upward of magnitude (), and thus the cart and the ground will be under compression and no relative motion will occur.
In contrast, if the half-amplitude exceeds the total weight for the same upward position of the rods, the reaction force from the ground to the cart will become negative. This means that an external hand is necessary to keep the cart immobile unless it is permanently glued to the floor. Equivalently, if for the same condition the external hand is removed, or the attachment below the cart is released, the cart will jump vertically upwards, and thus the center of mass (CM) of the system “cart + inertial drive” will perform a vertical shot. Furthermore, according to elementary mechanics, after the CM reaches its upper point (possessing zero velocity), it will return and crash on the ground with the same velocity as in the departure but of the opposite sign.
It may be useful to relate the above mechanics to the case of the well-known mass-spring system . In our case, the elastic spring is assumed to be under the mass . If we compress the spring by a small contraction (i.e., ) and then leave it, the mass will simply perform a vertical oscillation in which the lower end of the spring will be permanently connected to the ground; therefore, the reaction force from the ground will be of a sinusoidal form in time . But if we compress the spring in such a way that the compressive force becomes much higher than that of the weight (i.e., ), when we will take our hand away from the spring it will be progressively released until it takes its initial undeformed length at which the velocity of mass will be maximum. Therefore, if the lower end of the spring is not attached to the ground, the entire system will jump, and its center of mass will perform a vertical upward shot. After this discussion, one may easily understand that the mass–spring system is quite analogous to the Dean drive because the projection of the lumped masses on the vertical axis of symmetry is a point that performs an oscillation. In addition, we recall that in all textbooks of college physics it is widely written that: “A point P moving on a circular path with a constant angular velocity is undergoing uniform circular motion. Its projection on the -axis undergoes simple harmonic motion. This can be compared with the projection of the linear vertical motion of an oscillating mass on a spring” (e.g., [157] (pp. 363–366)).
In other words, the Dean drive operates like a catapult, very similar to the mass–spring system. The difference is that while in the latter case (mass–spring) the mechanical energy is initially stored in the elastic spring and then it is converted into kinetic energy of the mass , in the former case (Dean drive), the kinetic energy of the mass of the cart will be provided by the two rotating masses . In more detail, with the cart being immobilized, when the connecting rods are horizontally oriented (), the vertical velocity component of the rotating masses is maximum, and the component of the total centrifugal force in the vertical direction is zero. In contrast, when (after a rotation of 90 degrees) the connecting rods become vertically oriented, the vertical velocity components of the rotating masses vanish, and the component of the total centrifugal force in the vertical direction becomes maximum. In the latter case, when the total centrifugal force is much larger than the total weight , the cart will be forced to jump upwards.
In a series of papers [96,97,98], the vertical position of the cart was found to fulfil the following equation of motion, which is a second-order ordinary differential equation:
with
Equation (A2) has been obtained, always the same, by using either of the following four alternative formulations [96,97,98]:
- Application of Newton’s second and third laws on the five involved rigid bodies in the powertrain (two masses, each of them , two massless beams, and the cart of mass ).
- Application of Newton’s second law to the center of mass of the system.
- Conservation of Linear Momentum.
- Lagrange equations (analytical mechanics).
Assuming the initial conditions, i.e., for the cart and (, ) for the connecting rods, the integration of Equation (A2) in time implies the following kinematic characteristics for the cart (of mass ):
Vertical position of the cart:
Vertical velocity of the cart:
Based on the above equation of motion, it may be seen that:
- The maximum upward travel length of the mass into vacuum is highly influenced by the second term in Equation (A4), and thus is achieved when the connecting beams are horizontally oriented () and at the same time the ground suddenly disappears. For example, this may happen when the cart is standing above a deep well, and then the two halves of the cover open rapidly [96,97,98].
- It is possible to control the angular velocity so that the cart remains immobilized into a vacuum for a while, but this can be undertaken only for almost half a rotation (less than 180 degrees) bounded by the vertical axis through the middle of the cart [96].
Assuming that at the initial time , the velocity of the cart vanishes () while the connecting beam lies below the horizontal level at a polar angle degrees; to preserve the zero velocity (), we need to vary the angular velocity in such a way that . Then, Equation (A2) becomes a second-order ordinary differential equation in the polar angle , as follows:
with the analytical solution
and therefore, the variable angular velocity will be
Clearly, Equation (A8) is valid between the lower and the upper point of the circular path (where the particle velocity of each rotating mass is horizontal), excluding these two saddle points at which the ODE (A6) is not well defined (the denominator vanishes, i.e., ).
- An analogous instantaneous immobilization of the cart into vacuum, between two saddle points, occurs for rotating masses moving along a figure-eight-shaped path [111].
- As a virtual exaggerated example, in the very hypothetical case in which two hydrogen atoms had nuclei in contact and the two associated electrons were moving in synchronization (contra-rotating) according to the Rutherford–Bohr’s model for the harmonic , the maximum height at which the hydrogen compound could fly when it was left free to move would be about 72 km [98].
The major conclusion of Appendix A is that the initial velocity of the center of mass of the mechanical system “cart + drive”, given as
highly depends on the position of the connecting beams at the initial time , where the external supporting force ceases by withdrawing the mechanical support. The linear term in Equation (A4) is the most critical magnitude which determines the maximum height of the jump within a time interval , both of which are approximated by (see Ref. [97]):
Appendix B. Repeated Vibrational Motion
The most critical issue in inertial propulsion is to find a way to offer support (mechanical or any other physical type) to the mechanical system, exactly when the cart reaches the upper position, thus becoming instantaneously immobilized, as it was when it started its first shot. If this support is possible, then it would be possible to keep the cart immobilized for a very short time-interval until the connecting beam takes the proper position again, and then a second vertical shot would be possible, as previously described in Appendix A, and so on [99]. Unfortunately, when the cart moves in a vacuum, such a holding mechanism from the environment is not known so far. Outside the mechanical engineering realm, vacuum fluctuations, gravito-electromagnetism, conversion of chemical energy (e.g., enzymes), and any other type of internal energy consumption (e.g., fusion) will probably keep scientists busy in the future.
In contrast to the abovementioned unfavorable motion in a vacuum, the existence of the friction on the ground (of coefficient ) or in the water is of major importance and can be considered to successfully control the motion of the cart. The motion is achieved due to the excess of the friction by the inertial forces or, in other words, by the capability of the CM to obtain a substantial initial velocity to ensure motion. It is worth mentioning that, based on previous studies [100,110], the repeated nature of the motion (contra-rotation) leads to a larger travelled distance than the usual amount of , which is well known in elementary physics (e.g., [157] (p. 116)).
Appendix C. Contra-Rotating Wipers
Let us consider two contra-rotating masses at the ends of rigid rods of length , which move like car wipers (see, Figure A1). This means that the masses start from the horizontal position (A1 and B2) at a zero velocity and after a rotation of 180 degrees take the horizontal position (A2 and B1) again at zero velocity. Obviously, the period consists of two half-rotations for each mass (see, Figure A1). Even though each mass moves only above the center of the associated circle, the time integral of the vertical inertial force component (i.e., the impulse ) vanishes in each half period (rotation by 180 degrees), because the change in the linear momentum (at A1–A2 and B1–B2) is zero, with a difference in aforementioned zero values at the ends.
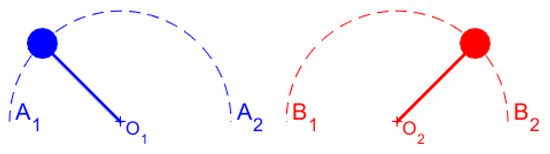
Figure A1.
Motion of two contra-rotating masses in the upper plane (from A1 to A2 and at the same time from B2 to B1, and vice versa).
Appendix D. Radial Displacement of a Satellite
Let us consider a satellite of mass which is in orbit around the Earth at height , thus moving on an (assumed) ideal circle of radius with denoting the Earth’s radius. It is well known that the measure of the velocity of the satellite (a vector tangent to the assumed circular orbit) is given by:
where is the gravitational constant and is the Earth’s mass.
Let us now assume that, by consuming an amount of energy, a mechanical component such as a dual gyroscope will change it orientation and thus move radially by distance (for example, if an astronaut of the satellite raises their two contra-rotating arms/forearms/hands by length , which is very close to the setup shown in [192], but in the horizontal direction). Then, we will wish to determine the new position of the center of mass of the satellite, measured from the Earth’s surface.
The conservation of the angular momentum with respect to the Earth’s center implies the following:
Hence,
Substituting (A11) into (A12), with one time for the radius and another time for , we eventually obtain
Equation (A13) shows that the center of mass of the satellite along the radius of the circular orbit will always remain at the same height above the Earth’s surface.
References
- Potier, O.N.R. The cancellation of gravity. Electron. Power 1965, 11, 111. [Google Scholar] [CrossRef]
- Farrall, A.W. An inertial propulsion system. Trans. ASAE 1966, 9, 586–587. [Google Scholar] [CrossRef]
- Hancock, R. (Ed.) Entry: “PROPULSION inertial”. In The Illustrated Encyclopedia of Science and Technology: HOW IT WORKS; Marshall Cavendish Ltd.: New York, NY, USA; London, UK, 1977; Volume 14, pp. 1874–1877. Available online: https://archive.org/details/howitworksillust14ralp/page/1874/mode/2up?q=inertial (accessed on 23 January 2024).
- Walgate, R. Eric Laithwaite defies Newton. New Sci. 1974, 14, 470. [Google Scholar]
- Engel, A.B.; Stiebitz, P.H. The cybernetics of inertial propulsion. Kybernetes 2009, 38, 141–157. [Google Scholar] [CrossRef]
- Fiala, H.E.; Fiala, J.E.; Fiala, J.-A. Inertial Propulsion Device to Move an Object Up and Down. U.S. Patent 8.066,226 B2, 29 November 2011. [Google Scholar]
- Goncharevich, I.F. Dynamics of Vibrational Transportation; Nauka: Moscow, Russia, 1972; p. 244. (In Russian) [Google Scholar]
- Blekhman, I.I. Vibrational Mechanics: Nonlinear Dynamic Effects, General Approach, Applications; World Scientific: Singapore, 2000; pp. 15+19. [Google Scholar]
- Kononenko, V.O. Vibrating Systems with a Limited Power Supply; Iliffe Books Ltd.: London, UK, 1969; p. 24. (In English) [Google Scholar]
- Blekhman, I.I. Synchronization in Science and Technology; ASME Press: New York, NY, USA, 1988; (In English, translated from Russian 1981). [Google Scholar]
- Majewski, T. Vibratory forces and synchronization in physical systems. Ing. Mecánica Tecnol. Desarro. 2013, 4, 119–128. [Google Scholar]
- Chen, L.; Pei, Z.; Tang, Z. Maximum power control of gyroscopic wave energy converter. E3S Web Conf. 2019, 118, 2022. [Google Scholar] [CrossRef]
- Townsend, N.; Shenoi, A. A gyroscopic wave energy recovery system for marine vessels. IEEE J. Ocean. Eng. 2012, 37, 271–280. [Google Scholar] [CrossRef]
- Tajmar, M. Advanced Space Propulsion Systems; Springer: Wien, NY, USA, 2002. [Google Scholar]
- Bruno, C.; Accettura, A.G. (Eds.) Advanced Propulsion Systems and Technologies: Today to 2020; Volume 223 Progress in Astronautics and Aeronautics; American Institute of Aeronautics and Astronautics: Reston, VI, USA, 2008. [Google Scholar]
- Millis, M.G.; Thomas, N.E. Responding to Mechanical Antigravity, NASA/TM-2006-214390, AIAA-2006-4913, December 2006. Available online: http://gltrs.grc.nasa.gov/reports/2006/TM-2006-214390.pdf (accessed on 23 January 2024).
- ElSheimy, N.; Youssef, A. Inertial sensors technologies for navigation applications: State of the art and future trends. Satell. Navig. 2020, 1, 2. [Google Scholar] [CrossRef]
- Lawerance, A. Modern Inertial Technologies: Navigation, Guidance and Control; Springer: New York, NY, USA, 1992. [Google Scholar]
- Rimrott, F.P.J. Introductory Attitude Dynamics; Springer: New York, NY, USA, 1989. [Google Scholar]
- Minetti, A.E.; Ardigó, L.P. Halteres used in ancient Olympic long jump. Nature 2002, 420, 141–142. [Google Scholar] [CrossRef]
- Provatidis, C.G. Simplified biomechanics for a possible explanation of the ancient Greek long jump using halteres. Univers. J. Eng. Sci. 2013, 1, 5–16. [Google Scholar] [CrossRef]
- Provatidis, C.G. On the maximum length of standing long jump using halters. Int. J. Multidiscip. Res. Stud. 2018, 1, 153–169. [Google Scholar]
- Citizendium. Available online: http://en.citizendium.org/wiki/Reactionless_propulsion (accessed on 23 January 2024).
- Todeschini, M. Motore a Forza Propulsive Centrifuga Alimentato ad Acqua Dissociate con Variazione di Velocita Graduale Automatic. Regno d’Italia, Ministero Delle Corporazioni, Brevetto Industriale No. 312496. 17 November 1933; See the First Two Pages of the Patent at the Website. Available online: www.circolotodeschini.com (accessed on 23 January 2024).
- Dean, N.L. System for Converting Rotary Motion into Unidirectional Motion. U.S. Patent 2,886,976, 19 May 1959. [Google Scholar]
- Dean, N.L. Variable Oscillator System. U.S. Patent 3,182,517, 11 May 1965. [Google Scholar]
- Campbell, J., Jr. The space drive problem. Astounding Sci. Fact Fict. 1960, 98, 83–106. [Google Scholar]
- Dempewolff, R.F. Engine with built-in wings. Pop. Mech. 1961, 116, 131–134, 264–266. [Google Scholar]
- Burridge, G. Toward antigravity. Rosicrucian Dig. 1962, XL, 136–139. [Google Scholar]
- Davis, W.O. The fourth law of motion. Analog 1962, 69, 83–104. Available online: http://www.rexresearch.com/dean/davis4.htm (accessed on 23 January 2024).
- Stine, G.H. Detesters, Phasers and Dean drives. Analog 1976, 96, 60–80. [Google Scholar]
- Campbell, J.W. (1962)-Interview by Fred Lerner. Available online: https://www.youtube.com/watch?v=SC-o9z-E010&ab_channel=FANACFanHistory (accessed on 23 January 2024).
- Stepanov, G.Y. Why is it impossible to have ‘Dean’s apparatus’? J. Priroda 1963, 7, 85–91. (In Russian) [Google Scholar]
- Di Bella, A. Apparatus for Imparting Motion to a Body. U.S. Patent 3,404,854, 8 October 1968. [Google Scholar]
- Di Bella, A. On propulsive effects of a rotating mass. In Proceedings of the Seventh Symposium Naval Hydrodynamics, Rome, Italy, 25–30 August 1968; Office of Naval Research-Department of The Navy, Arlington, VI, USA. Cooper, R.D., Doroff, S.W., Eds.; pp. 1373–1396. [Google Scholar]
- Available online: https://en.wikipedia.org/wiki/Viviani%27s_curve (accessed on 23 January 2024).
- Therriault, C. Wing Movement for Ornithopters and Apparatus of the Like. U.S. Patent 6,227,483 B1, 8 May 2001. [Google Scholar]
- Kuchinov, E. Quesalid’s Knots: A Guide to the Soviet Union’s Esoteric Research Institutes. Available online: https://sreda.v-a-c.org/en/read-01 (accessed on 23 January 2024).
- Tolchin, V.N. Sily Inertsii Kak Istochnik Postupatel’nogo Dvizheniia; Translation: Forces of Inertia as a Source of Translational Motion; Permskoe Knizhnoe Izdatel’stvo: Perm, Russia, 1977. [Google Scholar]
- Tolchin Drive-Short Original Film Copy. Available online: https://www.youtube.com/watch?v=DOXoaYs790M&ab_channel=stclairtechrd (accessed on 23 January 2024).
- Laithwaite, E.R. Propulsion Without Wheels, 2nd ed.; English Universities Press: London, UK, 1970. [Google Scholar]
- Wikipedia. Available online: https://en.wikipedia.org/wiki/Eric_Laithwaite (accessed on 23 January 2024).
- Laithwaite, E.R. The Engineer through the Looking Glass|The Royal Institution: Science Lives Here. Available online: https://www.rigb.org/explore-science/explore/video/engineer-through-looking-glass-looking-glass-house-1974 (accessed on 7 January 2024).
- Bruce De Palma. Available online: https://en-academic.com/dic.nsf/enwiki/1876830 (accessed on 23 January 2024).
- DePalma, B. The Tuning Fork Experiment, In: R.L. Dione, 1976 (ISBN 553-02723-150). Available online: http://www.brucedepalma.com/n-machine/spinning-ball-experiment/ (accessed on 23 January 2024).
- Available online: http://rexresearch.com/depalma2/depalm.htm (accessed on 23 January 2024).
- Available online: https://depalma.pairsite.com/gyrodrop.html (accessed on 23 January 2024).
- Hayasaka, H.; Takeuchi, S. Anomalous weight reduction on a gyroscope’s right rotations around the vertical axis on the earth. Phys. Rev. Lett. 1989, 63, 2701–2704. [Google Scholar] [CrossRef] [PubMed]
- Adelberger, E.G. Science correspondence on paper by Hayasaka & Takeuchi. Nature 1990, 345, 121. [Google Scholar]
- Faller, J.E.; Hollander, W.J.; Nelson, P.G.; McHugh, M.P. Gyroscope-weighing experiment with a null result. Phys. Rev. Lett. 1990, 64, 825–826. [Google Scholar] [CrossRef]
- MacCallum, M. Does a spinning mass really lose weight? New Sci. 1990, 1704, 30. [Google Scholar]
- Nitschke, J.M.; Wilmarth, P.A. Null result for the weight change of a spinning gyroscope. Phys. Rev. Lett. 1990, 64, 2115–2116. [Google Scholar] [CrossRef] [PubMed]
- Quinn, T.J.; Picard, A. The mass of spinning rotors: No dependence on speed or sense of rotation. Nature 1990, 343, 732–735. [Google Scholar] [CrossRef]
- Salter, S.H. Good vibrations for physics. Nature 1990, 343, 509–510. [Google Scholar] [CrossRef]
- Imanishi, A.; Maruyama, K.; Midorikawa, S.; Morimoto, T. Observation against the weight-reduction of spinning gyroscopes. J. Phys. Soc. Jpn. 1991, 60, 1150–1152. [Google Scholar] [CrossRef]
- Hayasaka, H.; Tanaka, H.; Hashida, T.; Chubachi, T.; Sugiyama, T. Possibility for the existence of anti-gravity: Evidence from a free-fall experiment using a spinning gyro. Specul. Sci. Technol. 1997, 20, 173–181. [Google Scholar]
- Luo, J.; Nie, Y.X.; Zhang, Y.Z.; Zhou, Z.B. Null result for violation of the equivalence principle with the free-fall rotating gyroscopes. Phys. Rev. D 2002, 65, 042005. [Google Scholar] [CrossRef]
- Labeysh, V.G. Experiments on asymmetrical mechanics. Galilean Electrodyn. 2000, 11, 8–11. [Google Scholar]
- Dmitriev, A.L.; Snegov, V.S. Measurements of mass: The weighing of a mechanical gyroscope with horizontal and vertical orientation of the spin axis. Meas. Tech. 2001, 44, 831–833. [Google Scholar] [CrossRef]
- Dmitriev, A.L. Frequency dependence of rotor’s free falling acceleration and inequality of inertial and gravity masses. arXiv 2011, arXiv:1101.4678. [Google Scholar]
- Dmitriev, A.L. Physical substantiation of an opportunity of artificial change of body weight. Phys. Procedia 2012, 38, 150–163. [Google Scholar] [CrossRef][Green Version]
- Dmitriev, A.L. Prospects of high-frequency gravimetry. Int. J. Circuits Syst. Signal Process. 2015, 9, 275–280. Available online: https://www.inase.org/library/2015/vienna/bypaper/APNE/APNE-37.pdf (accessed on 23 January 2024).
- Provatidis, C.G. Free fall of a symmetrical gyroscope in vacuum. Eur. J. Phys. 2021, 42, 065011. [Google Scholar] [CrossRef]
- Wayte, R. The phenomenon of weight-reduction of a spinning wheel. Meccanica 2007, 42, 359–364. [Google Scholar] [CrossRef]
- Lőrincz, I.; Tajmar, M. Identification of error sources in high precision weight measurements of gyroscopes. Measurement 2015, 73, 453–461. [Google Scholar] [CrossRef]
- Provatidis, C.G. Forced precession in a spinning wheel supported on a rotating pivot. Mech. Res. Commun. 2013, 52, 46–51. [Google Scholar] [CrossRef]
- Provatidis, C.G. Forced precession of a gyroscope with application to the Laithwaite’s engine. Eur. J. Phys. 2021, 42, 035003. [Google Scholar] [CrossRef]
- Allen, J.E. Quest for a novel force: A possible revolution in aerospace. Prog. Aerosp. Sci. 2003, 39, 1–60. [Google Scholar] [CrossRef]
- Meek, J. Bae’s Anti-Gravity Research Braves X-Files Ridicule. The Guardian, Mon 27 Mar 2000. Available online: https://www.theguardian.com/science/2000/mar/27/uknews (accessed on 23 January 2024).
- Anonymous. Project Greenglow and the Battle with Gravity. News, 23 March 2016. Available online: https://www.bbc.com/news/magazine-35861334 (accessed on 23 January 2024).
- Interview from Ron Evans. Available online: https://www.youtube.com/watch?v=BwI7Ij-5cMA&ab_channel=TimVentura (accessed on 23 January 2024).
- Anonymous. Science Does the Impossible: February 2003 Cover Story. Popular Mechanics. Available online: https://archive.ph/20070930015205/http://www.popularmechanics.com/science/research/1282281.html?page=3 (accessed on 23 January 2024).
- Anonymous. Boeing Internal Report Looks at Propellentless Propulsion. Available online: https://www.spacedaily.com/news/rocketscience-02t.html (accessed on 23 January 2024).
- BBC-News, Boeing Tries to Defy Gravity. Monday. 29 July 2002. Available online: http://news.bbc.co.uk/2/hi/science/nature/2157975.stm (accessed on 23 January 2024).
- Wikipedia: Eugene Podkletnov. Available online: https://en.wikipedia.org/wiki/Eugene_Podkletnov#cite_note-8 (accessed on 23 January 2024).
- Millis, M.G. Breakthrough Propulsion Physics Research Program. AIP Conf. Proc. 1997, 387, 1297–1302. [Google Scholar]
- Millis, M.G. NASA breakthrough propulsion physics program. Acta Astronaut. 1999, 44, 175–182. [Google Scholar] [CrossRef]
- Millis, M.G. Assessing potential propulsion breakthroughs. Annu. N. Y. Acad. Sci. 2005, 1065, 441–461. [Google Scholar] [CrossRef] [PubMed]
- Millis, M.G.; Davis, E.W. Frontiers of Propulsion Science; American Institute of Aeronautics and Astronautics Inc.: Reston, VA, USA, 2009. [Google Scholar]
- Millis, M.G. Progress in revolutionary propulsion physics, Paper IAC-10-C4.8.7. In Proceedings of the 61st International Astronautical Congress, Prague, Czech Republic, 27 September–1 October 2010. [Google Scholar]
- Robertson, D.B. Propulsion Method and Apparatus Utilizing Centrifugal Force; Number WO 01/46584 A3; World Intellectual Property Organization (WIPO): Karlsruhe, Germany, 2001. [Google Scholar]
- Hampton, S.M. From Dean Drives and Davis Mechanics: Inertial Propulsion and the Manipulation of Time in Symmetrical Systems©; Ebook; Apple Communications: London Mills, IL, USA, 2011. [Google Scholar]
- Hampton, S.M. Asymmetric Impulse Drive. AIAA 2022-4391. ASCEND 2022 (24–26 October 2022, Las Vegas, Nevada & Online). Session. In Frontiers in Deep Space Propulsion; View Video Presentation. Available online: https://video.aiaa.org/title/b3dbbfb4-564b-4cb4-bbd3-8965c3a40be4 (accessed on 23 January 2024).
- Tsiriggakis, V.T.; Provatidis, C.G.; Frigas, S. U.S. Patent Application for an “Antigravity Mechanism”. U.S. Patent 61/110,307, 31 October 2008. [Google Scholar]
- Provatidis, C.G.; Tsiriggakis, V.T. A new concept and design aspects of an ‘antigravity’ propulsion mechanism based on inertial forces. In Proceedings of the 46th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Nashville, TN, USA, 25–28 July 2010. Paper AIAA 2010-6684. [Google Scholar]
- Provatidis, C.G. A device that can produce net impulse using rotating masses. Engineering 2020, 2, 648–657. [Google Scholar] [CrossRef][Green Version]
- Pipes, L.A.; Harville, L.R. Applied Mathematics for Engineers and Physicists, 3rd ed.; McGraw-Hill: New York, NY, USA, 1981; pp. 494–496. [Google Scholar]
- Provatidis, C.G.; Gamble, M.A. Support forces in a synchronized rotating spring-mass system and its electromagnetic equivalent. Int. J. Appl. Electromagn. Mech. 2013, 41, 313–333. [Google Scholar] [CrossRef]
- Manning, J. Space, Propulsion & Energy Sciences International Forum-A Journalist’s Notes. Infin. Energy 2012, 103, 18–23. [Google Scholar]
- Valone, T. Inertial Propulsion: Concept and experiment, Part I. In Proceedings of the Intersociety Energy Conversion Engineering Conference, Monterey, CA, USA, 7–12 August 1994. [Google Scholar]
- Valone, T. Inertial Propulsion: Concept and experiment, Part II. In Proceedings of the Intersociety Energy Conversion Engineering Conference, Monterey, CA, USA, 7–12 August 1994; AIAA-94-4167-CP. pp. 1484–1489. [Google Scholar] [CrossRef]
- Valone, T.; Cox, J. Inertial Propulsion: Patent Collection; Integrity Research Institute: Washington, DC, USA, 2008. [Google Scholar]
- Valone, T.F. Eric Laithwaite Report: Gyromagnetic Engineering Genius–Publications, Inventions & News Clips; IRI PR-02-005; Integrity Research Institute: Beltsville, MD, USA, 2006. [Google Scholar]
- Almesallmy, M. Experimental and Analytical Investigation of Inertial Propulsion Mechanisms and Motion Simulation of Rigid-Multi-Body Mechanical Systems. Ph.D. Thesis, University of Rhode Island, Kingston, RI, USA, 2006. [Google Scholar]
- Guiad, D.; Nilvetti, F.; Pappalardo, C.M. Dry friction influence on cart pendulum dynamics. Int. J. Mech. 2009, 3, 31–38. [Google Scholar]
- Provatidis, C.G. Some issues on inertia propulsion mechanisms using two contra-rotating masses. Theory Mech. Mach. 2010, 8, 34–41. Available online: http://tmm.spbstu.ru/15/Provatidis_15.pdf (accessed on 23 January 2024).
- Provatidis, C.G. A study of the mechanics of an oscillating mechanism. Int. J. Mech. 2011, 5, 263–274. Available online: https://www.naun.org/main/NAUN/mechanics/17-093.pdf (accessed on 23 January 2024).
- Provatidis, C.G. An overview of the mechanics of oscillating mechanisms. Am. J. Mech. Eng. 2013, 1, 58–65. [Google Scholar] [CrossRef][Green Version]
- Provatidis, C.G. Repeated vibrational motion using an inertial drive. Vib. Acoust. Res. J. 2019, 1, 27–43. Available online: https://www.cansrg.com/journals/varj/2019/70.pdf (accessed on 23 January 2024).
- Provatidis, C.G. On the inertial propulsion of floating objects using contra-rotating masses. Mech. Res. Commun. 2014, 62, 117–122. [Google Scholar] [CrossRef]
- Ikuta, K.; Aritomi, S.; Kabashima, T. Tiny silent linear cybernetic actuator driven by piezoelectric device with electromagnetic clamp. In Proceedings of the IEEE Micro Electro Mechanical Systems, Travemunde, Germany, 4–7 February 1992; pp. 232–237. [Google Scholar] [CrossRef]
- Aoyama, H.; Iwata, F.; Sasaki, A. Desktop flexible manufacturing system by movable miniature robots-miniature robots with micro tool and sensor. In Proceedings of the 1995 IEEE International Conference on Robotics and Automation, Nagoya, Japan, 21–27 May 1995; Volume 1, pp. 660–665. [Google Scholar] [CrossRef]
- Zesch, W.; Buchi, R.; Codourey, A.; Siegwart, R. Inertial drives for micro- and nanorobots: Two novel mechanisms. In Proceedings of the Microrobotics and Micromechanical Systems, Philadelphia, PA, USA, 18 October 1995; pp. 80–88. [Google Scholar] [CrossRef]
- Buchi, R.; Zesch, W.; Codourey, A.; Siegwart, R. Inertial drives for micro- and nanorobots: Analytical study. Microrobotics Micromechanical Syst. 1995, 2593, 89–97. [Google Scholar] [CrossRef]
- Yoshikawa, H.; Kagiwada, T.; Harada, H.; Mimura, M. Improvement of propulsion mechanism based on the inertial force. In Towards Synthesis of Micro-/Nano-Systems; Kimura, F., Horio, K., Eds.; Springer: London, UK, 2007; pp. 333–334. [Google Scholar]
- Ju, J.; Wang, Q.; Zhang, K. Design and analysis of a novel micro-robot driving platform. Proc IMechE-Part C J. Mech. Eng. Sci. 2019, 233, 3849–3857. [Google Scholar] [CrossRef]
- Vatholomeos, P.; Papadopoulos, E. Dynamics, design and simulation of a novel micro-robotic platform employing vibration micro-actuators. ASME J. Dyn. Syst. Meas. Control 2006, 128, 122–133. [Google Scholar] [CrossRef]
- Vartholomeos, P.; Papadopoulos, E. Analysis and experiments on the force capabilities of centripetal-force-actuated microrobotic platforms. IEEE Trans. Robot. 2008, 24, 588–599. [Google Scholar] [CrossRef]
- Provatidis, C.G. Design of a propulsion cycle for endless sliding on frictional ground using rotating masses. Univers. J. Mech. Eng. 2014, 2, 35–43. [Google Scholar] [CrossRef]
- Provatidis, C.G. Mechanics of Dean drive on frictional ground. J. Mech. Des. Vib. 2014, 1, 10–19. Available online: https://pubs.sciepub.com/jmdv/1/1/3/index.html (accessed on 23 January 2024). [CrossRef]
- Provatidis, C.G. Unidirectional motion using rotating masses along figure-eight-shaped trajectories. J. Braz. Soc. Mech. Sci. Eng. 2015, 37, 397–409. [Google Scholar] [CrossRef]
- Provatidis, C.G. Progress in an antigravity mechanism using inertial masses. In Space, Propulsion & Energy Sciences International Forum (SPESIF-2011); [CR-ROM]; University of Maryland: College Park, MD, USA, 2011. [Google Scholar]
- Provatidis, C.G. Older and contemporary attempts for inertial propulsion. Gen. Sci. J. 2011, 14. Available online: http://gsjournal.net/Science-Journals/Essays/View/3772 (accessed on 23 January 2024).
- Gamble, M. History of Boeing control moment gyros (CMG). In Proceedings of the Presentation in Seventh International Conference On Future Energy (COFE7), Embassy Suites, Albuquerque, NM, USA, 30 July–1 August 2015. Boeing 15-00051-EOT. [Google Scholar]
- Gamble, M. Linear propulsion. In Proceedings of the Presentation in Seventh International Conference On Future Energy (COFE7), Embassy Suites, Albuquerque, NM, USA, 30 July–1 August 2015. [Google Scholar]
- Samokhvalov, V.N. Research on, and measurement of, force effects during mass-dynamic interaction. Galilean Electrodyn. GED East 2015, 26, 3–11. [Google Scholar]
- Samokhvalov, V.N. Non-electromagnetic force interaction in presence of rotating masses in vacuum. Int. J. Unconv. Sci. 2016, 1, 68–80. Available online: http://www.unconv-science.org/en/e1/samokhvalov/ (accessed on 23 January 2024).
- Allen, D.P., Jr.; Dunning-Davies, J. Neo-Newtonian Mechanics with Extension to Relativistic Velocities, 18th ed.; Part 1: Non-Radiative Effects; Kindle Direct Publishing: Seattle, WA, USA, 2023. [Google Scholar]
- Milković, V. Gravitational Machines: From Leonardo da Vinci to the Latest Discoveries; Veljko Milkovic Research & Development Center: Novi Sad, Serbia, 2013; ISBN 978-86-88883-03-0. [Google Scholar]
- Allen, D.P.; Provatidis, C.G. Inclined large-angle pendulum may produce endless linear motion of a cart when friction is negligible. WSEAS Trans. Appl. Theor. Mech. 2022, 17, 184–197. Available online: https://wseas.com/journals/mechanics/2022/a465111-016(2022).pdf (accessed on 23 January 2024). [CrossRef]
- Provatidis, C. Teaching the fixed spinning top using four alternative formulations. WSEAS Trans. Adv. Eng. Educ. 2021, 18, 80–95. [Google Scholar] [CrossRef]
- Provatidis, C.G. Revisiting the spinning top. Int. J. Mater. Mech. Eng. 2012, 1, 71–88. Available online: https://www.academia.edu/27516500/Revisiting_the_Spinning_Top (accessed on 23 January 2024).
- Loukanov, I.A. Vibration propulsion of a mobile robot. IOSR J. Mech. Civ. Eng. 2015, 12, 23–33. Available online: https://www.academia.edu/65248904/Vibration_Propulsion_of_a_Mobile_Robot (accessed on 23 January 2024).
- Loukanov, I.A. Application of inertial forces for generating unidirectional motion. Proc. Sci. Conf. Univ. Rousse 2014, 53. Available online: https://www.researchgate.net/publication/314067949_Application_of_Inertial_Forces_for_Generating_Unidirectional_Motion (accessed on 23 January 2024).
- Loukanov, I.A.; Uziak, J. Upon improving the prediction of the flow rate of sonic pump. Int. J. Eng. Res. Appl. 2013, 3, 393–398. Available online: https://www.ijera.com/papers/Vol3_issue1/BF31393398.pdf (accessed on 23 January 2024).
- Lukanov, I.A.; Vitliemov, V.G.; Ivanov, I.V. Dynamics of a mobile mechanical system with vibration propulsion (VibroBot). Int. J. Res. Eng. Sci. (IJRES) 2016, 4, 44–51. [Google Scholar]
- Cook, R.L. Device for Conversion of Centrifugal Force to Linear Force and Motion. U.S. Patent 4,238,968, 16 December 1980. [Google Scholar]
- Thornson, B.R. Apparatus for Developing a Propulsion Force. U.S. Patent No. 4,631,971, 30 December 1986. [Google Scholar]
- Foster, R.E. Converting Rotary Motion into Unidirectional Motion. U.S. Patent 3653269, 4 April 1972. [Google Scholar]
- Hoshino, M. Propulsion Apparatus Using Centrifugal Force. U.S. Patent 20050139022, 30 June 2005. [Google Scholar]
- Chung, T.B. Internal Propulsion Apparatus of Closed System Using a Coriolis Force. International Patent WO 03/087574 A1, 23 October 2003. [Google Scholar]
- Tanner, M.A. Resonant Maglev Centrifugal Propulsion. U.S. Patent 2007/0079663 A1, 12 April 2007. [Google Scholar]
- Farrall, A.W. Inertial Propulsion Device. U.S. Patent US3266233A, 16 August 1966. [Google Scholar]
- Robertson, G.A.; Murad, P.A.; Davis, E. New frontiers in space propulsion sciences. Energy Convers. Manag. 2008, 49, 436–452. [Google Scholar] [CrossRef]
- Robertson, G.A.; Webb, D.W. The death of rocket science in the 21st century. Phys. Procedia 2011, 20, 319–330. [Google Scholar] [CrossRef]
- MrEcodynamic, ZDF Planet e-Die Schwung Maschine. Online in 2 Parts at. Available online: http://www.youtube.com/watch?v=pfk6uykIrUs (accessed on 23 January 2024).
- Laithwaite, E.; Dawson, W. Propulsion System. U.S. Patent 5,860,317, 19 January 1999. [Google Scholar]
- Hilscher, G. Trägheit der Masse mobilisiert die Energietechnik: Mit dem findigen Johann Klimpfinger auf Entdeckungstour durch Archive und seine experimentelle Welt. NET-J. 2011, 16, 46–50. Available online: http://www.borderlands.de/net_pdf/NET0311S46-50.pdf (accessed on 23 January 2024).
- Anonymous. Kreisel Präzessions Antrieb (Gyro Precession Drive). Available online: https://www.youtube.com/watch?v=nstIIZZadAM&ab_channel=gyro2012 (accessed on 23 January 2024).
- Stoney, W. Method of Propulsion. Irish Patent Application IE 20190160 A2, 3 August 2022. [Google Scholar]
- Myshkin, N.P. Dvizheniye tela, nakhod yashegosya v potoke luchistoi energii. Zhyrnal Rus. Fiz.-Him. Obs. 1906, 3, 149. (In Russian) [Google Scholar]
- Kozyrev, N.A. Prichinnaya ili nesimmetrichnaya mekhanika v lineinom priblizhenii, Pulkovo. GAO AN SSSR 1958, 90. (In Russian) [Google Scholar]
- Kozyrev, N.A. On the possibility of experimental investigation of the properties of time. In Time in Science and Philosophy; Elsevier: Prague, Czech Republic, 1971; pp. 111–132. [Google Scholar]
- Available online: http://shipov.com/gennady-i-shipov/ (accessed on 23 January 2024).
- Wikipedia. Available online: https://en.wikipedia.org/wiki/Torsion_field_(pseudoscience) (accessed on 23 January 2024).
- Linevich, E.I.; Ezshov, A.F. The inertial motor. New Energy Technol. 2004, 3, 12–15. [Google Scholar]
- Kouznetsov, D. Support of non-traditional concepts. Far East J. Mech. Eng. Phys. 2010, 1, 1–6. Available online: https://www.pphmj.com/abstract/5076.htm (accessed on 23 January 2024).
- Shipov, G. Inertial Propulsion in Russia: Dr. Gennady Shipov on Torsion Physics & Inertial Propulsion. Interview to American Antigravity.Com. 2012, pp. 1–8. Available online: http://shipov.com/files/200506_news09.pdf (accessed on 23 January 2024).
- Sorokin, V. Available online: http://www.ntv.ru/novosti/84720/video (accessed on 23 January 2024).
- Naumov, A. Russian Scientists Test Perpetual Motion Machine in Space. PRAVDA Newspaper, 14 April 2009. Available online: http://english.pravda.ru/science/tech/14-04-2009/107399-russian_scientists-0 (accessed on 22 January 2024).
- Wikipedia. Available online: https://en.citizendium.org/wiki/Valery_Menshikov (accessed on 23 January 2024).
- Wikipedia. Available online: http://en.wikipedia.org/wiki/Yubileiny (accessed on 23 January 2024).
- Zhao, C.; Zhu, H.; Zhang, Y. Synchronization of two coupled exciters in a vibrating system of spatial motion. Acta Mech. Sin. 2010, 26, 477–493. [Google Scholar] [CrossRef]
- Zhao, C.; Zhang, Y.; Wen, B. Synchronisation and general dynamic symmetry of a vibrating system with two exciters rotating in opposite directions. Chin. Phys. B 2010, 19, 030301. [Google Scholar] [CrossRef]
- Chen, X.; Liu, J.; Li, L. Dynamics of the vibration system driven by three homodromy eccentric rotors using control synchronization. Appl. Sci. 2021, 11, 7691. [Google Scholar] [CrossRef]
- Hambling, D. EmDrive: China’s Radical New Space Drive, Wired 6 February 2013. Available online: https://www.wired.co.uk/article/emdrive-and-cold-fusion (accessed on 23 January 2024).
- Halliday, D.; Resnick, R. Physics; International Edition; Wiley: New York, NY, USA, 1966. [Google Scholar]
- Casey, J. Geometrical derivation of Lagrange’s equations for a system of particles. Am. J. Phys. 1994, 62, 836–847. [Google Scholar] [CrossRef]
- Casey, J. Applying the principle of angular momentum to constrained systems of point masses. Am. J. Phys. 2014, 82, 165–168. [Google Scholar] [CrossRef]
- Laithwaite E 1994 Heretics BBC2 Television London; Plus Private Demonstrations and Imperial College Christmas Lectures. Available online: http://youtube.com/watch?v&tnqx3d;KnNUTOxHoto (accessed on 4 April 2020).
- Pinheiro, M.J. On Newton’s third law and its symmetry-breaking effects. Phys. Scr. 2010, 84, 055004. [Google Scholar] [CrossRef][Green Version]
- Gutsche, G.J. Inertial Propulsion; and You Thought You Knew Everything about Physics; CreateSpace Independent Publishing Platform: Toronto, ON, Canada, 2018. [Google Scholar]
- Gutsche, G.J. Device for Efficient Self-Contained Inertial Vehicular Propulsion. U.S. Patent 9,995,284 B1, 12 January 2018. [Google Scholar]
- Allen, D.P., Jr. Foundations of Gutschian Mechanics: Part 1: Basics, 6th ed.; Kindle Direct Publishing: Seattle, WA, USA, 2019. [Google Scholar]
- Provatidis, C.G. A Review on antigravity, levitation, resonance, and devices inspired by the ouroboros serpent. Rose+Croix J. 2012, 9, 18–47. Available online: https://www.academia.edu/download/50150834/vol9_18_47_provatidis.pdf (accessed on 23 January 2024).
- Manning, J. Escape from Gravity: Is the ancient promise of freedom from the pull of earth alive and well at NASA and elsewhere? In Forbidden Science: From Ancient Technologies to Free Energy; Douglas Kenyon, J., Ed.; Bear & Co: Rochester, VT, USA, 2008; Chapter 13. [Google Scholar]
- Gerjuoy, E. On Newton’s third law and the conservation of momentum. Am. J. Phys. 1949, 17, 477–482. [Google Scholar] [CrossRef]
- Martins, A.A.; Pinheiro, M.J. On the nature of the propulsive force of asymmetric capacitors in the atmosphere. Phys. Procedia 2011, 20, 103–111. [Google Scholar] [CrossRef]
- Martins, A.A.; Pinheiro, M.J. On the nature of the propulsive force of asymmetric capacitors in a vacuum. Phys. Procedia 2011, 20, 112–119. [Google Scholar] [CrossRef]
- Stephenson, A. XX. On induced stability. Lond. Edinb. Dublin Phil. Mag. J. Sci. 1908, 15, 233–236. [Google Scholar] [CrossRef]
- Kapitsa, P.L. Dynamic stability of the pendulum when the point of suspension is oscillating. J. Exp. Theor. Phys. 1951, 21, 588–597. (In Russian) [Google Scholar]
- Blekhman, I.I.; Dresig, H.; Shishkina, E. On the theory of the Indian magic rope. In Selected Topics in Vibrational Mechanics; Blekhman, I.I., Ed.; World Scientific: Singapore, 2004; pp. 139–149. [Google Scholar]
- Cross, R. Laithwaite’s heavy spinning disk demonstration. Phys. Teach. 2014, 52, 349–350. [Google Scholar] [CrossRef]
- Davidowsky, P.; Rogers, M. Debunking a video on YouTube as an authentic research experience. Phys. Teach. 2015, 53, 304–306. [Google Scholar] [CrossRef]
- Sheheitli, H. On the dynamics of a spinning top under high-frequency excitation: Part I—Pivot point under vertical harmonic vibration. Nonlinear Dyn. 2017, 90, 765–779. [Google Scholar] [CrossRef]
- Sheheitli, H. On the dynamics of a spinning top under high-frequency excitation. Part II: Pivot point under horizontal harmonic vibration. Nonlinear Dyn. 2017, 90, 2269–2276. [Google Scholar] [CrossRef]
- LaViolette, P.A. Secrets of Antigravity Propulsion: Tesla, UFOs, and Classified Aerospace Technology; Bear & Company: Rochester, VT, USA, 2008. [Google Scholar]
- Childress, D.H. The Antigravity Handbook, 3rd ed.; Adventures Unlimited Press: Kampton, IL, USA, 2010. [Google Scholar]
- Passaro, V.M.N.; Cuccovillo, A.; Vaiani, L.; De Carlo, M.; Campanella, C.E. Gyroscope technology and applications: A review in the industrial perspective. Sensors 2017, 17, 2284. [Google Scholar] [CrossRef] [PubMed]
- Usubamatov, R. Theory of Gyroscopic Effects for Rotating Objects: Gyroscopic Effects and Applications; Springer: Cham, Switzerland, 2020. [Google Scholar] [CrossRef]
- Shipov, G. Four-Dimensional Gyroscope, Demonstrating the Violation of the Momentum Conservation Law during the Absolute Electic Collision with the Wall. U.S. Patent US20040166482A1, 15 February 2001. [Google Scholar]
- Solomon, B.T. An Introduction to Gravity Modification: A guide to Using Laithwaite’s and Podkletnov’s Experiments and the Physics of Forces for Empirical Results, 2nd ed.; Universal-Publishers: Boca Raton, FL, USA, 2012; pp. 67–81, 309–326. [Google Scholar]
- Solomon, B.T. Gravitational acceleration without mass and noninertia fields. Phys. Essays 2011, 24, 327–337. [Google Scholar] [CrossRef]
- Bjerke, E.; Pehrsson, B. Development of a Nonlinear Mechatronic Cube: The Jumping and Balancing Cube. Master’s Thesis, Chalmers University of Technology, Gothenburg, Sweden, 2016. [Google Scholar]
- Elliott, D.S. Momentum Control Systems and Their Application in Robotic Systems. Ph.D. Thesis, Cornell University, Ithaca, NY, USA, 2019. [Google Scholar]
- Elliott, D.S.; Peck, M.; Nesnas, I.A.D. Optimal solution for torque capability of control moment gyroscopes. In Proceedings of the 2019 IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 March 2019; pp. 1–17. [Google Scholar] [CrossRef]
- Elliott, D.S.; Peck, M.A. Dynamics and control of polyhedral surface robots with control moment gyroscopes. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Grapevine, TX, USA, 9–13 January 2017. AIAA 2017-1050, Session: Spacecraft Robotics. [Google Scholar] [CrossRef]
- CMG-Rover: NASA Has Supported Researchers in Cornell University to Develop Technologies to Use It for Locomotion Purposes (Say) in Mars. Available online: https://www.spacecraftresearch.com/cmg-rover (accessed on 23 January 2024).
- Gajamohan, M.; Merz, M.; Thommen, I.; D’Andrea, R. The Cubli: A cube that can jump up, balance, and ‘walk’. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Algavre, Portugal, 7–12 October 2012; pp. 3722–3727. Available online: https://www.youtube.com/watch?v=n_6p-1J551Y&ab_channel=GajamohanMohanarajah (accessed on 23 January 2024).
- NASA’s Helical Engine and Other Reactionless Drives. Available online: https://www.youtube.com/watch?v=yNro9yiVZno&t=3s&ab_channel=PhysicsUnsimplified (accessed on 23 January 2024).
- Gyroscopic Precession Powered Car. Available online: https://www.youtube.com/watch?v=zOGlHC56Brs&t=4s&ab_channel=anisotropicplus (accompanied by 12 more movies) (accessed on 23 January 2024).
- YouTube: Falcon Space Demonstrates Gyroscopic Propellentless Propulsion (Part 2). Available online: https://www.youtube.com/watch?v=OPPnmAFcPiw&ab_channel=CharlieC (accessed on 23 January 2024).
- Raptis, Y.; Kourouklis, G.A. A tribute to the work of the late Professor Evangelos Anastassakis (1938–2000). Phys. Status Solidi (B) 2001, 223, 1–13. [Google Scholar] [CrossRef]
- Ünker, F.; Çuvalci, O. Gyroscopic inertial thruster (GIT). In Proceedings of the 9th International Automotive Technologies Congress, Bursa, Turkey, 7–8 May 2018; pp. 686–695. [Google Scholar]
- Gerocs, A.; Korka, Z.-I.; Biró, I.; Cojocaru, V. Analytical investigation of an inertial propulsion system using rotating masses. J. Phys. Conf. Ser. 2020, 1426, 012031. [Google Scholar] [CrossRef]
- Gerocs, A.; Gillich, G.-R.; Nedelcu, D.; Korka, Z.-I. A multibody inertial propulsion drive with symmetrically placed balls rotating on eccentric trajectories. Symmetry 2020, 12, 1422. [Google Scholar] [CrossRef]
- Timofte, S.; Miclosina, C.-O.; Cojocaru, V.; Gerocs, A.; Korka, Z.-I. Inertial propulsion of a mobile platform driven by two eccentric bodies. Appl. Sci. 2023, 13, 9511. [Google Scholar] [CrossRef]
- Sprenger, A.R.; Scholz, C.; Ldov, A.; Wittkowski, R.; Löwen, H. Inertial self-propelled particles in anisotropic environments. Commun. Phys. 2023, 6, 301. [Google Scholar] [CrossRef]
- Frolov, A.V. New Aerospace Technologies; Independent Publisher: St.-Petersburg, Russia, 2017; ISBN 978-5-7679-3883-4. [Google Scholar]
- McCulloch, M.E. Low-acceleration dwarf galaxies as tests of quantised inertia. Astrophys Space Sci. 2017, 362, 57. [Google Scholar] [CrossRef][Green Version]
- McCulloch, M.E. Physics from the Edge: A New Cosmological Model for Inertia; World Scientific: Singapore, 2014. [Google Scholar]
- McCulloch, M.E. Can the Podkletnov effect be explained by quantised inertia? Phys. Procedia 2011, 20, 134–139. [Google Scholar] [CrossRef]
- Allan Williams, University Research Inspires New Commercial Advances in Satellite Propulsion, 27 April 2022. Available online: https://www.plymouth.ac.uk/news/university-research-inspires-new-commercial-advances-in-satellite-propulsion (accessed on 23 January 2024).
- Mike McCulloch, Using New Physics to Get to Alpha Centauri in a Human Lifetime (19 January 2022). Available online: https://www.youtube.com/watch?v=45E822mP59Q (accessed on 23 January 2024).
- Orf, D. The ‘Impossible’ Quantum Drive Supposedly Defies Newton’s Laws of Motion, Popular Mechanics, 16 November 2023. Available online: https://www.popularmechanics.com/space/satellites/a45850635/quantum-drive-space-test (accessed on 23 January 2024).
- Plain, C. Breaking: Satellite Failure Scuttles First of Its Kind in Space Test of Physics Defying Quantum Drive. The Debrief, 12 February 2024. Available online: https://thedebrief.org/breaking-satellite-failure-scuttles-first-of-its-kind-in-space-test-of-physics-defying-quantum-drive/ (accessed on 23 January 2024).
- Anonymous. Rogue Space Systems Operations Team is Announcing the Suspension of The active Phase of a Partially Successful Mission. 9 February 2024. Available online: https://rogue.space/suspension_of_barry1_operations (accessed on 23 January 2024).
- Aurigema, A.N.; Buhler, C.R. System and Method for Generating Forces Using Asymmetrical Electrostatic Pressure. U.S. Patent 11,511,891 B2, 29 November 2022. [Google Scholar]
- Buhler, C. Propellantless Propulsion Device. Available online: http://www.youtube.com/watch?v=WhsKMWOYuYo (accessed on 23 January 2024).
- Goebel, D.M.; Katz, I. Fundamentals of Electric Propulsion: Ion and Hall Thrusters; Wiley: Hoboken, NJ, USA, 2008. [Google Scholar]
- Forward, R.L. Guidelines to antigravity. Am. J. Phys. 1963, 31, 166–170. [Google Scholar] [CrossRef]
- Mashhoon, B.; Hehl, F.W.; Theiss, D.S. On the gravitational effects of rotating masses: The Thirring-Lense papers. Gen. Relativ. Gravit. 1984, 16, 711–750. [Google Scholar] [CrossRef]
- Wikipedia, Entry: Mach’s Principle. Available online: https://en.wikipedia.org/wiki/Mach%27s_principle (accessed on 23 January 2024).
- Tajmar, M. Homopolar artificial gravity generator based on frame-dragging. Acta Astronaut. 2010, 66, 1297–1301. [Google Scholar] [CrossRef]
- Millis, M.G. Inertial frames and breakthrough propulsion physics. Acta Astronaut. 2017, 138, 85–94. [Google Scholar] [CrossRef]
- Wisdom, J. Swimming in spacetime: Motion by cyclic changes in body shape. Science 2003, 299, 1865–1869. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).